A Sparse-Reconstruction-Based Fast Localization Algorithm for Mixed Far-Field and Near-Field Sources
-
摘要: 协方差向量具有比原始阵列输出更高的信噪比增益，该文将远近场混合源模型扩展到协方差域，并针对稀疏重构远近场混合源定位算法时间复杂度高的问题，提出了一种基于协方差域阵列信号模型和广义近似消息传递(GAMP)-变分贝叶斯推断(VBI)的远近场混合源定位改进算法(FN-GAMP-CVBI)，实现了计算效率与定位精度的有效平衡。数值仿真表明，与现有的远近场混合源定位算法相比，该文所提算法具有更高的远近场源定位精度和较低的计算时间。湖试数据结果进一步验证了该文所提算法的高效性和有效性。Abstract:
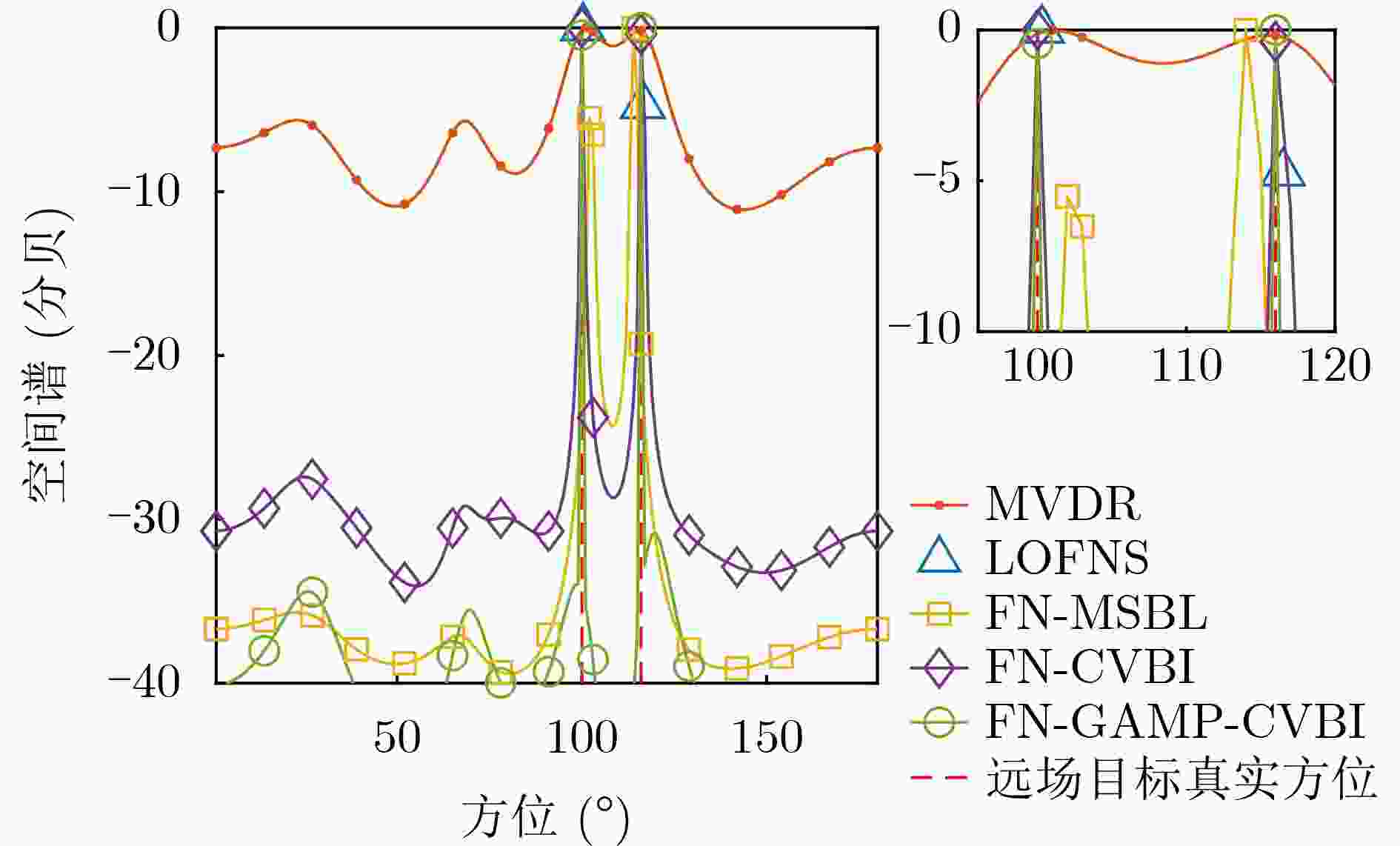
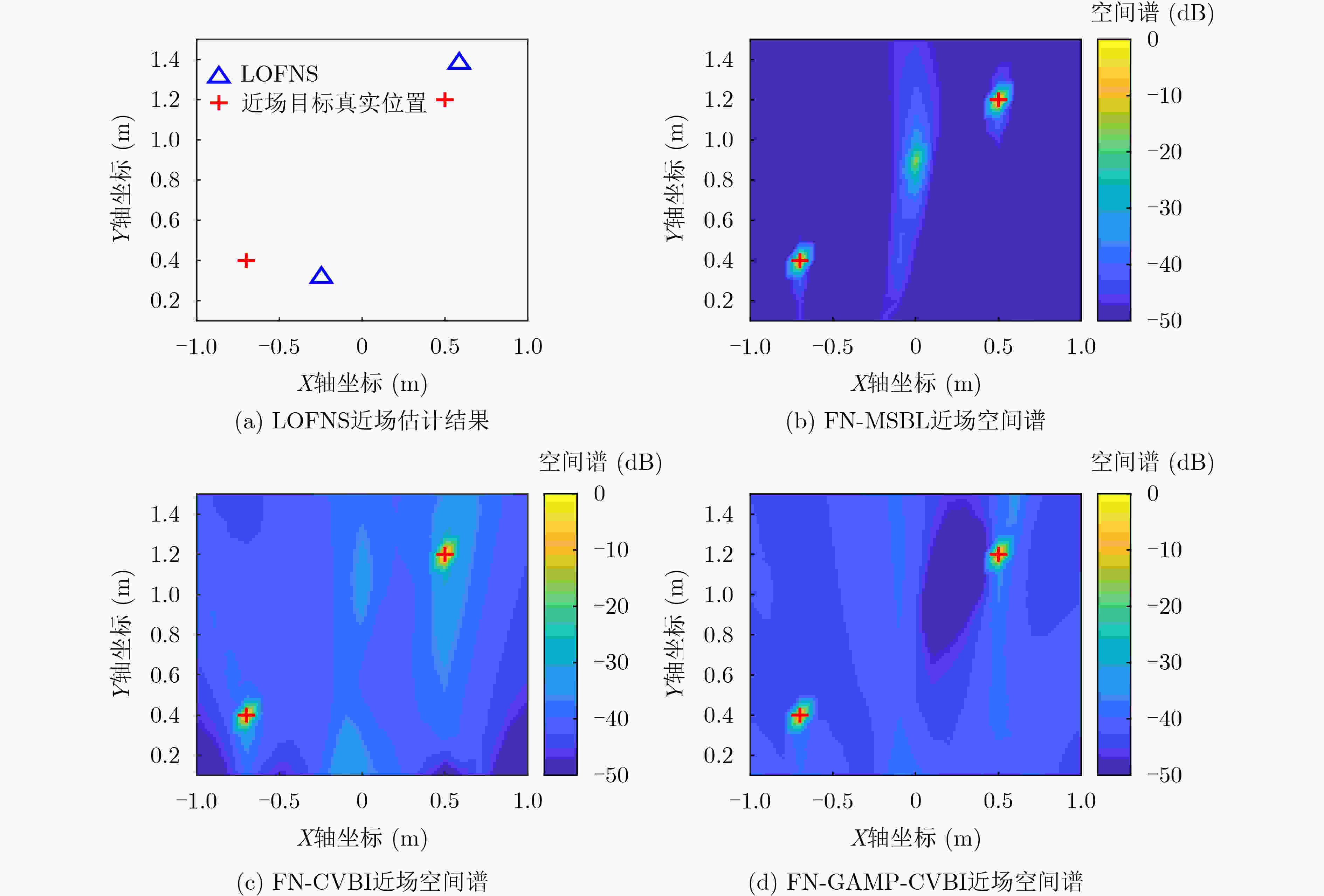
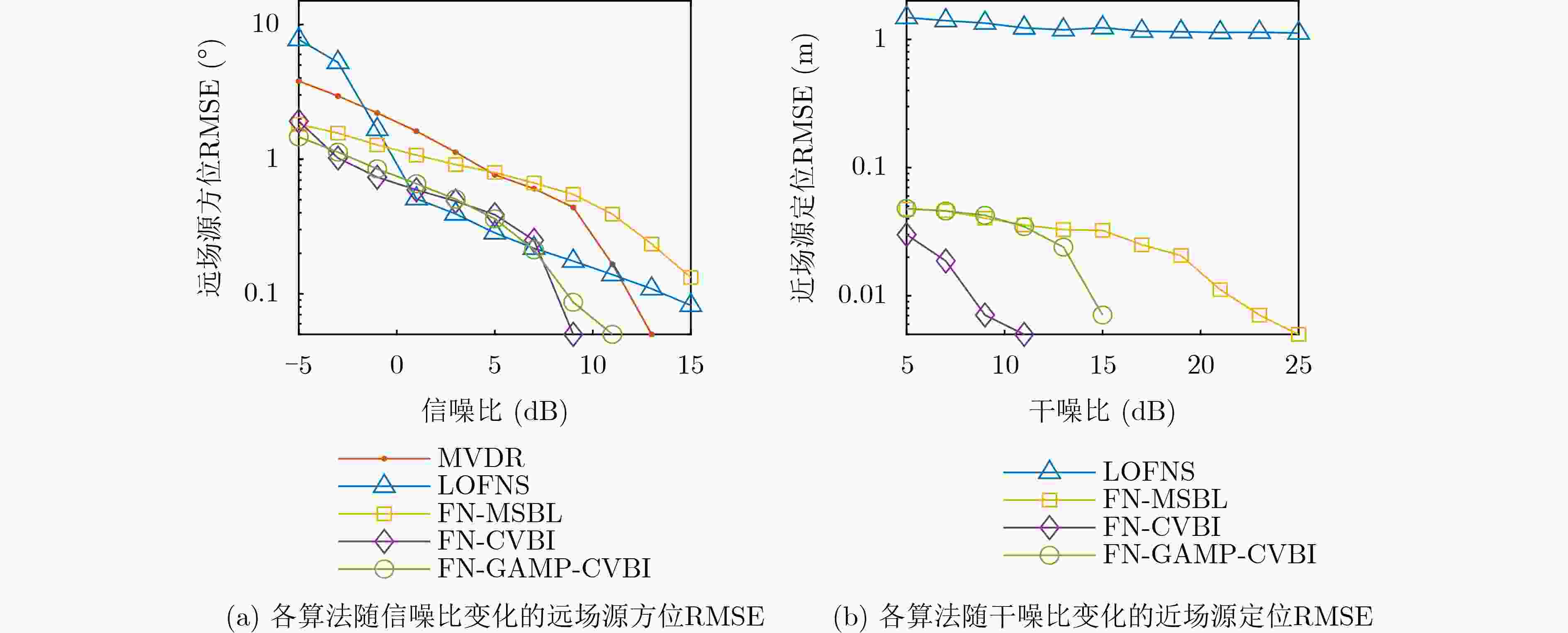
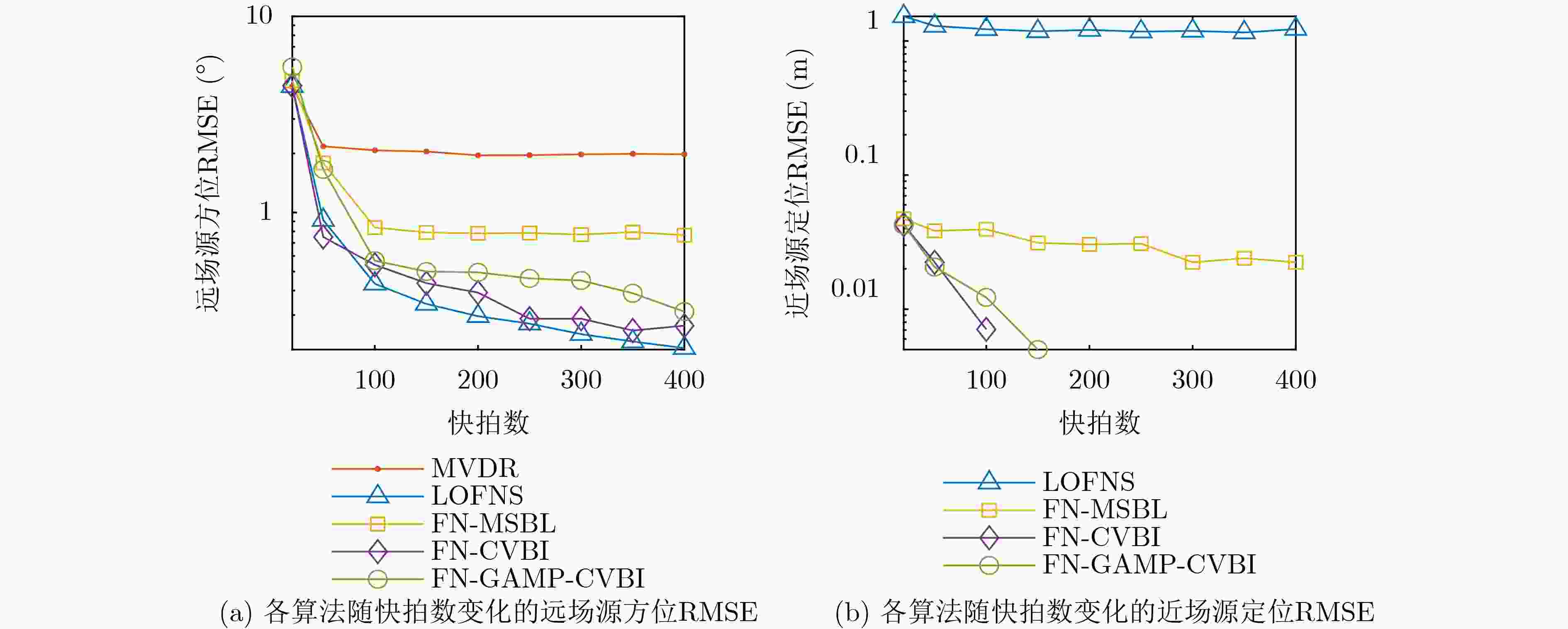
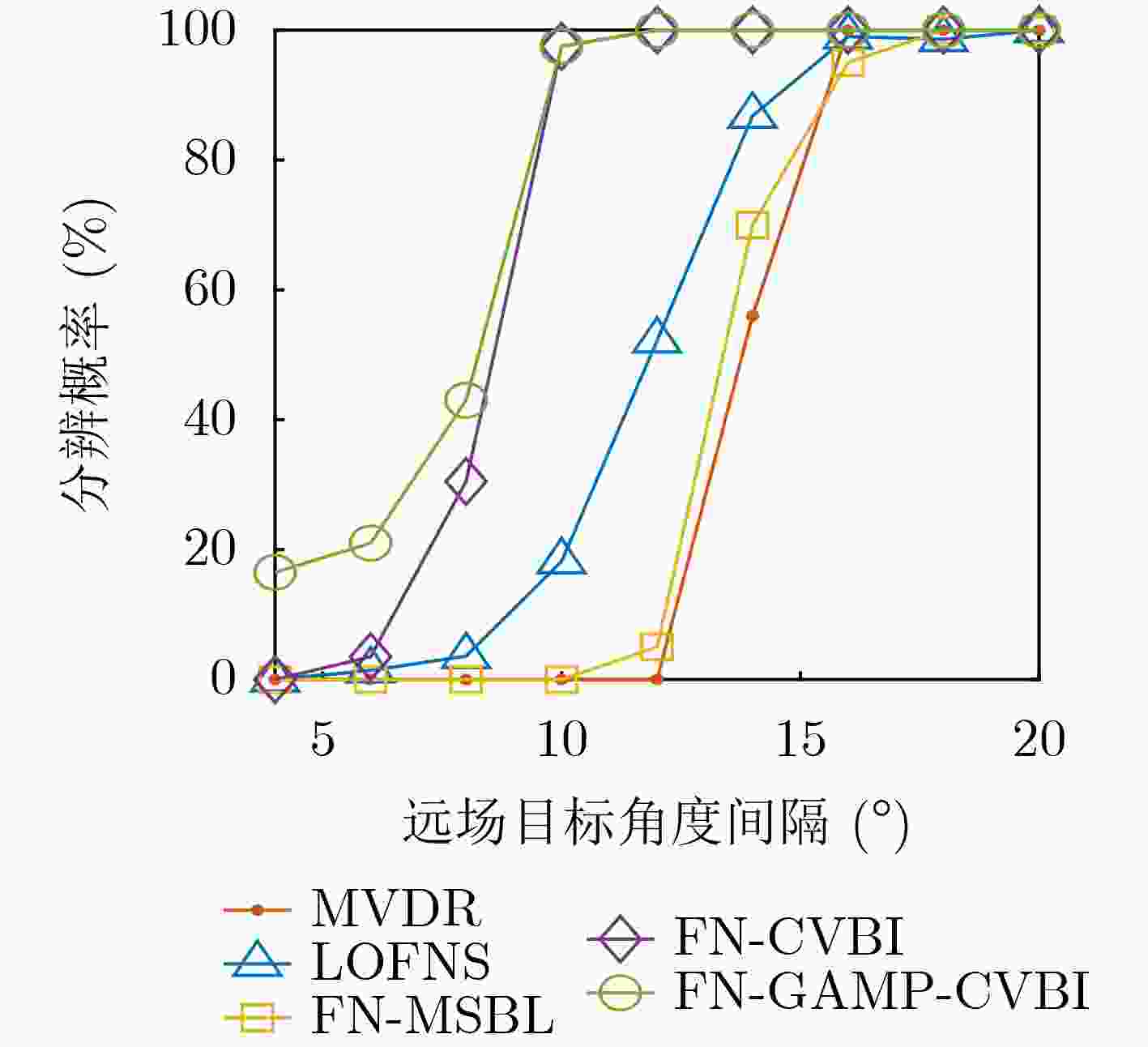
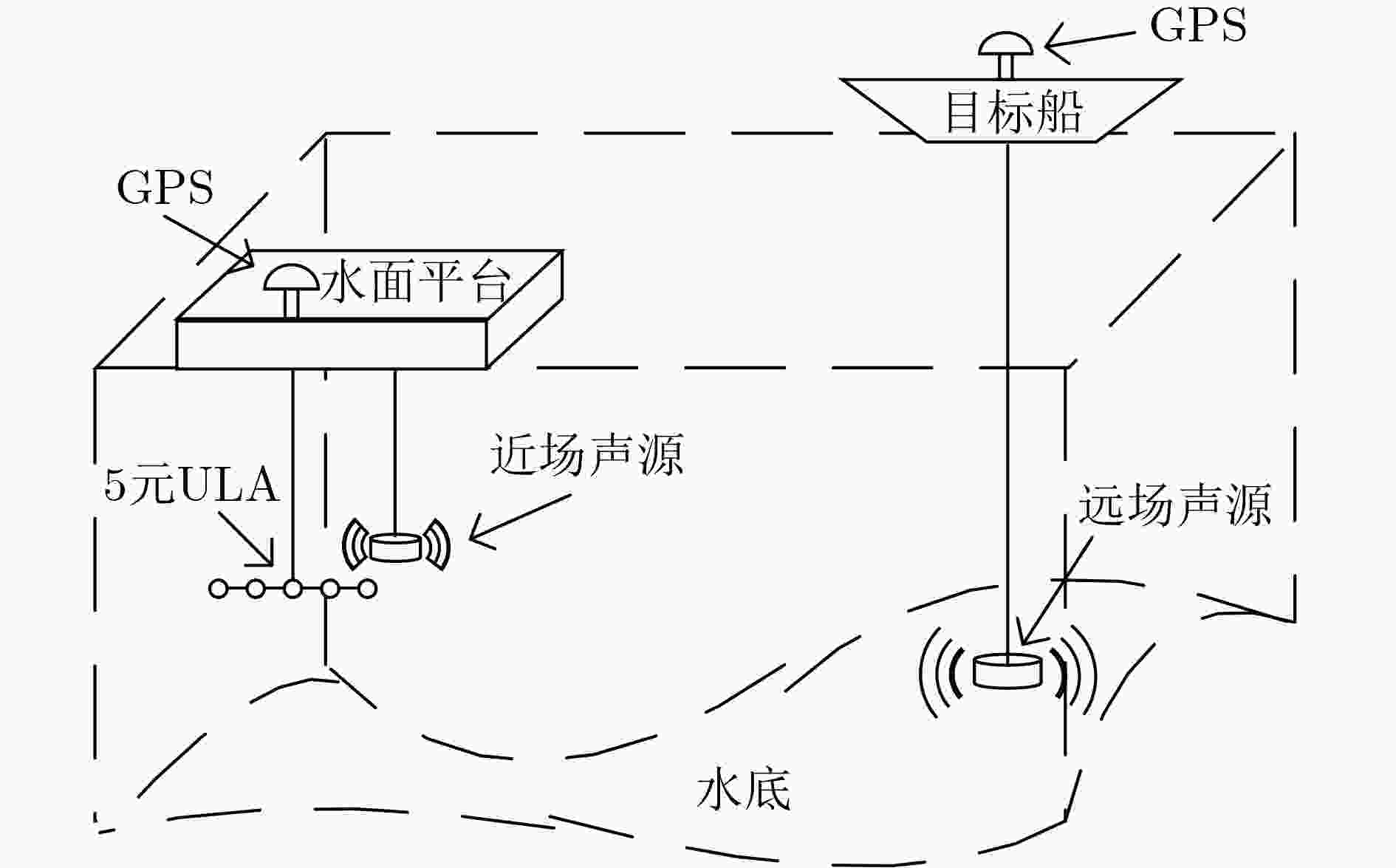
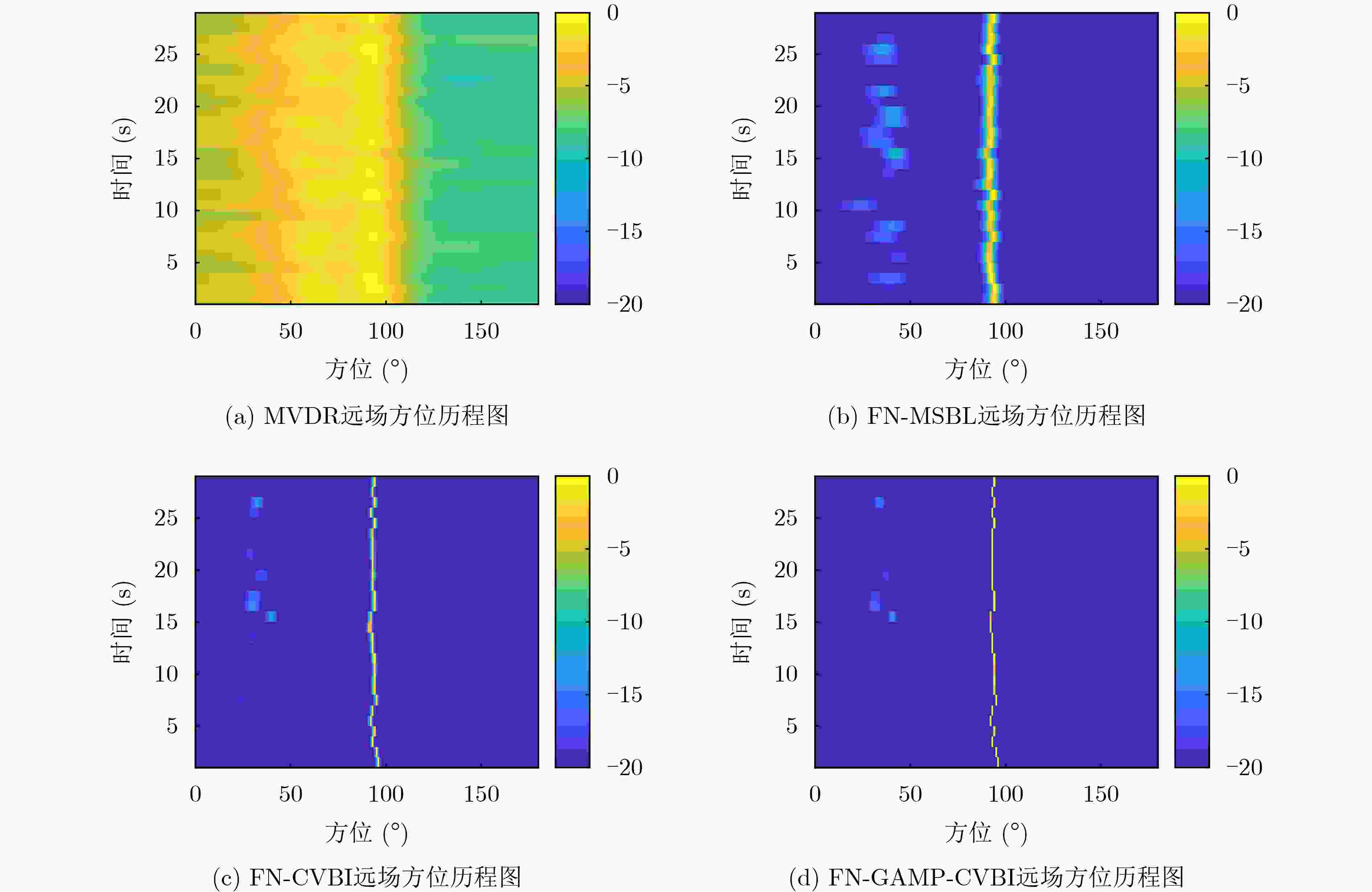
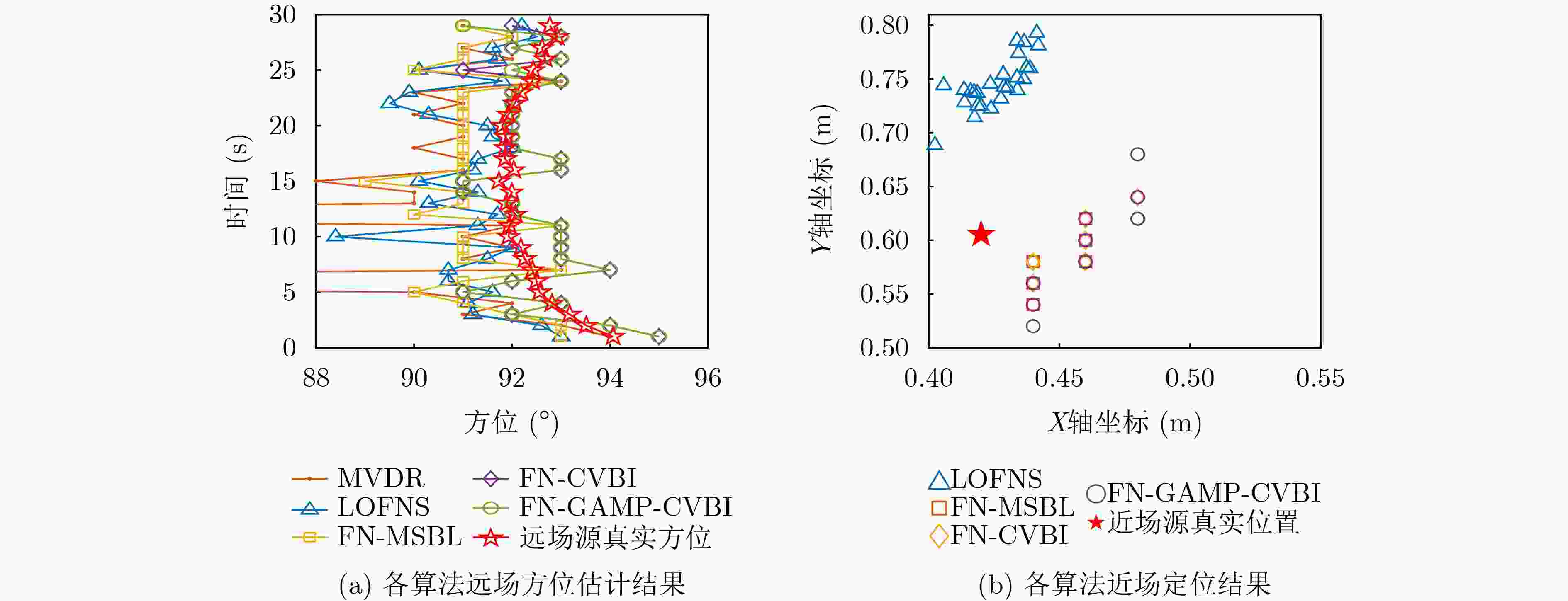
Objective Source localization is a critical research area in array signal processing, with applications in radar, sonar, and wireless communications. Traditional localization methods, which are based on either far-field or near-field models individually, face significant challenges in effectively separating and localizing mixed far-field and near-field sources. Existing algorithms, such as subspace-based methods, suffer from high computational complexity, limited localization accuracy, and degraded performance in low Signal-to-Noise Ratio (SNR) scenarios. In addition, these methods assume that near-field sources are located within the Fresnel Region, leading to localization errors and a reduction in effective array aperture. Improved algorithms, such as Multiple Sparse Bayesian Learning for Far and Near-field sources (FN-MSBL), successfully overcame these limitations and achieved higher localization accuracy. However, the high computational cost of matrix inversion during each iteration restricts its real-time applicability. Therefore, this paper aims to address these limitations and issues by proposing a novel algorithm that not only develops a sparse representation model for mixed near-field and far-field sources based on the covariance domain but also integrates sparse reconstruction with the Generalized Approximate Message Passing (GAMP) and Variational Bayesian Inference (VBI) frameworks. The primary goal is to achieve high-precision localization of mixed sources while significantly reducing computational costs, thereby enabling real-time applicability. Methods The proposed algorithms, termed Covariance-based VBI for Far and Near-field sources (FN-CVBI) and Covariance-based GAMP-VBI for Far and Near-field sources (FN-GAMP-CVBI), are developed through several key methods. First, a unified sparse representation model for mixed far-field and near-field sources is constructed based on the covariance vector. This model leverages the improved SNR of the covariance vector compared to the original array output, enabling more accurate far-field Direction Of Arrival (DOA) estimation. Second, to mitigate the estimation errors in the sample covariance matrix, a pre-whitening operation is applied to the covariance vector. This step effectively minimizes the correlation between the elements of the covariance vector, thereby enhancing the robustness of the sparse reconstruction algorithm. Third, a hierarchical Bayesian model is established to enforce sparsity, and VBI is employed to estimate the parameters. The VBI framework iteratively updates the posterior distributions of the hidden variables, ensuring convergence to a near-optimal solution. Fourth, to address the significant computational complexity associated with traditional VBI methods, the GAMP algorithm is embedded into the VBI framework. GAMP replaces the computationally expensive matrix inversion operations in VBI, significantly reducing the computational burden. The detailed implementation steps of GAMP are provided in Table 1 . In conclusion, by combining the advantages of sparse reconstruction, VBI, and GAMP, the proposed algorithm not only improves localization accuracy but also significantly reduces computational complexity, making it suitable for real-time applications.Results and Discussions The proposed algorithm FN-GAMP-CVBI demonstrates significant improvements in both localization accuracy and computational efficiency. Computational complexity analysis demonstrates that the algorithm significantly reduces computational costs ( Table 2 ). In terms of localization accuracy, the proposed algorithms, FN-CVBI and FN-GAMP-CVBI, both outperform compared methods such as LOFNS and FN-MSBL (Fig.3 ,Fig.4 ), particularly in low SNR and sufficient snapshots scenarios (Fig.5 ,Fig.6 ), and demonstrate superior performance in resolving closely spaced far-field sources (Fig.7 ). Experimental validation using lake trial data further confirms the effectiveness of the proposed algorithms, as evidenced by sharper spectral peaks and minimal false peaks in the background noise of Bearing Time Recording (BTR) (Fig.9 ). In addition, FN-CVBI achieves the highest accuracy in far-field DOA estimation and near-field localization. The computational time of FN-GAMP-CVBI is reduced by up to 95% compared to FN-MSBL, making the algorithm highly efficient for real-time applications (Table 4 ). Overall, the proposed FN-GAMP-CVBI algorithm strikes an effective balance between localization accuracy and computational efficiency.Conclusions This paper presents a novel approach to mixed far-field and near-field source localization by integrating sparse reconstruction with the GAMP-VBI framework. The proposed FN-GAMP-CVBI algorithm addresses the limitations of traditional methods, offering a balanced trade-off between computational efficiency and localization accuracy. The simulation results demonstrate superior performance, particularly in scenarios with sufficient snapshots and low SNR. Experimental validation further confirms the effectiveness and efficiency of the proposed algorithms. Overall, the proposed FN-GAMP-CVBI algorithm strikes an effective balance between localization accuracy and computational efficiency. Its ability to simultaneously handle both far-field and near-field sources, combined with its low computational complexity, positions it as a promising solution for real-time mixed source localization in complex environments. -
表 1 基于GAMP计算近似后验的算法流程
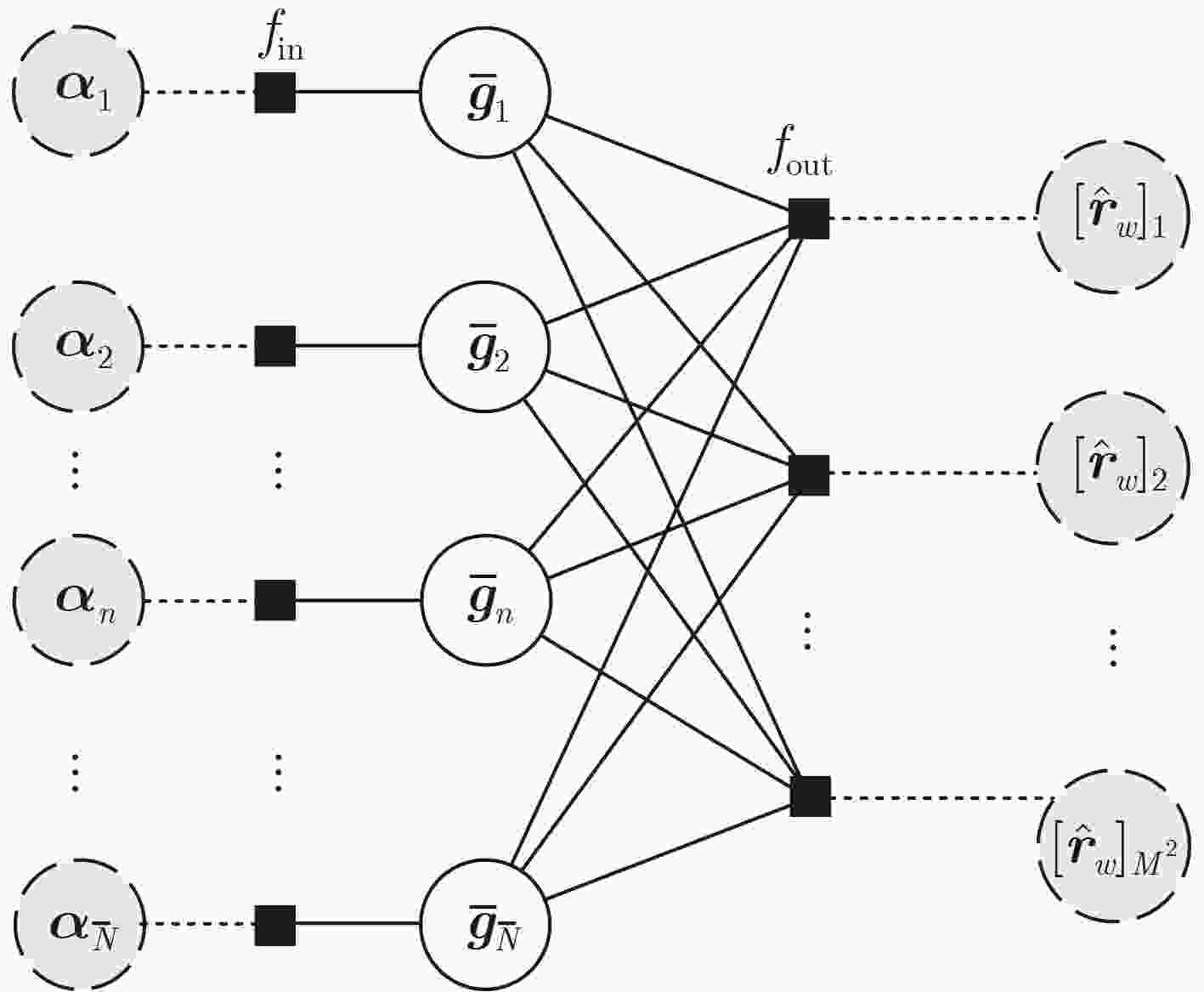
输入：参数估计${\boldsymbol{\alpha}} $、${\beta _0}$，协方差向量${\hat {\boldsymbol{r}}_w}$，过完备字典$ {\bar{\boldsymbol{ \Phi}} _w} $。 (1). 初始化：$l = 1$，${\hat {\boldsymbol{g}}^{(0)}} = {\boldsymbol{0}}$，${{\boldsymbol{s}}^{(0)}} = {\boldsymbol{0}}$，${\boldsymbol{S}} = {\left| {{{\bar {\boldsymbol{\Phi}} }_w}} \right|^2}$，${\boldsymbol{\tau}} _g^{(0)} = {{\boldsymbol{\alpha}} ^{ - 1}}$。 (2). 循环执行如下步骤 (a) 输出线性步骤 $\begin{gathered} {\boldsymbol{\tau}} _p^{(l)} = {\boldsymbol{S\tau}} _g^{(l - 1)} \\ {\boldsymbol{\mu}} _p^{(l)} = {{\bar {\boldsymbol{\Phi}} }_w}{{\hat {\boldsymbol{g}}}^{(l - 1)}} - {\boldsymbol{\tau}} _p^{(l)} \circ {{\boldsymbol{s}}^{(l - 1)}} \\ \end{gathered} $ (25) (b) 输出非线性步骤 $ \begin{gathered} {{\boldsymbol{s}}^{(l)}} = \left( {1 - {\lambda _g}} \right){{\boldsymbol{s}}^{(l - 1)}} + {\lambda _g}{{\boldsymbol{g}}_{out}}\left( {{{\hat r}_w},{\boldsymbol{\mu}} _p^{(l)},{\boldsymbol{\tau}} _p^{(l)},{\beta _0}} \right) \\ {\boldsymbol{\tau}} _s^{(l)} = - {{g'}_{out}}\left( {{{\hat {\boldsymbol{r}}}_w},{\boldsymbol{\mu}} _p^{(l)},{\boldsymbol{\tau}} _p^{(l)},{{\boldsymbol{\beta}} _0}} \right) \end{gathered} $ (26) (c) 输入线性步骤 $\begin{gathered} {\boldsymbol{\tau}} _q^{(l)} = {{\boldsymbol{1}} \mathord{\left/ {\vphantom {1 {{S^{\rm T}}\tau _s^{(l)}}}} \right. } {{{\boldsymbol{S}}^{\rm T}}{\boldsymbol{\tau}} _s^{(l)}}} \\ {\boldsymbol{\mu}} _q^{(l)} = {{\hat {\boldsymbol{g}}}^{(l - 1)}} + {\boldsymbol{\tau }}_q^{(l)} \circ \left( {{{\bar {\boldsymbol{\Phi}} }_w}^{\rm H}{{\boldsymbol{s}}^{(l)}}} \right) \end{gathered} $ (27) (d) 输入非线性步骤 $ \begin{gathered} {{\hat {\boldsymbol{g}}}^{(l)}} = \left( {1 - {\lambda _g}} \right){{\hat {\boldsymbol{g}}}^{(l - 1)}} + {\lambda _g}{g_{in}}({\boldsymbol{\mu}} _q^{(l)},{\boldsymbol{\tau}} _q^{(l)},{\boldsymbol{\alpha}} ) \\ {\boldsymbol{\tau}} _g^{(l)} = {\boldsymbol{\tau}} _q^{(l)} \circ {{g'}_{in}}({\boldsymbol{\mu}} _q^{(l)},{\boldsymbol{\tau}} _q^{(l)},{\boldsymbol{\alpha}} ) \end{gathered} $ (28) (e)令$l = l + 1$，循环执行(a)到(e)步直到迭代次数$l$和容差$ \xi = {{{{{\left\| {{{\hat g}^{(l)}} - {{\hat g}^{(l - 1)}}} \right\|}_2}} \mathord{\left/ {\vphantom {{{{\left\| {{{\hat g}^{(l)}} - {{\hat g}^{(l - 1)}}} \right\|}_2}} {\left\| {{{\hat g}^{(l)}}} \right\|}}} \right. } {\left\| {{{\hat g}^{(l)}}} \right\|}}_2} $满足条件$l \geqslant {G_l}$或$\xi \leqslant {G_\zeta }$时停止迭代，其中${G_l}$为设定最大GAMP迭代次数，${G_\zeta }$为设定的容差门限。 (3). 输出：$\bar g$的近似后验分布的估计结果$ q(\bar g) = \mathcal{C}\mathcal{N}(\hat \mu ,\hat \Sigma ) $，其均值和方差为 $ \left\{ \begin{gathered} \hat {\boldsymbol{\mu}} = {{\hat {\boldsymbol{g}}}^{(l)}} \\ \hat {\boldsymbol{\Sigma}} = diag\left\{ {{\boldsymbol{\tau}} _g^{(l)}} \right\} \\ \end{gathered} \right. $ (29) 
下载: 导出CSV
表 2 各算法的单次迭代时间复杂度
算法 时间复杂度 FN-MSBL $O\left( {\left( {\bar N - 1} \right)\left( {{M^2} + MT} \right) + {{\left( {\bar N - 1} \right)}^2}M + {M^3} + {M^2}T} \right)$ FN-CVBI $ O\left( {\max \left\{ {{{\bar N}^3} + {{\bar N}^2}{M^2},\bar N{M^4} + {{\bar N}^2}{M^2} + {M^6}} \right\}} \right) $ FN-GAMP-CVBI $O\left( {\bar N{M^2}} \right)$
下载: 导出CSV
表 4 各算法远近场混合源定位结果的统计对比
算法 远场RMSE
(度)近场RMSE
(米)平均计算时间
(秒)LOFNS 1.427 0.139 0.240 FN-MSBL 1.374 0.046 3.784 FN-CVBI 0.804 0.045 3.828 FN-GAMP-CVBI 0.819 0.049 0.184
下载: 导出CSV
-
[1] LIANG Guolong, CHEN Yu, WANG Jinjin, et al. Enhanced noise resilience in passive tone detection via broad-receptive field complex-valued convolutional neural networks[J]. The Journal of the Acoustical Society of America, 2024, 155(6): 3968–3982. doi: 10.1121/10.0026438. [2] DU Zhiyao, HAO Yu, QIU Longhao, et al. Sparsity-based direction-of-arrival estimation in the presence of near-field and far-field interferences for small-scale platform sonar arrays[J]. The Journal of the Acoustical Society of America, 2024, 156(5): 2989–3005. doi: 10.1121/10.0034240. [3] LEE J H, CHEN Y M, and YEH C C. A covariance approximation method for near-field direction-finding using a uniform linear array[J]. IEEE Transactions on Signal Processing, 1995, 43(5): 1293–1298. doi: 10.1109/78.382421. [4] LIANG Junli and LIU Ding. Passive localization of mixed near-field and far-field sources using two-stage MUSIC algorithm[J]. IEEE Transactions on Signal Processing, 2010, 58(1): 108–120. doi: 10.1109/TSP.2009.2029723. [5] HE Jin, SWAMY M N S, and AHMAD M O. Efficient application of MUSIC algorithm under the coexistence of far-field and near-field sources[J]. IEEE Transactions on Signal Processing, 2012, 60(4): 2066–2070. doi: 10.1109/TSP.2011.2180902. [6] ZUO Weiliang, XIN Jingmin, ZHENG Nanning, et al. Subspace-based localization of far-field and near-field signals without eigendecomposition[J]. IEEE Transactions on Signal Processing, 2018, 66(17): 4461–4476. doi: 10.1109/tsp.2018.2853124. [7] LI Chenmu, LIANG Guolong, QIU Longhao, et al. An efficient sparse method for direction-of-arrival estimation in the presence of strong interference[J]. The Journal of the Acoustical Society of America, 2023, 153(2): 1257–1271. doi: 10.1121/10.0017256. [8] WANG Bo, LIU Juanjuan, and SUN Xiaoying. Mixed sources localization based on sparse signal reconstruction[J]. IEEE Signal Processing Letters, 2012, 19(8): 487–490. doi: 10.1109/lsp.2012.2204248. [9] CHEN Mengya, LIN Wei, ZHAO Yongwei, et al. Gridless mixed-field sources localisation algorithm based on covariance matrix reconstruction[J]. Journal of Physics: Conference Series, 2024, 2849: 012117. doi: 10.1088/1742-6596/2849/1/012117. [10] QI Meibin, REN Weijie, and XIANG Houhong. Separation of mixed near-field and far-field sources and DOA estimation based on deep learning[C]. ICAIT 2023 - 2023 IEEE 15th International Conference on Advanced Infocomm Technology, Hefei, China, 2023: 226–233. doi: 10.1109/ICAIT59485.2023.10367306. [11] LIANG Guolong, ZHAO Benbin, and FAN Zhan. Direction of arrival estimation under near-field interference using matrix filter[J]. Journal of Computational Acoustics, 2015, 23(4): 1540007. doi: 10.1142/S0218396X1540007X. [12] HAWKES M and NEHORAI A. Acoustic vector-sensor correlations in ambient noise[J]. IEEE Journal of Oceanic Engineering, 2001, 26(3): 337–347. doi: 10.1109/48.946508. [13] 邱龙皓, 梁国龙, 王燕, 等. 稀疏贝叶斯学习远近场混合源定位方法[J]. 声学学报, 2018, 43(1): 1–11. doi: 10.15949/j.cnki.0371-0025.2018.01.001.QIU Longhao, LIANG Guolong, WANG Yan, et al. Mixed near-field and far-field sources localization method using sparse Bayesian learning[J]. Acta Acustica, 2018, 43(1): 1–11. doi: 10.15949/j.cnki.0371-0025.2018.01.001. [14] 刘章孟. 基于信号空域稀疏性的阵列处理理论与方法[D]. [博士论文], 国防科学技术大学, 2012.LIU Zhangmeng. Spatial sparsity-based theory and methodsof array signal processing[D]. [Ph. D. dissertation], National University of Defense Technology, 2012. [15] AL-SHOUKAIRI M, SCHNITER P, and RAO B D. A GAMP-based low complexity sparse bayesian learning algorithm[J]. IEEE Transactions on Signal Processing, 2018, 66(2): 294–308. doi: 10.1109/TSP.2017.2764855. [16] LI Ninghui, ZHANG Xiaokuan, ZONG Binfeng, et al. An off-grid direction-of-arrival estimator based on sparse Bayesian learning with three-stage hierarchical Laplace priors[J]. Signal Processing, 2024, 218: 109371. doi: 10.1016/j.sigpro.2023.109371. [17] TIPPING M E. Sparse Bayesian learning and the relevance vector machine[J]. The Journal of Machine Learning Research, 2001, 1: 211–244. doi: 10.1162/15324430152748236. [18] TZIKAS D G, LIKAS A C, and GALATSANOS N P. The variational approximation for Bayesian inference[J]. IEEE Signal Processing Magazine, 2008, 25(6): 131–146. doi: 10.1109/msp.2008.929620. [19] RANGAN S. Generalized approximate message passing for estimation with random linear mixing[C]. IEEE International Symposium on Information Theory, St. Petersburg, Russia, 2011: 2168–2172. doi: 10.1109/ISIT.2011.6033942. -
图(10) / 表(4)
计量
- 文章访问数: 36
- HTML全文浏览量: 20
- PDF下载量: 4
- 被引次数: 0
下载:
