稀疏圆阵的双深度Q学习非均匀阵列位置优化设计

陈涛; 梁曜鹏; 陈旭; 詹磊

doi:10.11999/JEIT250125

稀疏圆阵的双深度Q学习非均匀阵列位置优化设计

doi: 10.11999/JEIT250125 cstr: 32379.14.JEIT250125

陈涛^{1, 4},
梁曜鹏^{1, 2},
陈旭^{1, 4, ,},
詹磊³

1.
哈尔滨工程大学信息与通信工程学院哈尔滨 150001
2.
中国西南电子技术研究所成都 610036
3.
成都能通科技股份有限公司成都 610045
4.
中国航空工业集团有限公司电磁频谱协同探测与智能认知联合技术中心哈尔滨 150001

基金项目: 国家自然科学基金(62071137)

详细信息

作者简介:
陈涛：男，教授，博士，研究方向为宽带信号检测处理与识别、数字接收机和信号DOA估计与定位技术

梁曜鹏：男，硕士生，研究方向为阵列信号处理、波达方向估计

陈旭：男，副教授，博士，研究方向为MIMO信号处理，毫米波雷达成像

詹磊：男，研究员，博士，研究方向为宽带信号处理、宽带接收器

通讯作者:
陈旭　xuchen95909@126.com

中图分类号: TN911.7
计量
- 文章访问数: 21
- HTML全文浏览量: 10
- PDF下载量: 1
- 被引次数: 0
出版历程
- 收稿日期: 2025-03-03
- 修回日期: 2025-08-28
- 网络出版日期: 2025-09-02

Double Deep Q-Network for Non-Uniform Position Optimization in Sparse Circular Arrays

CHEN Tao^{1, 4},
LIANG Yaopeng^{1, 2},
CHEN Xu^{1, 4
, ,},
ZHAN Lei³

1.
College of Information and Communication Engineering, Harbin Engineering University, Harbin 150001, China
2.
Southwest China Institute of Electronic Technology, Chengdu 610036, China
3.
Chengdu LandTop Technology Co., Ltd, Chengdu 610045, China
4.
AVIC United Technology Center for Electromagnetic Spectrum Collaborative Detection and Intelligent Cognition, Aviation Industry Corporation of China, Harbin 150001, China

Funds: The National Natural Science Foundation of China (62071137)

摘要

摘要: 针对工程应用中阵元位置和阵元数量受限条件下的稀疏圆形阵列布阵场景，为了满足在通道数有限的前提下保证阵列波达方向(DOA)估计性能的需求，该文提出一种基于双深度Q学习(DDQN)的稀疏圆形阵列优化设计算法，实现了更加灵活和高效的阵列优化设计策略生成。首先，为了保证优化阵列的DOA估计精度以及角度分辨力，以最小化2维DOA估计Ziv-Zakai下界(ZZB)和峰值旁瓣电平(PSL)为优化目标完成稀疏圆形阵列优化问题建模。然后，构造动作空间、状态空间、奖励值函数等模型，采用DDQN算法对优化问题进行求解，最终设计出稀疏圆形优化阵列。实验结果表明，在布阵场景受限条件下，算法收敛性能良好，稀疏圆形阵列优化设计的有效性得到验证，且设计出的稀疏圆形优化阵列具备稳健的DOA估计综合性能。
- 阵列优化设计 /
- 稀疏圆形阵列 /
- DOA估计 /
- 深度强化学习
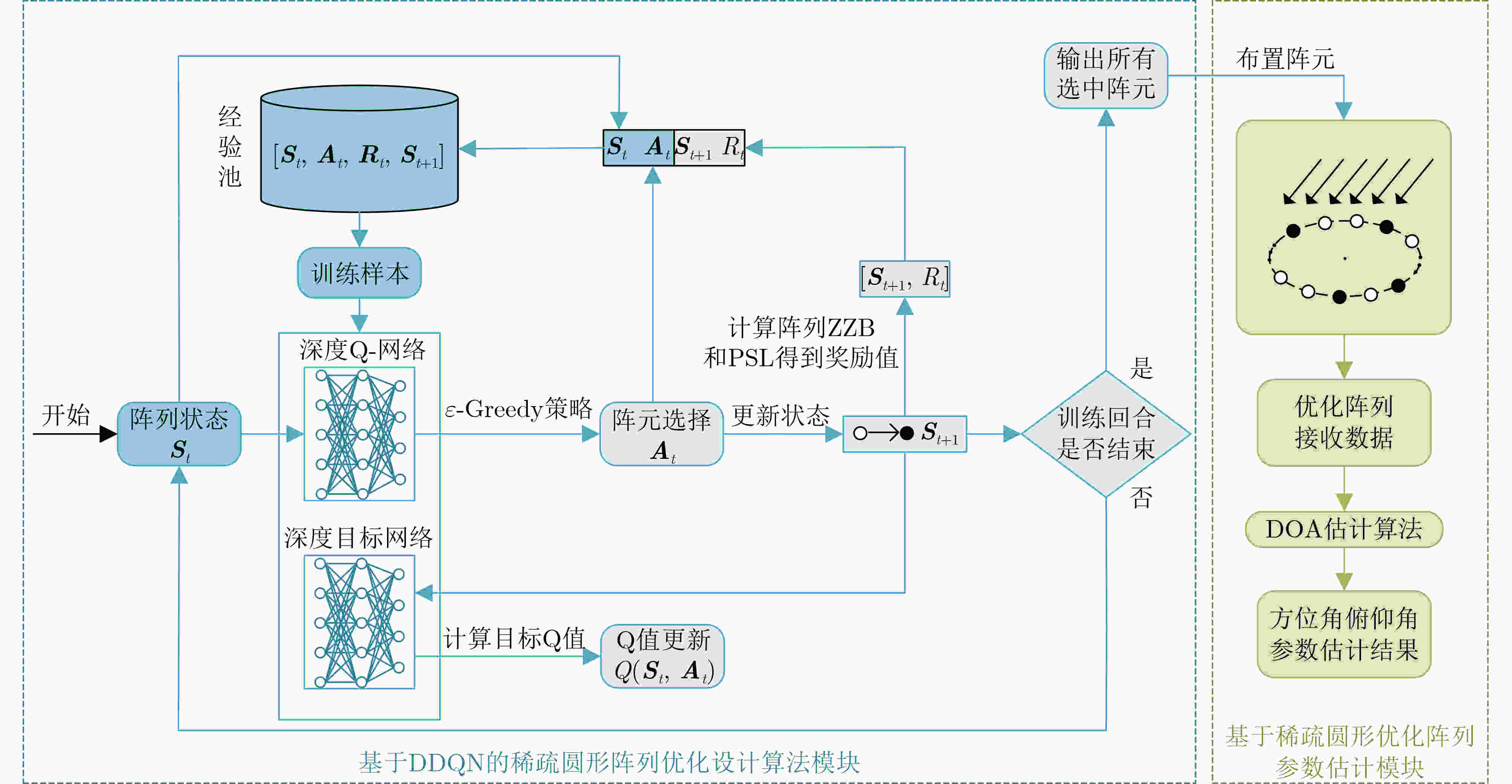
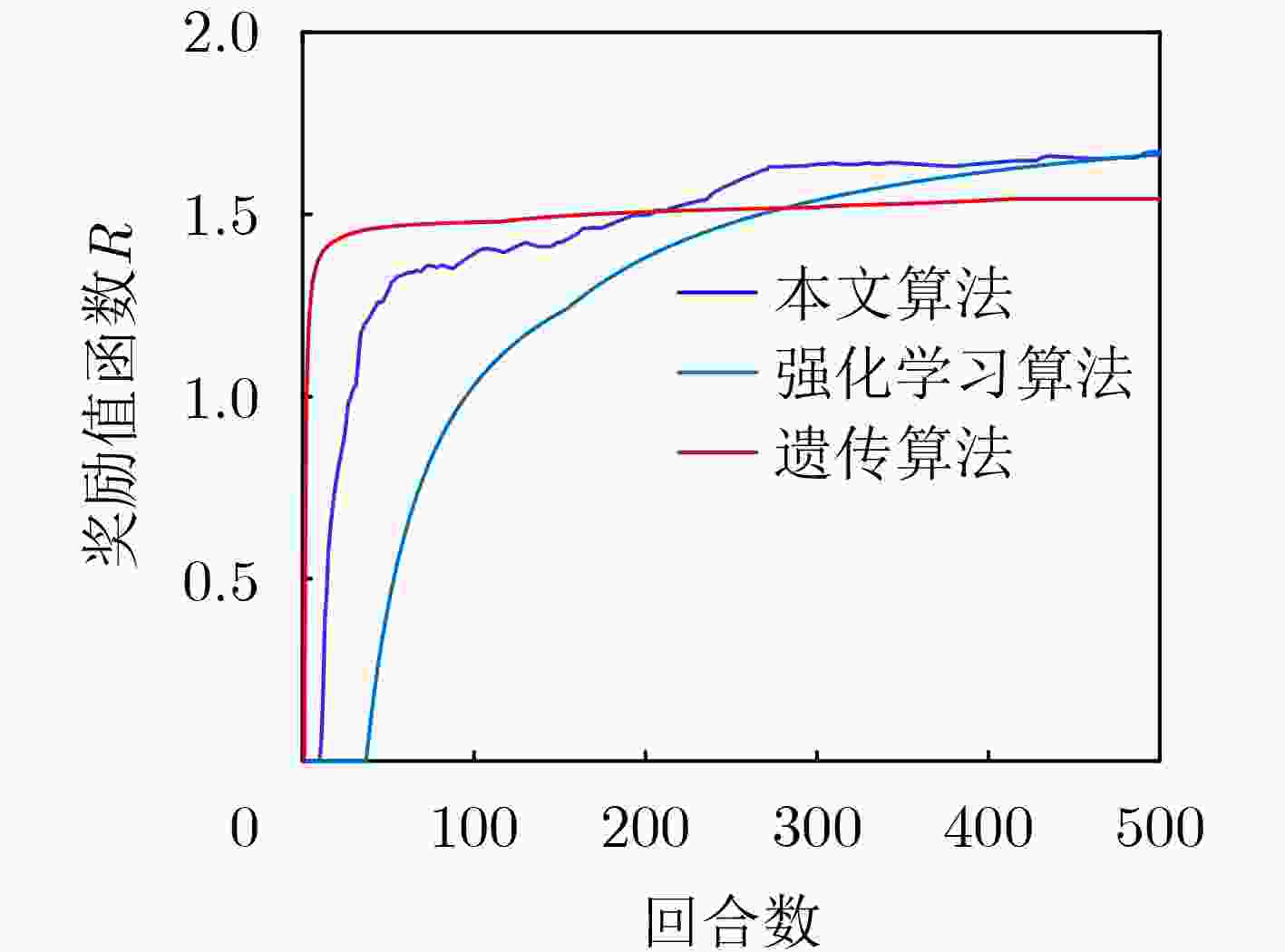
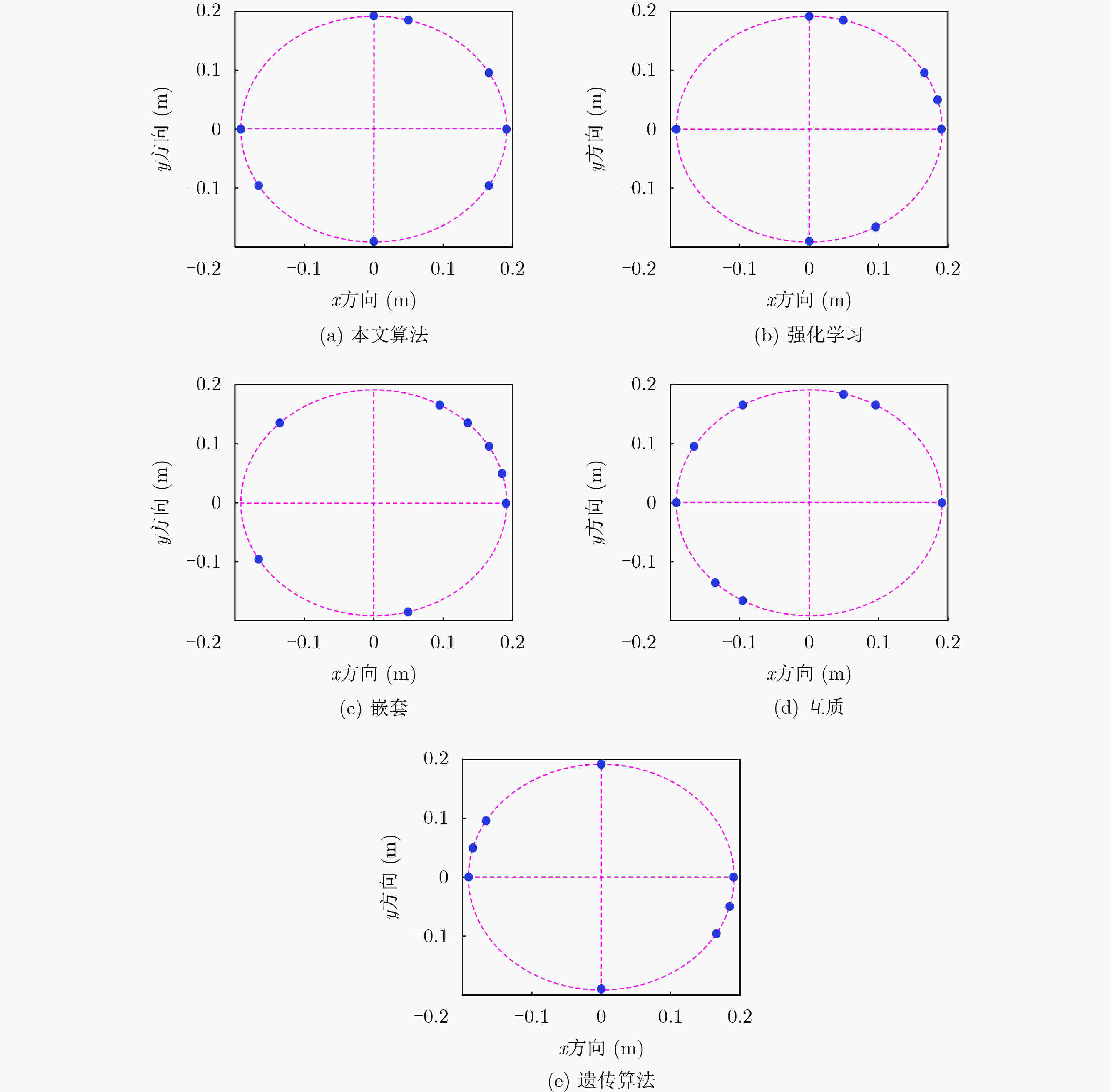
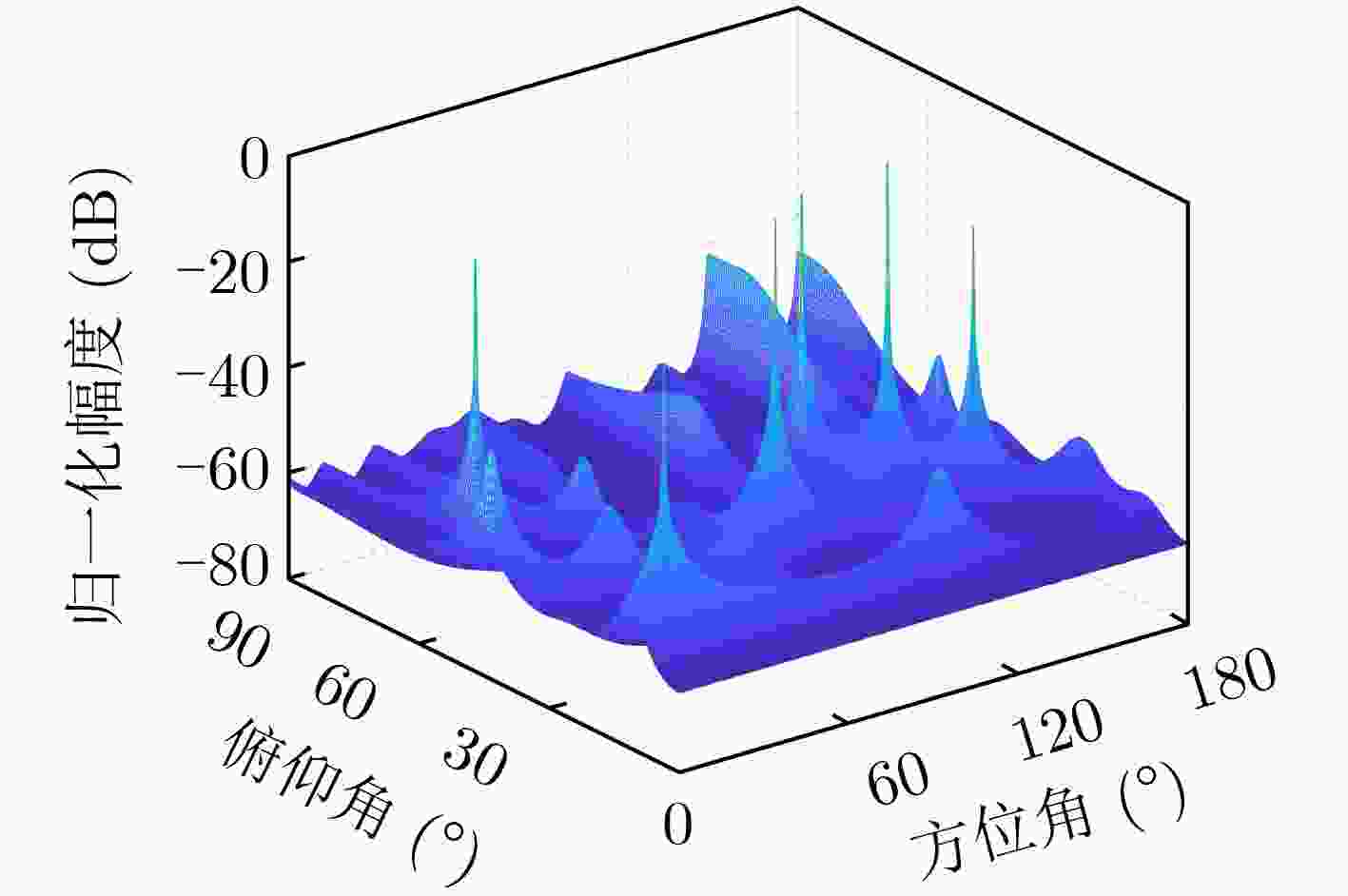
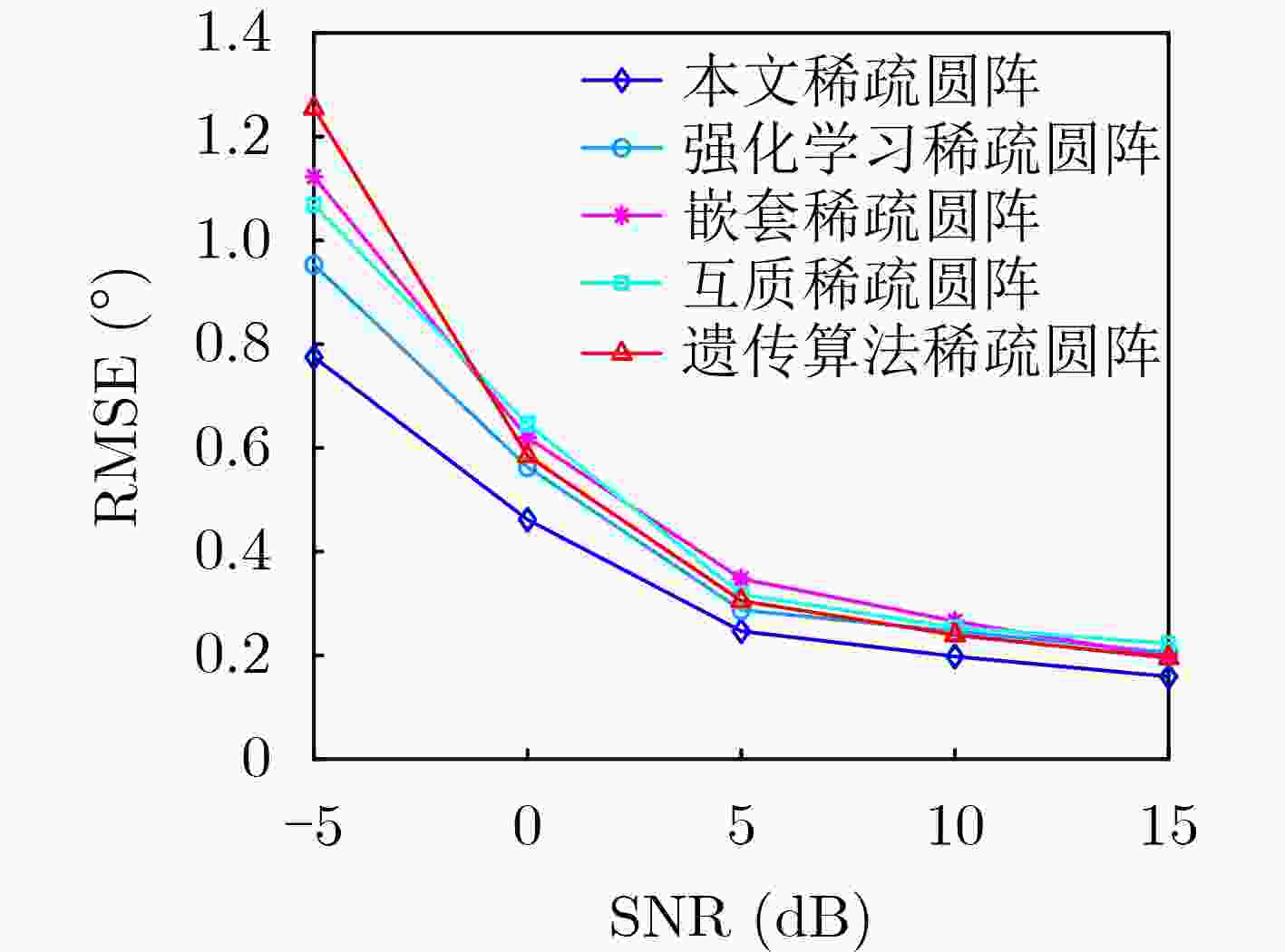
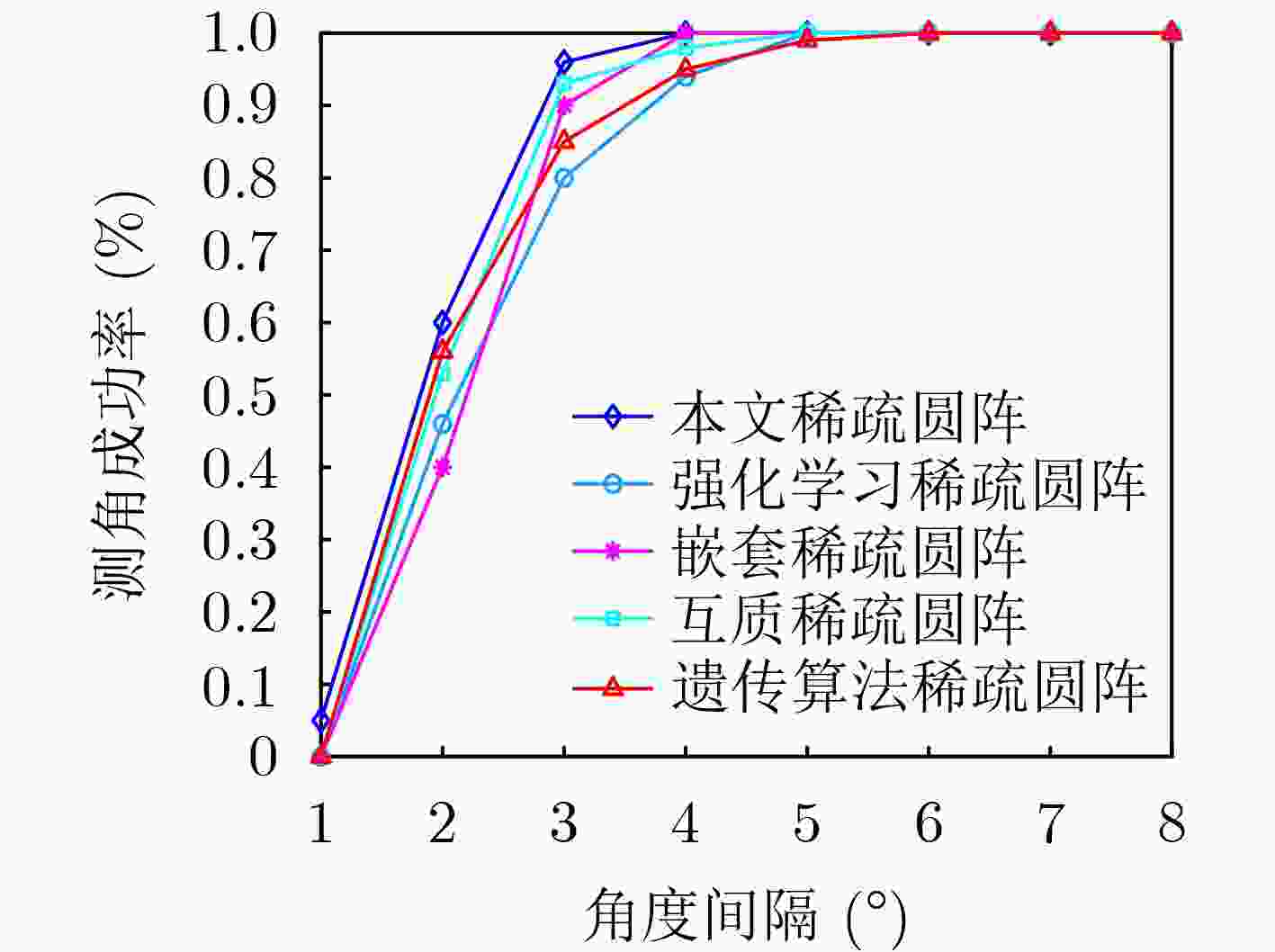
Abstract: Objective To address sparse circular array deployment in practical engineering scenarios, where the number and positions of array elements are constrained, this study proposes an optimization algorithm based on Double Deep Q-Networks (DDQN) to maintain Direction-of-Arrival (DOA) estimation performance under limited channel conditions. This method enables flexible and efficient array design strategies and overcomes challenges that conventional optimization approaches are unable to resolve effectively. The sparse circular array design problem is formulated by minimizing the two-dimensional DOA estimation Ziv–Zakai Bound (ZZB) and Peak Sidelobe Level (PSL) as joint objectives to ensure both angular resolution and estimation accuracy. The state space, action space, and reward function are constructed accordingly, and the DDQN algorithm is employed to solve the optimization task. Experimental results demonstrate that the proposed method achieves stable convergence and robust DOA estimation performance under deployment constraints, and confirm its practical effectiveness. Methods To optimize sparse circular arrays under structural and channel limitations, a DDQN-based design approach is proposed. The method selects a subset of elements from a uniform circular array to maximize DOA estimation accuracy and angular resolution while satisfying constraints on the number of antennas and inter-element spacing. The array design task is cast as a constrained optimization problem with the two-dimensional DOA ZZB and PSL as the performance metrics. Within the reinforcement learning framework, the state space reflects potential array configurations, the action space corresponds to candidate element selections, and the reward function is derived from the optimization objectives. Once trained, the DDQN model outputs an optimized sparse array configuration that balances resolution and sidelobe suppression under the given constraints. Results and Discussions Simulation results show that the reward function of the proposed algorithm converges as the number of training episodes increases (Fig. 8). In contrast, traditional reinforcement learning algorithms exhibit slower convergence and yield suboptimal solutions, while genetic algorithms tend to suffer from premature convergence. The designed sparse circular array satisfies the optimization constraints, including the maximum inter-element spacing requirement (Fig. 9(a)). Under a six-source scenario, the array demonstrates robust DOA estimation capability, effectively resolving multiple incident signals DOA estimation problem (Fig. 10). In evaluations of DOA estimation with Root Mean Squared Error (RMSE) under varying Signal-to-Noise Ratio (SNR) conditions (Fig. 11), the proposed array achieves an estimation error below 0.5° when SNR is ≥ 0 dB. Compared with other sparse circular arrays, it achieves the lowest RMSE, indicating superior estimation performance. In angular resolution tests, the proposed array also exhibits lower PSL values (Table 3) and a higher angle estimation success rate. When the angular separation is ≥ 3°, the success rate exceeds 95% (Fig. 12), confirming the array’s high DOA estimation accuracy and strong angular resolution. Conclusions This study formulates sparse circular array optimization as a constrained problem with the maximum inter-element spacing as a design constraint. To enhance both DOA estimation accuracy and angular resolution, the two-dimensional DOA estimation ZZB and PSL are minimized as joint objectives function. A DDQN algorithm with a dual-network structure is employed to solve the optimization problem and generate the array configuration. Simulation experiments verify that, under channel limitations, the proposed array satisfies the imposed constraints and achieves the intended optimization goals. Compared with other sparse circular arrays, the design demonstrates superior overall DOA estimation performance.
- Array optimization design /
- Sparse circular array /
- Direction-of-Arrival (DOA) estimation /
- Deep Reinforcement Learning (DRL)

HTML全文

图 1 稀疏圆形阵列优化设计场景

下载: 全尺寸图片幻灯片

图 2 DOA估计下界对比示意图

下载: 全尺寸图片幻灯片

图 3 阵列方向图

下载: 全尺寸图片幻灯片

图 4 DOA估计空间谱图

下载: 全尺寸图片幻灯片

图 5 基于DDQN的稀疏圆形阵列优化设计算法

下载: 全尺寸图片幻灯片

图 7 不同稀疏圆形优化阵列布阵示意图

下载: 全尺寸图片幻灯片

图 6 不同算法奖励值函数收敛效果图

下载: 全尺寸图片幻灯片

图 8 DOA估计空间谱图

下载: 全尺寸图片幻灯片

图 9 不同阵列DOA估计RMSE随信噪比变化曲线

下载: 全尺寸图片幻灯片

图 10 不同阵列测角成功率曲线

下载: 全尺寸图片幻灯片

1 基于DDQN的稀疏圆形阵列优化设计算法伪代码

(1) 分别根据$L$、$M$和$Ns$生成阵列状态空间$S$，根据Na生成阵　　列选取动作空间$A$
(2) for i = 1:episode
(3) 　${S_t} = {S_0}$，根据深度Q-网络的输出采用ε-Greedy策略选取　　　动作${A_t}$，得到待选取阵元
(4) 　执行动作${A_t}$，选取该阵元，${S_t}({A_t}) = 1$
(5) 　根据式(15)计算当前状态阵列对应的ZZB和PSL，得到奖　　　励值$R({S_t},{A_t})$
(6) 　更新状态得到${S_{t + 1}}$，由深度目标网络计算目标Q值
(7) 　将$[{S_t},{A_t},{R_t},{S_{t{\text{ + 1}}}}]$存放到经验池，随机抽取样本进行　　　训练
(8) 　根据式(17)更新$Q$值，记录储存${Q_l}$
(9) 　计算阵元选取奖赏值${R_i} = {{\mathrm{sum}}}({{\text{Q}}_i},1)$
(9) 　更新${S_t} = {S_{t + 1}}$，${A_t} = {A_{t + 1}}$
(10) end
(11) ${\mathrm{sort}}({R_{{\mathrm{all}}}},M - 4)$，输出最终被选中的$M - 4$个阵元
(12) 将输出阵元与对最大阵元间距进行约束的阵元组合构成　　 $M$阵元稀疏圆形优化阵列

下载: 导出CSV

表 2 不同稀疏圆形阵列的阵元选取情况

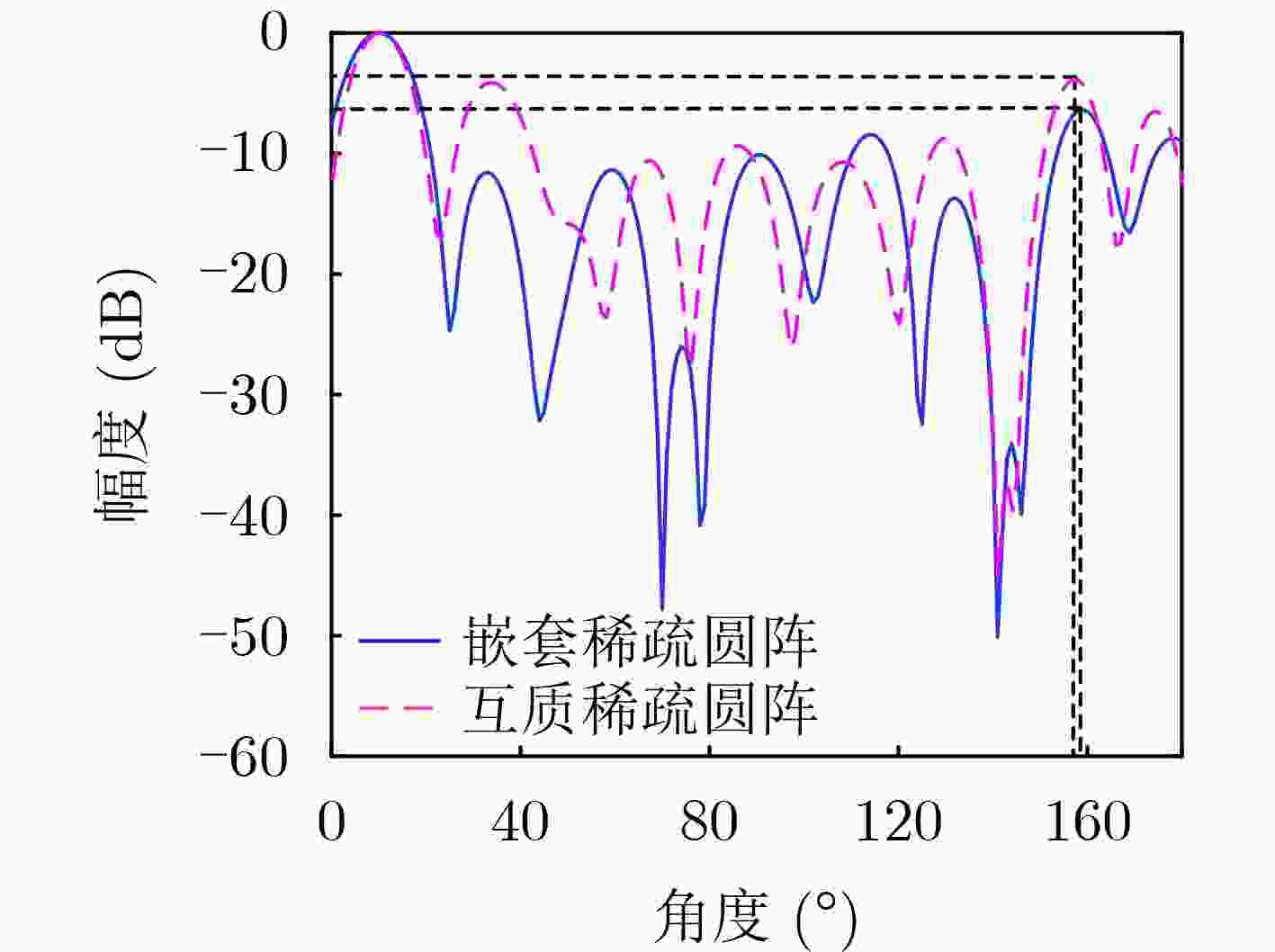
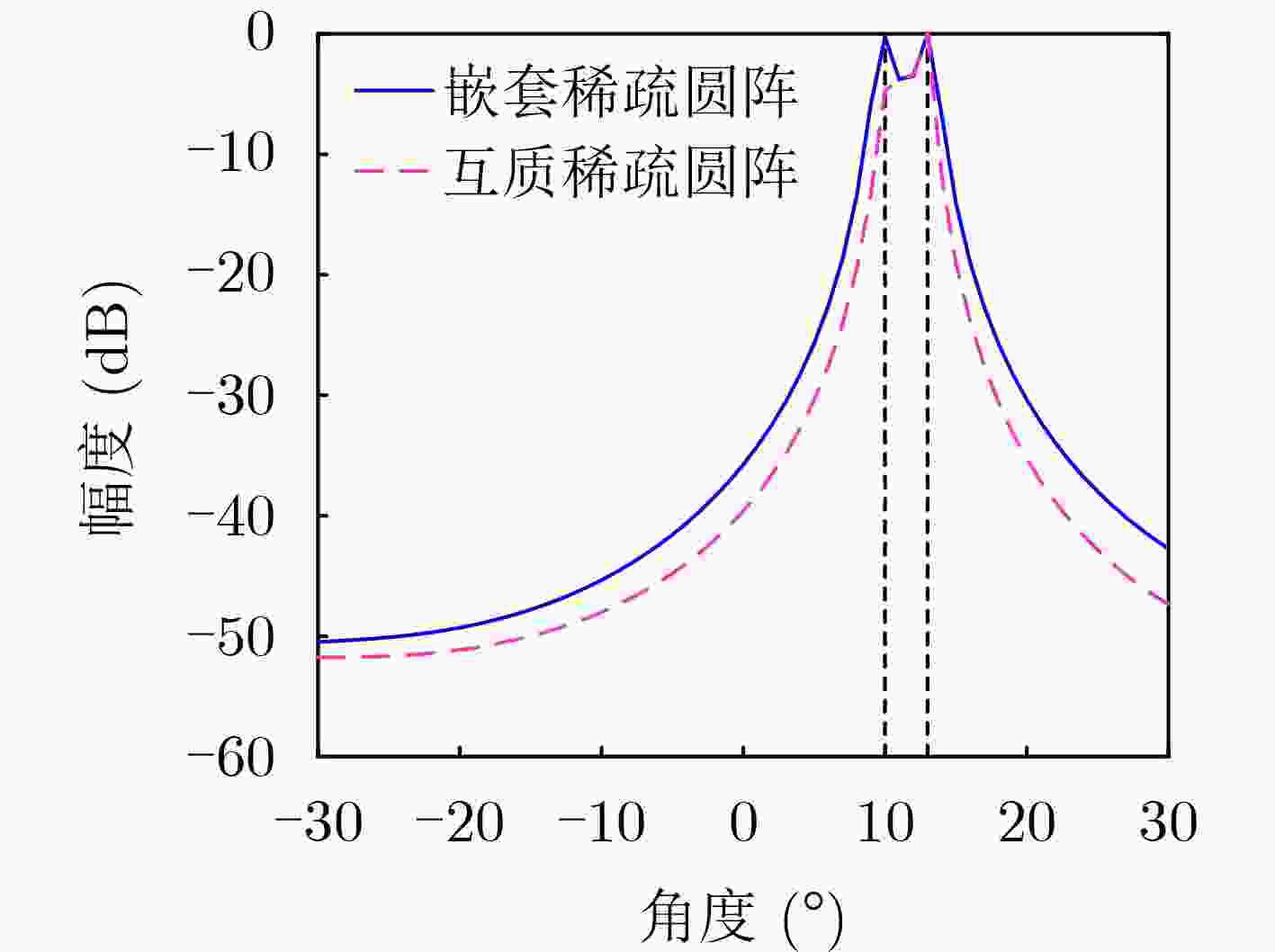
稀疏圆形阵列类型	阵元选取情况
本文算法	[1,3,6,7,13,15,19,23]
强化学习	[1,2,3,6,7,13,19,21]
嵌套	[1,2,3,4,5,10,15,20]
互质	[1,5,6,9,11,13,16,17]
遗传算法	[1,7,11,12,13,19,23,24]

下载: 导出CSV

表 3 不同稀疏圆阵的PSL(dB)

稀疏圆阵类型	本文算法	强化学习	嵌套	互质	遗传算法
PSL	–6.80	–4.10	–5.60	–4.25	–4.08

下载: 导出CSV

参考文献(20)

[1]	SINGH U and KAMAL T S. Synthesis of thinned planar concentric circular antenna arrays using biogeography-based optimisation[J]. IET Microwaves, Antennas & Propagation, 2012, 6(7): 822–829. doi: 10.1109/ET2ECN.2012.6470099.
[2]	GIL G T, LEE J Y, KIM H, et al. Comparison of UCA-OAM and UCA-MIMO systems for sub-THz band line-of-sight spatial multiplexing transmission[J]. Journal of Communications and Networks, 2021, 23(2): 83–90. doi: 10.23919/JCN.2021.000013.
[3]	HU Weiwei and WANG Qiang. DOA estimation for UCA in the presence of mutual coupling via error model equivalence[J]. IEEE Wireless Communications Letters, 2020, 9(1): 121–124. doi: 10.1109/LWC.2019.2944816.
[4]	LI Ping, LI Jianfeng, and ZHAO Gaofeng. Low complexity DOA estimation for massive UCA with single snapshot[J]. Journal of Systems Engineering and Electronics, 2022, 33(1): 22–27. doi: 10.23919/JSEE.2022.000003.
[5]	CAO Bin, XIONG Cong, GONG Linshu, et al. Two-dimensional direction of arrival estimation based on nested circular array[C]. Proceedings of 2022 IEEE USNC-URSI Radio Science Meeting, Denver, USA, 2022: 124–125. doi: 10.23919/USNC-URSI52669.2022.9887477.
[6]	ZHANG Xin, SUN Rongchen, GUO Kaifeng, et al. Coprime circular array DOA estimation method[C]. Proceedings of 2023 6th International Conference on Communication Engineering and Technology, Xi’an, China, 2023: 132–136. doi: 10.1109/ICCET58756.2023.00030.
[7]	ZHANG Zongyu, SHI Zhiguo, and GU Yujie. Ziv-zakai bound for DOAs estimation[J]. IEEE Transactions on Signal Processing, 2023, 71: 136–149. doi: 10.1109/TSP.2022.3229946.
[8]	ZHANG Zongyu, SHI Zhiguo, SHAO Cunqi, et al. Ziv–Zakai bound for 2D-DOAs estimation[J]. IEEE Transactions on Signal Processing, 2024, 72: 2483–2497. doi: 10.1109/TSP.2024.3375636.
[9]	PETKO J S and WERNER D H. Pareto optimization of thinned planar arrays with elliptical mainbeams and low sidelobe levels[J]. IEEE Transactions on Antennas and Propagation, 2011, 59(5): 1748–1751. doi: 10.1109/TAP.2011.2122212.
[10]	于波, 陈客松, 朱盼, 等. 稀布圆阵的降维优化方法[J]. 电子与信息学报, 2014, 36(2): 476–481. doi: 10.3724/SP.J.1146.2013.00526. YU Bo, CHEN Kesong, ZHU Pan, et al. An optimum method of sparse concentric rings array based on dimensionality reduction[J]. Journal of Electronics & Information Technology, 2014, 36(2): 476–481. doi: 10.3724/SP.J.1146.2013.00526.
[11]	JIANG Yi, ZHANG Shu, GUO Qiang, et al. Synthesis of uniformly excited concentric ring arrays using the improved integer GA[J]. IEEE Antennas and Wireless Propagation Letters, 2016, 15: 1124–1127. doi: 10.1109/LAWP.2015.2496173.
[12]	GUO Qiang, WANG Yani, YUAN Ding, et al. Optimization of sparse concentric ring arrays based on multiple constraints[J]. IEEE Antennas and Wireless Propagation Letters, 2020, 19(5): 781–785. doi: 10.1109/LAWP.2020.2980166.
[13]	LANG Rongling, XU Hao, GAO Fei, et al. Improving DOA estimation of GNSS interference through sparse non-uniform array reconfiguration[J]. Chinese Journal of Aeronautics, 2025, 38(8): 103384. doi: 10.1016/j.cja.2024.103384.
[14]	ZHANG Binchao, JIN Cheng, CAO Kaiqi, et al. Cognitive conformal antenna array exploiting deep reinforcement learning method[J]. IEEE Transactions on Antennas and Propagation, 2022, 70(7): 5094–5104. doi: 10.1109/TAP.2021.3096994.
[15]	FILIK T and TUNCER T E. Design and evaluation of V-shaped arrays for 2-D DOA estimation[C]. Proceedings of 2008 IEEE International Conference on Acoustics, Speech and Signal Processing, Las Vegas, USA, 2008: 2477–2480. doi: 10.1109/ICASSP.2008.4518150.
[16]	CHEN Zezong, HE Chao, ZHAO Chen, et al. Enhanced target detection for HFSWR by 2-D MUSIC based on sparse recovery[J]. IEEE Geoscience and Remote Sensing Letters, 2017, 14(11): 1983–1987. doi: 10.1109/LGRS.2017.2745048.
[17]	薛青, 来东, 徐勇军, 等. 基于分布式联邦学习的毫米波通信系统波束配置方法[J]. 电子与信息学报, 2024, 46(1): 138–145. doi: 10.11999/JEIT221536. XUE Qing, LAI Dong, XU Yongjun, et al. Beam configuration for millimeter wave communication systems based on distributed federated learning[J]. Journal of Electronics & Information Technology, 2024, 46(1): 138–145. doi: 10.11999/JEIT221536.
[18]	DING Yu, HAN Huimei, LU Weidang, et al. DDQN-based trajectory and resource optimization for UAV-Aided MEC secure communications[J]. IEEE Transactions on Vehicular Technology, 2024, 73(4): 6006–6011. doi: 10.1109/TVT.2023.3335210.
[19]	冯伟杨, 林思雨, 冯婧涛, 等. 基于Q学习的蜂窝车联网边缘计算系统PC-5/Uu接口联合卸载策略[J]. 电子学报, 2024, 52(2): 385–395. doi: 10.12263/DZXB.20220922. FENG Weiyang, LIN Siyu, FENG Jingtao, et al. Q-Learning based joint PC-5/Uu offloading strategy for C-V2X based vehicular edge computing system[J]. Acta Electronica Sinica, 2024, 52(2): 385–395. doi: 10.12263/DZXB.20220922.
[20]	CHEN Tao, WANG Xilin, SHI Lin, et al. Array sparse optimization method based on adaptive genetic algorithm[C]. IET International Radar Conference, 2020: 1271–1275. doi: 10.1049/icp.2021.0648. (查阅网上资料,无法确认作者的全拼信息是否正确).