Modeling and Simulation Analysis of Inter-satellites Pseudo-code Ranging for Space Gravitational Wave Detection
-
摘要: 为满足空间引力波探测中时延干涉算法(TDI)对米级精度星间距数据的需求,基于激光链路建立星间绝对距离测量系统。该文以空间引力波探测太极计划为背景,通过分析空间引力波探测中星间测距的实现原理,设计了基于伪随机码(PRN)低深度相位调制的星间测距模型,分析了测距精度的主要影响因素,并基于直接数字合成器(DDS)模拟外差干涉信号,进行了伪码测距系统的FPGA仿真验证。仿真结果表明,采用该模型可获得的理论测距精度可达厘米量级,达到了空间引力波探测的米级精度需求。该激光测距方案对卫星导航和天基引力波探测的工程应用具有参考价值。Abstract:
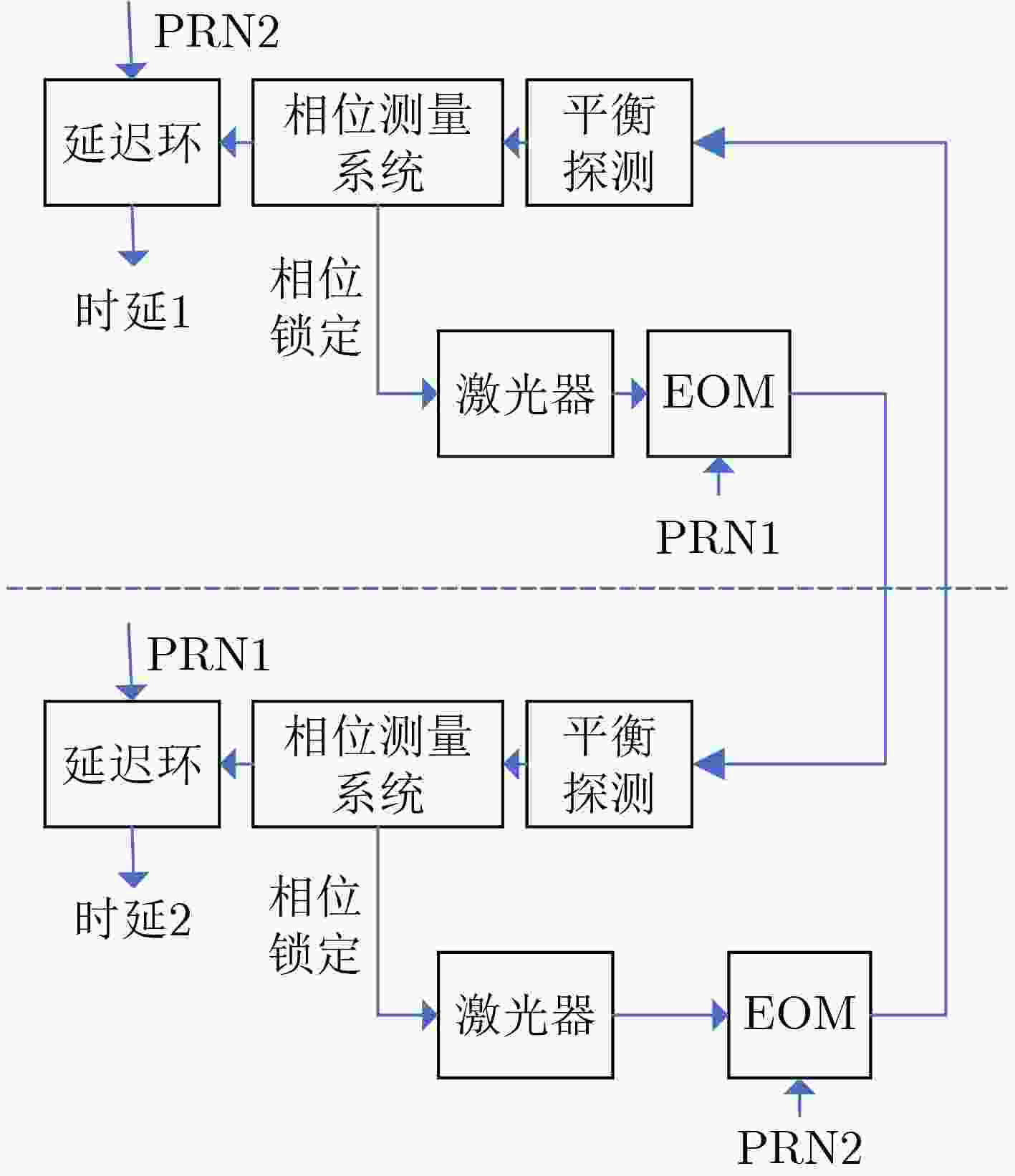
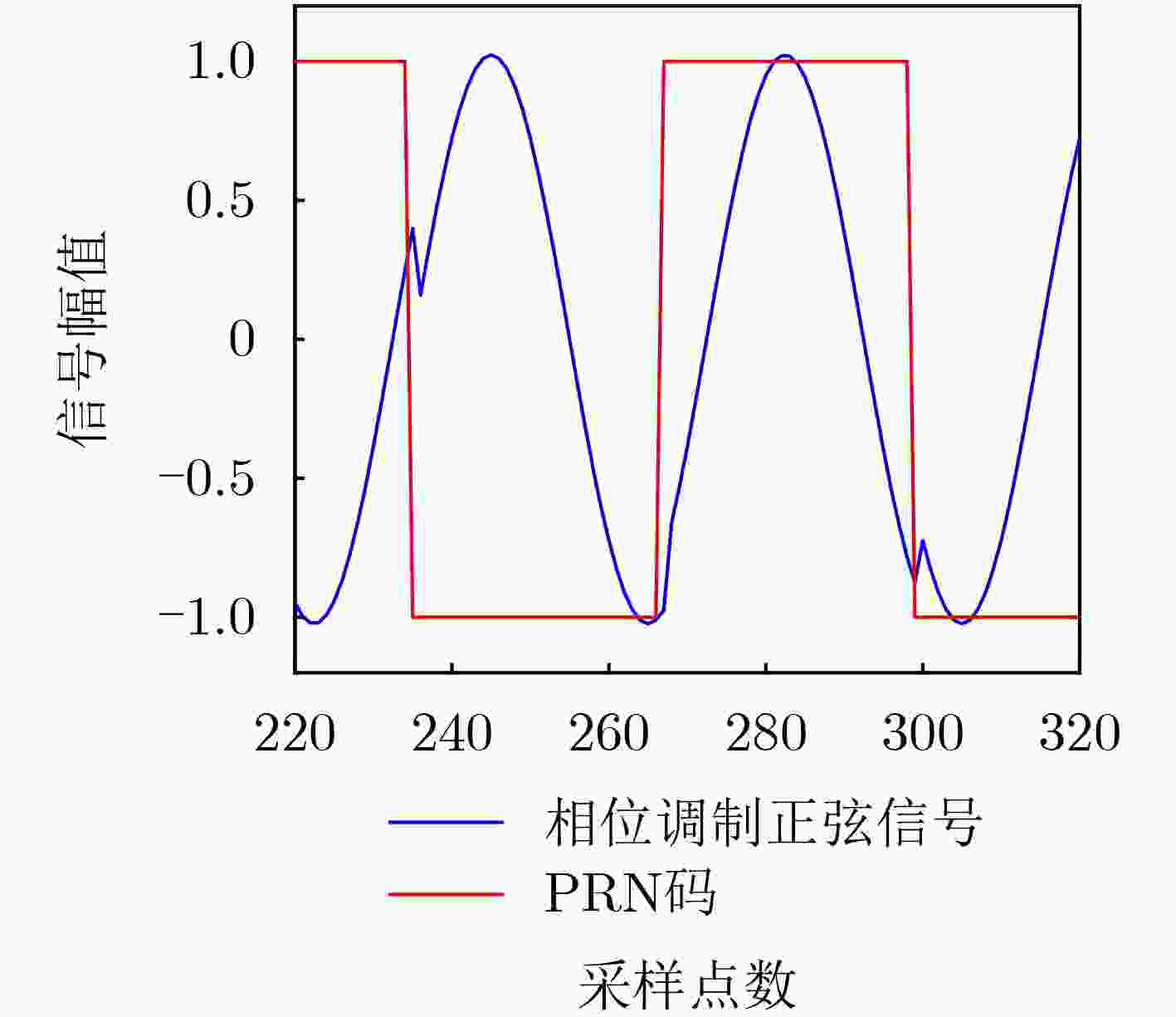
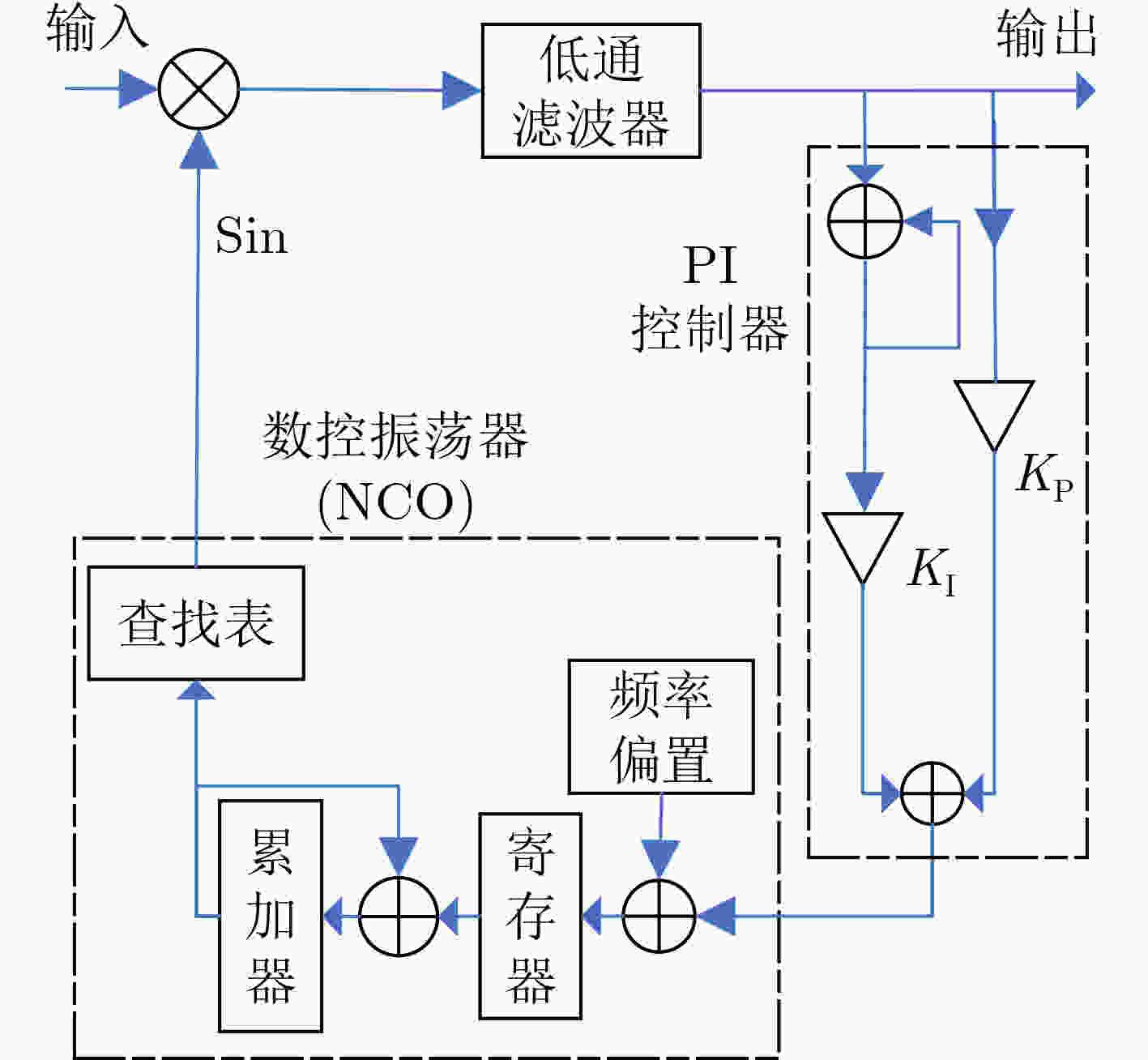
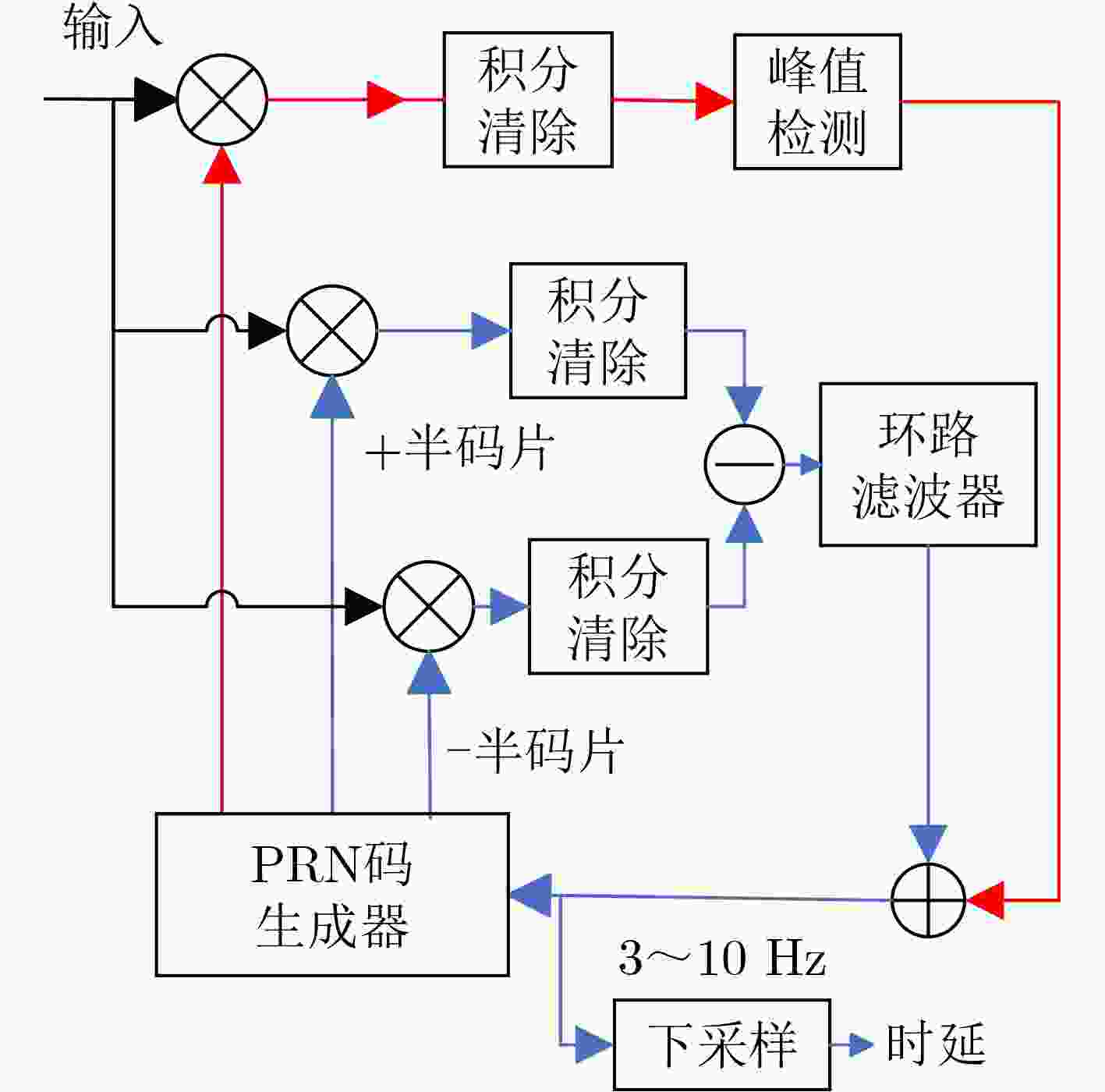
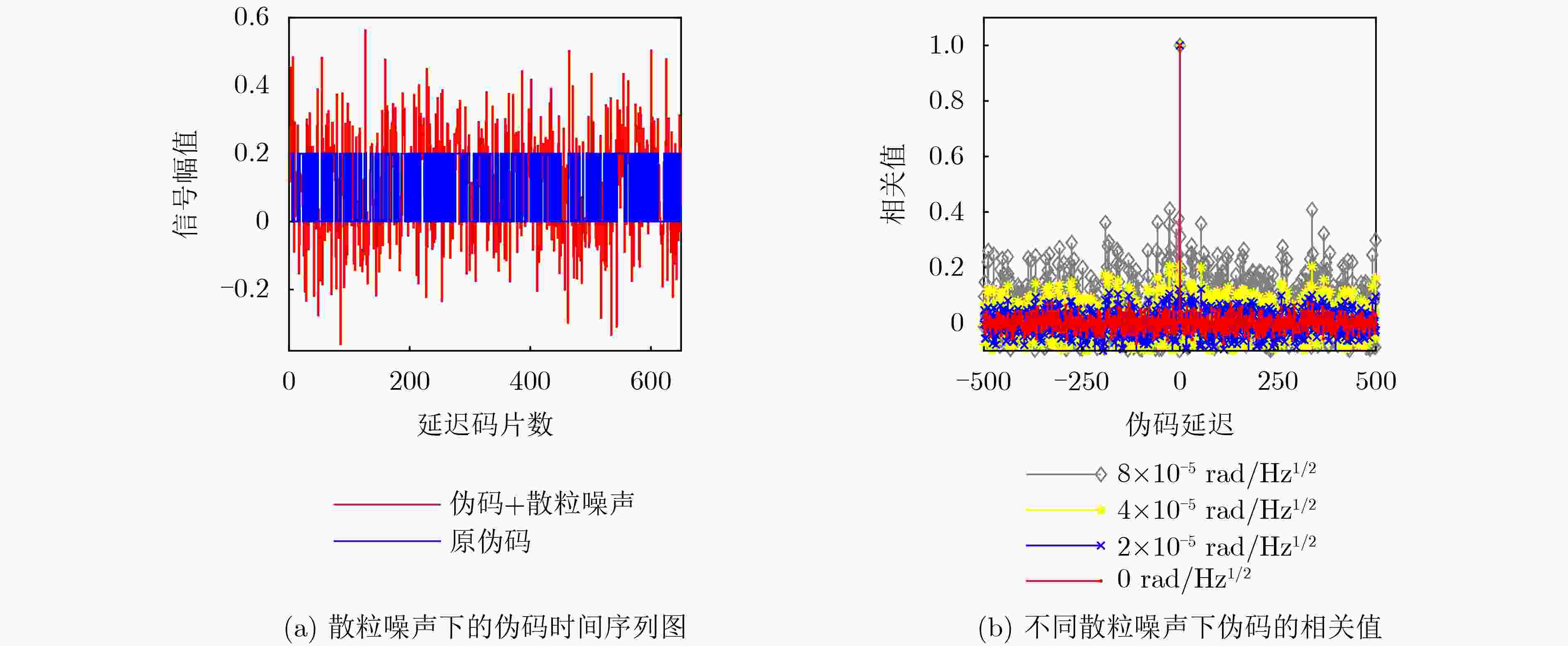
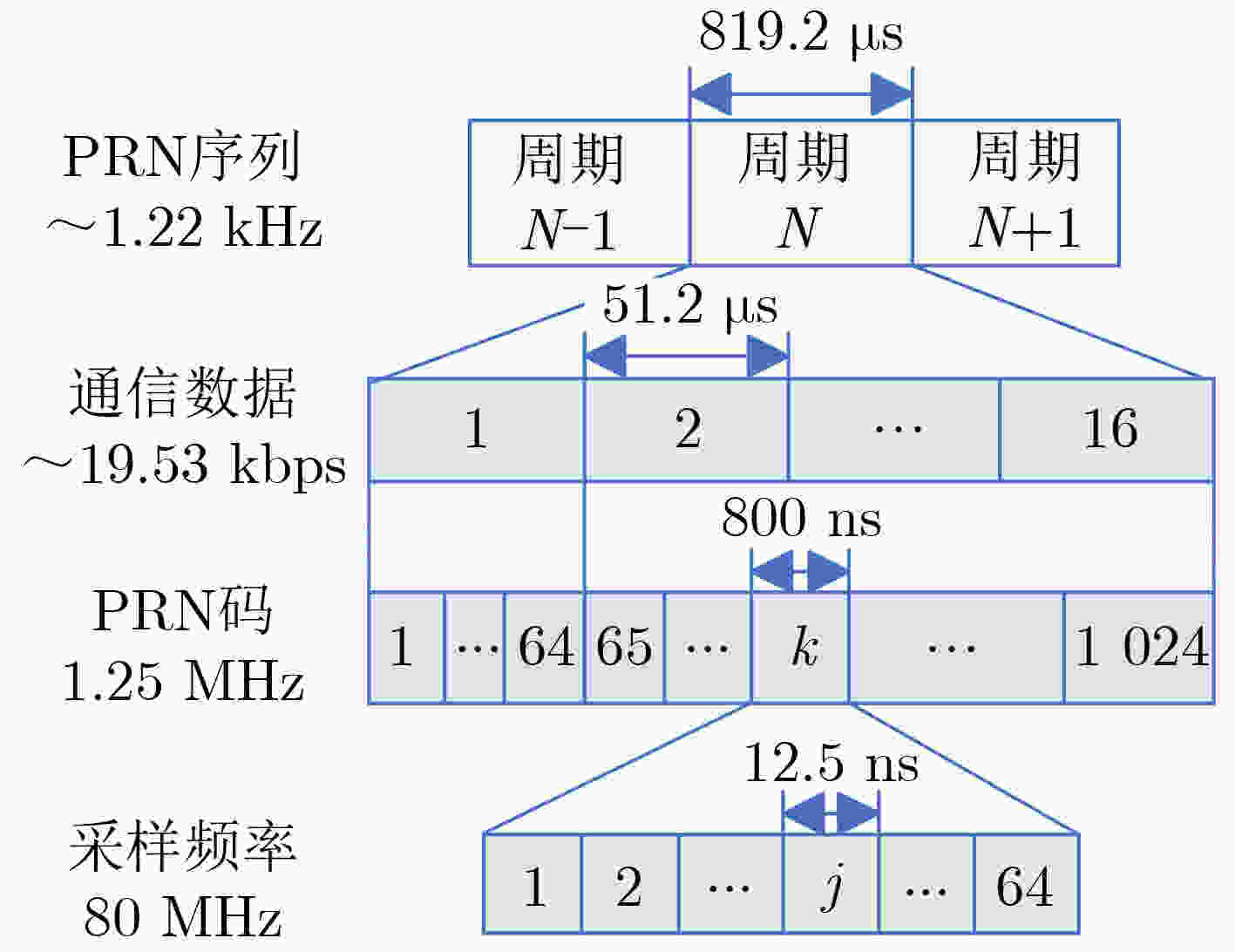
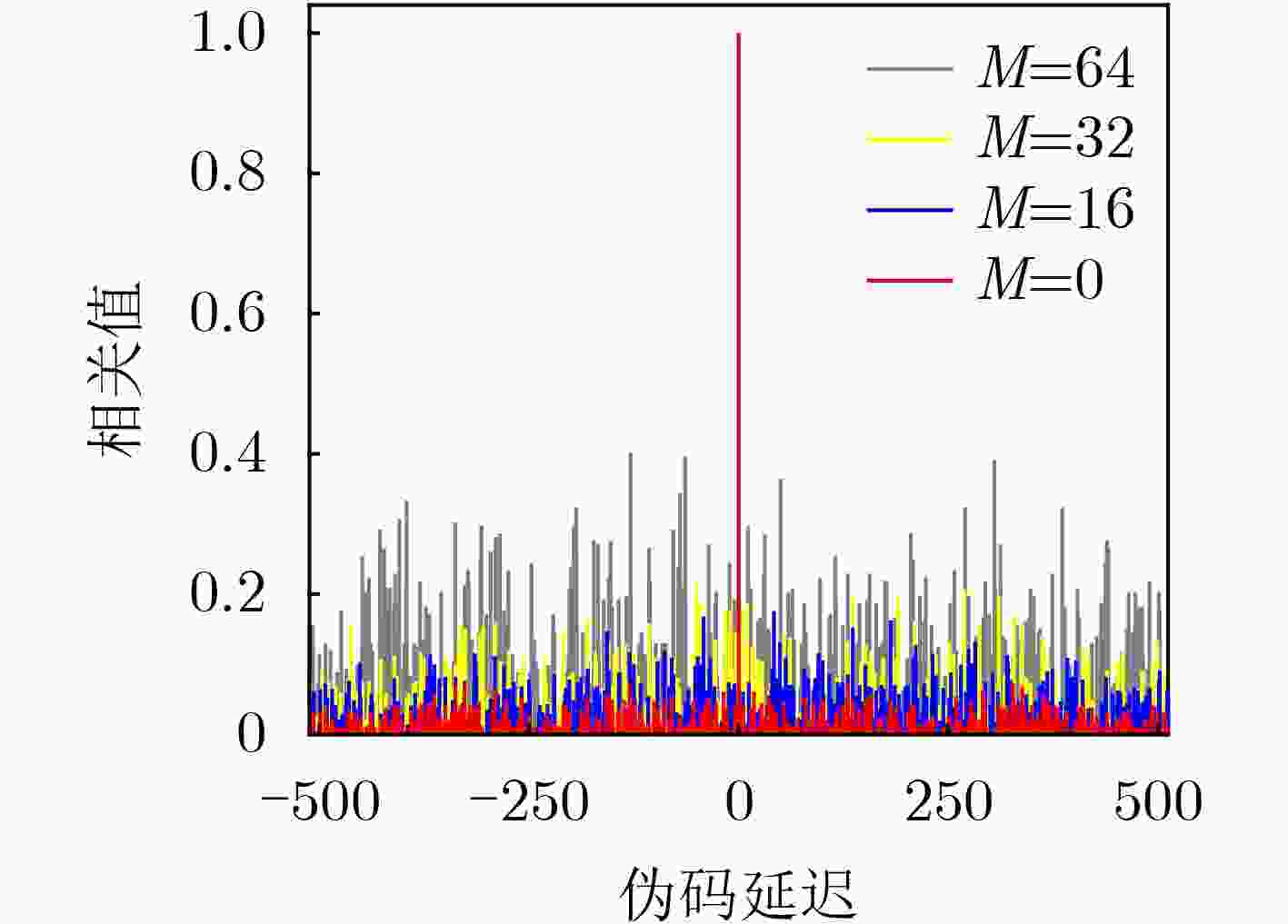
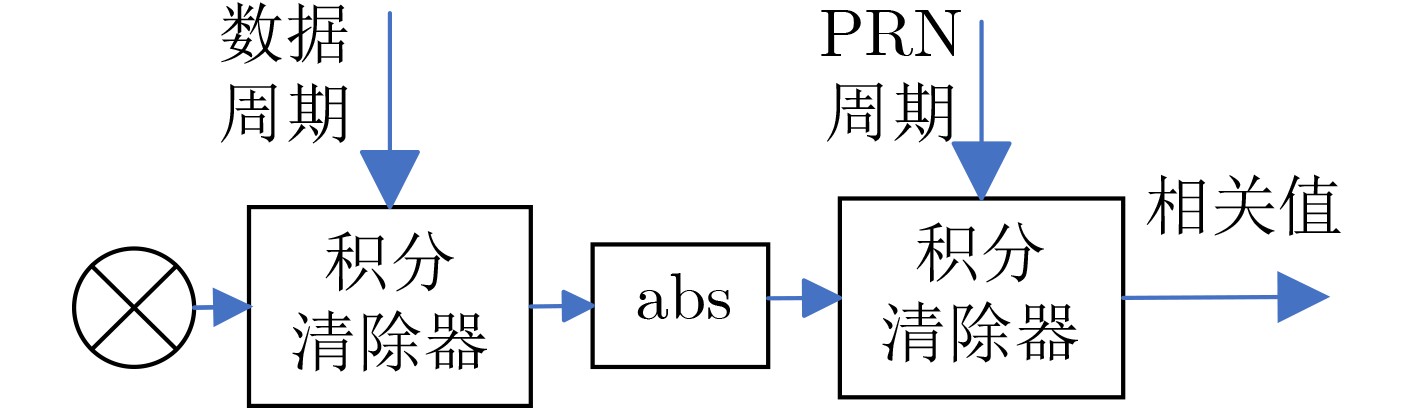
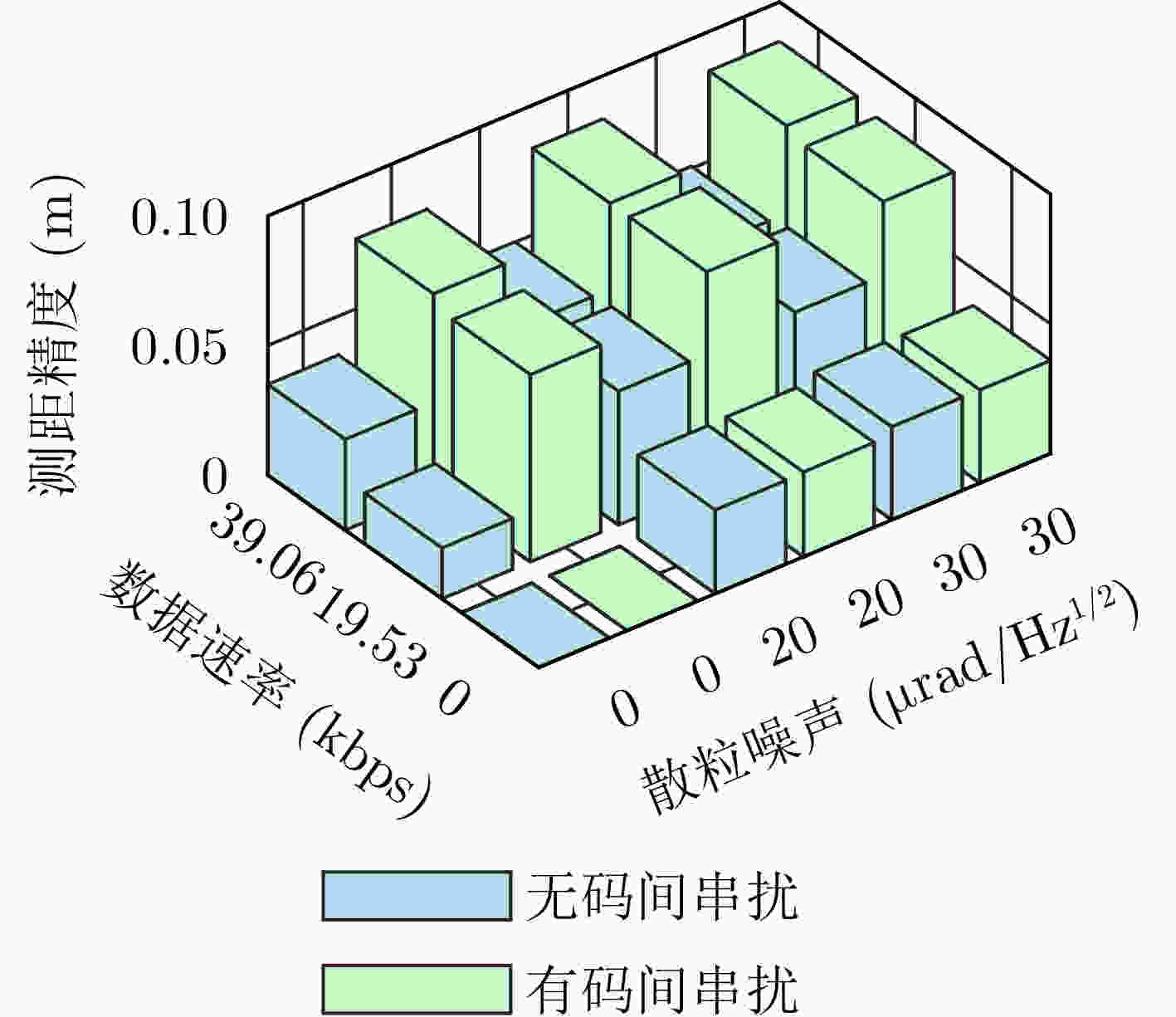
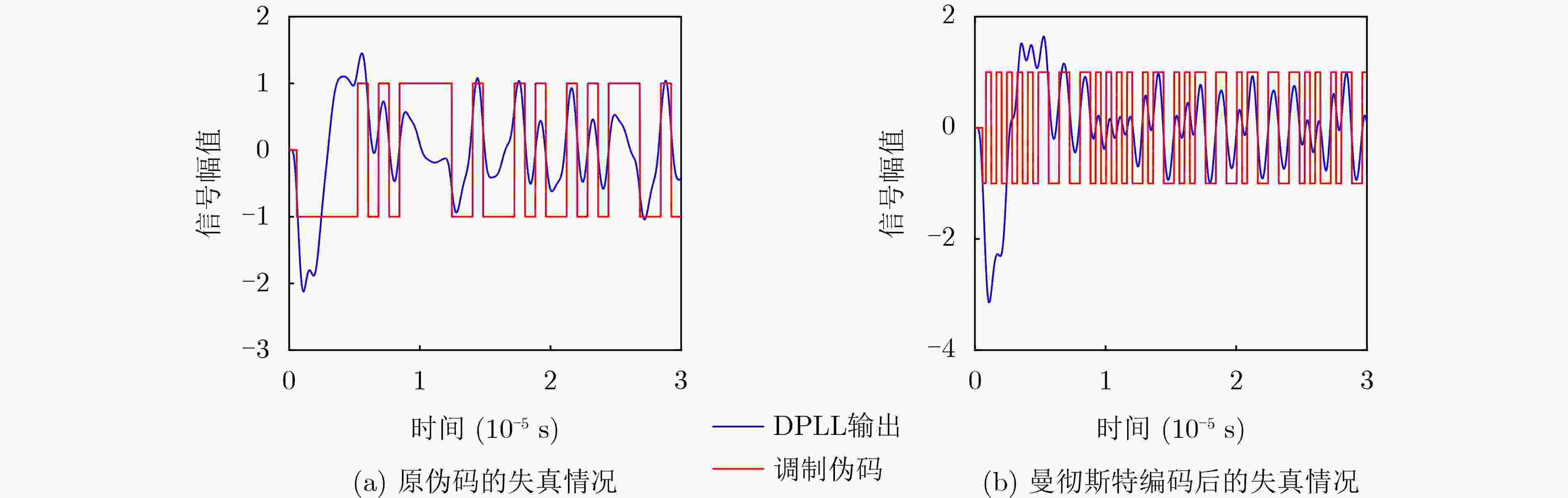
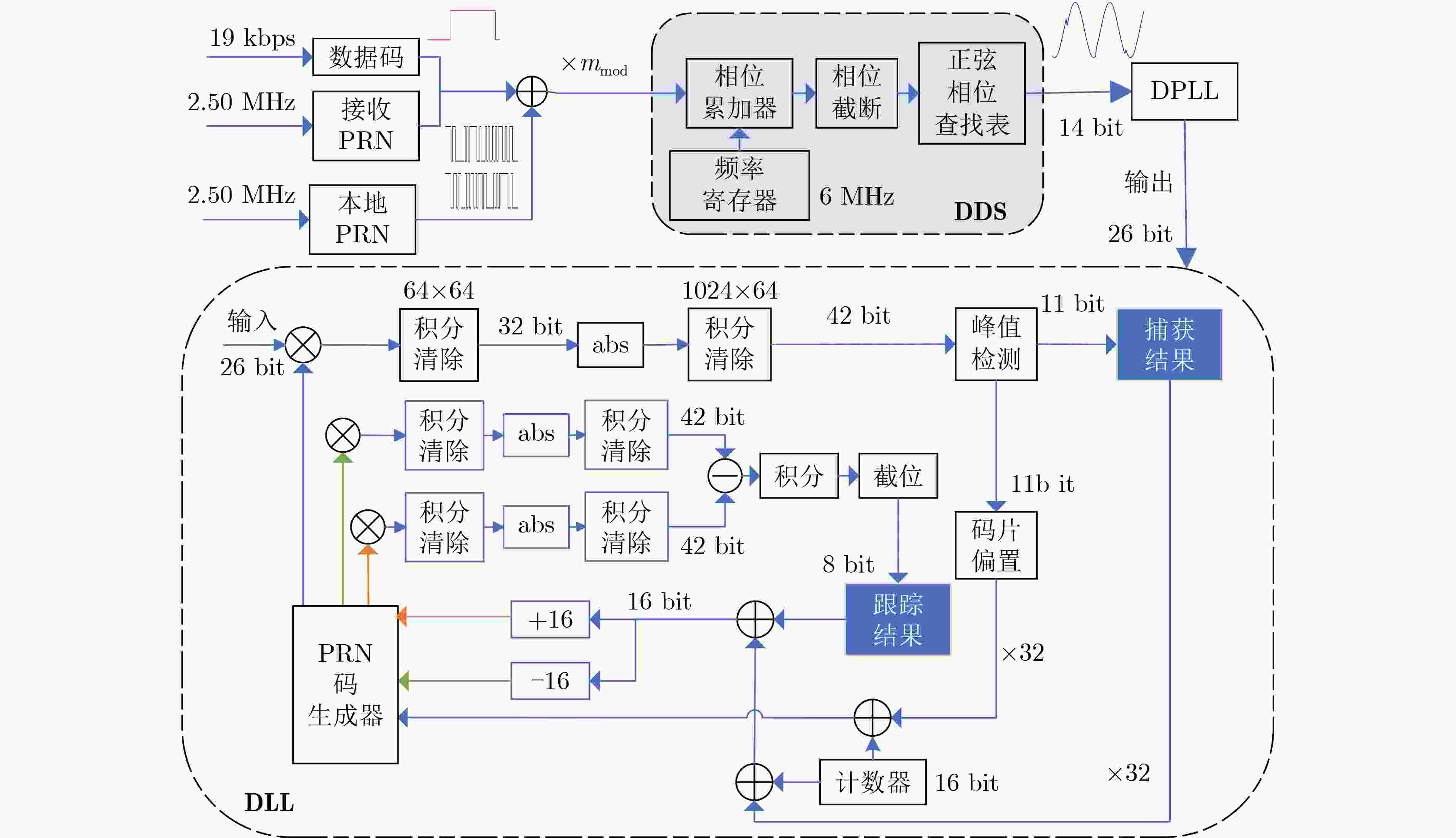
Objective Inter-satellite laser interferometry for space gravitational wave detection is constrained by orbital dynamics and other perturbations, which cause continuous variations in inter-satellite distances. Therefore, laser frequency noise becomes the dominant noise source in the inter-satellite interferometry system. To suppress this noise, the Time Delay Interferometry (TDI) algorithm is applied during data post-processing, where a virtual equal-arm interferometer is synthesized by shifting and combining data streams. However, accurate TDI combinations depend on precise knowledge of absolute inter-satellite distances at the picometer level. Any deviation in these measurements may propagate into errors in the final processed data. To address this issue, an inter-satellite ranging scheme based on Pseudo-Random Noise (PRN) is proposed. This method enables both inter-satellite ranging and data communication, providing theoretical support for autonomous satellite navigation as well as inter-satellite ranging and communication in space-based gravitational wave missions. Methods To reduce power consumption and spacecraft mass, the inter-satellite ranging task is implemented using existing laser links for scientific measurement. Only a small fraction of the available power is allocated to the ranging subsystem to avoid degrading the phase stability of science measurements. A low-depth Binary Phase-Shift Keying (BPSK) modulation scheme based on PRN is proposed to enable laser ranging and data communication as auxiliary functions of the high-precision inter-satellite interferometry system. The ranging system architecture incorporates a Digital Phase-Locked Loop (DPLL) for carrier synchronization and a Delay-Locked Loop (DLL) for PRN code synchronization. Theoretical limitations of ranging accuracy are systematically analyzed, including contributions from shot noise, integration time, inter-code interference, optical data bit encoding, and the impulse response of the DPLL. These analyses guide improvements in both the DPLL and DLL designs. A Direct Digital Synthesizer (DDS) is used to generate the heterodyne signal. Simulation verification of unidirectional ranging, bidirectional ranging and inter-satellite data communication is performed on a Field Programmable Gate Array (FPGA) platform. Results and Discussions The simulation results ( Table 2 ,Table 3 ) demonstrate that the optimization methods proposed in (Fig.9 ,Fig.11 ) effectively reduce the effects of data encoding and inter-code interference on the ranging accuracy of the delay-locked tracking loop, respectively. As shown in (Table 4 ), in a single delay-locked tracking loop, the dominant factor limiting ranging accuracy is data bit encoding for optical communication when the local PRN code is absent; otherwise, shot noise becomes the primary source of error. (Fig.16 ) illustrates the distortion of the PRN code caused by the phasemeter pulse response, and shows that Manchester encoding significantly mitigates this distortion. The final simulation results after applying all optimization techniques are summarized in (Table 5 ). With a modulation depth of approximately 0.4 rad, corresponding to an equivalent optical power of less than 4%, the Root Mean Square (RMS) errors for both unidirectional and bidirectional ranging are approximately 3 cm at a measurement rate of 3 Hz with an 80 MHz sampling frequency. For unidirectional ranging with data streams encoded at 19 kbps and 39 kbps, the corresponding RMS ranging errors are approximately 5 cm and 20 cm, respectively. Bidirectional ranging supports data transmission only at 19 kbps, yielding an RMS error of approximately 6 cm. When the phase modulation depth is reduced to 0.2 rad (corresponding to an equivalent optical power below 1%), the RMS ranging error is approximately 6 cm; if 19 kbps data are transmitted simultaneously, the RMS error increases to approximately 12 cm. These simulation results confirm that sub-meter absolute distance resolution is achievable under all tested conditions.Conclusions Based on the Taiji plan, an absolute distance measurement scheme utilizing low-depth phase modulation of PRN codes is proposed. A receiver model based on a DPLL and a DLL is established. The limiting factors affecting inter-satellite ranging accuracy are analyzed, leading to improvements in the ranging model. The simulation results, following comprehensive optimizations, show that the primary limiting factors of ranging accuracy are unavoidable shot noise and the encoding of data bits for optical communication. At a clock sampling rate of 80 MHz, with a PRN code phase modulation depth of 0.4 rad, the bidirectional ranging RMS error is approximately 6 cm when communication data is encoded at 19 kbps. When the modulation depth is reduced to 0.2 rad, the RMS error increases to approximately 12 cm while transmitting 19 kbps data concurrently. These simulation results demonstrate a clear improvement over meter-level accuracy, and the ranging model offers valuable insights for space gravitational wave detection and satellite autonomous navigation. Given the complexity of clock synchronization, it is assumed in this study that the clocks of the transmitter and receiver are fully synchronized. Further research will address clock synchronization issues, and electrical and optical experiments will be conducted to assess the performance of the proposed architecture in future work. -
表 1 散粒噪声与载噪比理论预估值
接收功率
${P_S}\left( {{\text{pW}}} \right)$相位噪声
$ \vartheta _{}^{{\mathrm{sn}}}\left( {{\text{μ rad/}}\sqrt {{\text{Hz}}} } \right) $载噪比
$ C/N^{{\mathrm{sn}}}\left( {{\text{dB}} \cdot {\text{Hz}}} \right) $1767.53 19.24 94.32 757.51 29.38 90.64 表 2 不同数据速率对应的DLL测距精度(m)
数据速率(kbps) 积分器个数 测距精度 19.53 1 0.0634 19.53 2 0.0196 39.06 1 0.1408 39.06 2 0.0769 表 3 存在本地PRN码时不同散粒噪声下对应的DLL测距精度(m)
散粒噪声
(μrad/Hz1/2)无本地PRN 有本地PRN 减去本地PRN 0 1.1005 ×10–90.3231 2.3550 ×10–920 0.0323 0.3326 0.0327 30 0.0359 0.3390 0.0359 表 4 单独DLL在不同情况下的测距精度(m)
散粒噪声
(μrad/Hz1/2)本地PRN码 数据速率(kbps) 0 19.53 39.06 0 无 1.1005 ×10–90.0196 0.0350 0 有 2.3550 ×10–90.0722 0.0769 20 无 0.0323 0.0516 0.0502 20 有 0.0327 0.0834 0.0834 30 无 0.0359 0.0536 0.0509 30 有 0.0359 0.0821 0.0848 表 5 不同条件对应DPLL与DLL的测距精度(m)
调制深度(rad) 数据速率
(kbps)单向/
双向测距载噪比(dB-Hz) 81.94 87.96 93.98 0.4 0 单 0.0302 0.0257 0.0061 0.4 0 双 0.0332 0.0336 0.0158 0.4 19 单 0.0547 0.0456 0.0111 0.4 19 双 0.0646 0.0642 0.0310 0.4 39 单 0.2033 0.1611 0.0422 0.2 0 单 0.0599 0.0452 0.0116 0.2 0 双 0.0632 0.0498 0.0123 0.2 19 单 0.1076 0.0812 0.0211 0.2 19 双 0.1236 0.0897 0.0235 -
[1] BENDER P L, BRILLET A, CIUFOLINI I, et al. LISA. Laser interferometer space antenna for the detection and observation of gravitational waves. An international project in the field of fundamental physics in space[R]. MPQ 233, 1998: 1–206. [2] LUO Jun, CHEN Lisheng, DUAN Huizong, et al. TianQin: A space-borne gravitational wave detector[J]. Classical and Quantum Gravity, 2016, 33(3): 035010. doi: 10.1088/0264-9381/33/3/035010. [3] LUO Ziren, WANG Yan, WU Yueliang, et al. The Taiji program: A concise overview[J]. Progress of Theoretical and Experimental Physics, 2021, 2021(5): 05A108. doi: 10.1093/ptep/ptaa083. [4] ESTEBAN DELGADO J J. Laser ranging and data communication for the laser interferometer space antenna[D]. [Ph. D. dissertation], Universidad de Granada, 2012. [5] ESTEBAN J J, GARCÍA A F, EICHHOLZ J, et al. Ranging and phase measurement for LISA[J]. Journal of Physics: Conference Series, 2010, 228: 012045. doi: 10.1088/1742-6596/228/1/012045. [6] REINHARDT J N, STAAB M, YAMAMOTO K, et al. Ranging sensor fusion in LISA data processing: Treatment of ambiguities, noise, and onboard delays in LISA ranging observables[J]. Physical Review D, 2024, 109(2): 022004. doi: 10.1103/PhysRevD.109.022004. [7] SUTTON A, MCKENZIE K, WARE B, et al. Laser ranging and communications for LISA[J]. Optics Express, 2010, 18(20): 20759–20773. doi: 10.1364/OE.18.020759. [8] 邓汝杰, 张艺斌, 刘河山, 等. 太极计划中的星间激光测距地面电子学验证[J]. 中国光学(中英文), 2023, 16(4): 765–776. doi: 10.37188/CO.2022-0041.DENG Rujie, ZHANG Yibin, LIU Heshan, et al. Ground electronics verification of inter-satellites laser ranging in the Taiji program[J]. Chinese Optics, 2023, 16(4): 765–776. doi: 10.37188/CO.2022-0041. [9] XIE Siyuan, ZENG Hanyu, PAN Yuhang, et al. Bi-directional PRN laser ranging and clock synchronization for TianQin mission[J]. Optics Communications, 2023, 541: 129558. doi: 10.1016/j.optcom.2023.129558. [10] EURINGER P, HECHENBLAIKNER G, SOUALL F, et al. Performance analysis of sequential carrier- and code-tracking receivers in the context of high-precision spaceborne metrology systems[J]. IEEE Transactions on Instrumentation and Measurement, 2024, 73: 1000510. doi: 10.1109/TIM.2023.3332388. [11] 刘河山, 高瑞弘, 罗子人, 等. 空间引力波探测中的绝对距离测量及通信技术[J]. 中国光学, 2019, 12(3): 486–492. doi: 10.3788/co.20191203.0486.LIU Heshan, GAO Ruihong, LUO Ziren, et al. Laser ranging and data communication for space gravitational wave detection[J]. Chinese Optics, 2019, 12(3): 486–492. doi: 10.3788/co.20191203.0486. [12] ZENG Hanyu, YAN Hao, XIE Siyuan, et al. Experimental demonstration of weak-light inter-spacecraft clock jitter readout for TianQin[J]. Optics Express, 2023, 31(21): 34648–34666. doi: 10.1364/OE.503164. [13] ESTEBAN J J, GARCÍA A F, BARKE S, et al. Experimental demonstration of weak-light laser ranging and data communication for LISA[J]. Optics Express, 2011, 19(17): 15937–15946. doi: 10.1364/OE.19.015937. [14] SWEENEY D M. Laser communications for LISA and the University of Florida LISA interferometry simulator[D]. [Ph. D. dissertation], University of Florida, 2012. [15] GERBERDING O, SHEARD B, BYKOV I, et al. Phasemeter core for intersatellite laser heterodyne interferometry: Modelling, simulations and experiments[J]. Classical and Quantum Gravity, 2013, 30(23): 235029. doi: 10.1088/0264-9381/30/23/235029. [16] 胡寿松. 自动控制原理[M]. 6版. 北京: 科学出版社, 2013: 209–213.HU Shousong. Principles of Automatic Control[M]. 6th ed. Beijing: Science Press, 2013: 209–213. [17] GARDNER F M. Phaselock Techniques[M]. 3rd ed. Hoboken: Wiley-Interscience, 2005. [18] 鲍爱达, 侯世豪, 郭鑫, 等. 星间链路通信收发一体化系统设计[J]. 计算机测量与控制, 2024, 32(8): 280–286. doi: 10.16526/j.cnki.11-4762/tp.2024.08.040.BAO Aida, HOU Shihao, GUO Xin, et al. Design of transceiver integrated system for inter-satellite link communication[J]. Computer Measurement & Control, 2024, 32(8): 280–286. doi: 10.16526/j.cnki.11-4762/tp.2024.08.040. [19] BARKE S. Inter-spacecraft frequency distribution for future gravitational wave observatories[D]. [Ph. D. dissertation], Gottfried Wilhelm Leibniz Universität Hannover, 2015. doi: 10.15488/8405. [20] HEINZEL G, ESTEBAN J J, BARKE S, et al. Auxiliary functions of the LISA laser link: Ranging, clock noise transfer and data communication[J]. Classical and Quantum Gravity, 2011, 28(9): 094008. doi: 10.1088/0264-9381/28/9/094008. [21] BRAUSE N C. Auxiliary function development for the LISA metrology system[D]. [Ph. D. dissertation], Institutionelles Repositorium der Leibniz Universität Hannover, 2018. doi: 10.15488/3511. [22] YAMAMOTO K, BYKOV I, REINHARDT J N, et al. Experimental end-to-end demonstration of intersatellite absolute ranging for the Laser Interferometer Space Antenna[J]. American Physical Society, 2024, 22(5): 054020. doi: 10.1103/PhysRevApplied.22.054020. -





 下载:
下载:

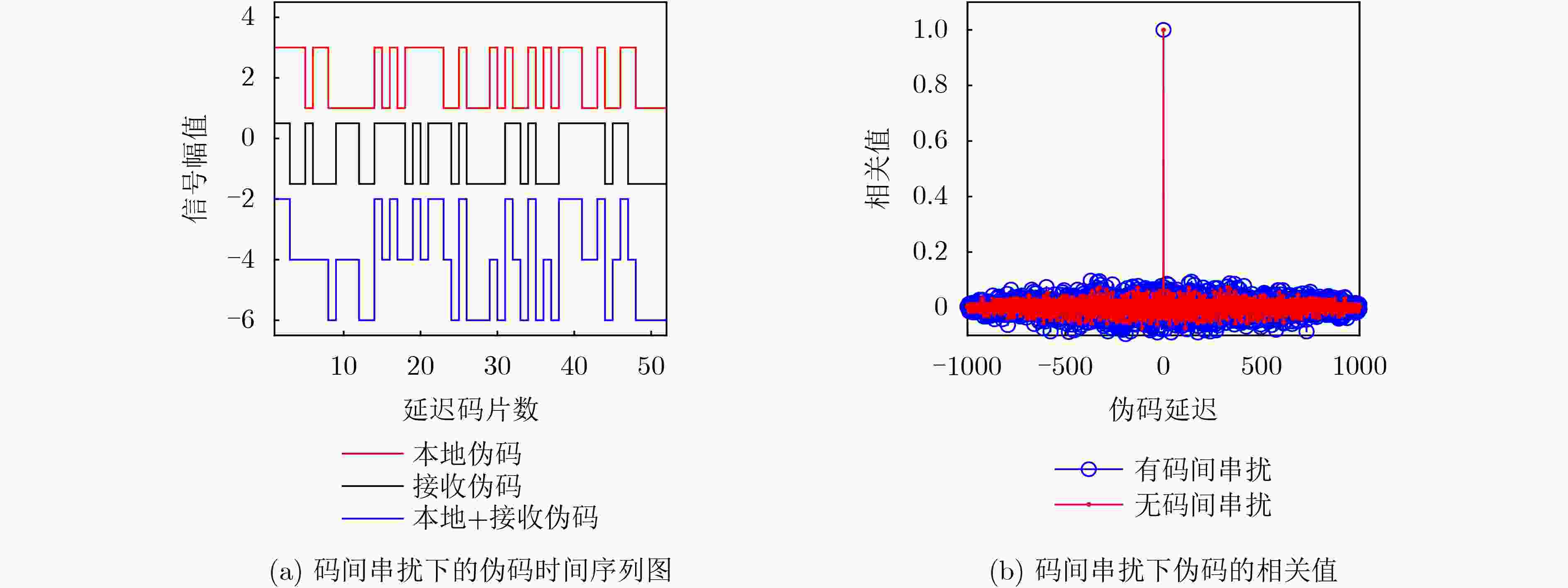
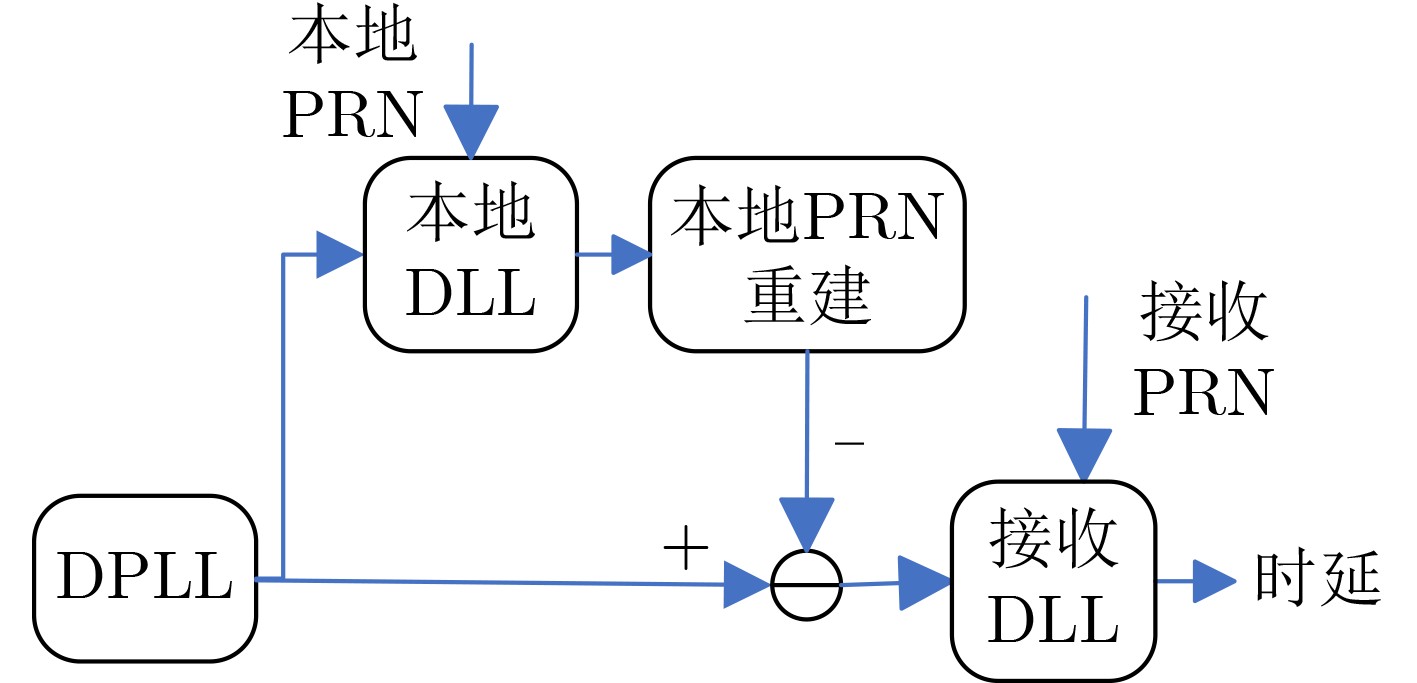
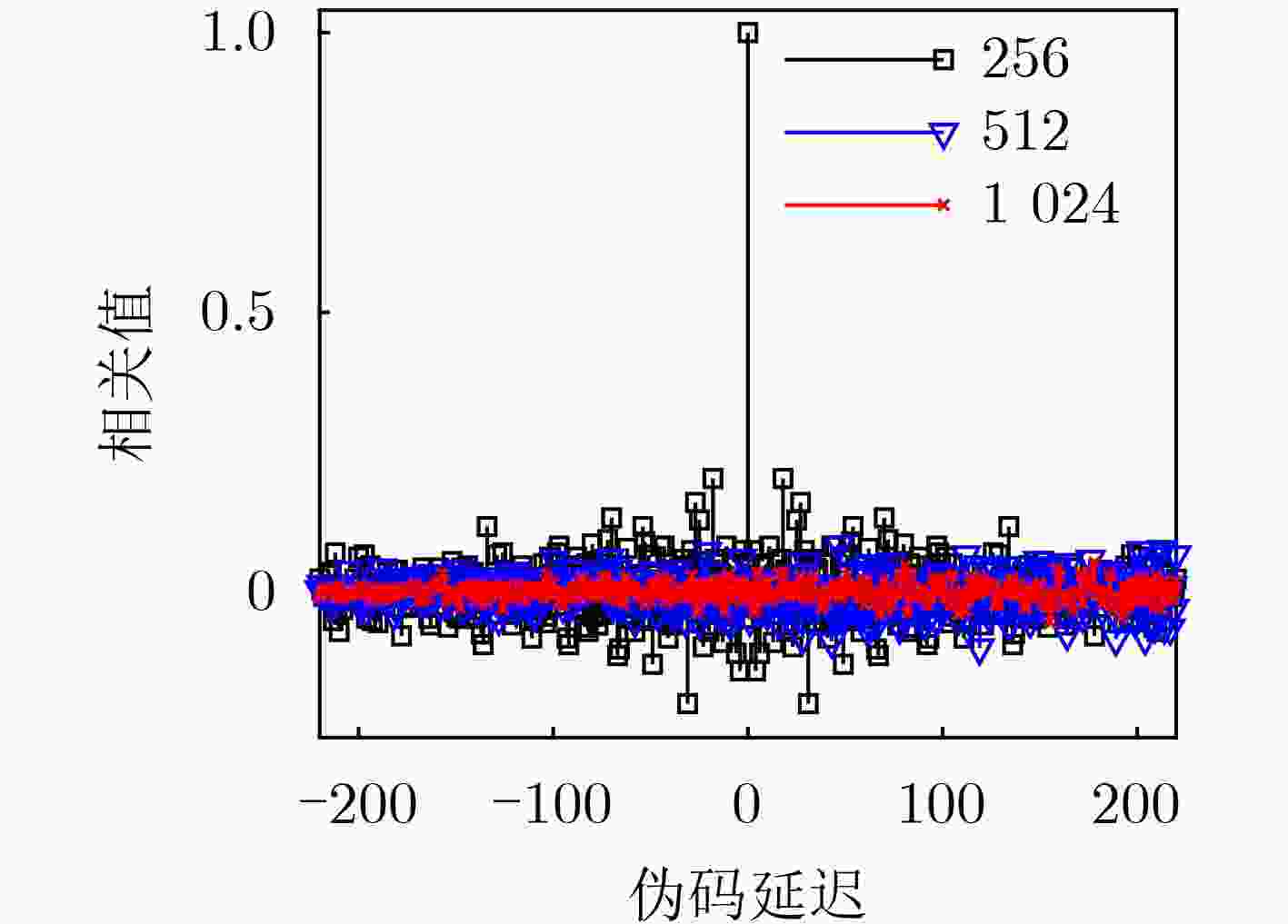
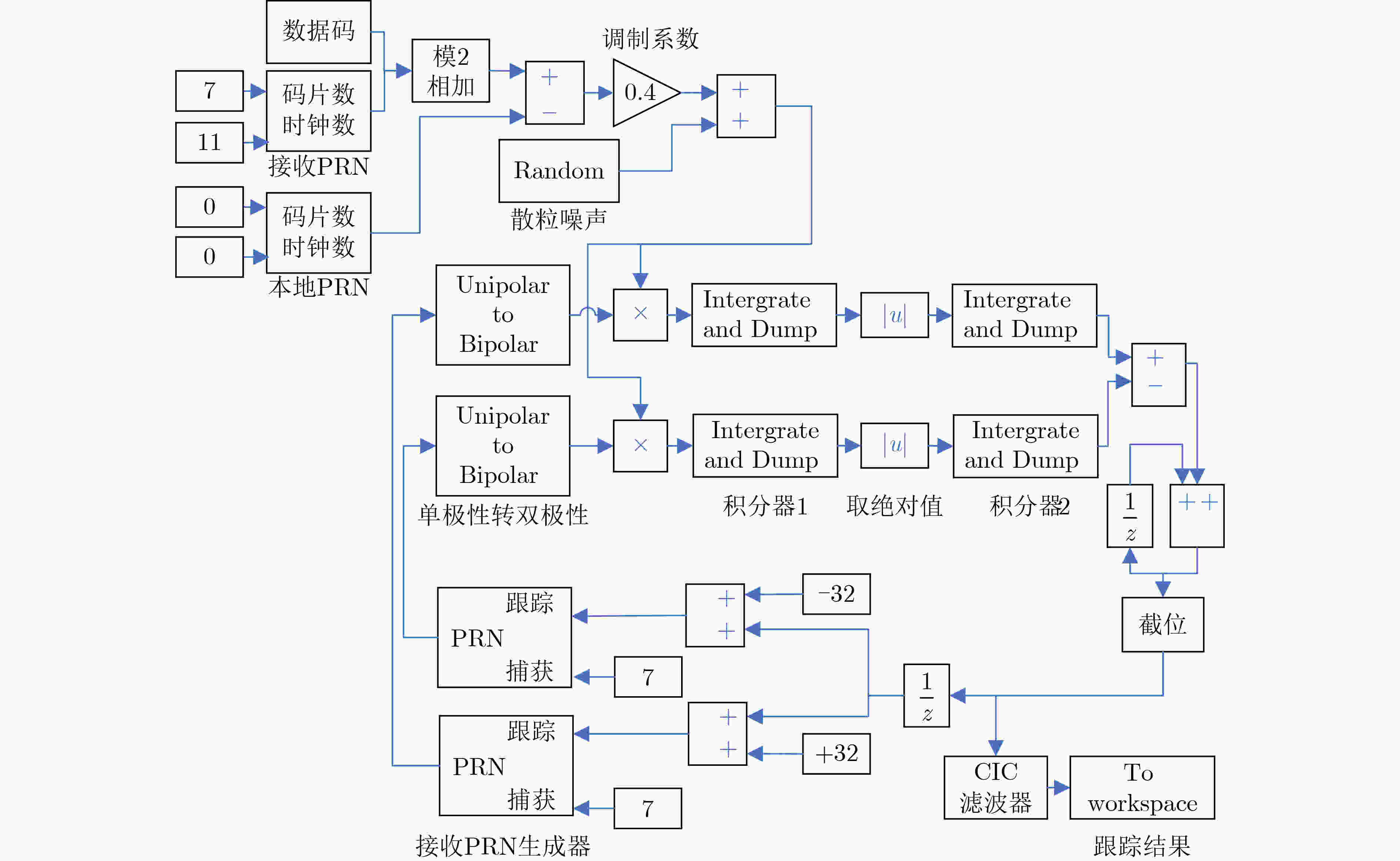


 下载:
下载:
