Multi-dimensional Performance Adaptive Content Caching in Mobile Networks Based on Meta Reinforcement Learning
-
摘要: 内容缓存技术被认为是提升移动网络服务性能的一种有效方法,其中缓存策略至关重要。为了提高缓存策略对用户动态业务性能需求的适应性,该文提出一种具备多维性能自适应能力的内容缓存策略。在该策略中,通过对传输时延效率、缓存命中率和缓存冗余指数多维指标进行建模,构造内容缓存联合优化问题,并设置动态加权参数模拟实际环境中用户业务性能需求的动态性。考虑到优化目标因用户需求动态变化导致的参数不确定性和动态性,该文引入了元强化学习算法(MAML-DDPG)以解决多目标动态优化问题,使缓存决策能够快速适应随时间变化的优化目标。在仿真实验中,评估了内容缓存策略对动态性能目标的适应能力,同时将所提策略与现有策略进行了多个维度的性能对比。实验结果表明,所提方案既能快速适应动态优化目标,又能保持良好的综合缓存性能。Abstract:
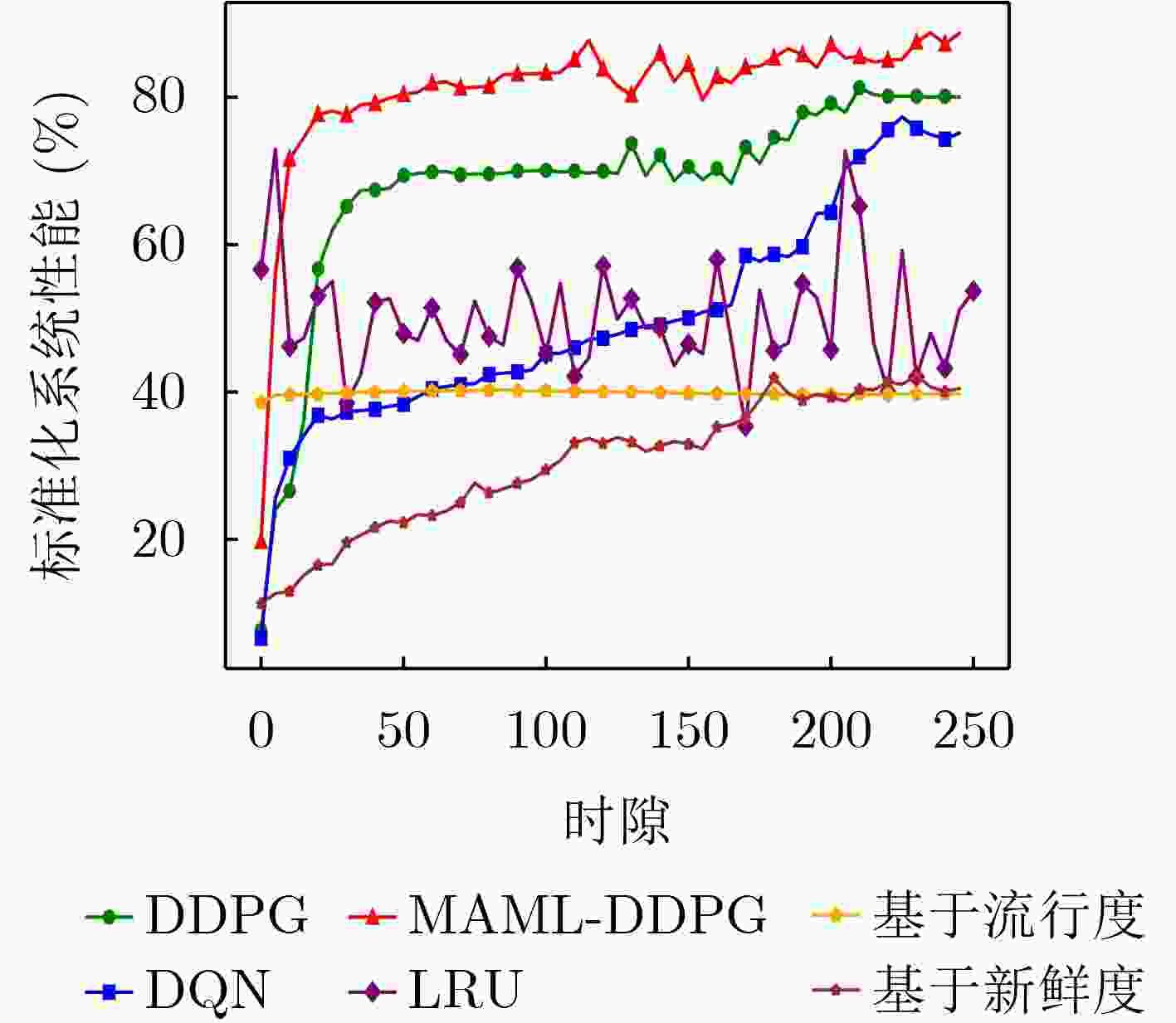
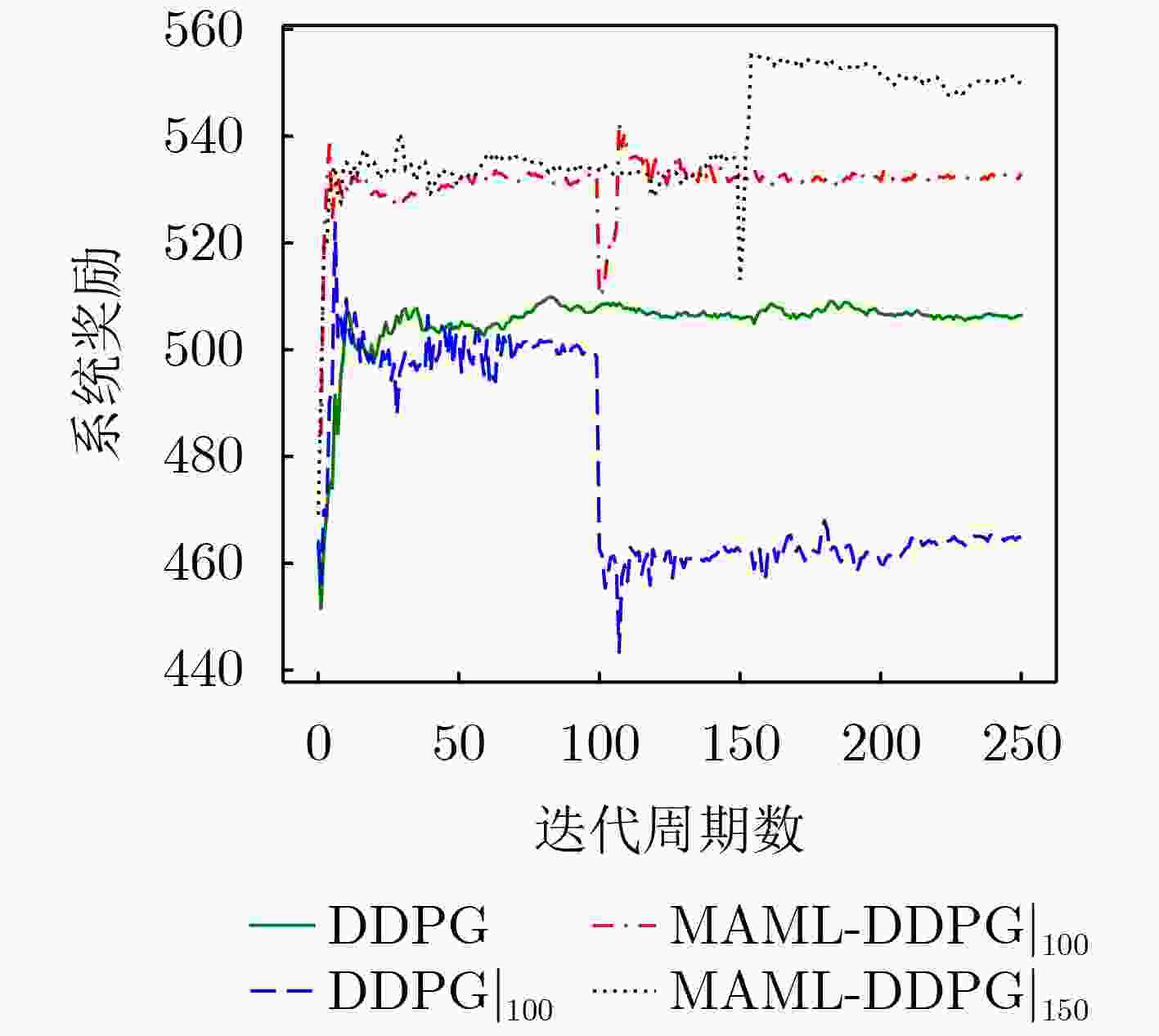
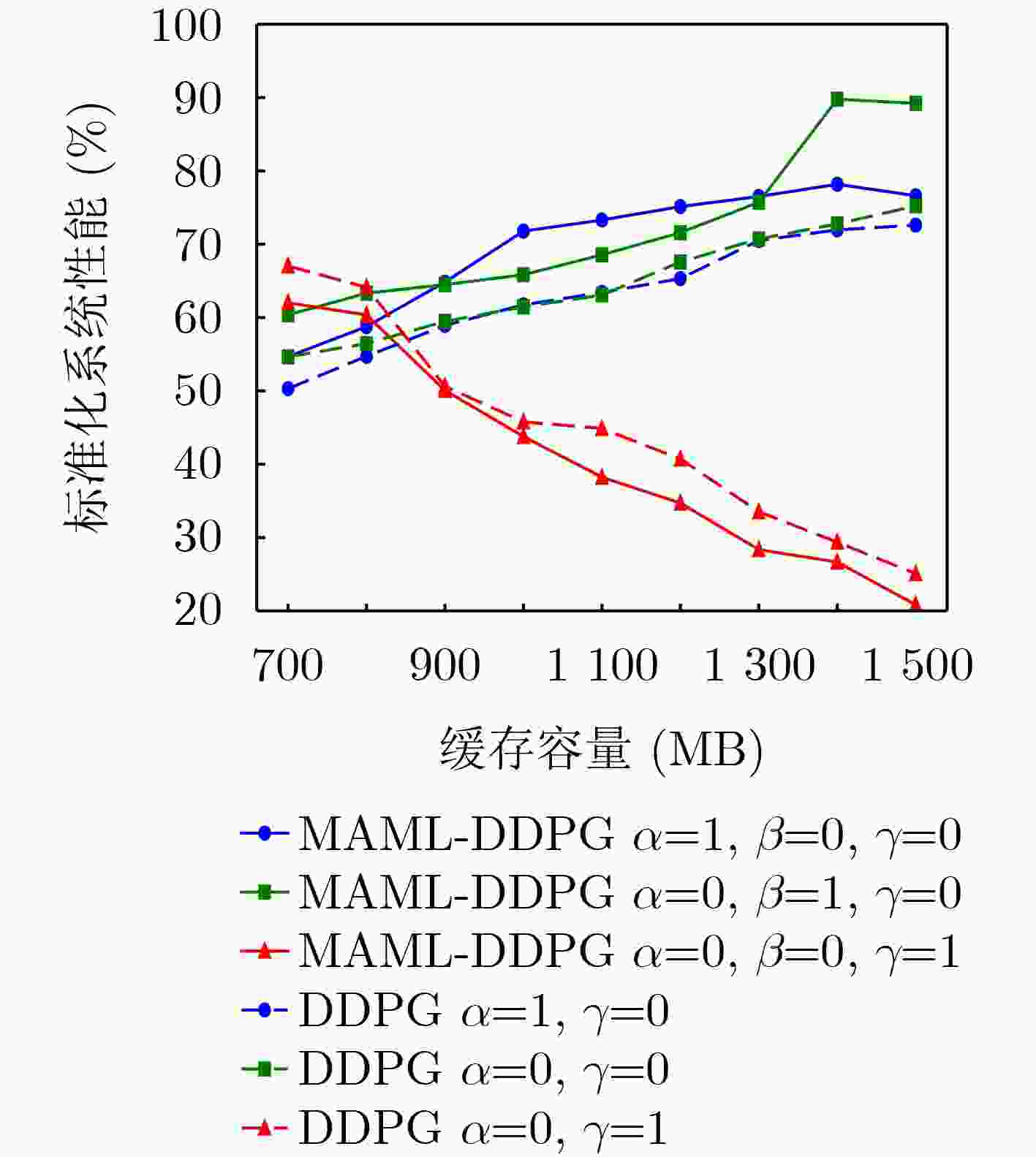
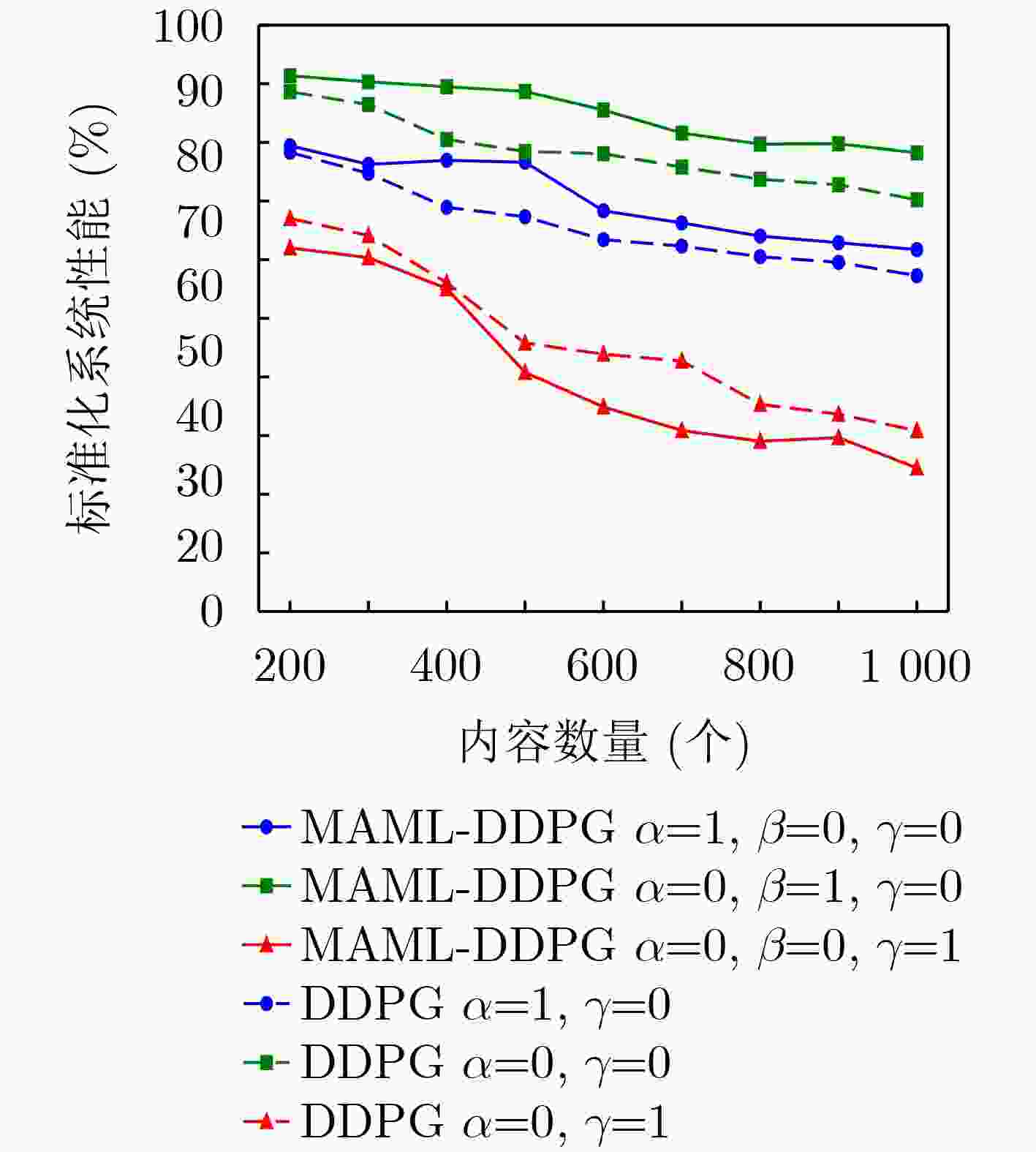
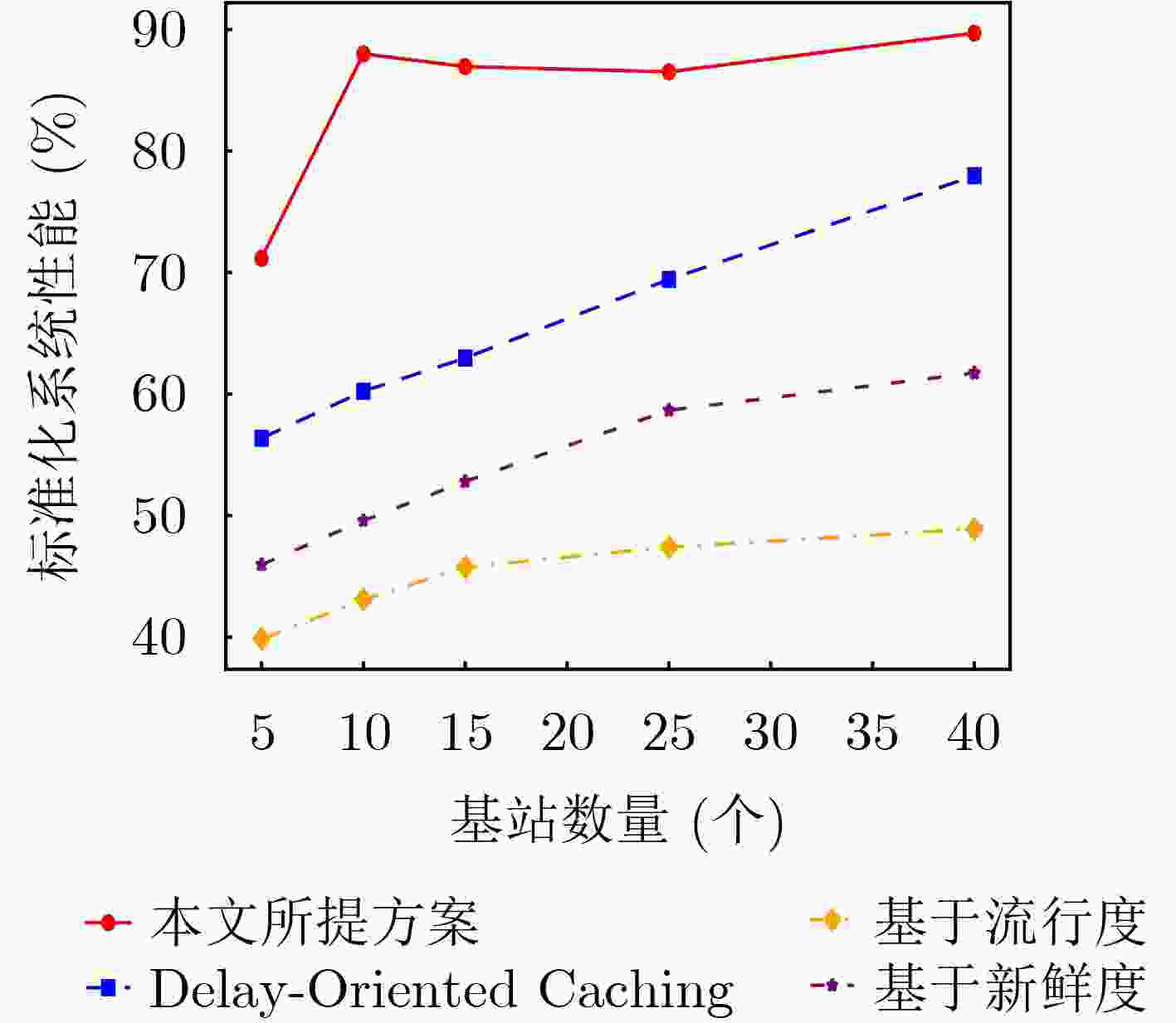
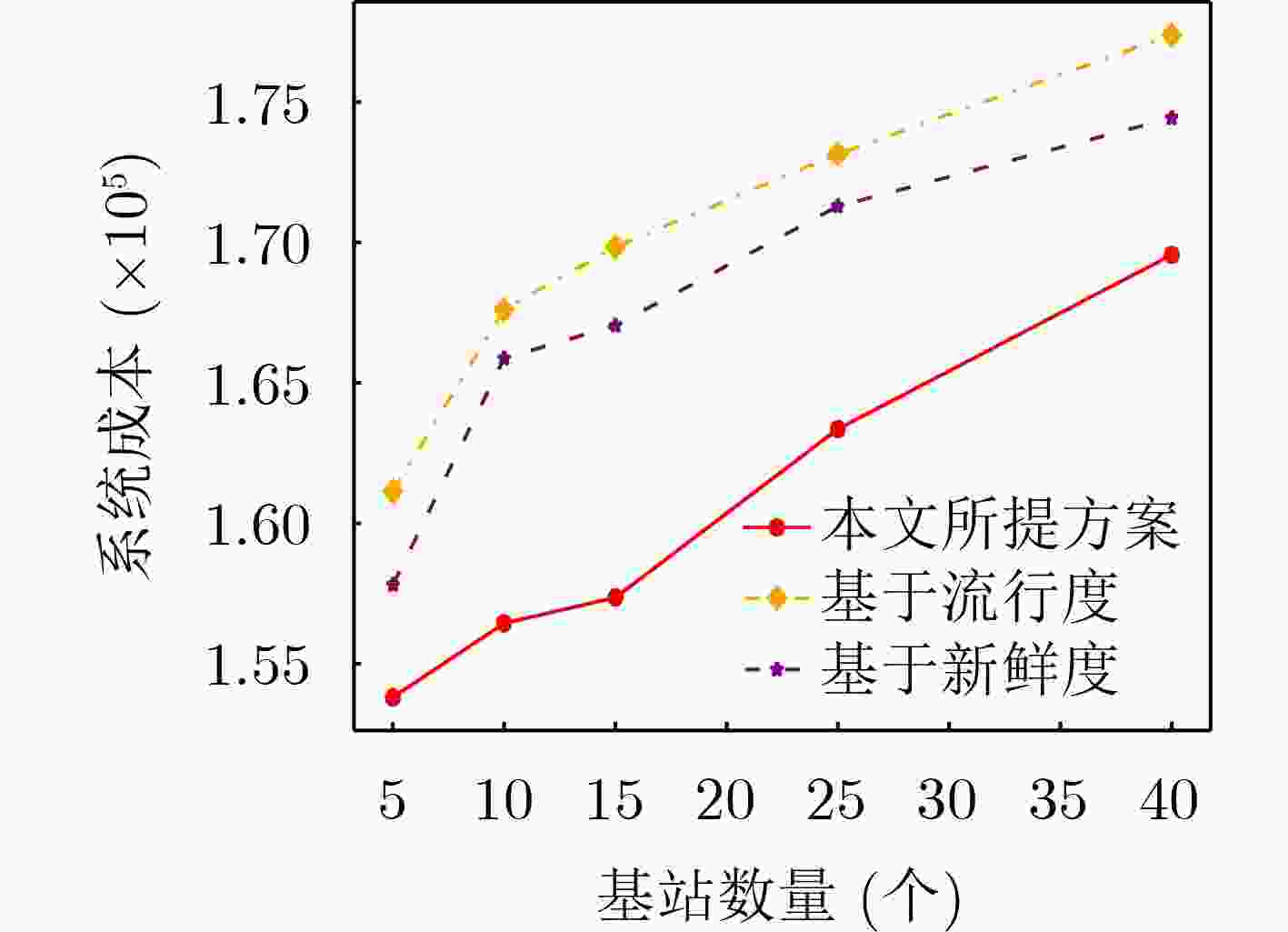
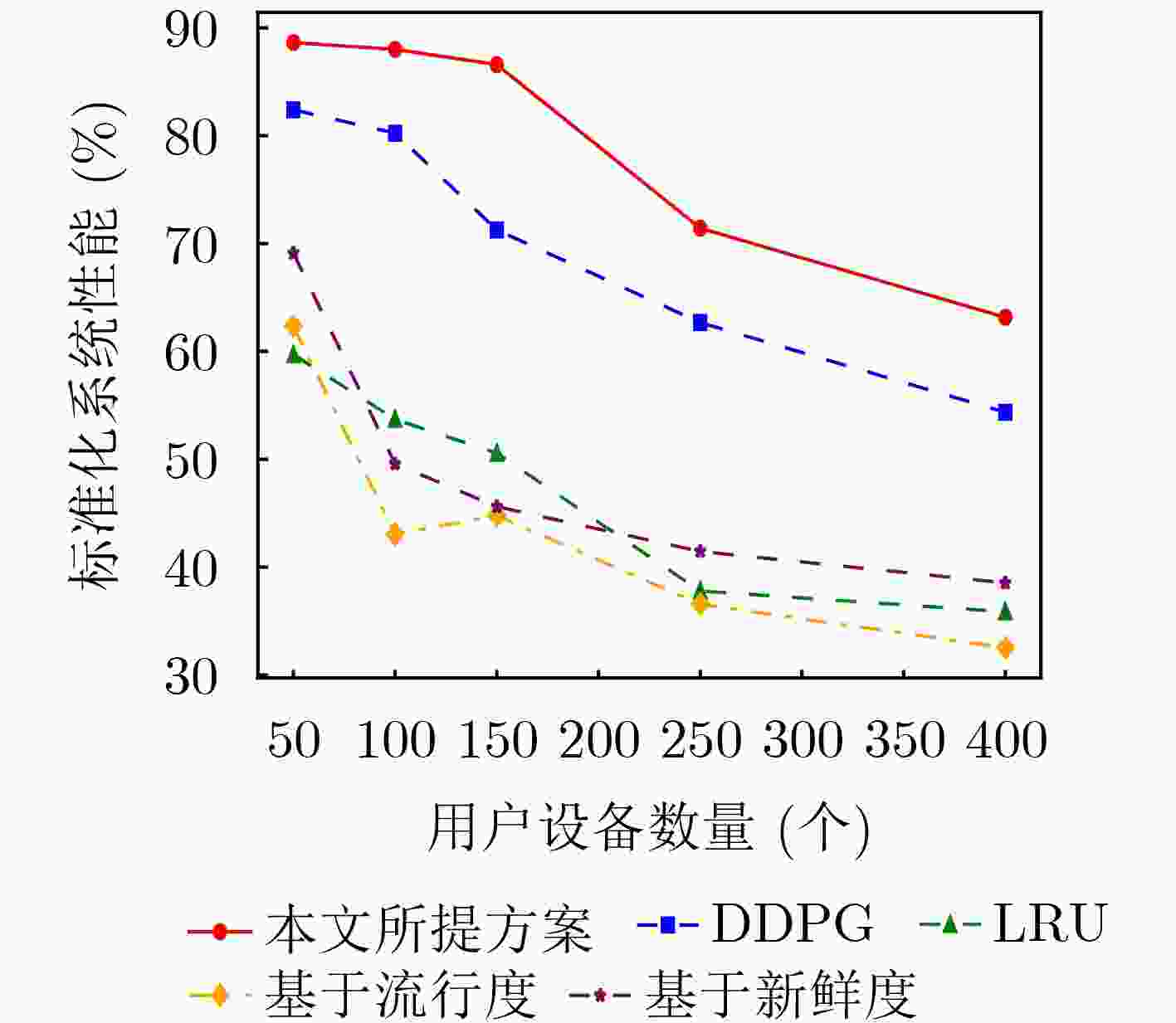
Objective Content caching enhances the efficiency of video services in mobile networks. However, most existing studies optimize caching strategies for a single performance objective, overlooking their combined effect on key metrics such as content delivery latency, cache hit rate, and redundancy rate. An effective caching strategy must simultaneously satisfy multiple performance requirements and adapt to their dynamic changes over time. This study addresses these limitations by investigating the joint optimization of content delivery latency, cache hit rate, and redundancy rate. To capture the interdependencies and temporal variations among these metrics, a meta-reinforcement learning-based caching decision algorithm is proposed. Built on conventional reinforcement learning frameworks, the proposed method enables adaptive optimization across multiple performance dimensions, supporting a dynamic and balanced content caching strategy. Methods To address the multi-dimensional objectives of content caching, namely, content delivery latency, cache hit rate, and redundancy rate, this study proposes a performance-aware adaptive caching strategy. Given the uncertainty and temporal variability of interrelationships among performance metrics in real-world environments, dynamic correlation parameters are introduced to simulate the evolving behavior of these metrics. The caching problem is formulated as a dynamic joint optimization task involving delivery latency efficiency, cache hit rate, and a cache redundancy index. This problem is further modeled as a Markov Decision Process (MDP), where the state comprises the content popularity distribution and the caching state from the previous time slot; the action represents the caching decision at the current time slot. The reward function is defined as a cumulative metric that integrates dynamic correlation parameters across latency, hit rate, and redundancy. To solve the MDP, a Model-Agnostic Meta-Reinforcement Learning Algorithm (MAML-DDPG) is proposed. This algorithm reformulates the joint optimization task as a multi-task reinforcement learning problem, enabling adaptation to dynamically changing optimization targets and improving decision-making efficiency. Results and Discussions This study compares the performance of MAML-DDPG with baseline algorithms under a gradually changing Zipf parameter (0.5 to 1.5). Results show that MAML-DDPG maintains more stable system performance throughout the change, indicating superior adaptability. The algorithm’s response to abrupt shifts in optimization objectives is further evaluated by modifying weight parameters during training. Specifically, the experiments include comparisons among DDPG, $ {\mathrm{D}\mathrm{D}\mathrm{P}\mathrm{G}|}_{100} $, $ \mathrm{M}\mathrm{A}\mathrm{M}\mathrm{L}{-\mathrm{D}\mathrm{D}\mathrm{P}\mathrm{G}|}_{100} $, and $ \mathrm{M}\mathrm{A}\mathrm{M}\mathrm{L}{-\mathrm{D}\mathrm{D}\mathrm{P}\mathrm{G}|}_{150} $, where $ {\mathrm{D}\mathrm{D}\mathrm{P}\mathrm{G}|}_{100} $ denotes a change in weight parameters at the 100th training cycle to simulate task mutation. Results show that the DDPG model exhibits a sharp drop in convergence value following the change and stabilizes at a lower performance level. In contrast, MAML-DDPG, although initially affected by the shift, recovers rapidly due to its meta-learning capability and ultimately converges to a higher-performing caching strategy. Conclusions This study addresses the content caching problem in mobile edge networks by formulating it as a joint optimization task involving cache hit rate, cache redundancy index, and delivery latency efficiency. To handle the dynamic uncertainty associated with these performance metrics, a MAML-DDPG is proposed. The algorithm enables rapid adaptation to changing optimization targets, improving decision-making efficiency. Simulation results confirm that MAML-DDPG effectively adapts to dynamic performance objectives and outperforms existing methods across multiple caching metrics. The findings demonstrate the algorithm’s capability to meet evolving performance requirements while maintaining strong overall performance. -
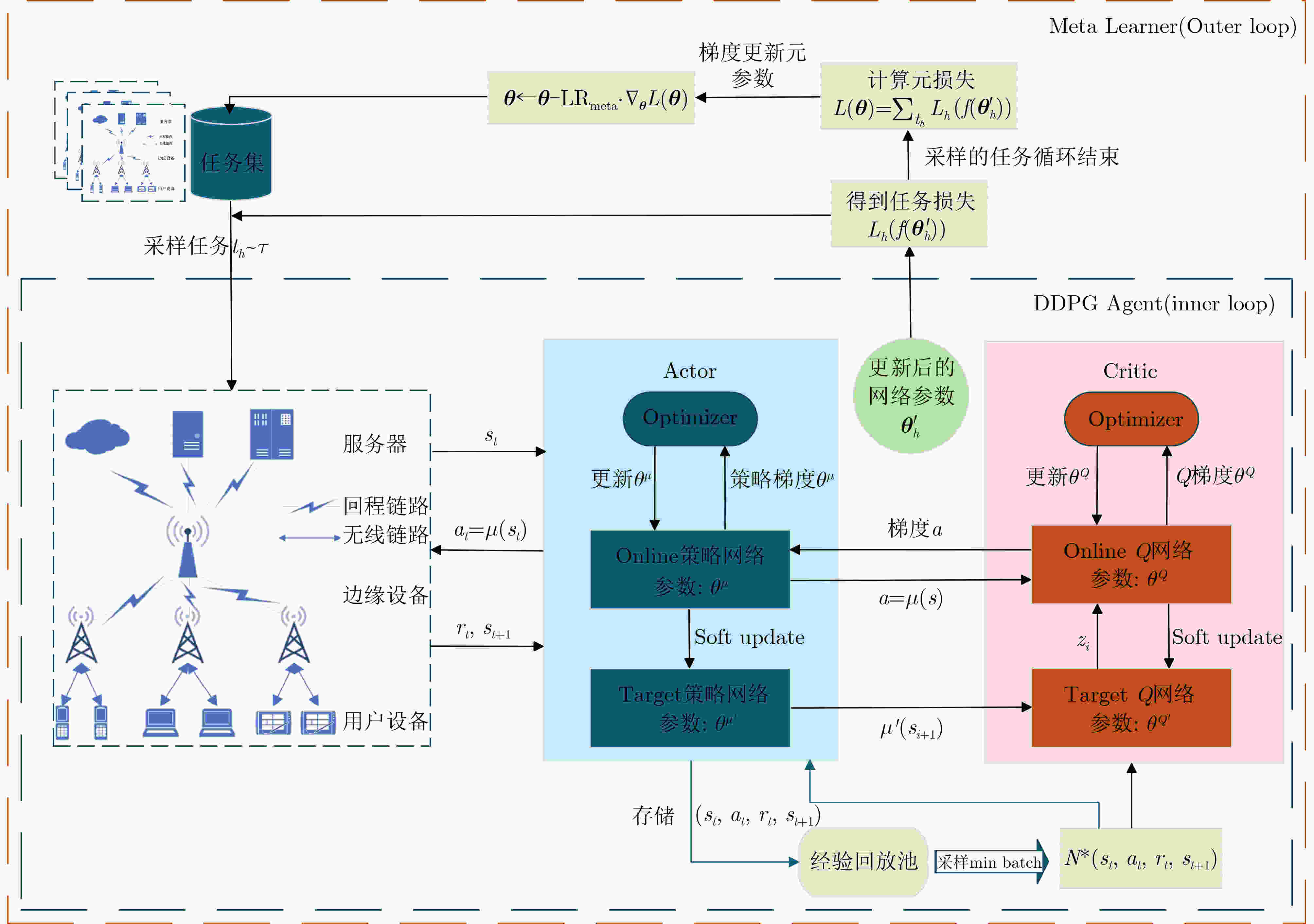
1 MAML-DDPG算法
(1) 初始化Actor和Critic网络参数:$ {\theta }^{\mu } $和$ {\theta }^{Q} $,及其对应的目标网络参数:$ {{\boldsymbol{\theta}} }^{{{{Q}}}^{{'}}}\leftarrow {{\boldsymbol{\theta}} }^{{{Q}}} $, $ {{\boldsymbol{\theta}} }^{{{\boldsymbol{\mu}} }^{{'}}}\leftarrow {{\boldsymbol{\theta}} }^{{\boldsymbol{\mu}} } $ (2) 初始化模型系数${\boldsymbol{ \phi }}=\left\{\alpha ,\beta ,\gamma \right\} $,任务集$ {{\tau}} $ (3) 采样任务批次$ {{{t}}}_{h}{\text{~}}{{\tau}} $ (4) 循环每个任务$ {{{t}}}_{{{h}}} $ (5) 根据s和Actor网络,得到动作a (6) 执行a,得到新状态$ {s}^{{'}} $和奖励r (7) 将元组$ \left(s,a,r,{s}^{{'}}\right) $存储到轨迹J中 (8) 使用$ f\left(\theta \right) $从缓存环境中采样K条轨迹$ J=\left\{\left({s}_{1},{a}_{1},\cdots ,{a}_{K}\right)\right\} $ (9) 根据式(14)计算$ {\nabla }_{{\boldsymbol{\theta}} }{L}_{{\boldsymbol{\theta}} }\left(f\left({\boldsymbol{\theta}} \right)\right) $ (10) 根据式(15)的梯度下降法更新参数 (11) 使用更新后的参数$ f\left({{\boldsymbol{\theta }}}_{h}^{{'}}\right) $再次采样K条轨迹$ {J}_{h}^{{'}}=\left\{\left({s}_{1},{a}_{1},\cdots ,{a}_{K}\right)\right\} $ (12) 根据式(14)计算损失$ {L}_{h}\left(f\left({{\boldsymbol{\theta}} }^{{'}}\right)\right) $ (13) 结束循环 (14) 由式(16)得到元损失$ L\left({\boldsymbol{\theta}} \right) $ (15) 根据式(14),使用每个$ {J}_{h}^{{'}} $和$ L\left({\boldsymbol{\theta}} \right) $和梯度更新元参数:${\boldsymbol{ \theta}} \leftarrow {\boldsymbol{\theta}} -{\mathrm{L}\mathrm{R}}_{\mathrm{m}\mathrm{e}\mathrm{t}\mathrm{a}}\cdot \nabla_{\theta }L\left({\boldsymbol{\theta}} \right) $ (16) 循环每个训练周期 (17) 获取当前模型系数$ {\phi }_{t} $并更新基站状态s (18) 如果$ {\phi }_{t}\ne {\phi }_{t-1} $ (19) 则构建目标任务$ {{{t}}}_{{{h}}} $,并将其记录至任务集$ \tau $,然后跳转至步骤(3)继续执行 (20) 否则,由$ {{{s}}}_{{{t}}} $和Actor网络得到$ {{{a}}}_{{{t}}} $,执行$ {{{a}}}_{{{t}}} $得到$ {s}_{t+1} $和$ {{\boldsymbol{r}}}_{{\boldsymbol{t}}} $并将元组$ \left({s}_{t},{a}_{t},{s}^{{'}},{r}_{t}\right) $存储到经验池D (21) 从D中采样并根据公式(14)计算$ {L}_{h}\left({\boldsymbol{\theta}} \right) $ (22) 根据式(15)更新网络参数 (23) 结束循环 -
[1] FU Yaru, LIU Jianqing, KE Junming, et al. Optimal and suboptimal dynamic cache update algorithms for wireless cellular networks[J]. IEEE Wireless Communications Letters, 2022, 11(12): 2610–2614. doi: 10.1109/LWC.2022.3211962. [2] LI Dongyang, ZHANG Haixia, DING Hui, et al. User-preference-learning-based proactive edge caching for D2D-assisted wireless networks[J]. IEEE Internet of Things Journal, 2023, 10(13): 11922–11937. doi: 10.1109/JIOT.2023.3244621. [3] LIN Peng, NING Zhaolong, ZHANG Zhizhong, et al. Joint optimization of preference-aware caching and content migration in cost-efficient mobile edge networks[J]. IEEE Transactions on Wireless Communications, 2024, 23(5): 4918–4931. doi: 10.1109/TWC.2023.3323464. [4] ZHANG Wanlu, LUO Jingjing, ZHENG Fuchun, et al. Decentralized collaborative caching in ultra-dense networks[J]. IEEE Wireless Communications Letters, 2024, 13(5): 1215–1219. doi: 10.1109/LWC.2024.3362595. [5] BATABYAL S. On the effect of redundant caching policy on multimedia streaming in D2D underlay network[C]. GLOBECOM 2023 - 2023 IEEE Global Communications Conference, Kuala Lumpur, Malaysia, 2023: 6747–6752. doi: 10.1109/GLOBECOM54140.2023.10437940. [6] LUONG N C, HOANG D T, GONG Shimin, et al. Applications of deep reinforcement learning in communications and networking: A survey[J]. IEEE Communications Surveys & Tutorials, 2019, 21(4): 3133–3174. doi: 10.1109/COMST.2019.2916583. [7] ZHOU Huan, WANG Zhenning, CHENG Nan, et al. Stackelberg-game-based computation offloading method in cloud–edge computing networks[J]. IEEE Internet of Things Journal, 2022, 9(17): 16510–16520. doi: 10.1109/JIOT.2022.3153089. [8] 陈祎鹏, 杨哲, 谷飞, 等. 一种基于博弈论的移动边缘计算资源分配策略[J]. 计算机科学, 2023, 50(2): 32–41. doi: 10.11896/jsjkx.220300198.CHEN Yipeng, YANG Zhe, GU Fei, et al. Resource allocation strategy based on game theory in mobile edge computing[J]. Computer Science, 2023, 50(2): 32–41. doi: 10.11896/jsjkx.220300198. [9] YAN Jia, BI Suzhi, DUAN Lingjie, et al. Pricing-driven service caching and task offloading in mobile edge computing[J]. IEEE Transactions on Wireless Communications, 2021, 20(7): 4495–4512. doi: 10.1109/TWC.2021.3059692. [10] SUN Mengying, XU Xiaodong, HUANG Yuzhen, et al. Resource management for computation offloading in D2D-aided wireless powered mobile-edge computing networks[J]. IEEE Internet of Things Journal, 2021, 8(10): 8005–8020. doi: 10.1109/JIOT.2020.3041673. [11] TENG Ziyi, FANG Juan, and LIU Yaqi. Combining Lyapunov optimization and deep reinforcement learning for D2D assisted heterogeneous collaborative edge caching[J]. IEEE Transactions on Network and Service Management, 2024, 21(3): 3236–3248. doi: 10.1109/TNSM.2024.3361796. [12] WU Pingyang, LI Jun, SHI Long, et al. Dynamic content update for wireless edge caching via deep reinforcement learning[J]. IEEE Communications Letters, 2019, 23(10): 1773–1777. doi: 10.1109/LCOMM.2019.2931688. [13] LIM J, KIM D, and YOO Y. Joint cache allocation and replacement for content-centric network-based private 5G networks: Deep reinforcement learning approach[J]. IEEE Access, 2024, 12: 56214–56225. doi: 10.1109/ACCESS.2024.3390429. [14] LIN Peng, LIU Yan, ZHANG Zhizhong, et al. Cost-aware task offloading and migration for wireless virtual reality using interactive A3C approach[J]. IEEE Transactions on Vehicular Technology, 2024, 73(7): 10850–10855. doi: 10.1109/TVT.2024.3374303. [15] TANG Ming and WONG V W S. Deep reinforcement learning for task offloading in mobile edge computing systems[J]. IEEE Transactions on Mobile Computing, 2022, 21(6): 1985–1997. doi: 10.1109/TMC.2020.3036871. -





 下载:
下载:


 下载:
下载:
