One-sided Personalized Differential Privacy Random Response Algorithm Driven by User Sensitive Weights
-
摘要: 单侧差分隐私机制具有敏感屏蔽特性,能确保攻击者无法显著降低其对记录敏感性的不确定性,但是该机制中的单侧差分隐私随机响应算法仅适用于敏感记录百分比较低的数据集。为克服上述算法在敏感记录百分比较高数据集中的局限性,该文提出一种新的算法——单侧个性化差分隐私随机响应算法。该算法引入敏感规范函数的定义,为不同用户的各项数据分别赋予不同的敏感级别,然后设计新的个性化采样方法,并基于用户数据权重值进行个性化采样和加噪处理。相对于单侧差分隐私随机响应算法,所提随机响应算法更细致地考虑到用户对不同数据的敏感程度。特别地,该文将综合权重值映射到需要添加的噪声量以满足严格的隐私保护要求。最后,在合成数据集和真实数据集上进行仿真实验,对比了单侧个性化差分隐私随机响应算法与现有的随机响应算法。实验结果表明,在不同的上限阈值下,所提算法不仅在敏感记录百分比较低时提供更优的数据效用,而且适用于敏感记录百分比较高的场景,并显著提高了查询结果的准确性和稳健性。Abstract:
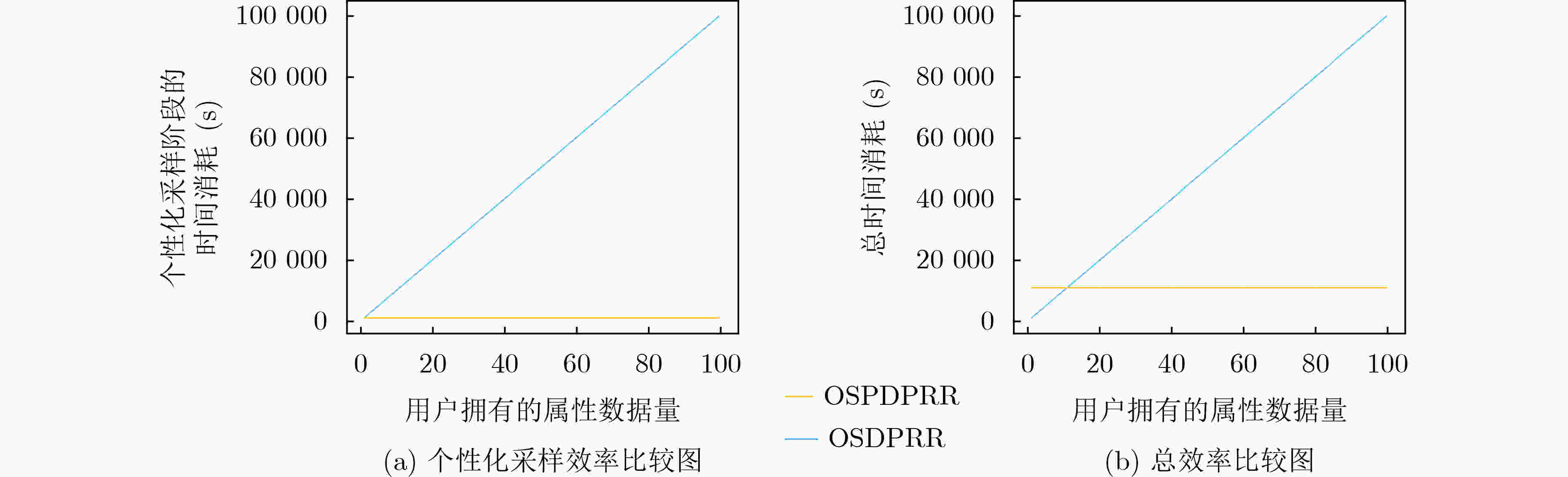
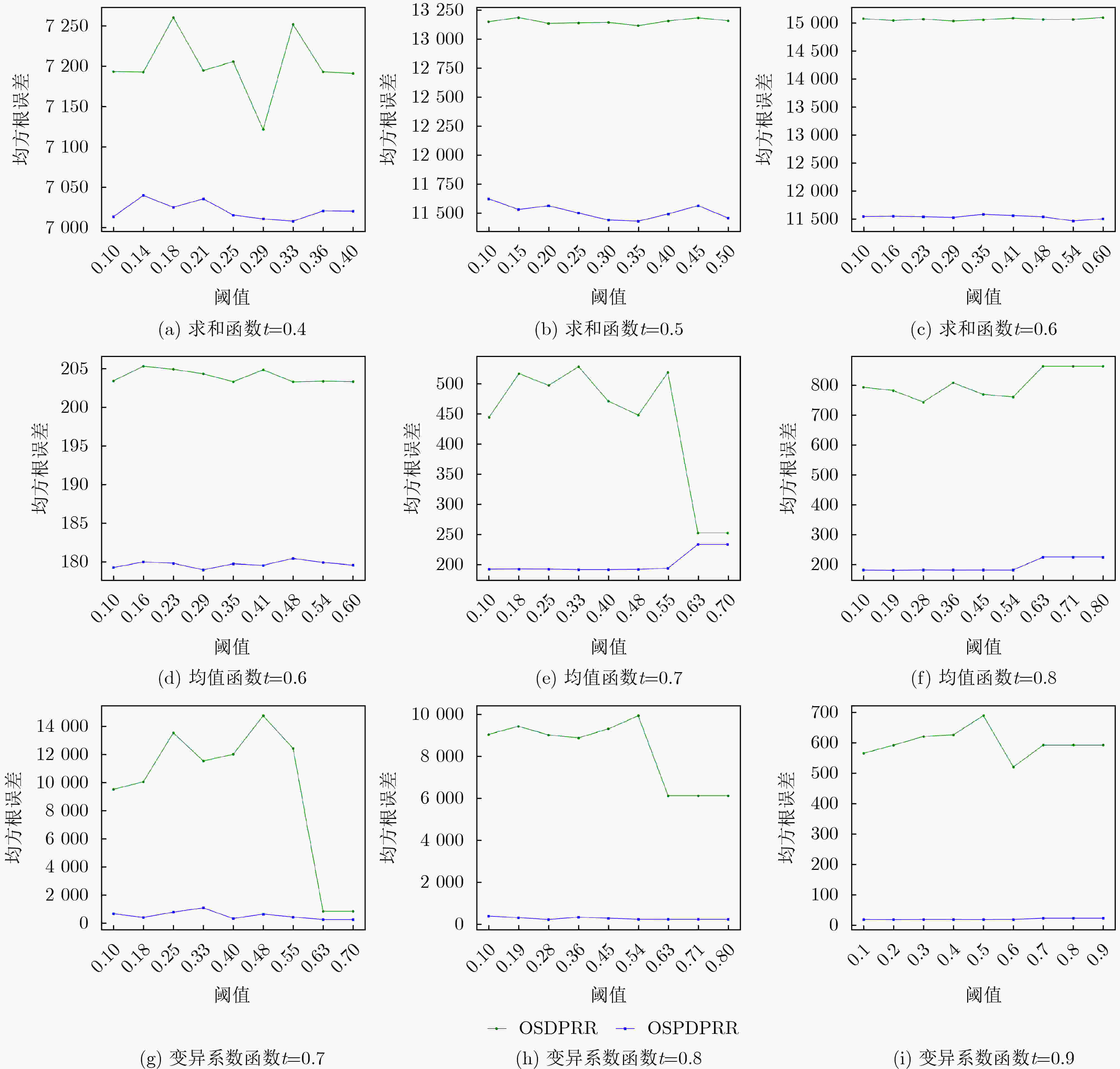
Objective One-sided differential privacy has received increasing attention in privacy protection due to its ability to shield sensitive information. This mechanism ensures that adversaries cannot substantially reduce uncertainty regarding record sensitivity, thereby enhancing privacy. However, its use in practical datasets remains constrained. Specifically, the random response algorithm under one-sided differential privacy performs effectively only when the proportion of sensitive records is low, but yields limited results in datasets with high sensitivity ratios. Examples include medical records, financial transactions, and personal data in social networks, where sensitivity levels are inherently high. Existing algorithms often fail to meet privacy protection requirements in such contexts. This study proposes an extension of the one-sided differential privacy random response algorithm by introducing user-sensitive weights. The method enables efficient processing of highly sensitive datasets while substantially improving data utility and maintaining privacy guarantees, supporting secure analysis and application of high-sensitivity data. Methods This study proposes a one-sided personalized differential privacy random response algorithm comprising three key stages: sensitivity specification, personalized sampling, and fixed-value noise addition. In the sensitivity specification stage, user data are mapped to sensitivity weight values using a predefined sensitivity function. This function reflects both the relative importance of each record to the user and its quantified sensitivity level. The resulting sensitivity weights are then normalized to compute a comprehensive sensitivity weight for each user. In the personalized sampling stage, the data sampling probability is adjusted dynamically according to the user’s comprehensive sensitivity weight. Unlike uniform-probability sampling employed in conventional methods, this personalized approach reduces sampling bias and improves data representativeness, thereby enhancing utility. In the fixed-value noise addition stage, the noise amount is determined in proportion to the comprehensive sensitivity weight. In high-sensitivity scenarios, a larger noise value is added to reinforce privacy protection; in low-sensitivity scenarios, the noise is reduced to preserve data availability. This adaptive mechanism allows the algorithm to balance privacy protection with utility across different application contexts. Results and Discussions The primary innovations of this study are reflected in three areas. First, a one-sided personalized differential privacy random response algorithm is proposed, incorporating a sensitivity specification function to allocate personalized sensitivity weights to user data. This design captures user-specific sensitivity requirements across data attributes and improves system efficiency by minimizing user interaction. Second, a personalized sampling method based on comprehensive sensitivity weights is developed to support fine-grained privacy protection. Compared with conventional approaches, this method dynamically adjusts sampling strategies in response to user-specific privacy preferences, thereby increasing data representativeness while maintaining privacy. Third, the algorithm’s sensitivity shielding property is established through theoretical analysis, and its effectiveness is validated via simulation experiments. The results show that the proposed algorithm outperforms the traditional one-sided differential privacy random response algorithm in both data utility and robustness. In high-sensitivity scenarios, improvements in query accuracy and robustness are particularly evident. When the data follow a Laplace distribution, for the sum function, the Root Mean Square Error (RMSE) produced by the proposed algorithm is approximately 76.67% of that generated by the traditional algorithm, with the threshold upper bound set to 0.6 ( Fig. 4(c) ). When the data follow a normal distribution, in the coefficient of variation function, the RMSE produced by the proposed algorithm remains below 200 regardless of whether the upper bound of the threshold t is 0.7, 0.8, or 0.9, while the RMSE of the traditional algorithm consistently exceeds 200 (Fig. 5(g,h,i) ). On real-world datasets, the proposed algorithm achieves higher data utility across all three evaluated functions compared with the traditional approach (Fig. 6 ).Conclusions The proposed one-sided personalized differential privacy random response algorithm achieves effective performance under an equivalent level of privacy protection. It is applicable not only in datasets with a low proportion of sensitive records but also in those with high sensitivity, such as healthcare and financial transaction data. By integrating sensitivity specification, personalized sampling, and fixed-value noise addition, the algorithm balances privacy protection with data utility in complex scenarios. This approach offers reliable technical support for the secure analysis and application of highly sensitive data. Future work may investigate the extension of this algorithm to scenarios involving correlated data in relational databases. -
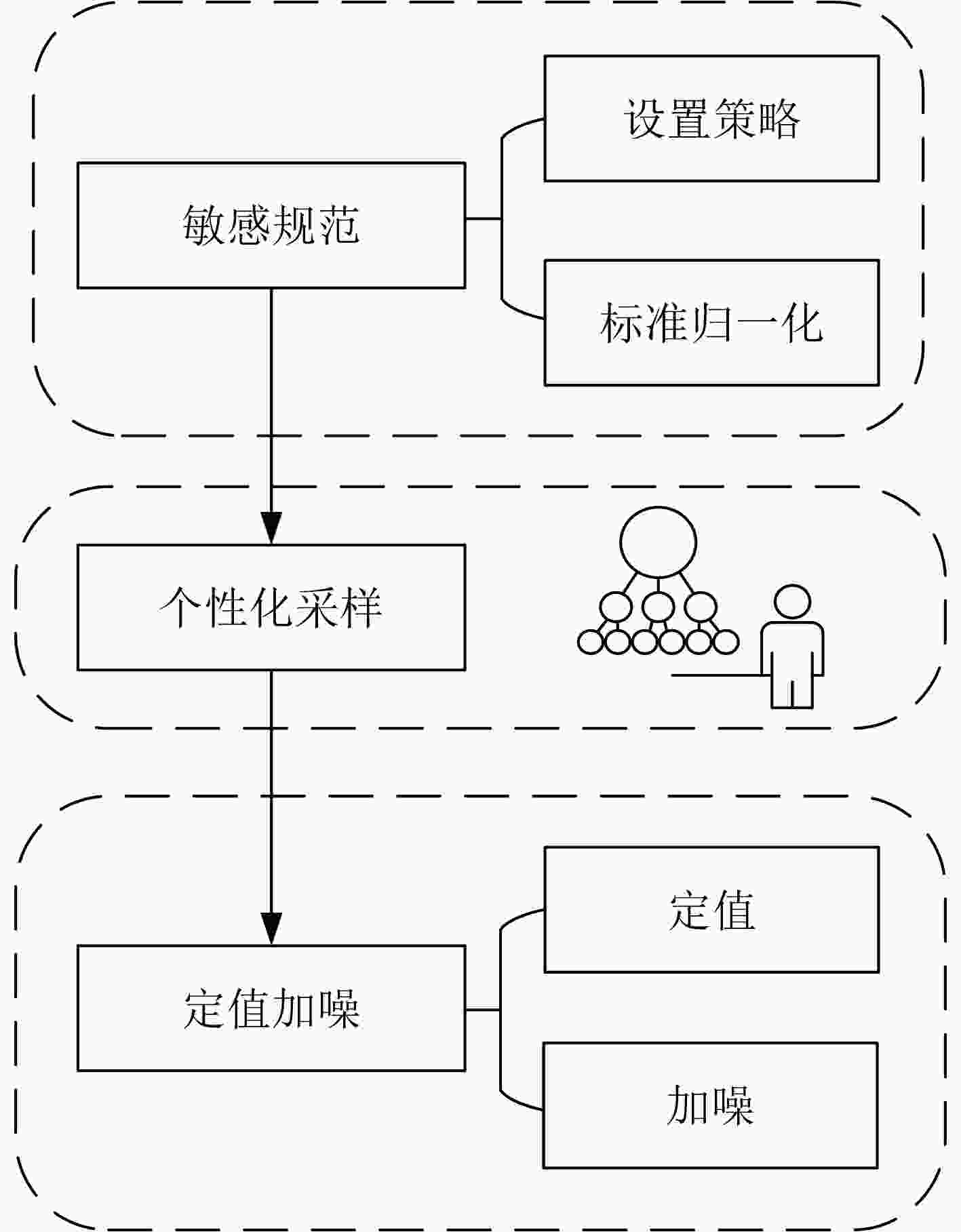
1 OSPDPRR算法.
输入:数据集$D$,拉普拉斯机制$\mathcal{M}$,用户集$U$,阈值$t$,查询函数${\boldsymbol{f}}$; 输出:扰动结果$\hat D$。 阶段1: (1) 对用户集$U$中的每个用户$u$,数据集$D$中的每条数据$x_i^u$,通过敏感规范函数$ S $计算出用户$u$的第$i$条数据的权重值$ w_i^u $。 (2) 将权重矩阵${\mathbf{w}}$进行标准归一化,计算得到标准权重矩阵${\mathbf{\bar w}}$。 (3) 计算正理想值${w^ + }$和负理想值${w^ - }$。 (4) 计算目标用户$u$到正理想值的距离$W_u^ + $和负理想值的距离$W_u^ - $。 (5) 计算每个用户$u$的综合权重值${M_u}$,得到综合权重值集合$C$。 阶段2: (6) 计算$A = \max C$, $B = \min C$。 (7) 计算每个用户$u$的采样概率${\pi _u}$,得到采样用户数据集$X$及采样用户的综合权重值集合$M$。 阶段3: (8) 通过方程$\varepsilon = {{\mathrm{e}}^m}$计算出隐私预算$\varepsilon $,其中$m$是集合$M$中的最小值。 (9) 定义$ {\Delta }{{\boldsymbol{f}}}=\underset{D={D}^{\prime }{\displaystyle \cup \left\{{X}_{u}\right\}},{X}_{u}\in D}{\max}\Vert {\boldsymbol{f}}(D)-{\boldsymbol{f}}({D}^{\prime })\Vert_l $,$D'$是数据集$D$的相邻数据集。 (10) 计算扰动结果$\hat D = f(D) + {\text{Lap}}(0,{{{\Delta {\boldsymbol{f}}}}}/{\varepsilon })$。 (11) 返回扰动结果$\hat D$。 -
[1] DWORK C. Differential privacy[C]. 33rd International Colloquium on Automata, Languages and Programming, Venice, Italy, 2006: 1–12. doi: 10.1007/11787006_1. [2] JORGENSEN Z, YU Ting, and CORMODE G. Conservative or liberal? Personalized differential privacy[C]. The 31st International Conference on Data Engineering, Seoul, Korea (South), 2015: 1023–1034. doi: 10.1109/ICDE.2015.7113353. [3] KOTSOGIANNIS I, DOUDALIS S, HANEY S, et al. One-sided differential privacy[C]. The 36th International Conference on Data Engineering, Dallas, USA, 2020: 493–504. doi: 10.1109/ICDE48307.2020.00049. [4] RATLIFF Z and VADHAN S. A framework for differential privacy against timing attacks[C]. ACM SIGSAC Conference on Computer and Communications Security, Salt Lake City, USA, 2024: 3615–3629. doi: 10.1145/3658644.3690206. [5] WANG Shiming, XIANG Liyao, CHENG Bowei, et al. Curator attack: When blackbox differential privacy auditing loses its power[C]. ACM SIGSAC Conference on Computer and Communications Security, Salt Lake City, USA, 2024: 3540–3554. doi: 10.1145/3658644.3690367. [6] LIU Junxu, LOU Jian, XIONG Li, et al. Cross-silo federated learning with record-level personalized differential privacy[C]. ACM SIGSAC Conference on Computer and Communications Security, Salt Lake City, 2024: 303–317. doi: 10.1145/3658644.3670351. [7] IMOLA J, CHOWDHURY A R, and CHAUDHURI K. Metric differential privacy at the user-level via the earth-mover’s distance[C]. ACM SIGSAC Conference on Computer and Communications Security, Salt Lake City, USA, 2024: 348–362. doi: 10.1145/3658644.3690363. [8] 魏立斐, 张无忌, 张蕾, 等. 基于本地差分隐私的异步横向联邦安全梯度聚合方案[J]. 电子与信息学报, 2024, 46(7): 3010–3018. doi: 10.11999/JEIT230923.WEI Lifei, ZHANG Wuji, ZHANG Lei, et al. A secure gradient aggregation scheme based on local differential privacy in asynchronous horizontal federated learning[J]. Journal of Electronics & Information Technology, 2024, 46(7): 3010–3018. doi: 10.11999/JEIT230923. [9] DU Minxin, YUE Xiang, CHOW S S M, et al. DP-Forward: Fine-tuning and inference on language models with differential privacy in forward pass[C]. ACM SIGSAC Conference on Computer and Communications Security, Copenhagen, Denmark, 2023: 2665–2679. doi: 10.1145/3576915.3616592. [10] DWORK C, KENTHAPADI K, MCSHERRY F, et al. Our data, ourselves: Privacy via distributed noise generation[C]. 25th International Conference on the Theory and Applications of Cryptographic Techniques, St. Petersburg, Russia, 2006: 486–503. doi: 10.1007/11761679_29. [11] GEHRKE J, HAY M, LUI E, et al. Crowd-blending privacy[C]. 32nd Annual Cryptology Conference on Advances in Cryptology, Santa Barbara, USA, 2012: 479–496. doi: 10.1007/978-3-642-32009-5_28. [12] YANG Bin, SATO I, and NAKAGAWA H. Bayesian differential privacy on correlated data[C]. ACM International Conference on Management of Data, Melbourne, Australia, 2015: 747–762. doi: 10.1145/2723372.2747643. [13] FU Yucheng and WANG Tianhao. Benchmarking secure sampling protocols for differential privacy[C]. ACM SIGSAC Conference on Computer and Communications Security, Salt Lake City, USA, 2024: 318–332. doi: 10.1145/3658644.3690257. [14] LU Mingjie and LIU Zhenhua. Improving accuracy of interactive queries in personalized differential privacy[C]. 6th International Conference on Frontiers in Cyber Security, Chengdu, China, 2024: 141–159. doi: 10.1007/978-981-99-9331-4_10. [15] NISSIM K, RASKHODNIKOVA S, and SMITH A. Smooth sensitivity and sampling in private data analysis[C]. Thirty-Ninth Annual ACM Symposium on Theory of Computing, San Diego, USA, 2007: 75–84. doi: 10.1145/1250790.1250803. [16] HUANG Wen, ZHOU Shijie, ZHU Tianqing, et al. Privately publishing internet of things data: Bring personalized sampling into differentially private mechanisms[J]. IEEE Internet of Things Journal, 2022, 9(1): 80–91. doi: 10.1109/JIOT.2021.3089518. [17] 朱友文, 王珂, 周玉倩. 一种满足个性化差分隐私的多方垂直划分数据合成机制[J]. 电子与信息学报, 2024, 46(5): 2159–2176. doi: 10.11999/JEIT231158.ZHU Youwen, WANG Ke, and ZHOU Yuqian. A multi-party vertically partitioned data synthesis mechanism with personalized differential privacy[J]. Journal of Electronics & Information Technology, 2024, 46(5): 2159–2176. doi: 10.11999/JEIT231158. [18] LIU Zhenhua, WANG Wenxin, LIANG Han, et al. Enhancing data utility in personalized differential privacy: A fine-grained processing approach[C]. Second International Conference on Data Security and Privacy Protection, Xi’an, China, 2025: 47–66. doi: 10.1007/978-981-97-8546-9_3. [19] LI Yijing, TAO Xiaofeng, ZHANG Xuefei, et al. Break the data barriers while keeping privacy: A graph differential privacy method[J]. IEEE Internet of Things Journal, 2023, 10(5): 3840–3850. doi: 10.1109/JIOT.2022.3151348. [20] LIU Jiandong, ZHANG Lan, LV Chaojie, et al. TPMDP: Threshold personalized multi-party differential privacy via optimal Gaussian mechanism[C]. 20th International Conference on Mobile Ad Hoc and Smart Systems, Toronto, Canada, 2023: 161–169. doi: 10.1109/MASS58611.2023.00027. [21] XU Chuan, DING Yingyi, CHEN Chao, et al. Personalized location privacy protection for location-based services in vehicular networks[J]. IEEE Transactions on Intelligent Transportation Systems, 2023, 24(1): 1163–1177. doi: 10.1109/TITS.2022.3182019. [22] ZHANG Mingyue, ZHOU Junlong, ZHANG Gongxuan, et al. APDP: Attribute-based personalized differential privacy data publishing scheme for social networks[J]. IEEE Transactions on Network Science and Engineering, 2023, 10(2): 922–933. doi: 10.1109/TNSE.2022.3224731. [23] GENG Quan, DING Wei, GUO Ruiqi, et al. Tight analysis of privacy and utility tradeoff in approximate differential privacy[C]. The 23rd International Conference on Artificial Intelligence and Statistics, Palermo, Italy, 2020: 89–99. [24] HUANG Wen, ZHOU Shijie, LIAO Yongjian, et al. Optimizing query times for multiple users scenario of differential privacy[J]. IEEE Access, 2019, 7: 183292–183299. doi: 10.1109/ACCESS.2019.2960283. [25] NIU Ben, CHEN Yahong, WANG Boyang, et al. AdaPDP: Adaptive personalized differential privacy[C]. IEEE Conference on Computer Communications, Vancouver, Canada, 2021: 1–10. doi: 10.1109/INFOCOM42981.2021.9488825. [26] HANEY S, MACHANAVAJJHALA A, and DING Bolin. Design of policy-aware differentially private algorithms[J]. Proceedings of the VLDB Endowment, 2015, 9(4): 264–275. doi: 10.14778/2856318.2856322. [27] BÖHLER J, BERNAU D, and KERSCHBAUM F. Privacy-preserving outlier detection for data streams[C]. 31st Annual IFIP WG 11.3 Conference on Data and Applications Security and Privacy XXXI, Philadelphia, USA, 2017: 225–238. doi: 10.1007/978-3-319-61176-1_12. [28] ASIF H, VAIDYA J, and PAPAKONSTANTINOU P A. Identifying anomalies while preserving privacy[J]. IEEE Transactions on Knowledge and Data Engineering, 2023, 35(12): 12264–12281. doi: 10.1109/TKDE.2021.3129633. [29] LI Xin, ZHU Hong, ZHANG Zhiqiang, et al. Item-oriented personalized LDP for discrete distribution estimation[C]. 28th European Symposium on Research in Computer Security, The Hague, The Netherlands, 2024: 446–466. doi: 10.1007/978-3-031-51476-0_22. [30] GOLDBERG A, FANTI G C, and SHAH N B. Batching of tasks by users of pseudonymous forums: Anonymity compromise and protection[J]. Proceedings of the ACM on Measurement and Analysis of Computing Systems, 2023, 7(1): 22. doi: 10.1145/3579335. [31] PAPPACHAN P, ZHANG Shufan, HE Xi, et al. Preventing inferences through data dependencies on sensitive data[J]. IEEE Transactions on Knowledge and Data Engineering, 2024, 36(10): 5308–5327. doi: 10.1109/TKDE.2023.3336630. [32] MCSHERRY F. Privacy integrated queries: An extensible platform for privacy-preserving data analysis[J]. Communications of the ACM, 2010, 53(9): 89–97. doi: 10.1145/1810891.1810916. [33] DWORK C, MCSHERRY F, NISSIM K, et al. Calibrating noise to sensitivity in private data analysis[C]. Third Theory of Cryptography Conference on Theory of Cryptography, New York, USA, 2006: 265–284. doi: 10.1007/11681878_14. [34] DEVAKUMAR K P. Data survey of COVID-19[EB/OL]. https://www.kaggle.com/datasets/imdevskp/corona-virus-report, 2024. -





 下载:
下载:





 下载:
下载:
