Multi-objective Remote Sensing Product Production Task Scheduling Algorithm Based on Double Deep Q-Network
-
摘要: 遥感产品的生产是一个涉及动态因素的多任务调度问题,任务之间存在资源竞争与冲突,且受生产环境实时变化的影响。如何实现自适应、多目标的高效调度成为问题关键。为此,该文创新性地提出一种基于双深度Q网络(DDQN)的多目标遥感产品生产任务调度算法(MORS),该方法可以有效降低遥感产品的生产时间,并实现节点资源的负载均衡。首先将多个产品输入处理单元生成相应的遥感算法,然后基于价值驱动的并行可执行筛选策略得到算法子集。在此基础上,设计一个能够感知遥感算法特征和节点特征的深度神经网络模型。通过综合遥感算法生产时间和节点资源状态设计奖励函数,采用DDQN算法训练模型,以确定待处理子集中每个遥感算法的最佳执行节点。在不同数量产品的仿真实验中,将MORS与先来先服务(FCFS)、轮询调度(RR)、遗传算法(GA)以及基于深度Q网络(DQN)的任务调度算法和基于双流深度Q网络(Dueling DQN)的任务调度算法进行全面对比。实验结果表明,MORS在遥感任务调度上相较于其它算法具有有效性和优越性。Abstract:
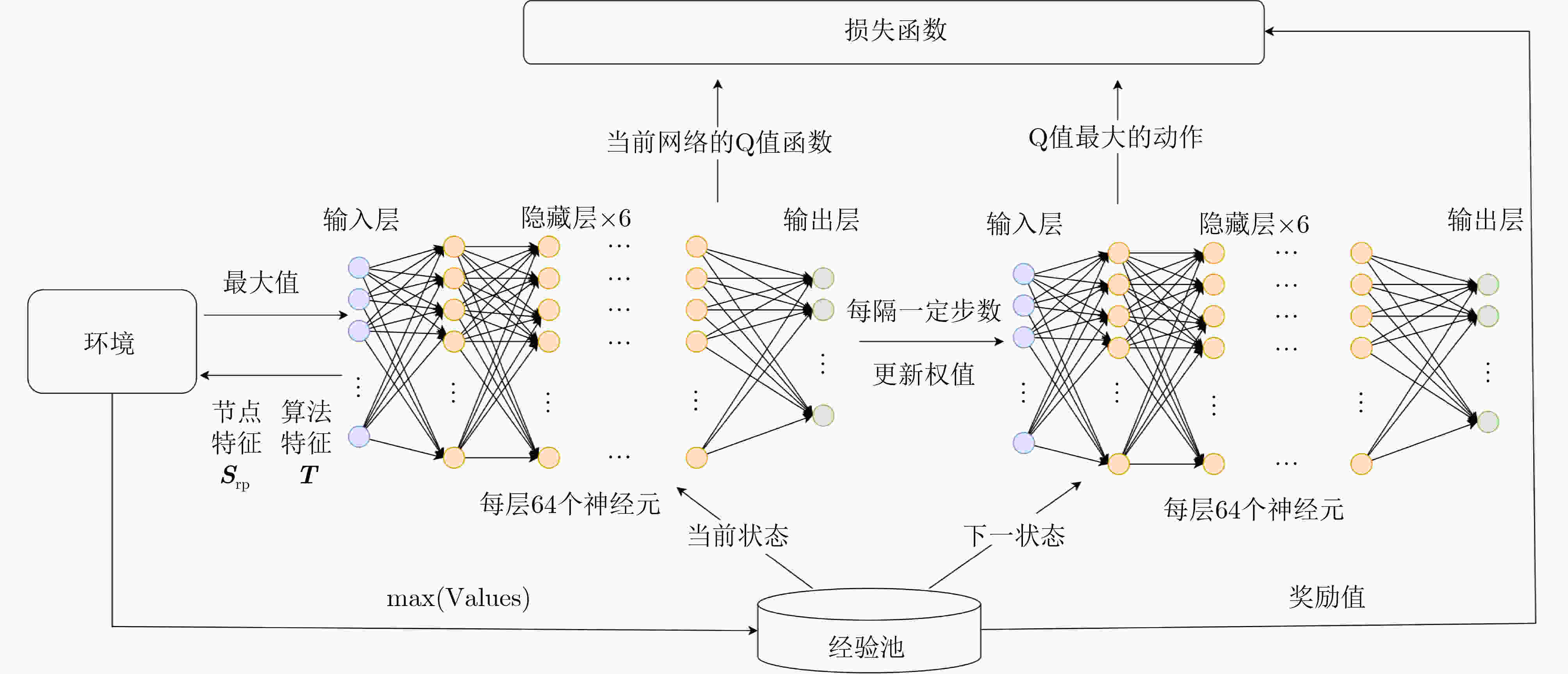
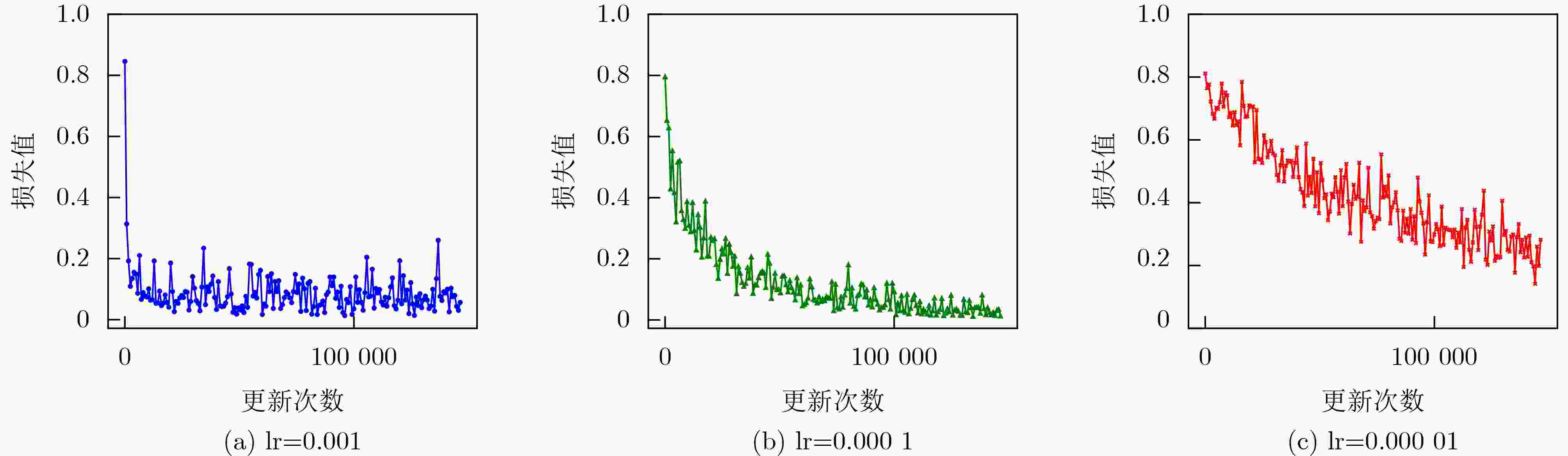
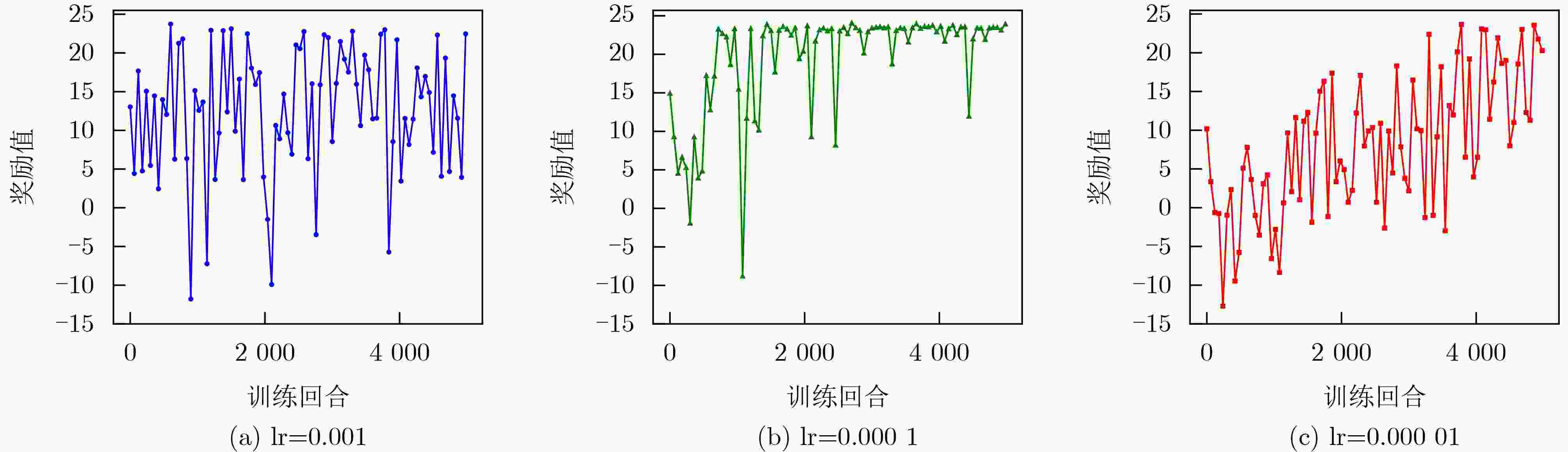
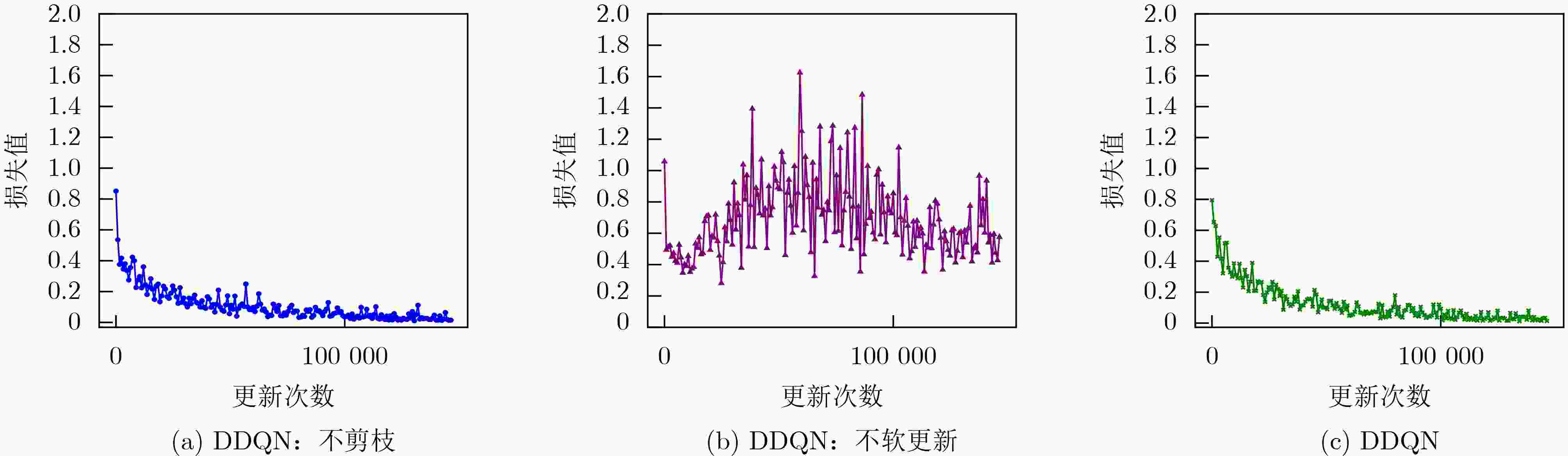
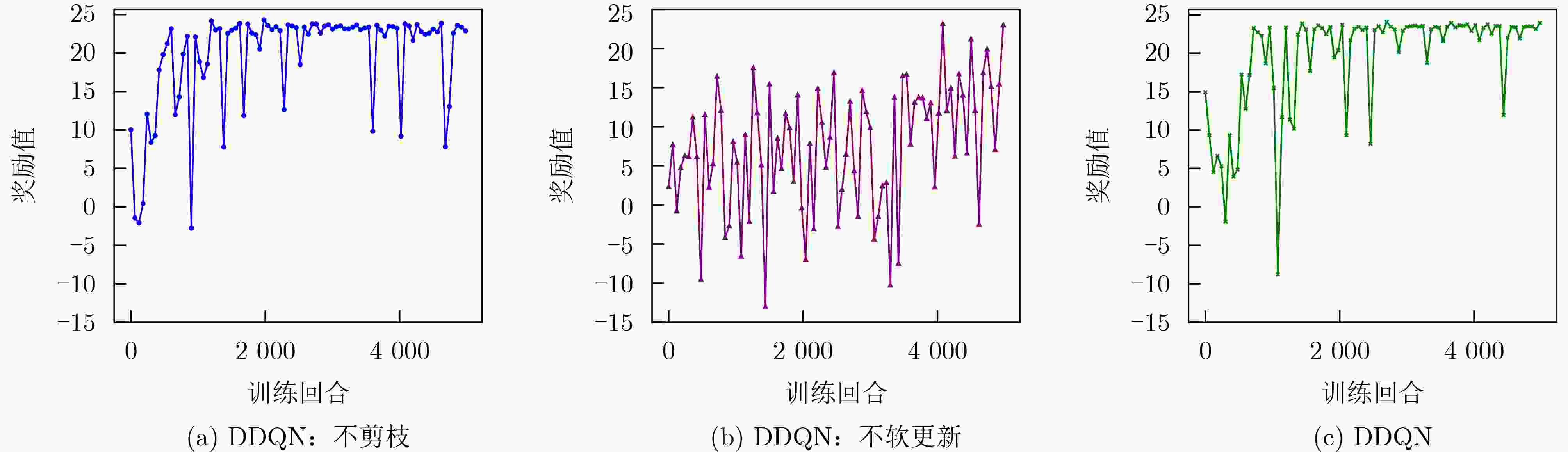
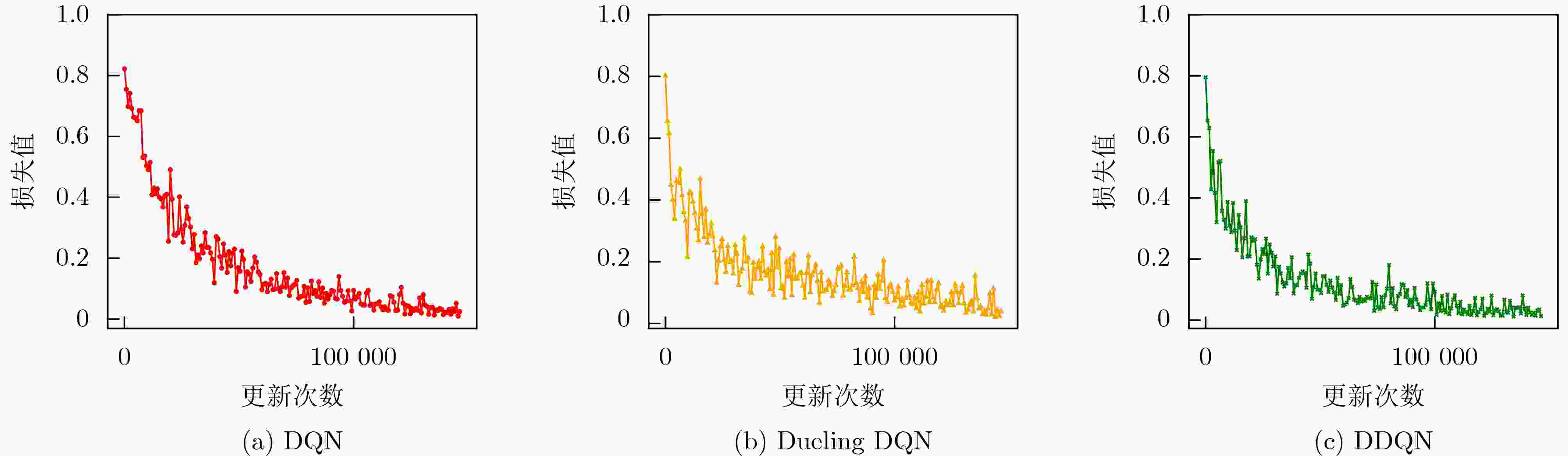
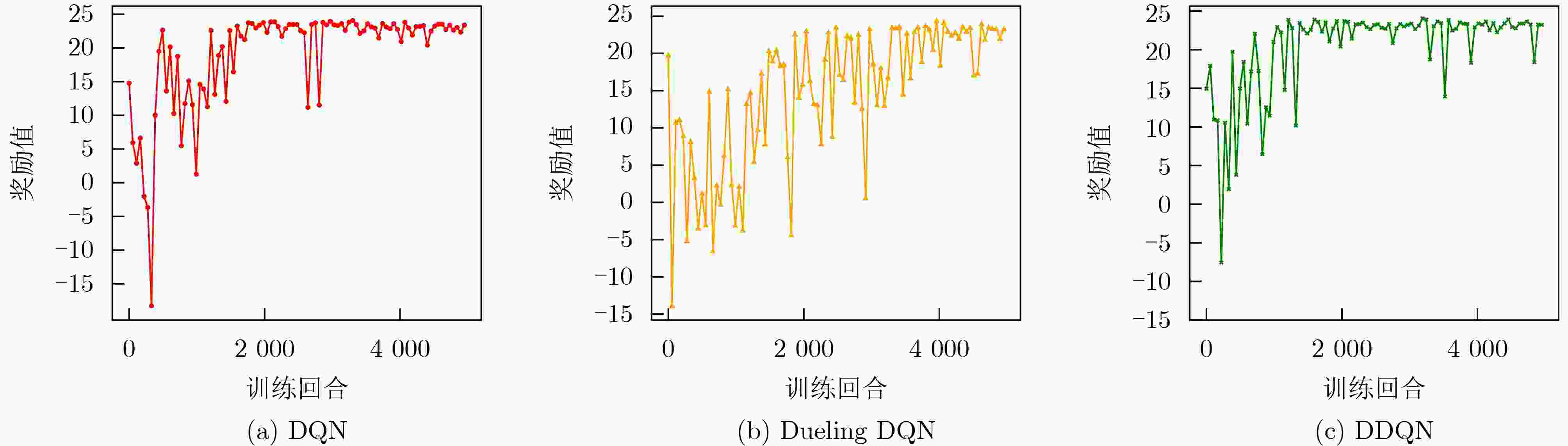
Objective Remote sensing product generation is a multi-task scheduling problem influenced by dynamic factors, including resource contention and real-time environmental changes. Achieving adaptive, multi-objective, and efficient scheduling remains a central challenge. To address this, a Multi-Objective Remote Sensing scheduling algorithm (MORS) based on a Double Deep Q-Network (DDQN) is proposed. A subset of candidate algorithms is first identified using a value-driven, parallel-executable screening strategy. A deep neural network is then designed to perceive the characteristics of both remote sensing algorithms and computational nodes. A reward function is constructed by integrating algorithm execution time and node resource status. The DDQN is employed to train the model to select optimal execution nodes for each algorithm in the processing subset. This approach reduces production time and enables load balancing across computational nodes. Methods The MORS scheduling process comprises two stages: remote sensing product processing and screening, followed by scheduling model training and execution. A time-triggered strategy is adopted, whereby all newly arrived remote sensing products within a predefined time window are collected and placed in a task queue. For efficient scheduling, each product is parsed into a set of executable remote sensing algorithms. Based on the model illustrated in Figure 2 , the processing unit extracts all constituent algorithms to form an algorithm set. An optimal subset is then selected using a value-driven parallel-executable screening strategy. The scheduling process is modeled as a Markov decision process, and the DDQN is applied to assign each algorithm in the selected subset to the optimal virtual node.Results and Discussions Simulation experiments use varying numbers of tasks and nodes to evaluate the performance of MORS. Comparative analyses are conducted against several baseline scheduling algorithms, including First-Come, First-Served (FCFS), Round Robin (RR), Genetic Algorithm (GA), Deep Q-Network (DQN), and Dueling Deep Q-Network (Dueling DQN). The results demonstrate that MORS outperforms all other algorithms in terms of scheduling efficiency and adaptability in remote sensing task scheduling. The learning rate, a critical hyperparameter in DDQN, influences the step size for parameter updates during training. When the learning rate is set to 0.00001 , the model fails to converge even after 5,000 iterations due to extremely slow optimization. A learning rate of0.0001 achieves a balance between convergence speed and training stability, avoiding oscillations associated with overly large learning rates (Figure 3 andFigure 4 ). The corresponding DDQN loss values show a steady decline, reflecting effective optimization and gradual convergence. In contrast, the unpruned DDQN initially declines sharply but plateaus prematurely, failing to reach optimal convergence. DDQN without soft updates shows large fluctuations in loss and remains unstable during later training stages, indicating that the absence of soft updates impairs convergence (Figure 5 ). Regarding decision quality, the reward values of DDQN gradually approach 25 in the later training stages, reflecting stable convergence and strong decision-making performance. Conversely, DDQN models without pruning or soft updates display unstable reward trajectories, particularly the latter, which exhibits pronounced reward fluctuations and slower convergence (Figure 6 ). A comparison of DQN, Dueling DQN, and DDQN reveals that all three show decreasing training loss, suggesting continuous optimization (Figure 7 ). However, the reward curve of Dueling DQN shows higher volatility and reduced stability (Figure 8 ). To further assess scalability, four sets of simulation experiments use 30, 60, 90, and 120 remote sensing tasks, with the number of virtual machine nodes fixed at 15. Each experimental configuration is evaluated using 100 Monte Carlo iterations to ensure statistical robustness. DDQN consistently shows superior performance under high-concurrency conditions, effectively managing increased scheduling pressure (Table 7 ). In addition, DDQN exhibits lower standard deviations in node load across all task volumes, reflecting more balanced resource allocation and reduced fluctuation in system utilization (Table 8 andTable 9 ).Conclusions The proposed MORS algorithm addresses the variability and complexity inherent in remote sensing task scheduling. Experimental results demonstrate that MORS not only improves scheduling efficiency but also significantly reduces production time and achieves balanced allocation of node resources. -
表 1 遥感算法属性
算法属性 描述 算法属性 描述 $ {a_{{\text{id}}}} $ 算法的唯一标识符 ${C_{{a_i}}}$ CPU配置 ${w_{{\text{id}}}}$ 所属遥感任务唯一标识 ${M_{{a_i}}}$ 内存大小 $ {N_{{a_i}}} $ 名称 ${S_{{a_i}}}$ 存储大小 $ {P_{{a_i}}} $ 优先级 $ {G_{{a_i}}} $ GPU要求 $ {\text{M}}{{\text{I}}_{{a_i}}} $ MIPS(百万条/s指令) ${R_{{a_i}}}$ 接收时间 $ {V_{{a_i}}} $ 任务的当前价值,初始值为0 ${U_{{a_i}}}$ 截至时间 $ {D_{{a_i}}} $ 输入数据的大小(GB) 表 2 物理机和虚拟机节点属性信息
节点属性 描述 ${\text{i}}{{\text{p}}_i}$ 节点的唯一标识符 $ {c_{{\text{v}}{{\text{m}}_i}}} $, ${c_{{\text{p}}{{\text{m}}_i}}}$ $ {c_{{\text{v}}{{\text{m}}_i}}} $第i个虚拟机的当前核心数,${c_{{\text{p}}{{\text{m}}_i}}}$第i个物理机的当前核心数 ${m_{{\text{v}}{{\text{m}}_i}}}$, $ {m_{{\text{p}}{{\text{m}}_i}}} $ ${m_{{\text{v}}{{\text{m}}_i}}}$第i个虚拟机的当前内存大小,${m_{{\text{p}}{{\text{m}}_i}}}$第i个物理机的当前内存大小 ${s_{{\text{v}}{{\text{m}}_i}}}$, ${s_{{\text{p}}{{\text{m}}_i}}}$ ${s_{{\text{v}}{{\text{m}}_i}}}$第i个虚拟机的当前存储大小,${s_{{\text{p}}{{\text{m}}_i}}}$第i个物理机的当前存储大小 ${b_{{\text{v}}{{\text{m}}_i}}}$, ${b_{{\text{p}}{{\text{m}}_i}}}$ ${b_{{\text{v}}{{\text{m}}_i}}}$第i个虚拟机的带宽,${b_{{\text{p}}{{\text{m}}_i}}}$第i个物理机的带宽,单位是GB/s ${p_{{\text{v}}{{\text{m}}_i}}}$, ${p_{{\text{p}}{{\text{m}}_i}}}$ ${p_{{\text{v}}{{\text{m}}_i}}}$第i个虚拟机处理单元的性能,${p_{{\text{p}}{{\text{m}}_i}}}$第i个物理机处理单元的性能 ${{r}}\_{t_{{\text{v}}{{\text{m}}_i}}}$, $r\_{t_{{\text{p}}{{\text{m}}_i}}}$ ${{r}}\_{t_{{\text{v}}{{\text{m}}_i}}}$第i个虚拟机运行的产品数,$r\_{t_{{\text{p}}{{\text{m}}_i}}}$第i个物理机运行的产品数 ${\text{vm\_}}{{\text{c}}_{{{\mathrm{pm}}_i}}}$ 第i个物理机上的虚拟机的数量 ${\mathrm{p}}\_{\mathrm{v}}$ 区分物理机和虚拟机的标识,1代表物理机,0代表虚拟机 表 3 节点参数
类型 参数 范围 类型 参数 范围 物理机 数量Number 2~5 虚拟机 数量Number 2~6 核心CPU 16 core 核心CPU 1~6 core 内存memory 32 GB 内存memory 4~8 GB 存储storage 200 GB 存储storage 10~50 GB 带宽bandwidth 2 GB/s 带宽bandwidth 2 GB/s 单元处理能力 9726 ~97260 MIPS单元处理能力 9726 MIPS表 4 遥感产品参数
参数 范围 参数 范围 每个任务的子任务数(算法) 1~5 core 算法所需内存 0.1~3.0 GB 算法需要的处理单元数 1~3 core 算法所需存储 2~10 GB 单元处理能力 9726 ~972600 MIPS遥感数据大小 0.1~10 GB 表 5 训练参数
参数 数值 参数 数值 轮次episodes 5000 更新频率update_frequency 50 ε衰减epsilon_decay 0.95 ${\alpha _1}$, ${\beta _1}$, ${\gamma _1}$ 0.5, 0.3, 0.2 ε最大值epsilon_max 1.0 ${\alpha _2}$, ${\beta _2}$, ${\gamma _2}$ 0.5, 0.3, 0.2 最小值exploration_min 0.01 ${\alpha _3}$, ${\beta _3}$, ${\gamma _3}$ 0.5, 0.3, 0.2 批次batch_size 64 ${w_{{\text{cpu}}}}$, ${w_{{\text{mem}}}}$, ${w_{{\text{str}}}}$ 0.5, 0.3, 0.2 学习率learning_rate 0.0001 表 6 控制变量测试:固定其他参数,单权重±25%扰动
权重 生产时间变化 负载 SLA达标率 ${\alpha _1}$±0.125 –9.2%~+11.8% 2.3% ±1.7% 表 7 不同产品数量下各算法与DDQN在任务完成时间上的对比及显著性检验结果
算法 min (n=30) P (n=30) min (n=60) P (n=60) min (n=90) P (n=90) min (n=120) P (n=120) FCFS 11.137 0 18.043 0 30.399 0 39.008 0 RR 7.346 0.062 14.504 0.030 20.201 0.046 28.126 0 GA 10.568 0 15.456 0 22.435 0 27.546 0 DQN 7.507 0.116 14.495 0.047 26.277 0 27.183 0 Dueling DQN 9.435 0 16.456 0 20.343 0 29.545 0 DDQN 7.272 - 14.197 - 19.235 - 25.886 - 表 8 不同产品数量下各算法与DDQN在物理机资源负载均衡值上的对比及显著性检验结果
算法 $ {{\mathrm{RL}}_{{\mathrm{pm}}}} $(n=30) P (n=30) $ {{\mathrm{RL}}_{{\mathrm{pm}}}} $(n=60) P (n=60) $ {{\mathrm{RL}}_{{\mathrm{pm}}}} $(n=90) P (n=90) $ {{\mathrm{RL}}_{{\mathrm{pm}}}} $(n=120) P (n=120) FCFS 0.177 0.016 0.143 0.031 0.214 0.002 0.212 0.001 RR 0.112 0.070 0.135 0.089 0.127 0.007 0.146 0.015 GA 0.137 0.038 0.148 0.024 0.196 0.052 0.206 0.004 DQN 0.159 0.047 0.134 0.040 0.150 0.006 0.136 0.057 Dueling DQN 0.159 0.034 0.158 0.027 0.145 0.051 0.166 0.014 DDQN 0.099 - 0.134 - 0.134 - 0.146 - 表 9 不同产品数量下各算法与DDQN在虚拟机资源负载均衡值上的对比及显著性检验结果
算法 $ {{\mathrm{RL}}_{{\text{vm}}}} $(n=30) P (n=30) $ {{\mathrm{RL}}_{{\text{vm}}}} $(n=60) P (n=60) $ {{\mathrm{RL}}_{{\text{vm}}}} $(n=90) P (n=90) $ {{\mathrm{RL}}_{{\text{vm}}}} $(n=120) P (n=120) FCFS 0.926 0.023 0.821 0.014 0.760 0.037 0.988 0.001 RR 0.694 0.085 0.787 0.079 0.828 0.027 0.786 0.039 GA 0.746 0.036 0.803 0.356 0.875 0.121 0.859 0.016 DQN 0.735 0.178 0.699 0.106 0.725 0.043 0.675 0.031 Dueling DQN 0.865 0.025 0.866 0.054 0.855 0.056 0.895 0.078 DDQN 0.719 - 0.768 - 0.787 - 0.773 - -
[1] AHMAD R. Smart remote sensing network for disaster management: An overview[J]. Telecommunication Systems, 2024, 87(1): 213–237. doi: 10.1007/s11235-024-01148-z. [2] 孙伟伟, 苏奋振, 侯西勇, 等. 遥感助力海岸带可持续发展—首届全国海岸带遥感大会总结[J]. 遥感学报, 2024, 28(4): 1123–1128. doi: 10.11834/jrs.20243538.SUN Weiwei, SUN Fenzhen, HOU Xiyong, et al. Remote sensing for sustainable development of coastal Zones-Summary of the first national conference on remote sensing of coastal zones[J]. National Remote Sensing Bulletin, 2024, 28(4): 1123–1128. doi: 10.11834/jrs.20243538. [3] XING Xiaoyue, YU Bailang, KANG Chaogui, et al. The synergy between remote sensing and social sensing in urban studies: Review and perspectives[J]. IEEE Geoscience and Remote Sensing Magazine, 2024, 12(1): 108–137. doi: 10.1109/MGRS.2023.3343968. [4] WANG Fumin, LI Jiale, PENG Dailiang, et al. Estimating soybean yields using causal inference and deep learning approaches with satellite remote sensing data[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2024, 17: 14161–14178. doi: 10.1109/JSTARS.2024.3435699. [5] GROSOF I, YANG Kunhe, SCULLY Z, et al. Nudge: Stochastically improving upon FCFS[C]. 2021 ACM SIGMETRICS/International Conference on Measurement and Modeling of Computer Systems, 2021: 11–12. doi: 10.1145/3410220.3460102. [6] PACHIPALA Y, SUREDDY K S, SRIYA KAITEPALLI A B S, et al. Optimizing task scheduling in cloud computing: An enhanced shortest job first algorithm[J]. Procedia Computer Science, 2024, 233: 604–613. doi: 10.1016/j.procs.2024.03.250. [7] BUSENHART C, HUNGERBÜHLER N, and XU W. A Variant of the round-robin scheduling problem[J]. Ars Combinatoria, 2024, 158: 81–92. doi: 10.61091/ars158-09. [8] GAWIEJNOWICZ S, LIN B M T, and MOSHEIOV G. Dynamic scheduling problems in theory and practice[J]. Journal of Scheduling, 2024, 27(3): 225–226. doi: 10.1007/s10951-023-00798-2. [9] ABO-ALSABEH R and SALHI A. The genetic algorithm: A study survey[J] Iraqi Journal of Science, 2022, 63(3): 1215–1231. doi: 10.24996/ijs.2022.63.3.27. [10] 陈亮, 李景山. 遥感卫星数据预处理系统复杂任务调度模型研究与实现[J]. 遥感信息, 2021, 36(5): 98–106. doi: 10.3969/j.issn.1000-3177.2021.05.014.CHEN Liang and LI Jingshan. Research and implementation of complex task scheduling model for remote sensing satellite data preprocessing system[J]. Remote Sensing Information, 2021, 36(5): 98–106. doi: 10.3969/j.issn.1000-3177.2021.05.014. [11] 赵斐, 陈昊, 白建东, 等. 基于改进蚁群算法的遥感信息处理负载均衡任务调度算法研究[J]. 计算机测量与控制, 2021, 29(11): 183–188. doi: 10.16526/j.cnki.11-4762/tp.2021.11.033.ZHAO Fei, CHEN Hao, BAI Jiandong, et al. One remote sensing information processing task allocation algorithm for collaborative planning based on knowledge model and genetic algorithm[J]. Computer Measurement & Control, 2021, 29(11): 183–188. doi: 10.16526/j.cnki.11-4762/tp.2021.11.033. [12] ZHANG Jianxiong, GUO Bing, DING Xuefeng, et al. An adaptive multi-objective multi-task scheduling method by hierarchical deep reinforcement learning[J]. Applied Soft Computing, 2024, 154: 111342. doi: 10.1016/j.asoc.2024.111342. [13] LI Guohao, LI Xuefei, LI Jing, et al. PTMB: An online satellite task scheduling framework based on pre-trained Markov decision process for multi-task scenario[J]. Knowledge-Based Systems, 2024, 284: 111339. doi: 10.1016/j.knosys.2023.111339. [14] HAN Xuefeng, HE Hongwen, WU Jingda, et al. Energy management based on reinforcement learning with double deep Q-learning for a hybrid electric tracked vehicle[J]. Applied Energy, 2019, 254: 113708. doi: 10.1016/j.apenergy.2019.113708. [15] 李奇儒, 耿霞. 基于改进DQN算法的机器人路径规划[J]. 计算机工程, 2023, 49(12): 111–120. doi: 10.19678/j.issn.1000-3428.0066348.LI Qiru and GENG Xia. Robot path planning based on improved DQN algorithm[J]. Computer Engineering, 2023, 49(12): 111–120. doi: 10.19678/j.issn.1000-3428.0066348. [16] WANG Xinwei, WU Guohua, XING Lining, et al. Agile earth observation satellite scheduling over 20 years: Formulations, methods, and future directions[J]. IEEE Systems Journal, 2021, 15(3): 3881–3892. doi: 10.1109/JSYST.2020.2997050. [17] 胡庆雷, 邵小东, 杨昊旸, 等. 航天器多约束姿态规划与控制: 进展与展望[J]. 航空学报, 2022, 43(10): 527351. doi: 10.7527/S1000-6893.2022.27351.HU Qinglei, SHAO Xiaodong, YANG Haoyang, et al. Spacecraft attitude planning and control under multiple constraints: Review and prospects[J]. Acta Aeronautica et Astronautica Sinica, 2022, 43(10): 527351. doi: 10.7527/S1000-6893.2022.27351. [18] 何奇恩, 李峰, 钟兴. 多目标算法在卫星区域覆盖调度及数传规划上的应用综述[J]. 遥感技术与应用, 2023, 38(4): 783–793. doi: 10.11873/j.issn.1004-0323.2023.4.0783.HE Qien, LI Feng, and ZHONG Xing. A review of the application of multi-objective algorithms in satellite regional coverage scheduling and data transmission planning[J]. Remote Sensing Technology and Application, 2023, 38(4): 783–793. doi: 10.11873/j.issn.1004-0323.2023.4.0783. [19] DROZDOWSKI M. Scheduling multiprocessor tasks—An overview[J]. European Journal of Operational Research, 1996, 94(2): 215–230. doi: 10.1016/0377-2217(96)00123-3. [20] 杨戈, 赵鑫, 黄静. 云环境下调度算法综述[J]. 电子技术应用, 2019, 45(9): 13–17,27. doi: 10.16157/j.issn.0258-7998.190547.YANG Ge, ZHAO Xin, and HUANG Jing. Overview of task scheduling algorithms in cloud computing[J]. Application of Electronic Technique, 2019, 45(9): 13–17,27. doi: 10.16157/j.issn.0258-7998.190547. [21] ELZEKI O M, RASHAD M Z, and ELSOUD M A. Overview of scheduling tasks in distributed computing systems[J]. International Journal of Soft Computing and Engineering (IJSCE), 2012, 2(3): 470–475. [22] KUCHUK H, MOZHAIEV O, KUCHUK N, et al. Devising a method for the virtual clustering of the internet of things edge environment[J]. Eastern-European Journal of Enterprise Technologies, 2024, 1(9): 60–71. doi: 10.15587/1729-4061.2024.298431. [23] WANG Jin. Virtual cluster model based on big data application[M]. LI Xiaolong. Advances in Intelligent Automation and Soft Computing. Cham: Springer, 2022: 61–66. doi: 10.1007/978-3-030-81007-8_8. [24] AGHAEI M, ASGHARI P, ADABI S, et al. Using recommender clustering to improve quality of services with sustainable virtual machines in cloud computing[J]. Cluster Computing, 2023, 26(2): 1479–1493. doi: 10.1007/s10586-022-03760-7. [25] GHASEMI A and KESHAVARZI A. Energy-efficient virtual machine placement in heterogeneous cloud data centers: A clustering-enhanced multi-objective, multi-reward reinforcement learning approach[J]. Cluster Computing, 2024, 27(10): 14149–14166. doi: 10.1007/s10586-024-04657-3. [26] HAN Xiaoyun, MU Chaoxu, ZHU Jiebei, et al. A safe virtual machine scheduling strategy for energy conservation and privacy protection of server clusters in cloud data centers[J]. IEEE Transactions on Sustainable Computing, 2024, 9(1): 46–60. doi: 10.1109/TSUSC.2023.3303637. [27] ZHU Xi, ZHANG Lei, and TANG Shaoqiang. Adaptive selection of reference stiffness in virtual clustering analysis[J]. Computer Methods in Applied Mechanics and Engineering, 2021, 376: 113621. doi: 10.1016/j.cma.2020.113621. [28] CHRAIBI A, BEN ALLA S, TOUHAFI A, et al. A novel dynamic multi-objective task scheduling optimization based on Dueling DQN and PER[J]. The Journal of Supercomputing, 2023, 79(18): 21368–21423. doi: 10.1007/s11227-023-05489-5. [29] MNIH V, KAVUKCUOGLU K, SILVER D, et al. Human-level control through deep reinforcement learning[J]. Nature, 2015, 518(7540): 529–533. doi: 10.1038/nature14236. [30] KOBAYASHI T and ILBOUDO W E L. t-soft update of target network for deep reinforcement learning[J]. Neural Networks, 2021, 136: 63–71. doi: 10.1016/j.neunet.2020.12.023. [31] HUANG Heqing, CHIU H C, SHI Qingkai et al. Balance seed scheduling via Monte Carlo planning[J]. IEEE Transactions on Dependable and Secure Computing, 2024, 21(3): 1469–1483. doi: 10.1109/TDSC.2023.3285293. -






 下载:
下载:


 下载:
下载:
