图结构数据驱动的非合作集群无线通信网络拓扑推断

侯长波; 付丁一; 宋振; 王斌; 周志超

doi:10.11999/JEIT250084

图结构数据驱动的非合作集群无线通信网络拓扑推断

doi: 10.11999/JEIT250084 cstr: 32379.14.JEIT250084

侯长波^{1, 2},
付丁一^1, ,,
宋振¹,
王斌¹,
周志超¹

1.
哈尔滨工程大学信息与通信工程学院哈尔滨 150001
2.
先进船舶通信与信息技术工业和信息化部重点实验室哈尔滨 150001

基金项目: 国家自然科学基金(U23A20271，中央高校基本科研业务费(3072024XX0808)

详细信息

作者简介:
侯长波：男，教授，研究方向为非合作无线通信网络拓扑预测、深度学习、宽带信号处理与认知无线电

付丁一：女，硕士生，研究方向为非合作无线通信网络拓扑预测与深度学习

宋振：男，博士生，研究方向为通信对抗与人工智能应用与多信号分离与识别

王斌：男，博士生，研究方向为信号处理与电磁辐射源定位

周志超：男，博士生，研究方向为非合作无线通信网络拓扑推理与图神经网络应用

通讯作者:
付丁一　fdy_0429@hrbeu.edu.cn

中图分类号: TN92
计量
- 文章访问数: 23
- HTML全文浏览量: 15
- PDF下载量: 1
- 被引次数: 0
出版历程
- 收稿日期: 2025-02-12
- 修回日期: 2025-09-15
- 网络出版日期: 2025-09-20

Graph-structured Data-driven Topology Inference for Non-cooperative Clustered Wireless Communication Networks

HOU Changbo^{1, 2},
FU Dingyi^{1
, ,},
SONG Zhen¹,
WANG Bin¹,
ZHOU Zhichao¹

1.
College of Information And Communication Engineering, Harbin Engineering University, Harbin 150001, China
2.
Key Laboratory of Advanced Marine Communication and Information Technology, Ministry of Industry and Information Technology, Harbin Engineering University, Harbin 150001, China

Funds: The National Natural Science Foundation of China (U23A20271), The Fundamental Research Funds for the Central Universities (3072024XX0808)

摘要

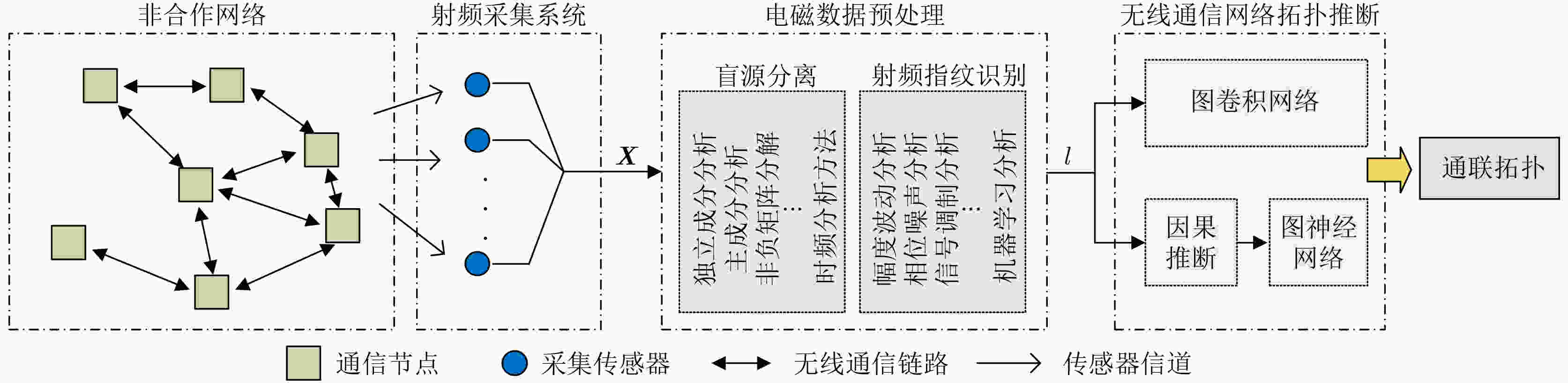
摘要: 集群目标通信网络在非合作场景中极大增加了电磁环境探测的难度。针对非合作环境下缺乏拓扑先验信息的挑战，该文提出基于图结构数据驱动的拓扑推断方法。通过场景假设分析与图神经网络建模，构建了基于因果推断与GNN结合的拓扑推断混合模型，其中因果推断包括多维霍克斯过程(MHP)、Peter–Clarks瞬时条件独立性检测(PCMCI)。实验表明在节点数8～13、连边概率0.45的条件下，PCMCI+GED方法的F1分数较PCMCI提升31.2%，较GCN方法提升23.9%。研究证实因果先验与图神经网络的协同机制可有效提高拓扑推断精度，50%节点特征输入的混合模型在保持93%精度的同时减少88.6%计算耗时，为大规模网络场景提供可行解决方案。
- 集群无线通信网络 /
- 网络拓扑推断 /
- 因果推理 /
- 图神经网络
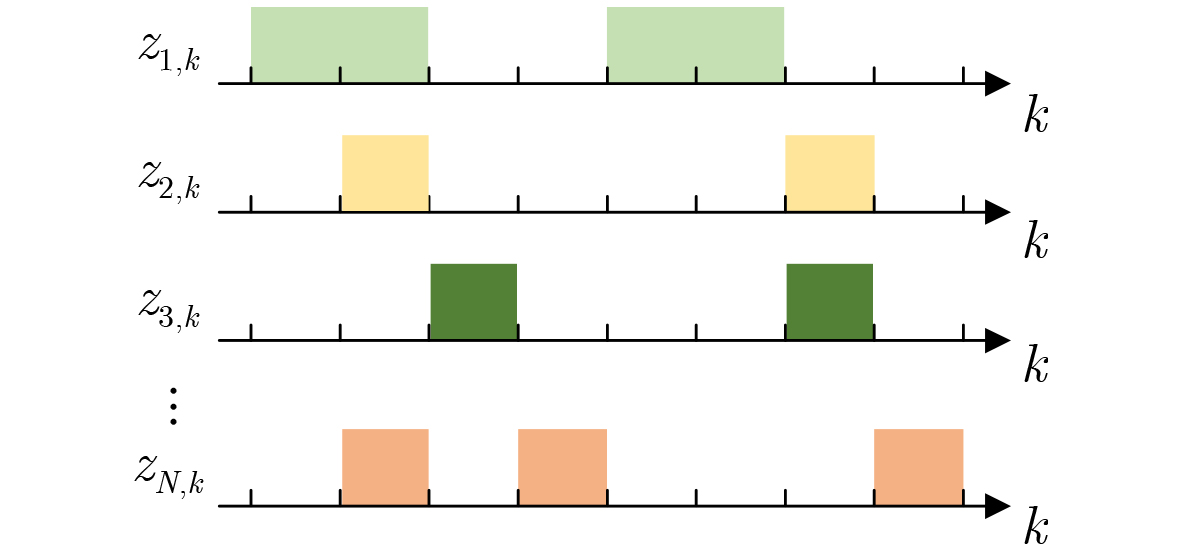
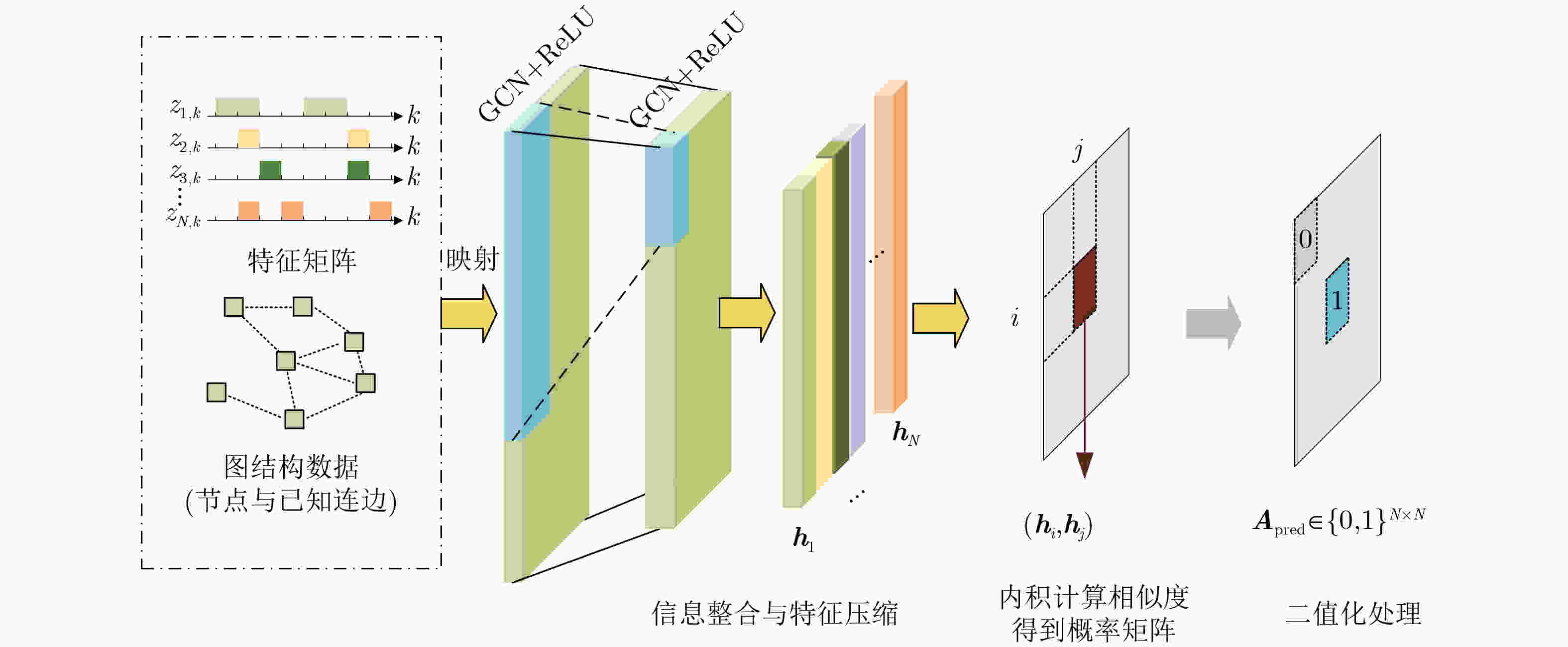
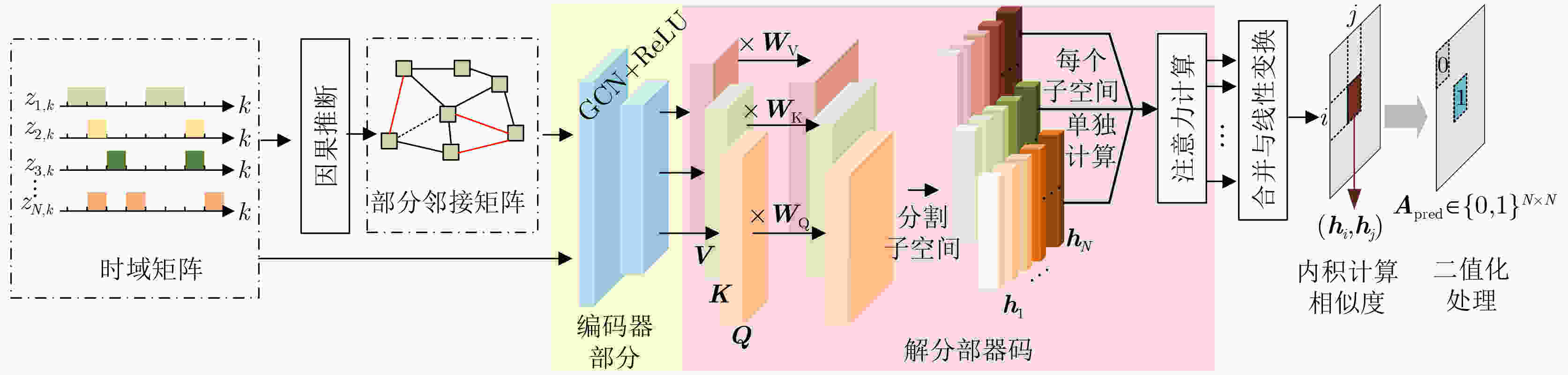
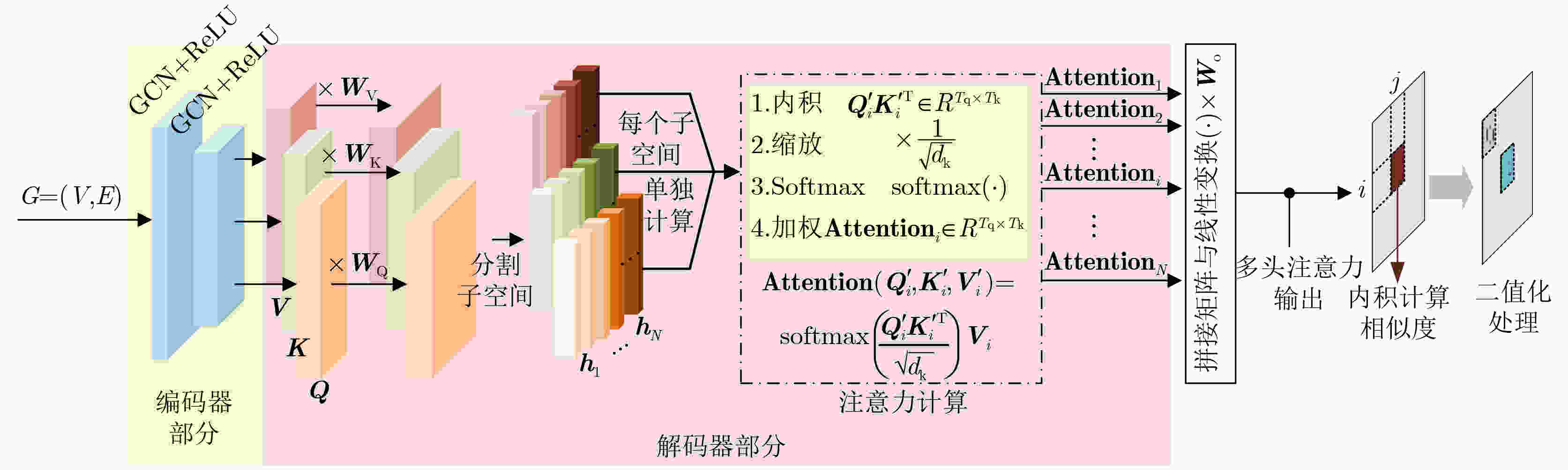
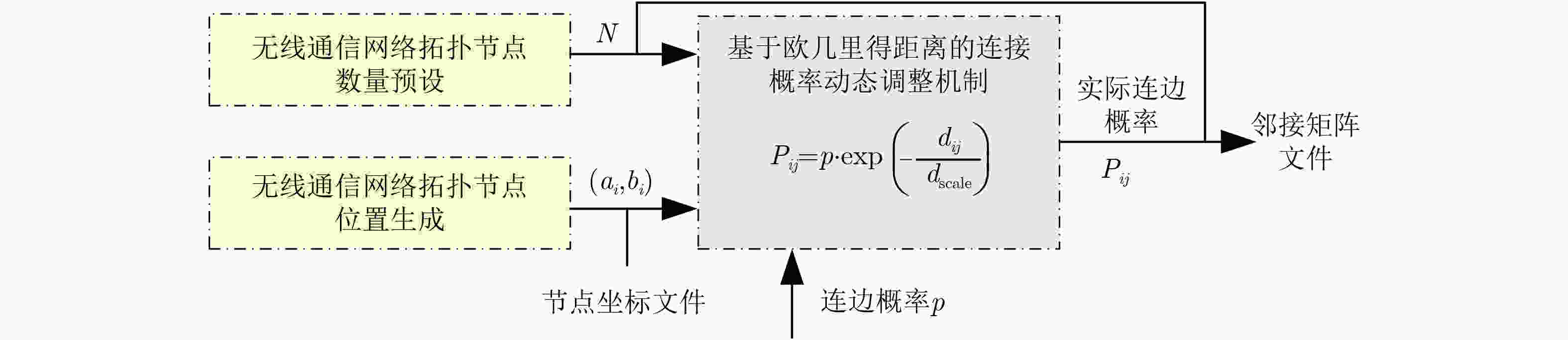
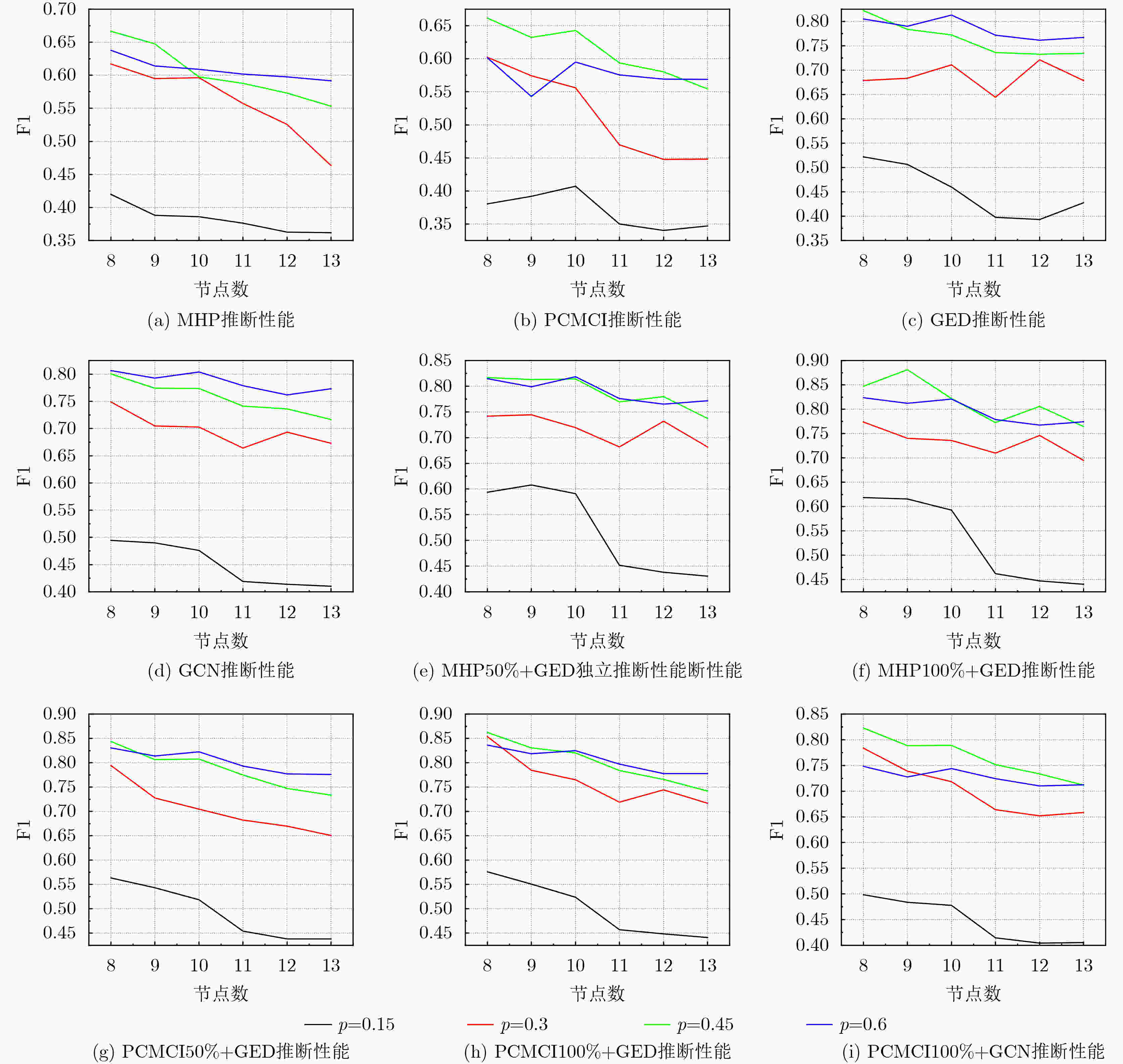
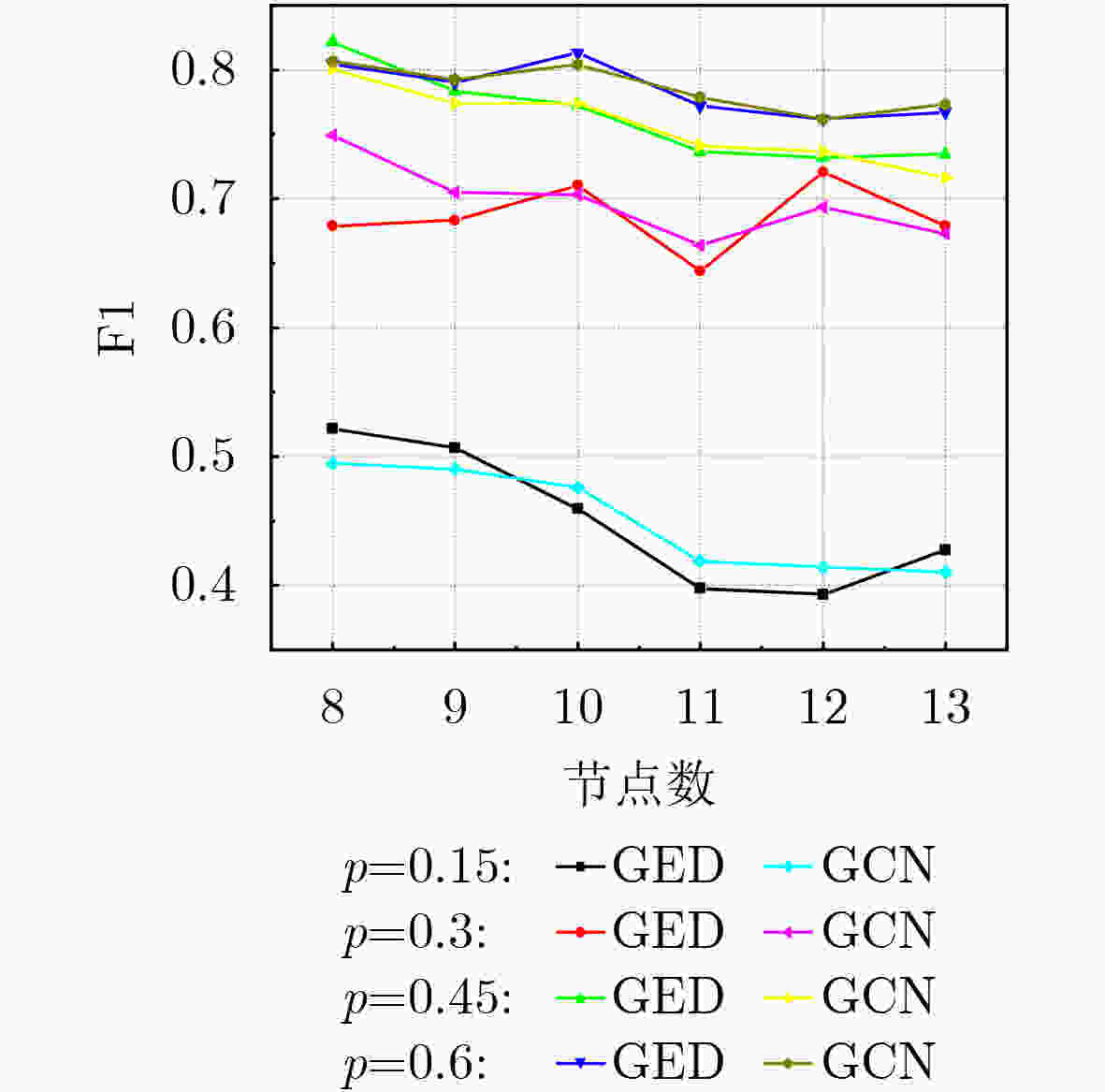
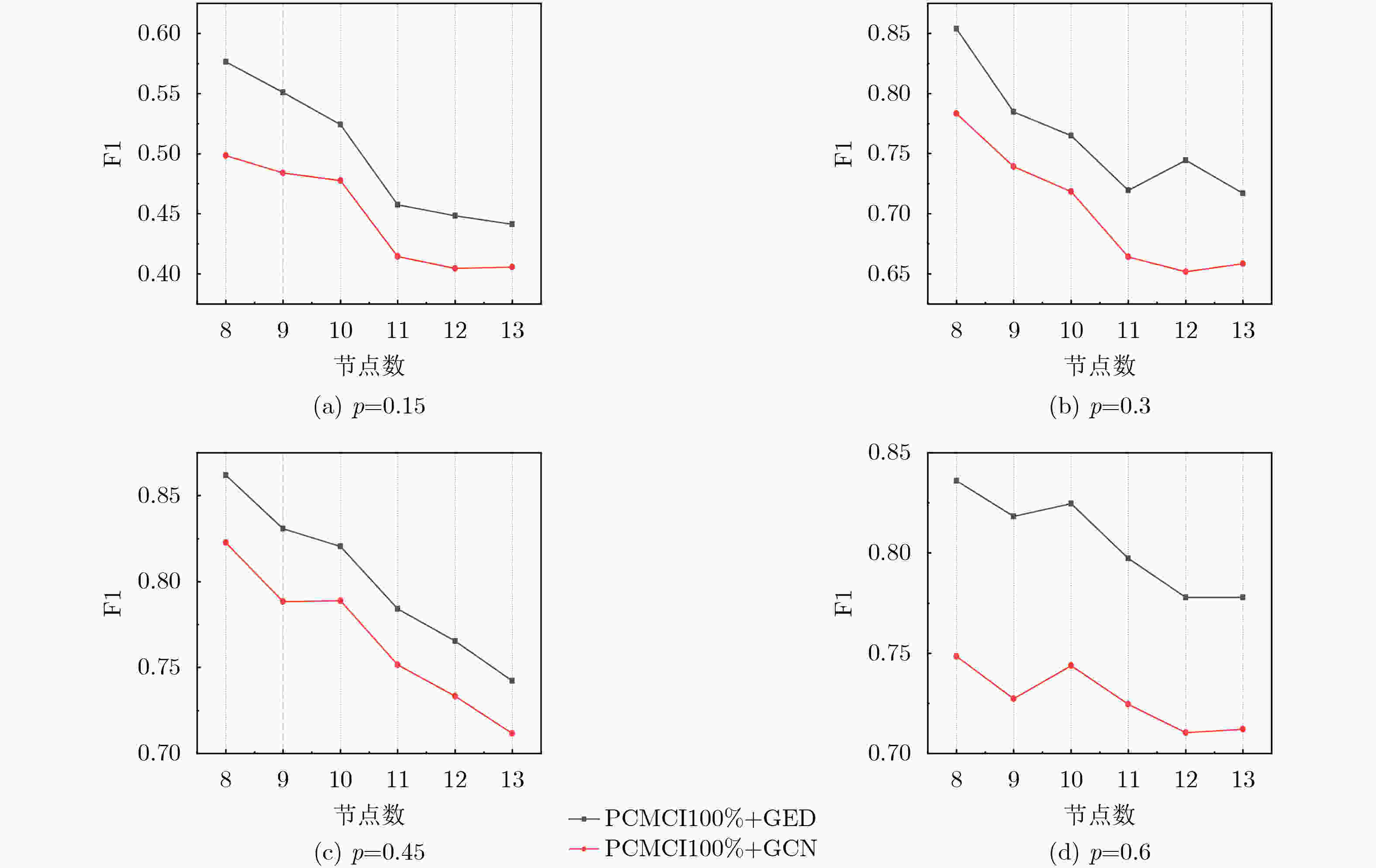
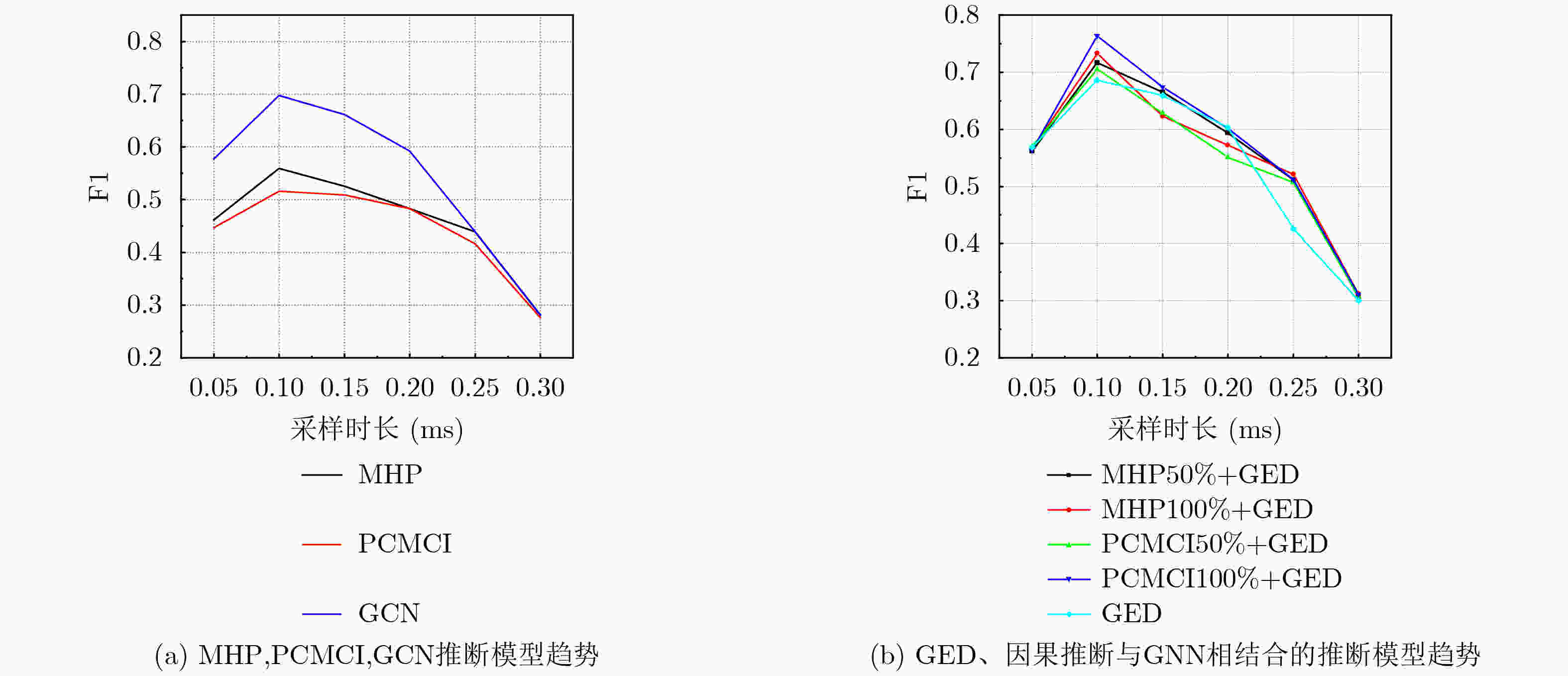
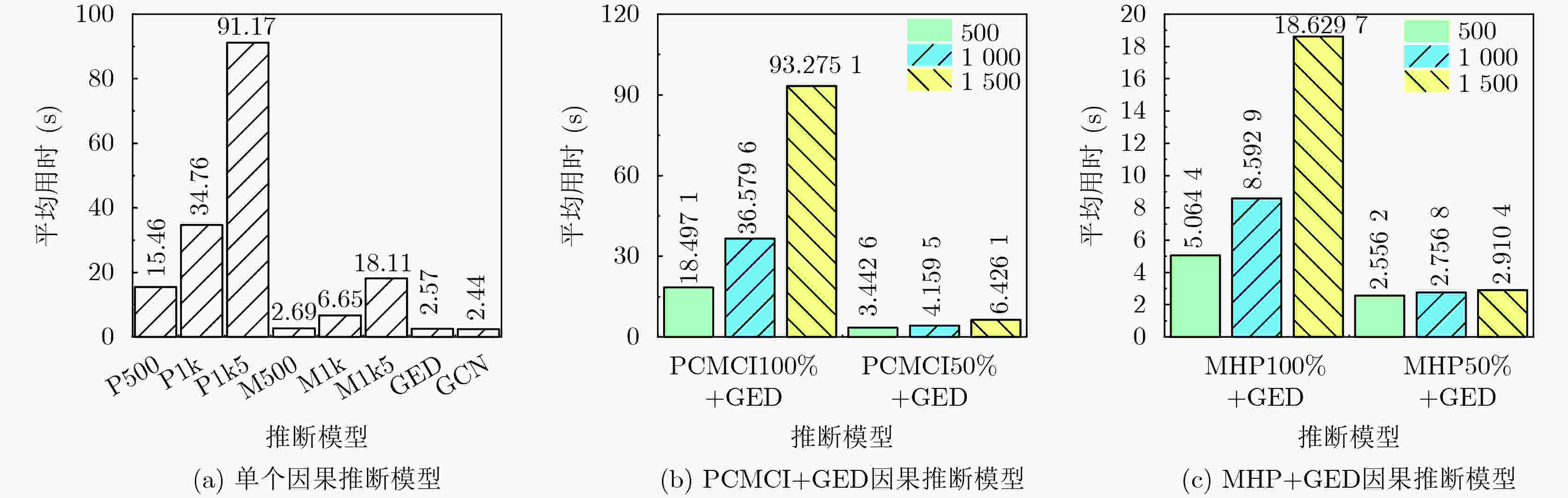
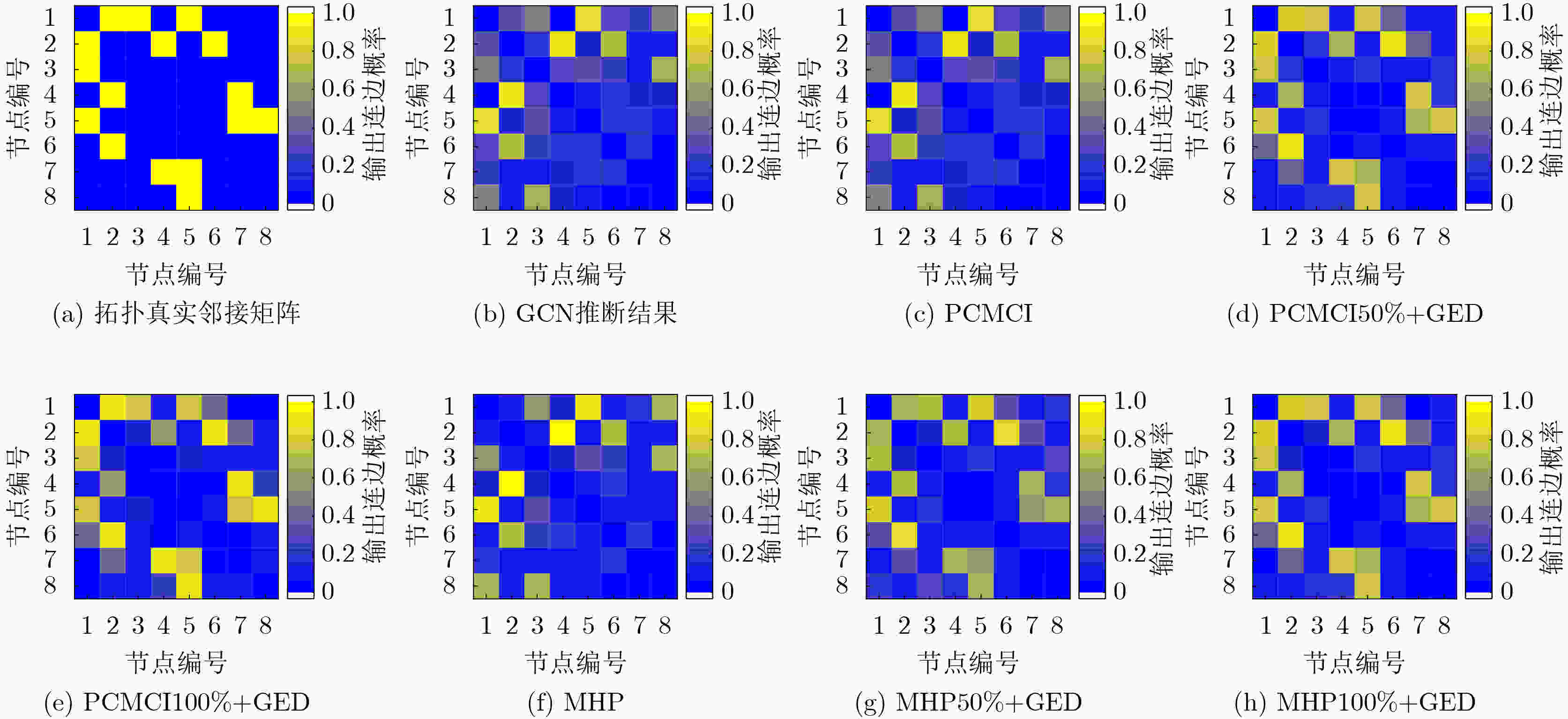
Abstract: Objective The emergence of clustered target communication networks complicates electromagnetic environment detection in non-cooperative scenarios, creating challenges for electromagnetic situation awareness and electronic countermeasures. Existing research seldom addresses topology prediction under conditions with no prior knowledge, where the absence of explicit structural information and the dynamic nature of the networks hinder accurate inference. This study investigates topology prediction for non-cooperative clustered wireless communication networks using graph-structured data-driven approaches. Specifically, it evaluates the performance of multiple topology inference methods, including the Multivariate Hawkes Process (MHP), Peter–Clark Momentary Conditional Independence (PCMCI), Graph Encoder–Decoder (GED), and Graph Convolutional Networks (GCN). The effects of network properties such as node count and edge probability on inference accuracy are analyzed. Additionally, a hybrid framework that integrates statistical models with graph-based learning is explored to improve inference accuracy and computational efficiency. Methods The proposed methodology combines causal inference with Graph Neural Network (GNN)–based learning. Adjacency matrices are first generated through causal discovery, using time-domain matrices derived from simulated wireless communication events. These matrices are constructed by thresholding power spectra to yield binary communication states. The GNN module subsequently refines the causal discovery output by suppressing false positives and optimizing global topology through encoder–decoder operations with multi-head attention mechanisms. To assess robustness, synthetic datasets are generated with NS-3 simulations under varying conditions: edge probabilities (0.15–0.60), node densities (8–13 nodes), sampling durations (0.05–0.30 ms), and node feature completeness (partial, 50%; full, 100%). Connectivity patterns are modeled by incorporating distance-adjusted edge probabilities. Performance evaluation uses F1-score, accuracy, recall, and inference time, with systematic comparison across baseline models (MHP, PCMCI, GCN, GED) and hybrid variants (PCMCI+GED, MHP+GED). Results and Discussions The PCMCI+GED hybrid framework consistently achieves superior topology prediction across diverse network configurations. At an edge probability of 0.45, PCMCI+GED with full node features attains an F1-score of 0.808, exceeding the performance of standalone PCMCI and GED by 31.1% and 4.9%, respectively (Fig. 7). This improvement arises from the synergy between causal priors and graph neural networks: PCMCI establishes preliminary causal relationships, while GED refines inference through global attention mechanisms that reduce false positives. Comparative analysis reveals that richer node features enhance topology inference in causal inference methods (Fig. 7). For example, MHP+GED with full features exceeds its 50% feature counterpart by 2.10%, and PCMCI+GED with full features improves by 3.04%. Yet, the most substantial gains come from combining causal inference with GED. Relative to standalone MHP with full features, MHP+GED improves by 30.65% with 50% features and 33.40% with full features. Similarly, PCMCI+GED improves by 34.43% and 38.51% under the same conditions. In contrast, relying solely on GNNs proves insufficient for modeling causal relationships. GED alone performs similarly to GCN, with Mean Absolute Error (MAE) and Root Mean Squared Error (RMSE) values of 0.0149 and 0.0206, respectively (Fig. 8). Without causal priors, GED offers no significant advantage over GCN; however, when priors are incorporated, GED outperforms GCN in inference accuracy (Fig. 9). Sampling duration analysis shows that 0.1 ms is optimal, balancing redundancy and information loss (Fig. 10, Table 2). Shorter intervals (0.05 ms) inflate computational costs through high-dimensional operations, whereas longer intervals (0.30 ms) obscure temporal dependencies, reducing the F1-score of PCMCI+GED with full features to 40.57% of its value at 0.1 ms. Efficiency evaluations highlight trade-offs between accuracy and runtime. With 50% node features, PCMCI+GED reduces inference time by 88.63% while retaining 96.96% of its F1-score. Under the same conditions, MHP+GED reduces inference time by 85.48% with only a 2.07% drop in performance (Fig. 11). PCMCI’s exponential complexity makes it computationally prohibitive in high-dimensional settings, whereas MHP’s quadratic scaling with node count and linear scaling with event frequency yield more modest efficiency gains. In low-dimensional settings, however, MHP’s event-driven computation leads to longer runtimes than PCMCI. Heatmap analysis further confirms the precision of the hybrid models. Adjacency matrices generated by PCMCI+GED and MHP+GED with full features closely align with the ground truth, demonstrating high predictive accuracy (Fig. 9). In sparse networks, standalone PCMCI introduces noise by linking non-interacting nodes, while GCN generates fragmented predictions due to the absence of causal priors. The hybrid framework alleviates these limitations by combining PCMCI’s local causal inference with GED’s global optimization. Overall, the hybrid framework addresses key shortcomings of individual methods: the high computational cost of PCMCI and MHP, and the limited interpretability of GNNs. By integrating causal discovery with graph-based deep learning, the model achieves state-of-the-art predictive accuracy while maintaining scalability. Its performance highlights the potential for real-time applications in resource-constrained environments, emphasizing the importance of balancing causal priors and data-driven learning for advancing non-cooperative wireless communication network analysis. Conclusions This study demonstrates the effectiveness of combining PCMCI-based causal inference with GED-enhanced GNN for topology prediction in non-cooperative clustered wireless communication networks. The hybrid model achieves state-of-the-art accuracy, particularly in dense networks, while partial node feature inputs substantially reduce computational overhead. Although the exponential complexity of PCMCI constrains scalability in high-dimensional settings, integration with GED alleviates this limitation through feature reduction and global optimization. The findings highlight the need to balance accuracy and efficiency in practical applications, where GCN offers a viable option for real-time inference. Future research will explore attention mechanisms and self-supervised learning to further enhance robustness. These advancements hold promise for improving electromagnetic situation awareness and electronic countermeasure strategies in dynamic adversarial environments.
- Clustered wireless communication networks /
- Network topology inference /
- Causal inference /
- Graph Neural Networks (GNN)

HTML全文

图 1 无线通信网络拓扑推断场景

下载: 全尺寸图片幻灯片

图 2 时域矩阵示例

下载: 全尺寸图片幻灯片

图 3 基于GCN的无线通信网络拓扑推断模型框架

下载: 全尺寸图片幻灯片

图 4 基于因果推断与图神经网络结合的拓扑推断结构框架图

下载: 全尺寸图片幻灯片

图 5 用于修正因果关系的GED框架图

下载: 全尺寸图片幻灯片

图 6 无线通信网络拓扑模型随机化方案

下载: 全尺寸图片幻灯片

图 7 不同网络结构下的各无线通信网络拓扑推断模型性能

下载: 全尺寸图片幻灯片

图 8 N与GED的性能对比

下载: 全尺寸图片幻灯片

图 9 有PCMCI作为先验信息下的GCN与GED性能对比

下载: 全尺寸图片幻灯片

图 10 不同时域矩阵采样时长下的拓扑推断模型性能趋势

下载: 全尺寸图片幻灯片

图 11 无线通信网络拓扑推断方法平均用时比较

下载: 全尺寸图片幻灯片

图 12 推断模型输出的邻接矩阵热力图

下载: 全尺寸图片幻灯片

表 1 NS-3无线通信网络仿真参数

参数名称	参数类型	值
SimTime	仿真总时间	4s
SinkStartTime	节点接收行为起始时间	1.000 1 s
SinkStopTime	节点接收行为停止时间	3.900 01 s
AppStartTime	应用层起始时间	2.000 1 s
AppStopTime	应用层停止时间	3.800 01 s
AppPacketRate	应用层数据速率	40 Kbit/(s·Hz)
PacketSize	数据包大小	1 000 Byte
LinkRate	链路数据速率	10 Mbit/(s·Hz)
DataRate	数据传输速率	10 Mbit/(s·Hz)
LinkDelay	链路延迟	2 ms

下载: 导出CSV

表 2 输入不同采样时长的时域矩阵情况下的拓扑推断模型平均F1分数

采样时长(ms)	MHP	PCMCI	GED	GCN	MHP50%+GED	MHP100%+GED	PCMCI50%+GED	PCMCI100%+GED
0.05	0.461 4	0.447 1	0.568 7	0.577 2	0.562 0	0.564 7	0.569 8	0.563 4
0.10	0.559 1	0.516 3	0.686 0	0.697 9	0.716 9	0.733 3	0.704 8	0.764 0
0.15	0.525 6	0.509 2	0.659 2	0.661 3	0.665 2	0.623 3	0.628 7	0.673 5
0.20	0.483 3	0.482 9	0.603 6	0.592 0	0.594 1	0.571 9	0.551 1	0.602 1
0.25	0.438 7	0.416 5	0.426 1	0.438 7	0.511 4	0.521 2	0.507 0	0.511 8
0.30	0.281 2	0.276 6	0.300 1	0.281 8	0.306 4	0.311 8	0.307 5	0.310 9

下载: 导出CSV

参考文献(32)

[1]	AL AJRAWI S and TRAN B. Mobile wireless ad-hoc network routing protocols comparison for real-time military application[J]. Spatial Information Research, 2024, 32(1): 119–129. doi: 10.1007/s41324-023-00535-z.
[2]	GOMES J E C, EHLERT R R, BOESCHE R M, et al. Surveying emerging network approaches for military command and control systems[J]. ACM Computing Surveys, 2024, 56(6): 143. doi: 10.1145/3626090.
[3]	AHMAD R B, KOLAWOLE S F, and CHINEDU P U. Design of multimedia mobile ad-hoc network for military applications: A review[J]. ATBU Journal of Science, Technology and Education, 2023, 11(4): 517–524.
[4]	MOHAMMED B A, AL-SHAREEDA M A, ALSADHAN A A, et al. Service based VEINS framework for vehicular Ad-hoc network (VANET): A systematic review of state-of-the-art[J]. Peer-to-Peer Networking and Applications, 2024, 17(4): 2259–2281. doi: 10.1007/s12083-024-01692-0.
[5]	ALMANSOR M J, DIN N M, BAHARUDDIN M Z, et al. Routing protocols strategies for flying Ad-Hoc network (FANET): Review, taxonomy, and open research issues[J]. Alexandria Engineering Journal, 2024, 109: 553–577. doi: 10.1016/j.aej.2024.09.032.
[6]	宋叶辉, 丁国如, 徐承龙, 等. 面向非合作无人机通信网络的通联拓扑推理技术[J]. 电子与信息学报, 2022, 44(3): 924–939. doi: 10.11999/JEIT211410. SONG Yehui, DING Guoru, XU Chenglong, et al. Communication topology inference technology for non-cooperative UAV communication network[J]. Journal of Electronics & Information Technology, 2022, 44(3): 924–939. doi: 10.11999/JEIT211410.
[7]	刘子彤, 丁国如, 王威, 等. 面向非合作无线网络的拓扑感知技术分析[J]. 指挥与控制学报, 2021, 7(2): 153–159. doi: 10.3969/j.issn.2096-0204.2021.02.0153. LIU Zitong, DING Guoru, WANG Wei, et al. Analysis of topology sensing technology for non-collaborative wireless networks[J]. Journal of Command and Control, 2021, 7(2): 153–159. doi: 10.3969/j.issn.2096-0204.2021.02.0153.
[8]	RÉAU M, RENAUD N, XUE L C, et al. DeepRank-GNN: A graph neural network framework to learn patterns in protein–protein interfaces[J]. Bioinformatics, 2023, 39(1): btac759. doi: 10.1093/bioinformatics/btac759.
[9]	JIANG Weiwei, LUO Jiayun, HE Miao, et al. Graph neural network for traffic forecasting: The research progress[J]. ISPRS International Journal of Geo-Information, 2023, 12(3): 100. doi: 10.3390/ijgi12030100.
[10]	LI Xiao, SUN Li, LING Mengjie, et al. A survey of graph neural network based recommendation in social networks[J]. Neurocomputing, 2023, 549: 126441. doi: 10.1016/j.neucom.2023.126441.
[11]	ZHOU Jie, CUI Ganqu, HU Shengding, et al. Graph neural networks: A review of methods and applications[J]. AI Open, 2020, 1: 57–81. doi: 10.1016/j.aiopen.2021.01.001.
[12]	LIU Zitong, WANG Wei, DING Guoru, et al. Topology sensing of non-collaborative wireless networks with conditional Granger causality[J]. IEEE Transactions on Network Science and Engineering, 2022, 9(3): 1501–1515. doi: 10.1109/TNSE.2022.3146465.
[13]	LIU Zitong, SUN Jiachen, SHEN Feng, et al. Topology sensing of wireless networks based on Hawkes process[J]. Mobile Networks and Applications, 2020, 25(6): 2459–2470. doi: 10.1007/s11036-020-01588-2.
[14]	SHARMA P, BUCCI D J, BRAHMA S K, et al. Communication network topology inference via transfer entropy[J]. IEEE Transactions on Network Science and Engineering, 2020, 7(1): 562–575. doi: 10.1109/TNSE.2018.2889454.
[15]	TILGHMAN P and ROSENBLUTH D. Inferring wireless communications links and network topology from externals using Granger causality[C]. Proceedings of the IEEE Military Communications Conference, San Diego, USA, 2013: 1284–1289. doi: 10.1109/MILCOM.2013.219.
[16]	MOORE M G and DAVENPORT M A. Analysis of wireless networks using Hawkes processes[C]. Proceedings of the 17th International Workshop on Signal Processing Advances in Wireless Communications (SPAWC), Edinburgh, UK, 2016: 1–5. doi: 10.1109/SPAWC.2016.7536795.
[17]	MOORE M G and DAVENPORT M A. A Hawkes’ eye view of network information flow[C]. Proceedings of 2016 IEEE Statistical Signal Processing Workshop, Palma de Mallorca, Spain, 2016: 1–5. doi: 10.1109/SSP.2016.7551779.
[18]	LAGHATE M and CABRIC D. Learning wireless networks’ topologies using asymmetric Granger causality[J]. IEEE Journal of Selected Topics in Signal Processing, 2018, 12(1): 233–247. doi: 10.1109/JSTSP.2017.2787478.
[19]	LIU Zitong, DING Guoru, WANG Zheng, et al. Cooperative topology sensing of wireless networks with distributed sensors[J]. IEEE Transactions on Cognitive Communications and Networking, 2021, 7(2): 524–540. doi: 10.1109/TCCN.2020.3019601.
[20]	SONG Yehui, DING Guoru, SUN Jiachen, et al. Topology tracking of dynamic UAV wireless networks[J]. Chinese Journal of Aeronautics, 2022, 35(11): 322–335. doi: 10.1016/j.cja.2021.08.012.
[21]	HE Dejun, WU Xinrong, YU Lu, et al. Recognition of non-cooperative radio communication relationships based on transformer[C]. Proceedings of the 8th International Conference on Communication and Information Processing, Beijing, China, 2022: 175–183. doi: 10.1145/3571662.3571688.
[22]	LI Pengxue, ZHA Haoran, and LIN Yun. Topology inference for low-resource non-cooperative cluster networks based on deep learning[C]. 2023 International Conference on Ubiquitous Communication (Ucom), Xi'an, China, 2023: 361–366. doi: 10.1109/Ucom59132.2023.10257608.
[23]	KOIZUMI T, WASA Y, and KISHIDA M. Information transfer-based topology identification of dynamic multi-agent systems[J]. IFAC-PapersOnLine, 2023, 56(2): 3948–3953. doi: 10.1016/j.ifacol.2023.10.1333.
[24]	CHANG Liang, ZHANG Ying, and ZHANG Qi. Dynamic topology identification of wireless communication networks based on Hawkes process[C]. Proceedings of the 2023 4th International Conference on Computing, Networks and Internet of Things, Xiamen, China, 2023: 693–700. doi: 10.1145/3603781.3603903.
[25]	SUN Rui. AITA: Accurate network topology recognition via active interception and topology analysis[C]. 2024 IEEE 4th International Conference on Electronic Technology, Communication and Information (ICETCI), Changchun, China, 2024: 6–10. doi: 10.1109/ICETCI61221.2024.10594668.
[26]	GAO Haoyang, LI Ning, and XIE Yuancheng. Hidden-SAGE: For the inference of complex autonomous system business relationships involving hidden links[J]. Electronics, 2024, 13(9): 1617. doi: 10.3390/electronics13091617.
[27]	GUAN Faqian, ZHU Tianqing, TONG Hanjin, et al. Topology modification against membership inference attack in Graph Neural Networks[J]. Knowledge-Based Systems, 2024, 305: 112642. doi: 10.1016/j.knosys.2024.112642.
[28]	ZHENG Tongya, WANG Xinchao, FENG Zunlei, et al. Temporal aggregation and propagation graph neural networks for dynamic representation[J]. IEEE Transactions on Knowledge and Data Engineering, 2023, 35(10): 10151–10165. doi: 10.1109/TKDE.2023.3265271.
[29]	ANSARI S, ALATRANY A S, ALNAJJAR K A, et al. A survey of artificial intelligence approaches in blind source separation[J]. Neurocomputing, 2023, 561: 126895. doi: 10.1016/j.neucom.2023.126895.
[30]	XIE Lingnan, PENG Linning, ZHANG Junqing, et al. Radio frequency fingerprint identification for Internet of Things: A survey[J]. Security and Safety, 2024, 3: 2023022. doi: 10.1051/sands/2023022.
[31]	RUNGE J, NOWACK P, KRETSCHMER M, et al. Detecting and quantifying causal associations in large nonlinear time series datasets[J]. Science Advances, 2019, 5(11): eaau4996. doi: 10.1126/sciadv.aau4996.
[32]	HAWKES A G. Spectra of some self-exciting and mutually exciting point processes[J]. Biometrika, 1971, 58(1): 83–90. doi: 10.1093/biomet/58.1.83.