时序信息驱动的并行交互式多模型水下目标跟踪算法

兰朝凤; 张桐基; 陈欢

doi:10.11999/JEIT250044

时序信息驱动的并行交互式多模型水下目标跟踪算法

doi: 10.11999/JEIT250044 cstr: 32379.14.JEIT250044

1.
哈尔滨理工大学测控技术与通信工程学院哈尔滨 150080
2.
哈尔滨理工大学模式识别与信息感知黑龙江省重点实验室哈尔滨 150080
3.
汉江国家实验室武汉 430000

基金项目: 国家自然科学基金(11804068)，黑龙江省优秀青年教师基础研究支持计划(YQJH2024064)

详细信息

作者简介:
兰朝凤：女，教授，博士生导师，研究方向为水下声信号分析与处理、智能任务规划与决策等

张桐基：男，硕士，研究方向为目标跟踪

陈欢：男，高级工程师，研究方向为水下声信号探测与识别，大型航行体的智能路径规划与决策

通讯作者:
陈欢　13545022860@139.com

中图分类号: TN713
计量
- 文章访问数: 51
- HTML全文浏览量: 12
- PDF下载量: 11
- 被引次数: 0
出版历程
- 收稿日期: 2025-01-20
- 修回日期: 2025-06-30
- 网络出版日期: 2025-07-04

Time-Series Information-Driven Parallel Interactive Multiple Model Algorithm for Underwater Target Tracking

1.
School of Measurement and Control Technology and Communication Engineering, Harbin University of Science and Technology, Harbin 150080, China
2.
Heilongjiang Province Key Laboratory of Pattern Recognition and Information Perception, Harbin University of Science and Technology, Harbin 150080, China
3.
Hanjiang National Laboratory, Wuhan 430000, China

Funds: The National Natural Science Foundation of China (11804068), Heilongjiang Provincial Outstanding Young Teachers Basic Research Support Programme (YQJH2024064)

摘要

摘要: 随着水下目标运动形式的多样化和复杂化，现有的交互式多模型算法(IMM)在面对目标状态切换时存在模型切换缓慢及跟踪精度不足的问题。为此，该文在经典IMM算法的基础上，提出一种基于时序信息的并行交互式多模型目标跟踪算法(TIP-IMM)。该算法通过比较相邻时刻的模型概率变化趋势，动态修正状态转移矩阵的参数，再经归一化处理实现状态转移矩阵的自适应更新。同时利用并行IMM框架和信息熵来动态更新模型概率，避免因过度修正状态转移矩阵而导致的跟踪精度下降。仿真结果表明，与现有算法相比，所提算法对目标的预测精度提高了3.52%～7.87%。同时模型的切换速度更快，有效地提高了水下目标跟踪精度。
- 水下目标跟踪 /
- 交互式多模型算法 /
- 状态转移矩阵 /
- 后验信息 /
- 自适应
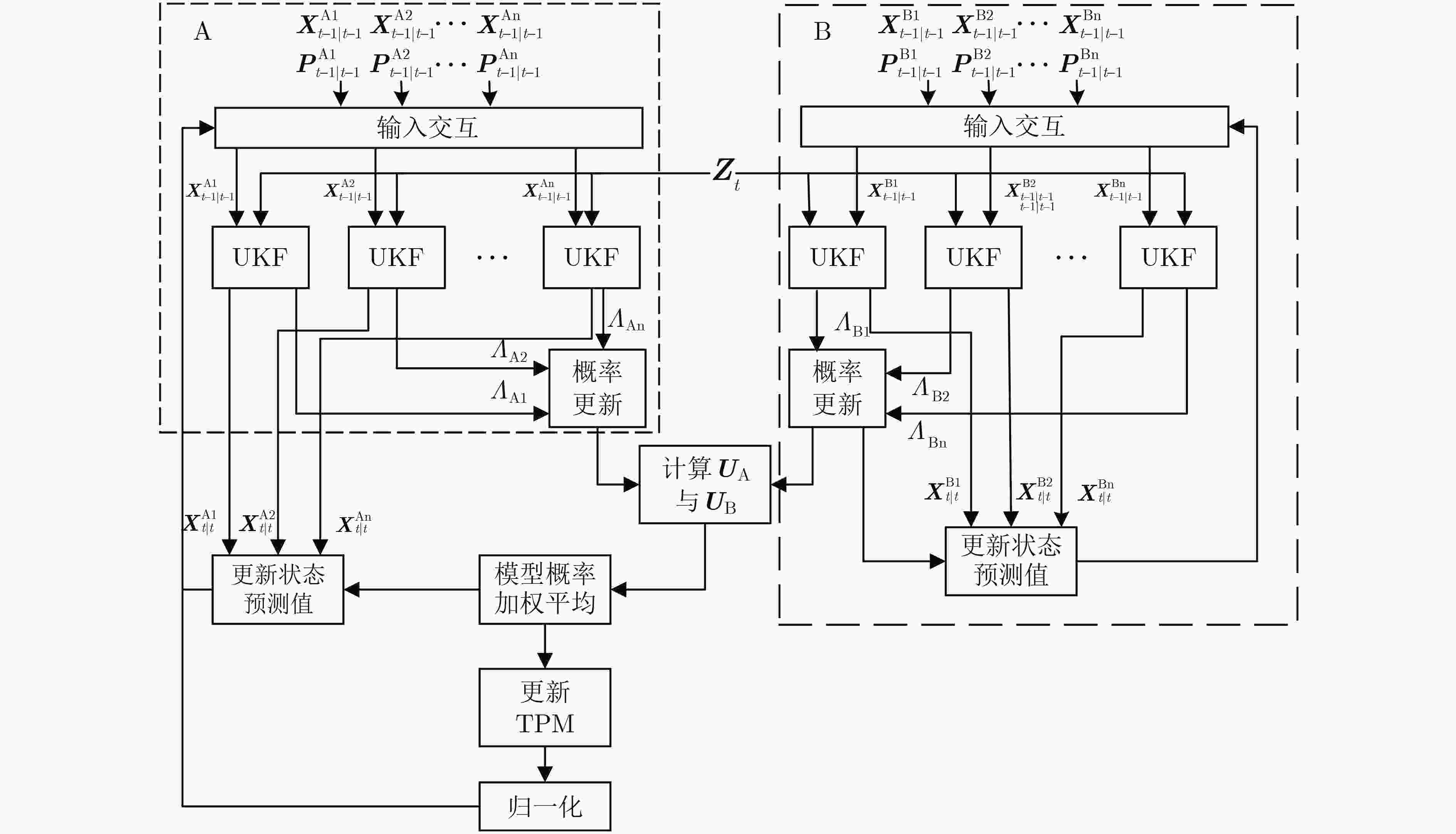
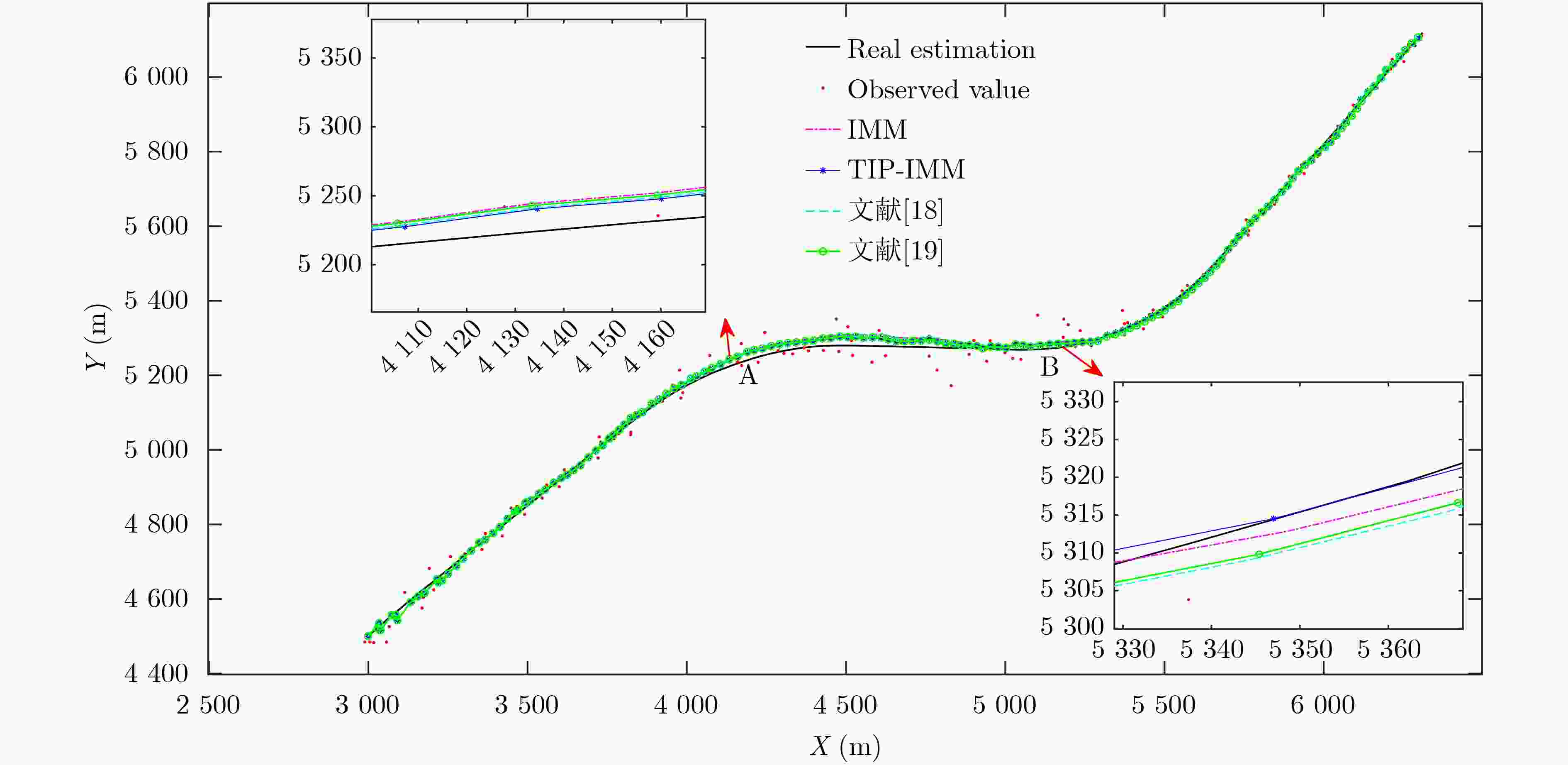
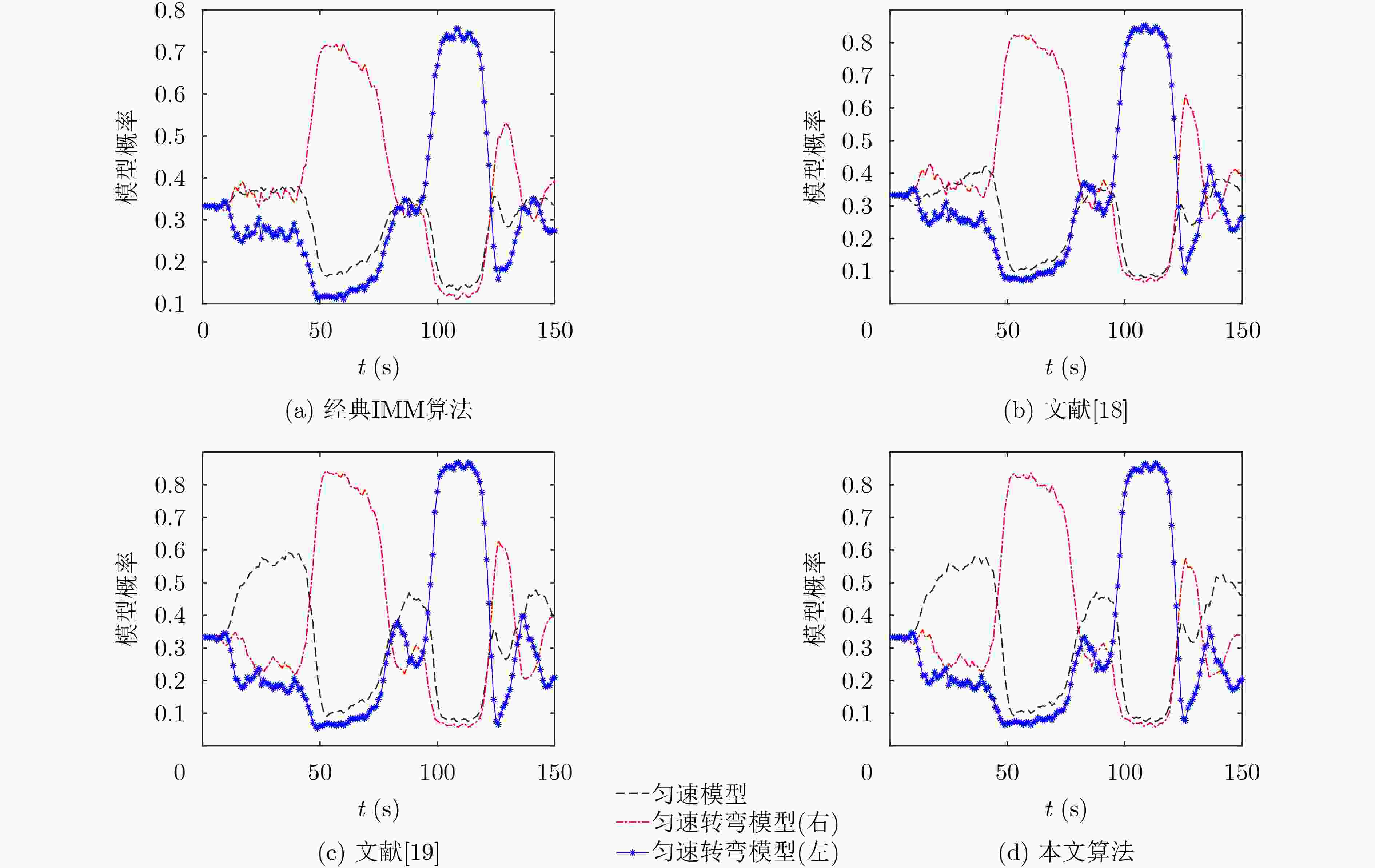
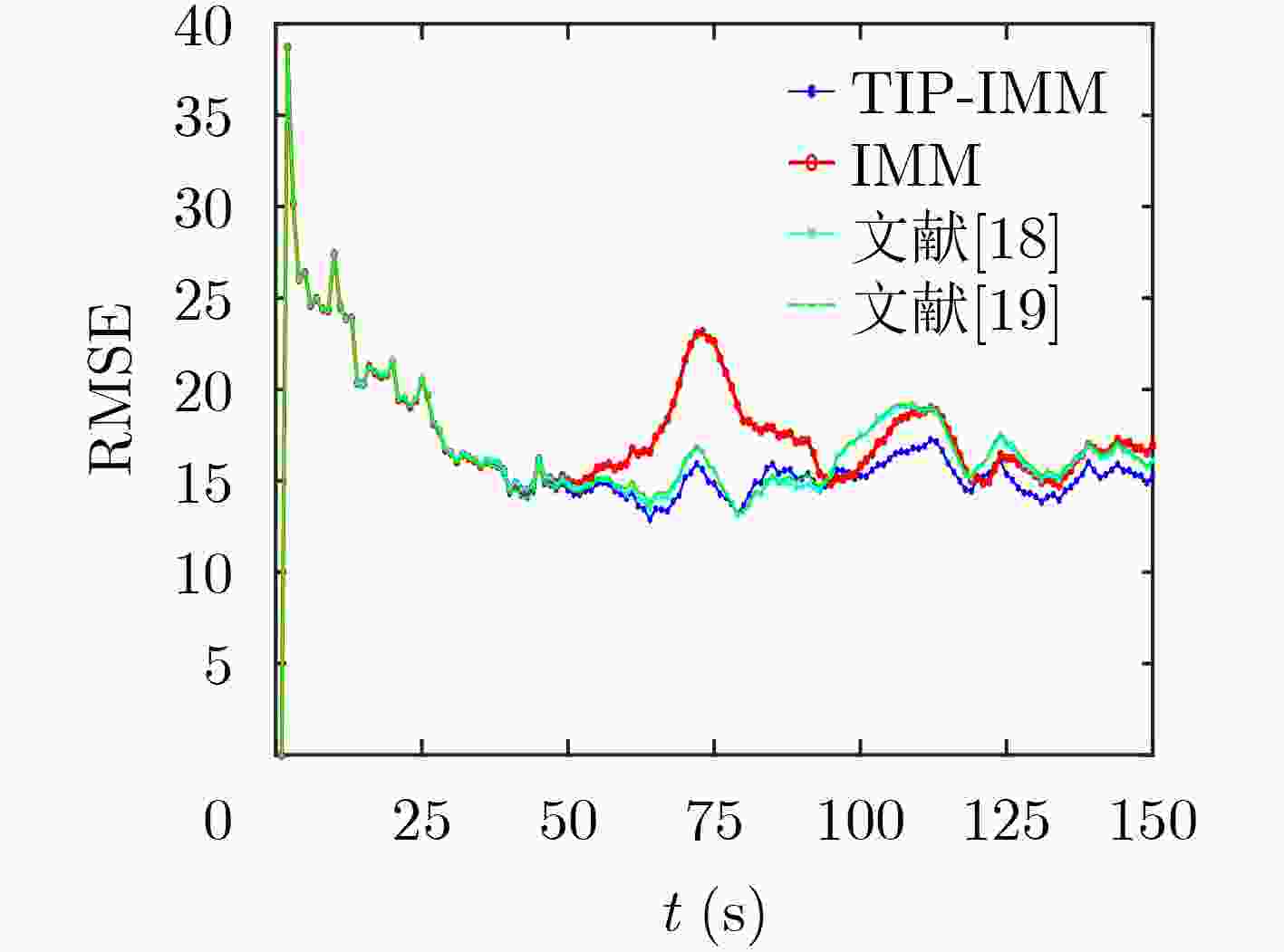
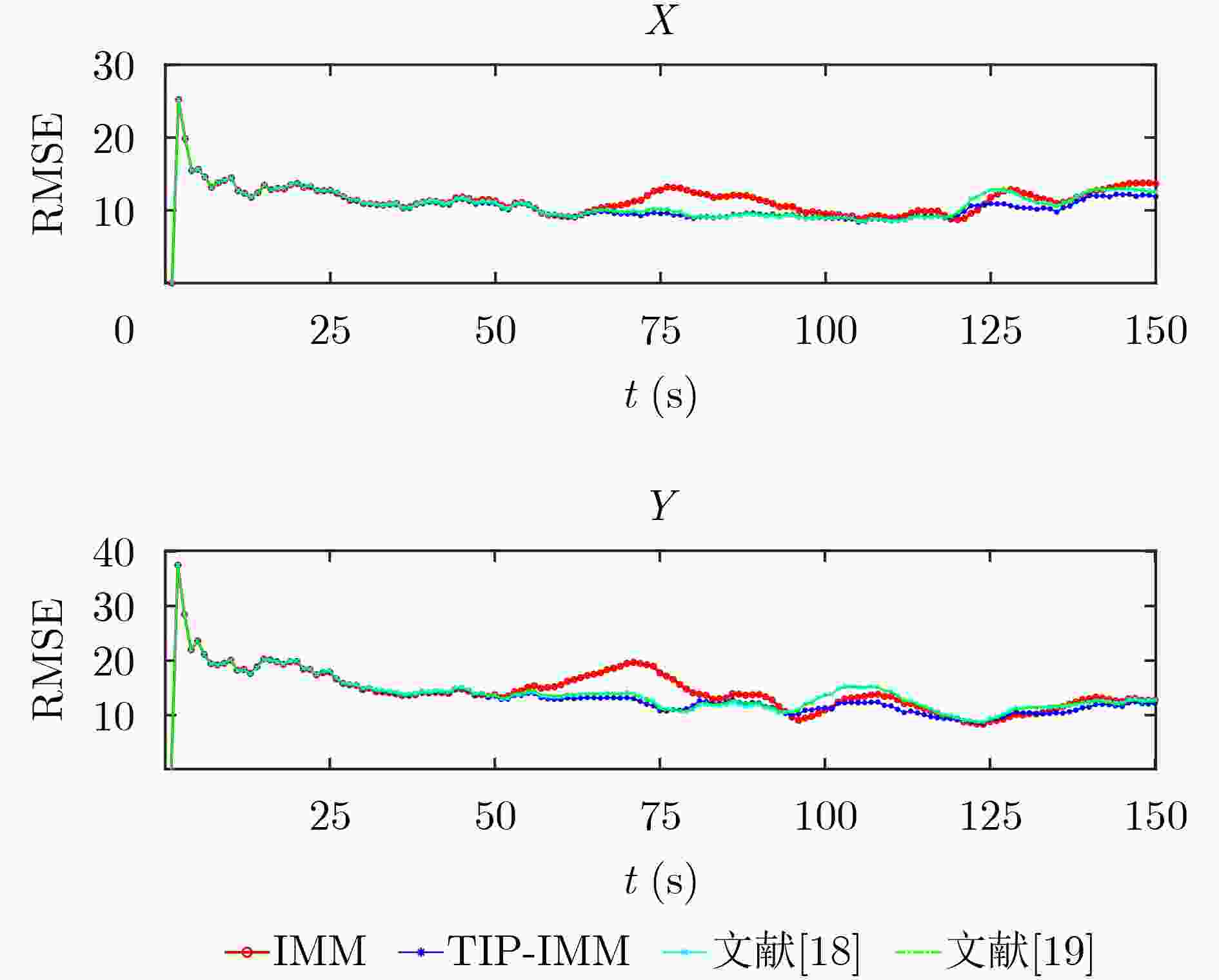
Abstract: Objective Accurate underwater target tracking is critical in marine surveillance, military reconnaissance, and resource management. The nonlinear, stochastic, and uncertain motion of underwater targets—exacerbated by complex environmental dynamics—limits the effectiveness of traditional tracking methods. The Interacting Multiple Model (IMM) algorithm addresses this challenge by integrating several motion models and adaptively switching between them based on the target’s dynamic state. Such adaptability enables improved tracking under abrupt motion transitions, such as submarine maneuvers or the irregular paths of unmanned underwater vehicles. However, the classical IMM algorithm relies on a fixed Transition Probability Matrix (TPM), which can delay model switching and reduce tracking accuracy in highly dynamic settings. To overcome these limitations, this paper proposes an adaptive IMM algorithm that incorporates timing information, parallel processing, and information entropy. These enhancements improve model-switching speed and accuracy, increase adaptability to environmental changes, and boost overall tracking performance and stability. Methods This study proposes a Temporal Information Parallel Interacting Multiple Model (TIP-IMM) target tracking algorithm that integrates temporal information, information entropy evaluation, and parallel processing to adaptively correct the TPM. At each time step, the algorithm identifies the model with the highest probability and assesses whether this model remains dominant across consecutive time steps. If consistent, it is designated the main model. The algorithm then evaluates changes in the main model’s probability relative to other models and updates the TPM based on defined correction rules. A parallel structure is introduced: Module A performs TPM correction, while Module B executes a standard IMM algorithm. Both modules operate concurrently. Information entropy is employed to quantify the uncertainty of the model probability distribution. When entropy is low in Module A, its corrected results are prioritized; when entropy is high, the system places greater reliance on Module B to ensure stable and robust performance under varying conditions. Results and Discussions The proposed TIP-IMM algorithm is evaluated through simulation experiments, demonstrating improved tracking accuracy and stability. True motion and observation trajectories are generated using predefined initial parameters and a motion model. Filtering results from TIP-IMM are compared with those of three benchmark algorithms. The estimated trajectories from TIP-IMM align more closely with the true trajectories, as confirmed by the enlarged views in panels A and B (Fig. 3). Analysis of model probability evolution during filtering indicates that TIP-IMM exhibits smaller fluctuations during model transitions and identifies the dominant model more rapidly than the comparison methods (Fig. 4). To quantify tracking performance, Root Mean Square Error (RMSE) serves as the evaluation metric. TIP-IMM consistently yields lower and smoother RMSE curves across the full trajectory and in both X and Y directions (Figs. 5 and 6). Furthermore, average RMSE (ARMSE) serves as a comprehensive indicator. TIP-IMM achieves lower errors in both position and velocity estimates (Table 2), consistent with the trend observed in RMSE analysis. Although the algorithm incurs a slightly higher runtime than the reference methods, its execution time remains within the millisecond range, meeting the real-time requirements of practical applications (Table 3). Conclusions This study proposes a TIP-IMM algorithm to address limitations of the classical IMM algorithm, particularly model-switching delays and over-smoothing during abrupt target motion changes. By incorporating temporal correlation of model probabilities, parallel processing, and information entropy, TIP-IMM improves responsiveness and transition smoothness in dynamic environments. Simulation experiments confirm that TIP-IMM achieves faster and more accurate model switching than existing methods. Compared with the traditional IMM and benchmark algorithms, TIP-IMM improves overall tracking accuracy by 3.52% to 7.87% across multiple scenarios. It also reduces estimation error recovery time while maintaining high accuracy during sudden motion transitions. These results demonstrate the algorithm’s enhanced adaptability, robustness, and stability, making it well suited for underwater target tracking applications.
- Underwater Target Tracking /
- Interacting Multiple Model (IMM) /
- Transition Probability Matrix (TPM) /
- Posterior Information /
- Adaptive

HTML全文

图 1 TIP-IMM算法流程

下载: 全尺寸图片幻灯片

图 2 4种算法跟踪轨迹对比图

下载: 全尺寸图片幻灯片

图 3 4种算法的模型概率曲线变化图

下载: 全尺寸图片幻灯片

图 4 不同算法的位置误差曲线与时间关系

下载: 全尺寸图片幻灯片

图 5 不同算法算在X方向和Y方向上的误差曲线与时间关系

下载: 全尺寸图片幻灯片

表 1 目标运动情况

时间(s)	1～40	41～70	71～90	91～115	116～150
运动状态	直线运动	匀速转弯 –1.2 °/s	直线运动	匀速转弯 1.8 °/s	直线运动

下载: 导出CSV

表 2 4种算法的误差对比

方法	ARMSE
	位置误差(m)			速度误差(m/s)
	位置整体误差	X方向	Y方向	X方向	Y方向
经典IMM	18.3600	11.4543	14.4556	1.0437	1.6767
文献[18]	17.6373	10.9372	13.9609	1.0408	1.6653
文献[19]	17.6248	10.9194	13.9302	1.0311	1.6653
本文算法(TIP-IMM)	17.0247	10.6614	13.3926	1.0190	1.6014

下载: 导出CSV

表 3 4种算法的运行时间

方法	总运行时常(ms)	平均运行时间(ms)
经典IMM	1160.7	11.16
文献[18]	2391.5	23.92
文献[19]	1817.3	18.17
本文算法(TIP-IMM)	2513.8	25.14

下载: 导出CSV

参考文献(26)

[1]	PERKOVIČ M, GUCMA L, and FEUERSTACK S. Maritime security and risk assessments[J]. Journal of Marine Science and Engineering, 2024, 12(6): 988. doi: 10.3390/jmse12060988.
[2]	PRASETYO K A, ANSORI A, and SUSETO B. Maritime defense strategy education as an effort of the indonesian government in maintaining maritime security[J]. International Journal of Asian Education, 2023, 4(1): 58–67. doi: 10.46966/ijae.v4i1.325.
[3]	YUE Wenrong, XU Feng, and YANG Juan. Tracking-by-detection algorithm for underwater target based on improved multi-kernel correlation filter[J]. Remote Sensing, 2024, 16(2): 323. doi: 10.3390/rs16020323.
[4]	JIA Shuyi, ZHANG Yun, and WANG Guohong. Highly maneuvering target tracking using multi-parameter fusion singer model[J]. Journal of Systems Engineering and Electronics, 2017, 28(5): 841–850. doi: 10.21629/JSEE.2017.05.03.
[5]	ZHANG Licheng, PENG Kun, ZHAO Xingmo, et al. New fuel consumption model considering vehicular speed, acceleration, and jerk[J]. Journal of Intelligent Transportation Systems, 2023, 27(2): 174–186. doi: 10.1080/15472450.2021.2000406.
[6]	DENG Mingjun, LI Shuhang, JIANG Xueqing, et al. Vehicle trajectory prediction method based on “Current” statistical model and cubature Kalman filter[J]. Electronics, 2023, 12(11): 2464. doi: 10.3390/electronics12112464.
[7]	HAN Guoxing, LIU Fuyun, DENG Jucai, et al. An adaptive vehicle tracking enhancement algorithm based on fuzzy interacting multiple model robust cubature Kalman filtering[J]. Circuits, Systems, and Signal Processing, 2024, 43(1): 191–223. doi: 10.1007/s00034-023-02497-x.
[8]	BLOM H A P and BAR-SHALOM Y. The interacting multiple model algorithm for systems with markovian switching coefficients[J]. IEEE Transactions on Automatic Control, 1988, 33(8): 780–783. doi: 10.1109/9.1299.
[9]	SUN Lifan, ZHANG Jinjin, YU Haofang, et al. Tracking of maneuvering extended target using modified variable dtructure multiple-model based on adaptive grid best model augmentation[J]. Remote Sensing, 2022, 14(7): 1613. doi: 10.3390/rs14071613.
[10]	XU Hong, PAN Qin, XU Heng, et al. Adaptive IMM smoothing algorithms for jumping markov system with mismatched measurement noise covariance matrix[J]. IEEE Transactions on Aerospace and Electronic Systems, 2024, 60(4): 5467–5480. doi: 10.1109/TAES.2024.3392552.
[11]	TIAN Ye, JIANG Hong, DING Quanxin, et al. Turn rate estimation based adaptive IMM algorithm for maneuvering target tracking[J]. Advanced Materials Research, 2012, 383/390: 5609–5614. doi: 10.4028/www.scientific.net/AMR.383-390.5609.
[12]	WANG Gang. ML estimation of transition probabilities in jump Markov systems via convex optimization[J]. IEEE Transactions on Aerospace and Electronic Systems, 2010, 46(3): 1492–1502. doi: 10.1109/TAES.2010.5545204.
[13]	LUO Yalun, LI Zhaoming, LIAO Yurong, et al. Adaptive Markov IMM based multiple fading factors strong tracking CKF for maneuvering hypersonic-target tracking[J]. Applied Sciences, 2022, 12(20): 10395. doi: 10.3390/app122010395.
[14]	许登荣, 程水英, 包守亮. 自适应转移概率交互式多模型跟踪算法[J]. 电子学报, 2017, 45(9): 2113–2120. doi: 10.3969/j.issn.0372-2112.2017.09.009. XU Dengrong, CHENG Shuiying, and BAO Shouliang. Interacting multiple model algorithm based on adaptive transition probability[J]. Acta Electronica Sinica, 2017, 45(9): 2113–2120. doi: 10.3969/j.issn.0372-2112.2017.09.009.
[15]	LEE I H and PARK C G. An improved interacting multiple model algorithm with adaptive transition probability matrix based on the situation[J]. International Journal of Control, Automation and Systems, 2023, 21(10): 3299–3312. doi: 10.1007/s12555-022-0989-4.
[16]	ZHANG Zhao, GUO Hongwu, HE Jiaxing, et al. Adaptive interactive multiple model target tracking algorithm based on markov matrix with acceleration correction factor[C]. Proceedings of 2022 China Automation Congress (CAC), Xiamen, China, 2022: 3227–3232. doi: 10.1109/CAC57257.2022.10055933.
[17]	XIE Guo, SUN Lanlan, WEN Tao, et al. Adaptive transition probability matrix-based parallel IMM algorithm[J]. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2021, 51(5): 2980–2989. doi: 10.1109/TSMC.2019.2922305.
[18]	王平波, 刘杨. 基于改进自适应IMM-UKF算法的水下目标跟踪[J]. 电子与信息学报, 2022, 44(6): 1999–2005. doi: 10.11999/JEIT211128. WANG Pingbo and LIU Yang. Underwater target tracking algorithm based on improved adaptive IMM-UKF[J]. Journal of Electronics & Information Technology, 2022, 44(6): 1999–2005. doi: 10.11999/JEIT211128.
[19]	王小敏, 雷筱, 张亚东. 基于改进自适应IMM算法的高速列车组合定位[J]. 电子与信息学报, 2024, 46(3): 817–825. doi: 10.11999/JEIT230251. WANG Xiaomin, LEI Xiao, and ZHANG Yadong. Combined positioning of high-speed train based on improved adaptive IMM algorithm[J]. Journal of Electronics & Information Technology, 2024, 46(3): 817–825. doi: 10.11999/JEIT230251.
[20]	LIBÓRIO M P, KARAGIANNIS R, DINIZ A M A, et al. The use of information entropy and expert opinion in maximizing the discriminating power of composite indicators[J]. Entropy, 2024, 26(2): 143. doi: 10.3390/e26020143.
[21]	LI Yuankai, LOU Jiaxin, TAN Xiaosu, et al. Adaptive kernel learning Kalman filtering with application to model-free maneuvering target tracking[J]. IEEE Access, 2022, 10: 78088–78101. doi: 10.1109/ACCESS.2022.3193101.
[22]	孙大军, 张艺翱, 滕婷婷, 等. 单站水下方位频率机动目标运动分析方法[J]. 声学学报, 2024, 49(4): 683–695. doi: 10.12395/0371-0025.2023077. SUN Dajun, ZHANG Yiao, TENG Tingting, et al. A single-platform underwater maneuvering target motion analysis method based on bearing and frequency measurements[J]. Acta Acustica, 2024, 49(4): 683–695. doi: 10.12395/0371-0025.2023077.
[23]	TIAN Feng, ZHANG Haoyu, and FU Weibo. Research on extended target-tracking algorithms of sea surface navigation radar[J]. Electronics, 2023, 12(3): 616. doi: 10.3390/electronics12030616.
[24]	GUO Caifa, DAI Zhengxu, YANG Lei, et al. Application of the strong tracking UKF in the maneuvering target tracking[J]. Journal of Physics: Conference Series, 2016, 679(1): 012048. doi: 10.1088/1742-6596/679/1/012048.
[25]	DAI Hongde, DAI Shaowu, CONG Yuancai, et al. Performance comparison of EKF/UKF/CKF for the tracking of ballistic target[J]. TELKOMNIKA Indonesian Journal of Electrical Engineering, 2012, 10(7). doi: 10.11591/telkomnika.v10i7.1564. (查阅网上资料,未找到本条文献页码信息,请确认).
[26]	LIU Haoran, JIANG Qiumei, QIN Yuha, et al. Double layer weighted unscented Kalman underwater target tracking algorithm based on sound speed profile[J]. Ocean Engineering, 2022, 266: 112982. doi: 10.1016/j.oceaneng.2022.112982.