航天器姿态系统的分数阶滑模容错控制器设计

张猛; 王利楠; 郑德智; 伊枭剑

doi:10.11999/JEIT250025

航天器姿态系统的分数阶滑模容错控制器设计

doi: 10.11999/JEIT250025 cstr: 32379.14.JEIT250025

1.
东南大学网络空间安全学院江苏南京 211189
2.
东南大学数学学院系统科学系江苏南京 211189
3.
北京理工大学前沿交叉科学研究院北京 100081
4.
北京理工大学机电学院北京 100081

基金项目: 国家自然科学基金(62325304, U22B2046, U24A20279)，江苏省应用数学科学研究中心(BK20233002)

详细信息

作者简介:
张猛：男，博士生，研究方向为无人系统故障诊断、分布式容错控制

王利楠：男，博士生，研究方向为非线性控制、分布式非光滑控制

郑德智：男，研究员，研究方向为临空信息探测、极端信号测量技术、传感器敏感机理

伊枭剑：男，副研究员，研究方向为无人系统可靠性与智能决策、故障预测与健康管理

通讯作者:
张猛　230239277@seu.edu.cn

中图分类号: TN911.7; TP13; V448.2
计量
- 文章访问数: 157
- HTML全文浏览量: 75
- PDF下载量: 29
- 被引次数: 0
出版历程
- 收稿日期: 2025-01-10
- 修回日期: 2025-05-13
- 网络出版日期: 2025-06-18
- 刊出日期: 2025-06-30

Fractional-Order Sliding Mode Fault-Tolerant Attitude Controller for Spacecraft

1.
School of Cyber Science and Engineering, southeast university, Nanjing 211189, China
2.
Department of Systems Science, Southeast University, Nanjing 211189, China
3.
Advanced Research Institute of Multidisciplinary Sciences, Beijing Institute of Technology, Beijing 100081, China
4.
School of Mechatronical Engineering, Beijing Institute of Technology, Beijing 100081, China

Funds: The National Natural Science Foundation of China (62325304, U22B2046, U24A20279), Jiangsu Provincial Scientific Research Center of Applied Mathematics (BK20233002)

摘要

摘要: 为解决执行器故障、外部干扰和内部参数不确定性导致的航天器姿态控制精度不足的问题，该文提出了一种新型的航天器姿态系统有限时间容错控制方法。通过对航天器姿态故障模型的分析，将执行器故障、惯性矩阵不确定性和外部环境干扰建模为集中干扰，并设计了有限时间观测器来补偿这些集中干扰。在此基础上，设计了一种新型的分数阶滑模容错控制器，以确保航天器的姿态角和角速度在有限时间内实现跟踪。最后，该文给出了一个仿真实例，并通过与现有算法对比，验证了所提出控制框架的有效性。
- 有限时间控制 /
- 执行器故障 /
- 容错控制 /
- 分数阶终端滑模
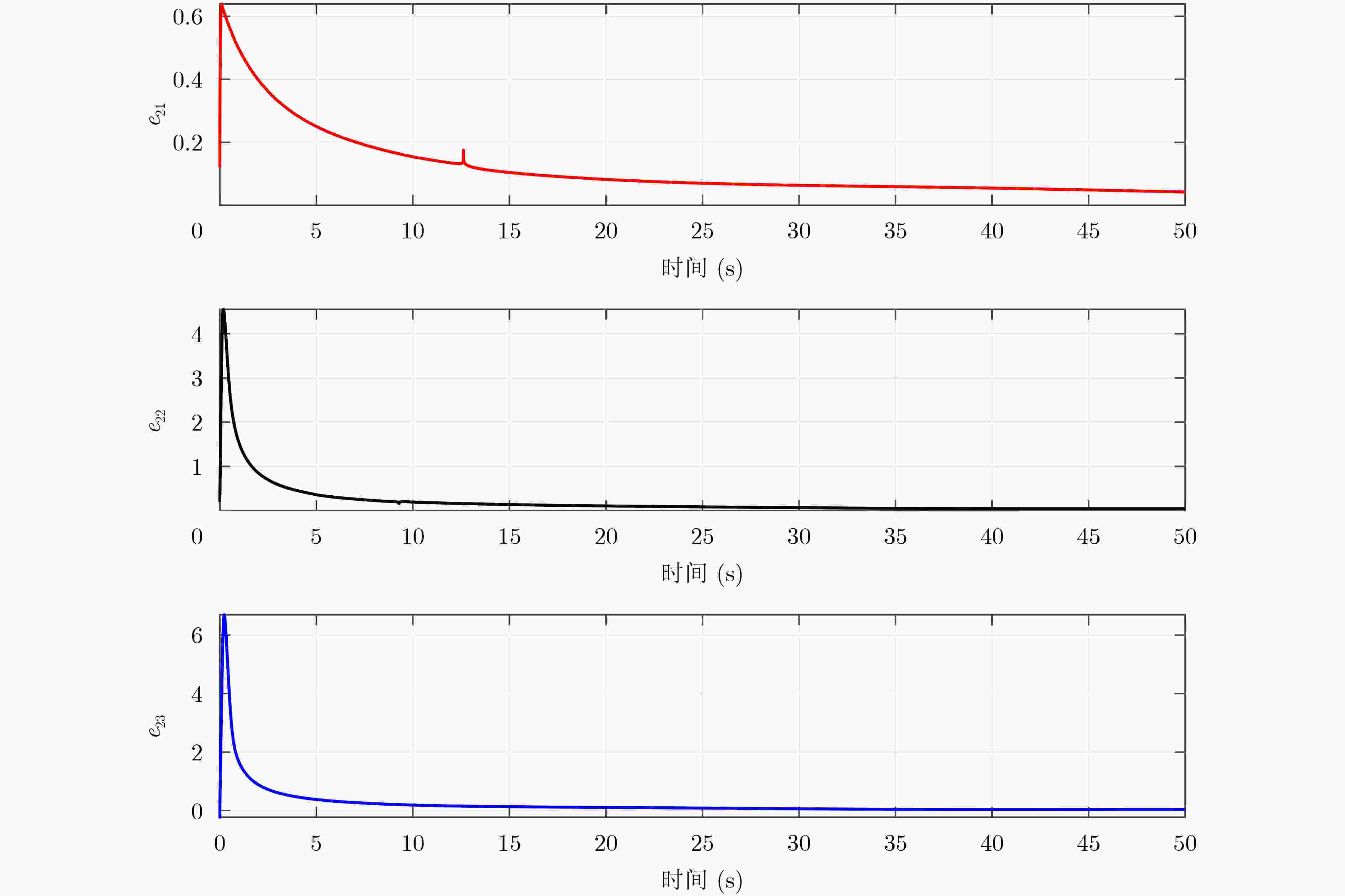
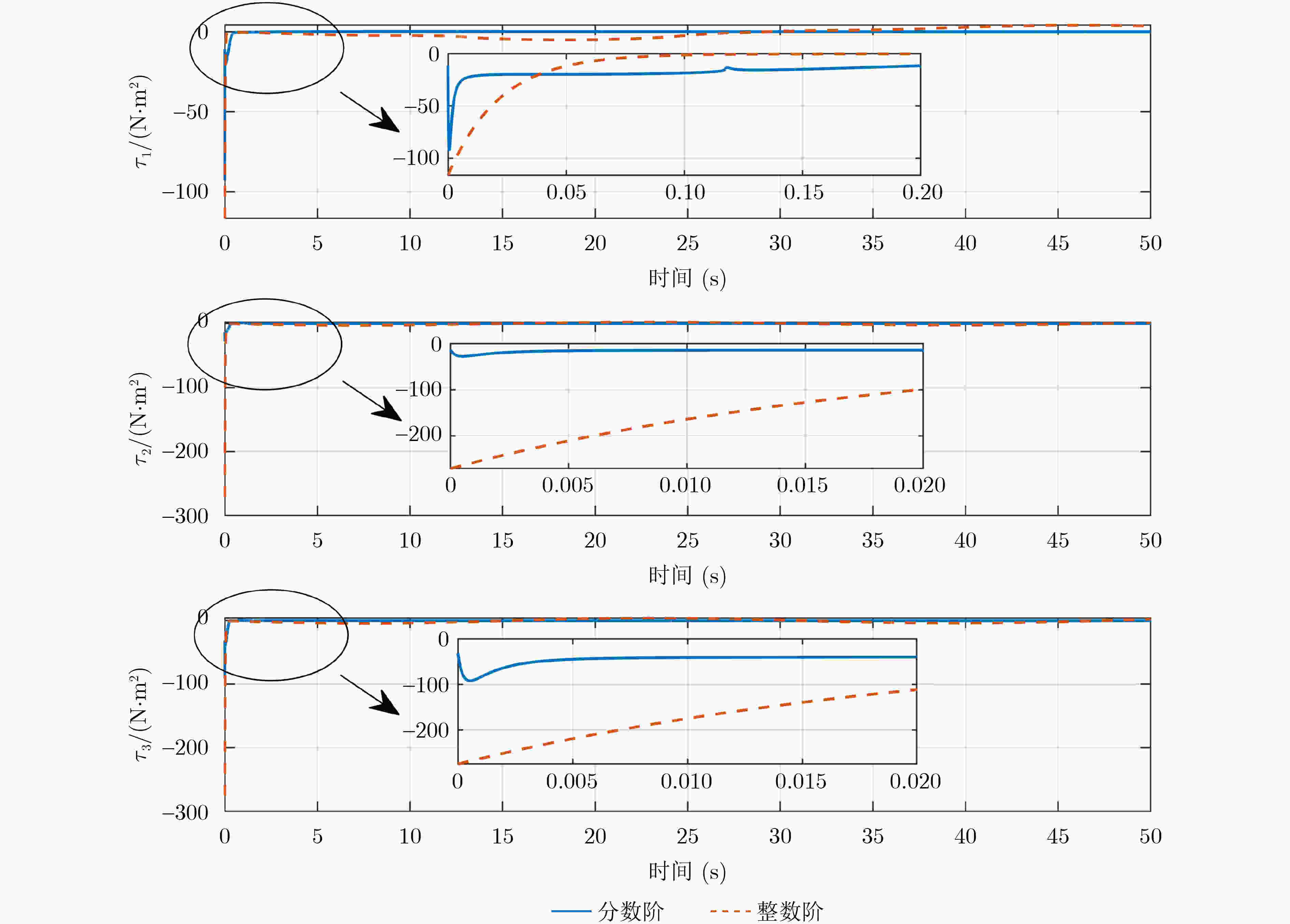
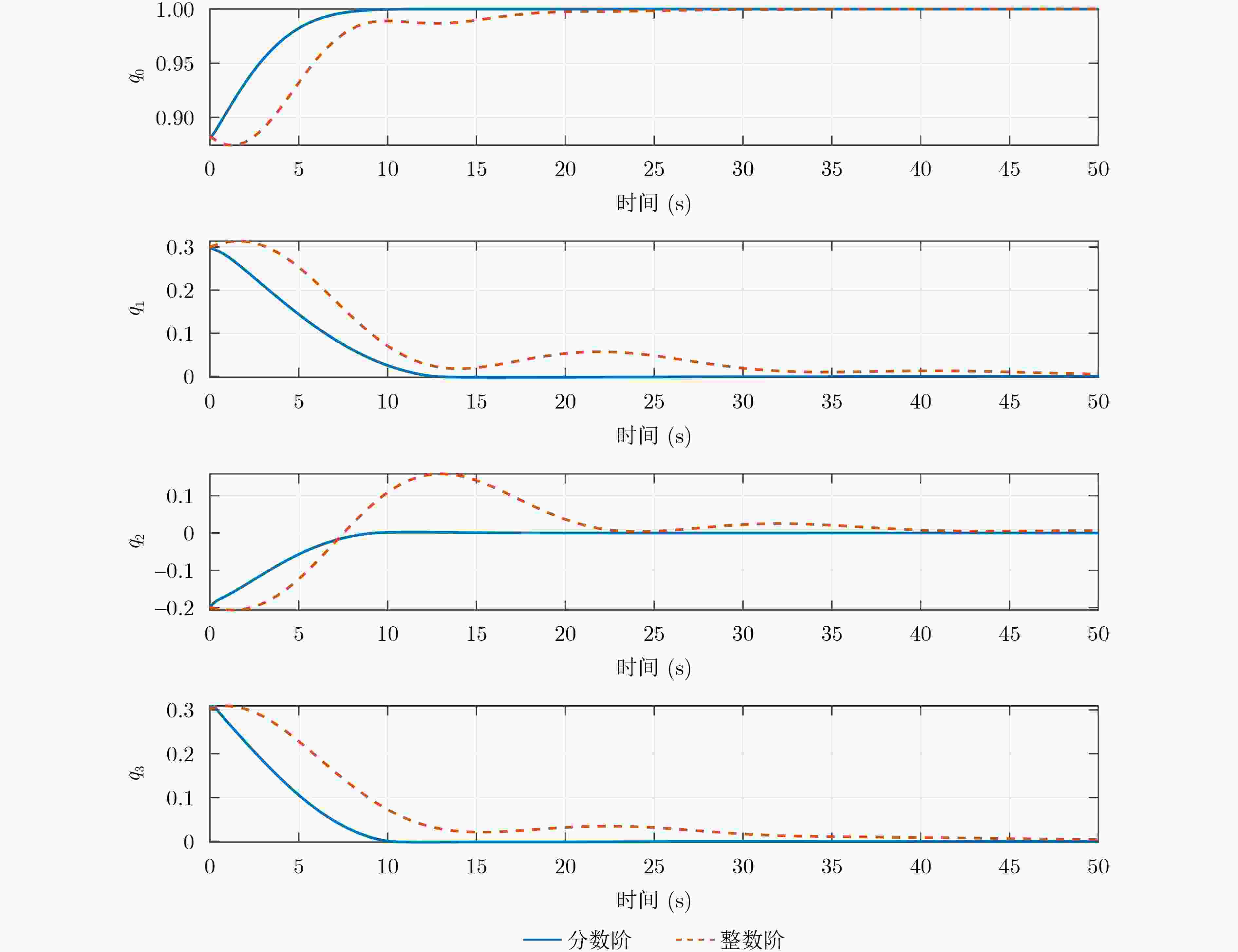
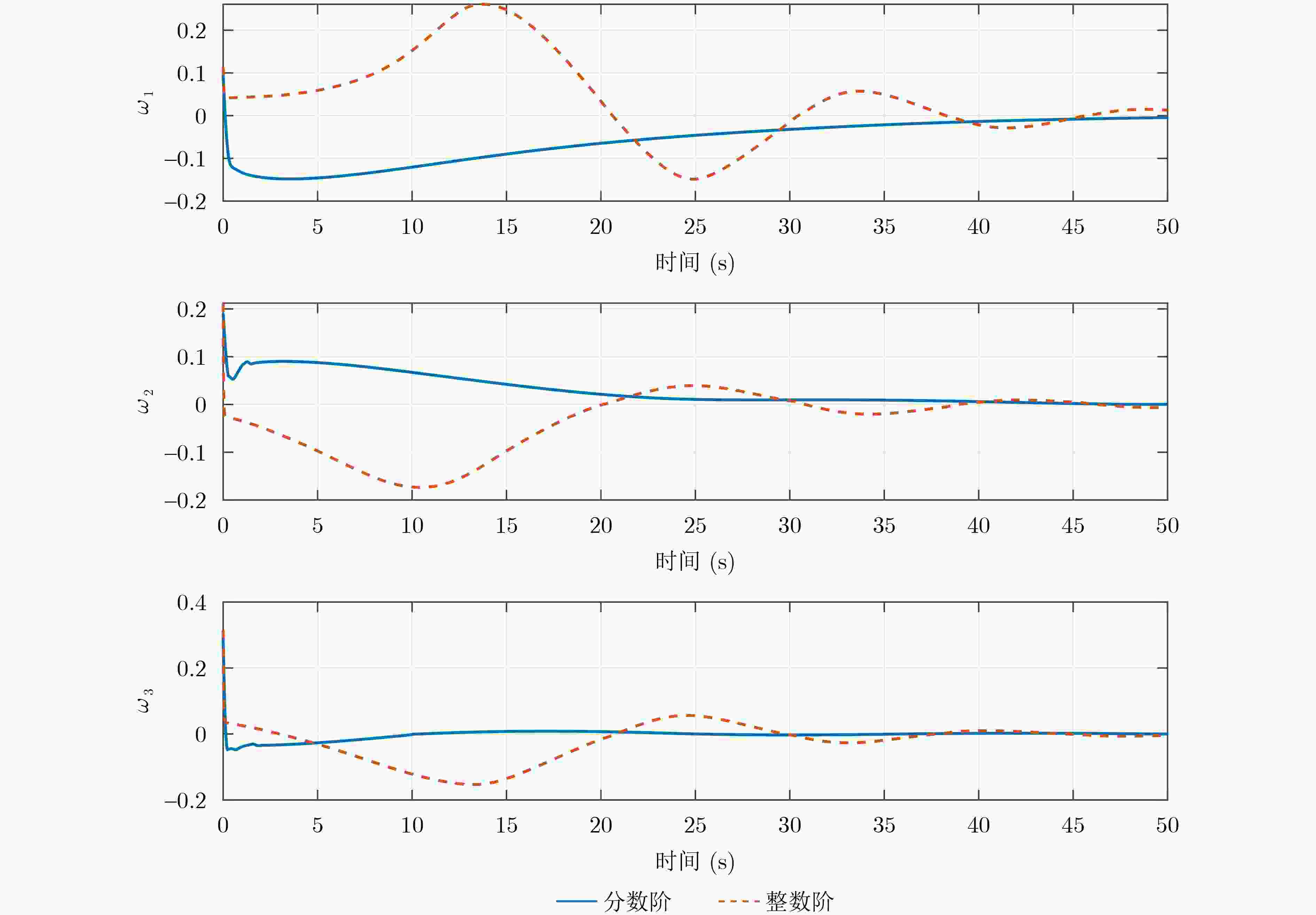
Abstract: Objective Spacecraft attitude control under complex operational conditions remains limited by inadequate controller adaptability, insufficient precision, and rapid chattering near the sliding surface. Fractional-Order Sliding Mode Control (FOSMC), which integrates fractional calculus into control algorithms, offers improved modeling flexibility and robustness. Compared with conventional integer-order controllers, fractional-order controllers yield smoother responses and enhanced dynamic behavior. This study proposes a novel fault-tolerant control strategy that combines FOSMC with fault accommodation mechanisms to achieve accurate spacecraft attitude tracking in the presence of system faults and environmental disturbances. Methods A finite-time disturbance observer is proposed to unify actuator faults, inertia uncertainties, and external disturbances into a single lumped term. This formulation allows for accurate estimation of both the system state and disturbances, supporting effective compensation. The observer’s fast convergence and robustness are analytically demonstrated using finite-time stability theory. To further accelerate convergence and mitigate the chattering typically observed in conventional sliding mode control, a finite-time fault-tolerant controller based on fractional-order sliding mode is developed. This controller ensures finite-time stabilization of spacecraft attitude and angular velocity. Results and Discussions To evaluate the effectiveness and performance advantages of the proposed method, a comparative analysis is conducted against an Integer-Order Sliding Mode Controller (IOSMC) using MATLAB simulations. Figure 1 shows the estimation error of the proposed finite-time observer, demonstrating its ability to rapidly and accurately estimate the lumped disturbance term. Figure 2 presents the attitude response trajectories under both control strategies, with blue and red lines corresponding to the fractional-order and integer-order controllers, respectively. Although both methods successfully track the desired attitude, the FOSMC exhibits significantly faster convergence. Figure 3 displays the angular velocity error curves, indicating that the FOSMC achieves finite-time stabilization. In comparison with the IOSMC, the proposed controller yields quicker convergence and reduced steady-state error. Figure 4 illustrates the control torque profiles, revealing that the FOSMC produces smoother torque outputs. Conclusions This study proposes a spacecraft attitude controller based on fractional-order sliding mode theory to reduce the high-frequency chattering observed near the sliding surface in conventional terminal sliding mode control. By incorporating fractional-order calculus into the control framework, a fault-tolerant strategy is developed to enhance the performance of spacecraft attitude systems under uncertain and faulty conditions. Simulation results validate the following advantages: (1) Compared with the IOSMC algorithm, the proposed controller achieves faster convergence and improved chattering suppression. (2) Actuator faults, inertia uncertainties, and external disturbances are consolidated into a unified disturbance term, which is accurately estimated by a finite-time disturbance observer for effective compensation. (3) The use of a fractional-order non-singular terminal sliding surface, together with Lyapunov-based analysis, provides a rigorous guarantee of finite-time stability. Moreover, the fractional-order sliding surface increases the design flexibility, allowing broader optimization of controller parameters. This work addresses finite-time fault-tolerant control for spacecraft attitude systems. Future research may investigate fixed-time fault-tolerant control approaches to further improve robustness and ensure consistent response times.
- Finite-time control /
- Actuator failure /
- Fault-tolerant control /
- Fractional-order terminal sliding mode

HTML全文

图 1 观测误差响应曲线

下载: 全尺寸图片幻灯片

图 4 航天器控制力矩响应曲线

下载: 全尺寸图片幻灯片

图 2 航天器姿态响应曲线

下载: 全尺寸图片幻灯片

图 3 角速度误差响应曲线

下载: 全尺寸图片幻灯片

表 1 执行器的故障分类

${\boldsymbol{\varGamma}} (t)$，${\boldsymbol{P}}(t)$	故障类型
${\rho _i}(t) = 0$	完全故障
$0 \lt {\rho _i}(t) \lt 1$	部分故障
${\rho _i}(t) = 1$	无故障
${\boldsymbol{\varGamma}} (t) = 0$	无偏差故障
${\boldsymbol{\varGamma}} (t) \ne 0$	偏差故障

下载: 导出CSV

参考文献(29)

[1]	江碧涛, 温广辉, 周佳玲, 等. 智能无人集群系统跨域协同技术研究现状与展望[J]. 中国工程科学, 2024, 26(1): 117–126. doi: 10.15302/J-SSCAE-2024.01.015. JIANG Bitao, WEN Guanghui, ZHOU Jialing, et al. Cross-domain cooperative technology of intelligent unmanned swarm systems: Current status and prospects[J]. Strategic Study of CAE, 2024, 26(1): 117–126. doi: 10.15302/J-SSCAE-2024.01.015.
[2]	王利楠, 温广辉, 伊枭剑. 状态约束下的多飞行器有限时间姿态一致性控制[J]. 现代防御技术, 2024, 52(2): 124–131. doi: 10.3969/j.issn.1009-086x.2024.02.014. WANG Linan, WEN Guanghui, and YI Xiaojian. Finite-time attitude consensus control of multiple unmanned aerial vehicles under state constraints[J]. Modern Defense Technology, 2024, 52(2): 124–131. doi: 10.3969/j.issn.1009-086x.2024.02.014.
[3]	胡子晅, 周佳玲, 王利楠, 等. 多BTT导弹滚转通道姿态约束下的固定时间姿态协调控制[J]. 系统工程与电子技术, 2024, 46(6): 2065–2072. doi: 10.12305/j.issn.1001-506X.2024.06.24. HU Zixuan, ZHOU Jialing, WANG Linan, et al. Fixed-time coordinated attitude control for roll channels of multiple BTT missiles with attitude constraints[J]. Systems Engineering and Electronics, 2024, 46(6): 2065–2072. doi: 10.12305/j.issn.1001-506X.2024.06.24.
[4]	YANG Ze, MA Jie, JI Ruihang, et al. IAR-STSCKF-based fault diagnosis and reconstruction for spacecraft attitude control systems[J]. IEEE Transactions on Instrumentation and Measurement, 2022, 71: 3526112. doi: 10.1109/TIM.2022.3212116.
[5]	GAO Han, XIA Yuanqing, ZHANG Jinhui, et al. Finite time fault tolerant output feedback attitude control of spacecraft formation with guaranteed performance[J]. International Journal of Robust and Nonlinear Control, 2021, 31(10): 4664–4688. doi: 10.1002/rnc.5504.
[6]	SHAO Xiaodong, HU Qinglei, SHI Yang, et al. Fault-tolerant control for full-state error constrained attitude tracking of uncertain spacecraft[J]. Automatica, 2023, 151: 110907. doi: 10.1016/j.automatica.2023.110907.
[7]	FAN Liming, HUANG Hai, and ZHOU Kaixing. Robust fault-tolerant attitude control for satellite with multiple uncertainties and actuator faults[J]. Chinese Journal of Aeronautics, 2020, 33(12): 3380–3394. doi: 10.1016/j.cja.2020.06.026.
[8]	MA Yajie, JIANG Bin, TAO Gang, et al. Minimum-eigenvalue-based fault-tolerant adaptive dynamic control for spacecraft[J]. Journal of Guidance, Control, and Dynamics, 2020, 43(9): 1764–1771. doi: 10.2514/1.G004394.
[9]	GAO Shihong, JING Yuanwei, DIMIROVSKI G M, et al. Adaptive fuzzy fault-tolerant control for the attitude tracking of spacecraft within finite time[J]. Acta Astronautica, 2021, 189: 166–180. doi: 10.1016/j.actaastro.2021.08.033.
[10]	MEI Yafei, LIAO Ying, GONG Kejie, et al. Fuzzy adaptive sliding mode fault estimation and fixed-time fault-tolerant control for coupled spacecraft based on SE(3)[J]. Aerospace Science and Technology, 2022, 126: 107673. doi: 10.1016/j.ast.2022.107673.
[11]	MENG Qingkai, YANG Hao, and JIANG Bin. Second-order sliding-mode on SO(3) and fault-tolerant spacecraft attitude control[J]. Automatica, 2023, 149: 110814. doi: 10.1016/j.automatica.2022.110814.
[12]	AMRR S M, SARKAR R, BANERJEE A, et al. Fault-tolerant finite-time adaptive higher order sliding mode control with optimized parameters for attitude stabilization of spacecraft[J]. International Journal of Robust and Nonlinear Control, 2022, 32(5): 2845–2863. doi: 10.1002/rnc.5934.
[13]	KHODAVERDIAN M and MALEKZADEH M. Fault-tolerant model predictive sliding mode control with fixed-time attitude stabilization and vibration suppression of flexible spacecraft[J]. Aerospace Science and Technology, 2023, 139: 108381. doi: 10.1016/j.ast.2023.108381.
[14]	BAI Yuzhi, SUN Huijie, WEN Jie, et al. Fault-tolerant control for the linearized spacecraft attitude control system with Markovian switching[J]. Journal of the Franklin Institute, 2022, 359(17): 9814–9835. doi: 10.1016/j.jfranklin.2022.08.054.
[15]	GUI Haichao. Observer-based fault-tolerant spacecraft attitude tracking using sequential Lyapunov analyses[J]. IEEE Transactions on Automatic Control, 2021, 66(12): 6108–6114. doi: 10.1109/TAC.2021.3062159.
[16]	LEE D. Fault-tolerant finite-time controller for attitude tracking of rigid spacecraft using intermediate quaternion[J]. IEEE Transactions on Aerospace and Electronic Systems, 2021, 57(1): 540–553. doi: 10.1109/TAES.2020.3024399.
[17]	CHEN Wei and HU Qinglei. Sliding-mode-based attitude tracking control of spacecraft under reaction wheel uncertainties[J]. IEEE/CAA Journal of Automatica Sinica, 2023, 10(6): 1475–1487. doi: 10.1109/JAS.2022.105665.
[18]	HU Qinglei, SHAO Xiaodong, and CHEN Wenhua. Robust fault-tolerant tracking control for spacecraft proximity operations using time-varying sliding mode[J]. IEEE Transactions on Aerospace and Electronic Systems, 2018, 54(1): 2–17. doi: 10.1109/TAES.2017.2729978.
[19]	DUAN Wenjie, WANG Dayi, and LIU Chengrui. Integral sliding mode fault-tolerant control for spacecraft with uncertainties and saturation[J]. Asian Journal of Control, 2017, 19(1): 372–381. doi: 10.1002/asjc.1365.
[20]	LABBADI M, BOUKAL Y, TALEB M, et al. Fractional order sliding mode control for the tracking problem of Quadrotor UAV under external disturbances[C]. 2020 European Control Conference (ECC), St. Petersburg, Russia, 2020: 1595–1600. doi: 10.23919/ECC51009.2020.9143707.
[21]	RAZMI H and AFSHINFAR S. Neural network-based adaptive sliding mode control design for position and attitude control of a quadrotor UAV[J]. Aerospace Science and Technology, 2019, 91: 12–27. doi: 10.1016/j.ast.2019.04.055.
[22]	WANG Hongbin, LI Ning, and LUO Qianda. Adaptive fractional-order nonsingular fast terminal sliding mode formation control of multiple quadrotor UAVs-based distributed estimator[J]. Asian Journal of Control, 2023, 25(5): 3671–3686. doi: 10.1002/asjc.3043.
[23]	MOFID O and MOBAYEN S. Robust fractional-order sliding mode tracker for quad-rotor UAVs: Event-triggered adaptive backstepping approach under disturbance and uncertainty[J]. Aerospace Science and Technology, 2024, 146: 108916. doi: 10.1016/j.ast.2024.108916.
[24]	AMRR S M and NABI M. Finite-time fault tolerant attitude tracking control of spacecraft using robust nonlinear disturbance observer with anti-unwinding approach[J]. Advances in Space Research, 2020, 66(7): 1659–1671. doi: 10.1016/j.asr.2020.06.019.
[25]	AMRR S M, BANERJEE A, and NABI M. Fault-tolerant attitude control of small spacecraft using robust artificial time-delay approach[J]. IEEE Journal on Miniaturization for Air and Space Systems, 2020, 1(3): 179–187. doi: 10.1109/JMASS.2020.3022685.
[26]	ZHANG Xin and SHI Ran. Adaptive fractional-order nonsingular fast terminal sliding mode control for manipulators[J]. Complexity, 2021, 2021(1): 7924953. doi: 10.1155/2021/7924953.
[27]	BHAT S P and BERNSTEIN D S. Finite-time stability of continuous autonomous systems[J]. SIAM Journal on Control and Optimization, 2000, 38(3): 751–766. doi: 10.1137/S0363012997321358.
[28]	SHTESSEL Y B, SHKOLNIKOV I A, and LEVANT A. Smooth second-order sliding modes: Missile guidance application[J]. Automatica, 2007, 43(8): 1470–1476. doi: 10.1016/j.automatica.2007.01.008.
[29]	HILFER R. Fractional diffusion based on Riemann-Liouville fractional derivatives[J]. The Journal of Physical Chemistry B, 2000, 104(16): 3914–3917. doi: 10.1021/jp9936289.