基于光量子传输距离矩阵构建的动态目标定位方法

周牧; 王敏; 曹静阳; 何维

doi:10.11999/JEIT250020

基于光量子传输距离矩阵构建的动态目标定位方法

doi: 10.11999/JEIT250020 cstr: 32379.14.JEIT250020

1.
重庆邮电大学通信与信息工程学院重庆 400065
2.
重庆邮电大学电子科学与工程学院重庆 400065

基金项目: 国家自然科学基金(62571074, 62501100)，重庆市自然科学基金(CSTB2025NSCQ-LZX0142)，重庆市技术创新与应用发展专项(重大项目)(CSTB2024TIAD-STX0035)

详细信息

作者简介:
周牧：男，博士生导师，研究方向为量子精密测量、无线定位与感知、多源信息融合与机器学习等

王敏：女，硕士生，研究方向为量子目标定位技术

曹静阳：女，博士生，研究方向为量子成像

何维：女，博士，研究方向为量子雷达

通讯作者:
周牧　zhoumu@cqupt.edu.cn

中图分类号: O431.2
计量
- 文章访问数: 58
- HTML全文浏览量: 25
- PDF下载量: 5
- 被引次数: 0
出版历程
- 收稿日期: 2025-01-10
- 修回日期: 2025-10-21
- 录用日期: 2025-11-03
- 网络出版日期: 2025-11-09

Dynamic Target Localization Method Based on Optical Quantum Transmission Distance Matrix Constructing

1.
School of Communications and Information Engineering, Chongqing University of Posts and Telecommunications, Chongqing 400065, China
2.
School of Electronic Science and Engineering, Chongqing University of Posts and Telecommunications, Chongqing 400065, China

Funds: The National Natural Science Foundation of China(62571074, 62501100), The Natural Science Foundation of Chongqing(CSTB2025NSCQ-LZX0142), The Special Project of Chongqing Technology Innovation and Application Development (Major Project)(CSTB2024TIAD-STX0035)

摘要

摘要: 利用纠缠态光量子的时间关联特性能够实现对目标的精确定位，但现有量子定位算法主要针对相对静止目标，难以适用于动态目标。于是，该文提出一种基于光量子传输距离矩阵构建的动态目标定位方法，以实现对运动目标的高精度定位。首先，通过对量子回波信号进行分析，结合符合计数结果估计背景噪声，优化检测阈值，实现了高灵敏度的目标检测。其次，利用速度测量矩阵进行自适应光量子分组，以提升定位系统的精确度。最后，通过构建光量子传输距离矩阵，求解光源坐标、目标位置与光量子传输距离的方程组，实现了动态目标位置估计。实测结果表明，该文方法实现了对动态目标的高精度定位，定位误差为厘米级，该方法定位误差在0.06 m内的置信概率达85%，相较于现有光量子定位方法的置信概率提高了69%，相较于传统单光子激光雷达动态目标定位方法提高了31%。
- 纠缠光量子 /
- 量子定位 /
- 动态目标 /
- 符合计数 /
- 传输距离矩阵
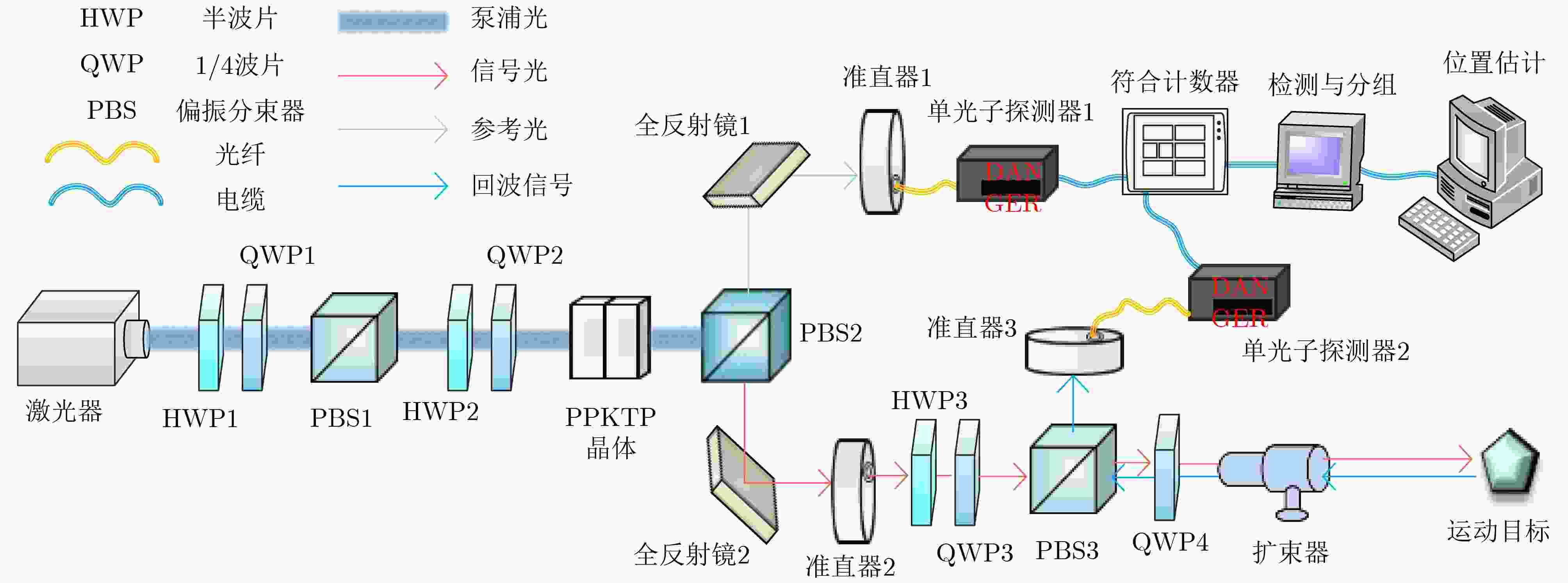
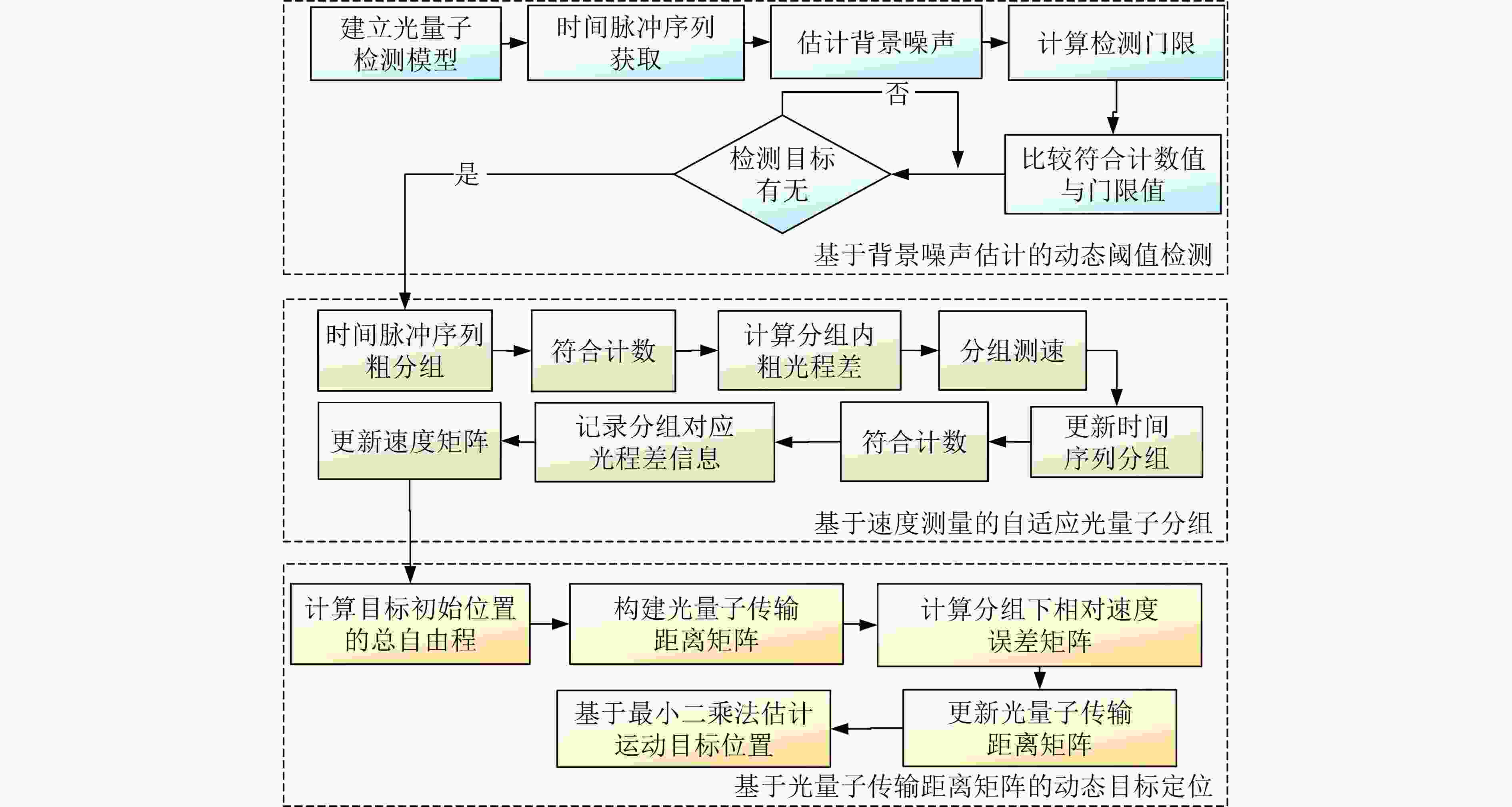
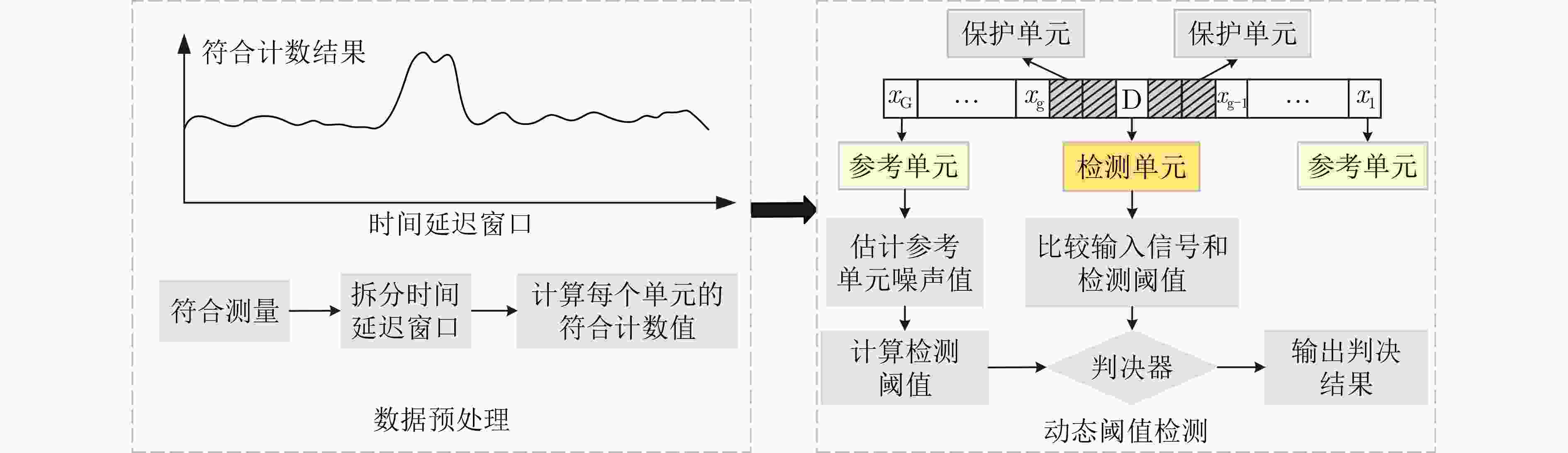
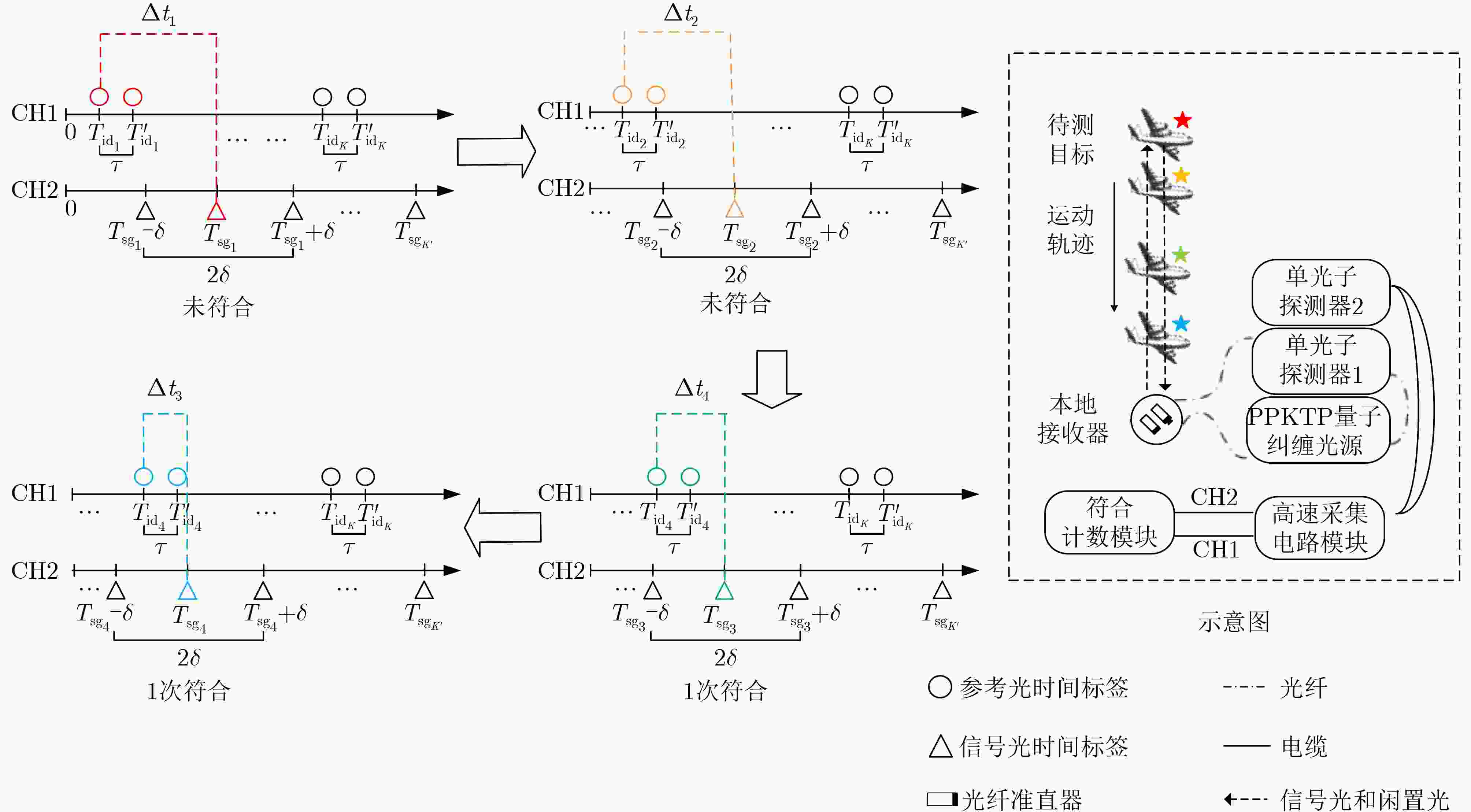
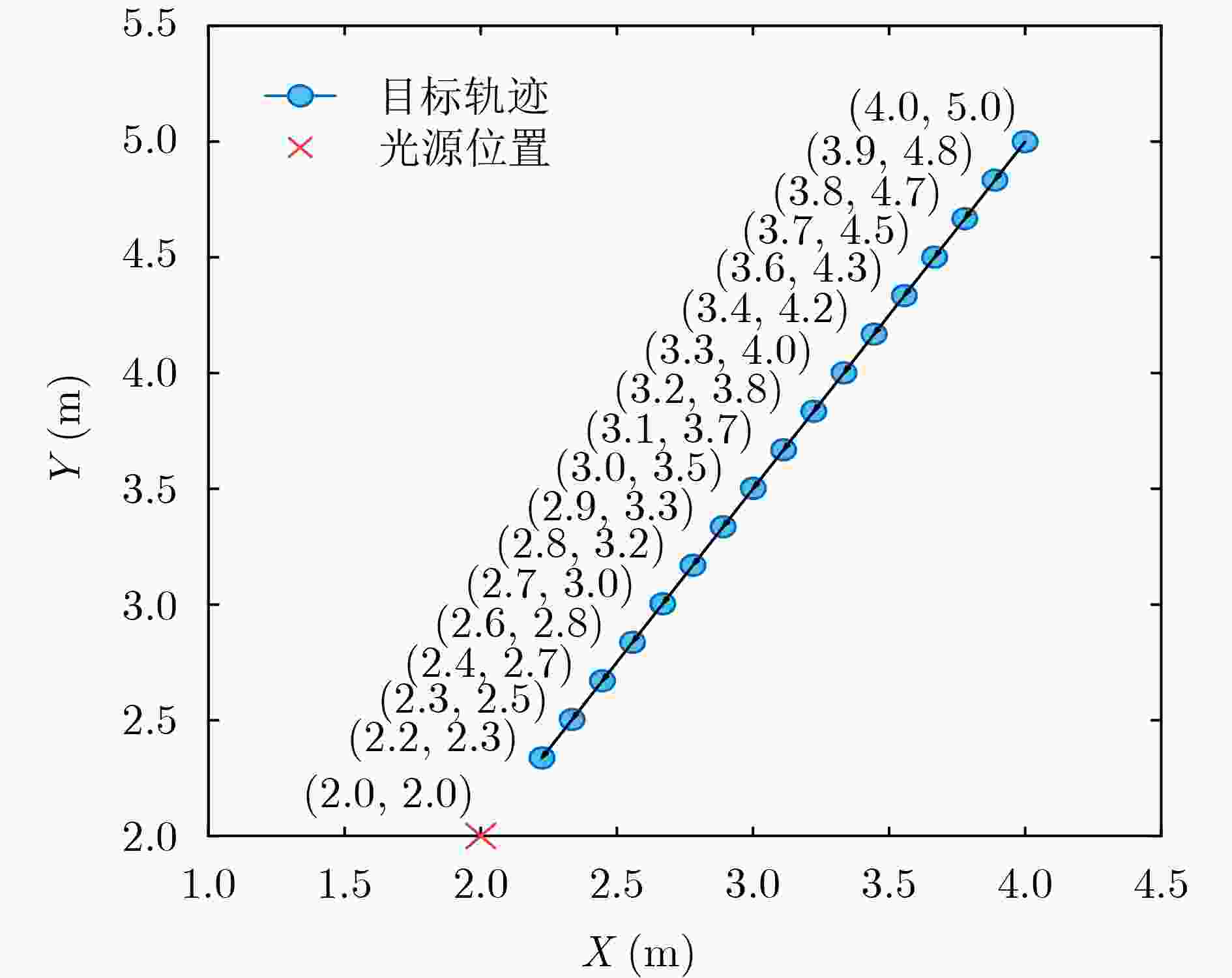
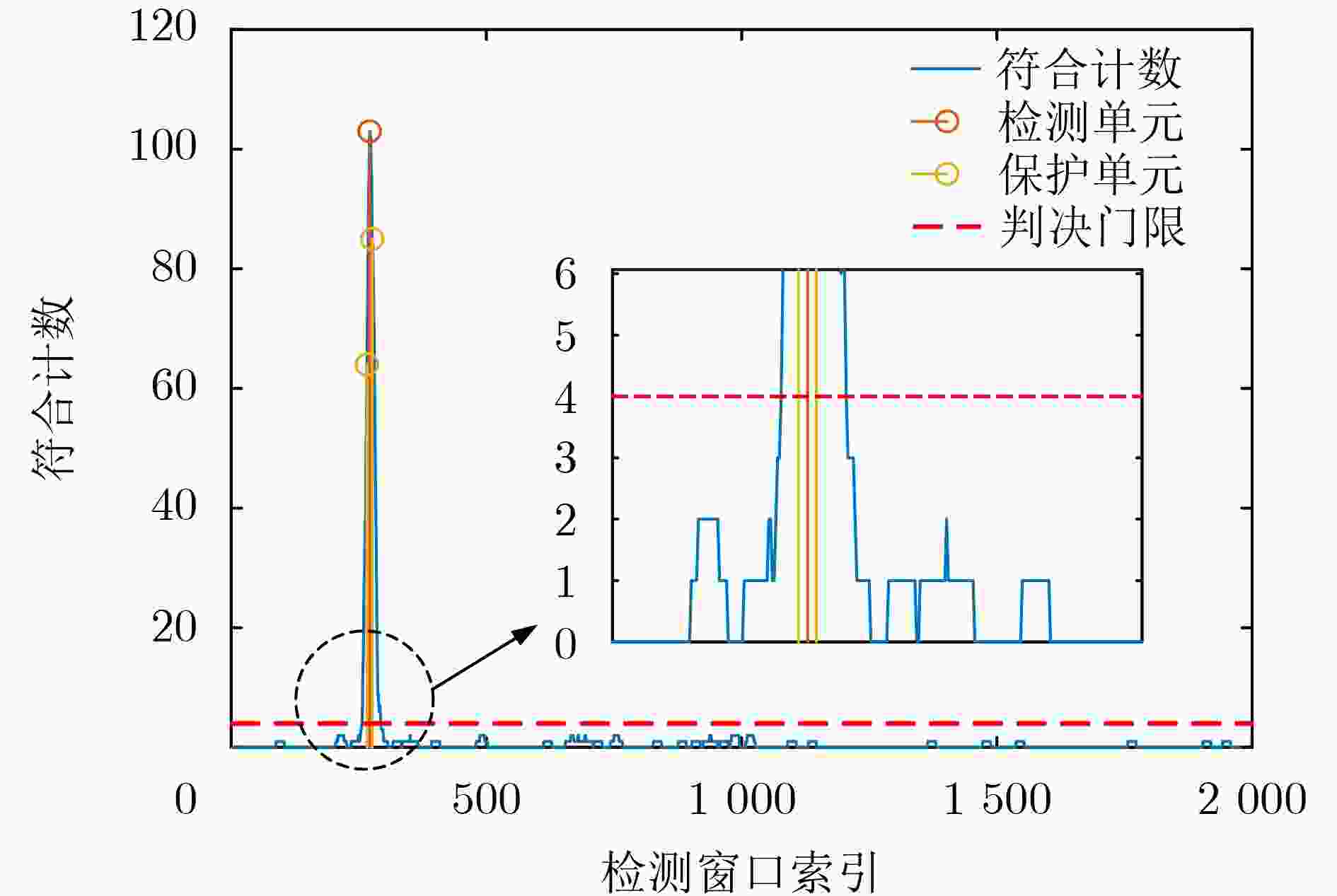
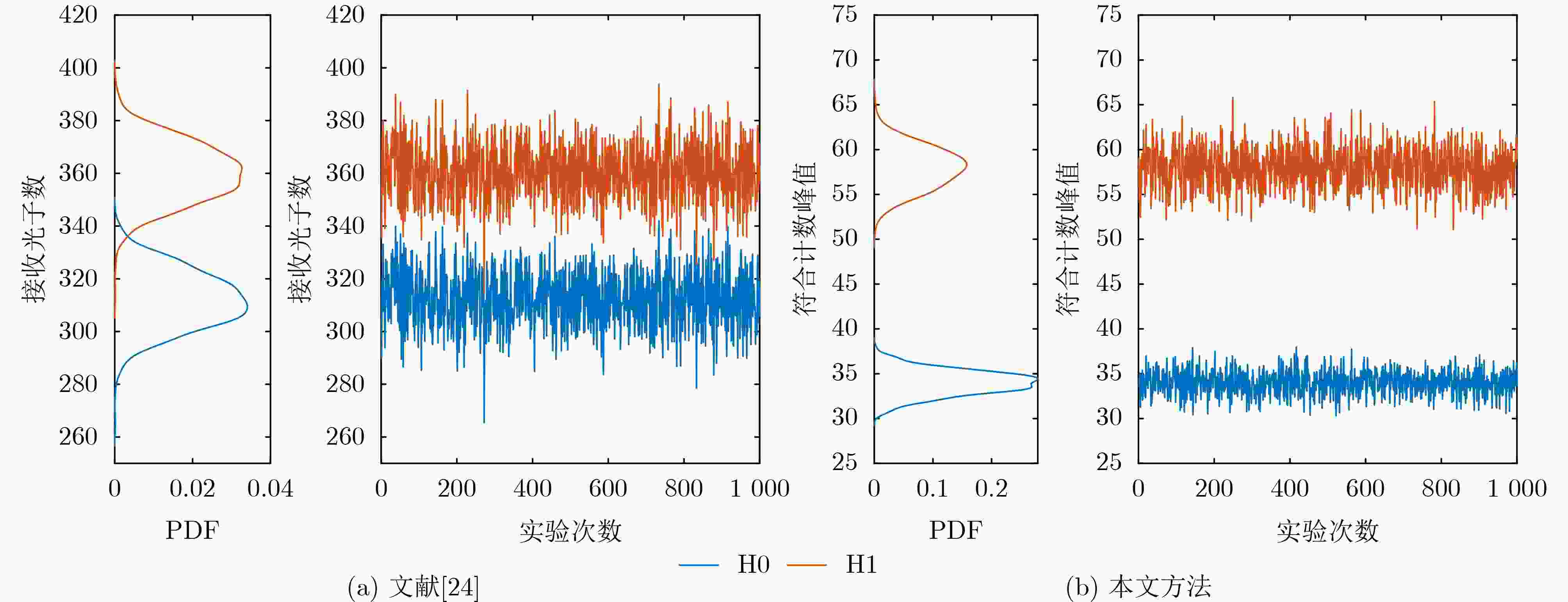
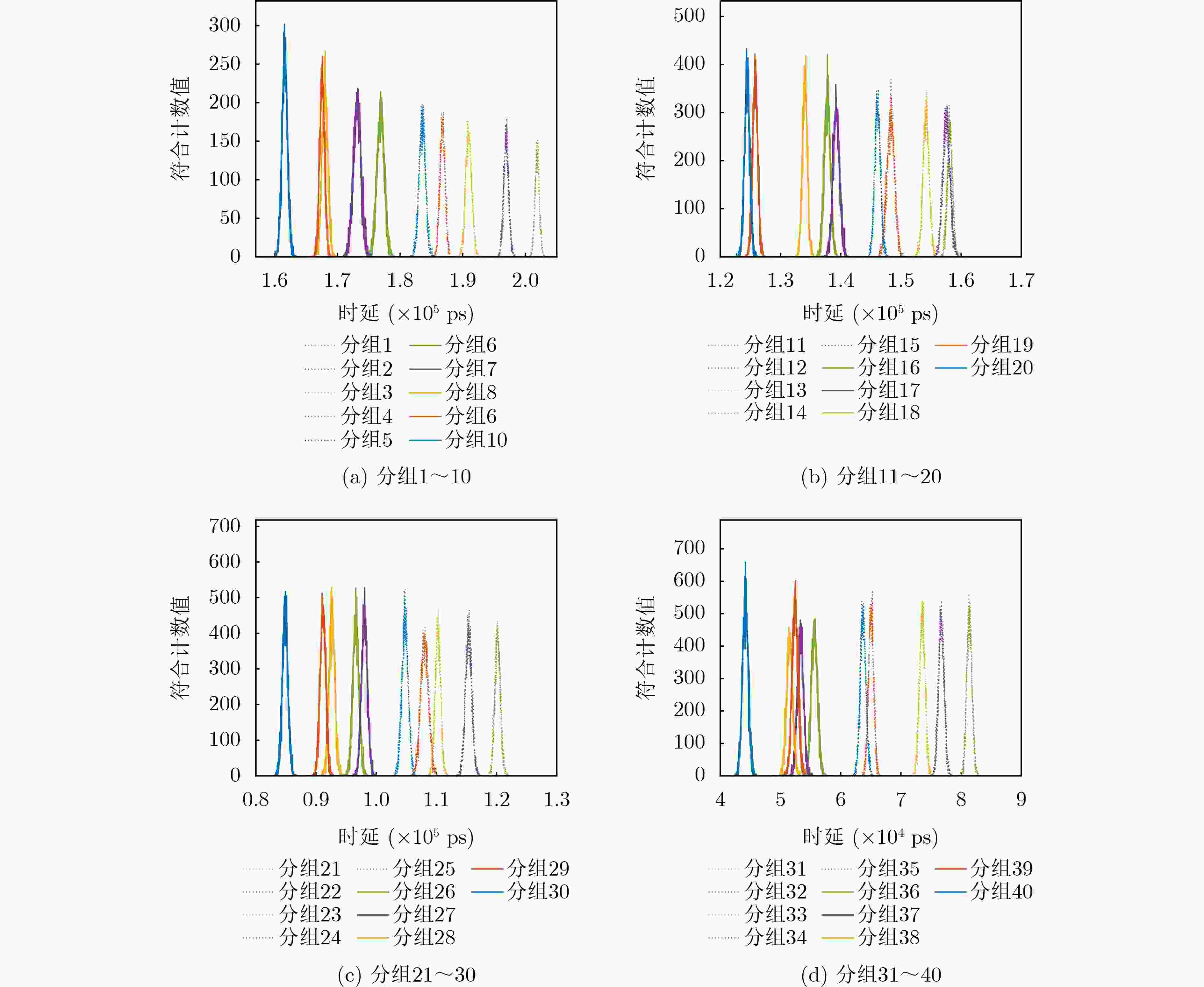
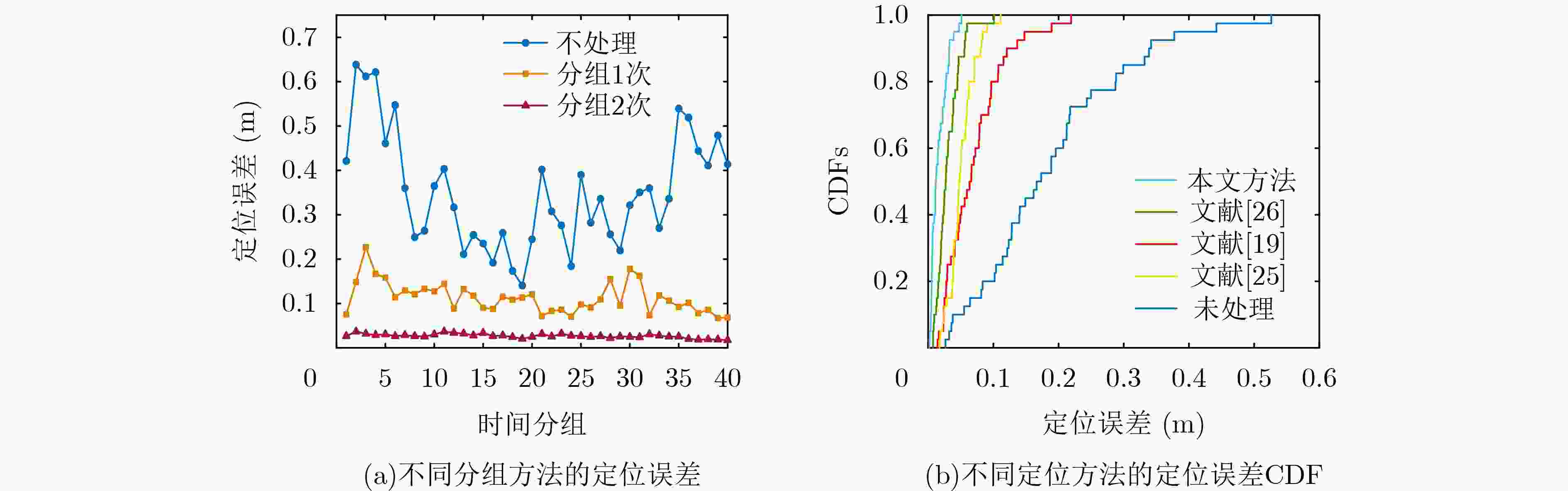
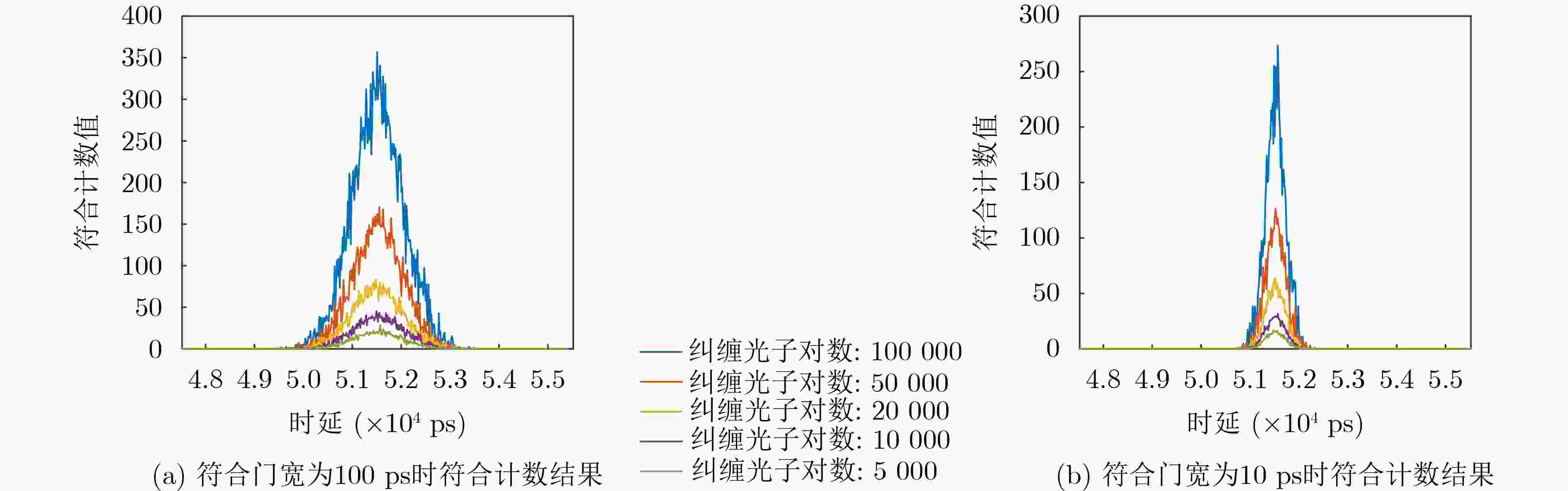
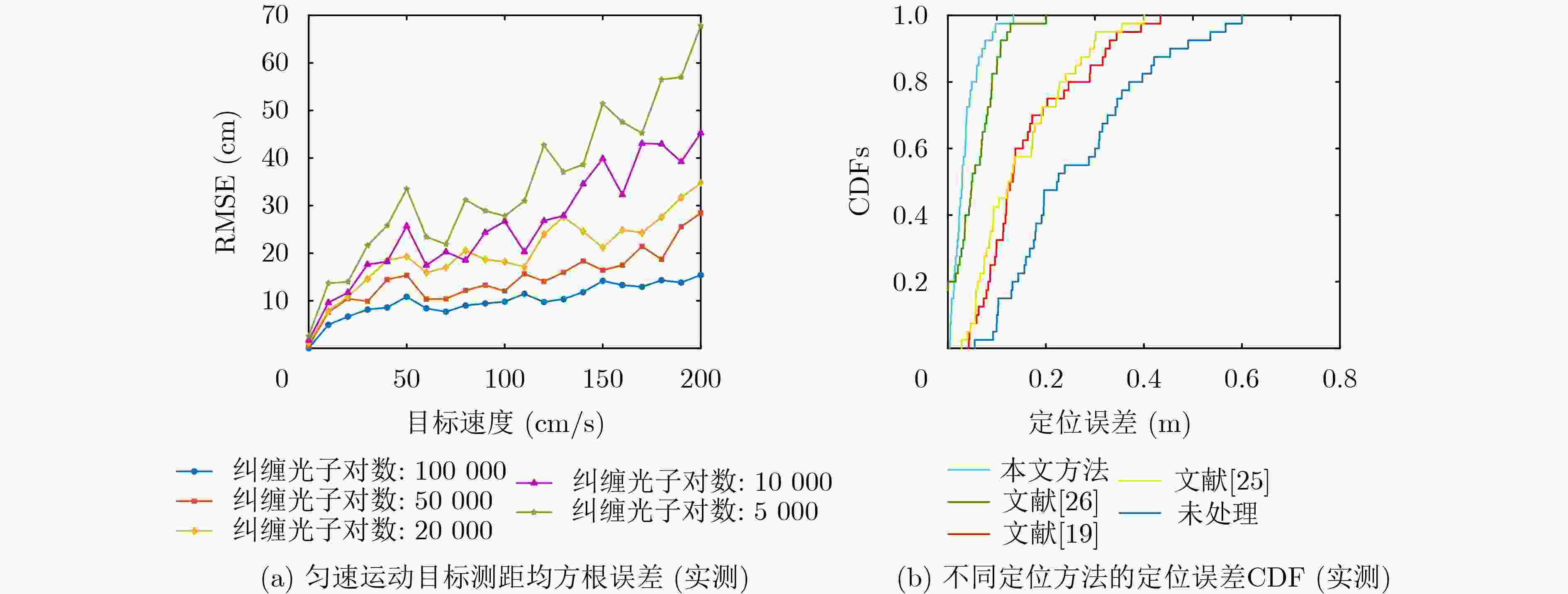
Abstract: Objective Quantum information research has grown rapidly with the integration of quantum mechanics, information science, and computer science. Grounded in principles such as quantum superposition and quantum entanglement, quantum information technology can overcome the limitations of traditional approaches and address problems that classical information technologies and conventional computers cannot resolve. As a core technology, space-based quantum information technology has advanced quickly, offering new possibilities to overcome the performance bottlenecks of conventional positioning systems. However, existing quantum positioning methods mainly focus on stationary targets and have difficulty addressing the dynamic variations in the transmission channels of entangled photon pairs caused by particles, scatterers, and noise photons in the environment. These factors hinder the detection of moving targets and increase positioning errors because of reduced data acquisition at fixed points during target motion. Traditional wireless signal-based localization methods also face challenges in dynamic target tracking, including signal attenuation, multipath effects, and noise interference in complex environments. To address these limitations, a dynamic target localization method based on constructing an optical quantum transmission distance matrix is proposed. This method achieves high-precision and robust dynamic localization, meeting the requirements for moving target localization in practical scenarios. It provides centimeter-level positioning accuracy and significantly enhances the adaptability and stability of the system for moving targets, supporting the future practical application of quantum-based dynamic localization technology. Methods To improve the accuracy of the dynamic target localization system, a dynamic threshold optical quantum detection model based on background noise estimation is proposed, utilizing the characteristics of optical quantum echo signals. A dynamic target localization optical path is established in which two entangled optical signals are generated through the Spontaneous Parametric Down-Conversion (SPDC) process. One signal is retained as a reference in a local Single-Photon Detector (SPD), and the other is transmitted toward the moving target as the signal light. The optical quantum echo signals are analyzed, and the background noise is estimated using a coincidence counting algorithm. The detection threshold is then dynamically adjusted and compared with the signals from the detection unit, enabling rapid detection of dynamic targets. To accommodate variations in quantum echo signals caused by target motion, an adaptive optical quantum grouping method based on velocity measurement is introduced. The time pulse sequence is initially coarsely grouped to calculate the rough velocity of the target. The grouping size is subsequently adjusted according to the target’s speed, updating the time grouping sequence and further optimizing the distance measurement accuracy to generate an updated velocity matrix. The photon transmission distance matrix is refined using the relative velocity error matrix. By constructing a system of equations involving the coordinates of the light source, the optical quantum transmission distance matrix, and the dynamic target coordinate sequence, the target position is estimated through the least squares method. This approach improves localization accuracy and effectively reduces errors arising from target motion. Results and Discussions The effectiveness of the proposed method is verified through both simulations and experimental validation on a practical measurement platform. The experimental results demonstrate that the dynamic threshold detection approach based on background noise estimation achieves high-sensitivity detection performance (Fig. 7). When a moving target enters the detection range, rapid identification is realized, enabling subsequent dynamic localization. The adaptive grouping method based on velocity measurement significantly improves the performance of the quantum dynamic target localization system. Through grouped coincidence counting, the problem of blurred coincidence counting peaks caused by target movement is effectively mitigated (Fig. 8), achieving high-precision velocity measurement (Table 1) and reducing localization errors associated with motion. Centimeter-level positioning accuracy is attained (Fig. 9). Furthermore, an entangled optical quantum experimental platform is established, with analyses focusing on measurement results under different velocities and localization performances across various methods. The findings confirm the reliability and adaptability of the proposed approach in improving distance measurement accuracy (Fig. 11). Conclusions A novel method for dynamic target localization in entangled optical quantum dynamics is proposed based on constructing an optical quantum transmission distance matrix. The method enhances distance measurement accuracy and optimizes the overall positioning accuracy of the localization system through a background noise estimation-based dynamic threshold detection model and a velocity measurement-based adaptive grouping approach. By integrating the optical quantum transmission distance matrix with the least squares optimization method, the proposed framework offers a promising direction for achieving more precise quantum localization systems and demonstrates strong potential for real-time dynamic target tracking. This approach not only improves the accuracy of dynamic quantum localization systems but also broadens the applicability of quantum localization technology in complex environments. It is expected to provide solid support for real-time quantum dynamic target localization and find applications in intelligent health monitoring, the Internet of Things, and autonomous driving.
- Entangled optical quantum /
- Quantum localization /
- Dynamic target /
- coincidence counting /
- Transmission distance matrix

HTML全文

图 1 基于光量子传输距离矩阵构建的动态目标定位方法光路结构图

下载: 全尺寸图片幻灯片

图 2 本文方法框架图

下载: 全尺寸图片幻灯片

图 3 基于背景噪声估计的动态阈值检测原理图

下载: 全尺寸图片幻灯片

图 4 动态目标纠缠光量子符合计数过程图

下载: 全尺寸图片幻灯片

图 5 运动目标轨迹图与光源位置图

下载: 全尺寸图片幻灯片

图 6 基于背景噪声估计的动态阈值检测示意图

下载: 全尺寸图片幻灯片

图 7 不同检测方法下的检测事件比较图

下载: 全尺寸图片幻灯片

图 8 运动目标不同时间分组下的符合计数结果

下载: 全尺寸图片幻灯片

图 9 自适应光量子分组定位结果

下载: 全尺寸图片幻灯片

图 10 纠缠光量子定位实验平台

下载: 全尺寸图片幻灯片

图 11 不同纠缠光量子对数符合计数结果

下载: 全尺寸图片幻灯片

图 12 实测实验结果

下载: 全尺寸图片幻灯片

表 1 分组测速误差表

误差(cm/s)	分组1次	分组2次
中位误差	5.01	1.83
中位误差	2.02	2.02
平均误差	1.04	1.04
最小误差	1.13	1.13
25%误差	1.96	1.96
75%误差	9.40	9.40

下载: 导出CSV

表 2 实验主要参数

名称	取值
激光器功率(${\text{mw}}$)	$40$
非线性晶体尺寸(${\text{m}}{{\text{m}}^3}$)	$1 \times 2 \times 20$
温度控制器精度($^\circ {\text{C}}$)	$0.01$
同步与符合模块时间测量范围(${\text{ms}}$)	$ \ge 1$
单光子探测器死时间(${\text{ns}}$)	$ \le 20$
单光子探测器暗计数($ {\text{Hz}} $)	$ \lt 500 $
单光子探测器饱和计数(${\text{MHz}}$)	$35$
单光子探测器探测效率	$ \gt 60\% $

下载: 导出CSV

参考文献(26)

[1]	HORODECKI R, HORODECKI P, HORODECKI M, et al. Quantum entanglement[J]. Reviews of Modern Physics, 2009, 81(2): 865–942. doi: 10.1103/RevModPhys.81.865.
[2]	ZHONG Shengyang. Quantum entanglement: An analysis via the orthogonality relation[J]. Foundations of Physics, 2023, 53(4): 75. doi: 10.1007/s10701-023-00710-0.
[3]	蔚娟, 张岩, 吴银花, 等. 双模压缩态量子相干性演化的实验研究[J]. 物理学报, 2023, 72(3): 034202. doi: 10.7498/aps.72.20221923. WEI Juan, ZHANG Yan, WU Yinhua, et al. Experimental demonstration on quantum coherence evolution of two-mode squeezed state[J]. Acta Physica Sinica, 2023, 72(3): 034202. doi: 10.7498/aps.72.20221923.
[4]	GENOVESE M. Real applications of quantum imaging[J]. Journal of Optics, 2016, 18(7): 073002. doi: 10.1088/2040-8978/18/7/073002.
[5]	GIOVANNETTI V, LLOYD S, and MACCONE L. Quantum-enhanced positioning and clock synchronization[J]. Nature, 2001, 412(6845): 417–419. doi: 10.1038/35086525.
[6]	LLOYD S. Enhanced sensitivity of photodetection via quantum illumination[J]. Science, 2008, 321(5895): 1463–1465. doi: 10.1126/science.1160627.
[7]	杨春燕, 吴德伟, 余永林, 等. 干涉式量子定位系统最优星座分布研究[J]. 测绘通报, 2009(12): 1–6. YANG Chunyan, WU Dewei, YU Yonglin, et al. Research on optimal constellation distribution of interferometric quantum positioning system[J]. Bulletin of Surveying and Mapping, 2009(12): 1–6.
[8]	ZHUANG Quntao. Quantum ranging with Gaussian entanglement[J]. Physical Review Letters, 2021, 126(24): 240501. doi: 10.1103/PhysRevLett.126.240501.
[9]	侯阿慧, 胡以华, 方佳节, 等. 平动小目标光子探测回波特性及测距误差研究[J]. 物理学报, 2022, 71(7): 074205. doi: 10.7498/aps.71.20211998. HOU Ahui, HU Yihua, FANG Jiajie, et al. Photon echo probability distribution characteristics and range walk error of small translational target for photon ranging[J]. Acta Physica Sinica, 2022, 71(7): 074205. doi: 10.7498/aps.71.20211998.
[10]	汪泳钦, 丛爽. 量子定位系统中的卫星间链路超前瞄准角跟踪补偿[J]. 导航定位学报, 2023, 11(2): 80–91. doi: 10.16547/j.cnki.10-1096.20230209. WANG Yongqin and CONG Shuang. Tracking compensation of inter satellite link point ahead angle in quantum positioning system[J]. Journal of Navigation and Positioning, 2023, 11(2): 80–91. doi: 10.16547/j.cnki.10-1096.20230209.
[11]	贺海, 杨鹏飞, 张鹏飞, 等. 基于1/4波片的腔增强自发参量下转换过程中双折射效应的补偿[J]. 物理学报, 2023, 72(12): 124203. doi: 10.7498/aps.72.20230422. HE Hai, YANG Pengfei, ZHANG Pengfei, et al. Birefringence compensation utilizing quarter-wave plates in cavity-enhanced spontaneous parametric down-conversion process[J]. Acta Physica Sinica, 2023, 72(12): 124203. doi: 10.7498/aps.72.20230422.
[12]	HE Hai, YANG Pengfei, ZHANG Pengfei, et al. Birefringence compensation utilizing quarter-wave plates in cavity-enhanced spontaneous parametric down-conversion process[J]. Acta Physica Sinica, 2023, 72(12): 124203. doi: 10.7498/aps.72.20230422. (查阅网上资料,本条文献是第11条文献的英文翻译信息,请确认).
[13]	KWIAT P G, MATTLE K, WEINFURTER H, et al. New high-intensity source of polarization-entangled photon pairs[J]. Physical Review Letters, 1995, 75(24): 4337–4341. doi: 10.1103/PhysRevLett.75.4337.
[14]	OMSHANKAR, VENKATARAMAN V, and GHOSH J. Unveiling quantum correlations of SPDC biphoton spatial modes using spatial light modulator[J]. Journal of Optics, 2024, 26(12): 125201. doi: 10.1088/2040-8986/ad89d8.
[15]	郭立新, 吴振森, 张民. 湍流大气中漫射目标光散射特性研究[J]. 电子与信息学报, 2001, 23(4): 388–395. GUO Lixin, WU Zhensen, and ZHANG Min. Light scattering from a diffuse target in the turbulent atmosphere[J]. Journal of Electronics and Information Technology, 2001, 23(4): 388–395.
[16]	LEE S M, KIM H, CHA M, et al. Polarization-entangled photon-pair source obtained via type-II non-collinear SPDC process with PPKTP crystal[J]. Optics Express, 2016, 24(3): 2941–2953. doi: 10.1364/OE.24.002941.
[17]	QUAN Runai, DONG Ruifang, and XIANG Xiao. High-precision nonlocal temporal correlation identification of entangled photon pairs for quantum clock synchronization[J]. Review of Scientific Instruments, 2020, 91(12): 123109. doi: 10.1063/5.0031166.
[18]	MAUGHAN N M, MOODY J W, and MILLER D R. Monte Carlo simulation of near-infrared light propagation through homogeneous mixed media[J]. Journal of Biomedical Optics, 2013, 18(10): 105007. doi: 10.1117/1.JBO.18.10.105007.
[19]	周牧, 张靖, 谢良波, 等. 基于自适应光源选择的纠缠光量子定位方法[J]. 电子与信息学报, 2022, 44(9): 3058–3064. doi: 10.11999/JEIT220212. ZHOU Mu, ZHANG Jing, XIE Liangbo, et al. Entangled light quantum positioning method based on adaptive light source selection[J]. Journal of Electronics & Information Technology, 2022, 44(9): 3058–3064. doi: 10.11999/JEIT220212.
[20]	HE Weiji, CHEN Yunfei, SIMA Boyu, et al. Performance characteristics of single photon pulse ranging system using Monte Carlo simulation[J]. Optik, 2013, 124(24): 6559–6564. doi: 10.1016/j.ijleo.2013.05.120.
[21]	HADFIELD R H, LEACH J, FLEMING F, et al. Single-photon detection for long-range imaging and sensing[J]. Optica, 2023, 10(9): 1124–1141. doi: 10.1364/optica.488853.
[22]	周牧, 嵇长银, 谢良波, 等. 基于符合计数滤波优化的光量子成像方法[J]. 电子与信息学报, 2023, 45(6): 2089–2097. doi: 10.11999/JEIT220627. ZHOU Mu, JI Changyin, XIE Liangbo, et al. Optical quantum imaging method based on filter optimization of coincidence counting[J]. Journal of Electronics & Information Technology, 2023, 45(6): 2089–2097. doi: 10.11999/JEIT220627.
[23]	龚建华. 用蒙特卡洛法计算几何平均自由程[J]. 合肥工业大学学报: 自然科学版, 1995, 18(2): 143–147. GONG Jianhua. Computation of the mean geometric free path by Monte Carlo's method[J]. Journal of Hefei University of Technology: Natural Science Edition, 1995, 18(2): 143–147.
[24]	LI Zhijian, LAI Jiancheng, WANG Chunyong, et al. Influence of dead-time on detection efficiency and range performance of photon-counting laser radar that uses a Geiger-mode avalanche photodiode[J]. Applied Optics, 2017, 56(23): 6680–6687. doi: 10.1364/AO.56.006680.
[25]	ZHOU Mu, WANG Qian, XIE Liangbo, et al. Passive target positioning on uncertain detection path based on entangled light quantum[J]. IEEE Transactions on Instrumentation and Measurement, 2023, 72: 7007714. doi: 10.1109/TIM.2023.3325857.
[26]	LI Zhikang, LIU Bo, WANG Huachuang, et al. Advancement on target ranging and tracking by single-point photon counting lidar[J]. Optics Express, 2022, 30(17): 29907–29922. doi: 10.1364/OE.464070.