针对SM4的选择明文攻击：线性运算带来的难题与对策

唐啸霖; 冯燕; 李志强; 郭叶; 龚关飞

doi:10.11999/JEIT250014

针对SM4的选择明文攻击：线性运算带来的难题与对策

doi: 10.11999/JEIT250014 cstr: 32379.14.JEIT250014

唐啸霖^{1, 2, 3},
冯燕^{1, 2, ,},
李志强^{1, 2},
郭叶^{1, 2},
龚关飞^{1, 2}

1.
集成电路制造技术重点实验室(中国科学院)北京 100029
2.
中国科学院微电子研究所北京 100029
3.
中国科学院大学北京 100049

基金项目: 国家重点研发计划(2020YFB2104600)

详细信息

作者简介:
唐啸霖：男，博士生，研究方向为集成电路硬件安全

冯燕：女，博士，正高级工程师，研究方向为集成电路硬件安全、IP/SoC设计与验证等

李志强：男，博士，研究员，博士生导师，研究方向为模拟/射频/毫米波集成电路设计

郭叶：女，博士生，高级工程师，研究方向为集成电路硬件验证、集成电路测试

龚关飞：男，硕士，高级工程师，研究方向为嵌入式软硬件协同设计、硬件安全等

通讯作者:
冯燕　fengyan@ime.ac.cn

中图分类号: TN402
计量
- 文章访问数: 114
- HTML全文浏览量: 60
- PDF下载量: 13
- 被引次数: 0
出版历程
- 收稿日期: 2025-01-09
- 修回日期: 2025-06-04
- 网络出版日期: 2025-06-14

A Chosen-Plaintext Method on SM4: Linear Operation Challenges and the Countermeasures

TANG Xiaolin^{1, 2, 3},
FENG Yan^{1, 2
, ,},
LI Zhiqiang^{1, 2},
GUO Ye^{1, 2},
GONG Guanfei^{1, 2}

1.
Key Laboratory of Fabrication Technologies for Integrated Circuits, Chinese Academy of Sciences, Beijing 100029, China
2.
Institute of Microelectronics of the Chinese Academy of Sciences, Beijing 100029, China
3.
University of Chinese Academy of Sciences, Beijing 100049, China

Funds: The National Key R&D Program of China (2020YFB2104600)

摘要

摘要: 在硬件安全领域，各种侧信道攻击已受到广泛关注，这类攻击利用硬件泄漏的物理信息来推断密钥等敏感信息，其中能量分析攻击是最受关注的侧信道攻击技术之一。针对高级加密标准的能量分析攻击方法相对成熟，对于SM4算法，由于其轮运算包含特殊的线性变换模块，使得能量分析攻击更加困难。针对SM4的选择明文攻击方法可以规避线性变换模块带来的运算复杂度，但这些方法面临以下难题：如何构造四轮选择明文、如何恢复初始密钥、如何分辨对称攻击结果，以及如何排除高相关性错误猜测值。该文在深入分析难题产生原因的基础上，提出了相应的对策，并对SM4算法实现进行了能量分析攻击实验，结果表明：所提应对策略，能有效解决在SM4的选择明文攻击过程中，线性运算带来的难题。
- SM4算法 /
- 能量分析攻击 /
- 选择明文 /
- 线性运算
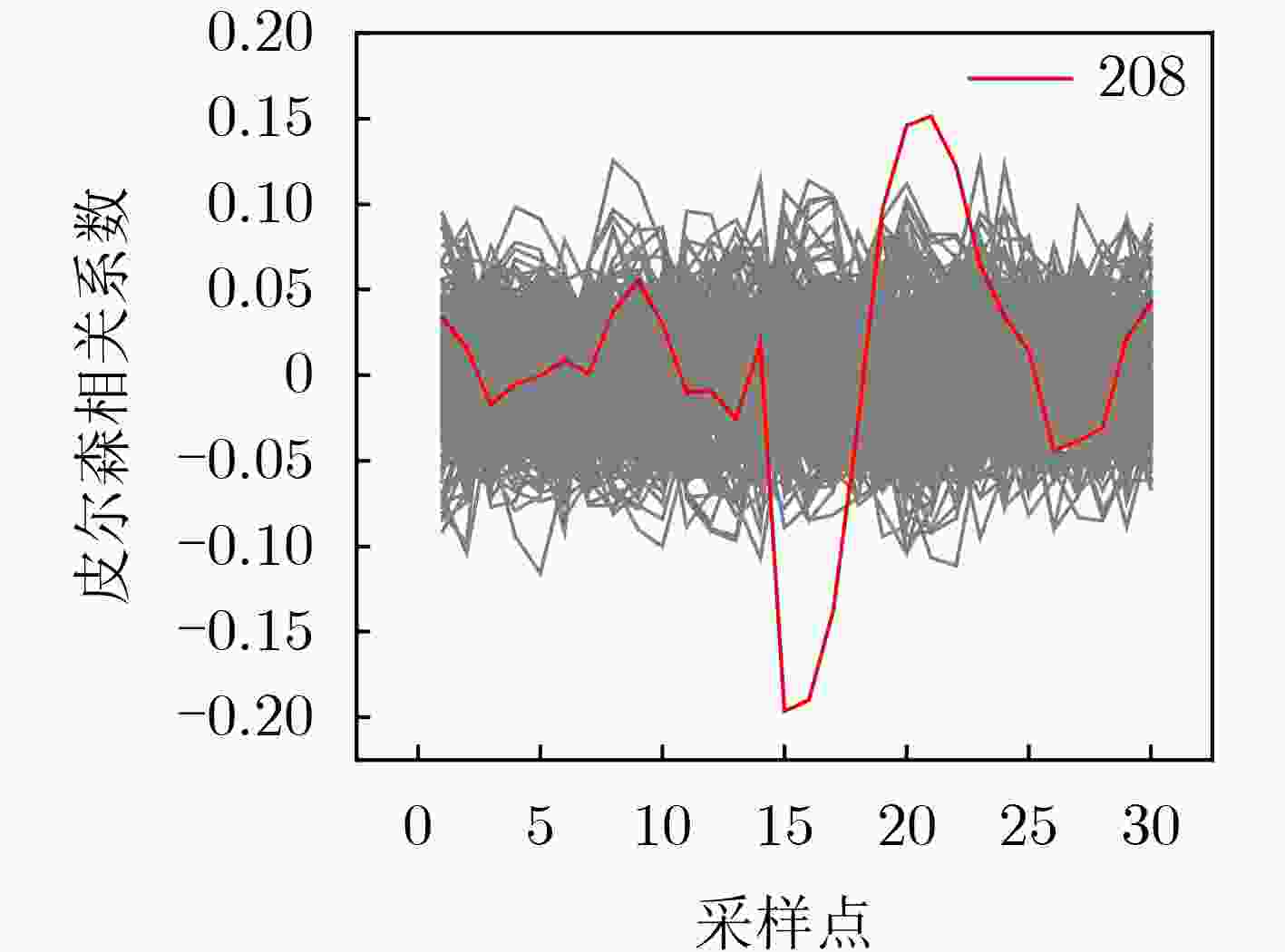
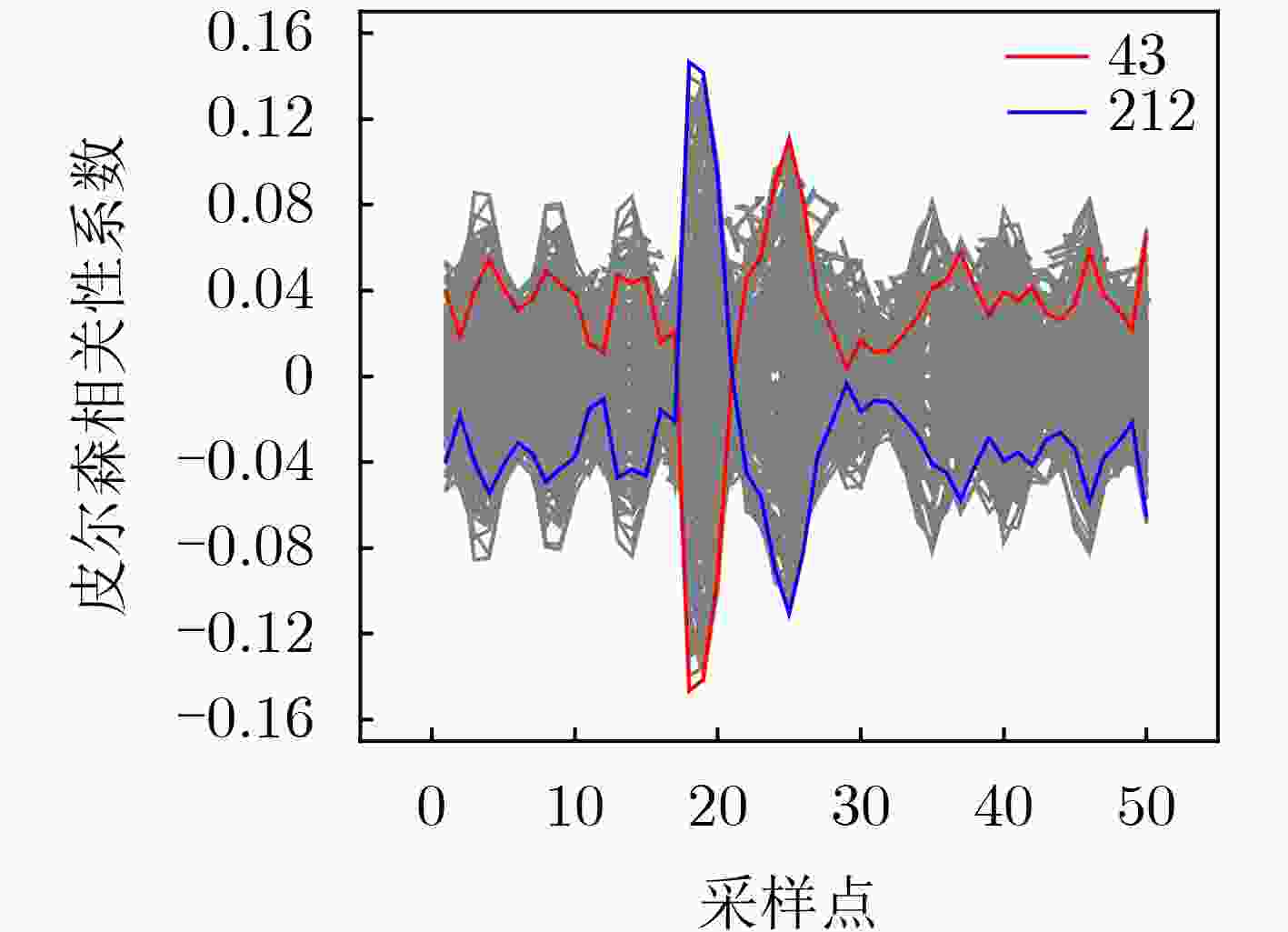
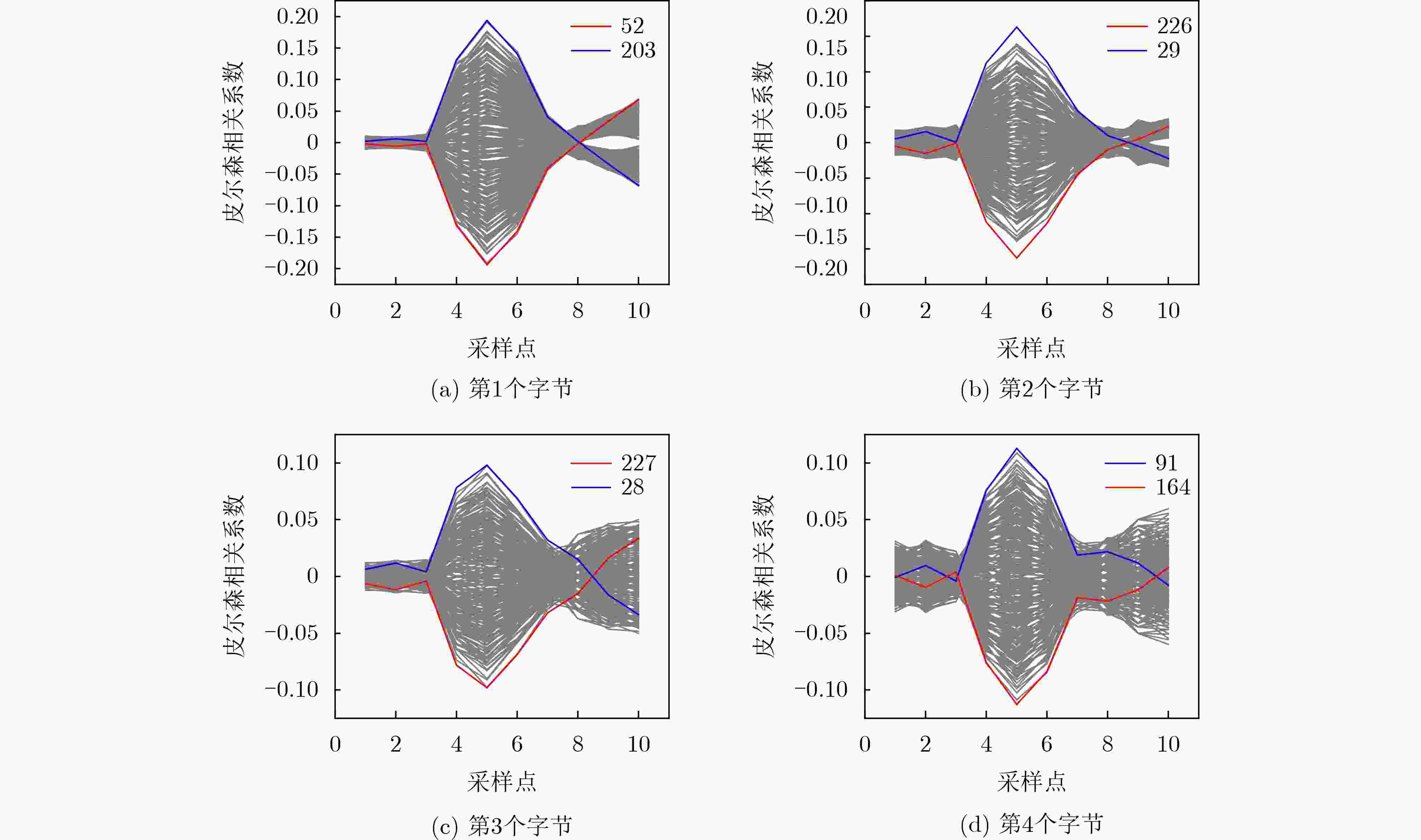
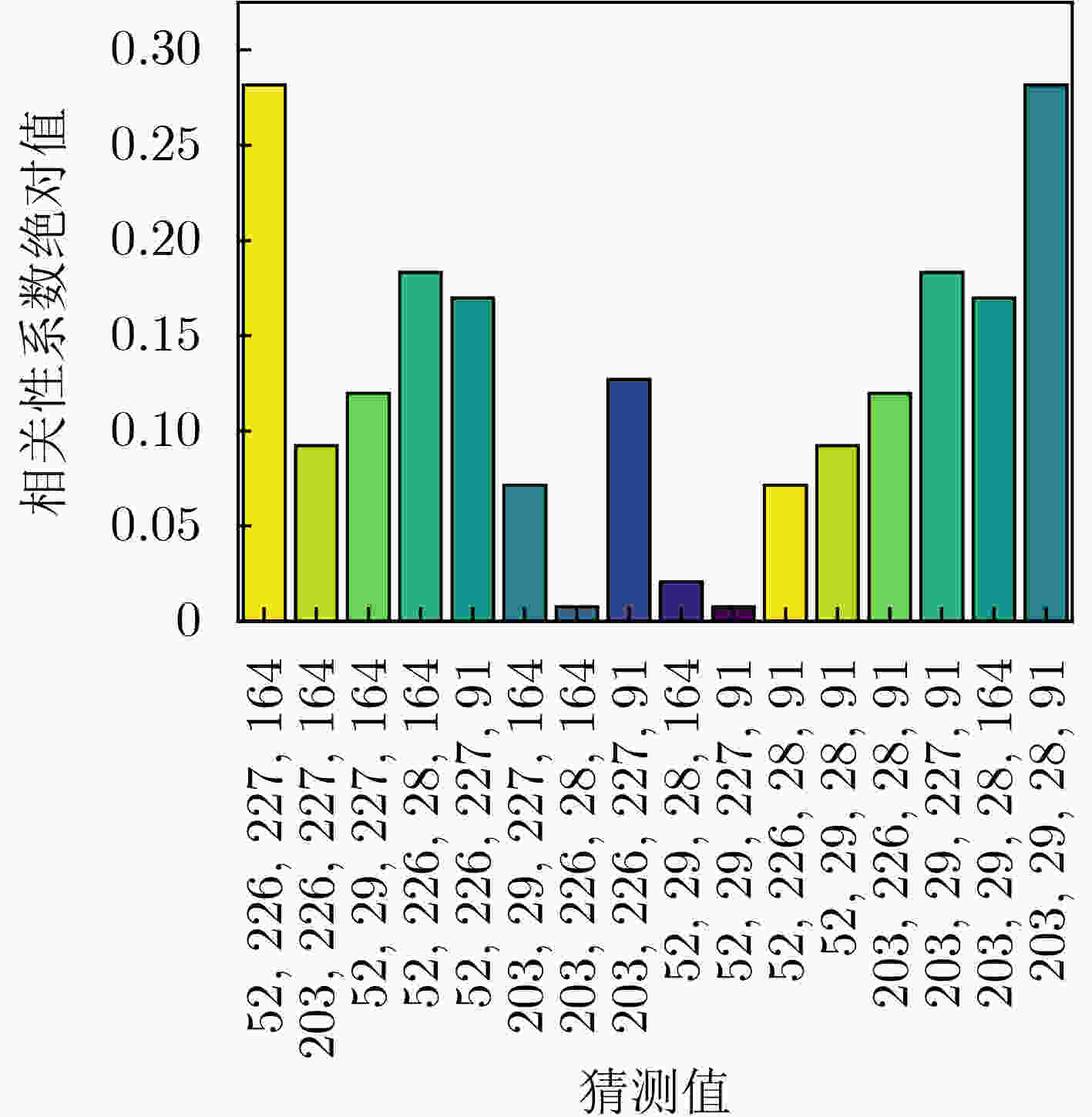
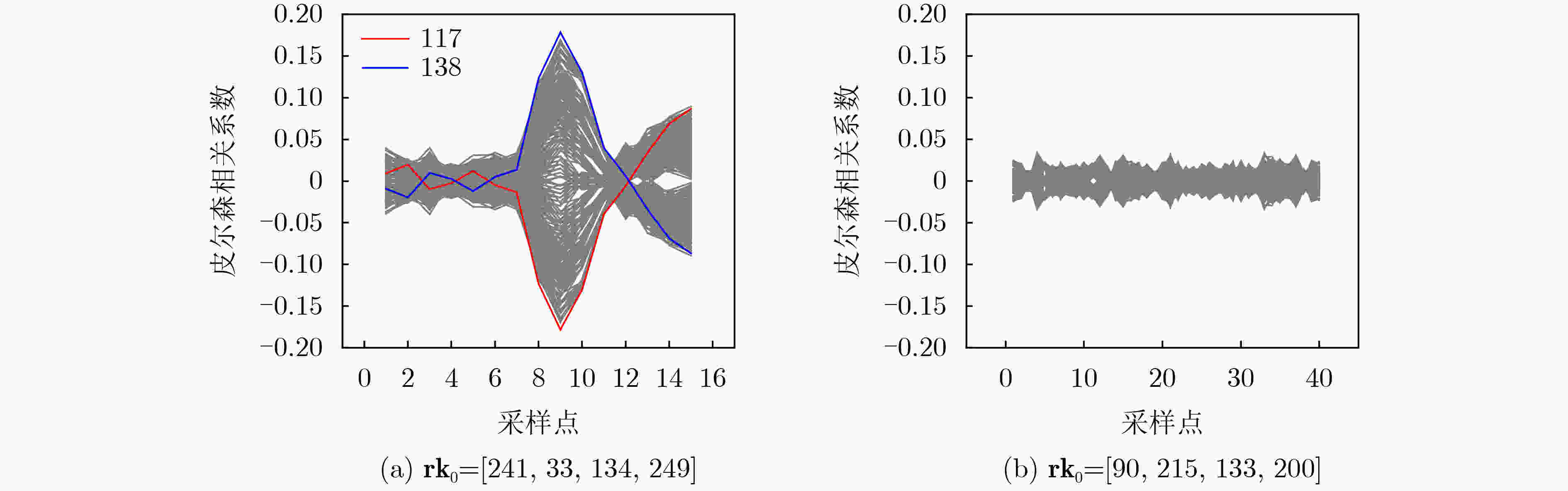
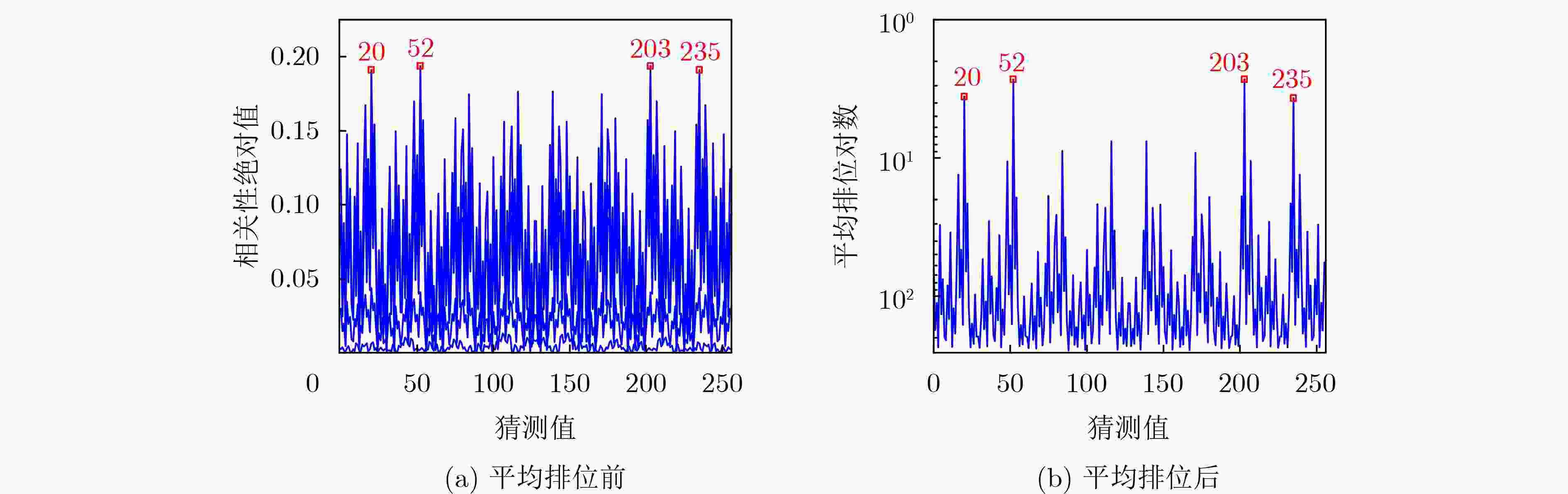
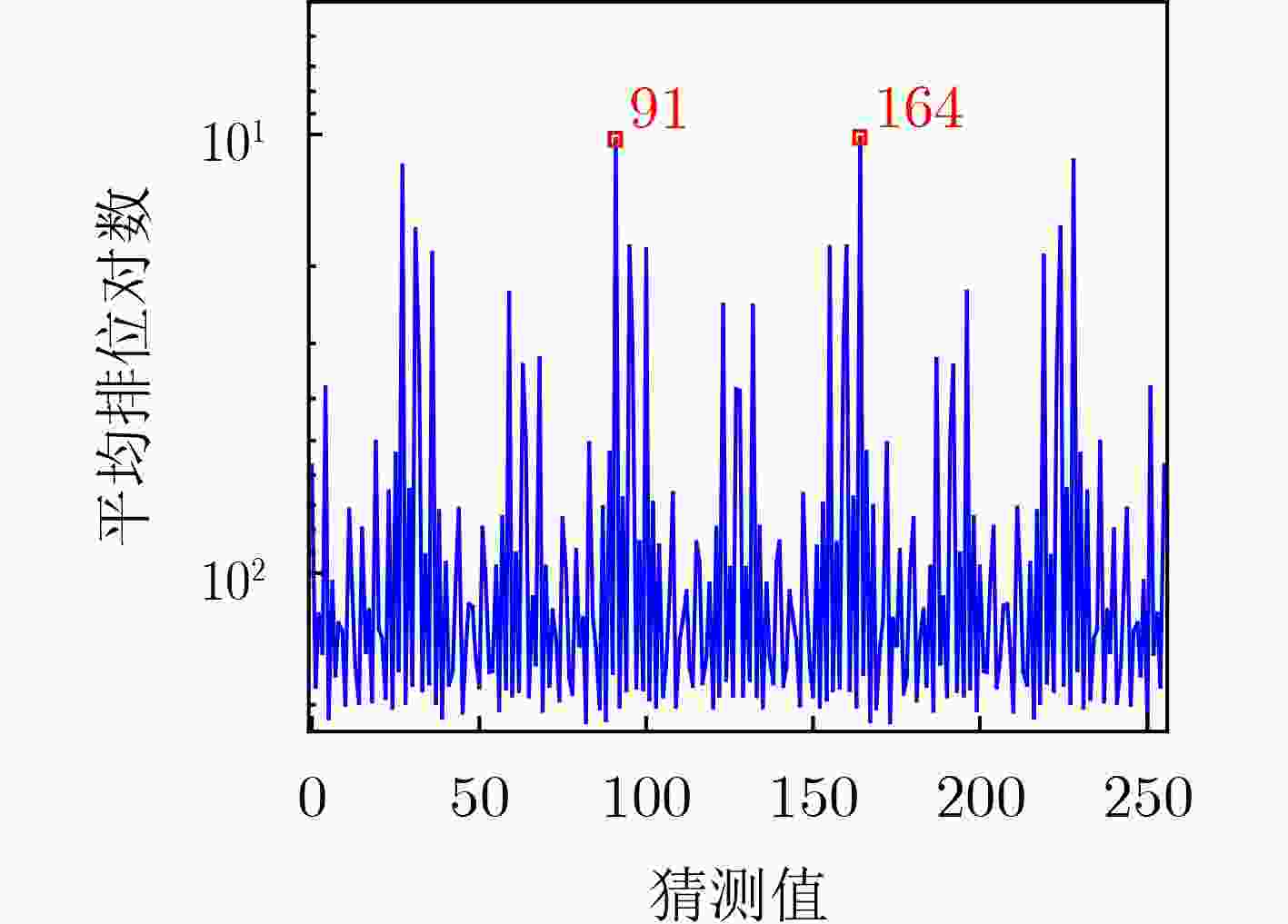
Abstract: Objective With increasing concerns over hardware security, techniques for exploiting hardware vulnerabilities have advanced rapidly. Among these, Side-Channel Attacks (SCAs) have received substantial attention for their ability to extract sensitive information via physical leakage. Power analysis, a prominent form of SCA, has been extensively applied to the Advanced Encryption Standard (AES). However, SM4—a block cipher issued by China’s State Cryptography Administration—presents greater challenges due to its unique linear transformation. Existing chosen-plaintext methods for attacking SM4 still encounter key limitations, including difficulty in constructing four-round chosen plaintexts, recovering initial keys from intermediate values, resolving symmetrical attack ambiguities, and filtering highly correlated incorrect guesses. This study systematically analyzes the root causes of these issues and proposes targeted countermeasures, effectively mitigating the constraints imposed by SM4’s linear operations. Methods This study systematically investigates the challenges in chosen-plaintext attacks on SM4 and proposes targeted countermeasures. To enable initial key recovery, the inverse transformation is expressed as a system of linear equations, and a new round-key derivation algorithm is developed. To facilitate the construction of four-round chosen plaintexts, additional critical constraints are incorporated into plaintext generation, yielding leak model expressions that are more concise and plaintext-dependent. To resolve symmetrical attack results, the set of 4-byte round-key candidates is reduced, and incorrect candidates are eliminated through analysis in subsequent rounds. To suppress interference from highly correlated false guesses, an average ranking method is applied. Results and Discussions The proposed countermeasures collectively resolve key limitations in chosen-plaintext attacks on SM4 and enhance attack efficiency. The key recovery algorithm (Algorithm 1) integrates Gaussian elimination with Boolean operations to extract round keys. For four-round plaintext construction, detailed expressions for the final three rounds are provided for the first time, expanding the number of valid values from 256 to at least 2³² (Table 1), thereby enabling the recovery of four round keys (Fig. 4). The number of symmetrical attack results is reduced from 16 to 2 (Fig. 5), and subsequent round verification identifies the correct candidate (Fig. 6). The average ranking method yields clearer attack traces when analyzing 50,000 plaintexts across 10 groups (Fig. 7). Conclusions The proposed countermeasures effectively address the challenges introduced by linear operations in chosen-plaintext attacks on SM4. Correlation Power Analysis (CPA)-based experiments demonstrate that: (1) the key recovery algorithm and plaintext generation strategy enable successful extraction of round keys and reconstruction of the initial key; (2) symmetrical attack results can be resolved using only seven attack sets; and (3) the average ranking method reduces interference from secondary correlation peaks. This study focuses on unprotected SM4 implementations; future work will extend the analysis to masked versions.
- SM4 algorithm /
- Power side-channel attack /
- Chosen-plaintext /
- Linear operation

HTML全文

图 1 CPA攻击第10轮密钥第1个字节结果

下载: 全尺寸图片幻灯片

图 2 第1个猜测值攻击结果

下载: 全尺寸图片幻灯片

图 3 轮函数F

下载: 全尺寸图片幻灯片

图 4 SM4第1轮猜测值的破解结果

下载: 全尺寸图片幻灯片

图 5 16种猜测值对应的相关性

下载: 全尺寸图片幻灯片

图 6 SM4第2轮猜测值第1个字节的破解结果

下载: 全尺寸图片幻灯片

图 7 平均排位前后的攻击结果对比

下载: 全尺寸图片幻灯片

图 8 掩码SM4，首轮密钥第4个字节攻击结果

下载: 全尺寸图片幻灯片

1 高斯消元法实现线性变换逆运算

输入：32 bit字C。
输出：32 bit字B。
(1) for ( i=0; i<32; i++ ) do
(2) 　for j in {0,2,10,18,24} do
(3) 　　${\boldsymbol{A}}{\text{[}}i{\text{][}}i - j{\text{] = 1}}$
//生成32×32的矩阵A
(4)${\boldsymbol{D}} = {\text{[}}{\boldsymbol{A}}{\text{ }}{\boldsymbol{C}}{\text{]}}$
//方程组左侧矩阵与右侧向量合并
(5) r=0
(6) for ( m=0; m<32; m++ ) do
(7) t=r
(8) 　for ( n=r; n<32; n++ ) do
(9) 　　if (D[n][m]==1) then
(10) 　　 t=n; break
//用t标记第各列中元素1出现的位置
(11) D[r,t]=D[t,r]
//通过第r行和第t行交换，确保A对角线上的元素为1
(12) for ( p=r+1; p<32; p++ ) do
(13) 　　 D[p]= D[p]$ \oplus $ D[r]
//通过行间异或运算，使矩阵下三角为0
(14) for ( i=31; i>0; i– – ) do
(15) 　for ( j=0; j<i; j++ ) do
(16) 　　if (D[j][i]==1) then
(17) D[j]= D[j]$ \oplus $ D[i]
//通过行间异或运算，使矩阵上三角为0
(18) return D[ ,[32]] //第33列为解

下载: 导出CSV

表 1 选择明文生成方法

第1轮攻击选择明文	第2轮攻击选择明文	第3轮攻击选择明文	第4轮攻击选择明文
$\begin{gathered} {X_0} = {\text{random(}}{\text{)}} \\ {X_1} = {\text{random(}}{\text{)}} \\ {X_2} = {\text{random(}}*{\text{)}} \\ {X_3} = {X_1} \oplus {X_2} \\ \end{gathered} $	$\begin{gathered} {X_1} = {\text{random(}}{\text{)}} \\ {X_2} = {\text{random(}}{\text{)}} \\ {X_3} = {X_2} \\ {X_0} = T({\bf{r}}{{\bf{k}}_0} \oplus {X_1}) \\ \end{gathered} $	$\begin{gathered} {X_0} = {\text{random(}}{\text{)}} \\ {X_1} = {\text{random(}}{\text{)}} \\ {X_2} = {X_0} \oplus {\bf{re}}{{\bf{s}}_0} \oplus \\ T({\bf{r}}{{\bf{k}}_1} \oplus {\bf{re}}{{\bf{s}}_0} \oplus {X_0} \oplus {X_1}) \\ {X_3} = {X_1} \oplus {X_2} \\ \end{gathered} $	$\begin{gathered} {X_3} = {\text{random(}}*{\text{)}} \\ {X_2} = {\bf{re}}{{\bf{s}}_1} \oplus T{\bf{(r}}{{\bf{k}}_2} \oplus {\bf{re}}{{\bf{s}}_1} \oplus {X_3}{\text{)}} \\ {X_1} = {X_2} \oplus {X_3} \\ {X_0} = {X_1} \oplus {\bf{re}}{{\bf{s}}_0} \\ \end{gathered} $
${X_4} = {\bf{re}}{{\bf{s}}_0} \oplus {X_0}$	$\begin{gathered} {X_4} = 0 \\ {X_5} = {\bf{re}}{{\bf{s}}_1} \oplus {X_1} \\ \end{gathered} $	$\begin{gathered} {X_4} = {X_0} \oplus {\bf{re}}{{\bf{s}}_0} \\ {X_5} = {X_0} \oplus {X_1} \oplus {X_2} \oplus {\bf{re}}{{\bf{s}}_0} \\ {X_6} = {\bf{re}}{{\bf{s}}_2} \oplus {X_2} \\ \end{gathered} $	$\begin{gathered} {X_4} = {X_0} \oplus {\bf{re}}{{\bf{s}}_0} \\ {X_5} = {X_1} \oplus {\bf{re}}{{\bf{s}}_1} \\ {X_6} = {\bf{re}}{{\bf{s}}_1} \\ {X_7} = {\bf{re}}{{\bf{s}}_3} \oplus {X_3} \\ \end{gathered} $
${{\mathrm{HW}}} ({\bf{re}}{{\bf{s}}_0} \oplus {X_0} \oplus {X_3})$	${{\mathrm{HW}}} ({\bf{re}}{{\bf{s}}_1} \oplus {X_1})$	${{\mathrm{HW}}} ({X_1} \oplus {\bf{re}}{{\bf{s}}_2} \oplus {X_0} \oplus {\bf{re}}{{\bf{s}}_0})$	${{\mathrm{HW}}} ({X_3} \oplus {\bf{re}}{{\bf{s}}_3} \oplus {\bf{re}}{{\bf{s}}_1})$

下载: 导出CSV

表 2 用错误的猜测值产生明文

$\begin{gathered} {X_1} = {\text{random(}}{\text{)}} \\ {X_2} = {\text{random(}}{\text{)}} \\ {X_3} = {X_2} \\ {X_0} = T({T^{ - 1}}({\text{res}}{'_0}) \oplus {X_1}) \\ \end{gathered} $
$ {X_4} = T({T^{ - 1}}({\bf{res}}{'_0}) \oplus {X_1}) \oplus T({\bf{r}}{{\bf{k}}_0} \oplus {X_1}) $
${\bf{re}}{{\bf{s}}_1} = T({\bf{r}}{{\bf{k}}_1} \oplus {X_4})$

下载: 导出CSV

参考文献(16)

[1]	王永娟, 樊昊鹏, 代政一, 等. 侧信道攻击与防御技术研究进展[J]. 计算机学报, 2023, 46(1): 202–228. doi: 10.11897/SP.J.1016.2023.00202. WANG Yongjuan, FAN Haopeng, DAI Zhengyi, et al. Advances in side channel attacks and countermeasures[J]. Chinese Journal of Computers, 2023, 46(1): 202–228. doi: 10.11897/SP.J.1016.2023.00202.
[2]	KOCHER P, JAFFE J, and JUN B. Differential power analysis[C]. The 19th Annual International Cryptology Conference on Advances in Cryptology - CRYPTO’99, Santa Barbara, USA, 1999: 388–397. doi: 10.1007/3-540-48405-1_25.
[3]	BRIER E, CLAVIER C, and OLIVIER F. Correlation power analysis with a leakage model[C]. The 6th International workshop on Cryptographic Hardware and Embedded Systems – CHES 2004, Cambridge, USA, 2004: 16–29. doi: 10.1007/978-3-540-28632-5_2.
[4]	WANG Shutong, GU Dawu, LIU Junrong, et al. A power analysis on SMS4 using the chosen plaintext method[C]. 2013 Ninth International Conference on Computational Intelligence and Security, Emeishan, China, 2013: 748–752, doi: 10.1109/CIS.2013.163.
[5]	SHAN Weijun, WANG Lihui, LI Qing, et al. A chosen-plaintext method of CPA on SM4 block cipher[C]. 2014 Tenth International Conference on Computational Intelligence and Security, Kunming, China, 2014: 363–366, doi: 10.1109/CIS.2014.57.
[6]	杜之波, 吴震, 王敏, 等. 针对SM4轮输出的改进型选择明文功耗分析攻击[J]. 通信学报, 2015, 36(10): 85–91. doi: 10.11959/j.issn.1000-436x.2015270. DU Zhibo, WU Zhen, WANG Min, et al. Improved chosen-plaintext power analysis attack against SM4 at the round-output[J]. Journal on Communications, 2015, 36(10): 85–91. doi: 10.11959/j.issn.1000-436x.2015270.
[7]	陈佳哲, 李贺鑫, 王蓓蓓. 改进的SM4算法的选择明文DPA攻击[J]. 清华大学学报: 自然科学版, 2017, 57(11): 1134–1138. doi: 10.16511/j.cnki.qhdxxb.2017.26.056. CHEN Jiazhe, LI Hexin, and WANG Beibei. Improved chosen-plaintext DPA on block cipher SM4[J]. Journal of Tsinghua University: Science and Technology, 2017, 57(11): 1134–1138. doi: 10.16511/j.cnki.qhdxxb.2017.26.056.
[8]	王敏, 杜之波, 吴震, 等. 针对SMS4轮输出的选择明文能量分析攻击[J]. 通信学报, 2015, 36(1): 2015016. doi: 10.11959/j.issn.1000-436x.2015016. WANG Min, DU Zhibo, WU Zhen, et al. Chosen-plaintext power analysis attack against SMS4 with the round-output as the intermediate data[J]. Journal on Communications, 2015, 36(1): 2015016. doi: 10.11959/j.issn.1000-436x.2015016.
[9]	TAOUIL M, ALJUFFRI A, and HAMDIOUI S. Power side channel attacks: Where are we standing?[C]. 2021 16th International Conference on Design & Technology of Integrated Systems in Nanoscale Era (DTIS), Montpellier, France, 2021: 1–6, doi: 10.1109/DTIS53253.2021.9505075.
[10]	迟浩. 基于对称密钥加密过程的侧信道分析研究与改进[D]. [硕士论文], 电子科技大学, 2024. doi: 10.27005/d.cnki.gdzku.2024.000843. CHI Hao. Research and improvement of side channel analysis based on symmetric encryption algorithm[D]. [Master dissertation], University of Electronic Science and Technology of China, 2024. doi: 10.27005/d.cnki.gdzku.2024.000843.
[11]	IYER V, WANG Meizhi, KULKARNI J, et al. A systematic evaluation of EM and power side-channel analysis attacks on AES implementations[C]. 2021 IEEE International Conference on Intelligence and Security Informatics (ISI), San Antonio, USA, 2021: 1–6. doi: 10.1109/ISI53945.2021.9624778.
[12]	周晓谊, 马纪新, 杜文才, 等. 一种求解有限域F_q上线性方程组的有效算法[J]. 海南大学学报: 自然科学版, 2010, 28(4): 306–310. doi: 10.3969/j.issn.1004-1729.2010.04.005. ZHOU Xiaoyi, MA Jixin, DU Wencai, et al. An efficient algorithm to solve linear equations over finite field F_q[J]. Natural Science Journal of Hainan University, 2010, 28(4): 306–310. doi: 10.3969/j.issn.1004-1729.2010.04.005.
[13]	王星阳. 基于FPGA的轻量级加密算法的侧信道研究与分析[D]. [硕士论文], 北京邮电大学, 2023. doi: 10.26969/d.cnki.gbydu.2023.002969. WANG Xingyang. Research and analysis of side channel of lightweight encryption algorithm based on FPGA[D]. [Master dissertation], Beijing University of Posts and Telecommunications, 2023. doi: 10.26969/d.cnki.gbydu.2023.002969.
[14]	ABDURAZZOKOV J. Dynamic S-box generation algorithm with improved strict avalanche criterion by selection of adjacency matrix parameters[C]. 2023 3rd International Conference on Technological Advancements in Computational Sciences (ICTACS), Tashkent, Uzbekistan, 2023: 393–398. doi: 10.1109/ICTACS59847.2023.10389847.
[15]	DUONG P P, NGUYEN H M, DAO B A, et al. S-boxes with optimal strict avalanche criterion using chaotic map[C]. 2024 9th International Conference on Integrated Circuits, Design, and Verification (ICDV), Hanoi, Vietnam, 2024: 85–90. doi: 10.1109/ICDV61346.2024.10616714.
[16]	JIN Xin, FENG Junhao, and HUANG Boyang. Side channel attack on SM4 algorithm with deep learning-based analysis[C]. 2022 IEEE International Conference on Advances in Electrical Engineering and Computer Applications (AEECA), Dalian, China, 2022: 749–752. doi: 10.1109/AEECA55500.2022.9919093.