Low-Complexity Transform Domain Orthogonal Time Frequency Space Channel Equalization Algorithm
-
摘要: 正交时频空(OTFS)调制在解决高速移动通信中的性能瓶颈方面具有独特优势,但传统均衡算法难以有效消除复杂环境下的符号间干扰(ISI)和多普勒间干扰(IDI),同时还存在复杂度高的问题。针对上述问题,该文提出一种低复杂度的基于分块矩阵的变换域OTFS信道均衡算法。首先,基于时延-多普勒(DD)域信道响应的分块稀疏性,结合保护间隔设计,逐步消除OTFS系统扩散引起的ISI,建立子块的均衡模型。其次,利用信道子矩阵托普利兹循环矩阵的性质,将其进行变换域处理变为对角矩阵,从而在均衡操作中消除IDI并降低算法复杂度。最后,在此算法的基础上引入判决反馈,进一步提升算法的性能增益。系统仿真表明,该文所提算法在复杂度与性能方面均具有良好的折中性能且适合多种实际场景,同时能在一定程度上降低信道估计过程中的导频开销,增加数据传输效率。Abstract:
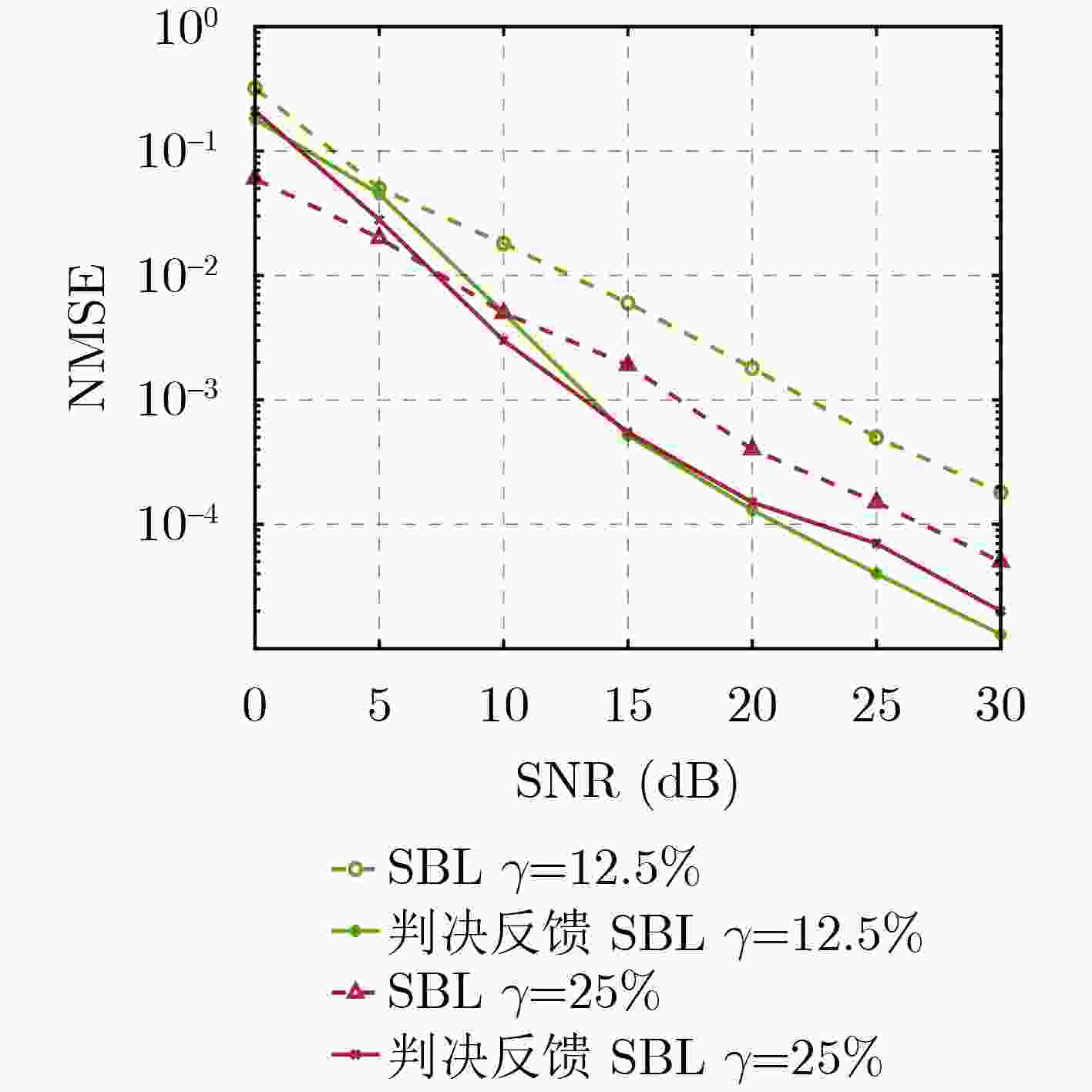
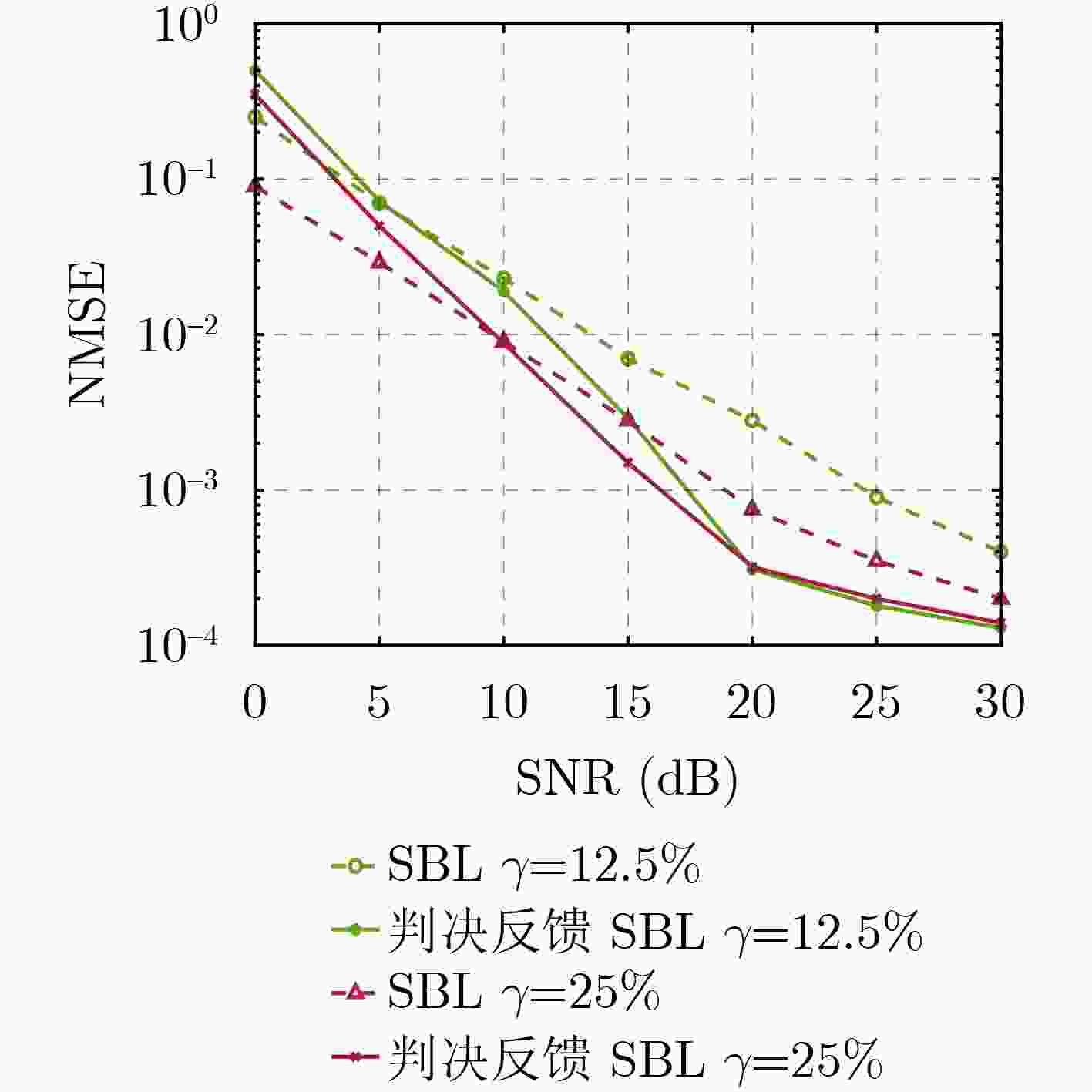
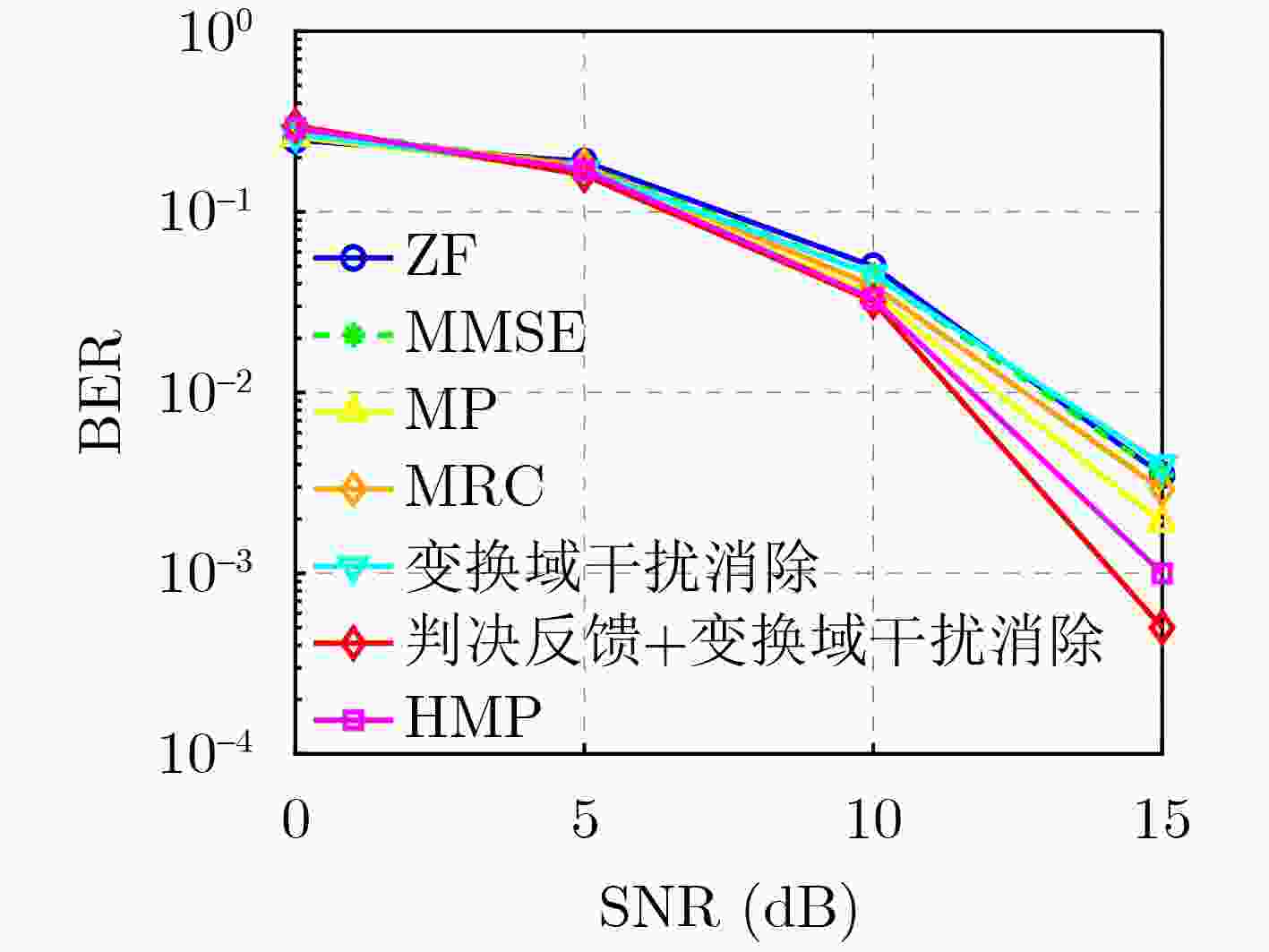
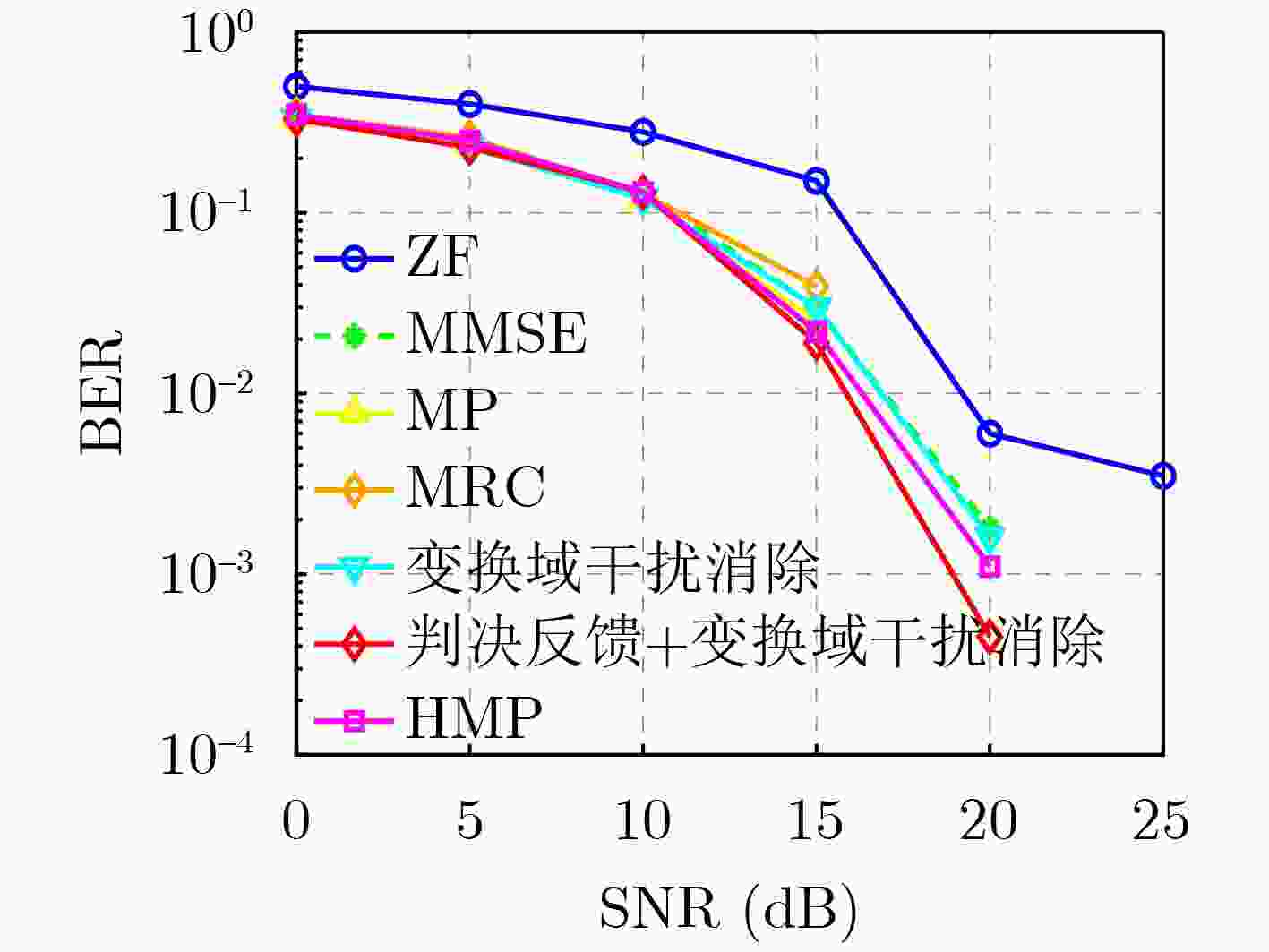
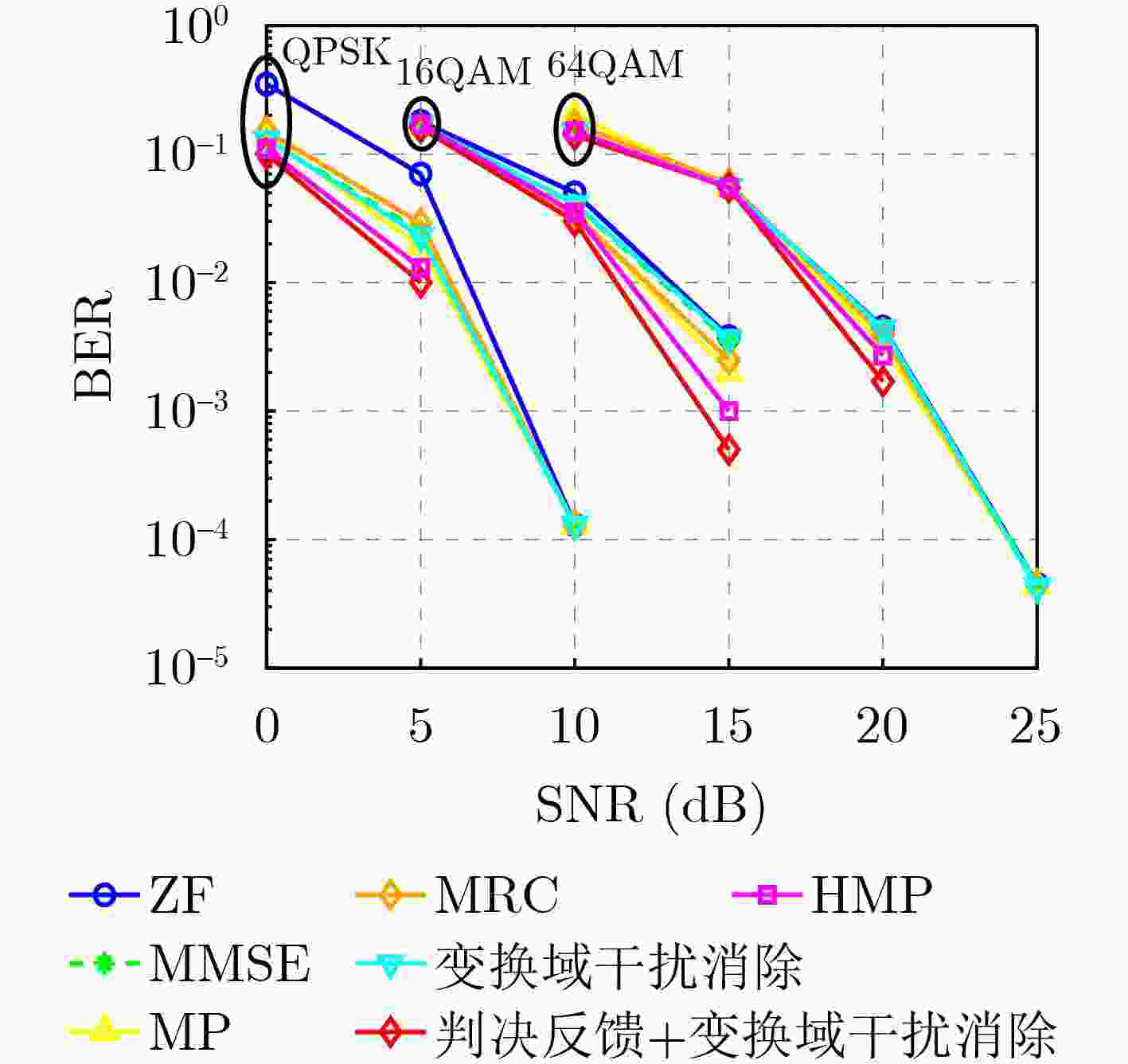
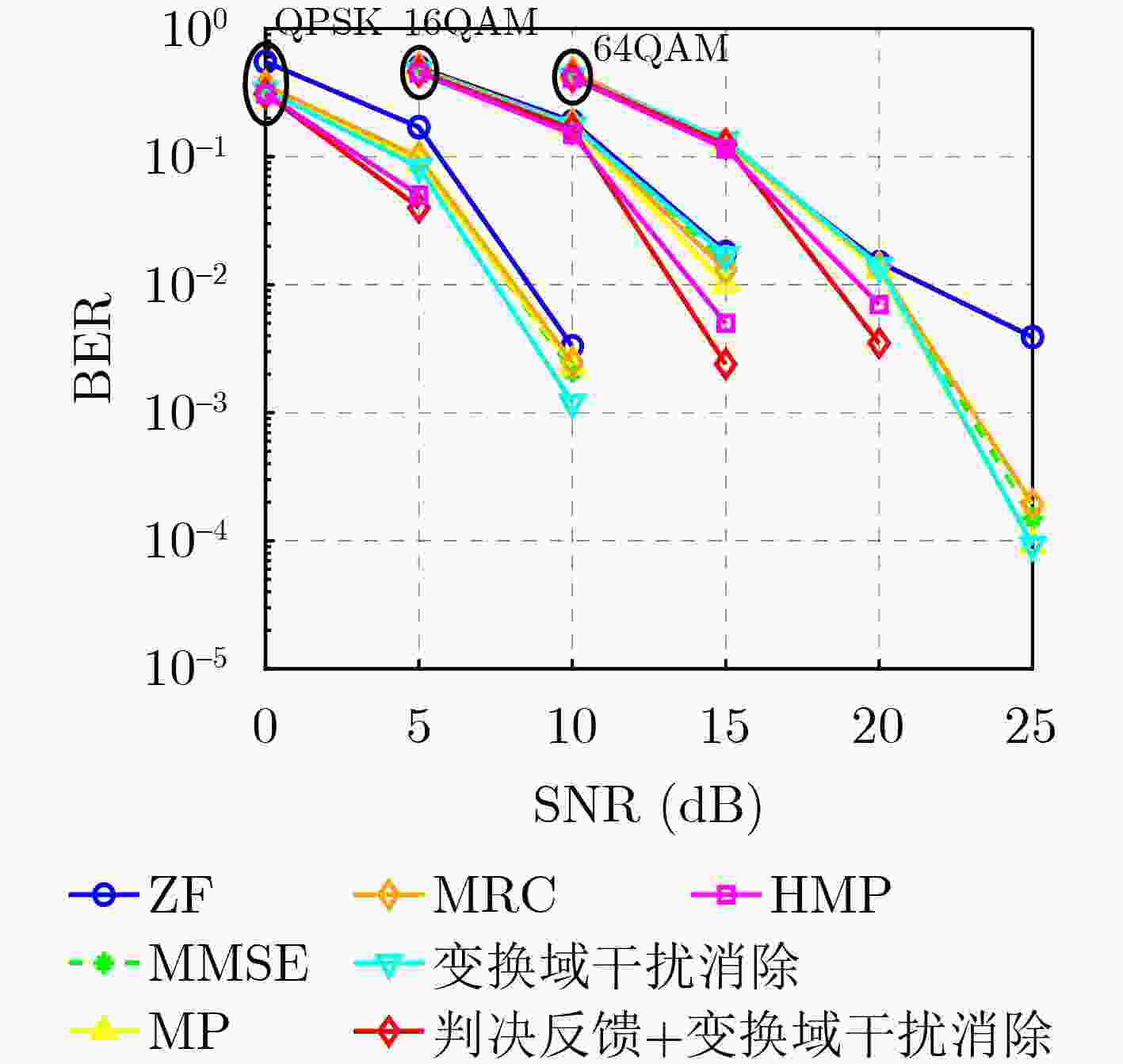
Objective Orthogonal Time Frequency Space (OTFS) modulation is a key technique for high-mobility communication systems, offering robustness against severe Doppler shifts and multipath fading. It provides notable advantages in dynamic environments such as vehicular networks, high-speed rail communications, and unmanned aerial vehicle systems, where conventional orthogonal frequency-division multiplexing fails due to rapid channel variations and dense scattering. However, standard equalization algorithms, including Zero Forcing (ZF) and Minimum Mean Square Error (MMSE), are often ineffective in mitigating Inter-Symbol Interference (ISI) and Inter-Doppler Interference (IDI) under rich-scatterer conditions. These methods also require large-scale matrix inversion, resulting in prohibitively high computational complexity, particularly on OTFS grids with high dimensionality (e.g., M = 32 subcarriers, N = 16 symbols per frame). Most existing studies adopt single-scatterer models that do not reflect the interference structure in practical multipath channels. This study proposes a low-complexity transform domain OTFS equalization algorithm that incorporates block matrix decomposition, transform domain diagonalization, and decision feedback strategies. The algorithm aims to (1) reduce complexity by exploiting block sparsity and structural features of the Delay-Doppler (DD) domain channel matrix, (2) improve interference suppression in time-varying Doppler and dense scattering environments, and (3) validate performance using the 3GPP Extended Vehicular A (EVA) channel model, which simulates realistic high-speed scenarios with user velocities ranging from 121.5 km/h to 607.5 km/h and multiple scattering paths. Methods The proposed algorithm operates in three key stages: (1) Block-Wise ISI Elimination: Leveraging the block-sparse structure of the DD-domain channel matrix, the algorithm partitions the channel into submatrices, each corresponding to a specific DD component. Guard intervals are introduced to suppress ISI arising from signal dispersion across the OTFS grid. Each submatrix K m,l is modeled as a Toeplitz circulant matrix, enabling iterative cancellation of interference by subtracting previously estimated symbols. (2) Transform Domain Diagonalization: Each Toeplitz circulant submatrix is diagonalized using Fourier-based operations. Specifically, the normalized FFT matrix F N is applied to K m,l , converting it into a diagonal form and transforming complex matrix inversion into element-wise division. This step reduces the computational complexity of MMSE equalization from $\mathcal{O}\left( M^3{{N^3}} \right)$ to $\mathcal{O}\left( {{N^3}} \right)$, where N denotes the Doppler dimension of the OTFS resource grid. (3) Decision Feedback Refinement: A closed-loop decision feedback mechanism is introduced to iteratively improve symbol estimates. The demodulated symbols are re-modulated and fed back to update the channel matrix, thereby enhancing estimation accuracy and lowering pilot overhead. The algorithm is evaluated using the 3GPP EVA channel model, which reflects practical high-speed communication scenarios with user velocities between 121.5 km/h and 607.5 km/h, time-varying Doppler shifts, and multiple scatterers. Key system parameters include 32 subcarriers (M = 32), 16 symbols per frame (N = 16), and modulation formats ranging from QPSK to 64QAM. Results and Discussions The performance of the proposed algorithm is evaluated against ZF, MMSE, Message Passing (MP), Maximal Ratio Combining (MRC), and Hybrid MP (HMP) detectors under scenarios: Complexity reduction. The algorithm achieves a computational complexity of $\mathcal{O}\left( {{N^3}} \right)$, markedly lower than that of ZF/MMSE and MP. Transform domain diagonalization simplifies matrix inversion into element-wise division, thereby eliminating $\mathcal{O}\left( {{N^3}} \right)$ operations.Interference Suppression: the algorithm yields a 2.5 dB Bit Error Ratio (BER) improvement over ZF and MMSE at 15 dB SNR under 16QAM modulation. The decision feedback mechanism further reduces the Normalized Mean Square Error (NMSE) by 12.5 dB while lowering pilot overhead by 50%. In high-speed scenarios, the algorithm maintains superior performance, outperforming MRC and HMP by 1.7 dB and 1.0 dB, respectively, under 64QAM modulation. Modulation Robustness: The algorithm consistently demonstrates performance gains across QPSK, 16QAM, and 64QAM. At high SNR with 64QAM, BER gains of 1.7 dB, 1.5 dB, and 1.0 dB are achieved over MRC, MP, and HMP, respectively. Transform domain processing efficiently diagonalizes the channel matrix and eliminates IDI, which is critical in scatterer-rich environments where non-diagonal components dominate interference.Practical Validation: Simulations using the 3GPP EVA model confirm the algorithm’s applicability in real-world high-mobility settings. Conclusions This study presents a low-complexity approach to OTFS channel equalization, addressing both computational and interference challenges in high-mobility scenarios. By leveraging the block-sparse structure of the DD-domain channel matrix and applying Fourier-based diagonalization, the algorithm achieves near-linear complexity while maintaining competitive BER performance. The decision feedback mechanism further enhances robustness, enabling adaptive channel estimation with reduced pilot overhead.Key contributions include: Block-sparse matrix decomposition that facilitates sequential ISI elimination through the use of guard intervals and Toeplitz circulant structures.Fourier-based diagonalization that replaces matrix inversion with element-wise division, reducing computational complexity by orders of magnitude.A closed-loop decision feedback scheme that improves NMSE by 12.5 dB while halving the required pilot overhead.Simulation results under the 3GPP EVA model confirm the algorithm’ suitability for high-speed applications, such as vehicular networks and high-speed rail communications. Future work will explore extensions to large-scale Multiple-Input Multiple-Output (MIMO) systems, adaptive channel tracking, and multi-user interference suppression, with the aim of integrating this framework into 6G URLLC systems. -
1 基于分块矩阵的OTFS干扰消除均衡算法
输入:DD域接收信号中的数据符号$ {{\boldsymbol{y}}^{\text{D}}} $,信道估计输出的DD域
等效矩阵H输出:DD域发送信号中的数据符号$ {\hat {\boldsymbol{x}}^{\text{D}}} $ (1) for $m = 1:M'$ (2) for $l = 1:L$ (3) ISI消除:
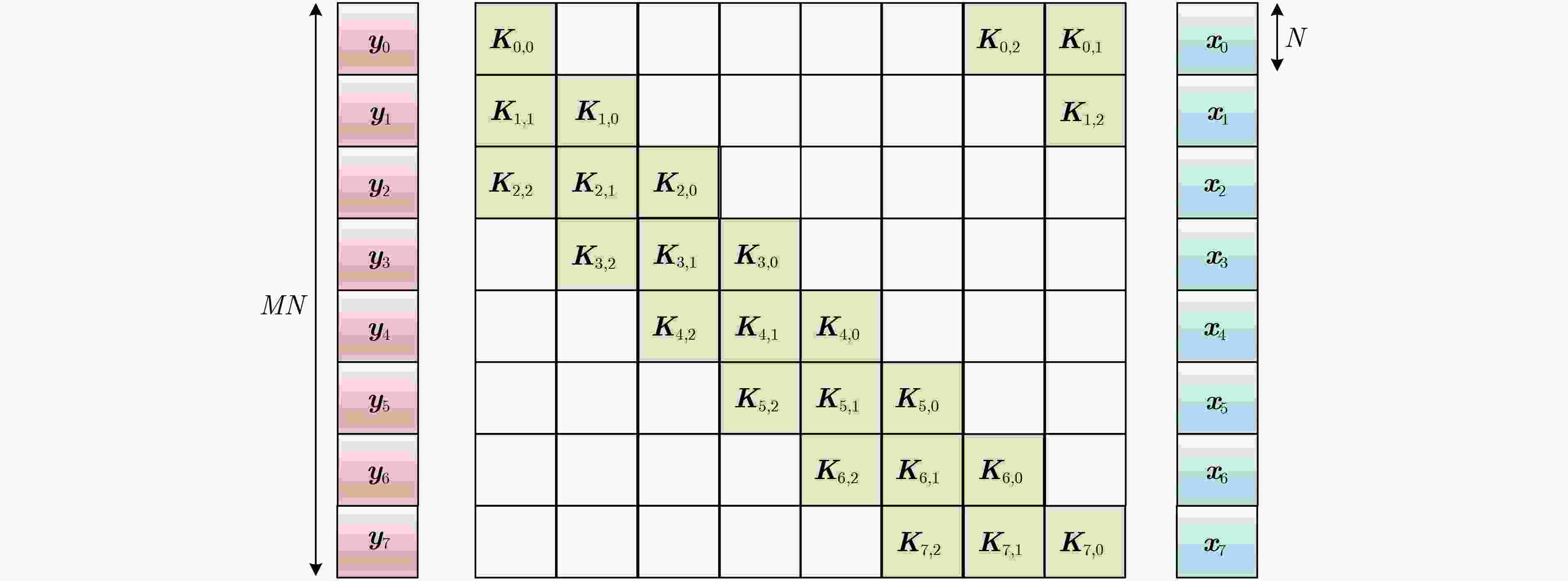
$ {{\boldsymbol{y}}}_{m}^{\text{LOS}}={{\boldsymbol{y}}}_{m}^{\text{D}}-{\displaystyle \sum _{l=1}^{L-1}{{\boldsymbol{K}}}_{m,l}\cdot {{\boldsymbol{x}}}_{m-l}}={{\boldsymbol{K}}}_{m,0}\cdot {{\boldsymbol{x}}}_{m}+{{\boldsymbol{z}}}_{m} $(4) end (5) 变换域矩阵表示:$ \vec {\boldsymbol{y}}_m^{{\text{LOS}}} = {\vec {\boldsymbol{K}}_{m,l}}{\vec {\boldsymbol{x}}_m} + {\vec {\boldsymbol{z}}_m} $ (6) 变换域信道均衡:$ {\vec {\boldsymbol{x}}_m} = {\left( {\vec {\boldsymbol{K}}_{m,l}^{\text{H}}{{\vec {\boldsymbol{K}}}_{m,l}} + {\sigma ^2}{\boldsymbol{I}}} \right)^{ - 1}}\vec {\boldsymbol{K}}_{m,l}^{\text{H}}\vec {\boldsymbol{y}}_m^{{\text{LOS}}} $ (7) 转换回DD域:$ {{\boldsymbol{x}}_m} ={\boldsymbol{ F}}_N^{\text{H}}{\vec {\boldsymbol{x}}_m} $ (8) end (9) 判决反馈:解调:${\mathop {\boldsymbol{x}}\limits^{\smile}}= \mathcal{D}\mathcal{Q}\left( {\boldsymbol{x}} \right) $ (10) 调制:$\mathop{\mathop {\boldsymbol{x}}\limits^{\smile}}\limits^\frown = \mathcal{Q}\left( {\mathop {\boldsymbol{x}}\limits^{\smile}} \right) $ (11) 信道估计更新:将$\mathop{\mathop {\boldsymbol{x}}\limits^{\smile}}\limits^\frown $和${\boldsymbol{y}}$输入相应信道估计算法中得到新的H (12) 均衡:重复本算法均衡过程得到最后的$ {\hat {\boldsymbol{x}}^{\text{D}}} $ 表 1 各均衡算法复杂度对比
算法 时间复杂度 ZF $\mathcal{O}\left( {{M^3}{N^3}} \right)$ MMSE $\mathcal{O}\left( {{M^3}{N^3}} \right)$ MP $\mathcal{O}\left( {M{N^2}VL{I_{{\text{MP}}}}} \right)$ MRC $\mathcal{O}\left( {LMN} \right)$ HMP $\mathcal{O}\left( {{{\left| Q \right|}^{P\left( {2k + 1} \right)}}} \right)$ 所提算法 $\mathcal{O}\left( {{N^3}} \right)$ 表 2 仿真系统参数
参数名称 参数值 子载波个数(M) 32 符号个数(N) 16 载波频率 5.9 GHz 子载波间隔 15 kHz 调制方式 QPSK/16QAM/64QAM 用户移动速度 121.5~607.5 km/h 信道模型 EVA[23] CP长度 7 天线配置 SISO 噪声模型 AWGN -
[1] BITHAS P S, KANATAS A G, DA COSTA D B, et al. On the double-generalized gamma statistics and their application to the performance analysis of V2V communications[J]. IEEE Transactions on Communications, 2018, 66(1): 448–460. doi: 10.1109/TCOMM.2017.2757466. [2] YANG Lu and ZHANG Wei. Beam tracking and optimization for UAV communications[J]. IEEE Transactions on Wireless Communications, 2019, 18(11): 5367–5379. doi: 10.1109/TWC.2019.2935972. [3] FAN Pingzhi, ZHAO Jing, and CHIH-LIN I. 5G high mobility wireless communications: Challenges and solutions[J]. China Communications, 2016, 13(2): 1–13. doi: 10.1109/CC.2016.7405718. [4] 廖勇, 罗渝, 荆亚昊. 6G新型时延多普勒通信范式: OTFS的技术优势、设计挑战、应用与前景[J]. 电子与信息学报, 2024, 46(5): 1827–1842. doi: 10.11999/JEIT231133.LIAO Yong, LUO Yu, and JING Yahao. 6G new time-delay Doppler communication paradigm: Technical advantages, design challenges, applications and prospects of OTFS[J]. Journal of Electronics & Information Technology, 2024, 46(5): 1827–1842. doi: 10.11999/JEIT231133. [5] YUAN Weijie, LI Shuangyang, WEI Zhiqiang, et al. New delay Doppler communication paradigm in 6G era: A survey of orthogonal time frequency space (OTFS)[J]. China Communications, 2023, 20(6): 1–25. doi: 10.23919/JCC.fa.2022-0578.202306. [6] LIU Haoyan, LIU Yanming, YANG Min, et al. On the characterizations of OTFS modulation over multipath rapid fading channel[J]. IEEE Transactions on Wireless Communications, 2023, 22(3): 2008–2021. doi: 10.1109/TWC.2022.3208161. [7] 廖勇, 李雪. 一种低复杂度的正交时频空系统接收机设计[J]. 电子与信息学报, 2024, 46(6): 2418–2424. doi: 10.11999/JEIT230625.LIAO Yong and LI Xue. Low complexity receiver design for orthogonal time frequency space systems[J]. Journal of Electronics & Information Technology, 2024, 46(6): 2418–2424. doi: 10.11999/JEIT230625. [8] LIAO Yong and LI Xue. Joint multi-domain channel estimation based on sparse Bayesian learning for OTFS system[J]. China Communications, 2023, 20(1): 14–23. doi: 10.23919/JCC.2023.01.002. [9] 方朝曦, 奚家熹, 王宗欣. 基于迫零均衡的单载波分块传输系统的误符号率分析[J]. 通信学报, 2010, 31(1): 80–84. doi: 10.3969/j.issn.1000-436X.2010.01.012.FANG Zhaoxi, XI Jiaxi, and WANG Zongxin. SER performance analysis of single carrier block transmission systems with zero-forcing equalization[J]. Journal on Communications, 2010, 31(1): 80–84. doi: 10.3969/j.issn.1000-436X.2010.01.012. [10] LIANG Yu, LI Lingjun, FAN Pingzhi, et al. Doppler resilient orthogonal time-frequency space (OTFS) systems based on index modulation[C]. 2020 IEEE 91st Vehicular Technology Conference (VTC2020-Spring), Antwerp, Belgium, 2020: 1–5. doi: 10.1109/VTC2020-Spring48590.2020.9129380. [11] SURABHI G D and CHOCKALINGAM A. Low-complexity linear equalization for OTFS modulation[J]. IEEE Communications Letters, 2020, 24(2): 330–334. doi: 10.1109/LCOMM.2019.2956709. [12] TIWARI S, DAS S S, and RANGAMGARI V. Low complexity LMMSE receiver for OTFS[J]. IEEE Communications Letters, 2019, 23(12): 2205–2209. doi: 10.1109/LCOMM.2019.2945564. [13] RAVITEJA P, PHAN K T, HONG Yi, et al. Interference cancellation and iterative detection for orthogonal time frequency space modulation[J]. IEEE Transactions on Wireless Communications, 2018, 17(10): 6501–6515. doi: 10.1109/TWC.2018.2860011. [14] 梁瑞璇. OTFS作用域及信号检测算法研究[D]. [硕士论文], 桂林电子科技大学, 2022. doi: 10.27049/d.cnki.ggldc.2022.000976.LIANG Ruixuan. Research on OTFS modulation domain and signal detection algorithm[D]. [Master dissertation], Guilin University of Electronic Technology, 2022. doi: 10.27049/d.cnki.ggldc.2022.000976. [15] LI Lingjun, LIANG Yu, FAN Pingzhi, et al. Low complexity detection algorithms for OTFS under rapidly time-varying channel[C]. 2019 IEEE 89th Vehicular Technology Conference (VTC2019-Spring), Kuala Lumpur, Malaysia, 2019: 1–5. doi: 10.1109/VTCSpring.2019.8746420. [16] XIANG Luping, LIU Yusha, YANG Lieliang, et al. Gaussian approximate message passing detection of orthogonal time frequency space modulation[J]. IEEE Transactions on Vehicular Technology, 2021, 70(10): 10999–11004. doi: 10.1109/TVT.2021.3102673. [17] 王丹, 李峰, 夏麒煜. 面向正交时频空的低复杂度信号检测算法[J]. 小型微型计算机系统, 2025, 46(2): 443–448. doi: 10.20009/j.cnki.21-1106/TP.2023-0448.WANG Dan, LI Feng, and XIA Qiyu. Low complexity signal detection algorithm for orthogonal time frequency space modulation[J]. Journal of Chinese Computer Systems, 2025, 46(2): 443–448. doi: 10.20009/j.cnki.21-1106/TP.2023-0448. [18] THAJ T and VITERBO E. Low complexity iterative rake decision feedback equalizer for zero-padded OTFS systems[J]. IEEE Transactions on Vehicular Technology, 2020, 69(12): 15606–15622. doi: 10.1109/TVT.2020.3044276. [19] 韩飞, 纪金伟, 刘成朋, 等. 一种MIMO-OTFS低复杂度信号检测算法[J]. 计算机测量与控制, 2023, 31(2): 190–195, 203. doi: 10.16526/j.cnki.11-4762/tp.2023.02.030.HAN Fei, JI Jinwei, LIU Chengpeng, et al. A low complexity MIMO-OTFS signal detection algorithm[J]. Computer Measurement & Control, 2023, 31(2): 190–195, 203. doi: 10.16526/j.cnki.11-4762/tp.2023.02.030. [20] LI Xiang, YUAN Weijie, and LI Zhongjie. Hybrid message passing detection for OTFS modulation[C]. 2023 IEEE Wireless Communications and Networking Conference, Glasgow, United Kingdom, 2023: 1–5. doi: 10.1109/WCNC55385.2023.10118784. [21] CHENG Junqiang, GAO Hui, XU Wenjun, et al. Low-complexity linear equalizers for OTFS exploiting two-dimensional fast Fourier transform[EB/OL]. https://doi.org/10.48550/arXiv.1909.00524, 2019. [22] 刘晨文. 基于OTFS调制的车载毫米波雷达通信一体化技术研究[D]. [硕士论文], 东南大学, 2021. doi: 10.27014/d.cnki.gdnau.2021.000409.LIU Chenwen. Research on mmWave automotive integrated radar and communication technology based on OTFS modulation[D]. [Master dissertation], Southeast University, 2021. doi: 10.27014/d.cnki.gdnau.2021.000409. [23] 任涛. OTFS接收机关键技术研究[D]. [硕士论文], 电子科技大学, 2024. doi: 10.27005/d.cnki.gdzku.2024.004692.REN Tao. Research on key technologies of OTFS receiver[D]. [Master dissertation], University of Electronic Science and Technology of China, 2024. doi: 10.27005/d.cnki.gdzku.2024.004692. [24] HUANG Ziyi, CAO Shuai, WEI Hua, et al. Research on channel estimation algorithm based on OTFS system[C]. 2022 IEEE 6th Information Technology and Mechatronics Engineering Conference (ITOEC), Chongqing, China, 2022: 352–356. doi: 10.1109/ITOEC53115.2022.9734425. [25] 蔡志镕. 基于LTE-V2X的信道估计与均衡研究[D]. [硕士论文], 重庆大学, 2022. doi: 10.27670/d.cnki.gcqdu.2022.003101.CAI Zhirong. Research on channel estimation and equalization based on LTE-V2X[D]. [Master dissertation], Chongqing University, 2022. doi: 10.27670/d.cnki.gcqdu.2022.003101. -





 下载:
下载:


 下载:
下载:
