通信干扰效能评估：<i>q</i>阶序对模糊集与CoCoSo-BM融合框架

宁晓燕; 王翔辰; 杨健; 陈增茂

doi:10.11999/JEIT241140

通信干扰效能评估：q阶序对模糊集与CoCoSo-BM融合框架

doi: 10.11999/JEIT241140 cstr: 32379.14.JEIT241140

1.
哈尔滨工程大学信息与通信工程学院哈尔滨 150001
2.
北京遥感设备研究所北京 100854

基金项目: 国家自然科学基金(62001139)，先进船舶通信与信息技术工业和信息化部重点实验室(AMCIT2101-05)

详细信息

作者简介:
宁晓燕：女，副教授，研究方向为5G通信物理层新技术、认知通信、军用数据链

王翔辰：男，硕士生，研究方向为通信干扰效能评估

杨健：男，研究员，研究方向为数据链、卫星通信、激光通信

陈增茂：男，副教授，研究方向为通信对抗、通信干扰建模、认知无线电技术

通讯作者:
陈增茂，　chenzengmao@hrbeu.edu.cn

中图分类号: TN92
计量
- 文章访问数: 88
- HTML全文浏览量: 34
- PDF下载量: 22
- 被引次数: 0
出版历程
- 收稿日期: 2024-12-27
- 修回日期: 2025-05-19
- 网络出版日期: 2025-06-10

Communication Jamming Effectiveness Evaluation: q-Rung Orthopair Fuzzy Set and CoCoSo-BM Fusion Framework

1.
College of Information and Communication Engineering, Harbin Engineering University, Harbin 150001, China
2.
(Beijing Remote Sensing Equipment Research Institute, Beijing 100854, China

Funds: The National Natural Science Foundation of China (62001139), The Advanced Ship Communications and Info-rmation Technology Industry and Key Laboratory of Ministry of Information Technology (AMCIT2101-05)

摘要

摘要: 在现代电子战的通信对抗中，干扰效能评估能够为抗干扰策略的选择提供决策依据，是无人系统实现智能抗干扰的关键技术。借鉴数学统计领域中最新提出的CoCoSo (Combined Compromise Solution)算法思想，该文提出基于q阶序对模糊集和CoCoSo-BM的通信干扰效能评估方法。首先，根据通信系统与干扰的特点建立通信干扰效能评估指标体系，并采用层次分析法(AHP)与离差最大化法结合的方法确定组合权重。其次，提出采用q阶序对模糊集解决干扰效能评估维度单一的问题，并且引入BM (Bonferroni Mean)算子改进CoCoSo评估方法没有考虑参数权重的问题。最后，通过仿真实验验证了该方法在不同通信抗干扰技术与不同干扰条件下的效能评估有效性和对不同通信环境干扰效果的区分度、敏感度。
- 干扰效能评估 /
- CoCoSo算法 /
- q阶序对模糊集 /
- BM算子 /
- 组合权重
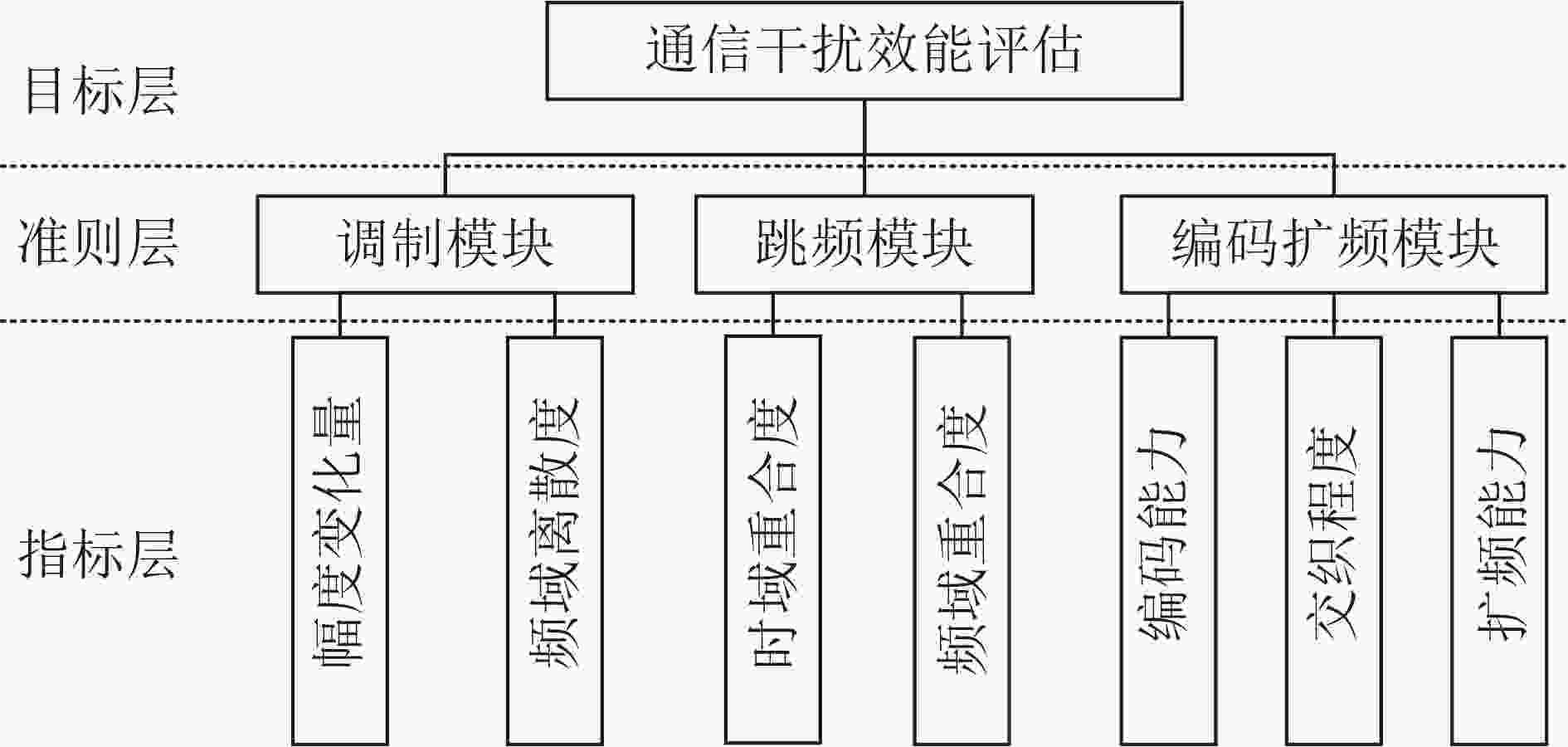
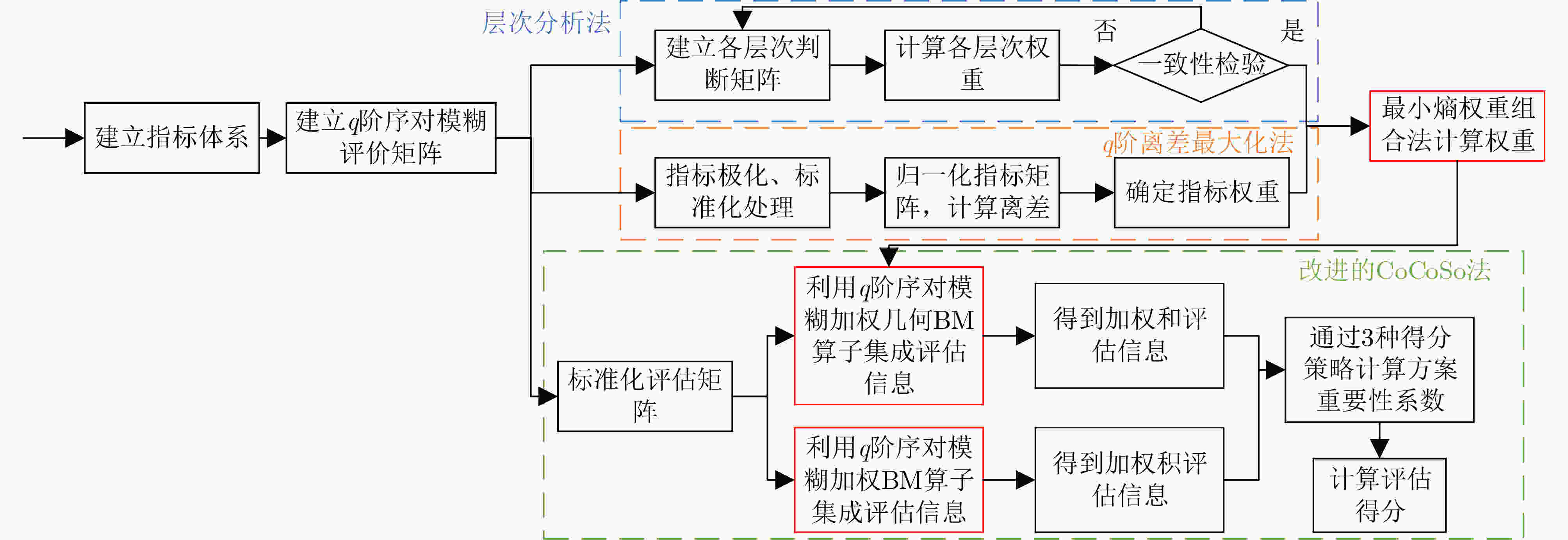
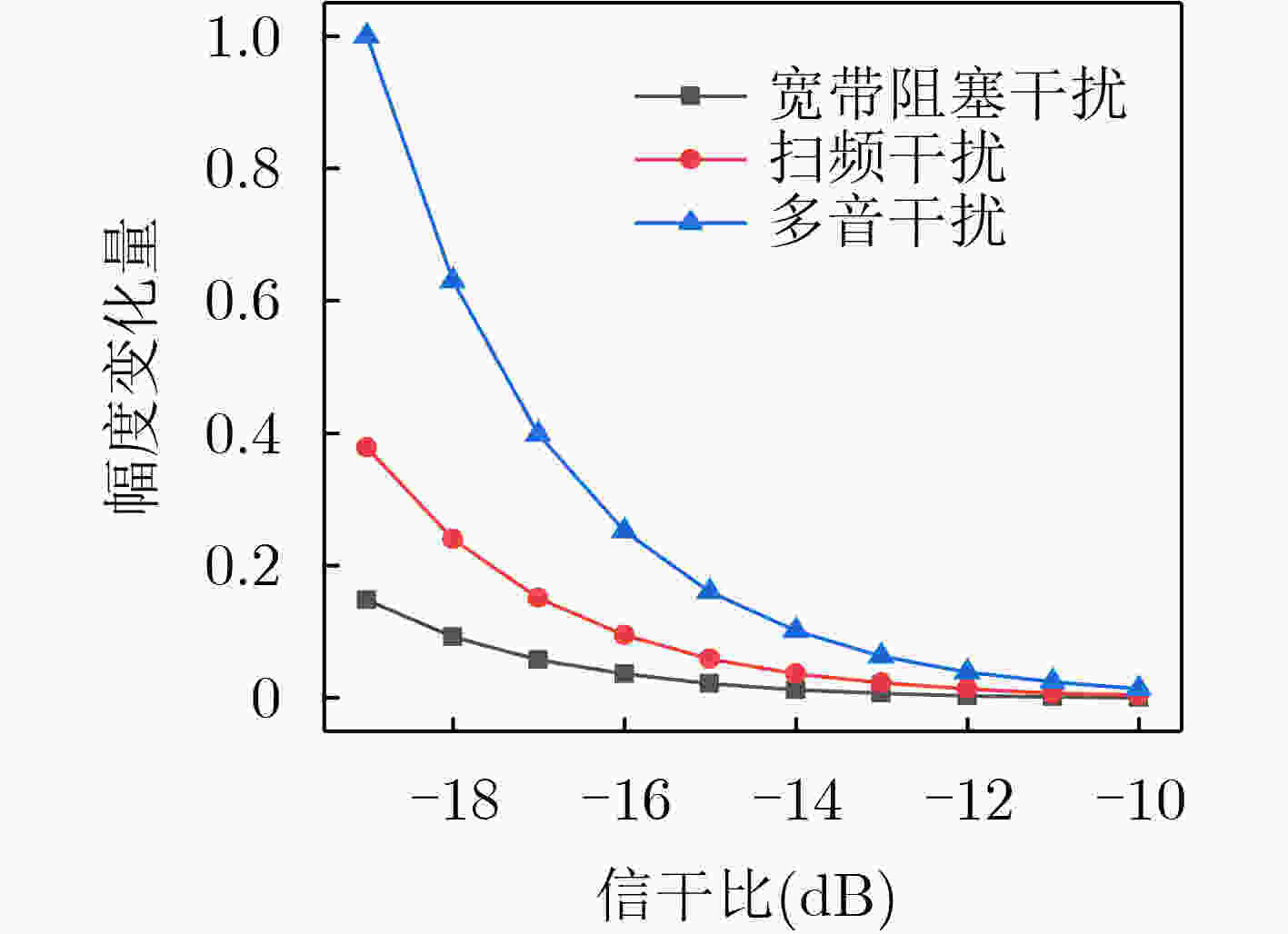
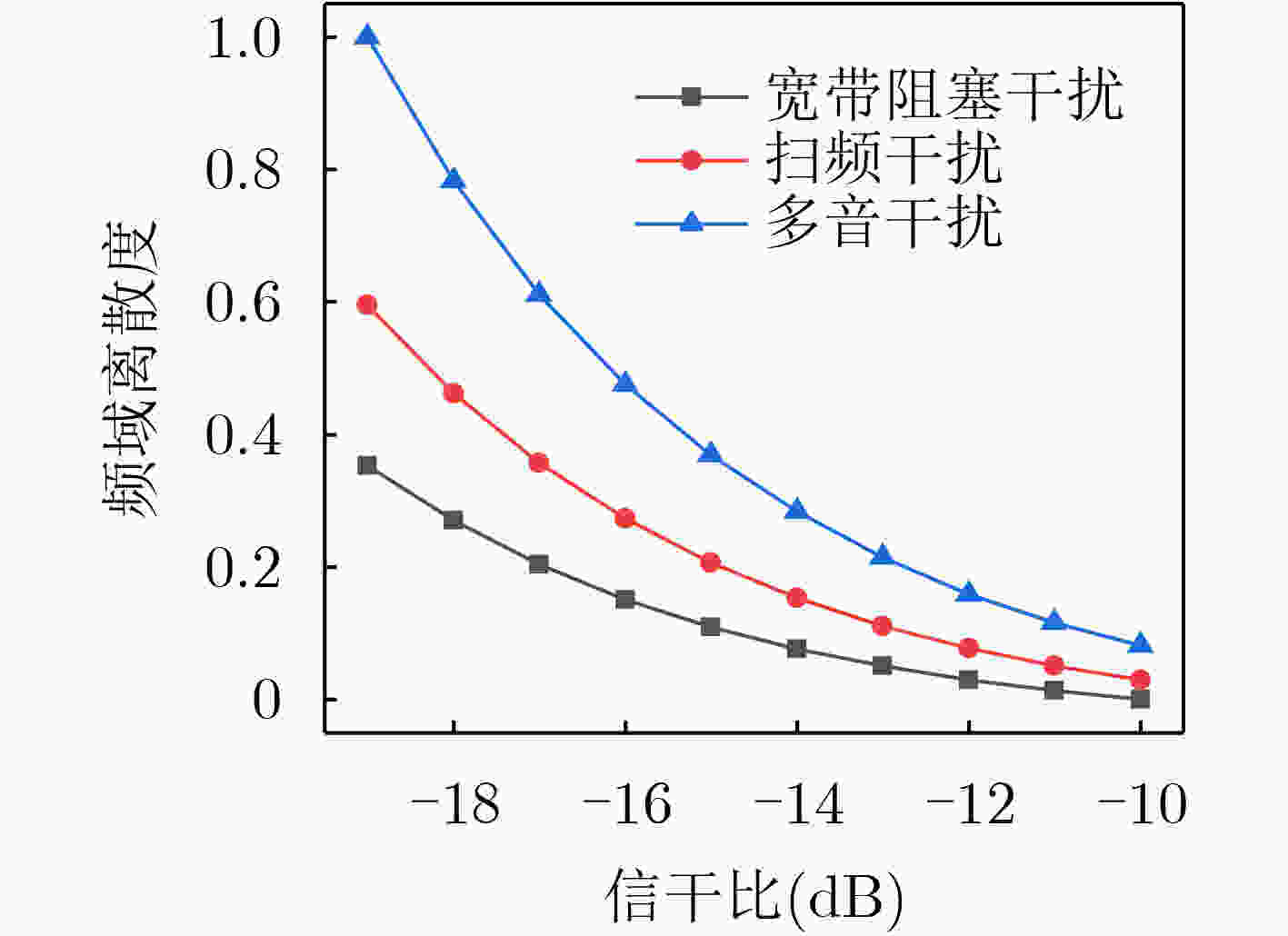
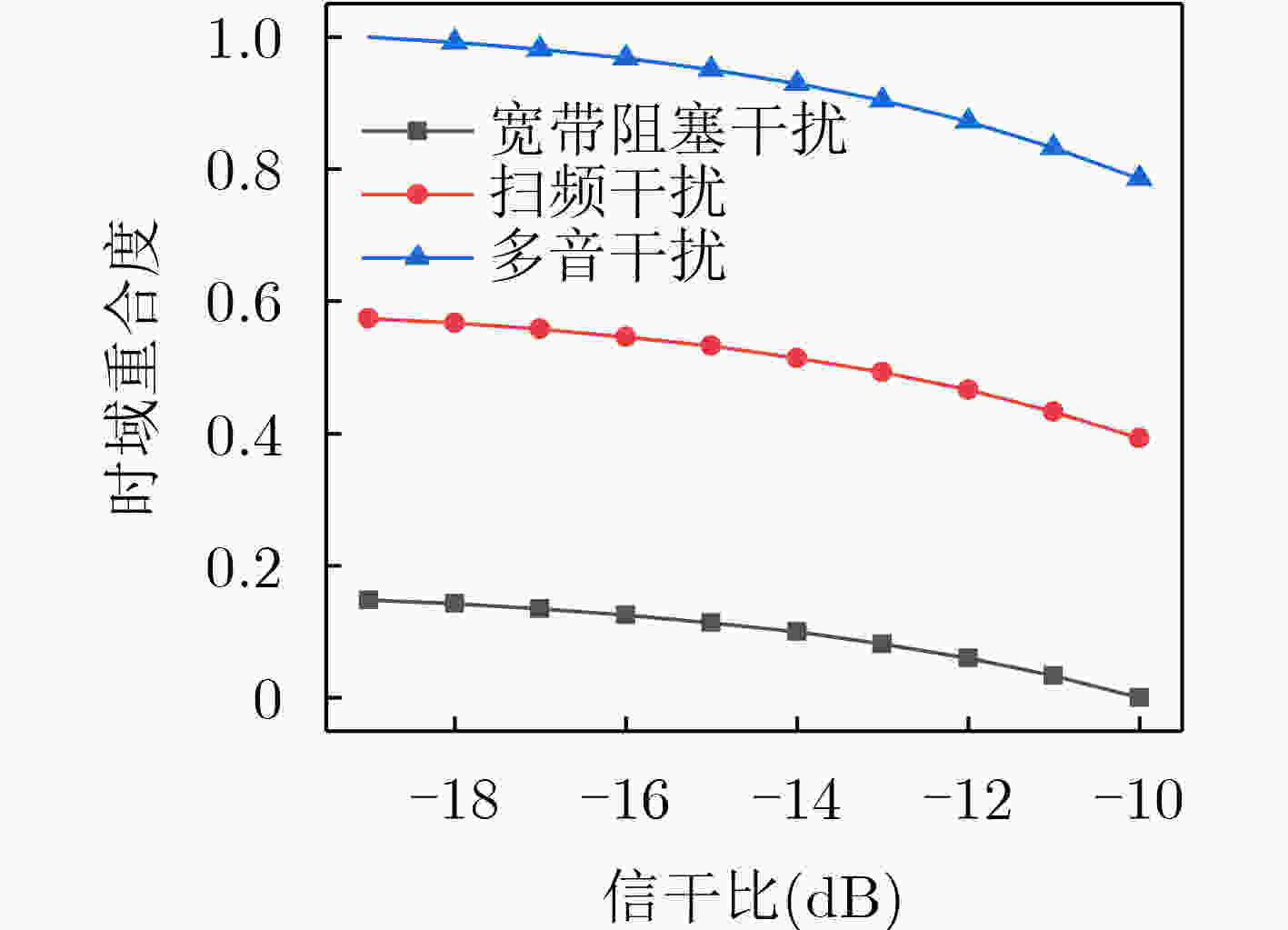
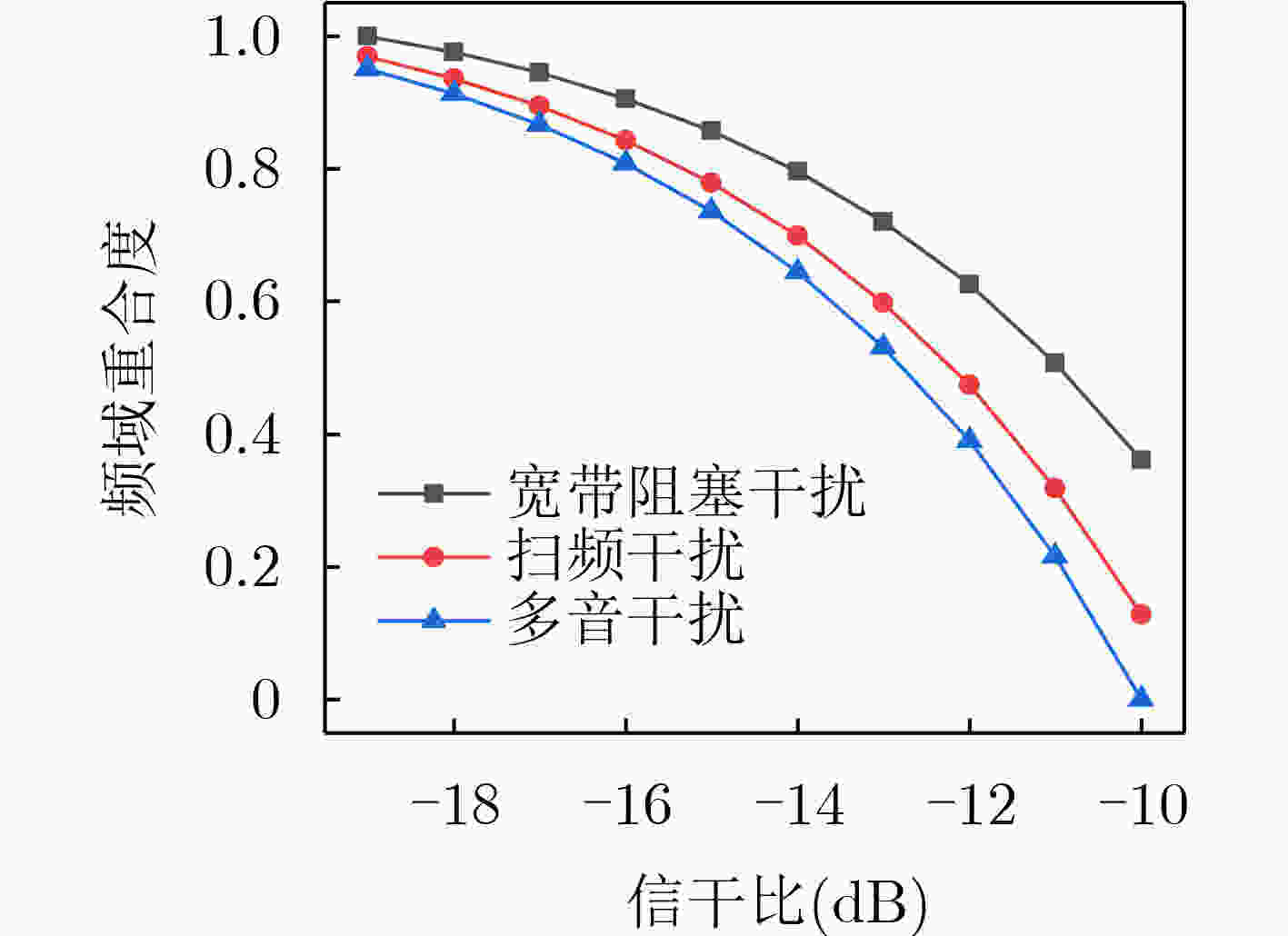
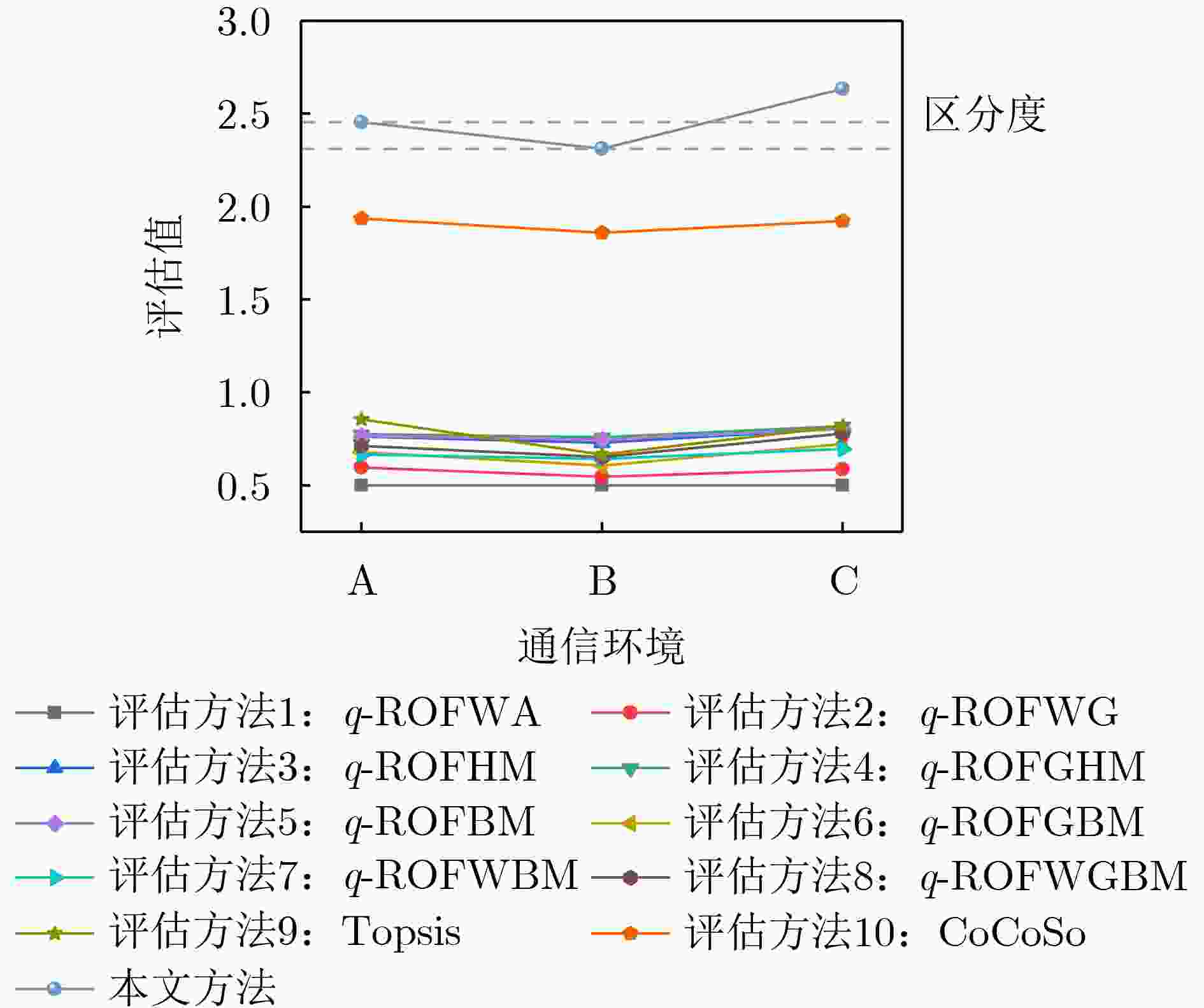
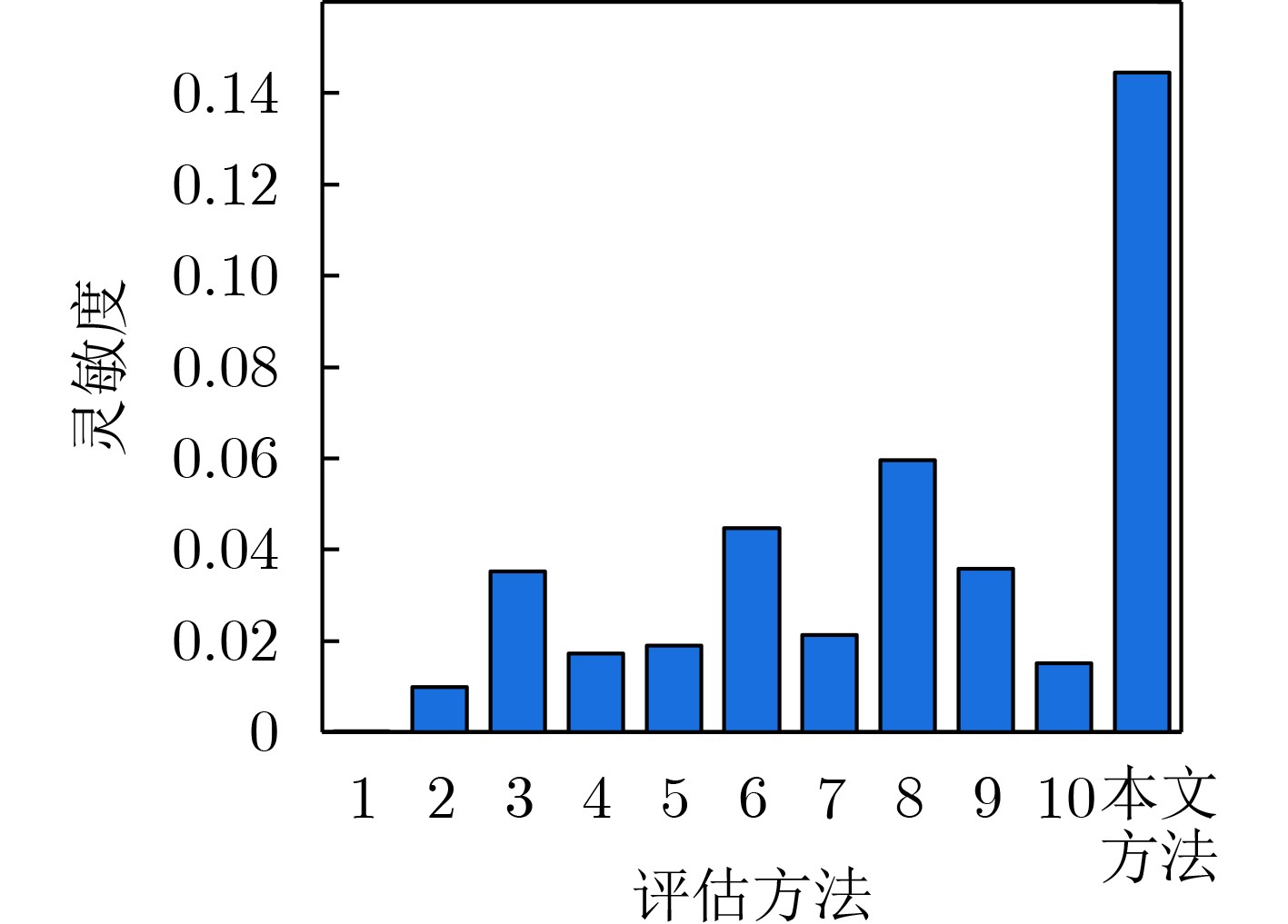
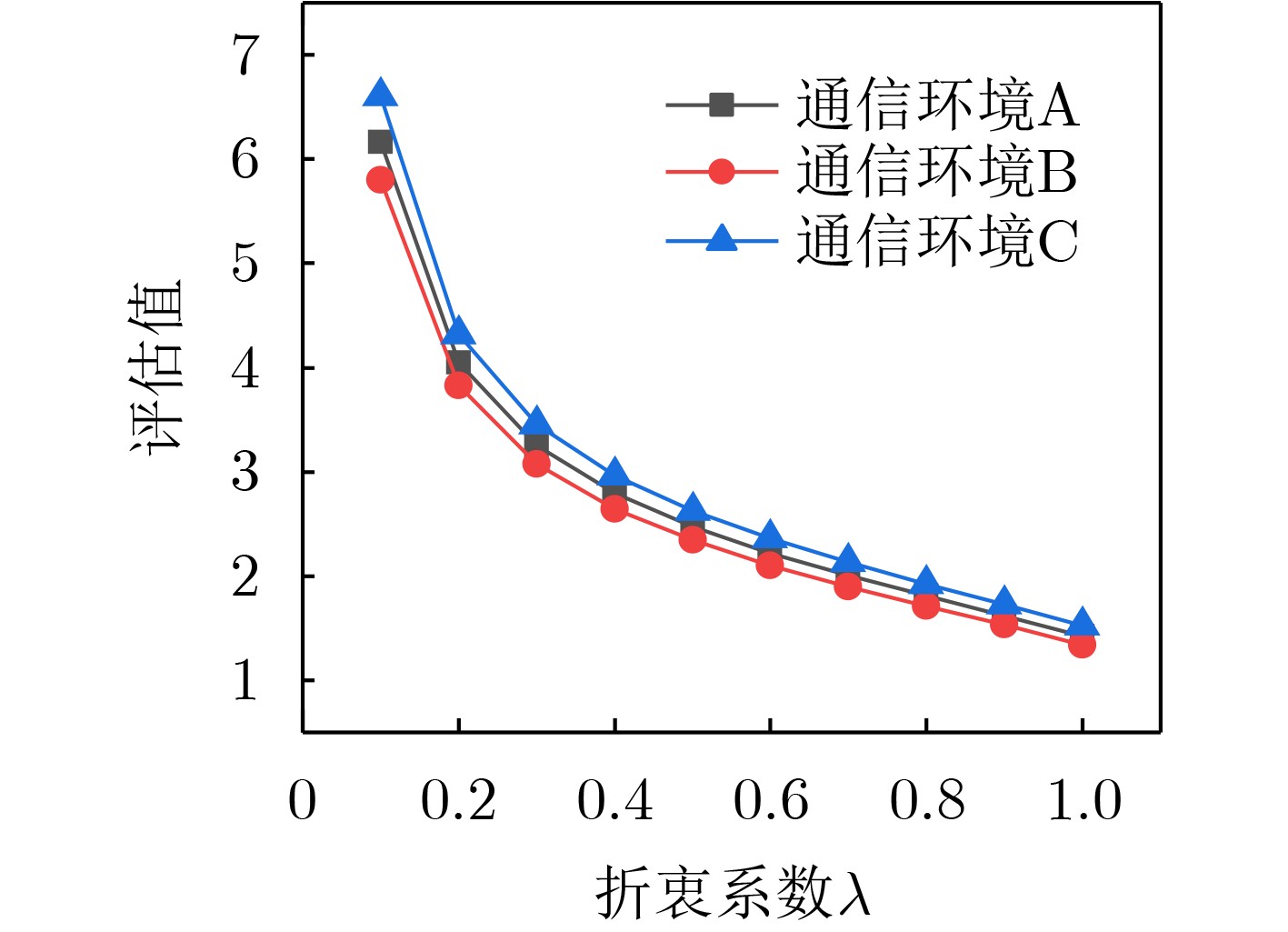
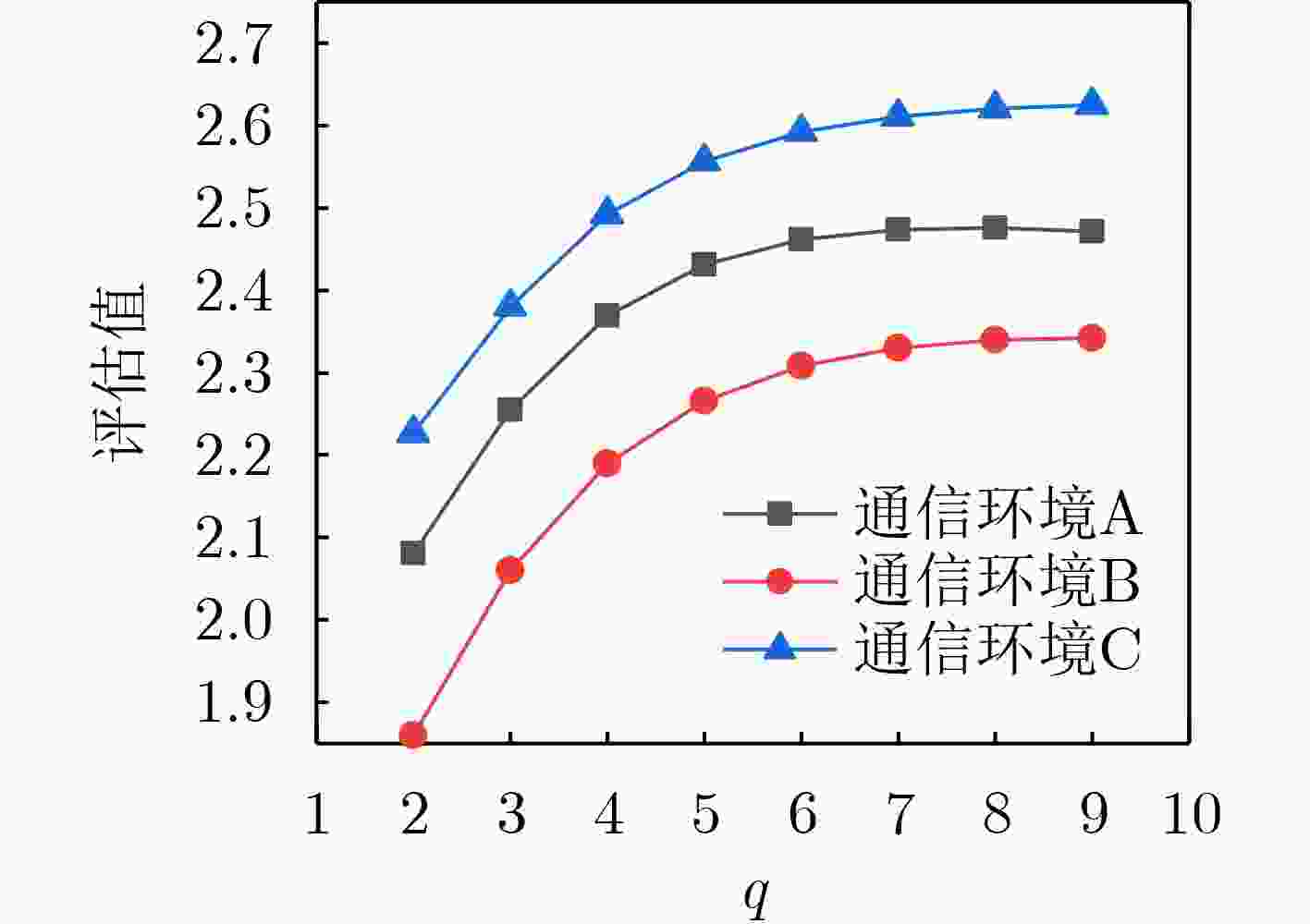
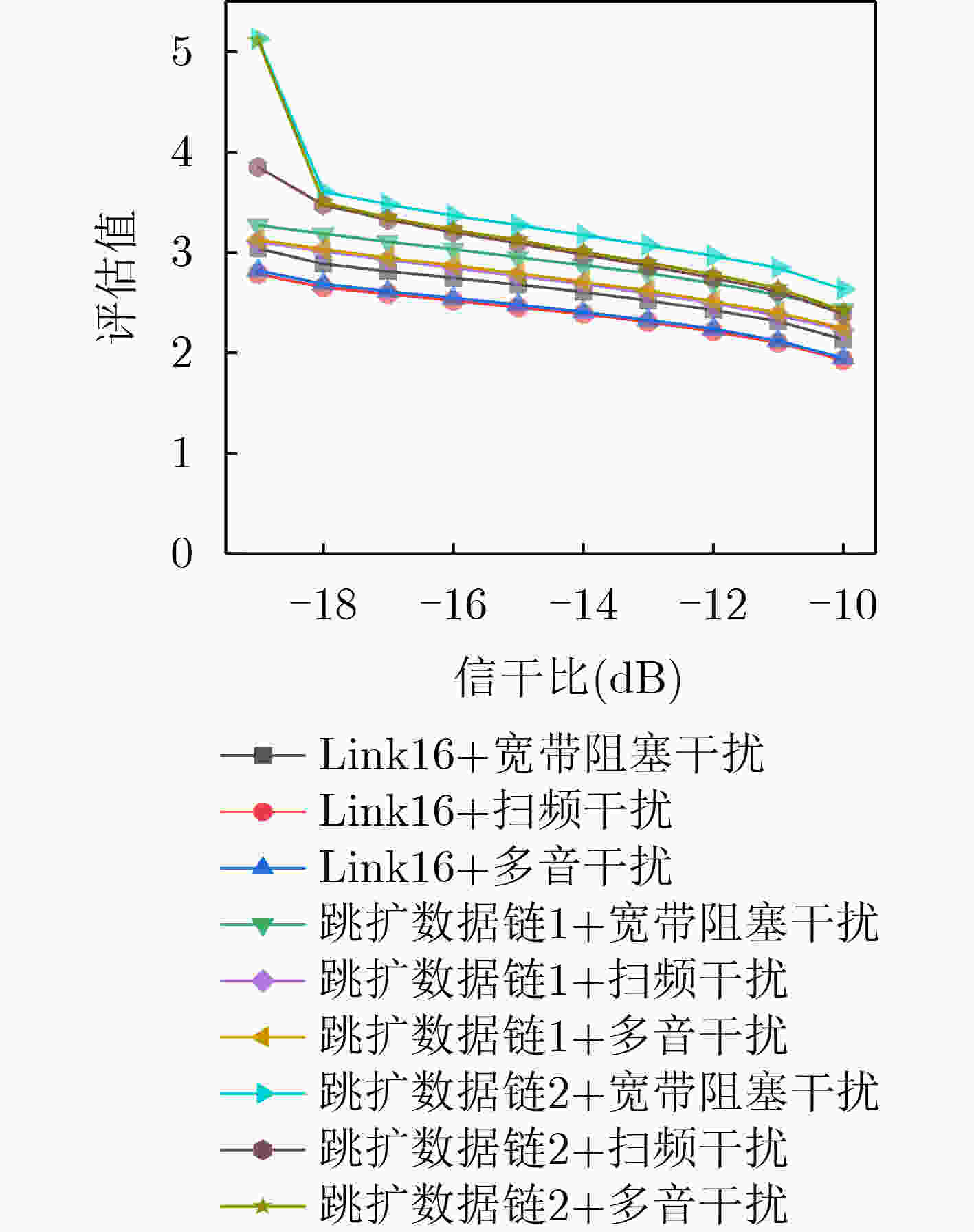
Abstract: Objective With the advancement of modern warfare and the development of communication countermeasure technologies, the evaluation of jamming efficiency is essential for supporting decision-making in anti-jamming strategy selection. It also plays a critical role in enabling intelligent countermeasures in unmanned systems. However, existing evaluation methods often lack comprehensiveness and exhibit low sensitivity. To address these limitations, this study proposes an evaluation method based on the q-rung orthopair fuzzy set and the Combined Compromise Solution (CoCoSo)-Bonferroni Mean (BM) approach, inspired by the recently developed CoCoSo algorithm in mathematical statistics. By integrating q-rung fuzzy ordinals and constructing a structured jamming efficiency evaluation framework, the proposed method improves the completeness and rationality of evaluation results. This approach provides a more effective means of assessing communication jamming efficiency. Methods The proposed evaluation method establishes a comprehensive index system for assessing communication jamming efficiency by integrating the characteristics of both communication systems and jamming techniques. The criterion layer is constructed based on anti-jamming technologies, while the index layer incorporates key indicators such as amplitude variation, frequency-domain dispersion, and time-domain coincidence degree. A combined weighting scheme is adopted using the Analytic Hierarchy Process (AHP) and the maximum deviation method to ensure both subjective and objective consistency. To overcome the limitations of single-dimensional evaluation, the q-rung orthopair fuzzy set is introduced, enabling more flexible representation of uncertainty. The CoCoSo method is applied to aggregate multiple scoring strategies, thereby enhancing the reliability of the evaluation results. To address the CoCoSo method’s limitation in parameter weighting, the BM operator is integrated into the model, ensuring a more balanced and comprehensive assessment. Results and Discussions Based on the established evaluation system, the proposed method utilizes simulation data (Figs. 3–6) and communication system parameters to construct the evaluation matrix. Standard normalization and q-rung fuzzy number transformation are applied to the collected data. The index weights are calculated using the combined AHP and maximum deviation methods. The CoCoSo-BM approach is then employed to comprehensively evaluate the index values under the specified communication environment. Comparative analysis with alternative evaluation methods (Fig. 7) indicates that the proposed method achieves higher discrimination capability across different communication scenarios. Sensitivity analysis (Fig. 8) further confirms its strong differentiation capacity. Evaluation results under varying q values, compromise coefficients, and communication environments (Figs. 9–11) demonstrate the method’s stability and robustness. Conclusions This study addresses the limitations of incompleteness and low discrimination in communication jamming efficiency evaluation by proposing a novel method based on the q-rung orthopair fuzzy set and CoCoSo-BM. By applying the q-rung orthopair fuzzy set—previously unused in communication efficiency assessments—and incorporating the BM operator into the CoCoSo framework, the proposed method enhances evaluation completeness and consistency. Simulation results under varied conditions demonstrate that: (1) the method achieves higher sensitivity than existing approaches; (2) the evaluation remains stable across different q values and compromise coefficients, enabling adaptive parameter selection; and (3) performance under varying jamming-to-signal ratios, system configurations, and jamming conditions confirms its robustness and adaptability in practical scenarios.
- Jamming efficiency evaluation /
- CoCoSo /
- q-rung orthopair fuzzy set /
- BM operator /
- Combined weighting

HTML全文

图 1 通信干扰效能评估指标体系

下载: 全尺寸图片幻灯片

图 2 改进的CoCoSo评估方法系统框图

下载: 全尺寸图片幻灯片

图 3 幅度变化量图

下载: 全尺寸图片幻灯片

图 4 频域离散度

下载: 全尺寸图片幻灯片

图 5 时域重合度

下载: 全尺寸图片幻灯片

图 6 频域重合度

下载: 全尺寸图片幻灯片

图 7 不同评估方法的评估结果

下载: 全尺寸图片幻灯片

图 8 不同评估方法的灵敏度

下载: 全尺寸图片幻灯片

图 9 不同折衷系数下的评估值

下载: 全尺寸图片幻灯片

图 10 不同q值下的评估值

下载: 全尺寸图片幻灯片

图 11 不同通信环境的评估值

下载: 全尺寸图片幻灯片

表 1 通信环境参数

通信环境	通信系统	信道编码	交织长度	ccsk扩频	干扰类型	干扰时段	干扰频段
环境A	Link16	RS(31,15)	109	(32,5)	扫频干扰	2/3	2/3
环境B	跳扩频数据链1	RS(15,11)	75	(8,3)	宽带阻塞干扰	1/3	1/3
环境C	跳扩频数据链2	RS(63,55)	126	(16,4)	多音干扰	全时段	全频段

下载: 导出CSV

表 2 综合评估矩阵

	环境A	环境B	环境C
幅度变化量	(0.0219,0.9781)	(0.0589,0.9411)	(0.1580,0.8420)
频域离散度	(0.1098,0.8902)	(0.2060,0.7940)	(0.3662,0.6338)
时域重合度	(0.5316,0.4684)	(0.1132,0.8868)	(0.9500,0.0500)
频域重合度	(0.7785,0.2215)	(0.8569,0.1431)	(0.7352,0.2648)
编码能力	(0.5162,0.4838)	(0.2667,0.7333)	(0.2170,0.7830)
交织程度	(0.7982,0.2018)	(0.8000,0.2000)	(0.8333,0.1667)
扩频能力	(0.8437,0.1563)	(0.6250,0.3750)	(0.7500,0.2500)

下载: 导出CSV

参考文献(19)

[1]	金山, 邹伟, 都琳. 美军武器数据链发展与启示[J]. 兵工自动化, 2021, 40(12): 8–11. doi: 10.7690/bgzdh.2021.12.003. JIN Shan, ZOU Wei, and DU Lin. Development and enlightenment of US military weapon data link[J]. Ordnance Industry Automation, 2021, 40(12): 8–11. doi: 10.7690/bgzdh.2021.12.003.
[2]	薛丽莎, 葛瑞星, 朱宇轩, 等. 基于SABEGAN的通信干扰信号生成与效能分析[J]. 系统工程与电子技术, 2024, 46(6): 2155–2163. doi: 10.12305/j.issn.1001-506X.2024.06.34. XUE Lisha, GE Ruixing, ZHU Yuxuan, et al. Generation and efficiency analysis of communication jamming signal based on SABEGAN[J]. Systems Engineering and Electronics, 2024, 46(6): 2155–2163. doi: 10.12305/j.issn.1001-506X.2024.06.34.
[3]	李威, 卢盈齐, 范成礼, 等. 基于组合赋权和改进VIKOR的动态威胁评估[J]. 航空兵器, 2022, 29(5): 66–75. doi: 10.12132/ISSN.1673-5048.2021.0254. LI Wei, LU Yingqi, FAN Chengli, et al. Dynamic threat assessment based on combination weighting and improved VIKOR[J]. Aero Weaponry, 2022, 29(5): 66–75. doi: 10.12132/ISSN.1673-5048.2021.0254.
[4]	汪霜玲, 李宇飞, 黄凯鹏, 等. 基于双基点模糊推理的智能系统评估方法[J]. 兵器装备工程学报, 2023, 44(1): 196–203. doi: 10.11809/bqzbgcxb2023.01.029. WANG Shuangling, LI Yufei, HUANG Kaipeng, et al. TOPSIS fuzzy inference-based method for evaluating the level of intelligence[J]. Journal of Ordnance Equipment Engineering, 2023, 44(1): 196–203. doi: 10.11809/bqzbgcxb2023.01.029.
[5]	孙志国, 肖硕, 吴毅杰, 等. 面向认知通信防护的穿透式干扰效能评估方法[J]. 通信学报, 2023, 44(11): 161–172. doi: 10.11959/j.issn.1000-436x.2023195. SUN Zhiguo, XIAO Shuo, WU Yijie, et al. Evaluation method of penetrating jamming effectiveness for cognitive communication protection[J]. Journal on Communications, 2023, 44(11): 161–172. doi: 10.11959/j.issn.1000-436x.2023195.
[6]	马丽丽, 孙志成, 安巧静, 等. 数据链系统综合抗干扰性能评估方法研究[J]. 电子技术应用, 2021, 47(5): 73–76,81. doi: 10.16157/j.issn.0258-7998.201108. MA Lili, SUN Zhicheng, AN Qiaojing, et al. Study of the comprehensive anti-jamming performance evaluation for data-link system[J]. Application of Electronic Technique, 2021, 47(5): 73–76,81. doi: 10.16157/j.issn.0258-7998.201108.
[7]	WEI Guiwu, GAO Hui, and WEI Yu. Some q-rung orthopair fuzzy Heronian mean operators in multiple attribute decision making[J]. International Journal of Intelligent Systems, 2018, 33(7): 1426–1458. doi: 10.1002/int.21985.
[8]	靳崇, 孙娟, 王永佳, 等. 基于直觉模糊TOPSIS和变权VIKOR的防空目标威胁综合评估[J]. 系统工程与电子技术, 2022, 44(1): 172–180. doi: 10.12305/j.issn.1001-506X.2022.01.22. JIN Chong, SUN Juan, WANG Yongjia, et al. Threat comprehensive assessment for air defense targets based on intuitionistic fuzzy TOPSIS and variable weight VIKOR[J]. Systems Engineering and Electronics, 2022, 44(1): 172–180. doi: 10.12305/j.issn.1001-506X.2022.01.22.
[9]	QIAO Wenbao. A novel MADM technique based on projection methods under q-rung orthopair fuzzy setting and its application to computer network security evaluation[J]. Journal of Intelligent & Fuzzy Systems, 2023, 45(1): 1029–1038. doi: 10.3233/JIFS-231351.
[10]	WANG Jie, WEI Guiwu, LU Jianping, et al. Some q-rung orthopair fuzzy Hamy mean operators in multiple attribute decision‐making and their application to enterprise resource planning systems selection[J]. International Journal of Intelligent Systems, 2019, 34(10): 2429–2458. doi: 10.1002/int.22155.
[11]	LIU Peide and LIU Junlin. Some q-rung orthopai fuzzy Bonferroni mean operators and their application to multi‐attribute group decision making[J]. International Journal of Intelligent Systems, 2018, 33(2): 315–347. doi: 10.1002/int.21933.
[12]	YAZDANI M, ZARATE P, KAZIMIERAS ZAVADSKAS E, et al. A Combined Compromise Solution (CoCoSo) method for multi-criteria decision-making problems[J]. Management Decision, 2019, 57(9): 2501–2519. doi: 10.1108/MD-05-2017-0458.
[13]	孙志国, 肖硕, 吴毅杰, 等. 基于迁移学习和参数优化的干扰效能评估方法[J]. 电子与信息学报, 2024, 46(6): 2515–2524. doi: 10.11999/JEIT230817. SUN Zhiguo, XIAO Shuo, WU Yijie, et al. Interference performance evaluation method based on transfer learning and parameter optimization[J]. Journal of Electronics & Information Technology, 2024, 46(6): 2515–2524. doi: 10.11999/JEIT230817.
[14]	孙志国, 刘传令, 肖硕, 等. 基于最优传递矩阵和相关系数的干扰效果评估方法[J/OL]. http://kns.cnki.net/kcms/detail/23.1390.u.20241204.1252.011.html, 2024. SUN Zhiguo, LIU Chuanling, XIAO Shuo, et al. Evaluation of jamming effect based on entropy weight of correlation coefficient and improved AHP[J/OL]. http://kns.cnki.net/kcms/detail/23.1390.u.20241204.1252.011.html, 2024.
[15]	YAGER R R. Generalized orthopair fuzzy sets[J]. IEEE Transactions on Fuzzy Systems, 2017, 25(5): 1222–1230. doi: 10.1109/TFUZZ.2016.2604005.
[16]	LYU Haimin, ZHOU Wanhuan, SHEN Shuilong, et al. Inundation risk assessment of metro system using AHP and TFN-AHP in Shenzhen[J]. Sustainable Cities and Society, 2020, 56: 102103. doi: 10.1016/j.scs.2020.102103.
[17]	袁彰求, 杨朝旭, 荣海军. 面向定性与定量指标的轻量化高空飞艇效能评估方法[J]. 系统工程与电子技术, 2025, 47(3): 817–826. doi: 10.12305/j.issn.1001-506X.2025.03.14. YUAN Zhangqiu, YANG Zhaoxu, and RONG Haijun. Lightweight effectiveness evaluation method for high altitude airships for both qualitative and quantitative indicators[J]. Systems Engineering and Electronics, 2025, 47(3): 817–826. doi: 10.12305/j.issn.1001-506X.2025.03.14.
[18]	WEI Guiwu, ZHAO Xiaofei, LIN Rui, et al. Uncertain linguistic Bonferroni mean operators and their application to multiple attribute decision making[J]. Applied Mathematical Modelling, 2013, 37(7): 5277–5285. doi: 10.1016/j.apm.2012.10.048.
[19]	DHRUVA S, KRISHANKUMAR R, PAMUCAR D, et al. Demystifying the stability and the performance aspects of CoCoSo ranking method under uncertain preferences[J]. Informatica, 2024, 35(3): 509–528. doi: 10.15388/24-INFOR565.