高斯过程认知学习的多机动目标泊松多伯努利混合滤波器

赵子文; 陈辉; 连峰; 张光华; 张文旭

doi:10.11999/JEIT241139

高斯过程认知学习的多机动目标泊松多伯努利混合滤波器

doi: 10.11999/JEIT241139 cstr: 32379.14.JEIT241139

1.
兰州理工大学自动化与电气工程学院兰州 730050
2.
西安交通大学自动化科学与工程学院西安 710049

基金项目: 国家自然科学基金 (62163023, 61873116, 62366031, 62363023)，甘肃省基础研究创新群体(25JRRA058)，中央引导地方科技发展资金项目(25ZYJA040)，甘肃省重点人才项目(2024RCXM86)，甘肃省军民融合发展专项资金(本基金无项目编号)

详细信息

作者简介:
赵子文：男，博士生，研究方向为多目标跟踪技术

陈辉：男，教授，博士生导师，博士，研究方向为多目标跟踪、数据融合、最优控制等

连峰：男，教授，博士生导师，博士，研究方向为目标跟踪、信息融合与传感器管理

张光华：男，副教授，博士生导师，博士，研究方向为信息融合与目标跟踪

张文旭：男，副教授，硕士生导师，博士，研究方向为深度强化学习、智能决策与数据挖掘和机器人技术

通讯作者:
陈辉　chenh@lut.edu.cn

中图分类号: TN911.7; TP274
计量
- 文章访问数: 127
- HTML全文浏览量: 66
- PDF下载量: 9
- 被引次数: 0
出版历程
- 收稿日期: 2024-12-27
- 修回日期: 2025-07-11
- 网络出版日期: 2025-07-25
- 刊出日期: 2025-08-27

Multiple Maneuvering Target Poisson Multi-Bernoulli Mixture Filter for Gaussian Process Cognitive Learning

1.
School of Automation and Electrical Engineering, Lanzhou University of Technology, Lanzhou 730050, China
2.
School of Automation Science and Engineering, Xi’an Jiaotong University, Xi’an 710049, China

Funds: The National Natural Science Foundation of China (62163023, 61873116, 62366031, 62363023), Gansu Provincial Basic Research Innovation Group of China (25JRRA058), The Central Government’s Funds for Guiding Local Science and Technology Development of China (25ZYJA040), Gansu Provincial Key Talent Project of China (2024RCXM86), Gansu Provincial Special Fund for Military-Civilian Integration Development of China

摘要

摘要: 针对复杂不确定环境下的多机动目标跟踪(MMTT)问题，该文提出一种基于高斯过程(GP)数据驱动的多目标跟踪方法。GP作为一种非参数贝叶斯方法，可通过有限样本灵活推断无限维函数，更能够灵活地自适应复杂多变的目标机动模式。通过GP算法学习多机动目标不确定的运动与观测模型，能有效克服传统多模型(MM)方法中因预设模型过多或模型失配所导致的性能退化问题。然后，利用泊松多伯努利混合(PMBM)建立多目标跟踪滤波的共轭先验递推结构，并使用GP学习未知的多目标动力学和观测模型，从而最终提出高斯过程多机动目标PMBM滤波器。仿真结果表明，该方法在复杂多变的MMTT任务中展现出较高的跟踪精度，验证了其在处理MMTT问题上的有效性和鲁棒性。
- 多机动目标跟踪 /
- 数据驱动 /
- 高斯过程 /
- 泊松多伯努利混合
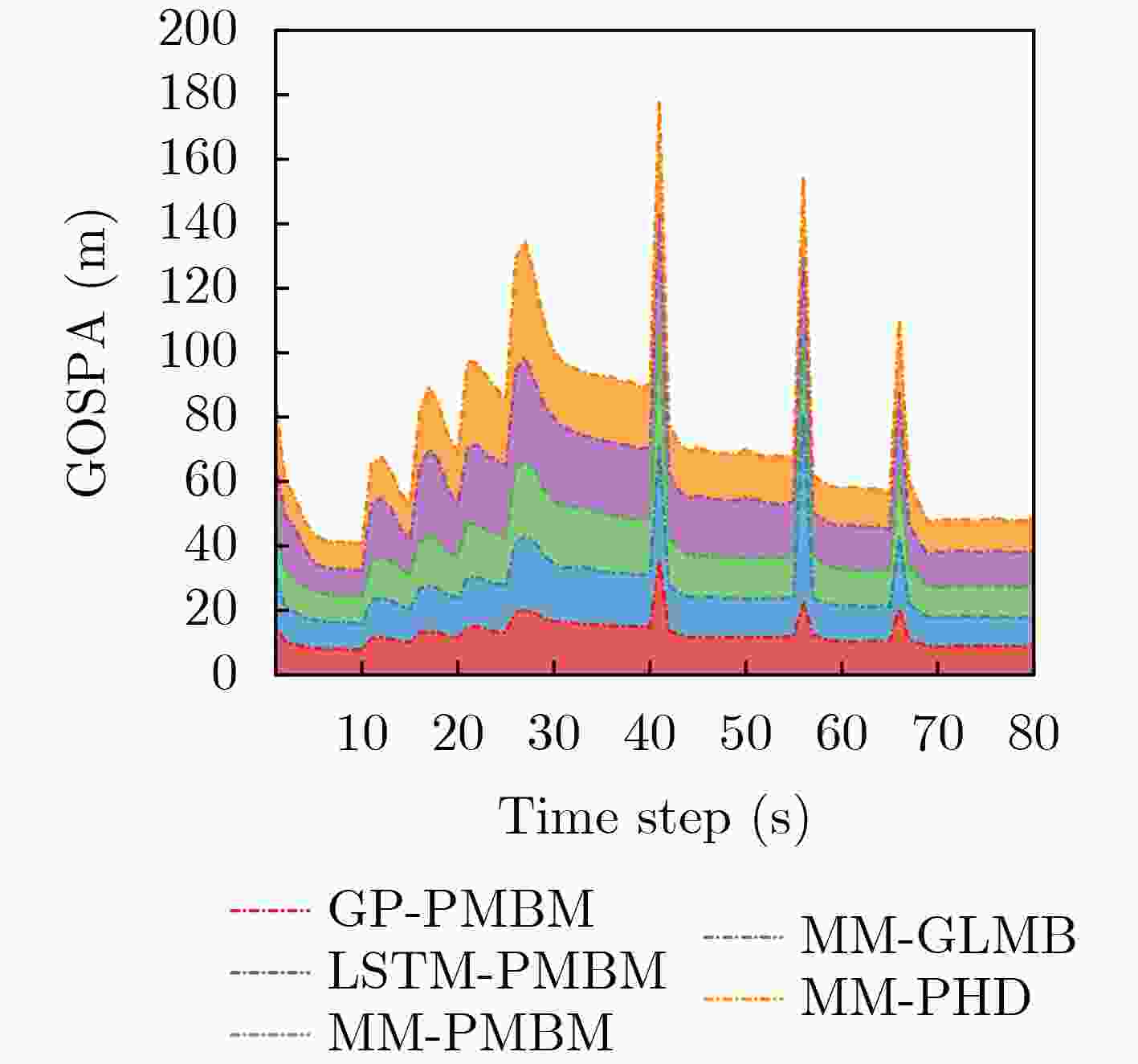
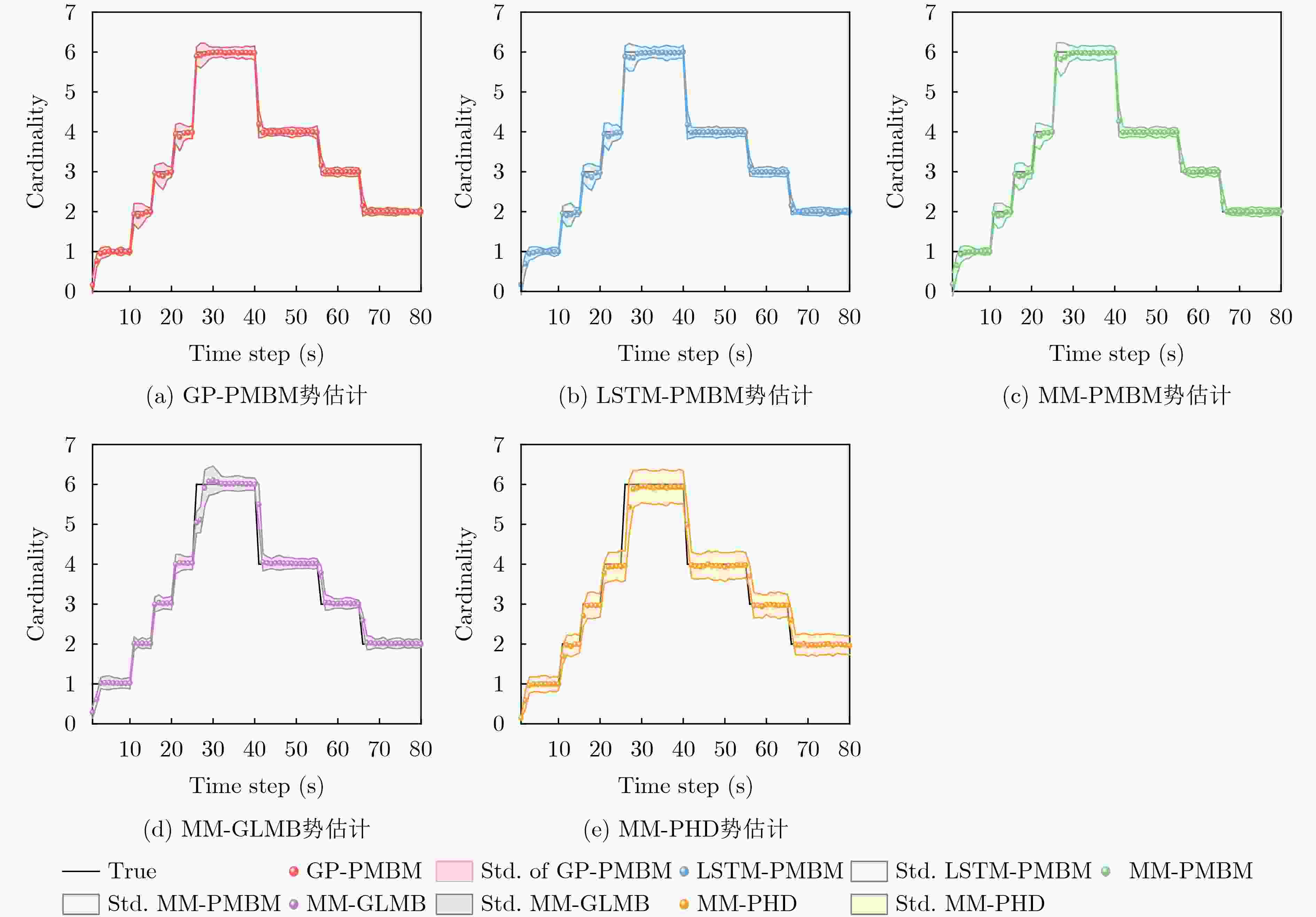
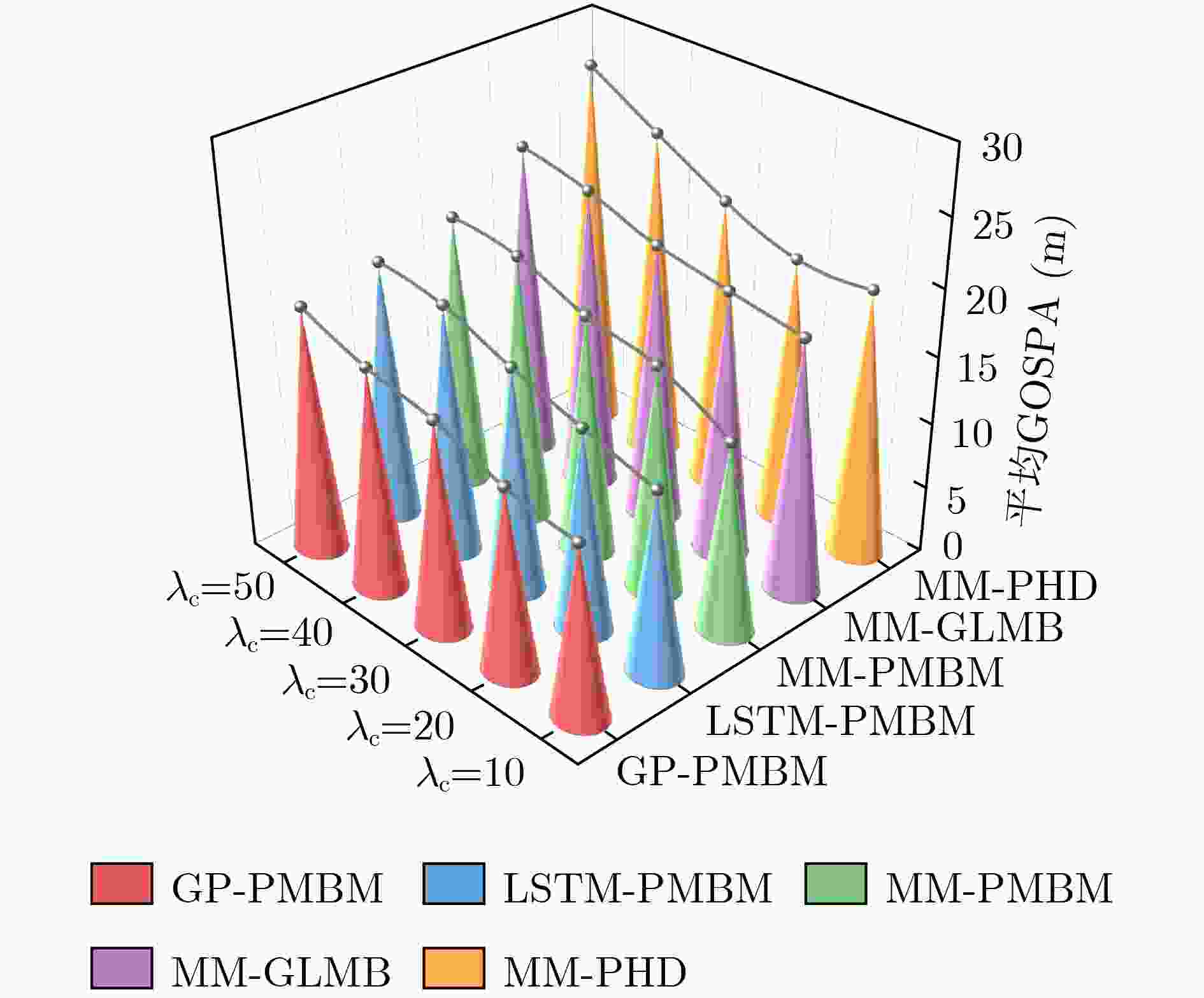
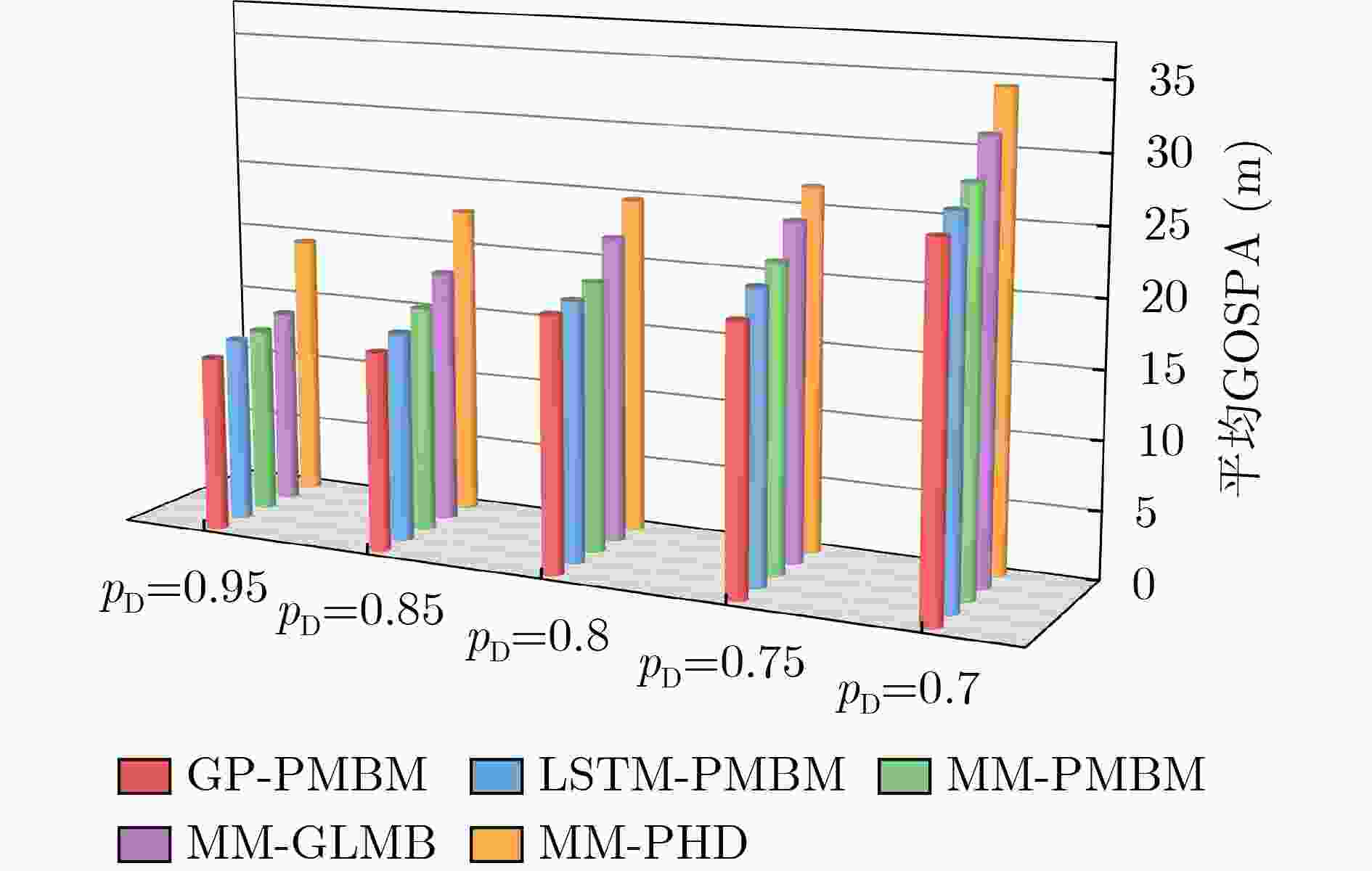
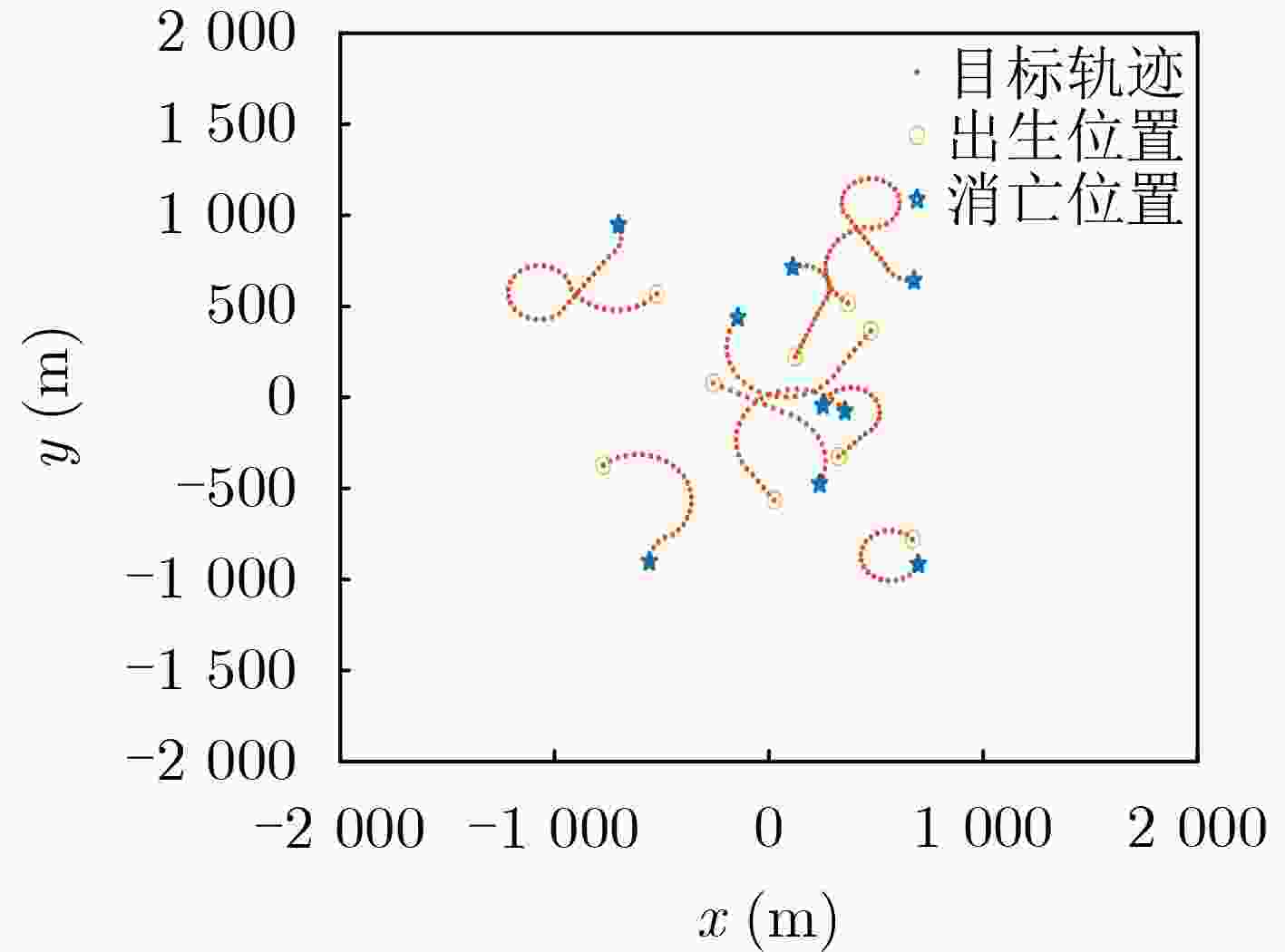
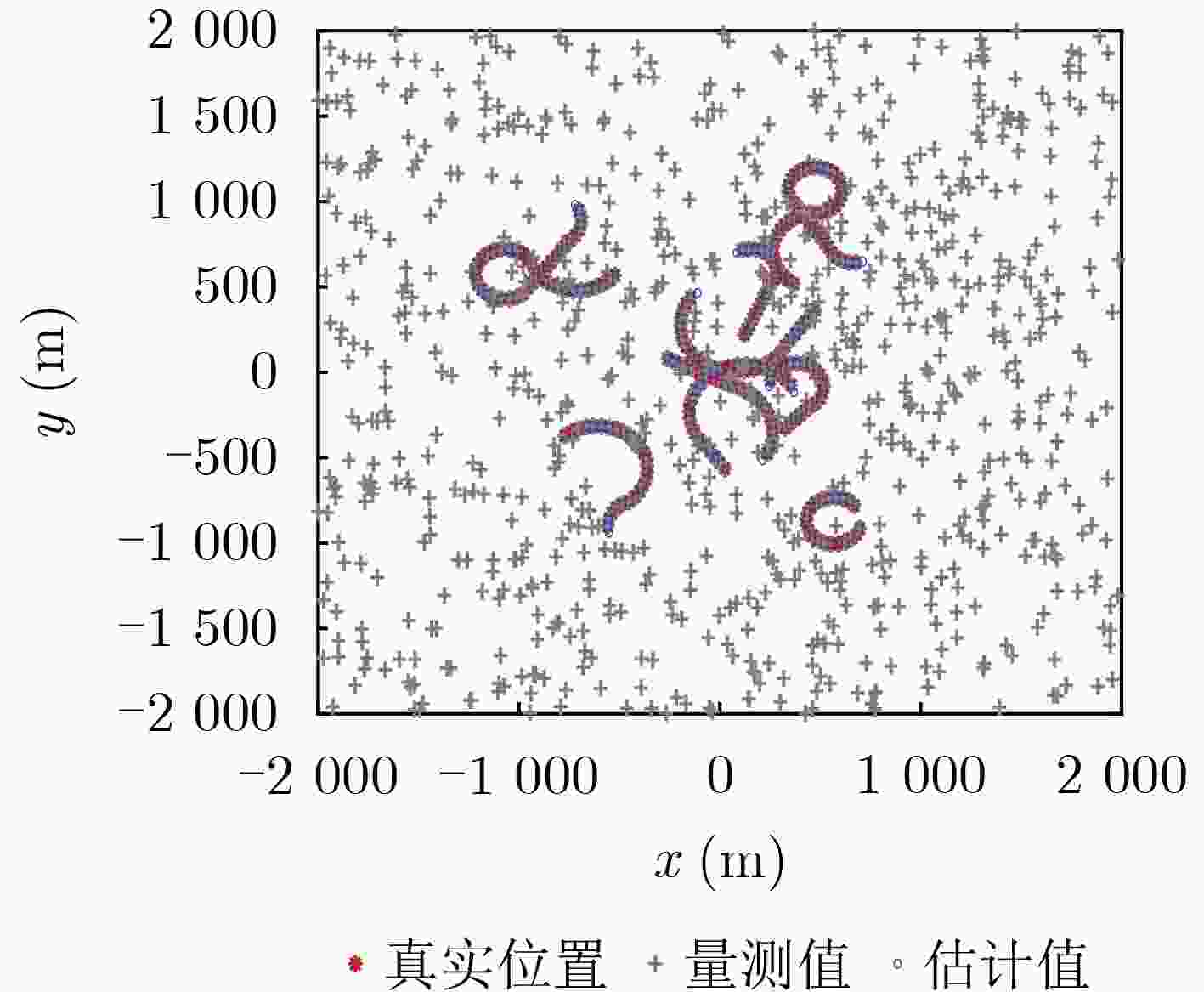
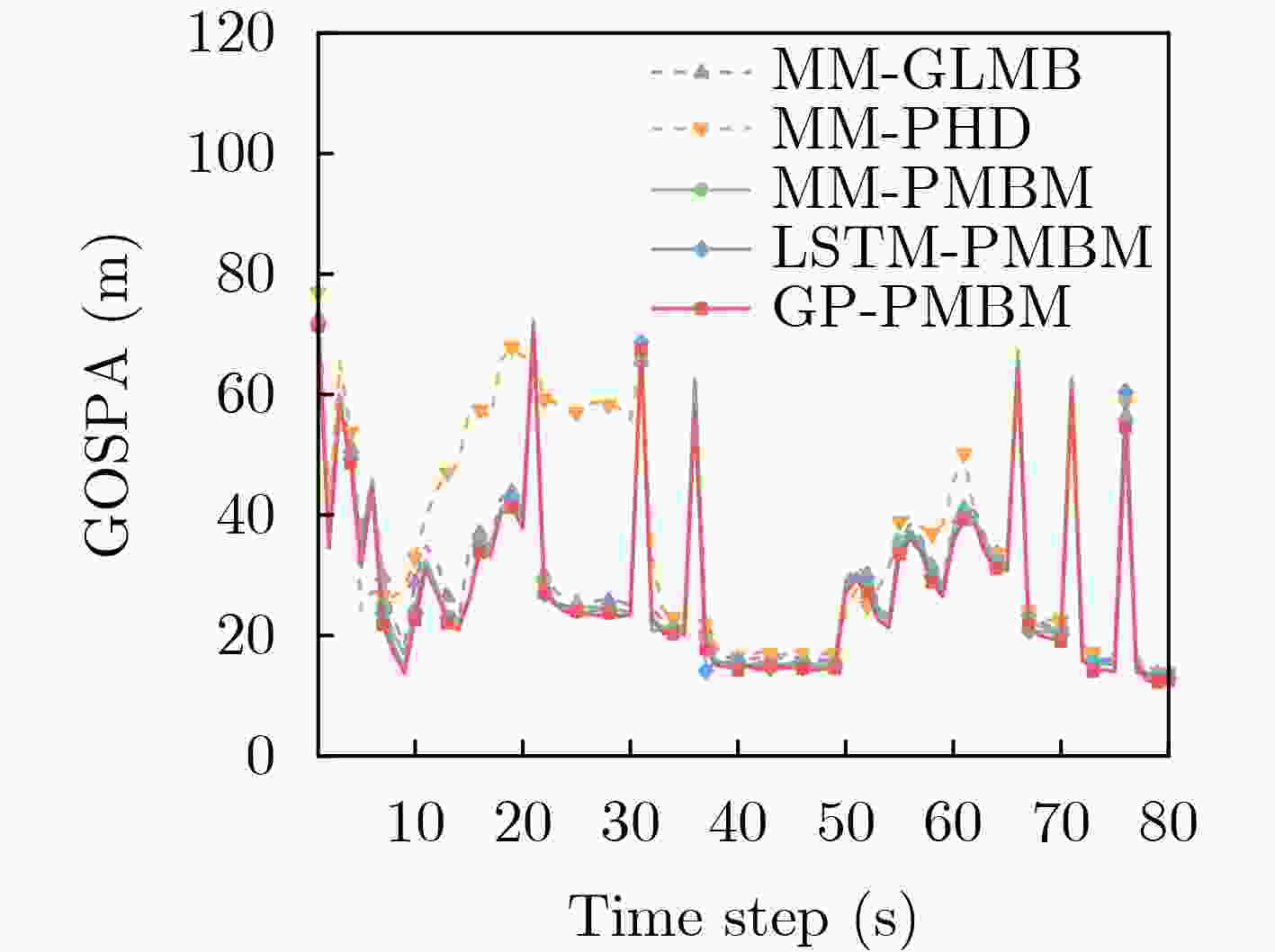
Abstract: Objective Multiple Maneuvering Target Tracking (MMTT) remains a critical yet challenging problem in radar signal processing and sensor fusion, particularly under complex and uncertain conditions. The primary difficulty arises from the unpredictable or highly dynamic nature of target motion. Conventional model-based methods, especially Multiple Model (MM) approaches, rely on predefined motion models to accommodate varying target behaviors. However, these methods face limitations, including sensitivity to initial parameter settings, high computational cost due to model switching, and degraded performance when actual target behavior deviates from the assumed model set. To address these limitations, this study proposes a data-driven MMTT method that combines Gaussian Process (GP) learning with the Poisson Multi-Bernoulli Mixture (PMBM) filter to improve robustness and tracking accuracy in dynamic environments without requiring extensive model assumptions. Methods The proposed method exploits the data-driven modeling capability of GP, a non-parametric Bayesian inference approach that learns high-dimensional, nonlinear function mappings from limited historical data without specifying explicit functional forms. In this study, GP models both the state transition and observation processes of multi-target systems, reducing the dependence on predefined motion models. During the offline phase, historical target trajectories and sensor measurements are collected to build a training dataset. The squared exponential kernel is selected for its smoothness and infinite differentiability, which effectively captures the continuity and dynamic characteristics of target state evolution. GP hyperparameters, including length scale, signal variance, and observation noise variance, are jointly optimized by maximizing the log-marginal likelihood, ensuring generalization and expressiveness in complex environments. In the online filtering phase, the trained GP models are incorporated into the PMBM filter, forming a recursive GP-PMBM filtering structure. Within this framework, the PMBM filter employs a Poisson point process to represent undetected targets and a multi-Bernoulli mixture to characterize the posterior state distribution of detected targets. During the prediction step, the GP-derived nonlinear state transition model is propagated using the Cubature Kalman Filter (CKF). In the update step, the GP-learned observation model refines state estimates, enhancing both tracking accuracy and robustness. Results and Discussions Extensive simulation experiments under two different MMTT scenarios validate the effectiveness and performance advantages of the proposed method. In Scenario 1, a moderate 2D surveillance environment with clutter and a varying number of targets is constructed. The GP-PMBM filter significantly outperforms existing methods, including LSTM-PMBM, MM-PMBM, MM-GLMB, and MM-PHD filters, based on the Generalized Optimal Sub-Pattern Assignment (GOSPA) metric (Fig. 3). In addition, the GP-PMBM filter achieves the lowest standard deviation in cardinality estimation, demonstrating high accuracy and stability (Fig. 4). Further experiments under different monitoring conditions confirm the robustness of GP-PMBM. When clutter rates vary, the GP-PMBM filter consistently achieves the lowest average GOSPA error, reflecting strong stability under interference (Fig. 5). As detection probability decreases, most algorithms show significant degradation in accuracy. However, GP-PMBM maintains superior tracking performance, achieving the lowest GOSPA distance across all detection conditions (Fig. 6). In Scenario 2, target motion becomes more complex, with increased maneuverability and higher–frequency birth–death dynamics. Despite these challenges, the GP-PMBM filter maintains superior tracking performance, even under highly maneuverable conditions and frequent target appearance and disappearance (Fig. 9, Fig. 10). Conclusions This study proposes a novel GP-PMBM filtering framework for MMTT in complex environments. By integrating the data-driven learning capability of the GP with the PMBM filter, the proposed method addresses the limitations of conventional model-based tracking approaches. The GP-PMBM filter automatically learns unknown motion and observation models from historical data, eliminating the dependence on predefined model sets and significantly improving adaptability. Simulation results confirm that the GP-PMBM filter achieves superior tracking accuracy, improved cardinality estimation, and enhanced robustness under varying clutter levels and detection conditions. These results indicate that the proposed method is well-suited for environments characterized by frequent maneuvering changes and uncertain target behavior. Future work will focus on extending the GP-PMBM framework to multi-maneuvering extended target tracking tasks to address more challenging scenarios.
- Multi-maneuvering target tracking /
- Data-driven /
- Gaussian Process (GP) /
- Poisson Multi-Bernoulli Mixture (PMBM)

HTML全文

图 2 跟踪结果

下载: 全尺寸图片幻灯片

图 1 多机动目标真实轨迹

下载: 全尺寸图片幻灯片

图 3 GOSPA堆叠面积

下载: 全尺寸图片幻灯片

图 4 多机动目标势估计

下载: 全尺寸图片幻灯片

图 5 不同杂波条件下的平均GOSPA

下载: 全尺寸图片幻灯片

图 6 不同检测概率条件下的平均GOSPA

下载: 全尺寸图片幻灯片

图 7 场景2中多机动目标真实轨迹

下载: 全尺寸图片幻灯片

图 8 场景2中跟踪结果

下载: 全尺寸图片幻灯片

图 9 场景2中势估计分条热度

下载: 全尺寸图片幻灯片

图 10 场景2中GOSPA误差

下载: 全尺寸图片幻灯片

表 1 目标初始状态和存活时间

目标	初始状态 (m, v/s, m, v/s)	存活时间 (s)
1	$ {\left[ {\begin{array}{*{20}{c}} { - 300}&0&{100}&0 \end{array}} \right]^{\rm T}} $	1～20
2	$ {\left[ {\begin{array}{*{20}{c}} {500}&0&{400}&0 \end{array}} \right]^{\rm T}} $	3～30
3	$ {\left[ {\begin{array}{*{20}{c}} {50}&0&{ - 600}&0 \end{array}} \right]^{\rm T}} $	5～30
4	$ {\left[ {\begin{array}{*{20}{c}} { - 800}&0&{ - 400}&0 \end{array}} \right]^{\rm T}} $	10～35
5	$ {\left[ {\begin{array}{*{20}{c}} {400}&0&{500}&0 \end{array}} \right]^{\rm T}} $	15～65
6	$ {\left[ {\begin{array}{*{20}{c}} { - 500}&0&{600}&0 \end{array}} \right]^{\rm T}} $	18～65
7	$ {\left[ {\begin{array}{*{20}{c}} {100}&0&{200}&0 \end{array}} \right]^{\rm T}} $	50～70
8	$ {\left[ {\begin{array}{*{20}{c}} {300}&0&{ - 350}&0 \end{array}} \right]^{\rm T}} $	55～75
9	$ {\left[ {\begin{array}{*{20}{c}} {700}&0&{ - 800}&0 \end{array}} \right]^{\rm T}} $	60～80

下载: 导出CSV

参考文献(38)

[1]	DAI Jinhui, PU Wenqiang, YAN Junkun, et al. Multi-UAV collaborative trajectory optimization for asynchronous 3-D passive multitarget tracking[J]. IEEE Transactions on Geoscience and Remote Sensing, 2023, 61: 5101116. doi: 10.1109/TGRS.2023.3239952.
[2]	DING Lintao, SHI Chenguang, and ZHOU Jianjiang. Collaborative route optimization and resource management strategy for multi-target tracking in airborne radar system[J]. Digital Signal Processing, 2023, 138: 104051. doi: 10.1016/j.dsp.2023.104051.
[3]	RAMACHANDRAN R K, FRONDA N, PREISS J A, et al. Resilient multi-robot multi-target tracking[J]. IEEE Transactions on Automation Science and Engineering, 2024, 21(3): 4311–4327. doi: 10.1109/TASE.2023.3295373.
[4]	KUMAR S and PARHI D R. Multi-target trajectory planning and control technique for autonomous navigation of multiple robots[J]. ISA Transactions, 2023, 138: 650–669. doi: 10.1016/j.isatra.2023.02.029.
[5]	WANG Qiang, HUANG Xiao, TAO Hao, et al. Marine navigation radar multi-target tracking using adaptive innovation sequence-based joint probability data association[C]. 2024 IEEE 13th Data Driven Control and Learning Systems Conference (DDCLS), Kaifeng, China, 2024: 511–516. doi: 10.1109/DDCLS61622.2024.10606901.
[6]	BLACK B, SELLERS T, LEI Tingjun, et al. Optimal multi-target navigation via graph-based algorithms in complex environments[C]. Proceedings of 2024 IEEE 33rd International Symposium on Industrial Electronics (ISIE), Ulsan, Korea, Republic of, 2024: 1–6. doi: 10.1109/ISIE54533.2024.10595682.
[7]	BLACKMAN S S. Multiple hypothesis tracking for multiple target tracking[J]. IEEE Aerospace and Electronic Systems Magazine, 2004, 19(1): 5–18. doi: 10.1109/MAES.2004.1263228.
[8]	MAHLER R P S. Statistical Multisource-Multitarget Information Fusion[M]. Boston: Artech, 2007.
[9]	RONG LI X and JILKOV V P. Survey of maneuvering target tracking. Part I. Dynamic models[J]. IEEE Transactions on Aerospace and Electronic Systems, 2003, 39(4): 1333–1364. doi: 10.1109/TAES.2003.1261132.
[10]	LI X R and JILKOV V P. Survey of maneuvering target tracking. Part V. Multiple-model methods[J]. IEEE Transactions on Aerospace and Electronic Systems, 2005, 41(4): 1255–1321. doi: 10.1109/TAES.2005.1561886.
[11]	MAHLER R. On multitarget jump-Markov filters[C]. 2012 15th International Conference on Information Fusion, Singapore, 2012: 149–156.
[12]	LI Xiaolong, SUN Zhi, YEO T S, et al. STGRFT for detection of maneuvering weak target with multiple motion models[J]. IEEE Transactions on Signal Processing, 2019, 67(7): 1902–1917. doi: 10.1109/TSP.2019.2899318.
[13]	MAHLER R P S. Advances In Statistical Multisource-Multitarget Information Fusion[M]. Boston: Artech House, 2014.
[14]	WEI Jingxin, LUO Feng, CHEN Shichao, et al. Robust fusion of GM-PHD filters based on geometric average[J]. Signal Processing, 2023, 206: 108912. doi: 10.1016/j.sigpro.2022.108912.
[15]	HUANG Qiao, XIE Lei, and SU Hongye. Estimations of time-varying birth cardinality distribution and birth intensity in Gaussian mixture CPHD filter for multi-target tracking[J]. Signal Processing, 2022, 190: 108321. doi: 10.1016/j.sigpro.2021.108321.
[16]	DAVIES E S and GARCÍA-FERNÁNDEZ á F. Information exchange track-before-detect Multi-Bernoulli filter for superpositional sensors[J]. IEEE Transactions on Signal Processing, 2024, 72: 607–621. doi: 10.1109/TSP.2024.3349769.
[17]	WEI Jingxin, LUO Feng, QI Jiawei, et al. Distributed fusion of Labeled Multi-Bernoulli filters based on arithmetic average[J]. IEEE Signal Processing Letters, 2024, 31: 656–660. doi: 10.1109/LSP.2024.3364506.
[18]	CAO Chenghu and ZHAO Yongbo. Multi-sensor multi-target tracking with generalized labeled multi-Bernoulli filter based on track-before-detect observation model using Gaussian belief propagation[J]. Digital Signal Processing, 2024, 153: 104618. doi: 10.1016/j.dsp.2024.104618.
[19]	ZHOU Yusong, ZHAO Jin, WU Sunyong, et al. A Poisson multi-Bernoulli mixture filter for tracking multiple resolvable group targets[J]. Digital Signal Processing, 2024, 144: 104279. doi: 10.1016/j.dsp.2023.104279.
[20]	GARCÍA-FERNÁNDEZ á F, XIA Yuxuan, and SVENSSON L. Poisson multi-Bernoulli mixture filter with general target-generated measurements and arbitrary clutter[J]. IEEE Transactions on Signal Processing, 2023, 71: 1895–1906. doi: 10.1109/TSP.2023.3278944.
[21]	VO B N and MA W K. The Gaussian mixture probability hypothesis density filter[J]. IEEE Transactions on Signal Processing, 2006, 54(11): 4091–4104. doi: 10.1109/TSP.2006.881190.
[22]	VO B N, SINGH S, and DOUCET A. Sequential Monte Carlo methods for multitarget filtering with random finite sets[J]. IEEE Transactions on Aerospace and Electronic Systems, 2005, 41(4): 1224–1245. doi: 10.1109/TAES.2005.1561884.
[23]	PUNITHAKUMAR K, KIRUBARAJAN T, and SINHA A. Multiple-model probability hypothesis density filter for tracking maneuvering targets[J]. IEEE Transactions on Aerospace and Electronic Systems, 2008, 44(1): 87–98. doi: 10.1109/TAES.2008.4516991.
[24]	PASHA S A, VO B N, TUAN H D, et al. A Gaussian mixture PHD filter for jump Markov system models[J]. IEEE Transactions on Aerospace and Electronic Systems, 2009, 45(3): 919–936. doi: 10.1109/TAES.2009.5259174.
[25]	GEORGESCU R and WILLETT P. The multiple model CPHD tracker[J]. IEEE Transactions on Signal Processing, 2012, 60(4): 1741–1751. doi: 10.1109/TSP.2012.2183128.
[26]	DONG Peng, JING Zhongliang, GONG Deren, et al. Maneuvering multi-target tracking based on variable structure multiple model GMCPHD filter[J]. Signal Processing, 2017, 141: 158–167. doi: 10.1016/j.sigpro.2017.06.004.
[27]	XUE Yu and FENG Xi’an. Joint multi-Gaussian mixture model and its application to multi-model multi-Bernoulli filter[J]. Digital Signal Processing, 2024, 153: 104616. doi: 10.1016/j.dsp.2024.104616.
[28]	REUTER S, SCHEEL A, and DIETMAYER K. The multiple model labeled multi-Bernoulli filter[C]. 2015 18th International Conference on Information Fusion (Fusion), Washington, USA, 2015: 1574–1580.
[29]	CAO Chenghu and ZHAO Yongbo. Multiple-model generalised labelled multi-Bernoulli filter with distributed sensors for tracking manoeuvring targets using belief propagation[J]. IET Radar, Sonar & Navigation, 2023, 17(5): 845–858. doi: 10.1049/rsn2.12382.
[30]	LI Guchong, KONG Lingjiang, YI Wei, et al. Multiple model Poisson multi-Bernoulli mixture filter for maneuvering targets[J]. IEEE Sensors Journal, 2021, 21(3): 3143–3154. doi: 10.1109/JSEN.2020.3022669.
[31]	SEEGER M. Gaussian processes for machine learning[J]. International Journal of Neural Systems, 2004, 14(2): 69–106. doi: 10.1142/S0129065704001899.
[32]	AFTAB W and MIHAYLOVA L. A Gaussian process regression approach for point target tracking[C]. 2019 22th International Conference on Information Fusion (FUSION), Ottawa, Canada, 2019: 1–8. doi: 10.23919/FUSION43075.2019.9011310.
[33]	AFTAB W and MIHAYLOVA L. A learning Gaussian process approach for maneuvering target tracking and smoothing[J]. IEEE Transactions on Aerospace and Electronic Systems, 2021, 57(1): 278–292. doi: 10.1109/TAES.2020.3021220.
[34]	SUN Mengwei, DAVIES M E, PROUDLER I K, et al. A Gaussian process regression based dynamical models learning algorithm for target tracking[EB/OL]. https://doi.org/10.48550/arXiv.2211.14162, 2022.
[35]	HU Zheng and LI Tiancheng. A particle Bernoulli filter based on Gaussian process learning for maneuvering target tracking[C]. Proceedings of 2022 30th European Signal Processing Conference (EUSIPCO), Belgrade, Serbia, 2022: 777–781. doi: 10.23919/EUSIPCO55093.2022.9909660.
[36]	GUO Qiang, TENG Long, YIN Tianxiang, et al. Hybrid-driven Gaussian process online learning for highly maneuvering multi-target tracking[J]. Frontiers of Information Technology & Electronic Engineering, 2023, 24(11): 1647–1656. doi: 10.1631/FITEE.2300348.
[37]	ARASARATNAM I and HAYKIN S. Cubature Kalman filters[J]. IEEE Transactions on Automatic Control, 2009, 54(6): 1254–1269. doi: 10.1109/TAC.2009.2019800.
[38]	RAHMATHULLAH A S, GARCíA-FERNáNDEZ á F, and SVENSSON L. Generalized optimal sub-pattern assignment metric[C]. 2017 20th International Conference on Information Fusion (Fusion), Xi’an, China, 2017: 1–8. doi: 10.23919/ICIF.2017.8009645.