基于扩展式博弈的组网雷达功率分配方法研究

叶方; 戚昌龙; 孙柳晴; 李一兵

doi:10.11999/JEIT241131

基于扩展式博弈的组网雷达功率分配方法研究

doi: 10.11999/JEIT241131

1.
哈尔滨工程大学信息与通信工程学院哈尔滨 150000
2.
哈尔滨工程大学先进船舶通信与信息技术重点实验室哈尔滨 150000

基金项目: 黑龙江省高等教育教学改革项目(SJGY20210233)

详细信息

作者简介:
叶方：女，教授，博士生导师，下一代移动通信及无线技术、网络资源分配、智能决策

戚昌龙：男，硕士生，研究方向为雷达资源分配

孙柳晴：女，硕士生，研究方向为干扰资源分配

李一兵：男，教授，博士生导师，通信信号处理，导航信号处理，图像信号处理，信息融合技术

通讯作者:
李一兵 email

中图分类号: TN974
计量
- 文章访问数: 28
- HTML全文浏览量: 18
- PDF下载量: 3
- 被引次数: 0
出版历程
- 收稿日期: 2024-12-25
- 修回日期: 2025-05-17
- 网络出版日期: 2025-06-09

Research on Power Allocation Method for Networked Radar Based on Extended Game Theory

1.
Institute of Information and Communication Engineering, Harbin Engineering University, Harbin 150000, China
2.
Key Laboratory of Advanced Ship Communication and Information Technology, Harbin Engineering University, Harbin 150000, China

Funds: Heilongjiang Higher Education Teaching Reform Project (SJGY20210233)

摘要

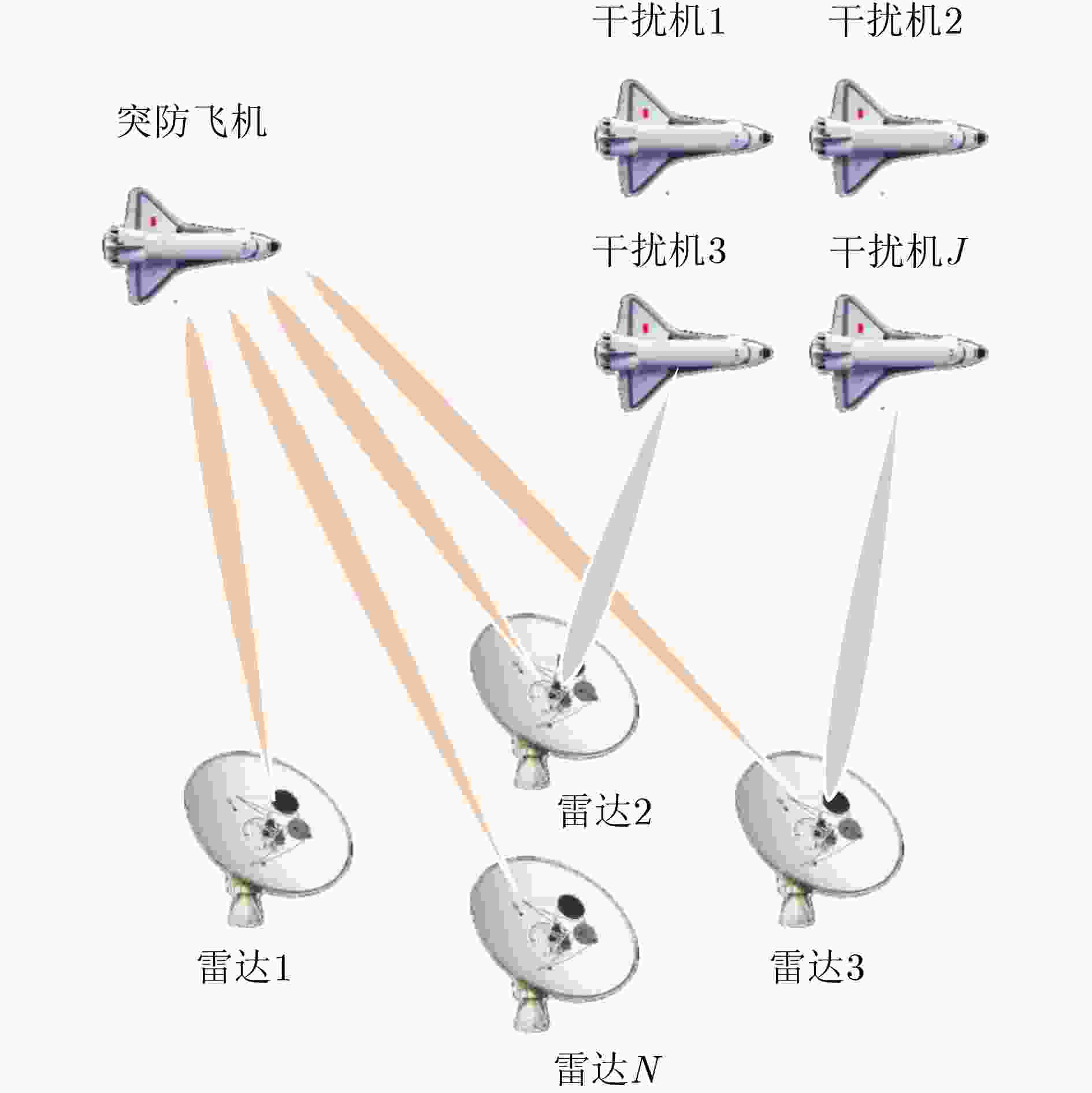
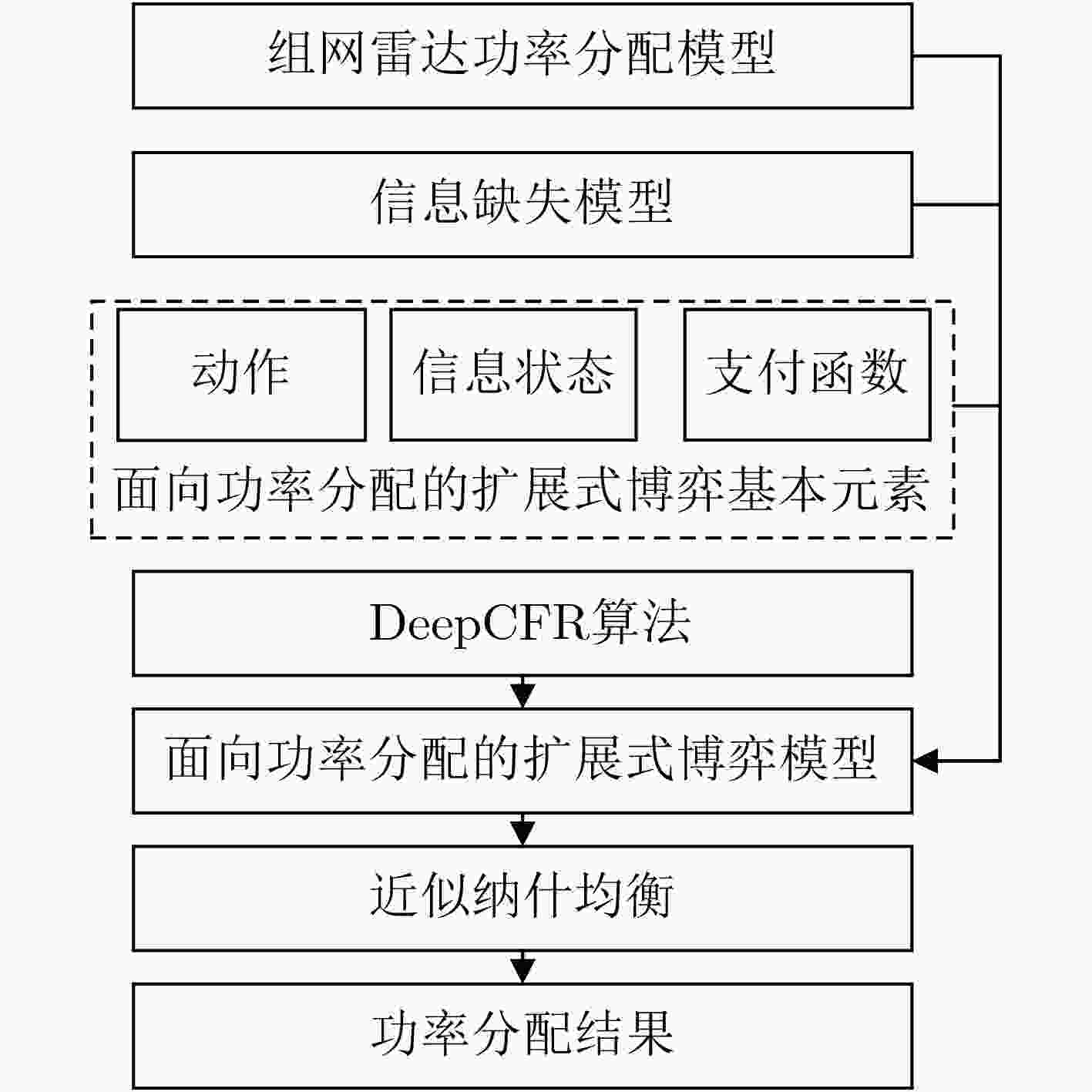
摘要: 组网雷达已成为对抗电子干扰的重要手段，然而随着干扰机集群化智能化发展，组网雷达在突防对抗中只能观测到部分信息，严重影响了对突防目标的检测性能。针对上述问题，该文提出一种基于扩展式博弈的组网雷达功率分配方法。该方法首先构造了组网雷达功率分配和对抗信息缺失模型，并结合扩展式博弈原理，建立了面向功率分配的扩展式博弈模型，在该博弈中，组网雷达可以通过信息集聚合对抗中不可观测的干扰机信息。在求解该文所构建博弈模型时，采用深度虚拟遗憾最小化算法(Deep CFR)，其通过结合深度学习与虚拟遗憾最小化，有效解决了传统方法在求解扩展式博弈中的存储与计算瓶颈。仿真结果表明，所提方法在部分观测信息约束条件下能有效对组网雷达进行功率分配，提高其对突防目标的检测概率。
- 组网雷达系统 /
- 扩展式博弈 /
- 功率分配
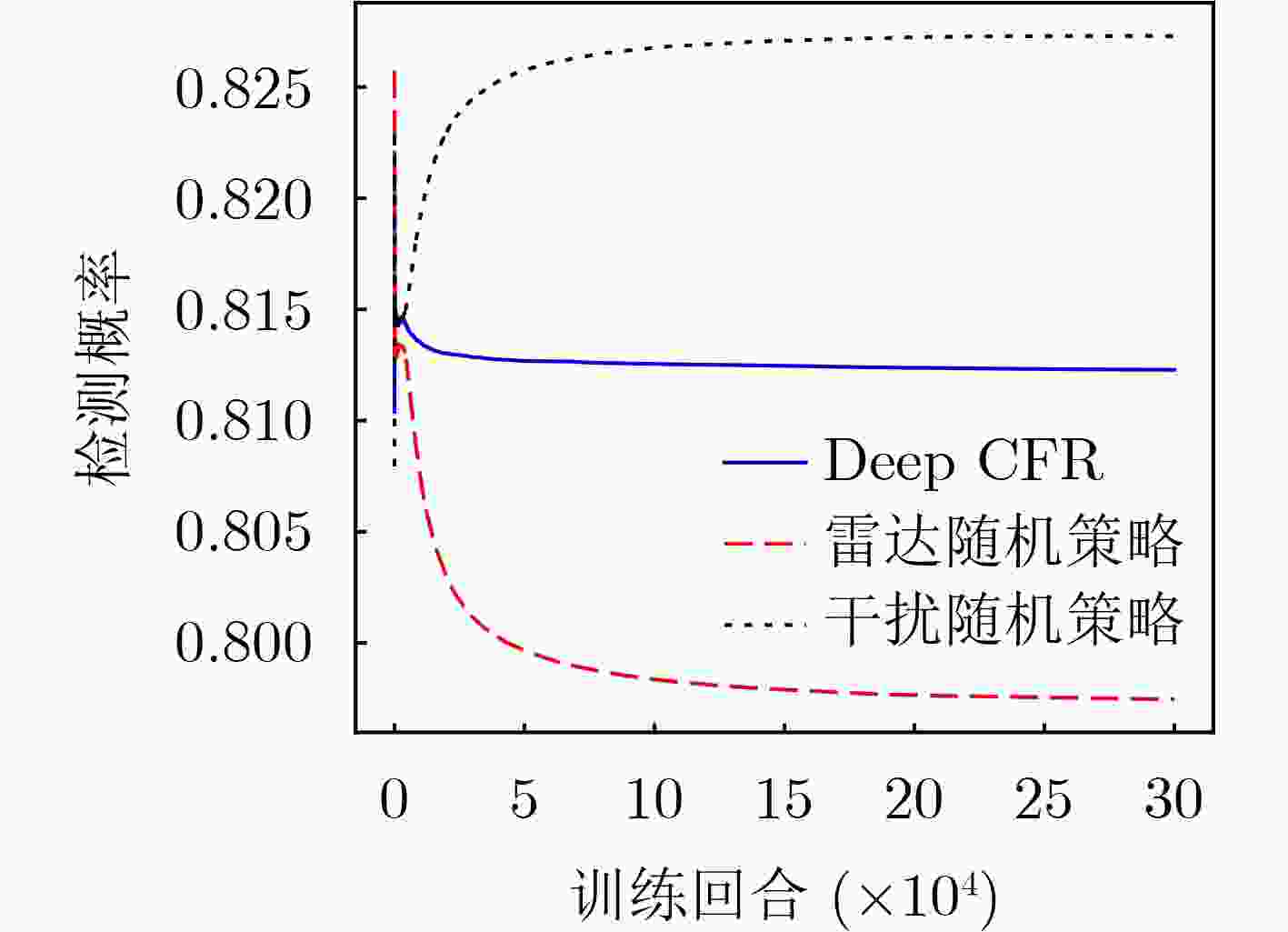
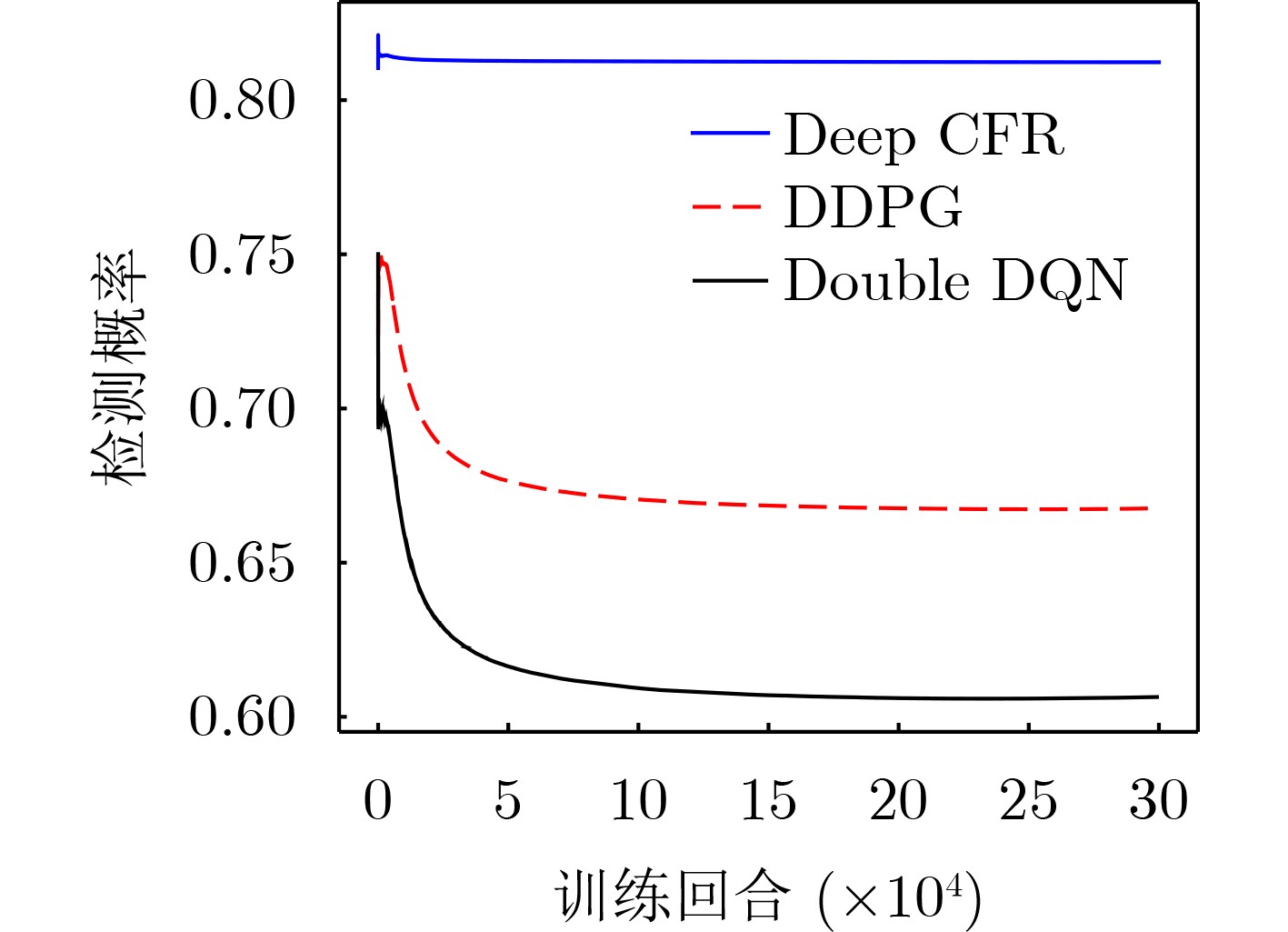
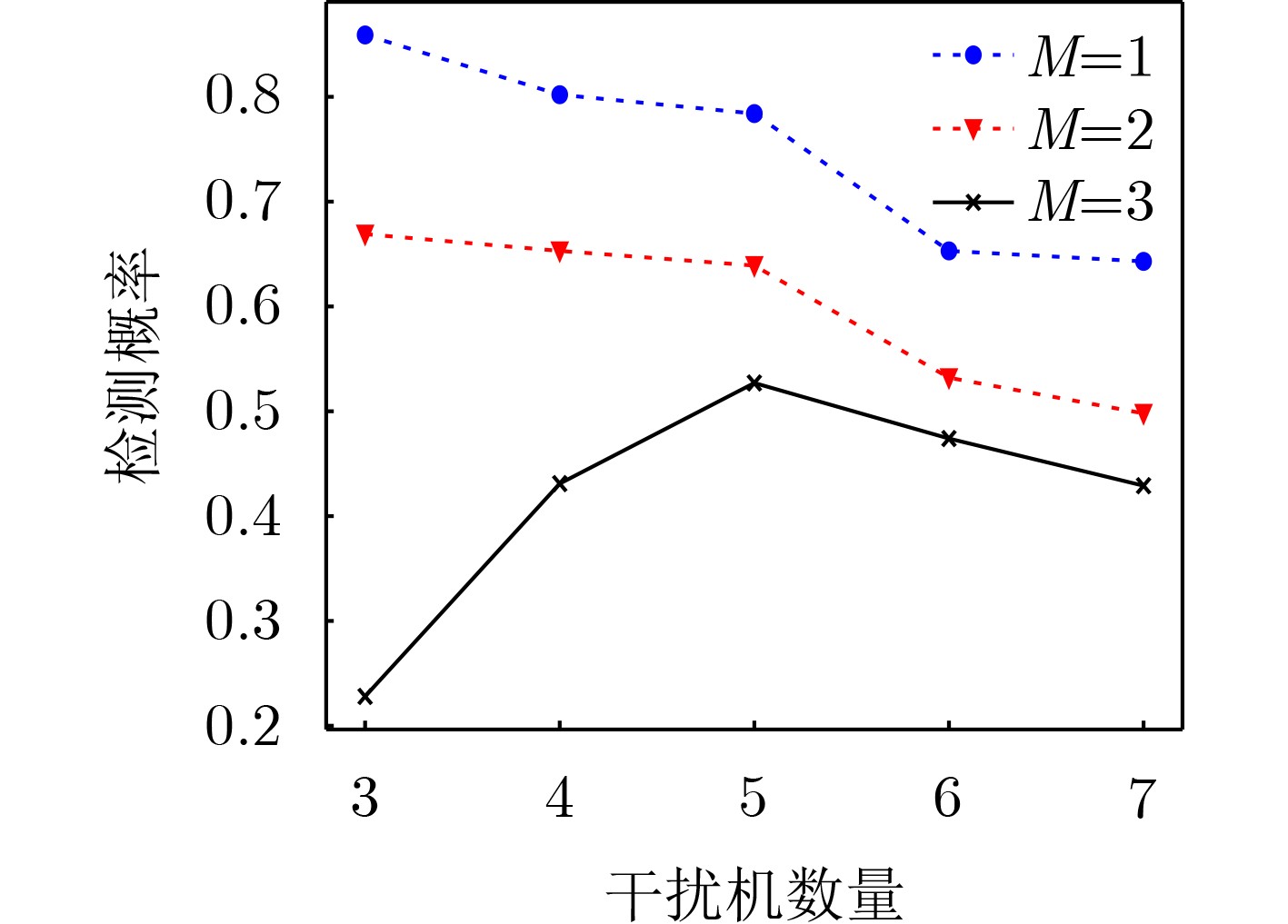
Abstract: Objective As jamming technology grows increasingly sophisticated, networked radar systems in penetration countermeasure scenarios often operate under partial information, which markedly reduces detection performance. Strategic power allocation can improve spatial and frequency diversity, thereby enhancing target detection. However, most existing methods optimize radar resource distribution in isolation, without accounting for the dynamic interactions between radars and jammers. To address this limitation, this paper proposes a power allocation method for networked radar based on extensive-form game theory. The allocation problem is modeled under partial observability, and the Deep Counterfactual Regret Minimization (Deep CFR) algorithm is employed to solve it. This approach increases the probability of successfully detecting penetration targets in adversarial environments. Methods A power allocation model for networked radar is developed in parallel with an information-loss model that captures the adversarial dynamics between networked radar and jammer swarms. Drawing on the principles of extensive-form games, the fundamental elements are defined and used to construct an extensive-form game model for radar power allocation. In this framework, networked radar aggregates observable information to mitigate the effects of unobservable jammer signals. To solve the game, the Deep CFR algorithm is employed, integrating deep learning with regret minimization to approximate Nash equilibrium strategies. This approach addresses the storage and computational challenges associated with traditional extensive-form game solutions. Simulation results confirm that the proposed method allocates radar power effectively under partial observation, improving the probability of target detection. Results and Discussions Simulation results show that under partial observation conditions, the proposed method achieves a detection probability of 0.813, exceeding the performance of random strategies, Deep Deterministic Policy Gradient (DDPG), and Double Deep Q-Network (Double DQN). While ensuring stable convergence, the method also reduces training time by 27.6% and 31.5% compared with DDPG and Double DQN, respectively. Sensitivity analysis indicates that detection performance declines with an increasing number of jammers due to stronger interference. Additionally, variations in the number of missing information elements (M) demonstrate that overall radar performance depends on both the extent of information loss and the intensity of coordinated jamming. When jamming degradation outweighs the benefits of reduced information loss, the detection probability decreases accordingly. Conclusions In modern electronic warfare, where jammers employ complex and adaptive interference strategies and networked radar systems operate with partial adversary information, this study proposes an effective approach to power resource management. By modeling the dynamic interaction between radar systems and jammer swarms through extensive-form game theory and applying the Deep CFR algorithm, simulation results demonstrate the following: (1) The near-Nash equilibrium strategy aligns with the optimal allocationobtained using the Sparrow Search Algorithm, confirming its validity; (2) The proposed method achieves higher detection probability (0.813) than random strategies, DDPG, and Double DQN; and (3) It reduces training time significantly compared with DDPG and Double DQN. Future work will extend this approach to other resource management dimensions, including waveform selection and beam dwell time optimization.
- Netted radar system /
- Extensive form game /
- Power allocation

HTML全文

图 1 组网雷达与干扰机群突防对抗场景图

下载: 全尺寸图片幻灯片

图 2 总体流程

下载: 全尺寸图片幻灯片

图 3 掷硬币游戏的博弈树示意图

下载: 全尺寸图片幻灯片

图 4 基于组网雷达功率分配的扩展式博弈树图

下载: 全尺寸图片幻灯片

图 5 训练过程

下载: 全尺寸图片幻灯片

图 6 基于Deep CFR算法求解的策略变化趋势图

下载: 全尺寸图片幻灯片

图 7 麻雀搜索算法寻优结果图

下载: 全尺寸图片幻灯片

图 8 算法对比结果

下载: 全尺寸图片幻灯片

图 9 参数变化下的检测概率曲线图

下载: 全尺寸图片幻灯片

1 流程1 Deep CFR算法流程

基于参数${\theta _p}$初始化每个玩家的优势网络$V\left( {I,a\|{\theta _p}} \right)$，使其对所有　输入返回0
初始化池化-采样优势记忆${\mathcal{M}_{V,1}}$，${\mathcal{M}_{V,2}}$和策略记忆${\mathcal{M}_\Pi }$
FOR CFR迭代数$t = 1:T$do
FOR每一个玩家$p = 1:P$do
FOR遍历数$k = 1:K$do
利用函数TRAVERSE$ (\varnothing,p,{\theta _1},{\theta _2},{\mathcal{M}_{V,p}},{\mathcal{M}_\Pi }) $从带有外　　　　部采样的博弈遍历过程中收集数据
END FOR
从初始值训练${\theta _p}$基于损失$\mathcal{L}({\theta _p}) = {\mathbb{E}_{(I,{t^\prime },{{\tilde r}^{{t^\prime }}})\text{～}{\mathcal{M}_{V,p}}}} $ 　　　$\left[ {{t^\prime }\displaystyle\sum\limits_a {{{\left( {{{\tilde r}^{{t^\prime }}}(a) - V(I,a\|{\theta _p})} \right)}^2}} } \right]$
END FOR
END FOR
基于损失$L({q_P}) = {E_{(I,{t^\cent},{s^{{t^\cent}}})\text{～}{M_P}}}\left[ {{t^\cent}\displaystyle\sum\limits_a {{{\left( {{s^{{t^\cent}}}(a) - P(I,a\|{q_P})} \right)}^2}} } \right]$ 　训练$ {\theta _\Pi } $

下载: 导出CSV

2 流程2 TRAVERSE函数流程

FUNCTION TRAVERSE$\left( {h,p,{\theta _1},{\theta _2},{\mathcal{M}_V},{\mathcal{M}_\Pi },t} \right)$
INPUT：历史h，遍历玩家p，每个玩家的遗憾网络参数$\theta $，玩　　家的优势记忆${\mathcal{M}_V}$，策略记忆${\mathcal{M}_\Pi }$，CFR 迭代t
IF$h = $终止THEN
RETURN玩家p的支付函数值
ELSE IF$h = $机会节点THEN
$a\～\sigma \left( h \right)$
RETURN TRAVERSE$\left( {h \cdot a,p,{\theta _1},{\theta _2},{\mathcal{M}_V},{\mathcal{M}_\Pi },t} \right)$
ELSE IF$P\left( h \right) = p$THEN
使用遗憾匹配基于预测出的优势$V\left( {I\left( h \right),a\|{\theta _p}} \right)$计算策略　　　${\sigma ^t}\left( I \right)$
FOR$a \in A\left( h \right)$do
$v(a) \leftarrow $TRAVERSE$\left( {h \cdot a,p,{\theta _1},{\theta _2},{\mathcal{M}_V},{\mathcal{M}_\Pi },t} \right)$
FOR$a \in A\left( h \right)$do
$\tilde r(I,a) \leftarrow v(a) - \sum\limits_{{a^\prime } \in A(h)} \sigma (I,{a^\prime }) \cdot v({a^\prime })$
将信息集及其行动优势值$\left( {I,t,{{\widetilde r}^t}\left( I \right)} \right)$插入到优势记忆　　　${\mathcal{M}_V}$中
ELSE
使用遗憾匹配基于预测出的优势$V\left( {I\left( h \right),a\|{\theta _{3 - p}}} \right)$计算策略　　　${\sigma ^t}\left( I \right)$。
将信息集及其行动概率$\left( {I,t,{\sigma ^t}\left( I \right)} \right)$插入到策略记忆${\mathcal{M}_\Pi }$中
从概率分布${\sigma ^t}\left( I \right)$中采样1个行动a。
RETURN TRAVERSE$\left( {h \cdot a,p,{\theta _1},{\theta _2},{\mathcal{M}_V},{\mathcal{M}_\Pi },t} \right)$

下载: 导出CSV

表 1 雷达的工作参数设置

参数名称	参数值
组网雷达总功率$ {P^{{\text{total}}}} $(kW)	1000
雷达节点发射天线增益${G_t}$(dB)	30
脉冲带宽$B$(MHz)	6
虚警概率${P_{fa}}$	$1 \times {10^{ - 4}}$
干扰机群总功率$P_j^{{\text{total}}}$(W)	60
干扰机发射天线增益${G_j}$/dB)	16
最小发射功率(kW)	0.1${P^{{\text{total}}}}$
最大发射功率(kW)	0.9${P^{{\text{total}}}}$

下载: 导出CSV

表 2 组网雷达动作序列与动作向量关系

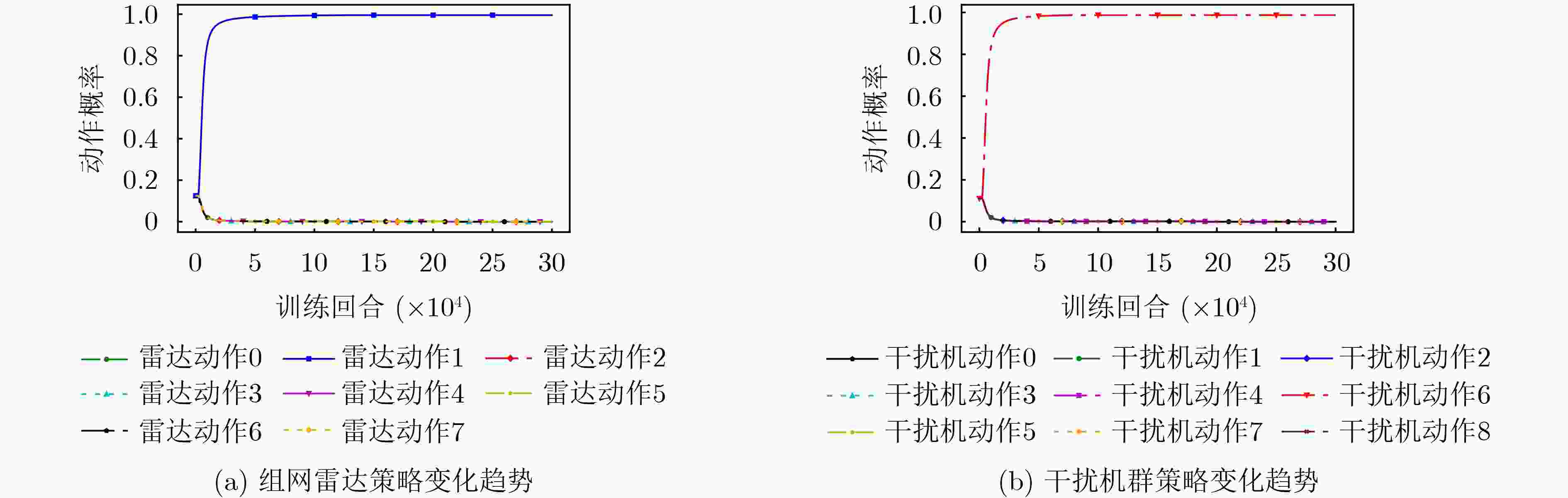
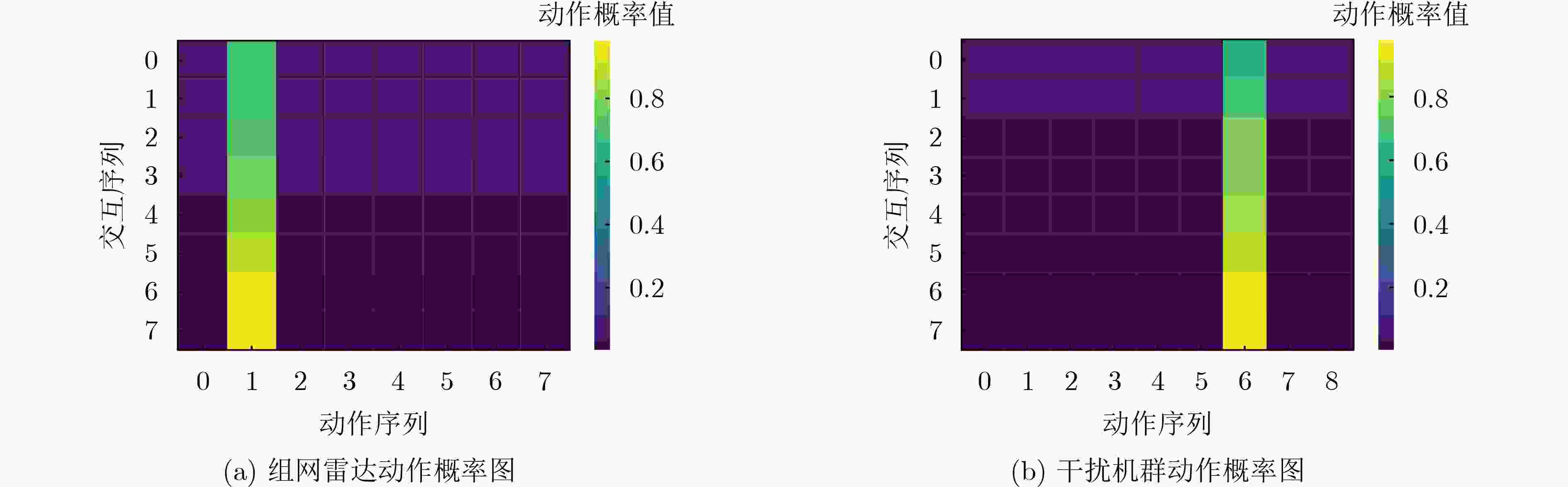
动作序列	雷达动作向量
0	[0, 0, 0]
1	[0, 0, 1]
2	[0, 1, 0]
3	[0, 1, 1]
4	[1, 0, 0]
5	[1, 0, 1]
6	[1, 1, 0]
7	[1, 1, 1]

下载: 导出CSV

表 3 干扰机群动作序列与动作向量关系

动作序列	干扰动作向量
0	[0, 0]
1	[0, 1]
2	[0, 2]
3	[1, 0]
4	[1, 1]
5	[1, 2]
6	[2, 0]
7	[2, 1]
8	[2, 2]

下载: 导出CSV

表 4 算法时间对比

算法种类	Deep CFR	DDPG	Double DQN
训练时间(min)	43.67	60.42	63.79
平均执行时间(ms)	9.41	10.52	9.95

下载: 导出CSV

参考文献(36)

[1]	ZHU Jingjing, ZHU Shengqi, XU Jingwei, et al. Discrimination of target and mainlobe jammers with FDA-MIMO radar[J]. IEEE Signal Processing Letters, 2023, 30: 583–587. doi: 10.1109/LSP.2023.3276630.
[2]	HE Bin and SU Hongtao. Game theoretic countermeasure analysis for multistatic radars and multiple jammers[J]. Radio Science, 2021, 56(5): 1–14. doi: 10.1029/2020RS007202.
[3]	时晨光, 蒋泽宇, 严牧, 等. 针对组网雷达的无人机集群航迹欺骗综合误差分析[J]. 电子与信息学报, 2024, 46(12): 4451–4458. doi: 10.11999/JEIT240289. SHI Chenguang, JIANG Zeyu, YAN Mu, et al. Comprehensive error in UAV cluster trajectory deception for networked radar[J]. Journal of Electronics & Information Technology, 2024, 46(12): 4451–4458. doi: 10.11999/JEIT240289.
[4]	孙明玮, 周瑜, 朴敏楠, 等. 雷达框架角约束下高空巡航导弹末制导策略[J]. 哈尔滨工程大学学报, 2021, 42(7): 1070–1075. doi: 10.11990/jheu.202003029. SUN Mingwei, ZHOU Yu, PIAO Minnan, et al. Terminal guidance strategy for a high-altitude cruise missile subject to the radar gimbal angle constraint[J]. Journal of Harbin Engineering University, 2021, 42(7): 1070–1075. doi: 10.11990/jheu.202003029.
[5]	刘鲁涛, 王璐璐, 陈涛. 基于改进DSets的无参数雷达信号分选算法[J]. 中国舰船研究, 2021, 16(4): 232–238. doi: 10.19693/j.issn.1673-3185.02012. LIU Lutao, WANG Lulu, and CHEN Tao. Non-parametric radar signal sorting algorithm based on improved DSets[J]. Chinese Journal of Ship Research, 2021, 16(4): 232–238. doi: 10.19693/j.issn.1673-3185.02012.
[6]	张忠民, 王雨鑫. 基于自适应的SSD算法和1.5维谱的新型雷达干扰识别[J]. 应用科技, 2021, 48(5): 54–59. doi: 10.11991/yykj.202012017. ZHANG Zhongmin and WANG Yuxin. New radar jamming recognition based on adaptive SSD algorithm and 1.5-dimensional spectrum[J]. Applied Science and Technology, 2021, 48(5): 54–59. doi: 10.11991/yykj.202012017.
[7]	SUN Hao, LI Ming, ZUO Lei, et al. Joint radar scheduling and beampattern design for multitarget tracking in netted colocated MIMO radar systems[J]. IEEE Signal Processing Letters, 2021, 28: 1863–1867. doi: 10.1109/LSP.2021.3108675.
[8]	LI Shengxiang, LIU Guangyi, ZHANG Kai, et al. DRL-based joint path planning and jamming power allocation optimization for suppressing netted radar system[J]. IEEE Signal Processing Letters, 2023, 30: 548–552. doi: 10.1109/LSP.2023.3270762.
[9]	YAN Junkun, LIU Hongwei, PU Wenqiang, et al. Joint threshold adjustment and power allocation for cognitive target tracking in asynchronous radar network[J]. IEEE Transactions on Signal Processing, 2017, 65(12): 3094–3106. doi: 10.1109/TSP.2017.2679693.
[10]	ZHANG Weiwei, SHI Chenguang, SALOUS S, et al. Convex optimization-based power allocation strategies for target localization in distributed hybrid non-coherent active-passive radar networks[J]. IEEE Transactions on Signal Processing, 2022, 70: 2476–2488. doi: 10.1109/TSP.2022.3173756.
[11]	SHI Chenguang, WANG Yijie, SALOUS S, et al. Joint transmit resource management and waveform selection strategy for target tracking in distributed phased array radar network[J]. IEEE Transactions on Aerospace and Electronic Systems, 2022, 58(4): 2762–2778. doi: 10.1109/TAES.2021.3138869.
[12]	LU Xiujuan, KONG Lingjiang, SUN Jun, et al. Joint online route planning and power allocation for multitarget tracking in airborne radar systems[C]. 2020 IEEE Radar Conference (RadarConf20), Florence, Italy, 2020: 1–6. doi: 10.1109/RadarConf2043947.2020.9266327.
[13]	易伟, 袁野, 刘光宏, 等. 多雷达协同探测技术研究进展: 认知跟踪与资源调度算法[J]. 雷达学报, 2023, 12(3): 471–499. doi: 10.12000/JR23036. YI Wei, YUAN Ye, LIU Guanghong, et al. Recent advances in multi-radar collaborative surveillance: Cognitive tracking and resource scheduling algorithms[J]. Journal of Radars, 2023, 12(3): 471–499. doi: 10.12000/JR23036.
[14]	KUANG Xiaofei, PENG Yu, JIN Biao, et al. Joint allocation of power and bandwidth for cognitive tracking netted radar[C]. 2021 International Conference on Control, Automation and Information Sciences (ICCAIS), Xi'an, China, 2021: 263–266. doi: 10.1109/ICCAIS52680.2021.9624621.
[15]	邝晓飞, 彭宇, 靳标, 等. 基于Stackelberg博弈的组网雷达功率分配方法[J]. 战术导弹技术, 2021(6): 38–46. doi: 10.16358/j.issn.1009-1300.2021.1.114. KUANG Xiaofei, PENG Yu, JIN Biao, et al. Power allocation method for netted radar based on Stackelberg game[J]. Tactical Missile Technology, 2021(6): 38–46. doi: 10.16358/j.issn.1009-1300.2021.1.114.
[16]	吴家乐, 时晨光, 周建江. 基于非合作博弈的组网雷达辐射功率控制算法[J]. 战术导弹技术, 2021(6): 11–19,37. doi: 10.16358/j.issn.1009-1300.2021.1.115. WU Jiale, SHI Chenguang, and ZHOU Jianjiang. Transmit power control algorithm of a radar network based on non-cooperative game theoretic model in confrontation scenarios[J]. Tactical Missile Technology, 2021(6): 11–19,37. doi: 10.16358/j.issn.1009-1300.2021.1.115.
[17]	SONG Xiufeng, WILLETT P, ZHOU Shengli, et al. The MIMO radar and jammer games[J]. IEEE Transactions on Signal Processing, 2012, 60(2): 687–699. doi: 10.1109/TSP.2011.2169251.
[18]	ZHANG Xiaobo, WANG Hai, RUAN Lang, et al. Joint channel and power optimisation for multi-user anti-jamming communications: A dual mode Q-learning approach[J]. IET Communications, 2022, 16(6): 619–633. doi: 10.1049/cmu2.12339.
[19]	GENG Jie, JIU Bo, LI Kang, et al. Multiagent reinforcement learning for antijamming game of frequency-agile radar[J]. IEEE Geoscience and Remote Sensing Letters, 2024, 21: 3504805. doi: 10.1109/LGRS.2024.3382041.
[20]	HART S and MAS-COLELL A. A simple adaptive procedure leading to correlated equilibrium[J]. Econometrica, 2000, 68(5): 1127–1150. doi: 10.1111/1468-0262.00153.
[21]	BROWN N and SANDHOLM T. Solving imperfect-information games via discounted regret minimization[C]. Proceedings of the 33rd AAAI Conference on Artificial Intelligence, Honolulu, USA, 2019: 1829–1836. doi: 10.1609/aaai.v33i01.33011829.
[22]	BROWN N, LERER A, GROSS S, et al. Deep counterfactual regret minimization[C]. Proceedings of the 36th International Conference on Machine Learning, Long Beach, USA, 2019: 793–802.
[23]	CHASLOT G, BAKKES S, SZITA I, et al. Monte-Carlo tree search: A new framework for game AI[C]. The 4th AAAI Conference on Artificial Intelligence and Digital Entertainment, Palo Alto, USA, 2008: 216–217. doi: 10.1609/aiide.v4i1.18700.
[24]	CHEN Yuxuan, ZHANG Li, LI Shijian, et al. RM-FSP: Regret minimization optimizes neural fictitious self-play[J]. Neurocomputing, 2023, 549: 126471. doi: 10.1016/j.neucom.2023.126471.
[25]	王跃东, 顾以静, 梁彦, 等. 伴随压制干扰与组网雷达功率分配的深度博弈研究[J]. 雷达学报, 2023, 12(3): 642–656. doi: 10.12000/JR23023. WANG Yuedong, GU Yijing, LIANG Yan, et al. Deep game of escorting suppressive jamming and networked radar power allocation[J]. Journal of Radars, 2023, 12(3): 642–656. doi: 10.12000/JR23023.
[26]	张大琳, 易伟, 孔令讲. 面向组网雷达干扰任务的多干扰机资源联合优化分配方法[J]. 雷达学报, 2021, 10(4): 595–606. doi: 10.12000/JR21071. ZHANG Dalin, YI Wei, and KONG Lingjiang. Optimal joint allocation of multijammer resources for jamming netted radar system[J]. Journal of Radars, 2021, 10(4): 595–606. doi: 10.12000/JR21071.
[27]	孙俊, 张大琳, 易伟. 多机协同干扰组网雷达的资源调度方法[J]. 雷达科学与技术, 2022, 20(3): 237–244,254. doi: 10.3969/j.issn.1672-2337.2022.03.001. SUN Jun, ZHANG Dalin, and YI Wei. Resource allocation for multi-jammer cooperatively jamming netted radar systems[J]. Radar Science and Technology, 2022, 20(3): 237–244,254. doi: 10.3969/j.issn.1672-2337.2022.03.001.
[28]	韩国玺, 何俊, 祁建清. 基于秩K准则的网络雷达对抗系统融合发现概率计算模型[J]. 海军工程大学学报, 2014, 26(1): 64–70. doi: 10.7495/j.issn.1009-3486.2014.01.014. HAN Guoxi, HE Jun, and QI Jianqing. Fused detection probability model of NRCS based on rank K criterion[J]. Journal of Naval University of Engineering, 2014, 26(1): 64–70. doi: 10.7495/j.issn.1009-3486.2014.01.014.
[29]	KORDIK A M, METCALF J G, CURTIS D D, et al. Graceful performance degradation and improved error tolerance via mixed-mode distributed coherent radar[J]. IEEE Sensors Journal, 2023, 23(5): 5251–5262. doi: 10.1109/JSEN.2023.3236487.
[30]	MA Hongguang, GUO Jinku, SONG Xiaoshan, et al. An approach to modeling cognitive antagonism with incomplete information[J]. IEEE Transactions on Computational Social Systems, 2024, 11(1): 795–802. doi: 10.1109/TCSS.2022.3233365.
[31]	王星, 王俊迪, 金政芝, 等. 机载雷达告警接收机发展现状及趋势[J]. 雷达学报, 2023, 12(2): 376–388. doi: 10.12000/JR22200. WANG Xing, WANG Jundi, JIN Zhengzhi, et al. Current situation and development demands for a radar warning receiver system[J]. Journal of Radars, 2023, 12(2): 376–388. doi: 10.12000/JR22200.
[32]	JAKOVAC M. Measurement and testing pulsed radar emission and parameters with spectrum analyser in time domain[C]. 2015 57th International Symposium ELMAR (ELMAR), Zadar, Croatia, 2015: 161–166. doi: 10.1109/ELMAR.2015.7334521.
[33]	SHI Shuqing, WANG Xiaobin, HAO Dong, et al. Solving poker games efficiently: Adaptive memory based deep counterfactual regret minimization[C]. 2022 International Joint Conference on Neural Networks (IJCNN), Padua, Italy, 2022: 1–11. doi: 10.1109/IJCNN55064.2022.9892417.
[34]	LI Kang, JIU Bo, PU Wenqiang, et al. Neural fictitious self-play for radar antijamming dynamic game with imperfect information[J]. IEEE Transactions on Aerospace and Electronic Systems, 2022, 58(6): 5533–5547. doi: 10.1109/TAES.2022.3175186.
[35]	JIANG Sen and WANG Bo. MADDPG based radar interference resource allocation decision[C]. 2024 China Automation Congress (CAC), Qingdao, China, 2024: 3204–3209. doi: 10.1109/CAC63892.2024.10864674.
[36]	IQBAL A, THAM M L, and CHANG Y C. Double deep Q-network-based energy-efficient resource allocation in cloud radio access network[J]. IEEE Access, 2021, 9: 20440–20449. doi: 10.1109/ACCESS.2021.3054909.