Sparse Channel Estimation and Array Blockage Diagnosis for Non-Ideal RIS-Assisted MIMO Systems
-
摘要: 针对非理想可重构智能超表面(RIS)辅助毫米波多输入多输出(MIMO)系统信道状态信息获取问题,该文提出一种稀疏级联信道参数与阵列阻塞向量联合估计方案。首先,设计信道训练帧结构,将接收信号建模为张量模型。然后,基于张量的平行因子分解模型,分析毫米波信道参数与阻塞向量之间的内在关联,实现对收发端空域信道参数的有效估计。基于这些空间角频率,构建出同时反映剩余信道参数和阻塞信息的耦合观测矩阵。最后,通过利用多径信道和阻塞向量的双稀疏特性,完成剩余信道参数的估计和阻塞诊断。仿真结果表明,所提方案的信道估计和阻塞诊断性能表现优于对照方案。
-
关键词:
- 毫米波MIMO /
- 可重构智能超表面(RIS) /
- 信道估计 /
- 阻塞诊断
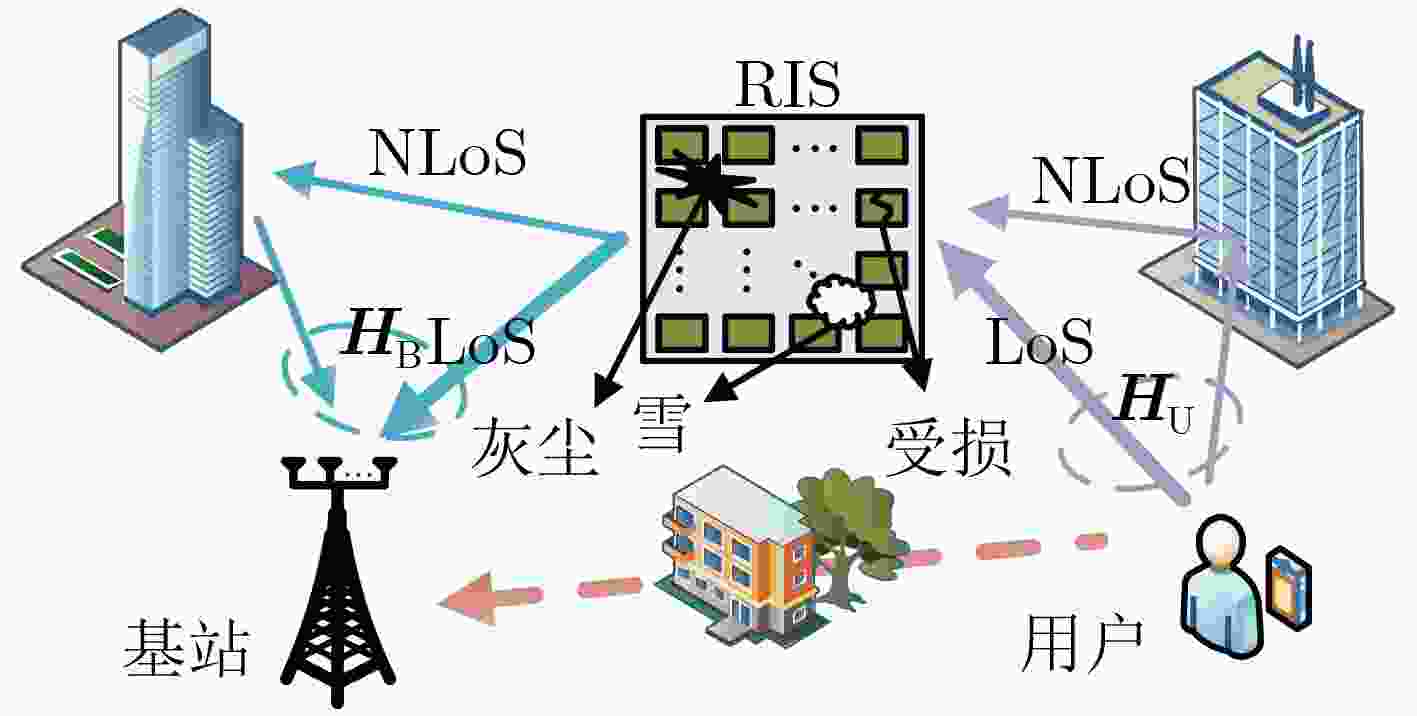
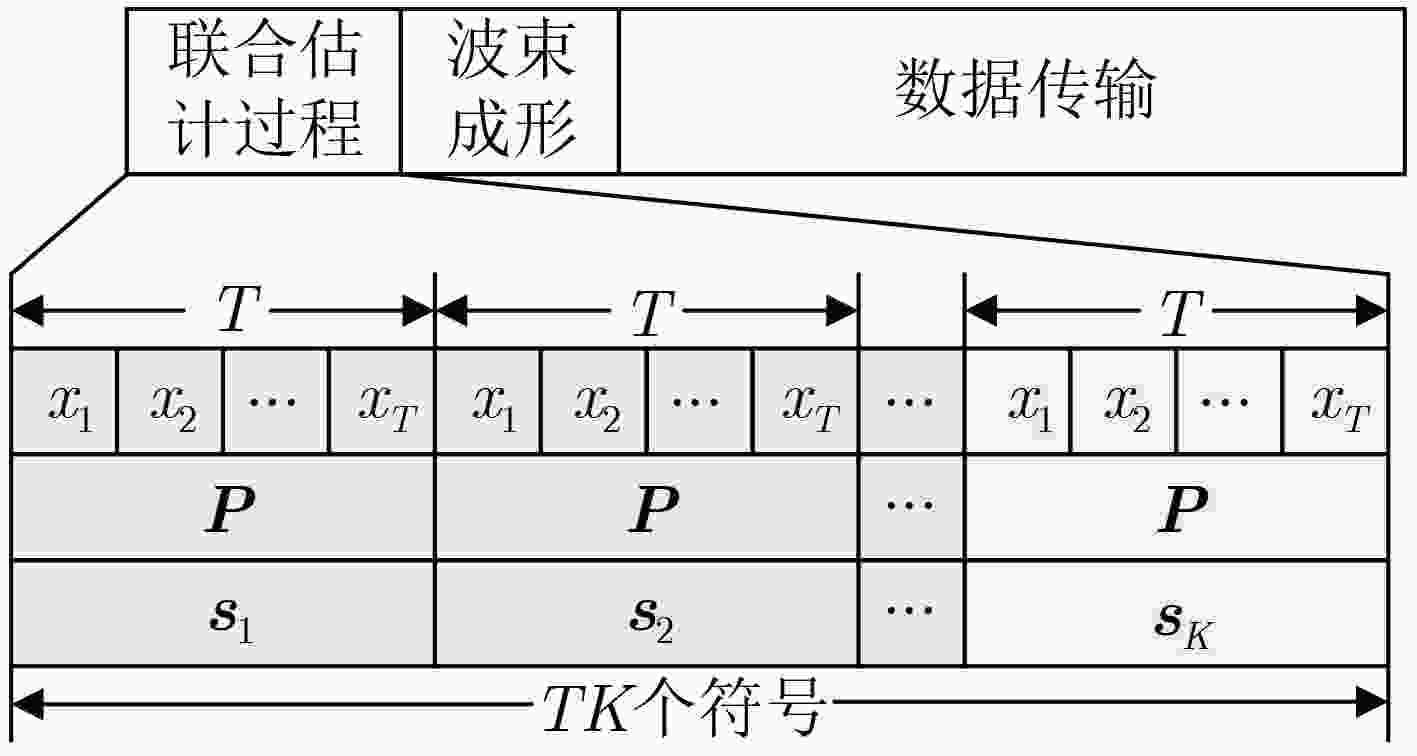
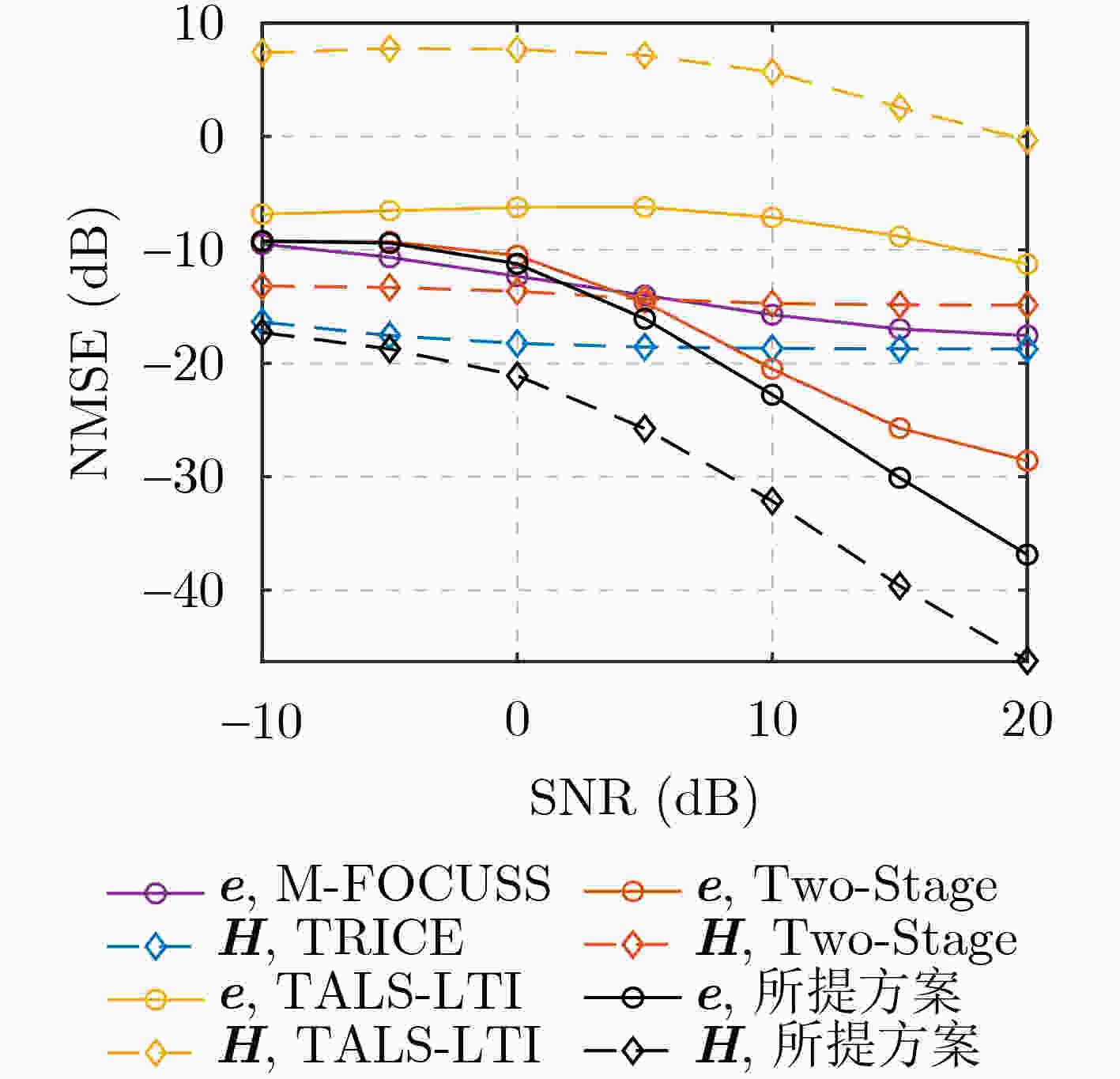
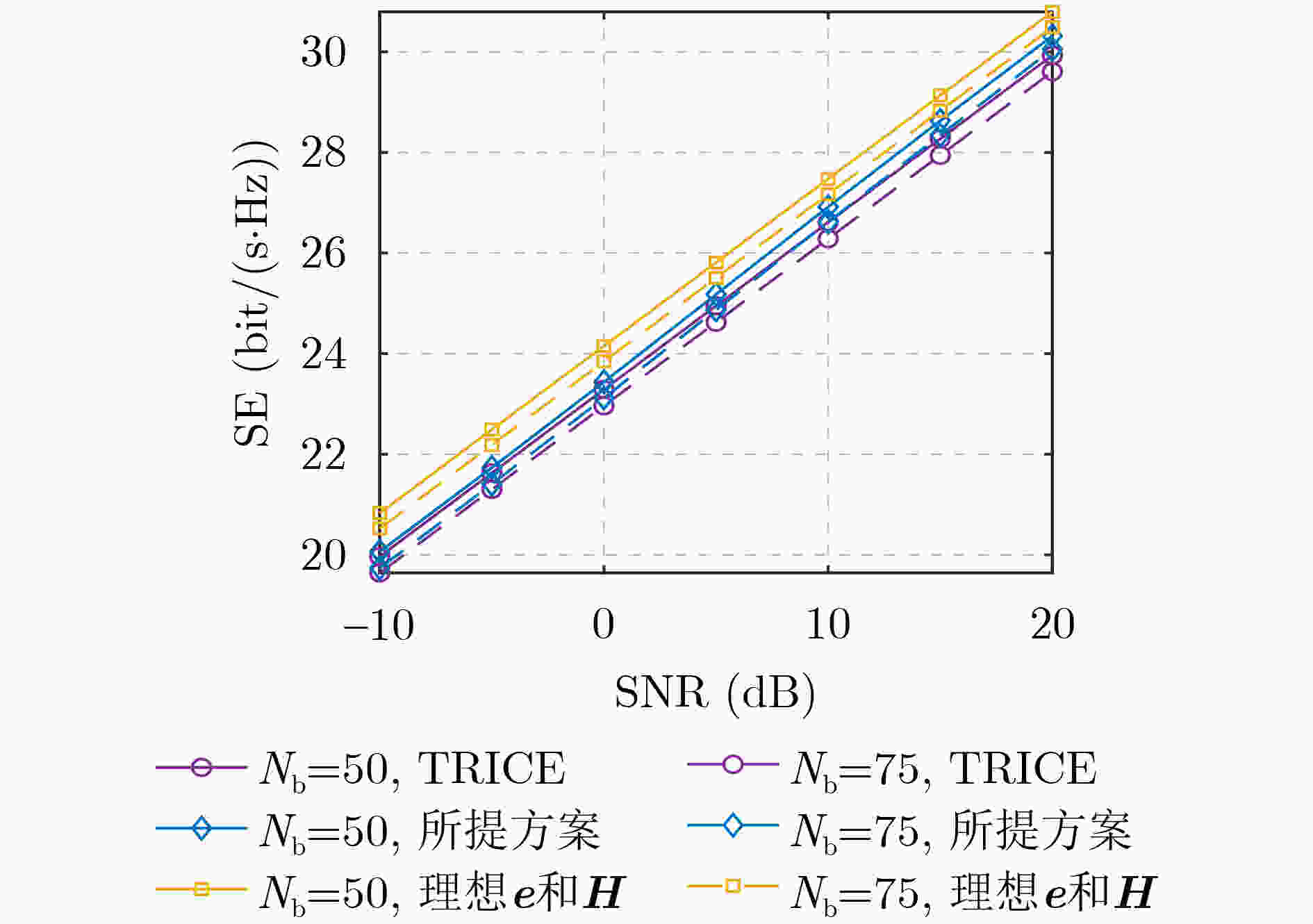
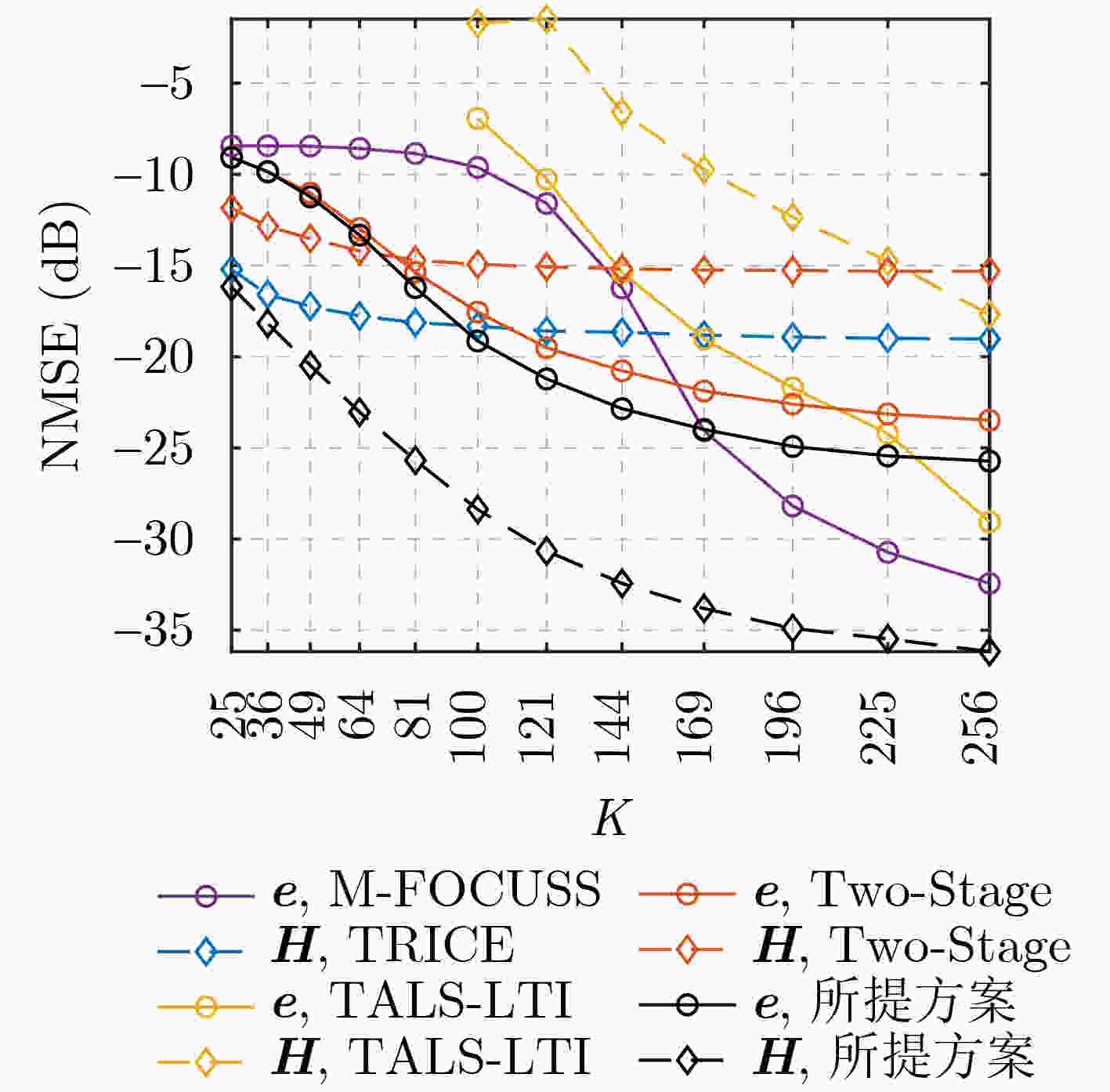
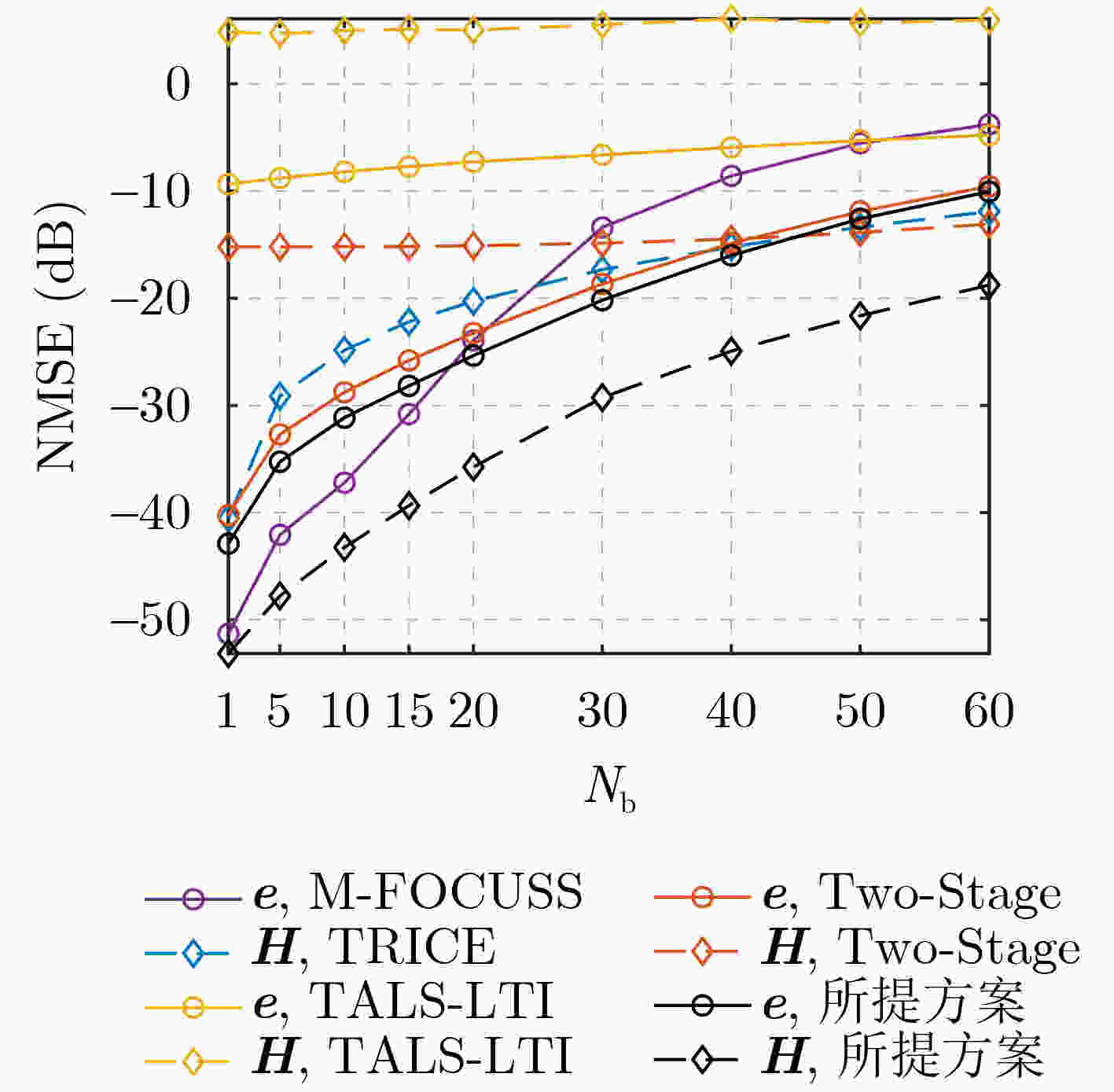
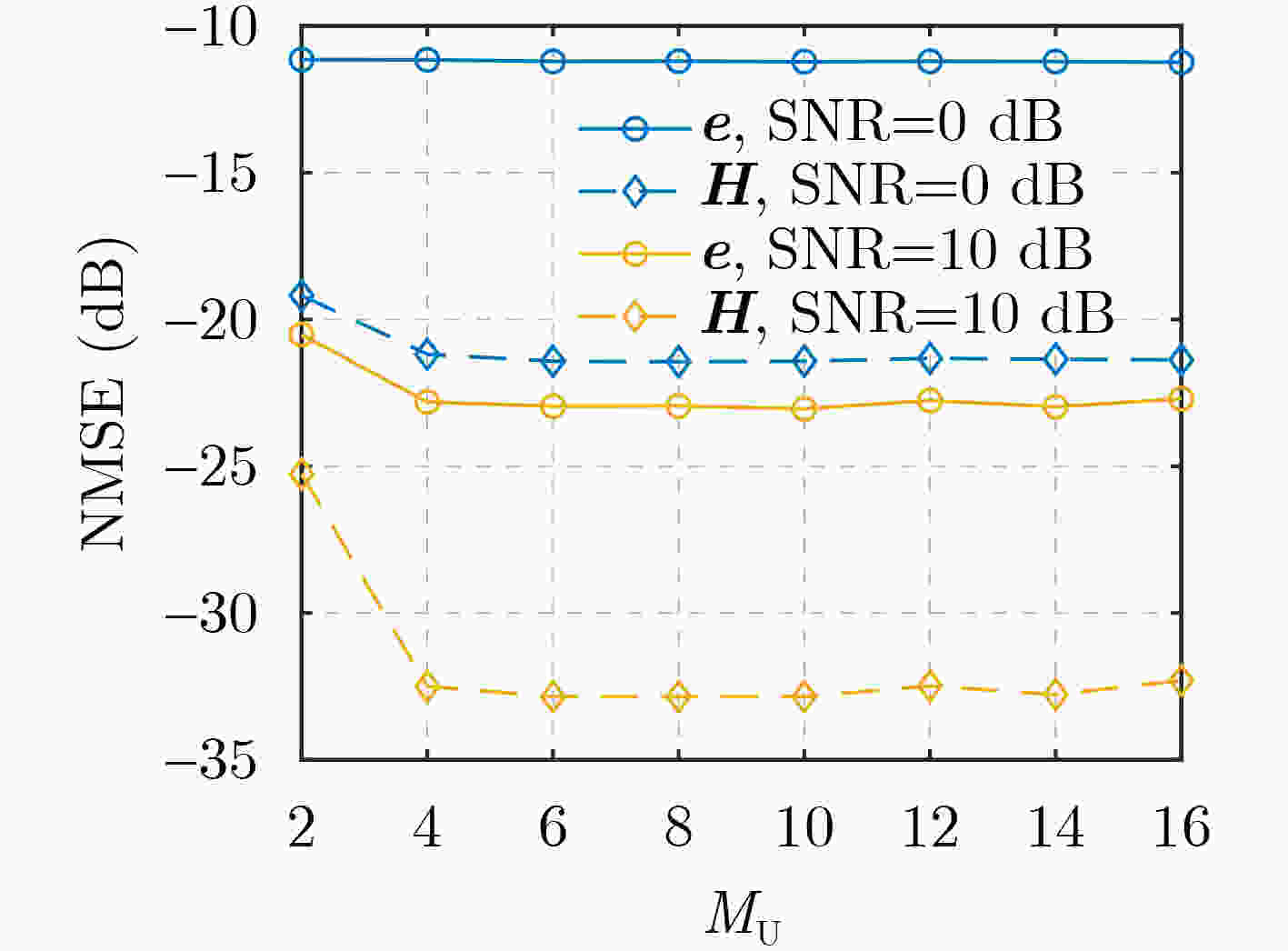
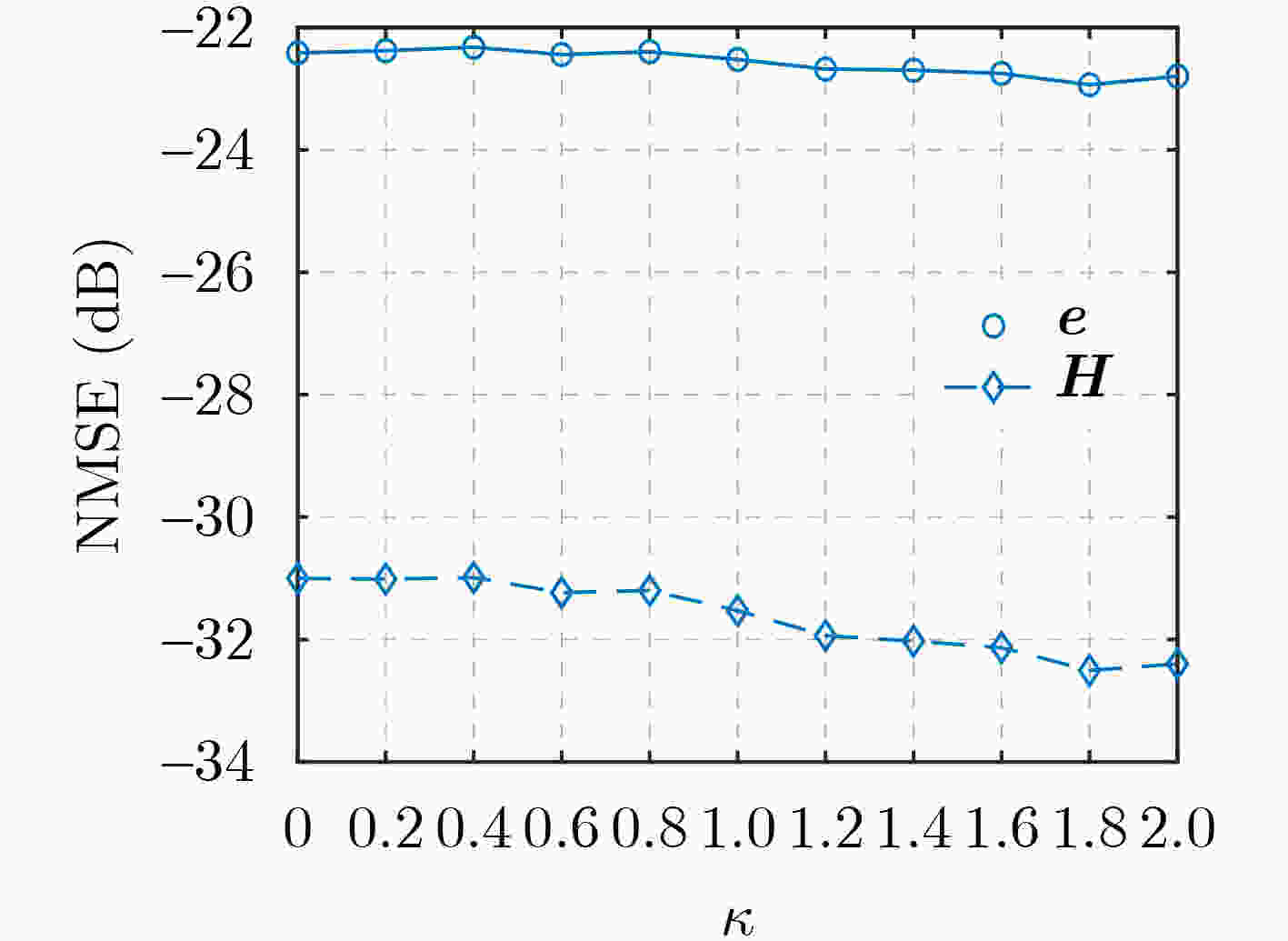
Abstract:Objective Reconfigurable Intelligent Surfaces (RISs) offer a promising approach to enhance Millimeter-Wave (mmWave) Multiple-Input Multiple-Output (MIMO) systems by dynamically manipulating wireless propagation. However, practical deployments are challenged by hardware faults and environmental blockages (e.g., dust or rain), which impair Channel State Information (CSI) accuracy and reduce Spectral Efficiency (SE). Most existing studies either overlook the interdependence between the CSI and blockage vector or fail to leverage the dual sparsity of multipath channels and blockage patterns. This study proposes a joint sparse channel estimation and blockage diagnosis scheme to overcome these limitations, thereby enabling reliable beamforming and enhancing system robustness in non-ideal RIS-assisted mmWave MIMO environments. Methods A third-order Parallel Factor (PARAFAC) decomposition model is constructed for the received signals using a tensor-based signal representation. The intrinsic relationship between mmWave channel parameters and the blockage vector is exploited to estimate spatial angular frequencies at the User Equipment (UE) and Base Station (BS) using Orthogonal Matching Pursuit (OMP). Based on these frequencies, a coupled observation matrix is formed to jointly capture residual channel parameters and blockage vector information. This matrix is reformulated as a Least Absolute Shrinkage and Selection Operator (LASSO) problem, which is solved using the Alternating Direction Method of Multipliers (ADMM) to estimate the blockage vector. The remaining channel parameters are then recovered using sparse reconstruction techniques by leveraging their inherent sparsity. Iterative refinement updates both the blockage vector and channel parameters, ensuring convergence under limited pilot overhead conditions. Results and Discussions For a non-ideal RIS-assisted mmWave MIMO system ( Fig. 1 ), a signal transmission framework is designed (Fig. 2 ), in which the received signals are represented as a third-order tensor. Leveraging the dual-sparsity of multipath channels and the blockage vector, a joint estimation scheme is developed (Algorithm 1 ), enabling effective parameter decoupling through tensor-based parallel factor decomposition and iterative optimization. Simulation results show that the proposed scheme achieves superior performance in both channel estimation and blockage diagnosis compared with baseline methods by fully exploiting dual-sparsity characteristics (Fig. 3 ). SE analysis confirms the detrimental effect of blockages on system throughput and highlights that the proposed scheme improves SE by compensating for blockage-induced impairments (Fig. 4 ). The method also demonstrates strong estimation accuracy under reduced pilot overhead (Fig. 5 ) and improved robustness as the number of blocked RIS elements increases (Fig. 6 ). A decline in spatial angular frequency estimation is observed with fewer UE antennas, which negatively affects overall performance; however, estimation stabilizes as antenna count increases (Fig. 7 ). Moreover, when Non-Line-of-Sight (NLoS) path contributions decrease, the scheme exhibits enhanced performance due to improved resolution between Line-of-Sight (LoS) and NLoS components (Fig. 8 ).Conclusions This study proposes a joint channel estimation and blockage diagnosis scheme for non-ideal RIS-assisted mmWave MIMO systems, based on the dual sparsity of multipath channels and blockage vectors. Analysis of the tensor-based parallel factor decomposition model reveals that the estimation of spatial angular frequencies at the UE and BS is unaffected by blockage conditions. The proposed scheme accounts for the contributions of NLoS paths, enabling accurate decoupling of residual channel parameters and blockage vector across different propagation paths. Simulation results confirm that incorporating NLoS path information improves both channel estimation accuracy and blockage detection. Compared with existing methods, the proposed approach achieves superior performance in both aspects. In practical scenarios, real-time adaptability may be challenged if blockage states vary more rapidly than channel characteristics. Future work will focus on enhancing the scheme’s responsiveness to dynamic blockage conditions. -
表 1 本文数学符号对照表
数学符号 符号说明 ${{\boldsymbol{A}}^*}$ 共轭 ${{\boldsymbol{A}}^\dagger }$ 伪逆 $\diamondsuit $ Khatri-Rao积 $ \otimes $ Kronecker积 ${[{\boldsymbol{a}}]_n}$ 向量${\boldsymbol{a}}$的第$n$个元素 ${[\mathcal{A}]_{(n)}}$ 张量$\mathcal{A}$的模式$n$展开 ${\text{diag(}} \cdot {\text{)}}$ 对角化 ${\text{vec(}} \cdot {\text{)}}$ 向量化 ${\text{unve}}{{\text{c}}_{M \times N}}( \cdot )$ 反向量化 $\left| \cdot \right|$ 取模 $ {\left\| \cdot \right\|_{\mathrm{F}}} $ Frobenius范数 $ {\left\| \cdot \right\|_{\mathrm{p}}} $ ${\mathrm{p}}$-范数 $\mathbb{E}\{ \cdot \} $ 均值 1 基于双稀疏的RIS辅助毫米波MIMO联合信道估计与阻塞诊断
(1) 输入:接收信号${{\boldsymbol{y}}_{k,t}}$,预编码信号${{\boldsymbol{p}}_t}$,组合矩阵${\boldsymbol{W}}$,相移向量${{\boldsymbol{s}}_k}$,$t = 1,2, \cdots ,T$,$k = 1,2, \cdots ,K$ (2) 根据导频传输协议,构造接收信号的张量模型$\mathcal{Y} \in {\mathbb{C}^{{N_{\text{B}}} \times T \times K}}$ (3) 构造张量$\mathcal{Y}$的模式1和模式2展开形式${[\mathcal{Y}]_{(1)}}$和${[\mathcal{Y}]_{(2)}}$,见式(14) (4) 构造1维字典矩阵$ {{{\bar {\boldsymbol A}}}_{\text{B}}} \in {\mathbb{C}^{{M_{\text{B}}} \times {{\bar L}_{\text{B}}}}} $和$ {{{\bar {\boldsymbol A}}}_{\text{U}}} \in {\mathbb{C}^{{M_{\text{U}}} \times {{\bar L}_{\text{U}}}}} $ (5) 根据式(15)和式(16),使用OMP算法估计${{\boldsymbol{\hat \theta }}_{\text{B}}}$和${{\boldsymbol{\hat \theta }}_{\text{U}}}$ (6) 根据${{\boldsymbol{\hat \theta }}_{\text{B}}}$和${{\boldsymbol{\hat \theta }}_{\text{U}}}$构$ {{{\hat {\boldsymbol A}}}_{\text{B}}} = [{\boldsymbol{a}}({\hat \theta _{{\text{B,}}1}}),{\boldsymbol{a}}({\hat \theta _{{\text{B,}}2}}), \cdots ,{\boldsymbol{a}}({\hat \theta _{{\text{B,}}{L_{\text{B}}}}})] $和${{{\hat {\boldsymbol A}}}_{\text{U}}} = [{\boldsymbol{a}}({\hat \theta _{{\text{U,}}1}}),{\boldsymbol{a}}({\hat \theta _{{\text{U,}}2}}), \cdots ,{\boldsymbol{a}}({\hat \theta _{{\text{U,}}{L_{\text{U}}}}})]$ (7) 构造张量$\mathcal{Y}$的模式3展开形式${[\mathcal{Y}]_{(3)}}$,见式(14) (8) 根据${[\mathcal{Y}]_{(3)}}$计算$ {{\bar {\boldsymbol B}}} = {[\mathcal{Y}]_{(3)}}{({({{\boldsymbol{P}}^{\text{T}}}{{\hat {\boldsymbol A}}}_{\text{U}}^*{{\boldsymbol{\varOmega }}_{\text{U}}}\diamondsuit {{\boldsymbol{W}}^{\text{T}}}{{{\hat {\boldsymbol A}}}_{\text{B}}}{{\boldsymbol{\varOmega }}_{\text{B}}})^{\text{T}}})^\dagger } $ (9) 根据式(12)将剩余信道参数和阻塞向量的观测矩阵表示为$ \begin{array}{*{20}{c}} {{{\bar {\boldsymbol B}}} = {{\boldsymbol{S}}^{\text{T}}}({\boldsymbol{\bar H}} + {\boldsymbol{D}}) + {\boldsymbol{\bar N}}} \end{array} $ (10) 初始化阻塞向量${{\boldsymbol{e}}^{(0)}} = {{{{\textit{1}}}}_N}$,即信道偏移矩阵${{\boldsymbol{D}}^{(0)}} = {{{{\textit{0}}}}_N}$ (11) $i \leftarrow i + 1$ (12) for $l = 1:L$ (13) 根据式(25),使用截断SVD分解求解$ {\boldsymbol{\hat b}}_{{\text{v}},l}^{(i)} $和$ {\boldsymbol{\hat b}}_{h,l}^{(i)} $ (14) 根据式(26)估计$ \hat {\boldsymbol{b}}_{{\text{v}},l}^{(i)} $和$ \hat {\boldsymbol{b}}_{{\text{h}},l}^{(i)} $,并重新构造$ {\boldsymbol{\hat b}}_{{\text{v}},l}^{(i)} $和$ {\boldsymbol{\hat b}}_{h,l}^{(i)} $ (15) 根据式(27)计算$ \hat \alpha _l^{(i)} $,并更新$ {{\boldsymbol{\hat{ \bar {\boldsymbol{H}}}}}^{(i)}} = \hat \alpha _l^{(i)}({\boldsymbol{\hat b}}_{{\text{v}},l}^{(i)} \otimes {\boldsymbol{\hat b}}_{{\text{h}},l}^{(i)}) $ (16) end (17) 根据式(28),确定$ {{\bar {\boldsymbol B}}}_2^{(i)} $中强度最大的列的索引${l_{{\text{LoS}}}}$,使用ADMM算法求解式(30)中的稀疏问题 (18) 判断${\left\| {{{\boldsymbol{e}}^{(i)}} - {{\boldsymbol{e}}^{(i - 1)}}} \right\|_2} \le \tau $或者$i \le {I_1}$是否满足,不满足则返回步骤(11) (19) 输出:${{\boldsymbol{\hat \theta }}_{\text{U}}}$, ${{\boldsymbol{\hat \theta }}_{\text{B}}}$, ${{\boldsymbol{\hat b}}_{\text{v}}}$, ${{\boldsymbol{\hat b}}_{\text{h}}}$, ${\boldsymbol{\hat \alpha }}$和${\boldsymbol{\hat e}}$ -
[1] 张建华, 王珩, 张宇翔, 等. 6G信道新特性与建模研究: 挑战、进展与展望[J]. 中国科学: 信息科学, 2024, 54(5): 1114–1143. doi: 10.1360/SSI-2023-0355.ZHANG Jianhua, WANG Heng, ZHANG Yuxiang, et al. Channel characteristics and modeling research for 6G: Challenges, progress, and prospects[J]. Scientia Sinica Informationis, 2024, 54(5): 1114–1143. doi: 10.1360/SSI-2023-0355. [2] WANG Chengxiang, YOU Xiaohu, GAO Xiqi, et al. On the road to 6G: Visions, requirements, key technologies, and testbeds[J]. IEEE Communications Surveys & Tutorials, 2023, 25(2): 905–974. doi: 10.1109/comst.2023.3249835. [3] DAJER M, MA Zhengxiang, PIAZZI L, et al. Reconfigurable intelligent surface: Design the channel–A new opportunity for future wireless networks[J]. Digital Communications and Networks, 2022, 8(2): 87–104. doi: 10.1016/j.dcan.2021.11.002. [4] HUANG Chongwen, ZAPPONE A, ALEXANDROPOULOS G C, et al. Reconfigurable intelligent surfaces for energy efficiency in wireless communication[J]. IEEE Transactions on Wireless Communications, 2019, 18(8): 4157–4170. doi: 10.1109/TWC.2019.2922609. [5] 郭甜, 张旭辉, 吴雨佳, 等. 可重构智能表面辅助的毫米波信道估计算法[J]. 电子与信息学报, 2023, 45(10): 3612–3621. doi: 10.11999/JEIT221232.GUO Tian, ZHANG Xuhui, WU Yujia, et al. Channel estimation algorithm for reconfigurable intelligent surface aided millimeter wave systems[J]. Journal of Electronics & Information Technology, 2023, 45(10): 3612–3621. doi: 10.11999/JEIT221232. [6] 李双志, 杨睿棋, 郭新, 等. 低导频开销RIS辅助毫米波MIMO系统参数化信道估计方案[J]. 通信学报, 2024, 45(9): 82–91. doi: 10.11959/j.issn.1000-436x.2024157.LI Shuangzhi, YANG Ruiqi, GUO Xin, et al. Low pilot overhead parametric channel estimation scheme for RIS-assisted mmWave MIMO systems[J]. Journal on Communications, 2024, 45(9): 82–91. doi: 10.11959/j.issn.1000-436x.2024157. [7] ZHOU Shaoqing, XU Wei, WANG Kezhi, et al. Spectral and energy efficiency of IRS-assisted MISO communication with hardware impairments[J]. IEEE Wireless Communications Letters, 2020, 9(9): 1366–1369. doi: 10.1109/lwc.2020.2990431. [8] PAPAZAFEIROPOULOS A, PAN Cunhua, KOURTESSIS P, et al. Intelligent reflecting surface-assisted MU-MISO systems with imperfect hardware: Channel estimation and beamforming design[J]. IEEE Transactions on Wireless Communications, 2022, 21(3): 2077–2092. doi: 10.1109/twc.2021.3109391. [9] CHEN Chunqi, WANG Manlin, XIA Bin, et al. Performance analysis and optimization of IRS-aided covert communication with hardware impairments[J]. IEEE Transactions on Vehicular Technology, 2023, 72(4): 5463–5467. doi: 10.1109/tvt.2022.3227342. [10] LI Liping, YING Run, LI Yingsong, et al. RIS array diagnosis for mmWave communication systems[J]. IEEE Signal Processing Letters, 2024, 31: 1980–1984. doi: 10.1109/lsp.2024.3427663. [11] MEDINA G, JIDA A S, PULIPALI S, et al. Millimeter-wave antenna array diagnosis with partial channel state information[C]. 2021-IEEE International Conference on Communications, Montreal, Canada, 2021: 1–5. doi: 10.1109/icc42927.2021.9500527. [12] SUN Rui, WANG Weidong, CHEN Li, et al. Diagnosis of intelligent reflecting surface in millimeter-wave communication systems[J]. IEEE Transactions on Wireless Communications, 2022, 21(6): 3921–3934. doi: 10.1109/twc.2021.3125734. [13] WU Tuo, PAN Cunhua, ZHI Kangda, et al. Exploit high-dimensional RIS information to localization: What is the impact of faulty element?[J]. IEEE Journal on Selected Areas in Communications, 2024, 42(10): 2803–2819. doi: 10.1109/jsac.2024.3414582. [14] LI Binrui, ZHANG Zhongpei, HU Zhenzhen, et al. Joint array diagnosis and channel estimation for RIS-aided mmWave MIMO system[J]. IEEE Access, 2020, 8: 193992–194006. doi: 10.1109/access.2020.3032775. [15] LI Binrui, ZHANG Zhongpei, and HU Zhenzhen. Channel estimation for reconfigurable intelligent surface‐assisted multiuser mmWave MIMO system in the presence of array blockage[J]. Transactions on Emerging Telecommunications Technologies, 2021, 32(11): e4322. doi: 10.1002/ett.4322. [16] GOMES P R B, DE ARAÚJO G T, SOKAL B, et al. Channel estimation in RIS-assisted MIMO systems operating under imperfections[J]. IEEE Transactions on Vehicular Technology, 2023, 72(11): 14200–14213. doi: 10.1109/tvt.2023.3279805. [17] MA Siqi, SHEN Wenqian, GAO Xinyu, et al. Robust channel estimation for RIS-aided millimeter-wave system with RIS blockage[J]. IEEE Transactions on Vehicular Technology, 2022, 71(5): 5621–5626. doi: 10.1109/tvt.2022.3153966. [18] PENG Zhendong, PAN Cunhua, ZHOU Gui, et al. Two-stage channel estimation for RIS-aided multiuser mmWave systems with reduced error propagation and pilot overhead[J]. IEEE Transactions on Signal Processing, 2023, 71: 3607–3622. doi: 10.1109/TSP.2023.3317729. [19] ZHENG Yu, WANG Qianli, REN Longfei, et al. RIS aided gridless 2D-DOA estimation via decoupled atomic norm minimization[J]. IEEE Transactions on Vehicular Technology, 2024, 73(10): 15733–15738. doi: 10.1109/TVT.2024.3401413. [20] LI Shuangzhi, LEI Haojie, DONG Zheng, et al. Two-stage channel estimation in mmWave MIMO systems with RIS blockage[J]. IEEE Wireless Communications Letters, 2024, 13(12): 3548–3552. doi: 10.1109/LWC.2024.3477504. [21] XIU Yue, WANG Wenyuan, and ZHANG Zhongpei. A message passing approach to acquire mm-Wave channel state information based on out-of-band data[J]. IEEE Access, 2018, 6: 45665–45680. doi: 10.1109/ACCESS.2018.2855688. [22] HE Jiguang, WYMEERSCH H, and JUNTTI M. Channel estimation for RIS-aided mmWave MIMO systems via atomic norm minimization[J]. IEEE Transactions on Wireless Communications, 2021, 20(9): 5786–5797. doi: 10.1109/TWC.2021.3070064. [23] GHEREKHLOO S, ARDAH K, DE ALMEIDA A L F, et al. Tensor-based channel estimation and reflection design for RIS-aided millimeter-wave MIMO communication systems[C]. 2021 55th Asilomar Conference on Signals, Systems, and Computers, Pacific Grove, USA, 2021: 1683–1689. doi: 10.1109/IEEECONF53345.2021.9723362. [24] TANG Gongguo, BHASKAR B N, SHAH P, et al. Compressed sensing off the grid[J]. IEEE Transactions on Information Theory, 2013, 59(11): 7465–7490. doi: 10.1109/TIT.2013.2277451. [25] AKDENIZ M R, LIU Yuanpeng, SAMIMI M K, et al. Millimeter wave channel modeling and cellular capacity evaluation[J]. IEEE Journal on Selected areas in Communications, 2014, 32(6): 1164–1179. doi: 10.1109/JSAC.2014.2328154. [26] ARDAH K, DE ALMEIDA A L F, and HAARDT M. A gridless CS approach for channel estimation in hybrid massive MIMO systems[C]. 2019 IEEE International Conference on Acoustics, Speech and Signal Processing, Brighton, United Kingdom, 2019: 4160–4164. doi: 10.1109/ICASSP.2019.8683049. [27] ARDAH K, GHEREKHLOO S, DE ALMEIDA A L F, et al. TRICE: A channel estimation framework for RIS-aided millimeter-wave MIMO systems[J]. IEEE Signal Processing Letters, 2021, 28: 513–517. doi: 10.1109/LSP.2021.3059363. [28] ZHOU Zhou, FANG Jun, YANG Linxiao, et al. Low-rank tensor decomposition-aided channel estimation for millimeter wave MIMO-OFDM systems[J]. IEEE Journal on Selected Areas in Communications, 2017, 35(7): 1524–1538. doi: 10.1109/JSAC.2017.2699338. -





 下载:
下载:


 下载:
下载:
