Rank-Two Beamforming Algorithm Based on Alternating Optimization Assisted by Intelligent Reflecting Surface
-
摘要: 针对智能反射面(IRS)辅助的下行多用户多输入单输出(MISO)系统,该文以最大化系统频谱效率为目标,在满足基站发射功率和IRS反射单元模约束的条件下,设计基站处主动波束成形向量和IRS的相移矩阵。首先为了实现更高的波束形成自由度,采用了基于空间时间块编码(STBC)的秩二波束形成方案。随后为了求解非凸深度耦合的优化问题,提出了一种交替优化算法。针对IRS相移矩阵的求解,提出了一种改进的黎曼流形共轭梯度法(IRMG)进行优化,同时使用加权最小均方误差(WMMSE)设计主动波束形成向量。仿真结果验证了所提算法具有更快的收敛速度,同时能有效提升系统频谱效率。Abstract:
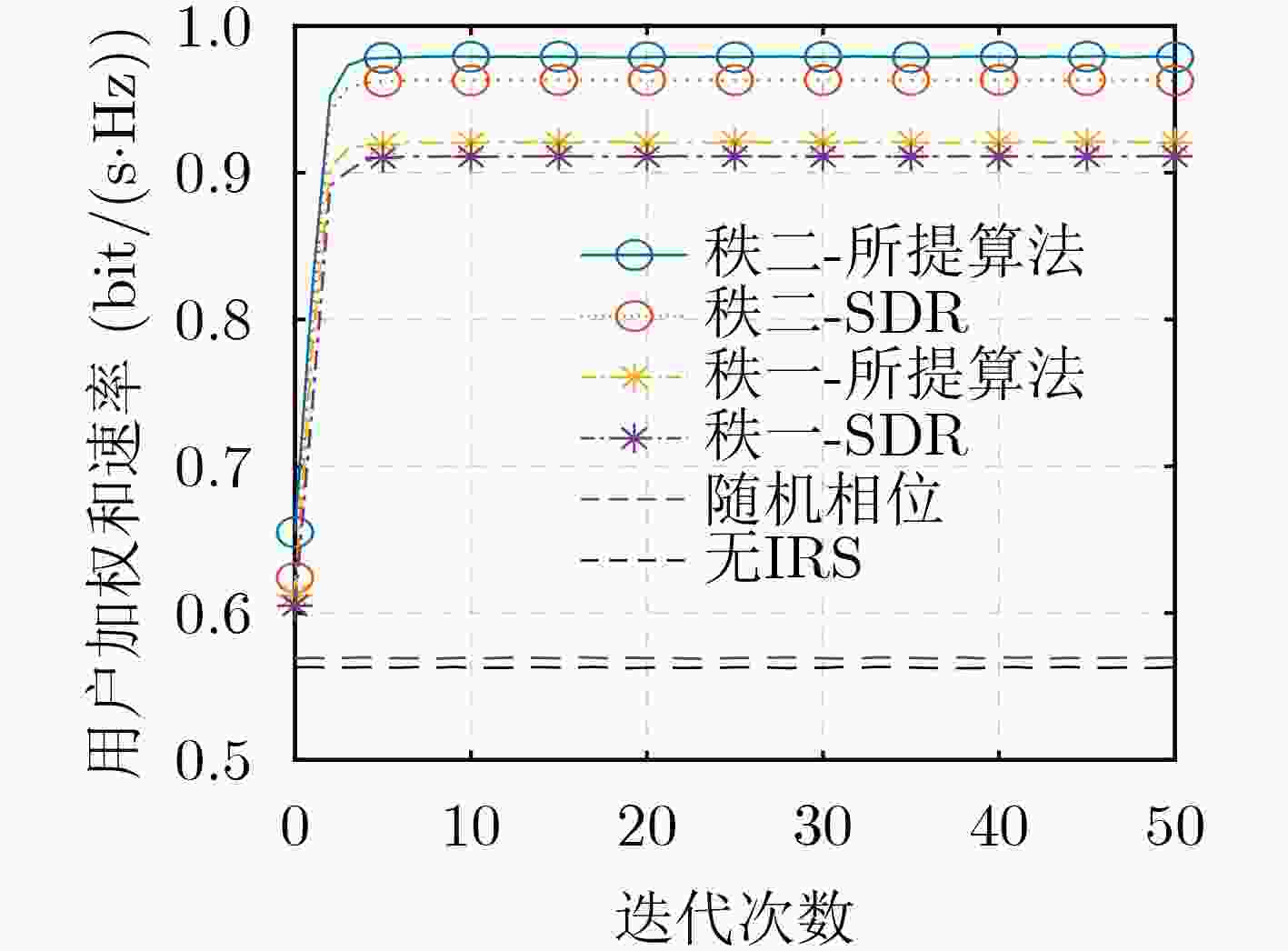
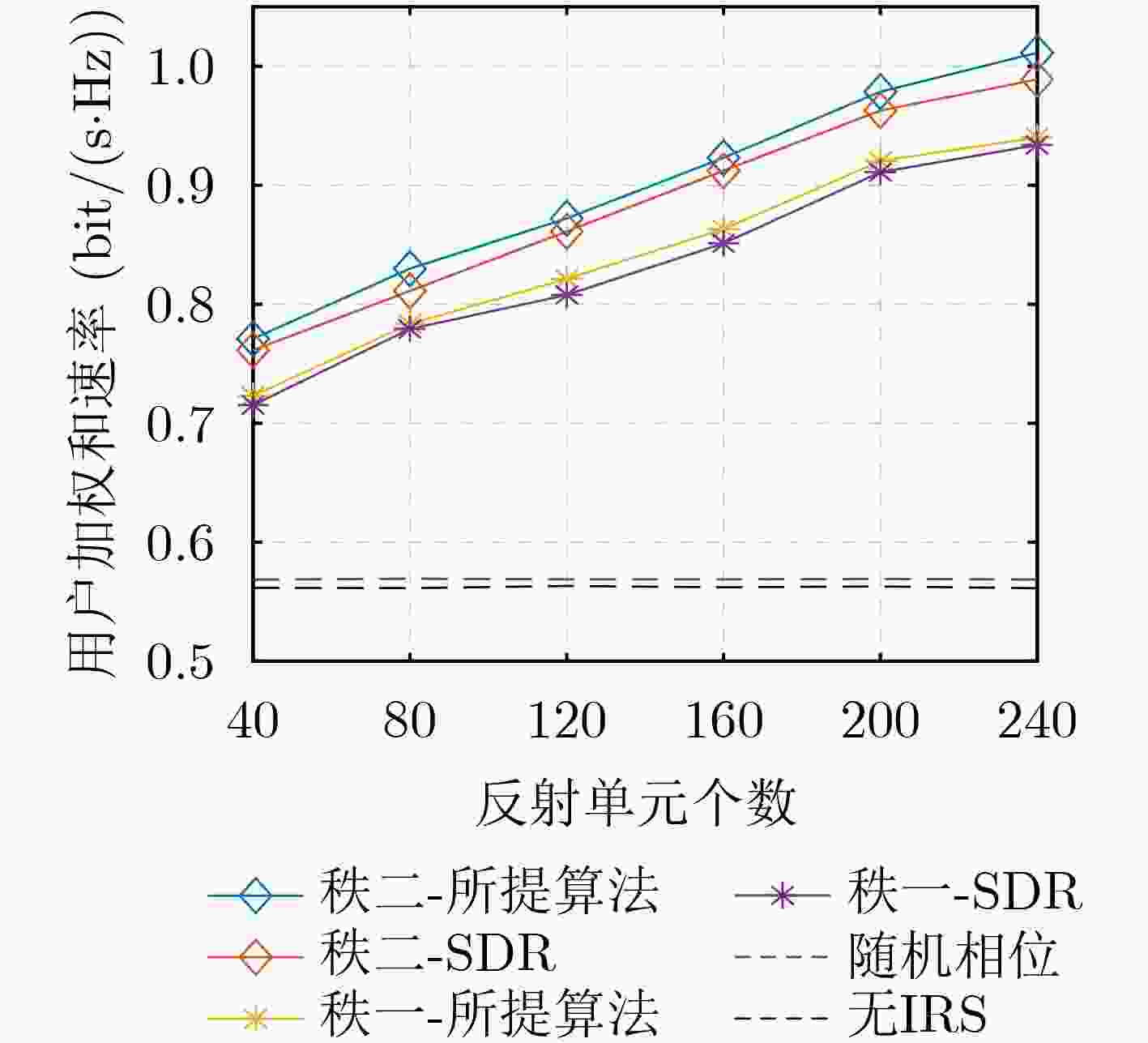
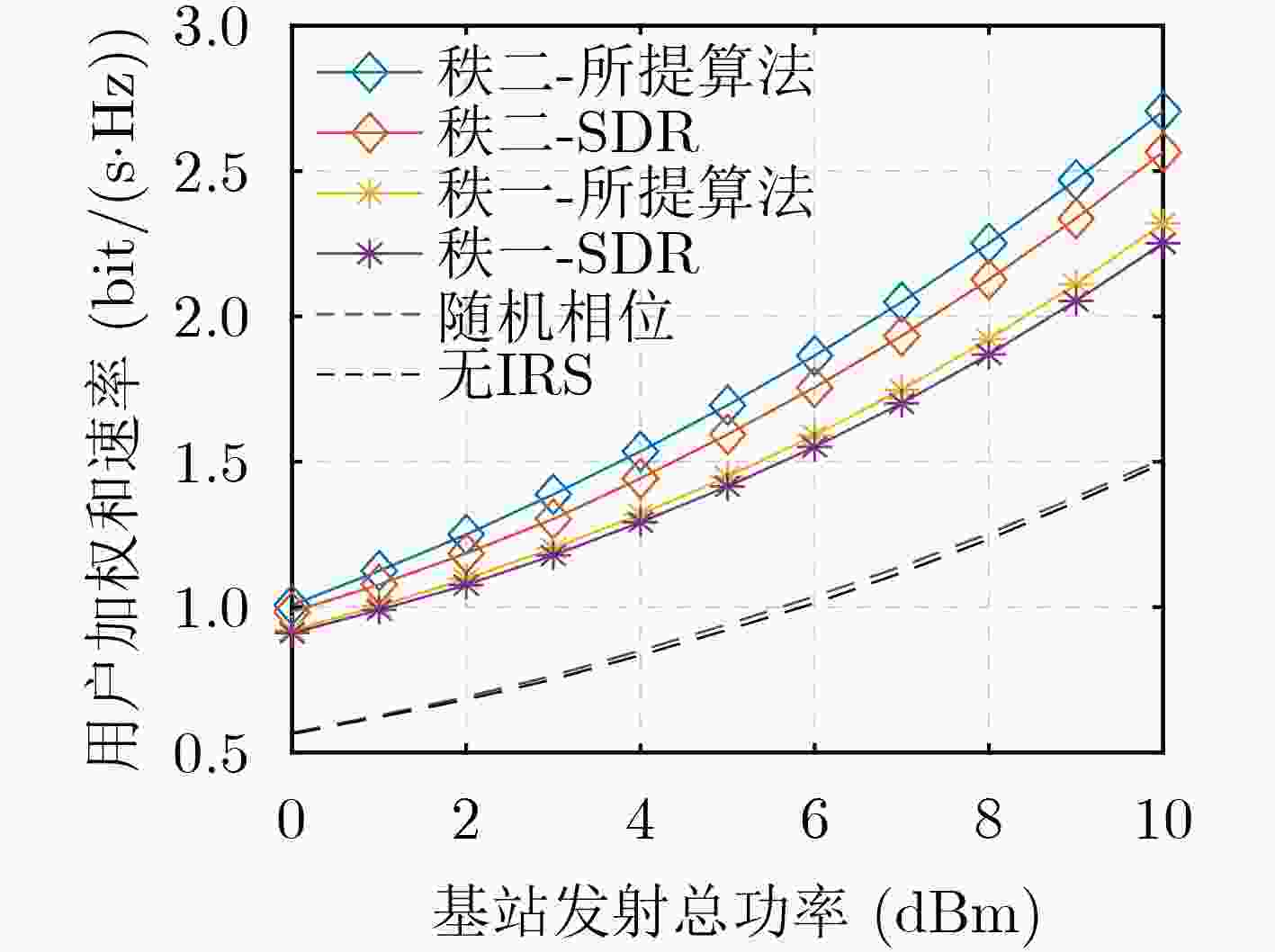
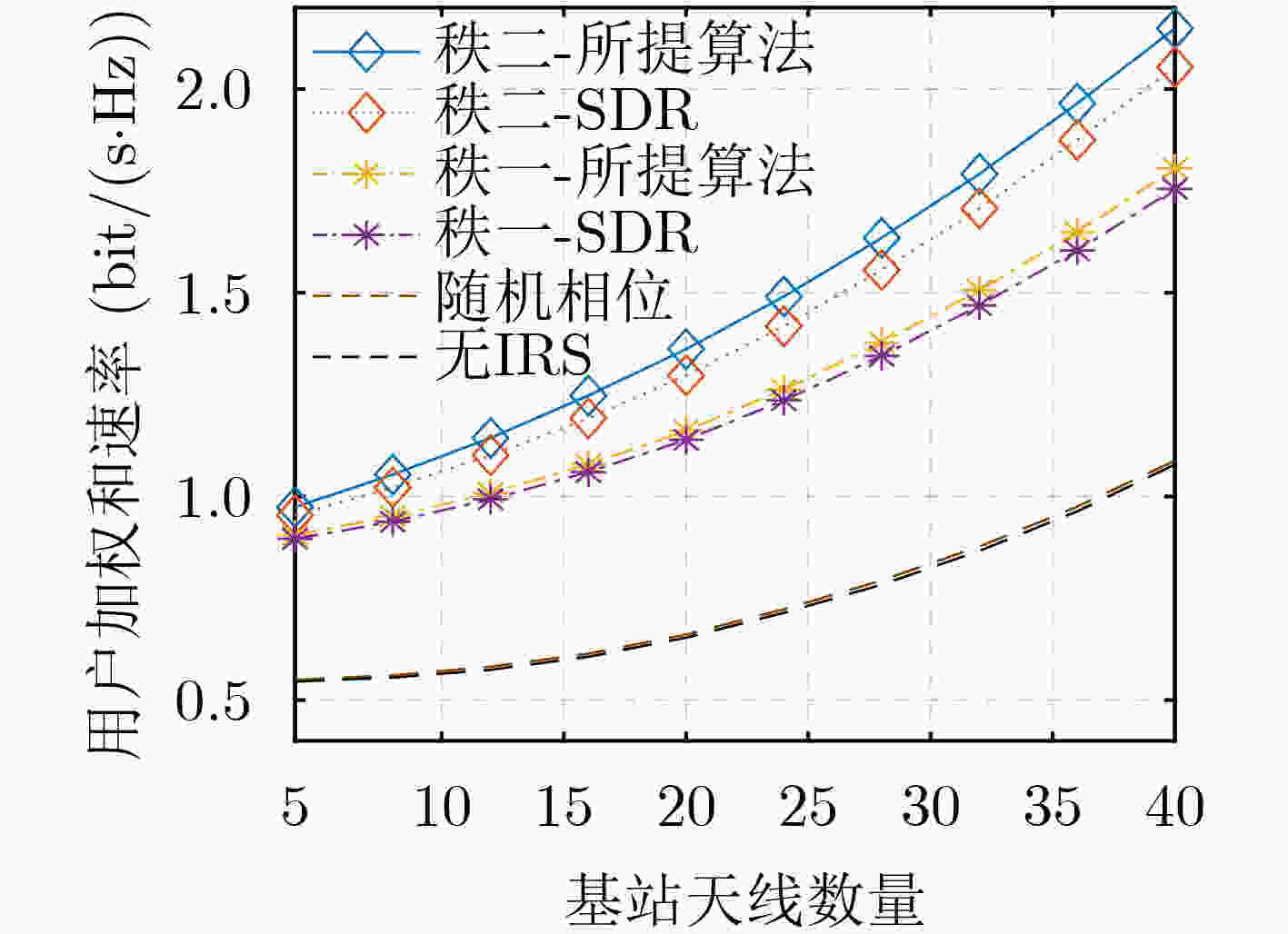
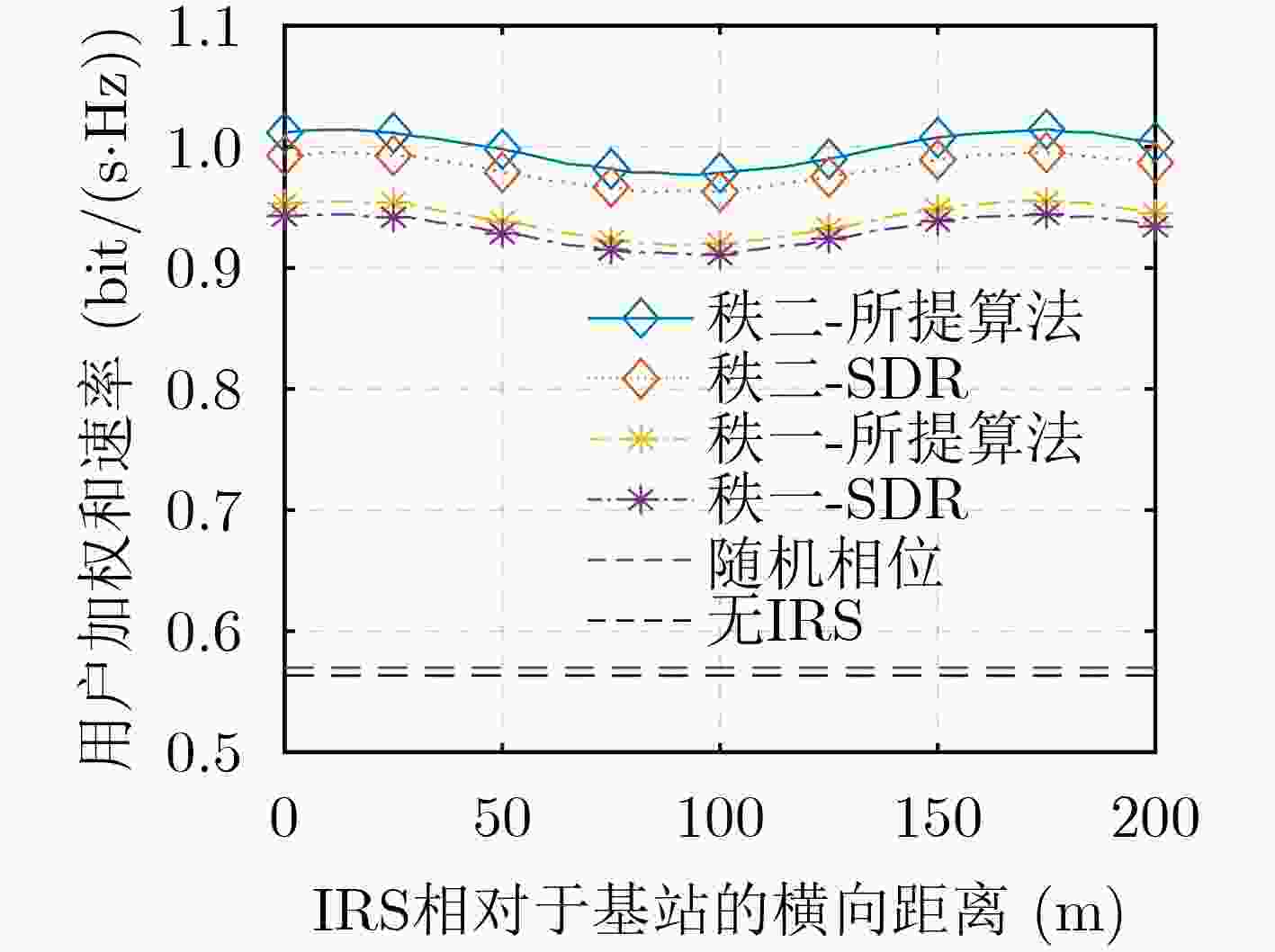
Objective To address the limitations of current optimization methods for Intelligent Reflecting Surface (IRS)-aided communication systems—such as high computational complexity, lack of closed-form solutions, and real-time transmission constraints—this study proposes an efficient joint active-passive beamforming algorithm to improve spectral efficiency and real-time performance. As the number of users increases, conventional rank-1 beamforming lacks sufficient design flexibility, highlighting the need for advanced approaches to avoid performance bottlenecks. This challenge is central to the practical deployment of large-scale Multiple-Input Single-Output (MISO) systems. Methods A hierarchical optimization framework is proposed to resolve the non-convex design problem in IRS-assisted MISO systems. A joint beamforming model is developed for downlink multi-user scenarios, incorporating Alamouti Space–Time Block Coding (STBC) and rank-2 beamforming to maximize the Weighted Sum Rate (WSR) under total power and IRS unit modulus constraints. The framework jointly optimizes the transmit and reflection matrices to improve spectral efficiency. To address the non-convexity of the formulation, an alternating optimization strategy is adopted. At the base station, a Weighted Minimum Mean-Square Error (WMMSE) algorithm is applied to refine the rank-2 beamforming design, and ensure efficient power allocation. For IRS phase shift optimization, an improved Riemannian Gradient Algorithm (RGA) is proposed. This algorithm integrates restart mechanisms and dynamic scaling vector transmission to accelerate convergence by avoiding local optima. Step size sensitivity is reduced using relaxed Wolfe conditions, which improves computational efficiency without loss of global optimality. Results and Discussions The improved Riemannian gradient optimization algorithm achieves faster convergence and markedly higher WSR performance, attributed to the incorporation of restart strategies and dynamic scaling vector transmission mechanisms, outperforming conventional algorithms ( Fig. 3 ). The proposed rank-2 beamforming scheme yields substantially better system performance than traditional rank-1 techniques (Fig. 3 ). Simulations further evaluate the effect of varying the number of IRS reflection elements. Across different configurations, the proposed algorithm consistently enhances WSR and outperforms benchmark algorithms (Fig. 4 ). In addition, it maintains robust performance under varying base station transmit power levels and antenna counts, with rank-2 beamforming preserving clear advantages over rank-1 designs (Fig. 5 ,Fig. 6 ). Finally, simulation results identify optimal IRS deployment positions. System performance peaks when the IRS is placed near the base station or users, whereas intermediate placement leads to performance degradation, highlighting the critical role of deployment strategy in practical applications (Fig. 7 ).Conclusions This study addresses the problem of spectral efficiency maximization in IRS-aided communication systems by proposing a joint rank-2 beamforming and alternating optimization framework. For transmit-side optimization, the WMMSE algorithm is applied to enable efficient power allocation in the rank-2 beamforming design. In parallel, an improved RGA is developed for optimizing the IRS phase shift matrix. This algorithm incorporates adaptive initial step selection based on relaxed Wolfe conditions and integrates restart strategies to avoid local optima. Simulation results confirm that the proposed framework achieves faster convergence and higher user sum rate performance compared to conventional algorithms. Moreover, rank-2 beamforming consistently provides superior system efficiency relative to traditional rank-1 methods across a range of scenarios. -
1 改进的黎曼共轭梯度搜索算法
输入:基站主动波束形成向量${{\boldsymbol{B}}}$,随机初始化${{\boldsymbol{\theta}} _0}$,重启阈值$\tau $,
求解精度${\varepsilon _1}$和最大迭代次数${I_{\mathrm{R}}}$;输出:IRS相移系数向量${{\boldsymbol{\theta}} }$; (1) 计算欧氏梯度${\nabla _{{{{\boldsymbol{\theta }}}_0}}}f$和黎曼梯度${\mathrm{gra}}{{\mathrm{d}}_{{{\boldsymbol{\theta}} _0}}}f$,根据式(12)确定初
始搜索方向${{\boldsymbol{\eta}} _0}$,迭代计数;(2) 循环 (3) 根据式(20)、式(21)选取搜索步长$ {\alpha _{t + 1}} $; (4) 根据式(15)的回缩操作在流形上确定${{{\boldsymbol{\theta}} }_{t + 1}}$:
$ {{{\boldsymbol{\theta}} }_{t + 1}} = {\mathcal{R}_{{{{\boldsymbol{\theta}} }_t}}}({\alpha _t}{{{\boldsymbol{\eta}} }_t}) $;(5) 根据式(13)计算$ {\beta _{t + 1}} $; (6) 根据式(14)计算传输函数$ \mathcal{T}_{{{{\boldsymbol{\theta}} }_t} \to {{{\boldsymbol{\theta}} }_{t + 1}}}^S $; (7) 根据式(19)计算搜索方向变化量$ {\bar \mu _t} $; (8) 根据式(18)计算下次迭代的搜索方向$ {{{\boldsymbol{\eta}} }_{t + 1}} $; (9) 更新$t = t + 1$; (10) 直到满足${\left\| {{\mathrm{gra}}{{\mathrm{d}}_{{{{\boldsymbol{\theta}} }_t}}}f} \right\|_2} \le {\varepsilon _1}$或$t = {I_{\mathrm{R}}}$。 2 互补松弛变量的二分搜索算法
输入:$ {\lambda _{\min }} = 0 $,$ {\lambda _{\max }} = \Re \left\{ {\displaystyle\sum\nolimits_{i = 1}^M {\displaystyle\sum\nolimits_{j = 1}^M {{{\boldsymbol{R}}}(i,j)} } } \right\} $,其中
$ {{\boldsymbol{R}} = }\displaystyle\sum\nolimits_{k = 1}^K {{s}_k^2{\zeta_k}{{{\boldsymbol{h}}}_k}{{\boldsymbol{h}}}_k^{\text{H}}} \in {\mathbb{C}^{M \times M}} $;输出:互补松弛变量$ \lambda $; (1) 由$ {\lambda _{\max }} $得到${{\boldsymbol{B}}}$,计算发射功率${P_{\mathrm{B}}} = \displaystyle\sum\nolimits_{k = 1}^K {{{\left\| {{{{\boldsymbol{B}}}_k}} \right\|}^2}} $; (2) 若${P_{\mathrm{B}}} = {P_{\mathrm{t}}}$,输出$ {\lambda _{\max }} $,并退出算法;若${P_{\mathrm{B}}} > {P_{\mathrm{t}}}$,则赋
值$ {\lambda _{\min }} = {\lambda _{\max }} $,$ {\lambda _{\max }} = 2{\lambda _{\max }} $,返回步骤(1);若${P_{\mathrm{B}}} < {P_{\mathrm{t}}}$
执行下一步;(3) 计算$\rho = \sqrt {{P_{\mathrm{t}}}/{P_{\mathrm{B}}}} $,令${{\boldsymbol{B}}} = \rho {{\boldsymbol{B}}}$,并计算此时系统${\mathrm{WSR}}$; (4) 令$ \lambda = ({\lambda _{\max }} + {\lambda _{\min }})/2 $,并计算$ {{\boldsymbol{R}}' = {\boldsymbol{R}}} + \lambda {{{\boldsymbol{I}}}_M} $,其中
$ {{{\boldsymbol{I}}}_M} $为单位矩阵;(5) 若$ {\mathrm{rank}}\left( {{{\boldsymbol{R}}'}} \right) < {{\boldsymbol{R}}} $,则令$ \lambda = ({\lambda _{\max }} + \lambda )/2 $,$ {\lambda _{\min }} = \lambda $;若
$ {\mathrm{rank}}\left( {{{\boldsymbol{R}}'}} \right) \ge {{\boldsymbol{R}}} $,则退出循环;(6) 由当前$ \lambda $,得到${{\boldsymbol{B}}}$, ${P_{\mathrm{B}}}$和$\rho $,令${{\boldsymbol{B}}} = \rho {{\boldsymbol{B}}}$并计算当前
${\mathrm{WSR}}$;(7) 当满足条件:${P_{\mathrm{B}}} \le {P_{\mathrm{t}}}$,$ \lambda = {\lambda _{\max }} $或${P_{\mathrm{B}}} > {P_{\mathrm{t}}}$,
$ \lambda = {\lambda _{\min }} $,则返回步骤(4),否则进行下一步;(8) 直到$ \lambda $, $ \left| {{\mathrm{WSR}}' - {\mathrm{WSR}}} \right| $和$ \left| {{P_{\mathrm{B}}} - {P_{\mathrm{t}}}} \right| $均小于阈值时,退出
算法;3 基于改进的黎曼共轭梯度搜索和WMMSE的交替优化算法
输入:信道信息${{\boldsymbol{H}}}$,设置截至阈值${\varepsilon _2}$和交替优化次数${I_{\mathrm{A}}}$; 输出:波束形成向量${{\boldsymbol{B}}}$、IRS相移系数向量${{\boldsymbol{\theta }}}$和${{\mathrm{WSR}}_1}$; (1) 初始化波束向量${{\boldsymbol{B}}}$和相移向量${{{\boldsymbol{\theta}} }_0}$,迭代计数$t = 0$; (2) 循环 (3) 根据式(24)和式(25)分别计算$ {{{\boldsymbol{s}}}_k} $和$ {\zeta _k} $; (4) 由算法2确定互补松弛变量$ \lambda $; (5) 根据式(26)计算${{\boldsymbol{B}}}$; (6) 由当前${{\boldsymbol{B}}}$和${{\boldsymbol{\theta}} }$更新信道信息${{\boldsymbol{H}}}$,并计算此时${{\mathrm{WSR}}_0}$; (7) 根据算法1求解相移向量${{\boldsymbol{\theta}} }$,并根据${{\boldsymbol{\theta }}}$更新${{\boldsymbol{H}}}$; (8) 由当前${{\boldsymbol{H}}}$, ${{\boldsymbol{B}}}$和${{\boldsymbol{\theta}} }$计算此时${{\mathrm{WSR}}_1}$; (9) 更新$t = t + 1$; (10) 直到满足${\left\| {{\mathrm{gra}}{{\mathrm{d}}_{{{\boldsymbol{{\theta }}}_t}}}f} \right\|_2} \le {\varepsilon _2}$或 $ t = {I_{\mathrm{A}}} $; 表 1 仿真参数设置
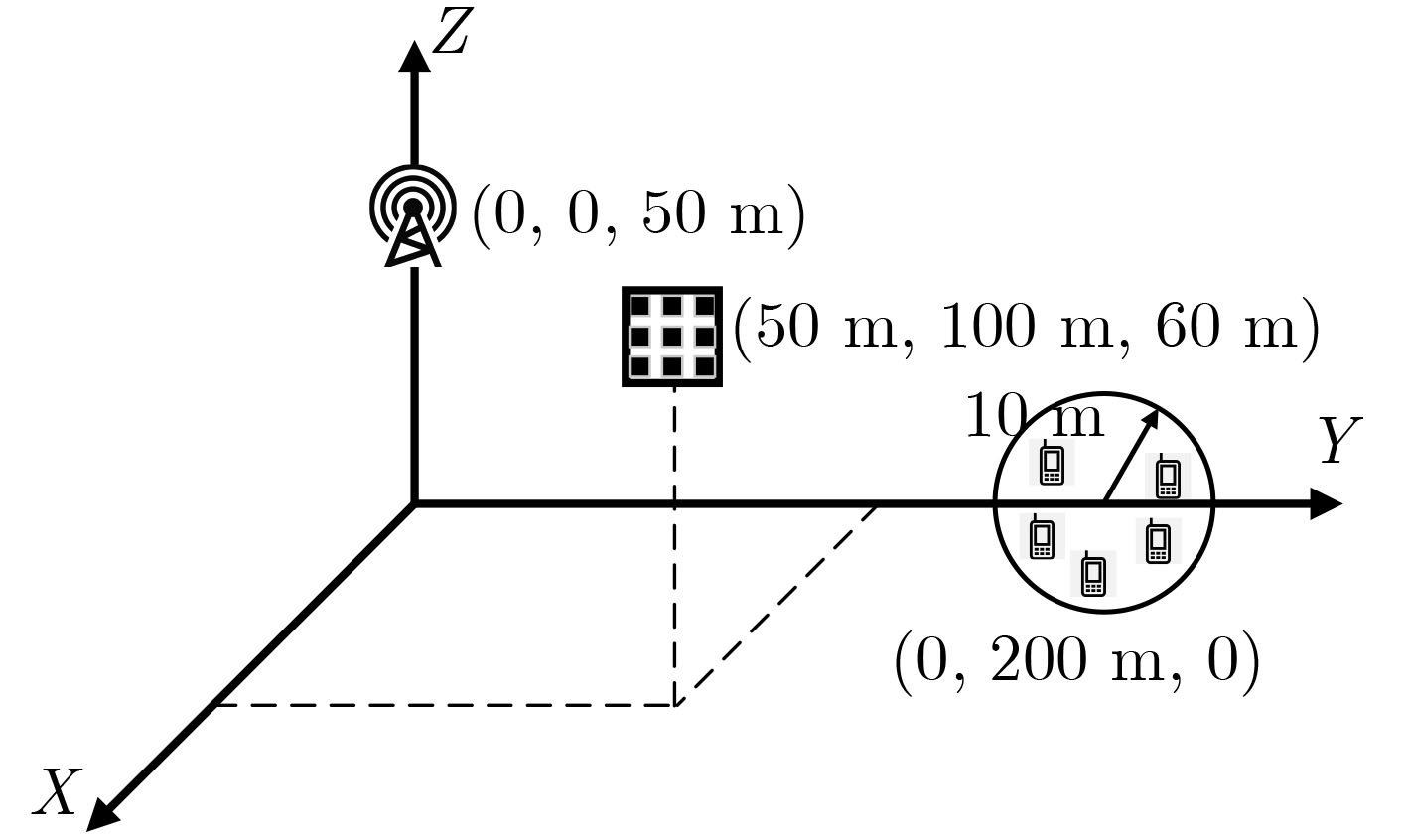
参数 参数值 参数 参数值 用户数 4 基站发射功率 0 dBm 基站天线个数 4 载波频率 4 GHz IRS反射单元个数 200 传输带宽 120 kHz IRS反射方位角$ v $ 45° 噪声功率谱密度 –170 dBm/Hz IRS反射俯仰角$ \varphi $ –45° 流形优化重启阈值 0.1 视距链路路径损耗(dB) 35.6 + 22.0 lgd ${{\boldsymbol{B}}}$, ${\theta }$和WSR截止阈值 0.0001 非视距链路路径损耗(dB) 32.6 + 36.7 lgd $ \lambda $截止阈值 0.001 视距链路莱斯因子$ \varepsilon $ 10 算法迭代次数${I_{\mathrm{A}}}$和${I_{\mathrm{R}}}$ 100 -
[1] PAN Cunhua, ZHOU Gui, ZHI Kangda, et al. An overview of signal processing techniques for RIS/IRS-aided wireless systems[J]. IEEE Journal of Selected Topics in Signal Processing, 2022, 16(5): 883–917. doi: 10.1109/JSTSP.2022.3195671. [2] WANG Xuehui, SHU Feng, SHI Weiping, et al. Beamforming design for IRS-aided decode-and-forward relay wireless network[J]. IEEE Transactions on Green Communications and Networking, 2022, 6(1): 198–207. doi: 10.1109/TGCN.2022.3145031. [3] 中国信息通信研究院IMT-2030(6G)推进组. 6G前沿关键技术研究报告[R]. 2022.China Academy of Information and Communications Technology IMT-2030(6G). Report of 6G frontier key technology research[R]. 2022. [4] ZHENG Beixiong, YOU Changsheng, MEI Weidong, et al. A survey on channel estimation and practical passive beamforming design for intelligent reflecting surface aided wireless communications[J]. IEEE Communications Surveys & Tutorials, 2022, 24(2): 1035–1071. doi: 10.1109/COMST.2022.3155305. [5] WANG Zhaorui, LIU Liang, ZHANG Shuowen, et al. Massive MIMO communication with intelligent reflecting surface[J]. IEEE Transactions on Wireless Communications, 2023, 22(4): 2566–2582. doi: 10.1109/TWC.2022.3212537. [6] ZHENG Beixiong and ZHANG Rui. Simultaneous transmit diversity and passive beamforming with large-scale intelligent reflecting surface[J]. IEEE Transactions on Wireless Communications, 2023, 22(2): 920–933. doi: 10.1109/TWC.2022.3199426. [7] 王沛兰. 智能反射面辅助毫米波大规模MIMO系统信号处理技术研究[D]. [博士论文], 电子科技大学, 2023. doi: 10.27005/d.cnki.gdzku.2023.000095.WANG Peilan. Research on signal processing techniques for intelligent reflecting surface-assisted millimeter-wave massive MIMO systems[D]. [Ph. D. dissertation], University of Electronic Science and Technology of China, 2023. doi: 10.27005/d.cnki.gdzku.2023.000095. [8] WU Qingqing and ZHANG Rui. Intelligent reflecting surface enhanced wireless network: Joint active and passive beamforming design[C]. IEEE Global Communications Conference, Abu Dhabi, United Arab Emirates, 2018: 1–6. doi: 10.1109/GLOCOM.2018.8647620. [9] WU Qingqing and ZHANG Rui. Intelligent reflecting surface enhanced wireless network via joint active and passive beamforming[J]. IEEE Transactions on Wireless Communications, 2019, 18(11): 5394–5409. doi: 10.1109/TWC.2019.2936025. [10] WU Qingqing and ZHANG Rui. Beamforming optimization for wireless network aided by intelligent reflecting surface with discrete phase shifts[J]. IEEE Transactions on Communications, 2020, 68(3): 1838–1851. doi: 10.1109/TCOMM.2019.2958916. [11] NING Boyu, CHEN Zhi, CHEN Wenjie, et al. Beamforming optimization for intelligent reflecting surface assisted MIMO: A sum-path-gain maximization approach[J]. IEEE Wireless Communications Letters, 2020, 9(7): 1105–1109. doi: 10.1109/LWC.2020.2982140. [12] ZHANG Shuowen and ZHANG Rui. Capacity characterization for intelligent reflecting surface aided MIMO communication[J]. IEEE Journal on Selected Areas in Communications, 2020, 38(8): 1823–1838. doi: 10.1109/JSAC.2020.3000814. [13] XU Xiaorong, REN Hengxu, BAO Jianrong, et al. An enhanced interference alignment strategy with MIL criterion and RCG algorithm for IRS-assisted multiuser MIMO[J]. IEEE Communications Letters, 2023, 27(3): 1001–1005. doi: 10.1109/LCOMM.2023.3237540. [14] ZHAO Mingmin, WU Qingqing, ZHAO Minjian, et al. Intelligent reflecting surface enhanced wireless networks: Two-timescale beamforming optimization[J]. IEEE Transactions on Wireless Communications, 2021, 20(1): 2–17. doi: 10.1109/TWC.2020.3022297. [15] JUNG M, SAAD W, DEBBAH M, et al. On the optimality of reconfigurable intelligent surfaces (RISs): Passive beamforming, modulation, and resource allocation[J]. IEEE Transactions on Wireless Communications, 2021, 20(7): 4347–4363. doi: 10.1109/TWC.2021.3058366. [16] GUO Huayan, LIANG Yingchang, CHEN Jie, et al. Weighted sum-rate maximization for reconfigurable intelligent surface aided wireless networks[J]. IEEE Transactions on Wireless Communications, 2020, 19(5): 3064–3076. doi: 10.1109/TWC.2020.2970061. [17] ZHU Fenghao, WANG Xinquan, HUANG Chongwen, et al. Robust beamforming for RIS-aided communications: Gradient-based manifold meta learning[J]. IEEE Transactions on Wireless Communications, 2024, 23(11): 15945–15956. doi: 10.1109/TWC.2024.3435023. [18] YE Junjie, HUANG Lei, CHEN Zhen, et al. Unsupervised learning for joint beamforming design in RIS-aided ISAC systems[J]. IEEE Wireless Communications Letters, 2024, 13(8): 2100–2104. doi: 10.1109/LWC.2024.3402235. [19] SIDIROPOULOS N D, DAVIDSON T N, and LUO Zhiquan. Transmit beamforming for physical-layer multicasting[J]. IEEE Transactions on Signal Processing, 2006, 54(6): 2239–2251. doi: 10.1109/TSP.2006.872578. [20] ZHOU Gui, PAN Cunhua, REN Hong, et al. Intelligent reflecting surface aided multigroup multicast MISO communication systems[J]. IEEE Transactions on Signal Processing, 2020, 68: 3236–3251. doi: 10.1109/TSP.2020.2990098. [21] HAN Huimei, ZHAO Jun, NIYATO D, et al. Intelligent reflecting surface aided network: Power control for physical-layer broadcasting[C]. IEEE International Conference on Communications, Dublin, Ireland, 2020: 1–7. doi: 10.1109/ICC40277.2020.9148827. [22] LI Ding, AN Qiaochu, SHI Yuanming, et al. Multigroup multicast transmission via intelligent reflecting surface[C]. 92nd IEEE Vehicular Technology Conference, Victoria, Canada, 2020: 1–6. doi: 10.1109/VTC2020-Fall49728.2020.9348503. [23] SHU Feng and WANG Jiangzhou. Secure multigroup multicast communication systems via intelligent reflecting surface[M]. SHU Feng and WANG Jiangzhou. Intelligent Reflecting Surface-Aided Physical-Layer Security. Cham: Springer, 2023: 171–190. doi: 10.1007/978-3-031-41812-9_8. [24] WANG Yajun, FANG Lili, CAI Shanjie, et al. Low-complexity algorithm for maximizing the weighted sum-rate of intelligent reflecting surface-assisted wireless networks[J]. IEEE Internet of Things Journal, 2024, 11(6): 10490–10499. doi: 10.1109/JIOT.2023.3326563. [25] WANG Kewei, QI Nan, GUAN Xin, et al. Transmit/passive beamforming design for multi-IRS assisted cell-free MIMO networks[J]. IEEE Systems Journal, 2023, 17(4): 6282–6291. doi: 10.1109/JSYST.2023.3307556. [26] SHI Mingli, LI Xiaohui, FAN Tao, et al. A low complexity algorithm for achievable rate maximization in mmWave systems aided by IRS[J]. IEEE Wireless Communications Letters, 2022, 11(10): 2215–2219. doi: 10.1109/LWC.2022.3197418. [27] AHMADINEJAD A and TALEBI S. Beamforming design via machine learning in intelligent reflecting surface-aided wireless communication[J]. Physical Communication, 2025, 68: 102586. doi: 10.1016/j.phycom.2024.102586. [28] XU Sai, DU Yanan, LIU Jiajia, et al. Weighted sum rate maximization in IRS-BackCom enabled downlink multi-cell MISO network[J]. IEEE Communications Letters, 2022, 26(3): 642–646. doi: 10.1109/LCOMM.2021.3140207. -





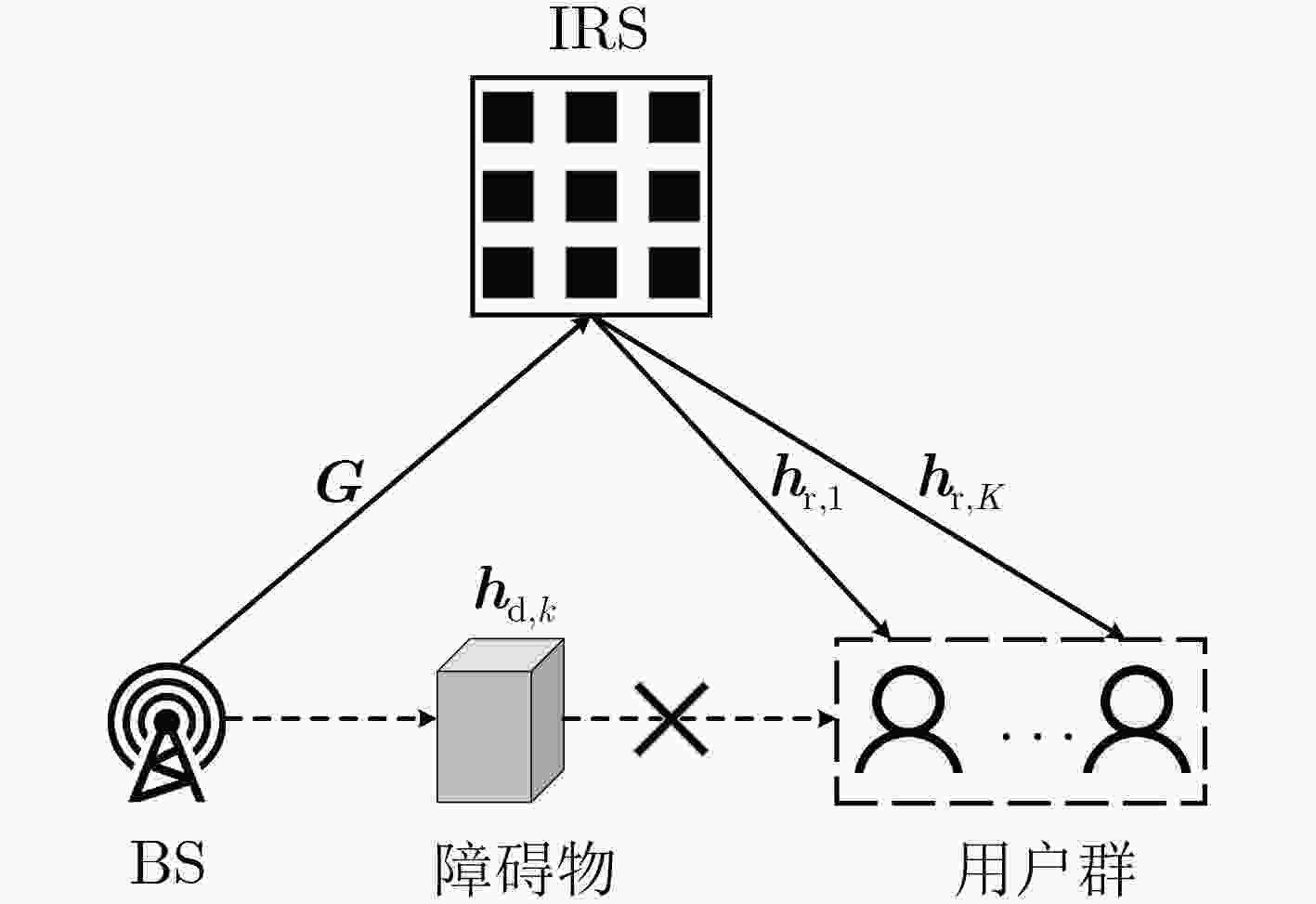
 下载:
下载:


 下载:
下载:
