Research on Fast Iterative TDOA Localization Method Based on Spatial Grid Gradients
-
摘要: 在无人机应用、空中旅游、应急救援等新兴业务驱动下,到达时差(TDOA)定位技术不断发展,逐渐成为低空智能网联的关键技术之一。但现有解析类迭代定位算法计算量过高,难以满足低延迟实时定位需求。因此,该文提出基于空间栅格梯度的TDOA快速迭代定位方法。在定位前,首先进行预处理,包括构建空间栅格、根据已建立的空间栅格计算栅格间的TDOA梯度,并基于这些梯度构建栅格迭代矩阵。在定位过程中,根据定位初值调用迭代矩阵,计算并补偿定位初值相对于目标位置的偏差,从而避免传统迭代定位的大量计算,显著降低计算时间。该文借鉴空间栅格化思路,进一步挖掘利用了栅格间的内在梯度关系,从而将栅格化框架融入到迭代补偿模型,克服了栅格宽度对经典栅格化算法的性能制约,提升了迭代定位时效性。依据仿真和实测数据可知,所提算法在保证定位精度的同时,相比传统迭代定位算法节省了76%以上的计算时间,满足低空智能网络的实时定位需求。Abstract:
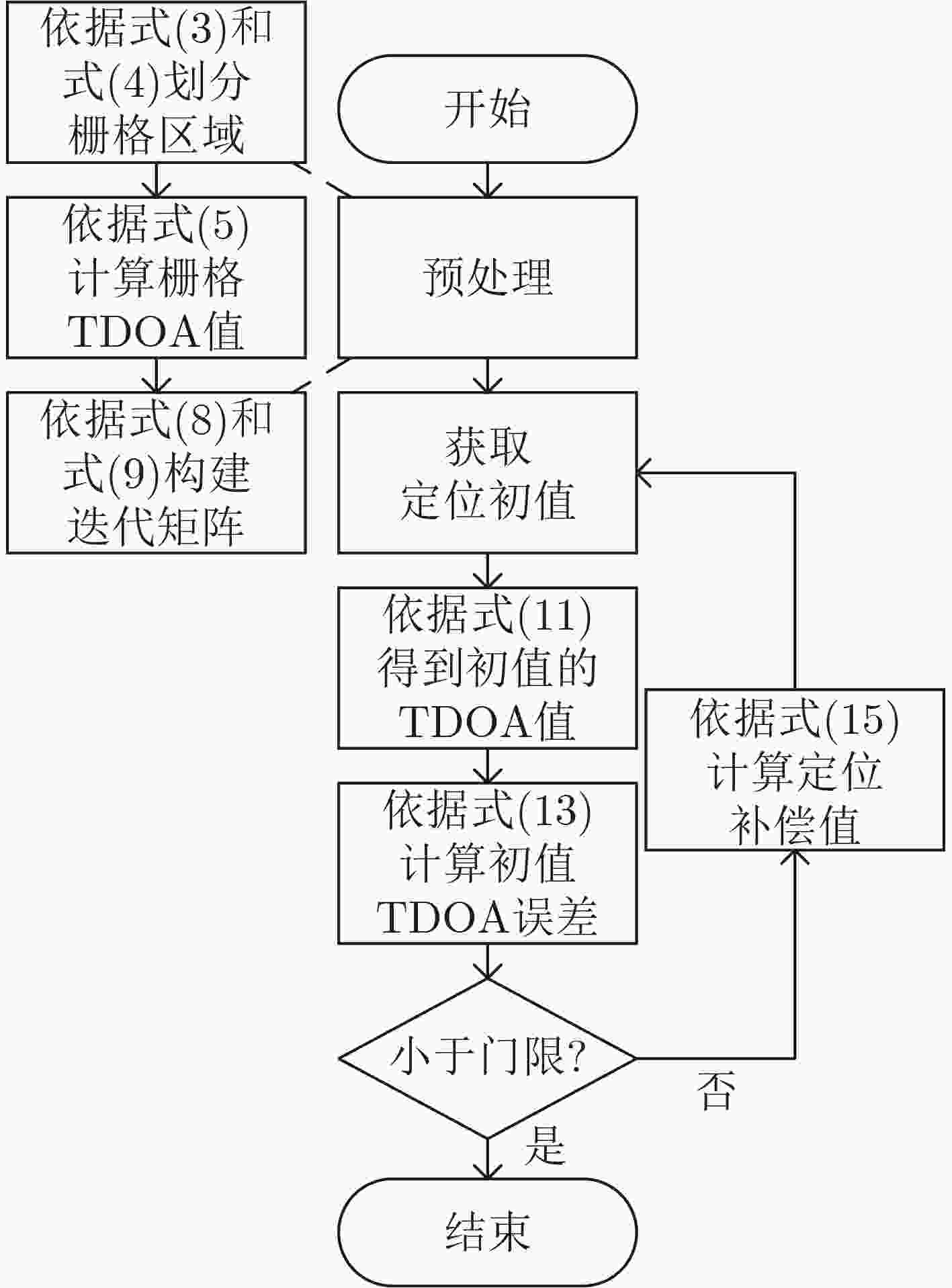
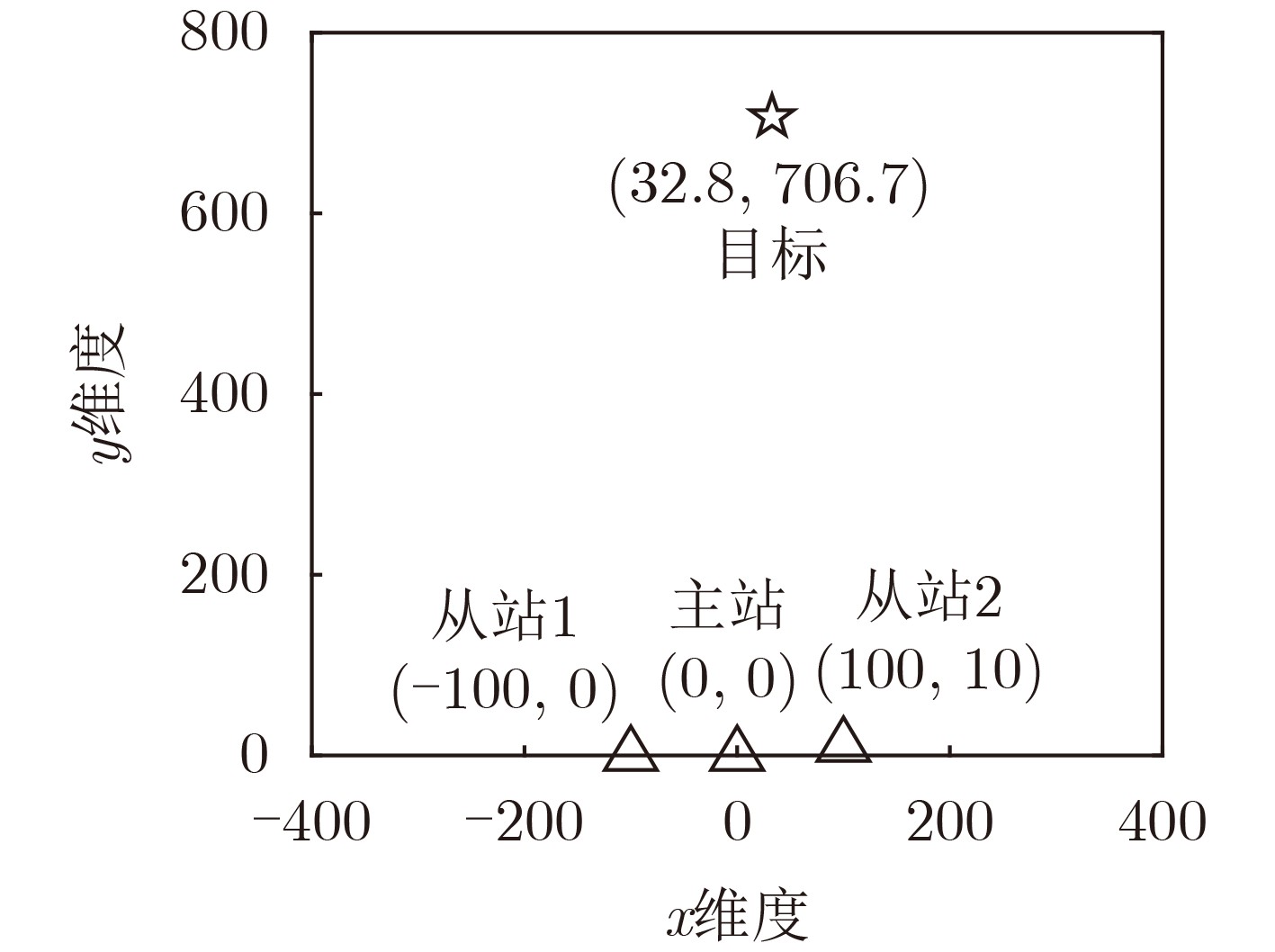
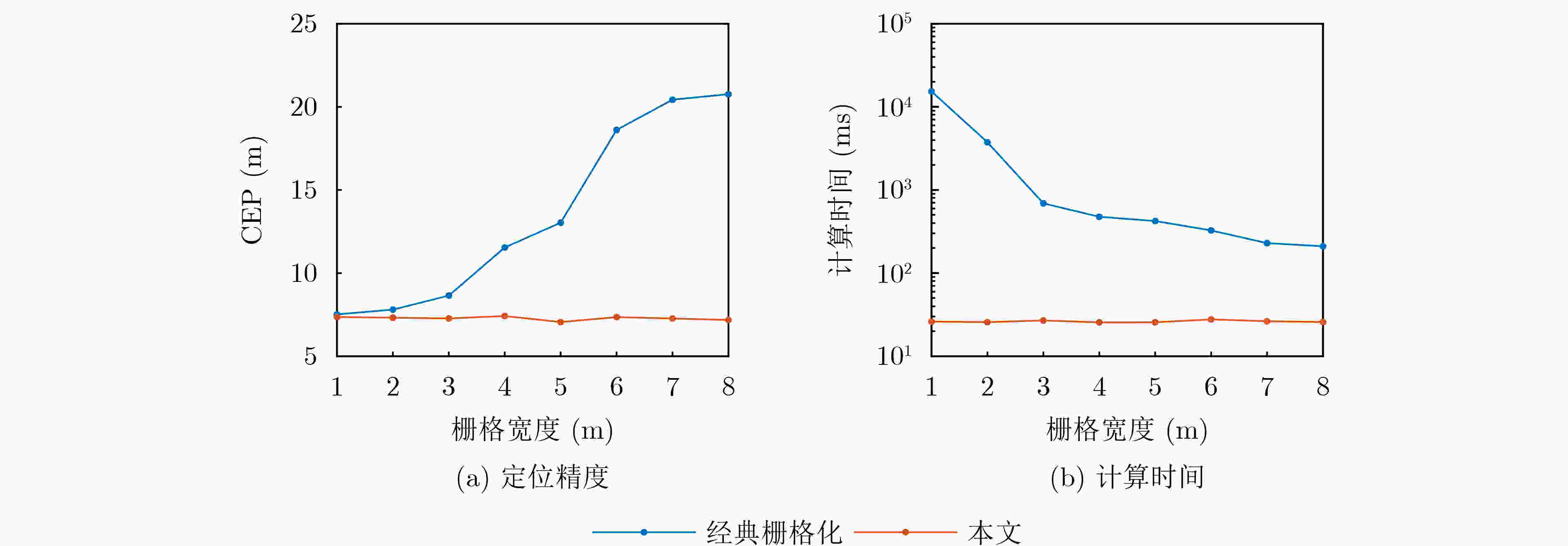
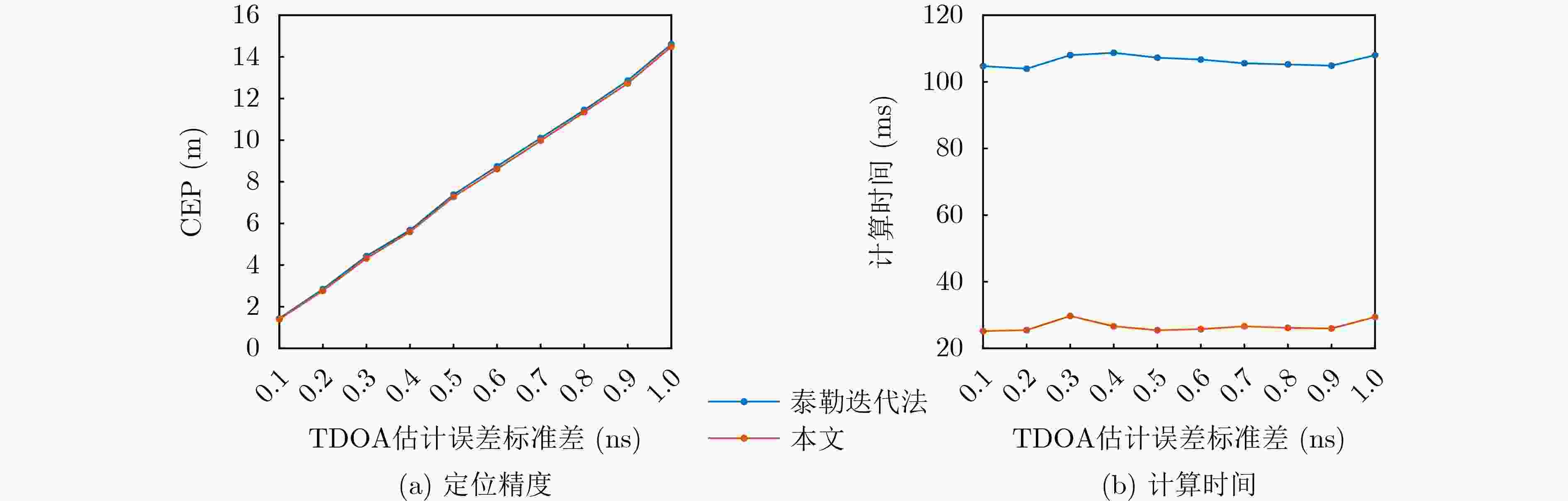
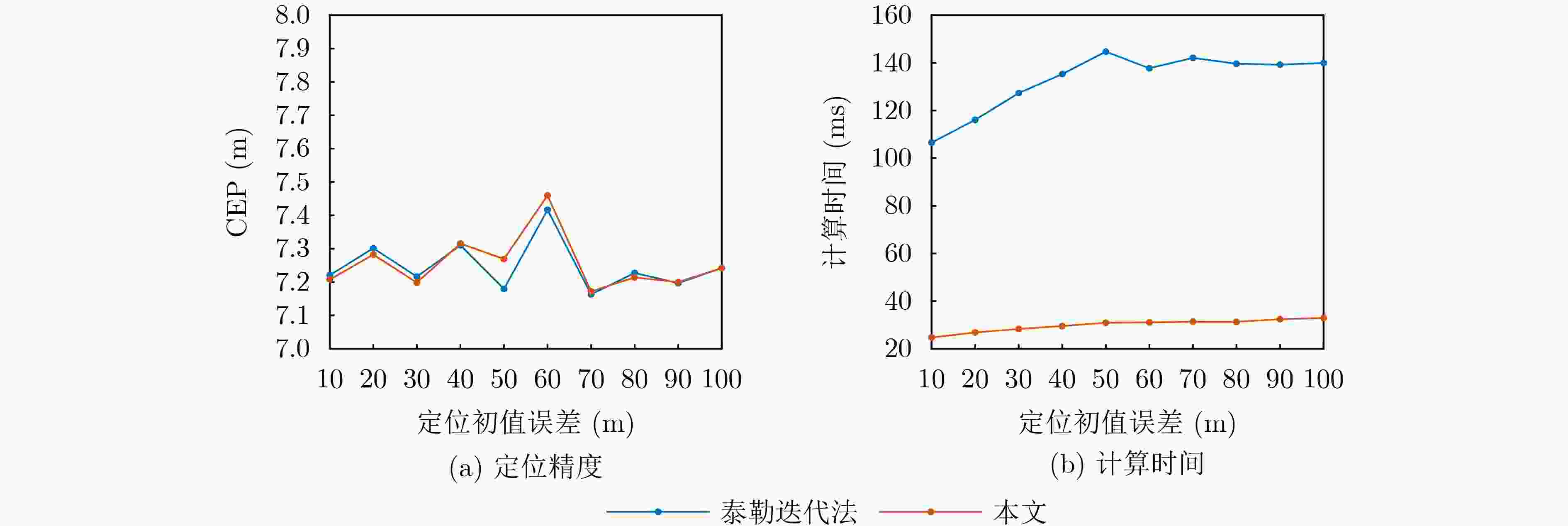
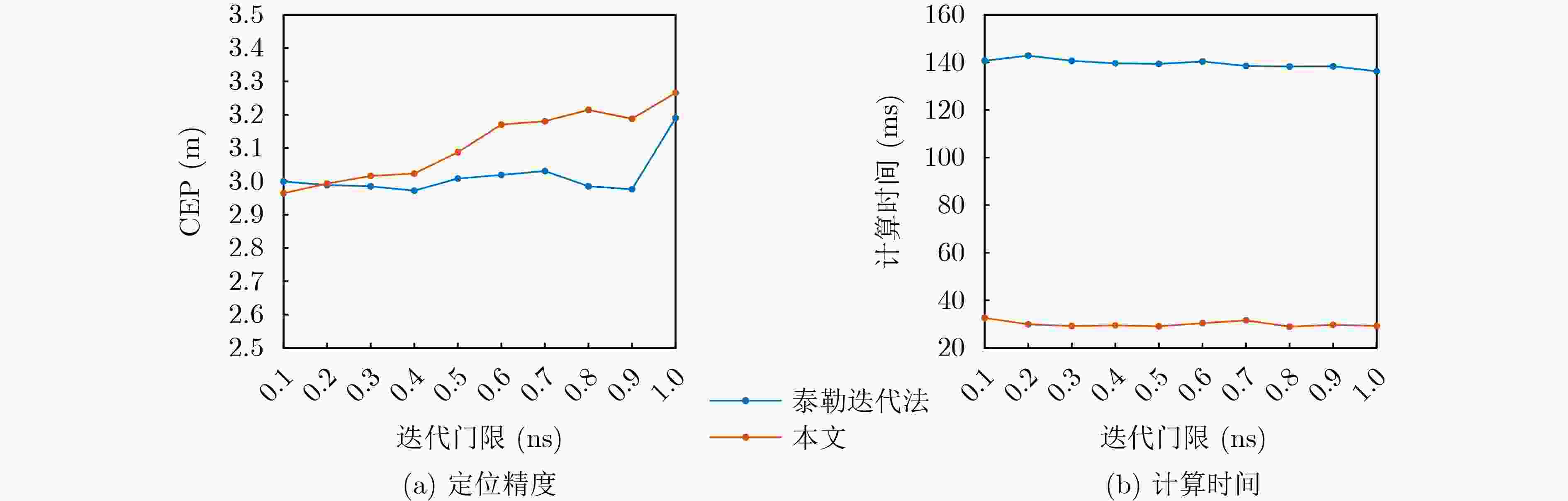
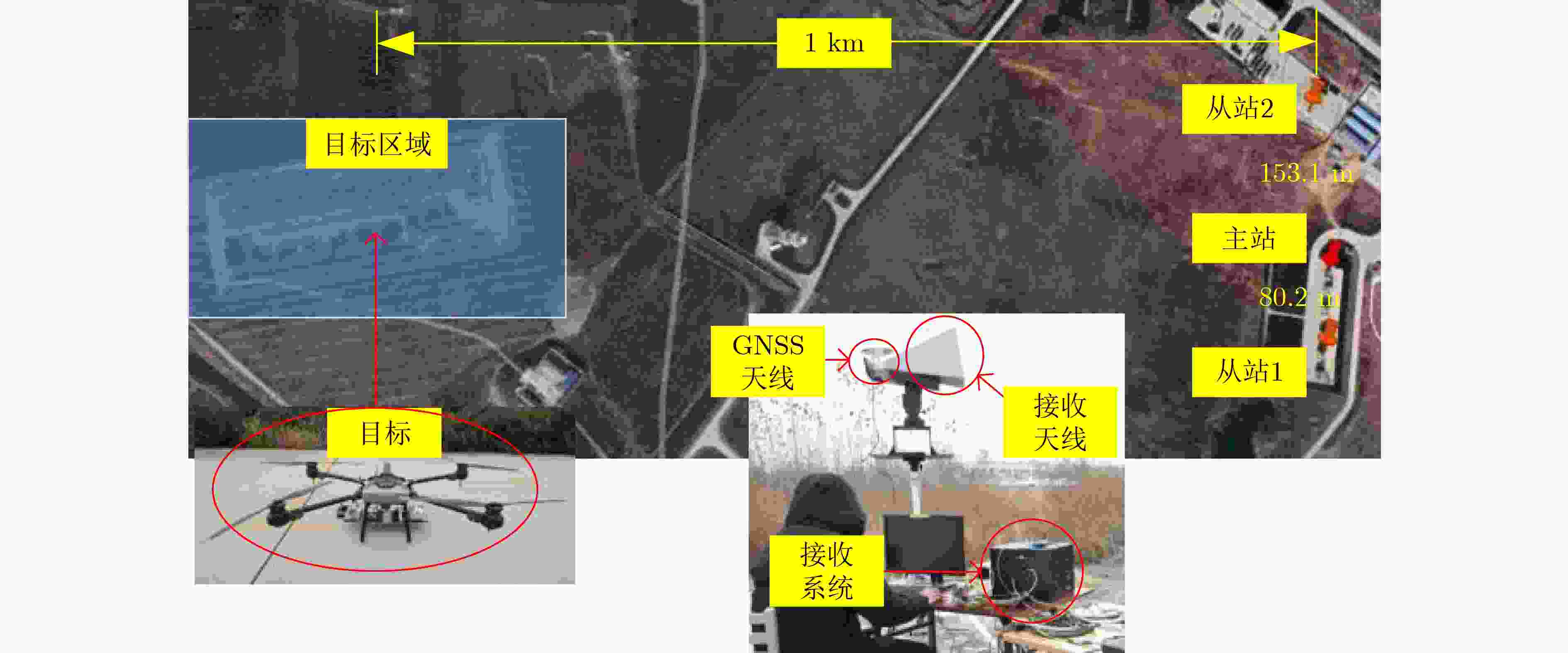
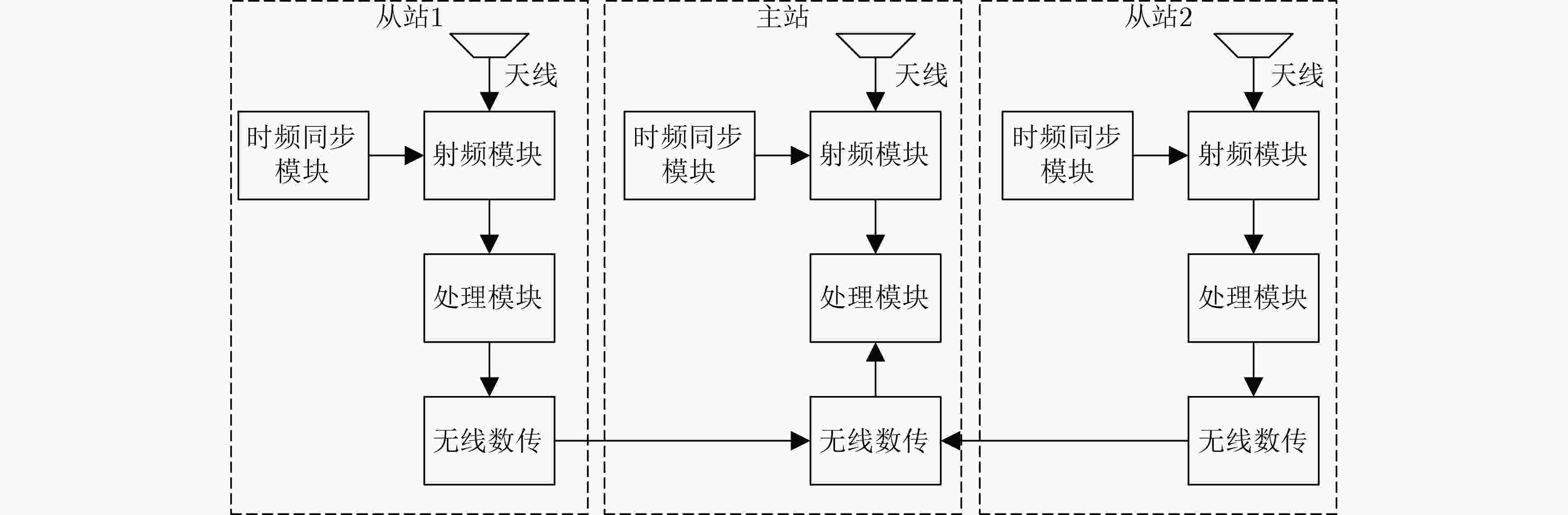
Objective In various application scenarios such as Unmanned Aerial Vehicle (UAV) formation, emergency rescue, and low-altitude intelligent networks, passive localization technologies that offer low latency and high precision are of significant practical value. The Time Difference of Arrival (TDOA) localization method is widely adopted for wireless signal source localization due to its ability to operate without requiring the target to actively transmit a signal and its strong adaptability to different environments. Among the various methods used to enhance the accuracy of TDOA localization, the Taylor Iterative Method has gained significant popularity. However, this method requires the calculation of a Taylor expansion for each iteration, resulting in a high computational load. This computational burden often leads to issues such as poor real-time performance and degraded accuracy, which hinder the application of TDOA localization technology in low-latency engineering contexts. To overcome these challenges, this paper proposes a novel TDOA rapid iterative localization method based on spatial grid gradients. The proposed method can significantly reduce computational time while maintaining high levels of localization accuracy. Methods The proposed approach is based on the concept of spatial gridization, incorporating insights derived from the inherent gradient relationships between neighboring grids. These relationships are leveraged to integrate the grid framework into an iterative compensation model. This integration addresses the performance limitations associated with grid width in traditional gridization algorithms, thereby enhancing the efficiency of the iterative localization process. The overall computational process is divided into two distinct stages: preprocessing and iterative localization. The preprocessing stage occurs during the system’s initialization phase and includes constructing the spatial grid, calculating the TDOA gradients between grid points, and establishing the grid-based iterative matrix. Once this preprocessing is complete, the results are stored and readily accessible for future localization processes. During the localization stage, the precomputed iteration matrix is directly invoked and the initial value for the target’s position. The method then calculates and compensates for the deviation between the initial value and the actual target position. By employing a grid-based approach, the significant computational workload typically encountered during iterative localization is shifted to the preprocessing phase. This leads to a marked reduction in localization time, significantly improving computational efficiency. Results and Discussions To validate the effectiveness and performance of the proposed algorithm, simulations and field experiments are conducted. The results are compared with those of the classic spatial gridization algorithm and the Taylor Iterative Method. It is observed that the classic spatial gridization algorithm experiences a significant loss in localization accuracy as the grid width increases, accompanied by a dramatic increase in computation time. In contrast, the proposed algorithm remains unaffected by grid width and outperforms the traditional spatial gridization method in both localization accuracy and computation time ( Fig. 3 ). A deeper comparison of the proposed algorithm with the Taylor Iterative Method is made by analyzing the effects of TDOA estimation errors, initial value errors, and iteration thresholds on the performance of both algorithms. Specifically, under varying TDOA estimation errors, the proposed algorithm reduces the average computation time by 76% compared to the Taylor Iterative Method, while maintaining similar localization accuracy (Fig. 4 ). Under varying initial value errors, the proposed algorithm reduces average computation time by 78%, with comparable localization accuracy (Fig. 5 ). As the iteration threshold increases, both algorithms experience a slight reduction in localization accuracy; however, their overall performance remains similar. In this scenario, the proposed algorithm still reduces computation time by approximately 76% when compared to the Taylor Iterative Method (Fig. 6 ). To further verify the applicability of the proposed algorithm in real-world scenarios, field experiments are also conducted. The field test results confirm the validity of the proposed method, demonstrating a 78% reduction in computation time compared to the Taylor Iterative Method, while maintaining comparable localization accuracy (Table 2 ).Conclusions The proposed TDOA fast iterative localization method, based on spatial grid gradients, effectively reduces computational complexity while maintaining localization accuracy. This method is well-suited for high real-time passive localization applications. It significantly enhances both the efficiency and practicality of TDOA localization systems. Future work will focus on expanding the applicability of this algorithm by integrating it with other localization techniques, such as Time of Arrival (TOA), Angle of Arrival (AOA), and Frequency Difference of Arrival (FDOA). This integration is expected to facilitate the development of low-altitude economic activities and contribute to advancing the capabilities of localization technologies. -
表 1 无人机辐射源信号参数
参数 数值 功率 30 dBm 载波频率 3.4 GHz 带宽 80 MHz 表 2 两种算法实测性能对比表
指标 方法 第1组 第2组 第3组 第4组 第5组 CEP(m) 泰勒迭代法 4.4 1.0 2.4 2.3 8.4 本文算法 3.4 1.4 2.5 2.4 7.1 计算时间(ms) 泰勒迭代法 11.8 12.4 12.0 11.8 12.1 本文算法 2.6 2.7 2.6 2.7 2.7 -
[1] LI Xujie, XU Yuan, TANG Jin, et al. A trusted multi-task distribution mechanism for Internet of vehicles based on smart contract[J]. China Communications, 2023, 20(4): 212–226. doi: 10.23919/JCC.fa.2022-0622.202304. [2] WANG Xue, WANG Shubo, GAO Xin, et al. AMTOS: An ADMM-based multilayer computation offloading and resource allocation optimization scheme in IoV-MEC system[J]. IEEE Internet of Things Journal, 2024, 11(19): 30953–30964. doi: 10.1109/JIOT.2024.3416171. [3] XU Shiwu, WEI Fen, and WU Yi. A novel fingerprint database regeneration method for accurate visible light positioning[J]. IEEE Transactions on Instrumentation and Measurement, 2024, 73: 2512613. doi: 10.1109/TIM.2024.3378255. [4] ZHAO Haitao, ZHAO Chunxi, ZHANG Tianyu, et al. Fishing net optimization: A learning scheme of optimizing multi-lateration stations in air-ground vehicle networks[J]. IEEE Signal Processing Letters, 2024, 31: 2965–2969. doi: 10.1109/LSP.2024.3479923. [5] FENG Simeng, ZHAO Yidi, KAI Liu, et al. Fine-grained particle swarm optimization for UAV trajectory design in FSO relay communication[C]. 2024 IEEE/CIC International Conference on Communications in China (ICCC), Hangzhou, China, 2024: 2029–2034. doi: 10.1109/ICCC62479.2024.10681835. [6] 邱佩雯, 钟奇, 俞越. 基于TDOA技术的无人机监测定位方法研究[J]. 中国无线电, 2024(3): 63–64,71.QIU Peiwen, ZHONG Qi, and YU Yue. Research on UAV monitoring and direction finding method based on TDOA[J]. China Radio, 2024(3): 63–64,71. [7] 罗智杰, 李首庆, 姚尧. 无人机典型定位算法研究[J]. 无线互联科技, 2023, 20(24): 141–144. doi: 10.3969/j.issn.1672-6944.2023.24.038.LUO Zhijie, LI Shouqing, and YAO Yao. Research on typical positioning algorithm of unmanned aerial vehicles[J]. Wireless Internet Science and Technology, 2023, 20(24): 141–144. doi: 10.3969/j.issn.1672-6944.2023.24.038. [8] 周明复, 叶方全, 卓智海. 无线电反制技术及其在无人机探测与反制领域的应用[J]. 警察技术, 2019(3): 21–23. doi: 10.3969/j.issn.1009-9875.2019.03.005.ZHOU Mingfu, YE Fangquan, and ZHUO Zhihai. Radio counter technology and its application in UAV detection and response[J]. Police Technology, 2019(3): 21–23. doi: 10.3969/j.issn.1009-9875.2019.03.005. [9] ZOU Yanbin and FAN Jingna. Source localization using TDOA measurements from underwater acoustic sensor networks[J]. IEEE Sensors Letters, 2023, 7(6): 6002604. doi: 10.1109/LSENS.2023.3274200. [10] 秦兆涛, 王俊, 魏少明, 等. 基于目标高度先验信息的多站时差无源定位方法[J]. 电子与信息学报, 2018, 40(9): 2219–2226. doi: 10.11999/JEIT171231.QIN Zhaotao, WANG Jun, WEI Shaoming, et al. Passive localization using TDOA measurements from multiple sensors based on priori knowledge of target altitude[J]. Journal of Electronics & Information Technology, 2018, 40(9): 2219–2226. doi: 10.11999/JEIT171231. [11] LI Jinzhou, LV Shouye, JIN Ying, et al. Geolocation and tracking by TDOA measurements based on space–air–ground integrated network[J]. Remote Sensing, 2023, 15(1): 44. doi: 10.3390/rs15010044. [12] FOY W H. Position-location solutions by taylor-series estimation[J]. IEEE Transactions on Aerospace and Electronic Systems, 1976, AES-12(2): 187–194. doi: 10.1109/TAES.1976.308294. [13] CHEN Jinming, LI Yu, YANG Xiaochao, et al. A two-stage aerial target localization method using time-difference-of-arrival measurements with the minimum number of radars[J]. Remote Sensing, 2023, 15(11): 2829. doi: 10.3390/rs15112829. [14] DOGANCAY K and HMAM H. 3D TDOA emitter localization using conic approximation[J]. Sensors, 2023, 23(14): 6254. doi: 10.3390/s23146254. [15] JIN Tian, LI Fangchi, QIN Honglei, et al. Differential time of arrival based opportunistic positioning for asynchronous cellular signals: Model, algorithms and experiments[J]. IEEE Transactions on Vehicular Technology, 2023, 72(10): 12983–12999. doi: 10.1109/TVT.2023.3274210. [16] 李帅辰, 武建锋. 基于Chan-Taylor和优化BP神经网络的5G室内定位算法[J]. 中国惯性技术学报, 2023, 31(8): 806–813,822. doi: 10.13695/j.cnki.12-1222/o3.2023.08.009.LI Shuaichen and WU Jianfeng. 5G indoor location algorithm based on Chan-Taylor and optimized BP neural network[J]. Journal of Chinese Inertial Technology, 2023, 31(8): 806–813,822. doi: 10.13695/j.cnki.12-1222/o3.2023.08.009. [17] 张岳, 蒲红平, 陈伟. 基于多策略蜜獾算法的TDOA定位[J]. 无线互联科技, 2024, 21(5): 1–6,23. doi: 10.3969/j.issn.1672-6944.2024.05.002.ZHANG Yue, PU Hongping, and CHEN Wei. TDOA localization based on multi-strategy honey badger algorithm[J]. Wireless Internet Science and Technology, 2024, 21(5): 1–6,23. doi: 10.3969/j.issn.1672-6944.2024.05.002. [18] 叶智慧, 吴红梅, 王佩, 等. 基于量子海鸥算法的运载火箭回收舱段时差定位方法[J]. 上海航天(中英文), 2023, 40(6): 121–135. doi: 10.19328/j.cnki.2096-8655.2023.06.016.YE Zhihui, WU Hongmei, WANG Pei, et al. TDOA positioning method of launch vehicle recovery cabin based on quantum seagull optimization algorithm[J]. Aerospace Shanghai (Chinese & English), 2023, 40(6): 121–135. doi: 10.19328/j.cnki.2096-8655.2023.06.016. [19] 李谦. 基于TDOA的无源定位技术及其节点优选方法研究[D]. [博士论文], 西安电子科技大学, 2021. doi: 10.27389/d.cnki.gxadu.2021.000055.LI Qian. Research on passive location technology and node selection method based on TDOA[D]. [Ph. D. dissertation], Xidian University, 2021. doi: 10.27389/d.cnki.gxadu.2021.000055. [20] 辛升, 张卫杰. 主动空间栅格定位算法研究[J]. 战术导弹技术, 2016(3): 96–100. doi: 10.16358/j.issn.1009-1300.2016.03.18.XIN Sheng and ZHANG Weijie. Research on algorithm based on grid search for location[J]. Tactical Missile Technology, 2016(3): 96–100. doi: 10.16358/j.issn.1009-1300.2016.03.18. [21] XIN Jihao, GE Xuyang, ZHANG Yuan, et al. High-precision time difference of arrival estimation method based on phase measurement[J]. Remote Sensing, 2024, 16(7): 1197. doi: 10.3390/rs16071197. -





 下载:
下载:


 下载:
下载:
