Joint Local Linear Embedding and Deep Reinforcement Learning for RIS-MISO Downlink Sum-Rate Optimization
-
摘要: 智能反射面(RIS)因其能调节电磁波的相位和幅度,被视为下一代无线通信的关键技术而被广泛研究。在RIS辅助多输入单输出(MISO)的通信系统中,信道状态维度随用户数量的增加呈平方级增长,导致深度强化学习(DRL)智能体在高维状态空间下面临训练开销大的挑战。针对此问题,该文提出一种基于局部线性嵌入(LLE)和软动作评论(SAC)的联合优化算法,通过随机搜索算法和LLE对信道状态进行降维,并将低维状态作为SAC算法的输入,联合优化基站波束成形与RIS相位偏移,最大化MISO系统的下行和速率。仿真结果表明,在用户数为40的场景下,所提算法在维持与SAC相当的和速率性能的同时,训练时间减少了18.3%,计算资源消耗降低了64.8%。且随着用户规模的扩大,算法的训练开销进一步下降,充分验证了其有效性。Abstract:
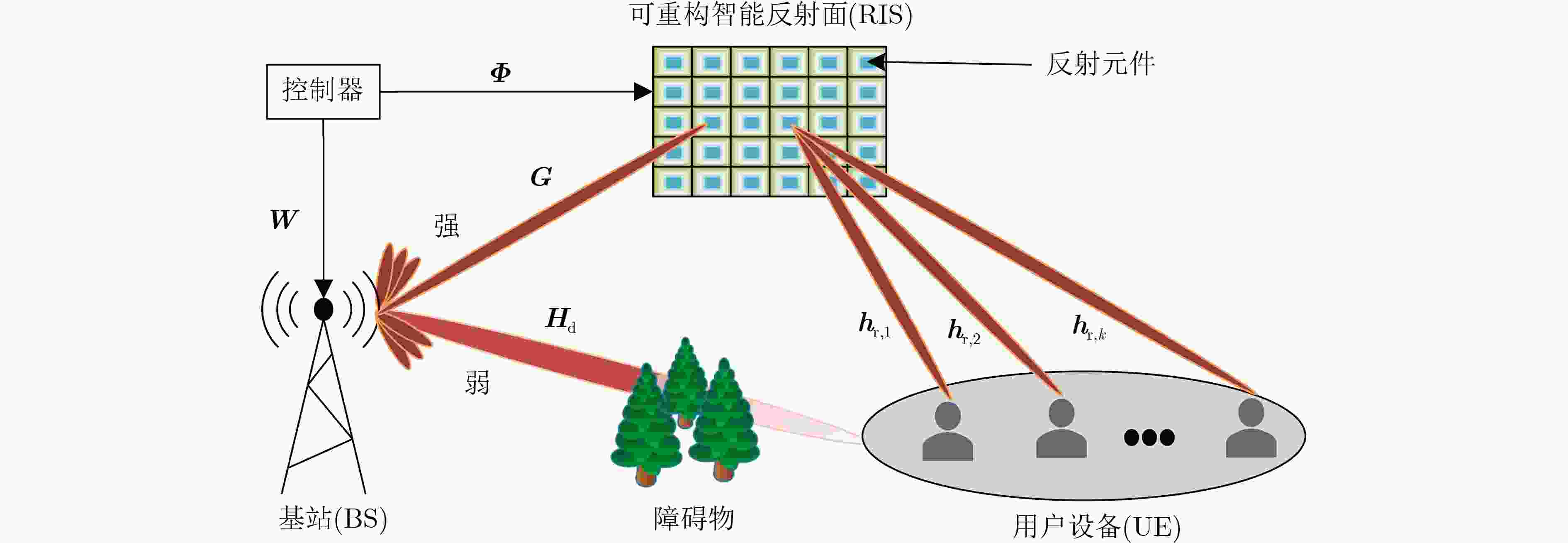
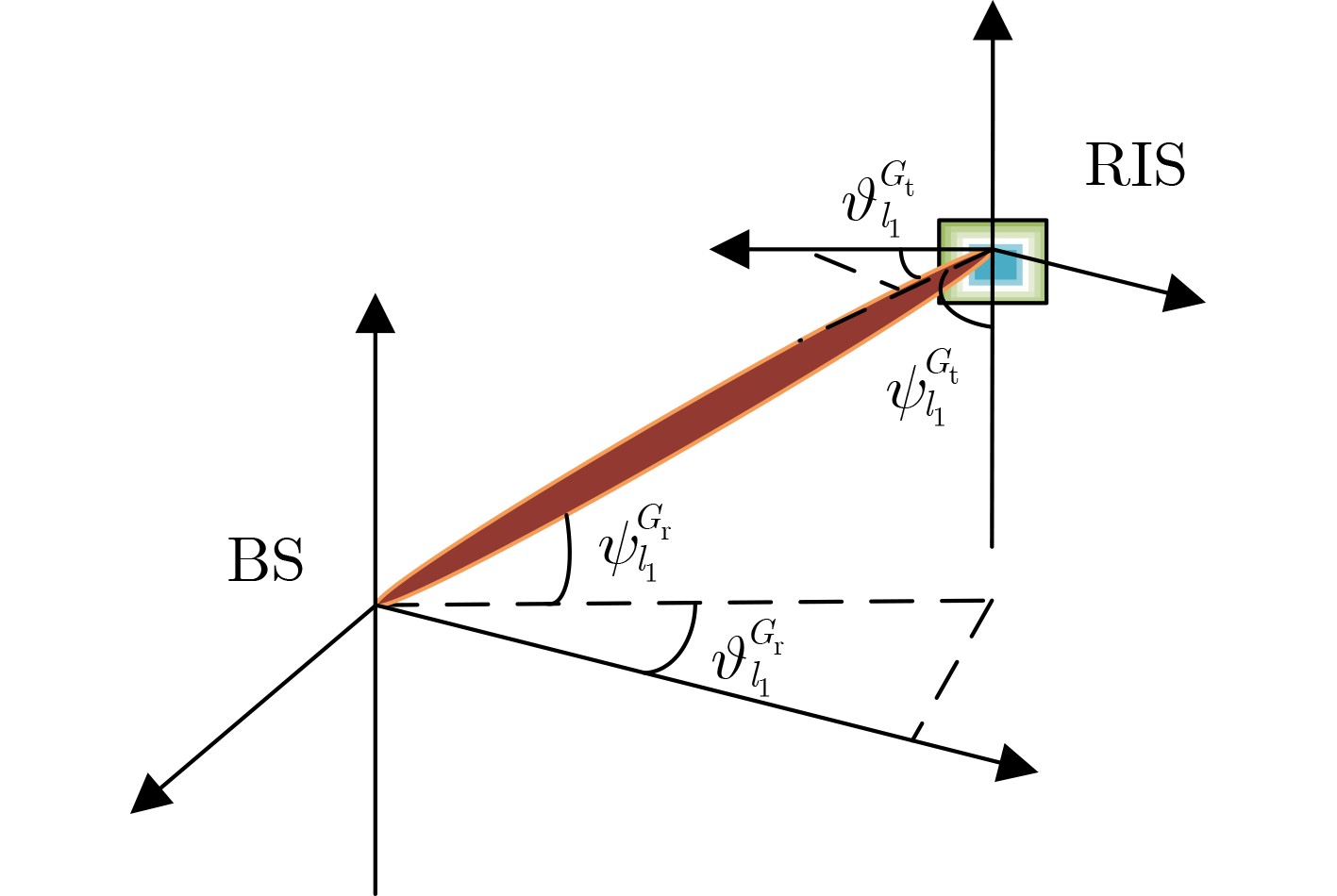
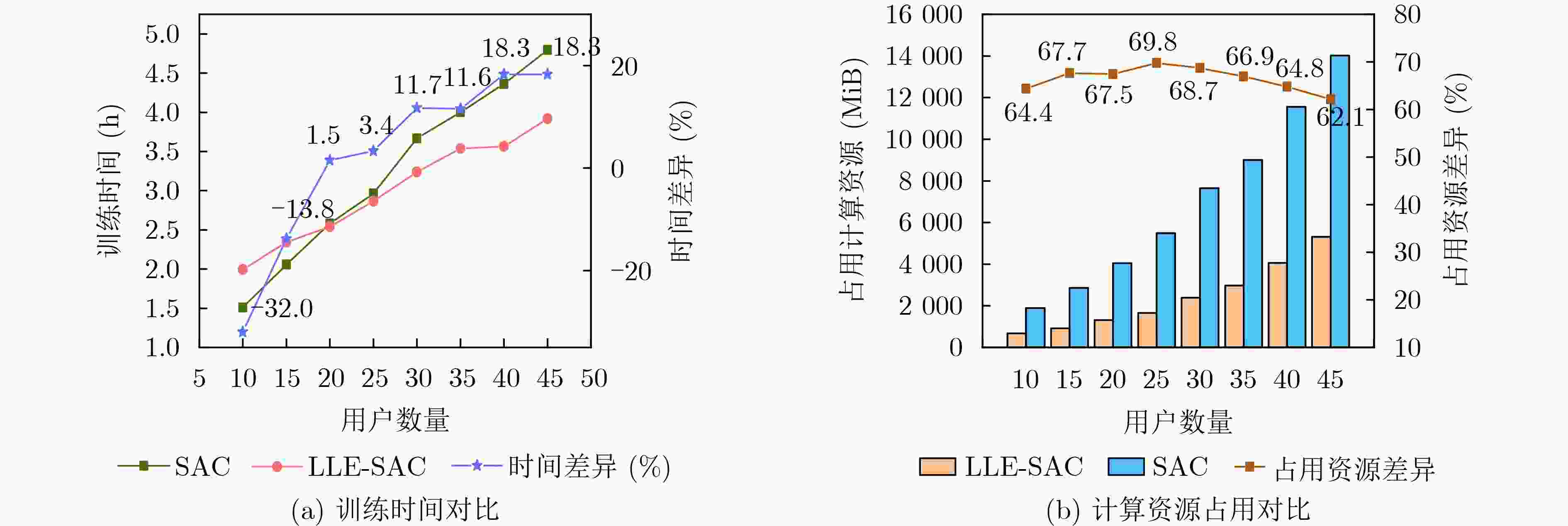
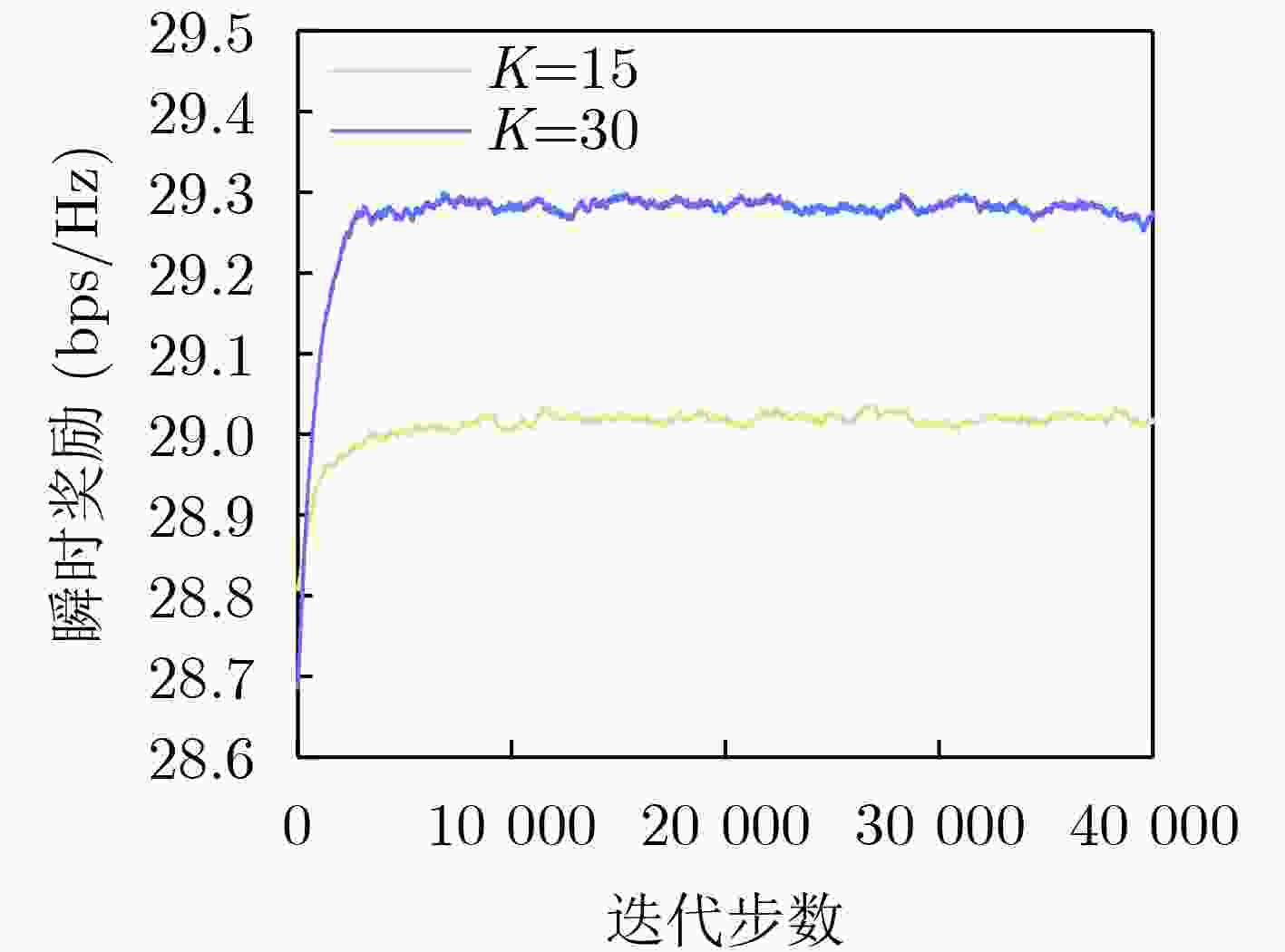
Objective Reconfigurable Intelligent Surfaces (RISs) enhance signal transmission efficiency for large-scale user networks by adaptively controlling signal propagation paths. In RIS-assisted Multiple Input Single Output (MISO) systems, Deep Reinforcement Learning (DRL) is widely employed to jointly optimize Base Station (BS) beamforming and RIS phase shifts. However, the channel state space expands quadratically with the number of users, leading to increased training overhead and reduced algorithm efficiency. To address this challenge, the LLE-SAC algorithm is proposed, in which Local Linear Embedding (LLE) is integrated for dimensionality reduction with the Soft Actor-Critic (SAC) algorithm for policy optimization. This joint framework aims to improve system throughput and training efficiency by reducing the complexity of the channel state representation, thereby enabling the construction of a scalable and intelligent communication system for RIS-assisted MISO in multi-user scenarios. Methods The LLE-SAC algorithm models the wireless environment as a cascaded channel comprising the links between the BS, RIS, and user equipment. To reduce the dimensionality of the high-dimensional channel state, the algorithm searches for the optimal number of neighboring nodes and low-dimensional features based on the principle of minimizing reconstruction error. These parameters are selected through a randomized search strategy to ensure minimal information loss during dimensionality reduction. The LLE algorithm is then applied using the identified optimal parameters to map the original high-dimensional state into a low-dimensional representation. Parameter selection in LLE is constrained to preserve the local geometric structure of the nonlinear channel data and achieve efficient dimensionality reduction. The resulting low-dimensional state, combined with the BS transmission power and user equipment receive power, forms the input state space for the SAC algorithm. Within the SAC framework, the state space comprises the reduced-dimension representation of the cascaded channel and the BS beamforming and RIS phase shift matrix from the previous time step. The action space consists of the current BS beamforming vectors and RIS phase shifts. The reward function is defined as the sum rate of the RIS-assisted MISO system, guiding the agent to iteratively optimize its beamforming strategy. By leveraging both channel state abstraction and historical control parameters, the agent dynamically selects actions that maximize the system sum rate under complex multi-user conditions. Results and Discussions The LLE-SAC algorithm reduces the dimensionality of the high-dimensional cascaded channel state. It then computes the BS beamforming vectors and RIS phase shifts based on the resulting low-dimensional representation to maximize the sum rate of the RIS-assisted MISO system. Simulation results demonstrate that LLE-SAC effectively identifies the optimal number of neighboring nodes and low-dimensional features to minimize reconstruction error ( Fig. 6 ,Fig. 7 ). For a system with 30 users, the minimum reconstruction error reaches 0.061 when the number of neighboring nodes is set to 2 and the dimensionality is reduced to 15, compressing the state space from7092 to 960. In terms of training overhead (Fig. 8 ), the LLE-SAC algorithm reduces training time by 18.3% and computational resource usage by 64.8% relative to the conventional SAC algorithm when the user count reaches 40. This efficiency gain increases with user scale, further reducing training overhead in large-scale scenarios. Under high transmission power (Fig. 9 ), the LLE-SAC algorithm achieves a higher sum rate than both the alternating optimization and semi-definite relaxation algorithms, while maintaining comparable performance to SAC. The algorithm also scales effectively with the number of transmit antennas, achieving increased sum rates and reduced inter-user interference, further confirming its effectiveness. Moreover, in ten independent runs using different random seeds (Fig. 10 ), the LLE-SAC algorithm consistently yields optimal sum rate performance, demonstrating both robustness and stability.Conclusions The proposed method addresses the challenge of high-dimensional channel states, which significantly increase the training overhead in RIS-assisted MISO systems, by integrating the LLE algorithm with the SAC framework. This integration enables effective dimensionality reduction of the cascaded channel state, thereby lowering training costs while maintaining sum rate performance. The simulation results demonstrate three key findings. First, when the number of users reaches 40, the LLE-SAC algorithm reduces training time by 18.3% and computational resource consumption by 64.8% compared to the SAC algorithm. Second, under increasing transmission power, the proposed method achieves superior sum rate performance relative to conventional optimization methods and performs comparably to SAC. Third, across different antenna configurations, the LLE-SAC algorithm yields improved sum rates with increasing transmission power, demonstrating its robustness and scalability. Future work will explore the application of the LLE-SAC algorithm in edge computing environments with large-scale user access. -
表 1 LLE-SAC实验相关参数
参数 描述 值 $M$ BS天线数量 25 $N$ RIS反射元件数量 36 ${L_{\rm G}}$ BS至RIS信道路径数 3 ${L_{{\rm r},k}}$ RIS至UE信道路径数 3 ${L_{{\rm d},k}}$ BS至UE信道路径数 10 $\delta _0^2$ 高斯白噪声方差 0.01 $U$ 训练步数 40000 ${{\mathrm{lr}}_{\mathrm{A}}}$ Actor网络学习率 0.001 ${{\mathrm{lr}}_{\mathrm{C}}}$ Critic网络学习率 0.01 $\Gamma $ 经验池大小 100000 $B$ 批处理数据大小 64 $\alpha $ 初始化熵系数 0.01 $\tau $ 目标网络软更新系数 0.001 -
[1] BASAR E, ALEXANDROPOULOS G C, LIU Yuanwei, et al. Reconfigurable intelligent surfaces for 6G: Emerging hardware architectures, applications, and open challenges[J]. IEEE Vehicular Technology Magazine, 2024, 19(3): 27–47. doi: 10.1109/MVT.2024.3415570. [2] BILOTTI F, BARBUTO M, HAMZAVI-ZARGHANI Z, et al. Reconfigurable intelligent surfaces as the key-enabling technology for smart electromagnetic environments[J]. Advances in Physics: X, 2024, 9(1): 2299543. doi: 10.1080/23746149.2023.2299543. [3] FENG Yijun, HU Qi, QU Kai, et al. Reconfigurable intelligent surfaces: Design, implementation, and practical demonstration[J]. Electromagnetic Science, 2023, 1(2): 0020111. doi: 10.23919/emsci.2022.0011. [4] GUO Huayan, LIANG Yingchang, CHEN Jie, et al. Weighted sum-rate maximization for intelligent reflecting surface enhanced wireless networks[C]. 2019 IEEE Global Communications Conference, Waikoloa, USA, 2019: 1–6. doi: 10.1109/GLOBECOM38437.2019.9013288. [5] 田心记, 孟浩然, 李兴旺, 等. 双STAR-RIS辅助下行NOMA系统中最大化和速率的方法[J]. 电子与信息学报, 2024, 46(9): 3537–3543. doi: 10.11999/JEIT240007.TIAN Xinji, MENG Haoran, LI Xingwang, et al. Method of maximizing sum rate for dual STAR-RIS assisted downlink NOMA systems[J]. Journal of Electronics & Information Technology, 2024, 46(9): 3537–3543. doi: 10.11999/JEIT240007. [6] ZHU Guangxu, LYU Zhonghao, JIAO Xiang, et al. Pushing AI to wireless network edge: An overview on integrated sensing, communication, and computation towards 6G[J]. Science China Information Sciences, 2023, 66(3): 130301. doi: 10.1007/s11432-022-3652-2. [7] LEE H, LEE B, YANG H, et al. Towards 6G hyper-connectivity: Vision, challenges, and key enabling technologies[J]. Journal of Communications and Networks, 2023, 25(3): 344–354. doi: 10.23919/JCN.2023.000006. [8] ZHONG Ruikang, LIU Yuanwei, MU Xidong, et al. AI empowered RIS-assisted NOMA networks: Deep learning or reinforcement learning?[J]. IEEE Journal on Selected Areas in Communications, 2022, 40(1): 182–196. doi: 10.1109/JSAC.2021.3126068. [9] HUANG Hongji, SONG Yiwei, YANG Jie, et al. Deep-learning-based millimeter-wave massive MIMO for hybrid precoding[J]. IEEE Transactions on Vehicular Technology, 2019, 68(3): 3027–3032. doi: 10.1109/TVT.2019.2893928. [10] HUANG Hao, XIA Wenchao, XIONG Jian, et al. Unsupervised learning-based fast beamforming design for downlink MIMO[J]. IEEE Access, 2019, 7: 7599–7605. doi: 10.1109/ACCESS.2018.2887308. [11] 陈真, 杜晓宇, 唐杰, 等. 基于深度强化学习的RIS辅助通感融合网络: 挑战与机遇[J]. 电子与信息学报, 2024, 46(9): 3467–3473. doi: 10.11999/JEIT240086.CHEN Zhen, DU Xiaoyu, TANG Jie, et al. DRL-based RIS-assisted ISAC network: Challenges and opportunities[J]. Journal of Electronics & Information Technology, 2024, 46(9): 3467–3473. doi: 10.11999/JEIT240086. [12] CHEN Peng, LI Xiao, MATTHAIOU M, et al. DRL-based RIS phase shift design for OFDM communication systems[J]. IEEE Wireless Communications Letters, 2023, 12(4): 733–737. doi: 10.1109/LWC.2023.3242449. [13] HUANG Chongwen, MO Ronghong, and YUEN C. Reconfigurable intelligent surface assisted multiuser MISO systems exploiting deep reinforcement learning[J]. IEEE Journal on Selected Areas in Communications, 2020, 38(8): 1839–1850. doi: 10.1109/JSAC.2020.3000835. [14] ZHANG Ruichen, XIONG Ke, LU Yang, et al. Energy efficiency maximization in RIS-assisted SWIPT networks with RSMA: A PPO-based approach[J]. IEEE Journal on Selected Areas in Communications, 2023, 41(5): 1413–1430. doi: 10.1109/JSAC.2023.3240707. [15] HUANG Chongwen, YANG Zhaohui, ALEXANDROPOULOS G C, et al. Multi-hop RIS-empowered terahertz communications: A DRL-based hybrid beamforming design[J]. IEEE Journal on Selected Areas in Communications, 2021, 39(6): 1663–1677. doi: 10.1109/JSAC.2021.3071836. [16] SAGLAM B, GURGUNOGLU D, and KOZAT S S. Deep reinforcement learning based joint downlink beamforming and RIS configuration in RIS-aided MU-MISO systems under hardware impairments and imperfect CSI[C]. 2023 IEEE International Conference on Communications Workshops, Rome, Italy, 2023: 66–72. doi: 10.1109/ICCWorkshops57953.2023.10283517. [17] IZENMAN A J. Introduction to manifold learning[J]. WIREs: Computational Statistics, 2012, 4(5): 439–446. doi: 10.1002/wics.1222. [18] ZHOU Xiaoping, WANG Peipei, YANG Zhe, et al. A manifold learning two-tier beamforming scheme optimizes resource management in massive MIMO networks[J]. IEEE Access, 2020, 8: 22976–22987. doi: 10.1109/ACCESS.2020.2964615. [19] ZHU Guangxu, LIU Dongzhu, DU Yuqing, et al. Toward an intelligent edge: Wireless communication meets machine learning[J]. IEEE Communications Magazine, 2020, 58(1): 19–25. doi: 10.1109/MCOM.001.1900103. [20] ZHU Fenghao, WANG Xinquan, HUANG Chongwen, et al. Robust beamforming for RIS-aided communications: Gradient-based manifold meta learning[J]. IEEE Transactions on Wireless Communications, 2024, 23(11): 15945–15956. doi: 10.1109/TWC.2024.3435023. [21] DE SOUZA JUNIOR W, GUERRA D W M, MARINELLO FILHO J C, et al. Manifold-based optimizations for RIS-aided massive MIMO systems[J]. IEEE Open Journal of the Communications Society, 2024, 5: 7913–7940. doi: 10.1109/OJCOMS.2024.3512662. [22] DAI Linglong and WEI Xiuhong. Distributed machine learning based downlink channel estimation for RIS assisted wireless communications[J]. IEEE Transactions on Communications, 2022, 70(7): 4900–4909. doi: 10.1109/TCOMM.2022.3175175. [23] HAARNOJA T, ZHOU A, HARTIKAINEN K, et al. Soft actor-critic algorithms and applications[EB/OL]. https://arxiv.org/abs/1812.05905, 2018. -





 下载:
下载:








 下载:
下载:
