Diffusion Model and Edge Information Guided Single-photon Image Reconstruction Algorithm
-
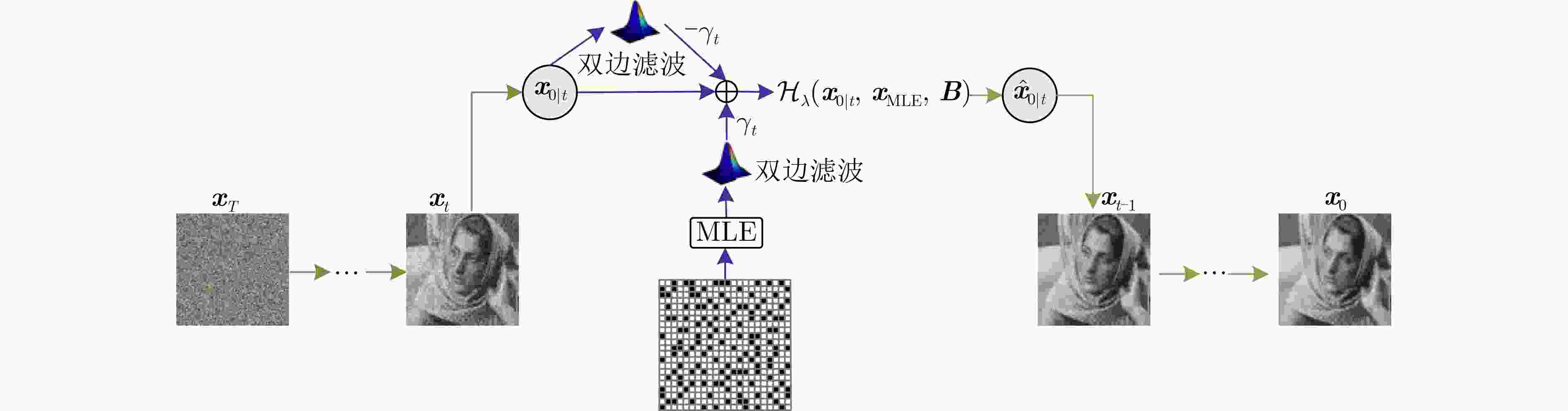
摘要: 在量子图像传感器(QIS)搭建的单光子成像系统中,场景信息蕴含于QIS输出的二值量化数据中,从二值比特流重建原始图像为极度不适定问题。针对现有重建算法在低过采样率重建质量低,对读出噪声敏感的问题,该文提出一种基于扩散模型和边缘信息引导的QIS图像重建算法,以实现快速高质量重建。该算法将测量子空间约束引入无条件的扩散模型反向扩散过程以满足数据一致性和自然图像数据分布的要求,最大似然估计算法重建图像的边缘轮廓成分作为辅助信息引导采样,在减少采样步数的同时提升重建质量。该算法在多个通用数据集上进行测试,并与典型的QIS图像重建算法和基于扩散模型的方法进行比较,实验结果表明,该算法有效地改善了图像重建质量,且对读出噪声具有较强的鲁棒性。Abstract:
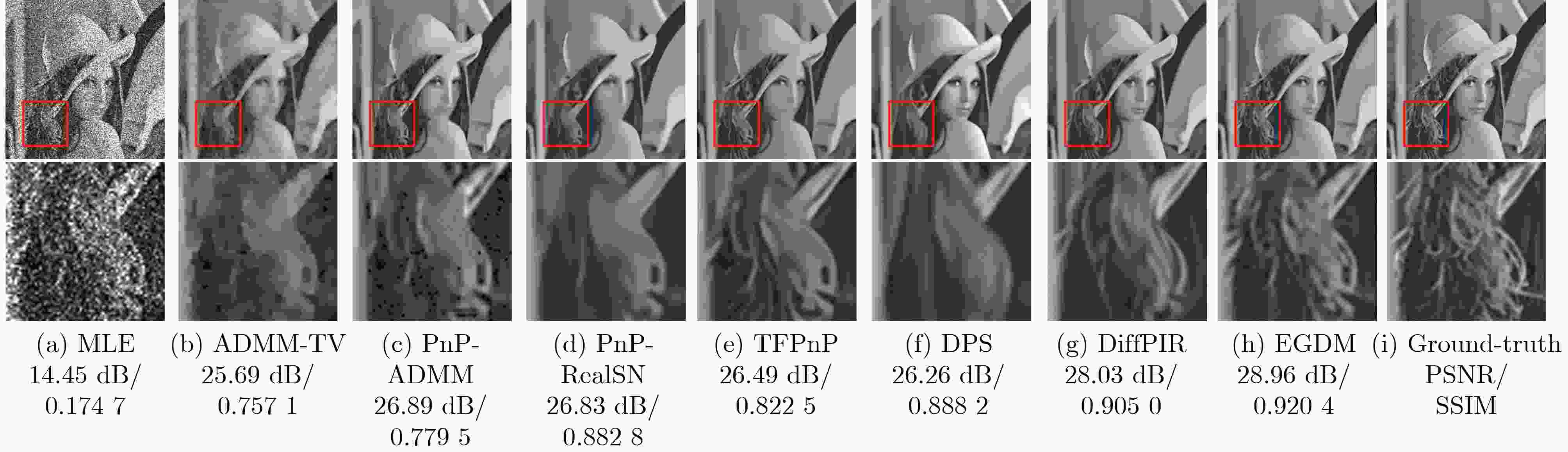
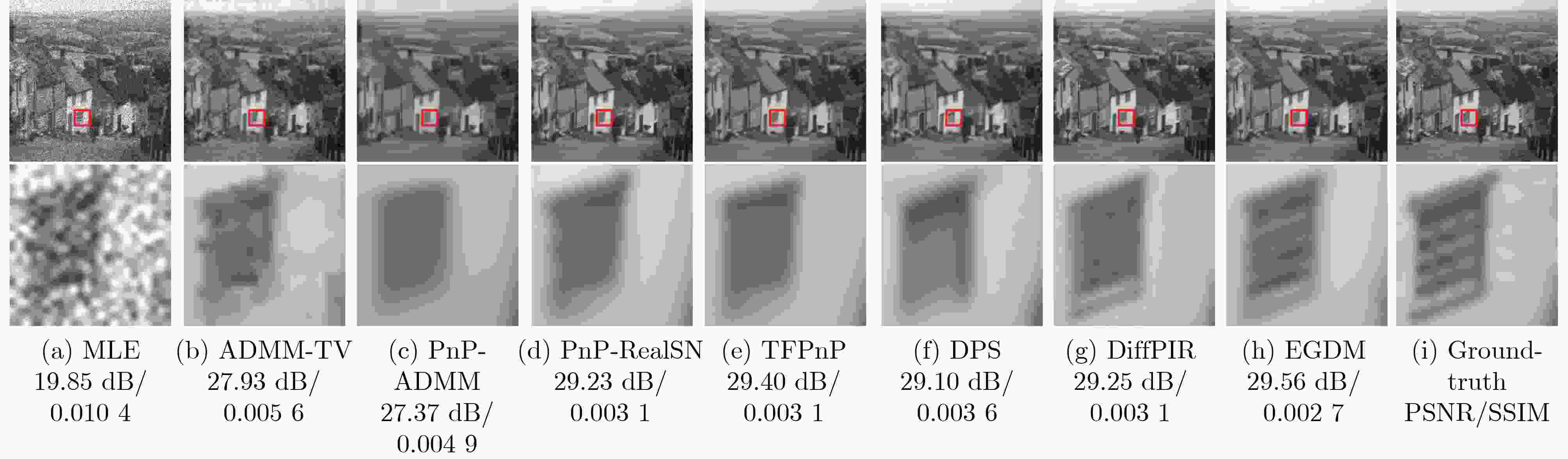
Objective Quanta Image Sensors (QIS) are solid-state sensors that encode scene information into binary bit-streams. The reconstruction for QIS consists of recovering the original scenes from these bit-streams, which is an ill-posed problem characterized by incomplete measurements. Existing reconstruction algorithms based on physical sensors primarily use maximum-likelihood estimation, which may introduce noise-like components and result in insufficient sharpness, especially under low oversampling factors. Model-based optimization algorithms for QIS generally combine the likelihood function with an explicit or implicit image prior in a cost function. Although these methods provide superior quality, they are computationally intensive due to the use of iterative solvers. Additionally, intrinsic readout noise in QIS circuits can degrade the binary response, complicating the imaging process. To address these challenges, an image reconstruction algorithm, Edge-Guided Diffusion Model (EGDM), is proposed for single-photon sensors. This algorithm utilizes a diffusion model guided by edge information to achieve high-speed, high-quality imaging for QIS while improving robustness to readout noise. Methods The proposed EGDM algorithm incorporates a measurement subspace constrained by binary measurements into the unconditional diffusion model sampling framework. This constraint ensures that the generated images satisfy both data consistency and the natural image distribution. Due to high noise intensity in latent variables during the initial reverse diffusion stages of diffusion models, texture details may be lost, and structural components may become blurred. To enhance reconstruction quality while minimizing the number of sampling steps, a bilateral filter is applied to extract edge information from images generated by maximum likelihood estimation. Additionally, the integration of jump sampling with a measurement subspace projection termination strategy reduces inference time and computational complexity, while preserving visual quality. Results and Discussions Experimental results on both the benchmark datasets, Set10 and BSD68 ( Fig. 6 ,Fig. 7 ,Table 2 ), and the real video frame (Fig. 8 ) demonstrate that the proposed EGDM method outperforms several state-of-the-art reconstruction algorithms for QIS and diffusion-based methods in both objective metrics and visual perceptual quality. Notably, EGDM achieves an improvement of approximately 0.70 dB to 3.00 dB compared to diffusion-based methods for QIS in terms of Peak Signal-to-Noise Ratio (PSNR) across all oversampling factors. For visualization, the proposed EGDM produces significantly finer textures and preserves image sharpness. In the case of real QIS video sequences (Fig. 8 ), EGDM preserves more detailed information while mitigating blur artifacts commonly found in low-light video capture. Furthermore, to verify the robustness of the reconstruction algorithm to readout noise, the reconstruction of the original scene from the measurements is conducted under various readout noise levels. The experimental results (Table 3 ,Fig. 9 ,Fig. 10 ) demonstrate the effectiveness of the proposed EGDM method in suppressing readout noise, as it achieves the lowest average Mean Squared Error (MSE) and superior quality compared to other algorithms in terms of PSNR, particularly at higher noise levels. Visually, EGDM produces the best results, with sharp edges and clear texture patterns even under severe noise conditions. Compared to the EGDM algorithm without acceleration strategies, the implementation of jump sampling and measurement subspace projection termination strategies reduces the execution time by 5 seconds and 1.9 seconds, respectively (Table 4 ). Moreover, EGDM offers faster computation speeds than other methods, including deep learning-based reconstruction algorithms that rely on GPU-accelerated computing. After thorough evaluation, these experimental findings confirm that the high-performance reconstruction and rapid imaging speed make the proposed EGDM method an excellent choice for practical applications.Conclusions This paper proposes a single-photon image reconstruction algorithm, EGDM, based on a diffusion model and edge information guidance, overcoming the limitations of traditional algorithms that produce suboptimal solutions in the presence of low oversampling factors and readout noise. The measurement subspace defined by binary measurements is introduced as a constraint in the diffusion model sampling process, ensuring that the reconstructed images satisfy both data consistency and the characteristics of natural image distribution. The bilateral filter is applied to extract edge components from the MLE-generated image as auxiliary information. Furthermore, a hybrid sampling strategy combining jump sampling with measurement subspace projection termination is introduced, significantly reducing the number of sampling steps while improving reconstruction quality. Experimental results on both benchmark datasets and real video frames demonstrate that: (1) Compared with conventional image reconstruction algorithms for QIS, EGDM achieves excellent performance in both average PSNR and SSIM. (2) Under different oversampling factors, EGDM outperforms existing diffusion-based reconstruction methods by a large margin. (3) Compared with existing techniques, the EGDM algorithm requires less computational time while exhibiting strong robustness against readout noise, confirming its effectiveness in practical applications. Future research could focus on developing parameter-free reconstruction frameworks that preserve imaging quality and extending EGDM to address more complex environmental challenges, such as dynamic low-light or high dynamic range imaging for QIS. -
Key words:
- Quanta Image Sensor (QIS) /
- Single-photon imaging /
- Diffusion model /
- Edge information
-
1 EGDM算法求解流程
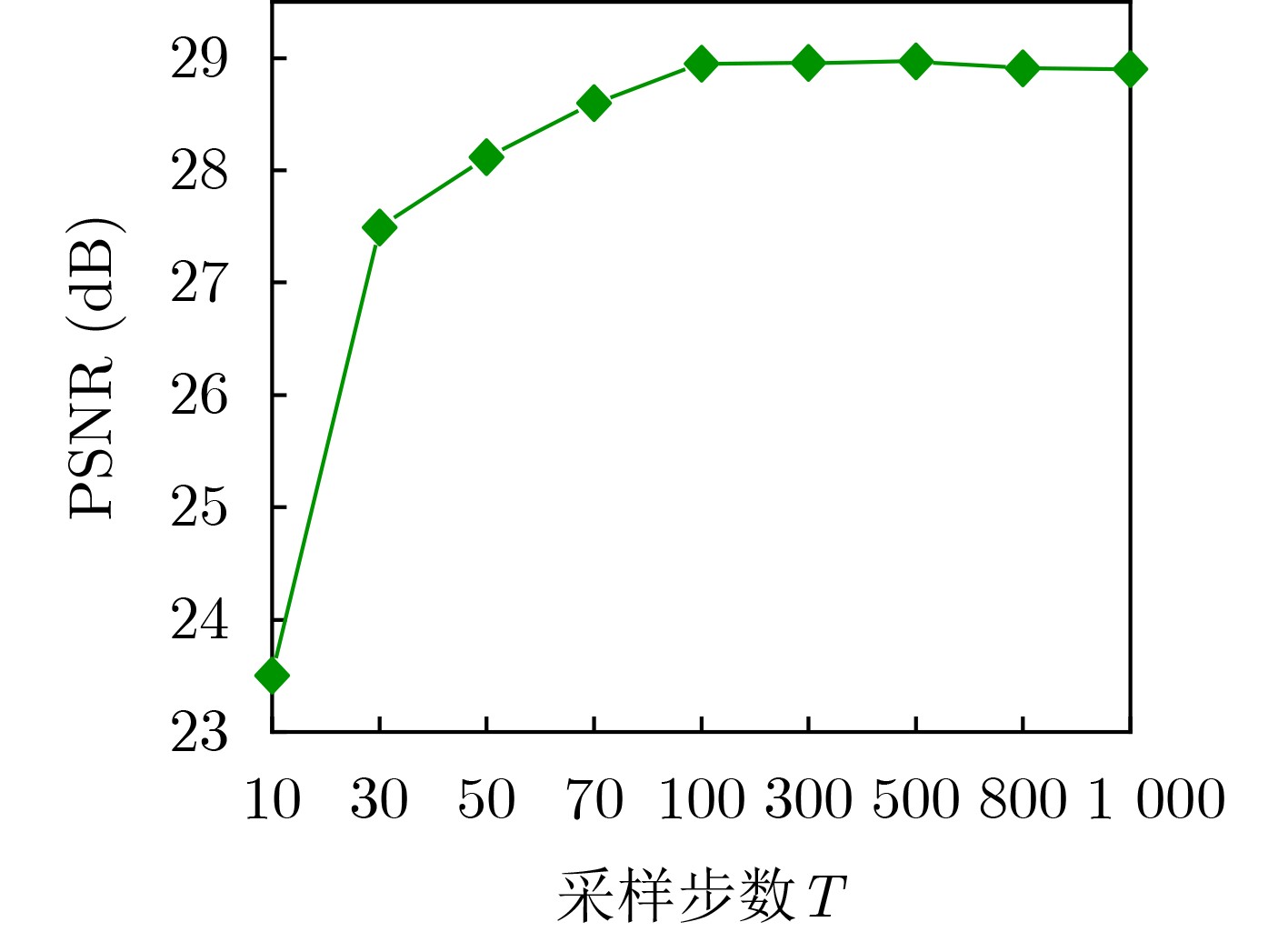
输入:二值测量值B,无条件预训练扩散模型$ {{\boldsymbol{\varepsilon}} _\theta } $,采样步数T 初始化:初始采样图像$ {{\boldsymbol{x}}_T} \sim \mathcal{N}\left( {0,{\boldsymbol{I}}} \right) $,t=T,参数:τ, $ {\gamma _t} $,
$\lambda $, $\delta,\mu $while t≥1: $ {{\boldsymbol{x}}_{0{|t}}} = \dfrac{1}{{\sqrt {{{{\bar \alpha }}_{t}}} }}\left( {{{\boldsymbol{x}}_{t}} - \sqrt {1 - {{{\bar \alpha }}_{t}}} {{{\boldsymbol{\varepsilon}} }_{\theta }}\left( {{{\boldsymbol{x}}_{t}},{t}} \right)} \right) $//利用预训练扩散模
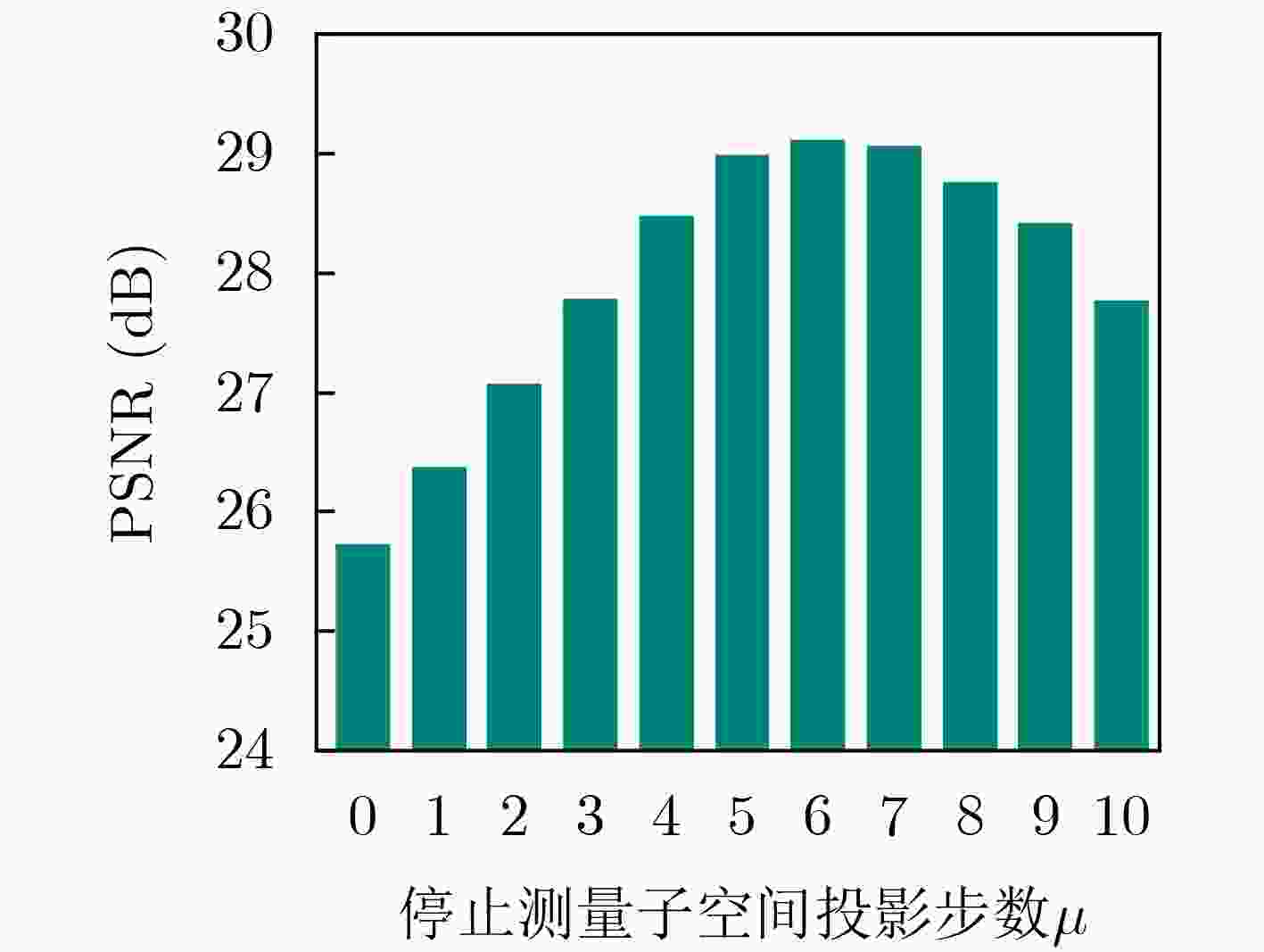
型从xt预测原始图像x0|tif t ≥$\mu $: $ {\hat {\boldsymbol{x}}_{0{|t}}} = {\mathcal{H}_{{\lambda ,}{{\gamma }_{t}}}}\left( {{{\boldsymbol{x}}_{0{|t}}},{{\boldsymbol{x}}_{{\mathrm{MLE}}}},{\boldsymbol{B}}} \right) $//融合边缘信息并向测量
子空间投影else: $ {\hat {\boldsymbol{x}}_{0{|t}}} = {{\boldsymbol{x}}_{0{|t}}} $//停止向测量子空间投影 end if $ {{{\boldsymbol{\varepsilon}}}^{\prime}_{t}} = \dfrac{1}{{\sqrt {1 - {{{\bar \alpha }}_{t}}} }}\left( {{{\boldsymbol{x}}_{t}} - \sqrt {{{{\bar \alpha }}_{t}}} {{\hat {\boldsymbol{x}}}_{0|t}}} \right) $//计算隐变量xt中的有效
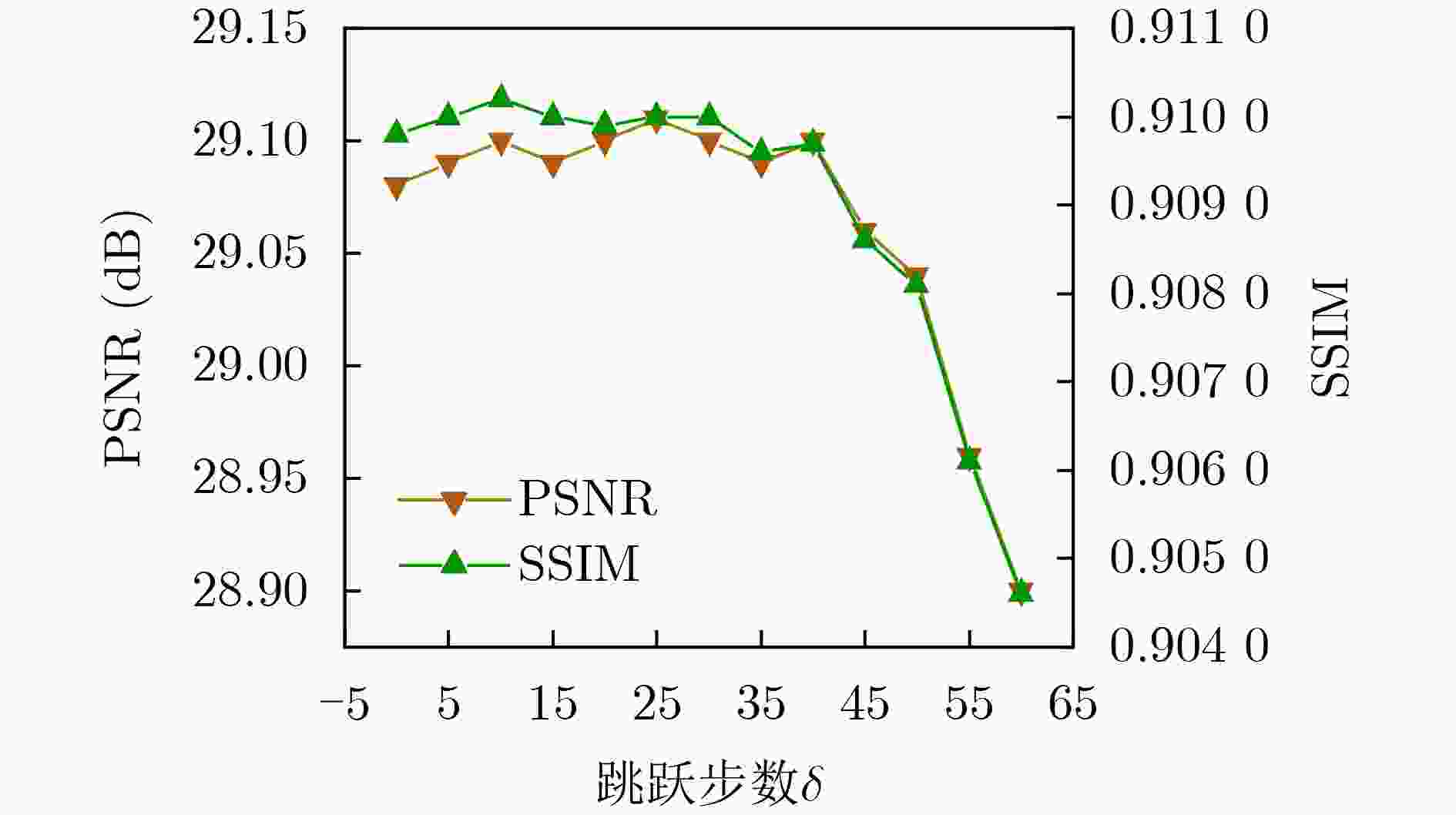
预测噪声$ {\boldsymbol{\varepsilon}} \sim \mathcal{N}\left( {0,{\boldsymbol{I}}} \right) $ if t =T: $ {{\boldsymbol{x}}_{t{ - }{\delta }}} = \sqrt {{{{\bar \alpha }}_{{t - }{\delta }}}} {\hat {\boldsymbol{x}}_{0{|t}}} + \sqrt {1 - {{{\bar \alpha }}_{{t - }{\delta }}}} [{\tau }{{\boldsymbol{\varepsilon}} '_{t}} + (1 - {\tau }){\boldsymbol{\varepsilon}} ] $//
跳跃采样t = t–δ else: $ {{\boldsymbol{x}}_{{t - }1}} = \sqrt {{{{\bar \alpha }}_{{t - }1}}} {\hat {\boldsymbol{x}}_{0{|t}}} + \sqrt {1 - {{{\bar \alpha }}_{{t} - 1}}} [\tau {{\boldsymbol{\varepsilon}} '_{t}} + (1 - {\tau }){\boldsymbol{\varepsilon}} ] $//反
向扩散获得xt–1t = t–1 end if end while 输出:重建图像$ {{\boldsymbol x}_0} $ 表 1 有/无引入边缘信息、测量子空间投影对算法所需迭代次数/平均PSNR (dB)/SSIM的影响
方法 K=4 K=6 K=8 K=10 w/o EG 100/26.56/0.860 1 100/28.95/0.907 4 100/30.29/0.928 2 100/31.23/0.939 6 w/o MP 95/25.67/0.838 8 85/27.08/0.873 2 75/28.05/0.892 7 75/28.77/0.906 9 w/ EG&MP 85/27.17/0.872 2 60/29.10/0.909 7 50/30.43/0.929 2 40/31.45/0.941 8 表 2 不同QIS重建算法在不同数据集下重建PSNR (dB)/SSIM对比
数据集 K MLE ADMM-TV PnP-ADMM PnP-RealSN TFPnP DPS DiffPIR EGDM Set10 4 14.49/0.214 8 24.25/0.648 0 25.83/0.722 5 25.43/0.815 4 24.84/0.733 2 24.01/0.768 9 26.40/0.854 2 27.17/0.872 2 6 17.62/0.323 9 26.17/0.717 9 28.47/0.813 8 28.18/0.885 7 27.65/0.796 5 27.97/0.889 5 28.40/0.894 6 29.10/0.909 7 8 19.98/0.415 5 27.20/0.736 4 29.72/0.845 1 29.82/0.916 1 29.70/0.854 0 29.71/0.919 3 29.69/0.917 4 30.43/0.929 2 10 21.88/0.491 0 27.93/0.747 2 30.51/0.863 9 30.48/0.925 0 31.29/0.894 2 29.99/0.919 7 30.72/0.931 3 31.45/0.941 8 BSD68 4 15.14/0.216 7 24.39/0.634 3 25.12/0.652 6 25.19/0.790 4 24.27/0.694 0 24.02/0.785 9 25.83/0.819 0 26.25/0.839 2 6 18.41/0.334 9 26.06/0.689 3 27.83/0.776 4 27.69/0.863 4 27.19/0.774 6 27.41/0.871 7 27.74/0.869 2 28.34/0.889 6 8 20.80/0.432 4 27.11/0.715 8 29.11/0.820 1 29.20/0.895 1 29.26/0.840 7 28.29/0.892 7 29.05/0.898 1 29.70/0.914 0 10 22.68/0.511 6 27.89/0.733 1 29.84/0.838 4 29.75/0.903 6 30.82/0.879 6 29.18/0.902 8 30.03/0.915 2 30.72/0.929 2 表 3 不同QIS重建算法在不同噪声强度下重建PSNR(dB)/MSE对比
$\sigma $ K MLE ADMM-TV PnP-ADMM PnP-RealSN TFPnP DPS DiffPIR EGDM 0.3 4 14.16/0.038 4 24.29/0.004 4 23.90/0.004 4 24.95/0.003 7 24.51/0.003 9 24.85/0.003 5 26.29/0.002 6 26.76/0.002 3 6 17.16/0.019 3 26.07/0.002 9 25.45/0.003 1 27.56/0.002 0 27.10/0.002 2 26.67/0.002 4 27.93/0.001 7 28.43/0.001 6 8 19.38/0.011 6 27.11/0.002 1 26.72/0.002 3 29.13/0.001 3 29.17/0.001 8 28.37/0.001 6 28.91/0.001 4 29.50/0.001 2 10 21.11/0.007 8 27.73/0.001 8 27.49/0.001 9 29.92/0.001 1 30.75/0.001 0 29.34/0.001 2 29.86/0.001 1 30.39/0.001 0 0.4 4 13.59/0.043 8 23.29/0.005 4 22.17/0.006 4 24.06/0.004 4 23.74/0.004 5 23.18/0.005 0 25.07/0.003 3 25.71/0.002 9 6 16.24/0.023 8 24.95/0.003 6 23.12/0.005 1 25.90/0.002 8 24.37/0.003 7 24.64/0.003 6 26.23/0.002 5 26.73/0.002 2 8 18.11/0.015 5 25.87/0.002 9 25.34/0.003 1 26.92/0.002 1 25.37/0.002 9 25.92/0.002 7 26.90/0.002 1 27.43/0.001 9 10 19.46/0.011 3 26.59/0.002 3 25.86/0.002 7 27.36/0.001 9 25.98/0.002 4 26.79/0.002 2 27.45/0.001 8 27.88/0.001 6 表 4 不同QIS重建算法在K=8时Set10数据集上的平均执行时间 (s)
算法 PnP-RealSN TFPnP DPS DiffPIR w/ SK& MSP w/o SK w/o MSP EGDM 运行时长 65.4 1.8 316.4 13.8 12.6 10.7 7.6 6.9 -
[1] FOSSUM E R, MA Jiaju, MASOODIAN S, et al. The quanta image sensor: Every photon counts[J]. Sensors, 2016, 16(8): 1260. doi: 10.3390/s16081260. [2] GYONGY I, AL ABBAS T, DUTTON N, et al. Object tracking and reconstruction with a quanta image sensor[C]. The International Image Sensor Workshop, Hiroshima, Japan, 2017: 4. [3] POLAND S P, KRSTAJIĆ N, MONYPENNY J, et al. A high speed multifocal multiphoton fluorescence lifetime imaging microscope for live-cell FRET imaging[J]. Biomedical Optics Express, 2015, 6(2): 277–296. doi: 10.1364/BOE.6.000277. [4] SEITZ P and THEUWISSEN A J P. Single-Photon Imaging[M]. Berlin, Heidelberg: Springer, 2011. doi: 10.1007/978-3-642-18443-7. [5] YANG Feng, LU Y M, SBAIZ L, et al. Bits from photons: Oversampled image acquisition using binary Poisson statistics[J]. IEEE Transactions on Image Processing, 2012, 21(4): 1421–1436. doi: 10.1109/TIP.2011.2179306. [6] CHAN S H, ELGENDY O A, and WANG Xiran. Images from bits: Non-iterative image reconstruction for quanta image sensors[J]. Sensors, 2016, 16(11): 1961. doi: 10.3390/s16111961. [7] YANG Feng, SBAIZ L, CHARBON E, et al. Image reconstruction in the gigavision camera[C]. The 2009 IEEE 12th International Conference on Computer Vision Workshops, ICCV Workshops, Kyoto, Japan, 2009: 2212–2219. doi: 10.1109/ICCVW.2009.5457554. [8] YANG Feng, LU Y M, SBAIZ L, et al. An optimal algorithm for reconstructing images from binary measurements[C]. SPIE 7533, Computational Imaging VIII, San Jose, USA, 2010: 75330K. doi: 10.1117/12.850887. [9] CHAN S H and LU Y M. Efficient image reconstruction for gigapixel quantum image sensors[C]. 2014 IEEE Global Conference on Signal and Information Processing, Atlanta, USA, 2014: 312–316. doi: 10.1109/GlobalSIP.2014.7032129. [10] CHAN S H, WANG Xiran, and ELGENDY O A. Plug-and-play ADMM for image restoration: Fixed-point convergence and applications[J]. IEEE Transactions on Computational Imaging, 2017, 3(1): 84–98. doi: 10.1109/TCI.2016.2629286. [11] RYU E, LIU Jialin, WANG Sicheng, et al. Plug-and-play methods provably converge with properly trained denoisers[C]. The 36th International Conference on Machine Learning, Long Beach, USA, 2019: 5546–5557. [12] WEI Kaixuan, AVILES-RIVERO A, LIANG Jingwei, et al. TFPnP: Tuning-free plug-and-play proximal algorithms with applications to inverse imaging problems[J]. The Journal of Machine Learning Research, 2022, 23(1): 16. [13] WANG Xingzheng . Single-photon cameras image reconstruction using vision transformer[C]. 2023 IEEE 3rd International Conference on Computer Communication and Artificial Intelligence, Taiyuan, China, 2023: 296–300. doi: 10.1109/CCAI57533.2023.10201259. [14] 胡铭菲, 左信, 刘建伟. 深度生成模型综述[J]. 自动化学报, 2022, 48(1): 40–74. doi: 10.16383/j.aas.c190866.HU Mingfei, ZUO Xin, and LIU Jianwei. Survey on deep generative model[J]. Acta Automatica Sinica, 2022, 48(1): 40–74. doi: 10.16383/j.aas.c190866. [15] XIANG Xuezhi, ABDEIN R, LV Ning, et al. InvFlow: Involution and multi-scale interaction for unsupervised learning of optical flow[J]. Pattern Recognition, 2024, 145: 109918. doi: 10.1016/j.patcog.2023.109918. [16] 厉行, 樊养余, 郭哲, 等. 基于边缘领域自适应的立体匹配算法[J]. 电子与信息学报, 2024, 46(7): 2970–2980. doi: 10.11999/JEIT231113.LI Xing, FAN Yangyu, GUO Zhe, et al. Edge domain adaptation for stereo matching[J]. Journal of Electronics & Information Technology, 2024, 46(7): 2970–2980. doi: 10.11999/JEIT231113. [17] LIN Xinmiao, LI Yikang, HSIAO J, et al. Catch missing details: Image reconstruction with frequency augmented variational autoencoder[C]. 2023 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, Canada, 2023: 1736–1745. doi: 10.1109/CVPR52729.2023.00173. [18] HO J, JAIN A, and ABBEEL P. Denoising diffusion probabilistic models[C]. The 34th International Conference on Neural Information Processing Systems, Vancouver, Canada, 2020: 574. [19] XIA Bin, ZHANG Yulun, WANG Shiyin, et al. Diffir: Efficient diffusion model for image restoration[C]. Tthe 2023 IEEE/CVF International Conference on Computer Vision, Paris, France, 2023: 13049–13059. doi: 10.1109/ICCV51070.2023.01204. [20] CHUNG H, KIM J, MCCANN M T, et al. Diffusion posterior sampling for general noisy inverse problems[C]. 2023 International Conference on Learning Representations, Kigali, Rwanda, 2023: 1–30. [21] FEI Ben, LYU Zhaoyang, PAN Liang, et al. Generative diffusion prior for unified image restoration and enhancement[C]. 2023 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, Canada, 2023: 9935–9946. doi: 10.1109/CVPR52729.2023.00958. [22] SONG Jiaming, MENG Chenlin, and ERMON S. Denoising diffusion implicit models[C]. The 9th International Conference on Learning Representations, Vienna, Austria, 2021: 1–20. [23] SONG Yang, SOHL-DICKSTEIN J, KINGMA D P, et al. Score-based generative modeling through stochastic differential equations[C]. The 9th International Conference on Learning Representations, Vienna, Austria, 2021: 1–36. [24] ZHU Yuanzhi, ZHANG Kai, LIANG Jingyun, et al. Denoising diffusion models for plug-and-play image restoration[C]. 2023 IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops, Vancouver, Canada, 2023: 1219–1229. doi: 10.1109/CVPRW59228.2023.00129. [25] BYERS R. A bisection method for measuring the distance of a stable matrix to the unstable matrices[J]. SIAM Journal on Scientific and Statistical Computing, 1988, 9(5): 875–881. doi: 10.1137/0909059. [26] WANG Yinhuai, YU Jiwen, and ZHANG Jian. Zero-shot image restoration using denoising diffusion null-space model[C]. 2023 International Conference on Learning Representations, Kigali, Rwanda, 2023: 1–31. [27] BURRI S, MARUYAMA Y, MICHALET X, et al. Architecture and applications of a high resolution gated SPAD image sensor[J]. Optics Express, 2014, 22(14): 17573–17589. doi: 10.1364/OE.22.017573. [28] DHARIWAL P and NICHOL A. Diffusion models beat GANs on image synthesis[C]. The 35th International Conference on Neural Information Processing Systems, 2021: 672. [29] CHI Yiheng, GNANASAMBANDAM A, KOLTUN V, et al. Dynamic low-light imaging with quanta image sensors[C]. The 16th European Conference on Computer Vision, Glasgow, UK, 2020: 122–138. doi: 10.1007/978-3-030-58589-1_8. [30] GNANASAMBANDAM A and CHAN S H. Image classification in the dark using quanta image sensors[C]. 2020 European Conference on Computer Vision, Glasgow, UK, 2020: 484–501. doi: 10.1007/978-3-030-58598-3_29. -





 下载:
下载:






 下载:
下载:
