Density Clustering Hypersphere-based Self-adaptively Oversampling Algorithm for Imbalanced Datasets
-
摘要: 不平衡数据分类是机器学习中的常见问题,过采样是解决方案之一。但现有过采样方法在处理复杂不均衡数据集时容易引入噪声样本导致类重叠,且无法有效解决低密度、小析取等子概念引起的类内不平衡问题。为此,该文提出一种基于超球体密度聚类的自适应过采样算法(DCHO),该算法通过计算少数类样本密度动态确定聚类中心,构建超球体并将超球体内少数类样本归入相应簇,再按照不均衡比调整超球体半径。同时,根据超球体内样本局部密度和半径大小自适应分配过采样权重,进而解决类内不平衡问题。为防止类重叠,过采样过程均在每个超球体内部进行。此外,为进一步增强少数类边界以及探索未知区域,该文还构建一种新的边界偏好随机过采样策略。实验结果表明,所提算法在避免类重叠的同时,强化了低密度子概念的表达,有效解决了类间与类内不平衡问题。Abstract:
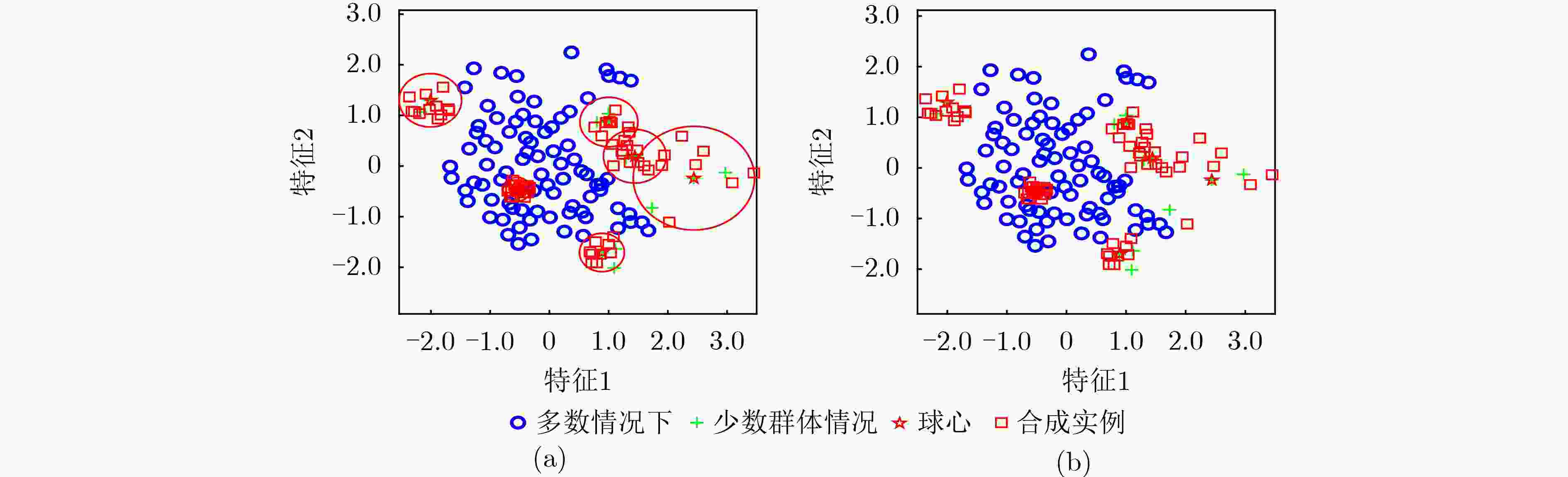
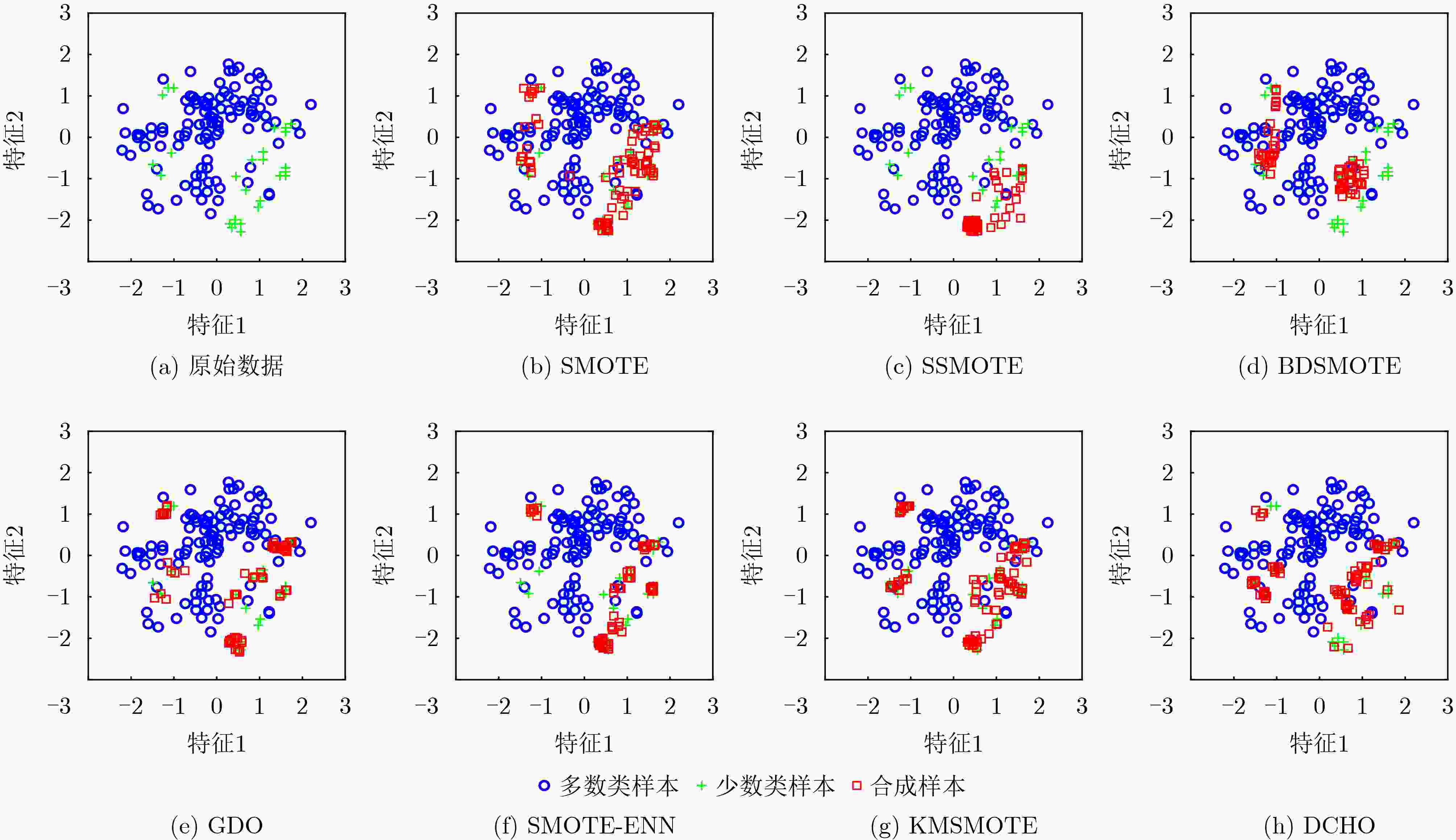
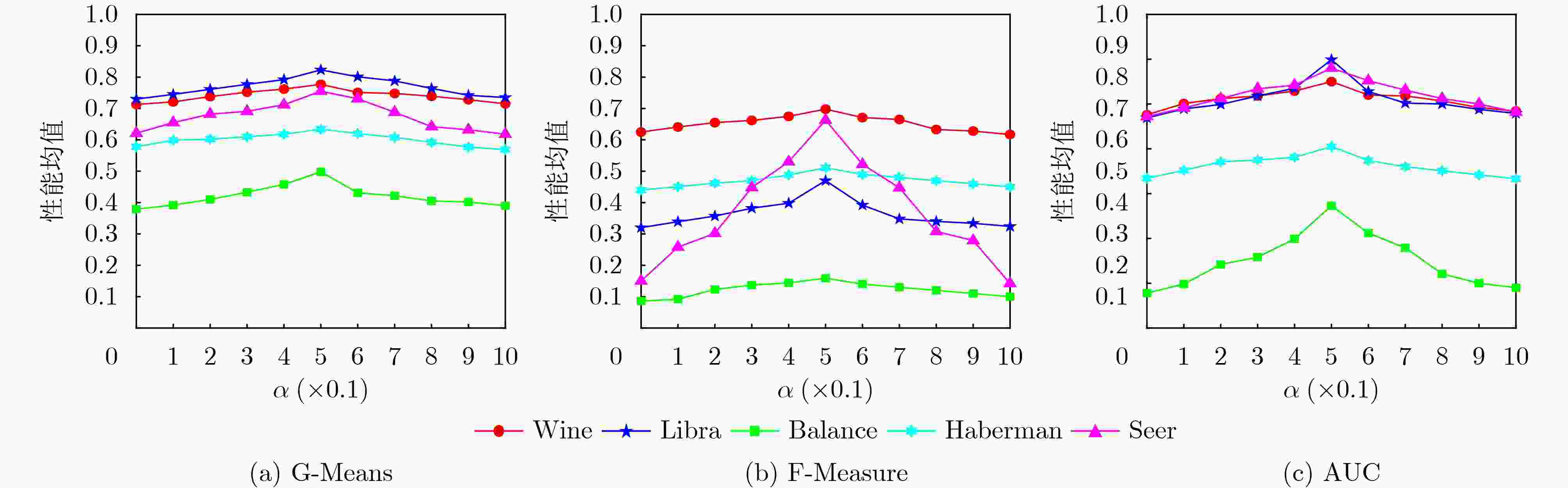
Objective Learning from imbalanced datasets presents significant challenges for the supervised learning community. Existing oversampling methods, however, have notable limitations when applied to complex imbalanced datasets. These methods can introduce noisy instances, leading to class overlap, and fail to effectively address within-class imbalance caused by low-density regions and small disjuncts. To overcome these issues, this study proposes the Density Clustering Hypersphere-based self-adaptively Oversampling algorithm (DCHO). Methods The DCHO algorithm first identifies clustering centers by dynamically calculating the density of minority class instances. Hyperspheres are then constructed around each center to guide clustering, and oversampling is performed within these hyperspheres to reduce class overlap. Oversampling weights are adaptively assigned according to the number of instances and the radius of each hypersphere, which helps mitigate within-class imbalance. To further refine the boundary distribution of the minority class and explore underrepresented regions, a boundary-biased random oversampling technique is introduced to generate synthetic samples within each hypersphere. Results and Discussions The DCHO algorithm dynamically identifies clustering centers based on the density of minority class instances, constructs hyperspheres, and assigns all minority class instances to corresponding clusters. This forms the foundation for oversampling. The algorithm further adjusts the influence of the cumulative density of instances within each hypersphere and the hypersphere radius on the allocation of oversampling weights through a defined trade-off parameter $ \alpha $. Experimental results indicate that this approach reduces class overlap and assigns greater oversampling weights to sparse, low-density regions, thereby generating more synthetic instances to improve representativeness and address within-class imbalance ( Fig. 7 ). When the trade-off parameter is set to 0.5, the algorithm effectively incorporates both density and boundary distribution, improving the performance of subsequent classification tasks (Fig. 11 ).Conclusions Comparative results with other popular oversampling algorithms show that: (1) The DCHO algorithm effectively prevents class overlap by oversampling exclusively within the generated hypersphere. Meanwhile, the algorithm adaptively assigns oversampling weights based on the local density of instances within the hypersphere and its radius, thereby addressing the within-class imbalance issue. (2) By considering the relationship between the hypersphere radius and the density of the minority class instances, the balance parameter $ \alpha $ is set to 0.5, which comprehensively addresses both the within-class imbalance caused by density and the enhancement of the minority class boundary distribution, ultimately improving classification performance on imbalanced datasets. (3) When applied to highly imbalanced datasets with complex boundaries, DCHO significantly improves the distribution of minority class instances, thereby enhancing the classifier’s generalization ability. -
Key words:
- Imbalanced dataset /
- Classification /
- Oversampling /
- Within-class imbalance /
- Hypersphere
-
1 基于密度的超球体过采样算法(DCHO
输入:$ {X}\text{=}\text{[}{{X}}_{\text{min}}\text{.}{{X}}_{\text{m}\text{a}\text{j}}\text{]} $:原始数据;$ {{X}}_{\text{min}} $:原始数据中的少数
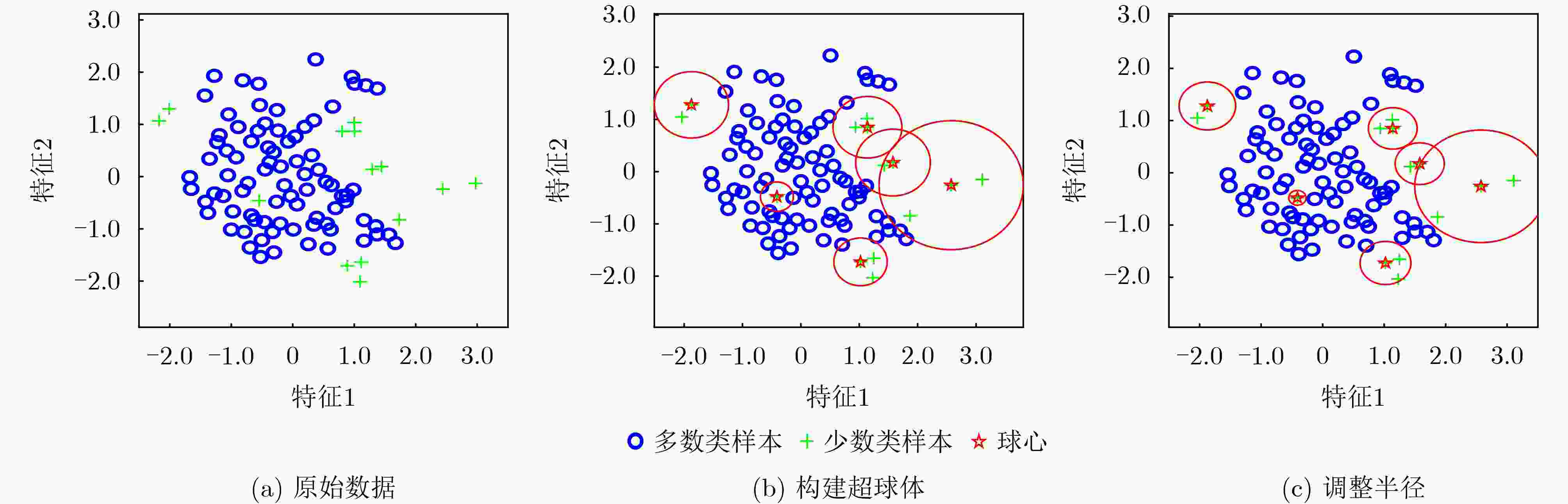
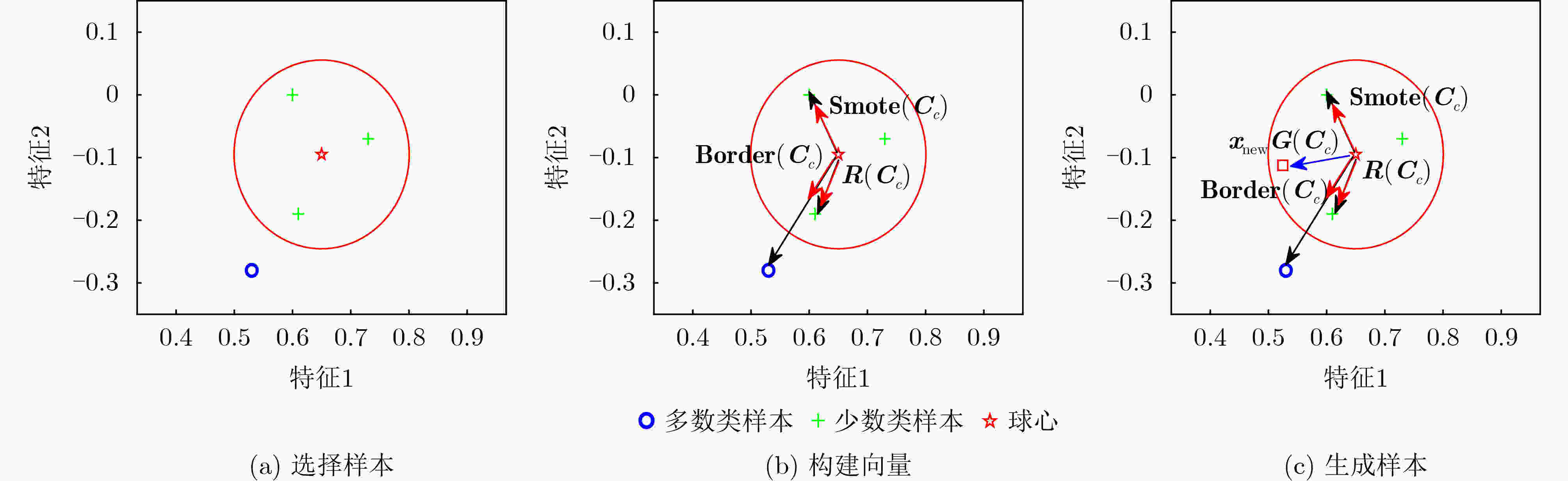
类样本集;$ {X}_{\text{m}\text{a}\text{j}} $:原始数据中的多数类样本集。输出:$ {{X}}_{\mathrm{n}\mathrm{e}\mathrm{w}} $:最终数据集包含原始数据集和生成的数据集 程序开始: 通过z-score方法对所有样本进行归一化处理。 步骤1 基于密度对少数类样本进行归簇. (1) $ {\boldsymbol{C}}_{{\text{min}}c}\text{=[}\text{ }\text{]} $ //存储归簇后的少数类子集 (2) 根据式(1)计算少数类样本$ {\boldsymbol{x}}_{\text{min}{i}} $的局部密度$ {\rho}_{{i}} $ (3) While 还有未被归簇的少数类样本$ {\boldsymbol{x}}_{\text{min}{i}} $ do//构建超球体
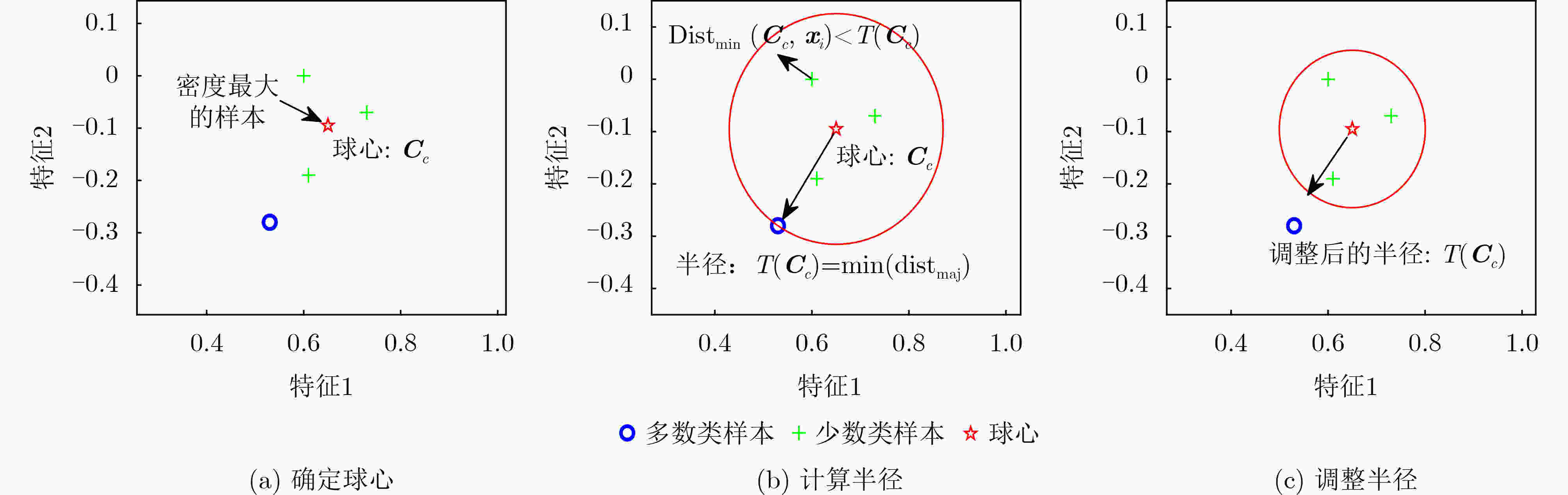
并执行聚类(4) 根据式(2)选取密度最大的少数类样本作为超球体球心$ {\boldsymbol{C}}_{{c}} $ (5) 根据式(3)计算超球体球心$ {\boldsymbol{C}}_{{c}} $和多数类样本$ {\boldsymbol{x}}_{\text{m}\text{aj}{i}} $之间的欧
式距离$ {\text{dist}}_{\text{maj}} $(6) 根据式(4)计算超球体的半径$ {T}\text{(}{\boldsymbol{C}}_{{c}}{)} $ (7) 根据式(5)计算超球体球心$ {\boldsymbol{C}}_{{c}} $和少数类样本$ {\boldsymbol{x}}_{\text{min}{i}} $之间的
欧式距离$ {\text{dist}}_{\text{min}} $(8) if $ {\text{dist}}_{\text{min}}\text{ < }{T}\text{(}{\boldsymbol{C}}_{{c}}\text{)} $ do (9) $ {\boldsymbol{C}}_{\text{min}{c}}\text{=}{\boldsymbol{C}}_{\text{min}\text{c}}\cup{\boldsymbol{x}}_{\text{min}\text{i}} $//将位于超球体内的少数类样本分
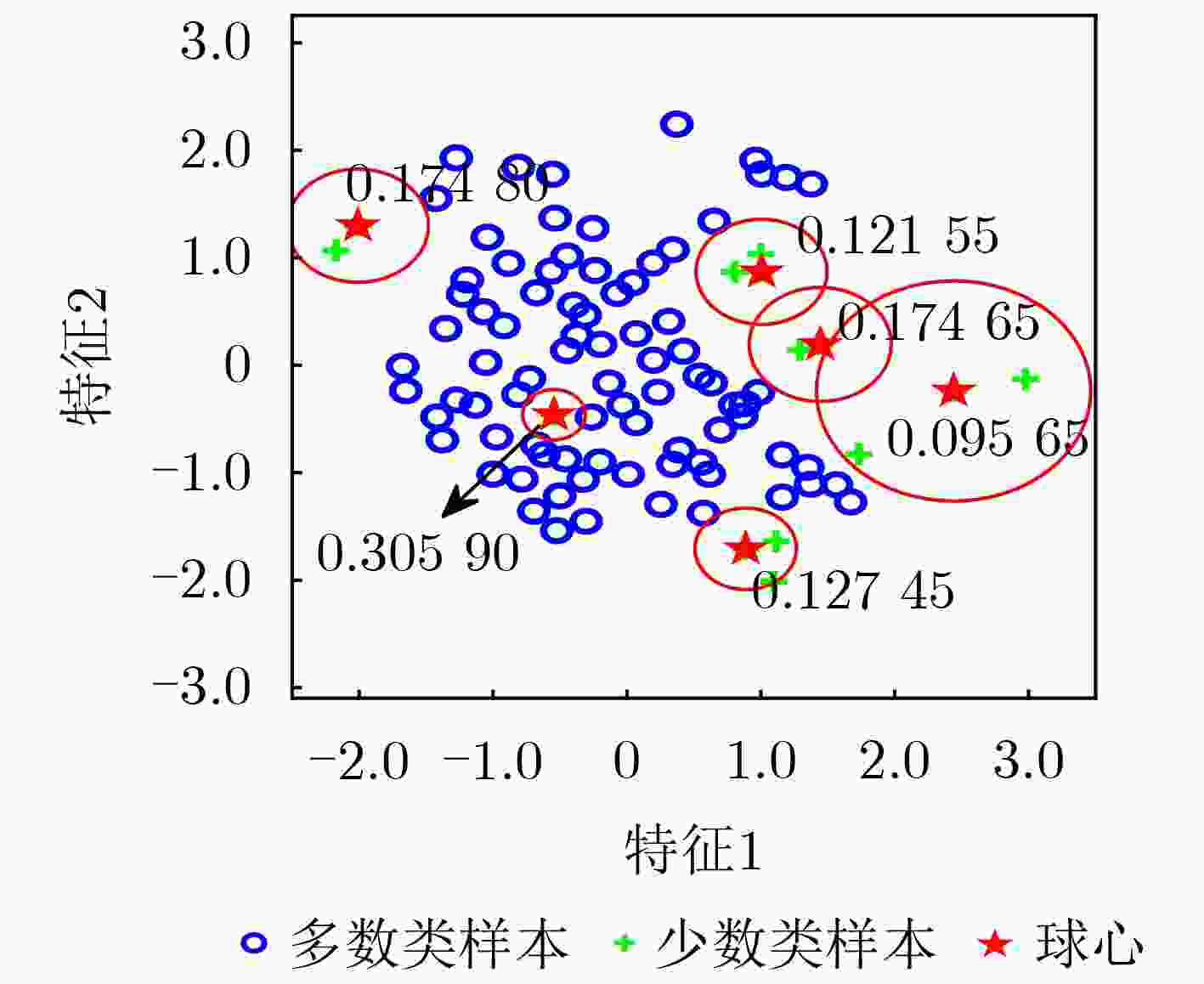
配到簇$ {\boldsymbol{C}}_{\text{min}{c}} $(10) 将$ {\boldsymbol{x}}_{\text{min}{i}} $从$ {{X}}_{\text{min}} $中移除 (11) end if (12) 根据式(7)和式(8)调整超球体的半径$ T $ (13) end while 步骤2 为每个超球体分配过采样权重 (1) for c$ \text{=1:}{C} $ do//对每个超球体(少数类样本簇)
$ {\boldsymbol{C}}_{\text{min}{c}}\text{,}\;\text{}{c}{=1,2,}\cdots \text{,}{C} $(2) 根据式(9)计算其权重影响因素${{p}}_{{c}} $ (3) 根据式(10)计算其权重影响因素$ {{q}}_{{c}} $ (4) 根据式(11)计算其权重$ {{w}}_{{c}} $ (5) end for (6) 根据式(12)计算过采样生成合成样本的总数量$ {{s}} $ (7) 根据式(13)计算每个超球体(少数类样本簇)$ {\boldsymbol{C}}_{\text{min}{c}} $ 需要生
成合成样本的数量$ {{N}}_{{c}} $步骤3 生成样本 (1) for c$ \text{=1:}{C} $ do //对每个超球体(少数类样本簇)
$ {\boldsymbol{C}}_{\text{min}{c}}\text{,}\;\text{}\text{c}\text{=1,2,}\cdots \text{,}{C} $(2) for $ {i}\text{=1:}{{N}}_{{c}} $ do (3) 根据式(14)–式(17)构造一个生成向量$ {{\boldsymbol{G}}}{(}{\boldsymbol{C}}_{{c}}\text{)} $ 。 (4) 根据式(18)生成新样本$ {{{\boldsymbol{x}}}}_{\text{new}} $ (5) $ {{X}}_{\mathrm{n}\mathrm{e}\mathrm{w}}\text{=}{{{X}}}\cup {{x}}_{\text{new}} $ //合并数据集 (6) end for (7) end for 表 1 数据集信息
数据集 特征数 少数类/多数类 少数类类别 不平衡比 Liver 6 145/200 1 1:1.38 Pima 8 268/500 1 1:1.87 Yeast 8 429/ 1055 2 1:2.46 Wine 13 48/130 1 1:2.71 Haberman 3 81/225 2 1:2.78 Spect 22 55/212 1 1:3.85 Yeast1 8 244/ 1240 3 1:5.08 Traffic 26 163473 /1215190 1 1:7.43 Pageblock 10 560/ 4913 1 1:8.77 Blabance 4 49/576 B 1:11.76 Libra 90 24/336 15 1:14.00 Seer 11 110411 /2422218 8 1:21.94 Yeast5 8 20/463 9 1:23.15 Yeast6 8 51/ 1433 5 1:28.10 Sensors 5 43790 /2176013 4 1:49.69 Iot1 10 109278 /6953328 9 1:63.63 表 2 参数信息
算法 参数 SMOTE $ {k}\text{=5} $ SSMOTE $ {k}\text{=5} $ BDSMOTE $ {k}\text{=5} $ ADASYN $ {k}\text{=5} $, $ \text{dth=0.75} $, $ \beta\text{=1} $ MWMOTE $ {{k}}_{\text{1}}{=5} $, $ {{k}}_{\text{2}}\text{=3} $, $ {{k}}_{\text{3}}\text{=}\left|{{S}}_{\text{min}}\right|\text{/2} $, $ {{C}}_{\text{p}}\text{=3} $, $ {{C}}_{\text{f}}\left(\text{th}\right)\text{=5} $, $ \text{CMAX=2} $ KMSMOTE $ {{c}}_{\text{thres}}\in \left\{\text{1,2}\right\} $,$ \text{itr=1} $ A-SUWO $ {{c}}_{\text{thres}}\in \text{{1,2}} $ SMOTE-NaN-DE $ \text{SFGSS=8} $,$ \text{SFHC=20} $,$ \text{Fl=0.1} $,$ \text{Fu=0.9}, \tau \text{1=0.1} $,$ \tau \text{2=0.03} $,$ \tau \text{3=0.07} $ GDO $ {k}\text{=5} $,$ {d}\text{=1} $ RBO $ \text{step=}\text{0} $, $ \text{iterations=5}\;\text{000} $, $ \gamma\in\text{{0.001, 0.01,}\cdots \text{, 10}} $ imFTP $ \text{mini-batch=200} $,学习率$ {=0.000\;2} $,训练轮数$ \text{=500} $ 表 3 以DCHO为对照算法的Holm检验结果
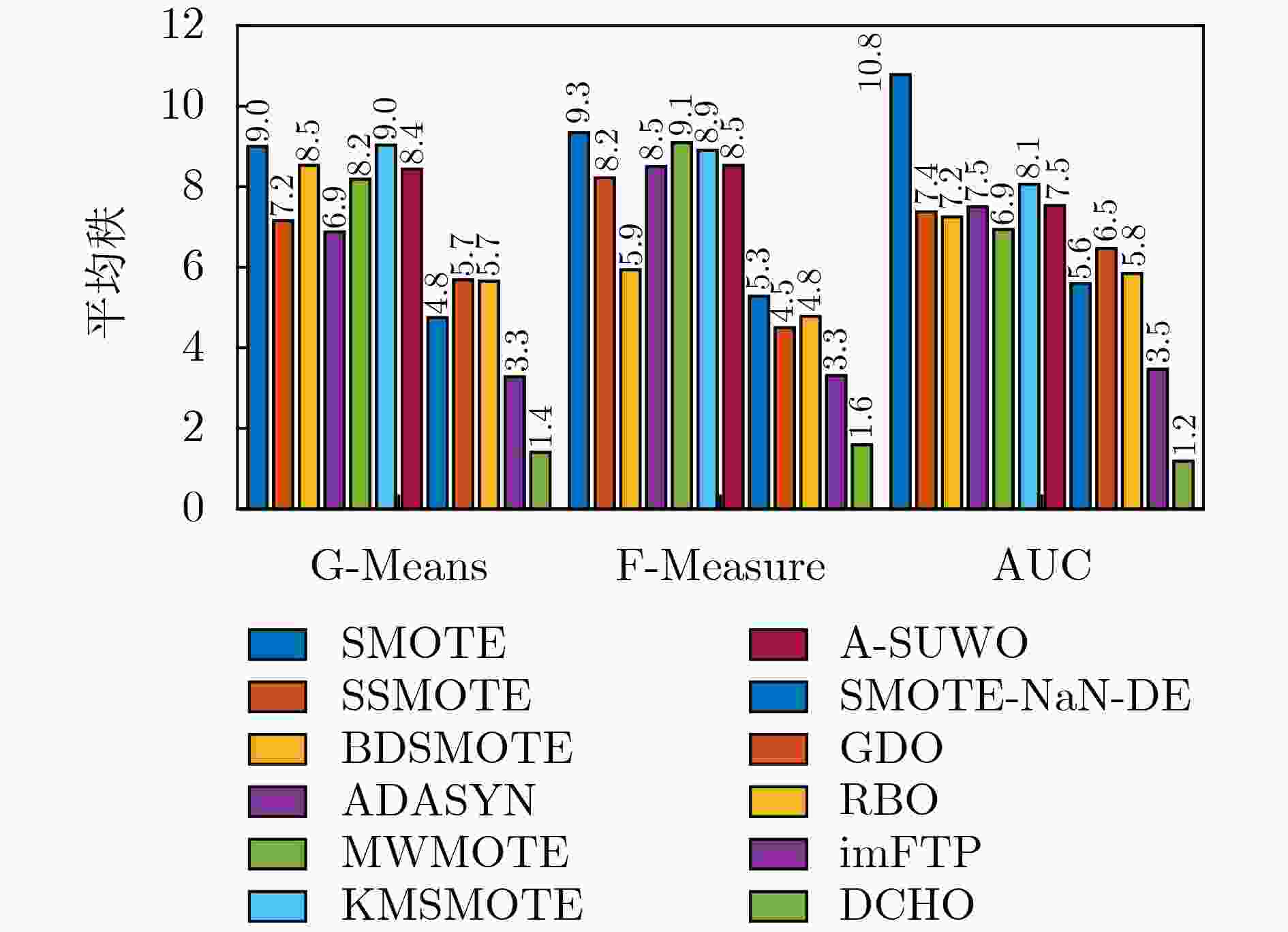
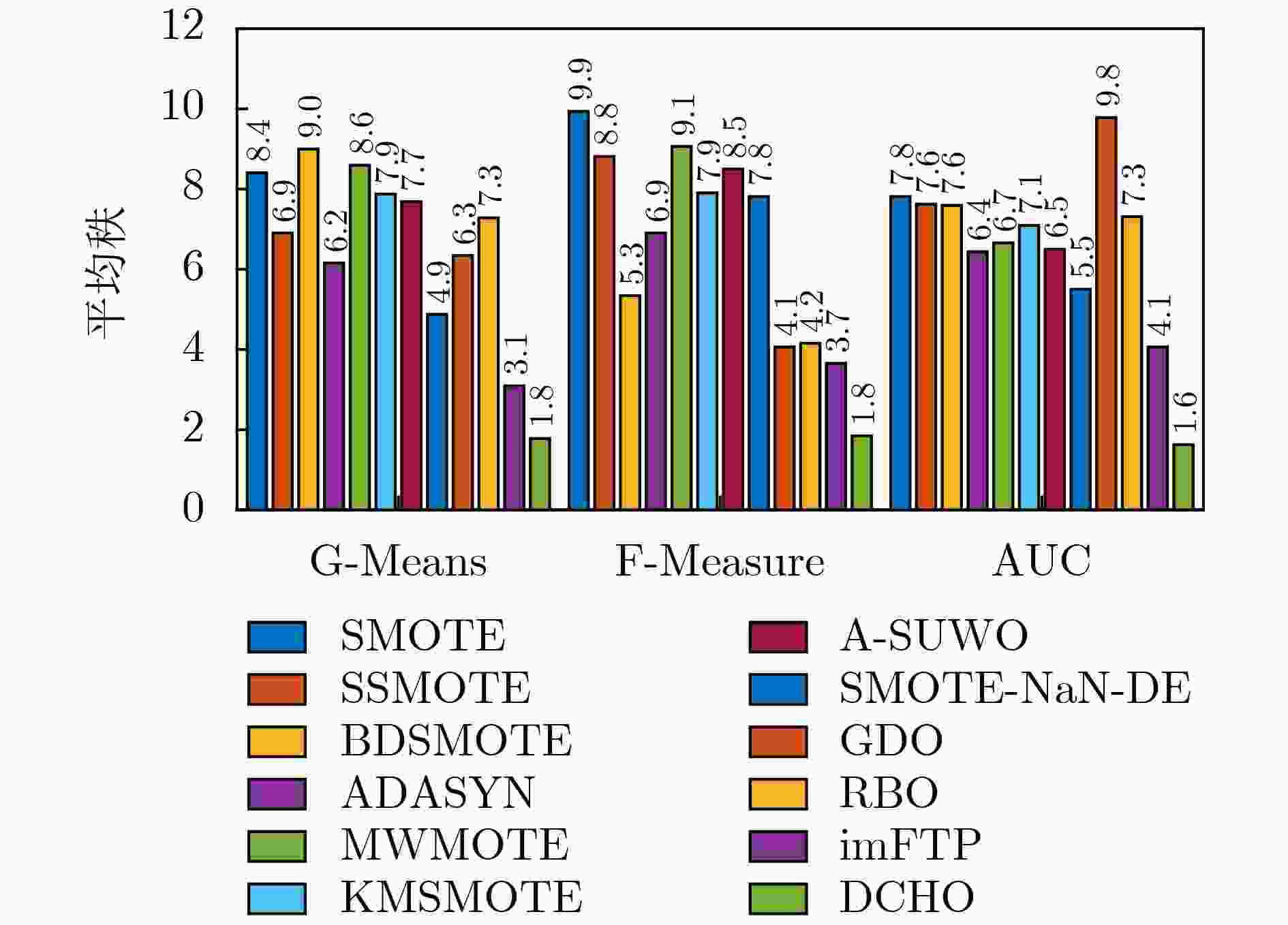
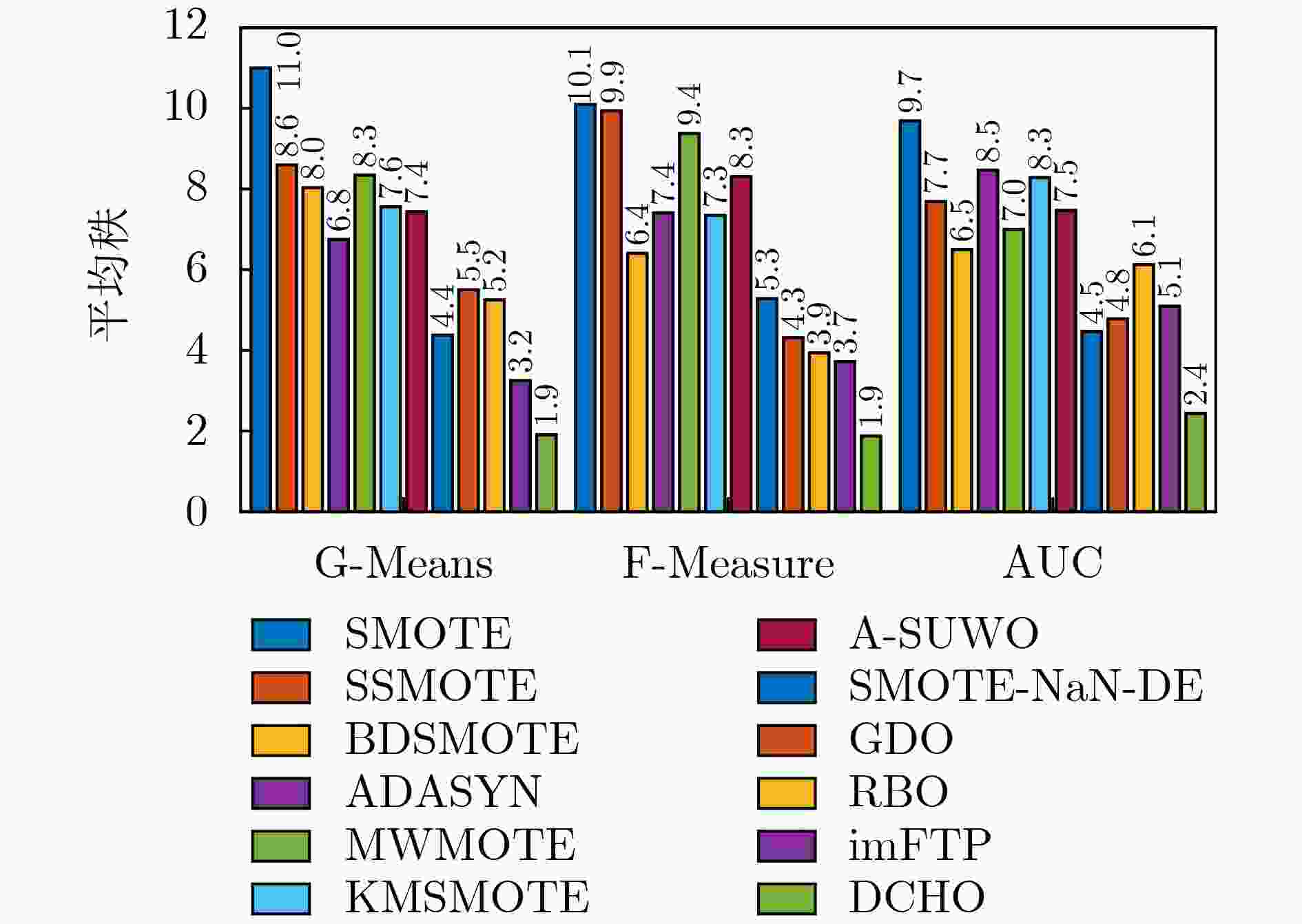
指标 方法 BPNN LDA SVM $ {\alpha }_{0.05} $ p-value $ {\alpha }_{0.05} $ p-value $ {\alpha }_{0.05} $ p-value G-Mean SMOTE 0.005 1 5.059 3e–14 0.005 6 2.121 9e–10 0.004 6 8.185 5e–20 SSMOTE 0.008 5 3.924 6e–09 0.010 2 5.118 2e–07 0.005 1 1.930 8e–12 BDSMOTE 0.005 6 1.026 2e–12 0.004 6 7.117 8e–12 0.006 3 7.305 8e–11 ADASYN 0.010 2 1.867 7e–08 0.016 9 1.513 7e–05 0.010 2 1.425 5e–07 MWMOTE 0.007 3 8.807 2e–12 0.005 1 7.387 0e–11 0.005 6 9.903 9e–12 KMSMOTE 0.004 6 4.126 4e–14 0.006 3 3.847 3e–09 0.007 3 1.319 8e–09 A-SUWO 0.006 3 1.854 6e–12 0.007 3 1.033 4e–08 0.008 5 2.791 6e–09 SMOTE-NaN-DE 0.025 3 4.103 0e–04 0.025 3 1.941 6e–03 0.025 3 5.795 1e–03 GDO 0.012 7 7.605 7e–06 0.012 7 6.725 0e–06 0.012 7 7.167 1e–05 RBO 0.016 9 8.786 1e–06 0.008 5 8.222 8e–08 0.016 9 2.113 1e–04 imFTP 0.05 0.044 9 0.05 0.183 7 0.05 0.130 2 F-measure SMOTE 0.004 6 3.998 2e–16 0.004 6 3.995 9e–17 0.004 6 1.506 4e–18 SSMOTE 0.008 5 1.095 5e–12 0.005 6 1.222 8e–13 0.005 1 5.028 4e–18 BDSMOTE 0.010 2 1.217 4e–06 0.012 7 8.114 6e–05 0.010 2 1.857 1e–07 ADASYN 0.007 3 1.591 7e–13 0.010 2 2.466 3e–08 0.007 3 3.965 8e–10 MWMOTE 0.005 1 2.424 1e–15 0.005 1 2.141 8e–14 0.005 7 3.626 4e–16 KMSMOTE 0.005 6 9.230 1e–15 0.007 3 5.281 4e–11 0.008 5 5.949 9e–10 A-SUWO 0.006 3 1.281 8e–13 0.006 3 1.037 9e–12 0.006 4 8.421 2e–13 SMOTE-NaN-DE 0.012 7 3.232 4e–05 0.008 5 9.650 7e–11 0.012 7 6.825 2e–05 GDO 0.025 3 9.487 2e–04 0.025 3 1.139 1e–02 0.016 9 3.974 0e–03 RBO 0.016 9 3.012 5e–04 0.016 9 8.401 2e–03 0.025 3 1.448 4e–02 imFTP 0.05 0.0483 0.05 0.038 1 0.05 0.028 5 AUC SMOTE 0.004 6 8.664 1e–20 0.005 1 6.308 3e–09 0.004 6 1.386 9e–11 SSMOTE 0.007 3 3.810 4e–10 0.005 6 1.629 9e–08 0.006 3 4.666 2e–07 BDSMOTE 0.008 5 7.865 0e–10 0.006 3 1.906 0e–08 0.010 2 7.684 4e–05 ADASYN 0.006 3 1.830 7e–10 0.016 9 4.235 2e–06 0.005 1 1.013 7e–08 MWMOTE 0.010 2 4.634 2e–09 0.010 2 1.618 9e–06 0.008 5 1.003 4e–05 KMSMOTE 0.005 1 6.136 5e–12 0.008 5 2.168 1e–07 0.005 6 2.621 1e–08 A-SUWO 0.005 6 1.522 2e–10 0.012 7 3.227 5e–06 0.007 3 1.279 2e–06 SMOTE-NaN-DE 0.025 3 4.715 8e–06 0.025 3 1.831 5e–04 0.05 0.044 5 GDO 0.012 7 5.944 4e–08 0.004 6 1.144 5e–13 0.025 3 2.064 7e–02 RBO 0.016 9 1.428 3e–06 0.007 3 7.611 1e–08 0.012 7 3.151 5e–04 imFTP 0.05 0.015 4 0.05 0.017 2 0.016 9 8.858 5e–03 表 4 使用不同采样策略的DCHO算法统计对比结果
数据集 DCHO-SMOTE DCHO-RAN DCHO Liver 0.638 2±0.044 1 ($\approx $) 0.623 7±0.057 7 (+) 0.639 4±0.040 7 Pima 0.735 2±0.030 1 (+) 0.735 3±0.028 1 (+) 0.748 5±0.026 5 Yeast 0.713 6±0.029 0 (+) 0.701 1±0.027 4 (+) 0.731 3±0.020 3 Wine 0.742 1±0.028 9 ($\approx $) 0.739 8±0.020 7 (+) 0.756 2±0.076 6 Haberman 0.619 4±0.053 2 ($\approx $) 0.601 1±0.051 1 (+) 0.622 8±0.040 5 Spect 0.742 5±0.043 5 ($ + $) 0.754 3±0.045 9 ($\approx $) 0.758 4±0.038 5 Yeast1 0.754 2±0.044 1 (+) 0.749 7±0.050 0 (+) 0.774 1±0.037 6 Traffic 0.882 4±0.032 4 (+) 0.888 0±0.032 9 ($\approx $) 0.893 5±0.028 6 Pageblock 0.864 0±0.043 8 ($ + $) 0.844 8±0.043 9 ($ + $) 0.869 6±0.043 6 Blabance 0.422 6±0.045 8 ($\approx $) 0.430 4±0.043 0 (+) 0.451 0±0.042 9 Libra 0.775 4±0.046 5 ($ + $) 0.772 1±0.048 4 ($ + $) 0.790 5±0.042 2 Seer 0.727 5±0.050 5 ($ + $) 0.728 1±0.050 2 ($ + $) 0.747 7±0.048 6 Yeast5 0.761 4±0.042 0 (+) 0.755 9±0.050 5 (+) 0.735 8±0.050 1 Yeast6 0.799 8±0.048 2 ($ + $) 0.806 8±0.051 7 ($ + $) 0.825 0±0.044 8 Sensors 0.799 2±0.053 2 (+) 0.799 2±0.054 6 (+) 0.824 2±0.049 2 Iot1 0.912 0±0.053 6 ($\approx $) 0.914 8±0.053 5 ($\approx $) 0.917 1±0.046 0 +/–/$\approx $ 11/0/5 13/0/3 -
[1] CHEN Zhuohang, CHEN Jinglong, FENG Yong, et al. Imbalance fault diagnosis under long-tailed distribution: Challenges, solutions and prospects[J]. Knowledge-Based Systems, 2022, 258: 110008. doi: 10.1016/J.KNOSYS.2022.110008. [2] CHEN Zheng, YANG Chen, ZHU Meilu, et al. Personalized retrogress-resilient federated learning toward imbalanced medical data[J]. IEEE Transactions on Medical Imaging, 2022, 41(12): 3663–3674. doi: 10.1109/TMI.2022.3192483. [3] TENG Hu, WANG Cheng, YANG Qing, et al. Leveraging adversarial augmentation on imbalance data for online trading fraud detection[J]. IEEE Transactions on Computational Social Systems, 2024, 11(2): 1602–1614. doi: 10.1109/TCSS.2023.3240968. [4] BLANCHARD A E, GAO Shang, YOON H J, et al. A keyword-enhanced approach to handle class imbalance in clinical text classification[J]. IEEE Journal of Biomedical and Health Informatics, 2022, 26(6): 2796–2803. doi: 10.1109/JBHI.2022.3141976. [5] CHEN M F, NACHMAN B, and SALA F. Resonant anomaly detection with multiple reference datasets[J]. Journal of High Energy Physics, 2023, 2023(7): 188. doi: 10.1007/JHEP07(2023)188. [6] 高雷阜, 张梦瑶, 赵世杰. 融合簇边界移动与自适应合成的混合采样算法[J]. 电子学报, 2022, 50(10): 2517–2529. doi: 10.12263/DZXB.20210265.GAO Leifu, ZHANG Mengyao, and ZHAO Shijie. Mixed-sampling algorithm combining cluster boundary movement and adaptive synthesis[J]. Acta Electronica Sinica, 2022, 50(10): 2517–2529. doi: 10.12263/DZXB.20210265. [7] 职为梅, 常智, 卢俊华, 等. 面向不平衡图像数据的对抗自编码器过采样算法[J]. 电子与信息学报, 2024, 46(11): 4208–4218. doi: 10.11999/JEIT240330.ZHI Weimei, CHANG Zhi, LU Junhua, et al. Adversarial autoencoders oversampling algorithm for imbalanced image data[J]. Journal of Electronics & Information Technology, 2024, 46(11): 4208–4218. doi: 10.11999/JEIT240330. [8] DU Guodong, ZHANG Jia, JIANG Min, et al. Graph-based class-imbalance learning with label enhancement[J]. IEEE Transactions on Neural Networks and Learning Systems, 2023, 34(9): 6081–6095. doi: 10.1109/TNNLS.2021.3133262. [9] JIN Xiaoyu, XIAO Fu, ZHANG Chong, et al. GEIN: An interpretable benchmarking framework towards all building types based on machine learning[J]. Energy and Buildings, 2022, 260: 111909. doi: 10.1016/J.ENBUILD.2022.111909. [10] 李帆, 张小恒, 李勇明, 等. 基于包络学习和分级结构一致性机制的不平衡集成算法[J]. 电子学报, 2024, 52(3): 751–761. doi: 10.12263/DZXB.20220712.LI Fan, ZHANG Xiaoheng, LI Yongming, et al. Imbalanced ensemble algorithm based on envelope learning and hierarchical structure consistency mechanism[J]. Acta Electronica Sinica, 2024, 52(3): 751–761. doi: 10.12263/DZXB.20220712. [11] LI Yanjiao, ZHANG Jie, ZHANG Sen, et al. Multi-objective optimization-based adaptive class-specific cost extreme learning machine for imbalanced classification[J]. Neurocomputing, 2022, 496: 107–120. doi: 10.1016/J.NEUCOM.2022.05.008. [12] 孙中彬, 刁宇轩, 马苏洋. 基于安全欠采样的不均衡多标签数据集成学习方法[J]. 电子学报, 2024, 52(10): 3392–3408. doi: 10.12263/DZXB.20240210.SUN Zhongbin, DIAO Yuxuan, and MA Suyang. An imbalanced multi-label data ensemble learning method based on safe under-sampling[J]. Acta Electronica Sinica, 2024, 52(10): 3392–3408. doi: 10.12263/DZXB.20240210. [13] TAO Xinmin, CHEN Wei, ZHANG Xiaohan, et al. SVDD boundary and DPC clustering technique-based oversampling approach for handling imbalanced and overlapped data[J]. Knowledge-Based Systems, 2021, 234: 107588. doi: 10.1016/J.KNOSYS.2021.107588. [14] SUN Zhongqiang, YING Wenhao, ZHANG Wenjin, et al. Undersampling method based on minority class density for imbalanced data[J]. Expert Systems with Applications, 2024, 249: 123328. doi: 10.1016/J.ESWA.2024.123328. [15] MA Tingting, LU Shuxia, and JIANG Chen. A membership-based resampling and cleaning algorithm for multi-class imbalanced overlapping data[J]. Expert Systems with Applications, 2024, 240: 122565. doi: 10.1016/J.ESWA.2023.122565. [16] TAO Xinmin, GUO Xinyue, ZHENG Yujia, et al. Self-adaptive oversampling method based on the complexity of minority data in imbalanced datasets classification[J]. Knowledge-Based Systems, 2023, 277: 110795. doi: 10.1016/J.KNOSYS.2023.110795. [17] LÓPEZ V ,FERNÁNDEZ A ,GARCÍA S, et al. An insight into classification with imbalanced data: Empirical results and current trends on using data intrinsic characteristics[J]. Information Sciences, 2013, 250: doi: 10.1016/j.ins.2013.07.007113-141. 2. [18] TAO Xinmin, ZHANG Xiaohan, ZHENG Yujia, et al. A MeanShift-guided oversampling with self-adaptive sizes for imbalanced data classification[J]. Information Sciences, 2024, 672: 120699. doi: 10.1016/J.INS.2024.120699. [19] JIANG Zhen, ZHAO Lingyun, LU Yu, et al. A semi-supervised resampling method for class-imbalanced learning[J]. Expert Systems with Applications, 2023, 221: 119733. doi: 10.1016/J.ESWA.2023.119733. [20] BUNKHUMPORNPAT C, SINAPIROMSARAN K, and LURSINSAP C. Safe-Level-SMOTE: Safe-level-synthetic minority over-sampling TEchnique for handling the class imbalanced problem[C]. The 13th Pacific-Asia Conference on Advances in Knowledge Discovery and Data Mining, Bangkok, Thailand, 2009. doi: 10.1007/978-3-642-01307-2_43. [21] LI Min, ZHOU Hao, LIU Qun, et al. WRND: A weighted oversampling framework with relative neighborhood density for imbalanced noisy classification[J]. Expert Systems with Applications, 2024, 241: 122593. doi: 10.1016/j.eswa.2023.122593. [22] PAN Tingting, ZHAO Junhong, WU Wei, et al. Learning imbalanced datasets based on SMOTE and Gaussian distribution[J]. Information Sciences, 2020, 512: 1214–1233. doi: 10.1016/j.ins.2019.10.048. [23] HAN Hui, WANG Wenyuan, and MAO Binghua. Borderline-SMOTE: A new over-sampling method in imbalanced data sets learning[C]. The International Conference on Intelligent Computing Advances in Intelligent Computing, Hefei, China, 2005: 878–887. doi: 10.1007/11538059_91. [24] HE Haibo, BAI Yang, GARCIA E A, et al. ADASYN: Adaptive synthetic sampling approach for imbalanced learning[C]. 2008 IEEE International Joint Conference on Neural Networks, Hong Kong, China, 2008: 1322–1328. doi: 10.1109/IJCNN.2008.4633969. [25] BARUA S, ISLAM M, YAO Xin, et al. MWMOTE--majority weighted minority oversampling technique for imbalanced data set learning[J]. IEEE Transactions on Knowledge and Data Engineering, 2014, 26(2): 405–425. doi: 10.1109/TKDE.2012.232. [26] MATHARAARACHCHI S, DOMARATZKI M, and MUTHUKUMARANA S. Enhancing SMOTE for imbalanced data with abnormal minority instances[J]. Machine Learning with Applications, 2024, 18: 100597. doi: 10.1016/J.MLWA.2024.100597. [27] KOZIARSKI M, KRAWCZYK B, and WOŹNIAK M. Radial-Based oversampling for noisy imbalanced data classification[J]. Neurocomputing, 2019, 343: 19–33. doi: 10.1016/j.neucom.2018.04.089. [28] DOUZAS G and BACAO F. Geometric SMOTE a geometrically enhanced drop-in replacement for SMOTE[J]. Information Sciences, 2019, 501: 118–135. doi: 10.1016/j.ins.2019.06.007. [29] XIE Yuxi, QIU Min, ZHANG Haibo, et al. Gaussian distribution based oversampling for imbalanced data classification[J]. IEEE Transactions on Knowledge and Data Engineering, 2022, 34(2): 667–679. doi: 10.1109/tkde.2020.2985965. [30] HOU Yaxin, DING Weiping, and ZHANG Chongsheng. imFTP: Deep imbalance learning via fuzzy transition and prototypical learning[J]. Information Sciences, 2024, 679: 121071. doi: 10.1016/J.INS.2024.121071. [31] LI Chuang, MAO Zhizhong, and JIA Mingxing. A real-valued label noise cleaning method based on ensemble iterative filtering with noise score[J]. International Journal of Machine Learning and Cybernetics, 2024, 15(9): 4093–4118. doi: 10.1007/S13042-024-02137-Z. [32] LAURIKKALA J. Improving identification of difficult small classes by balancing class distribution[C]. The 8th Conference on Artificial Intelligence in Medicine in Europe Artificial Intelligence in Medicine, Cascais, Portugal, 2001: 63–66. doi: 10.1007/3-540-48229-6_9. [33] NAPIERAŁA K, STEFANOWSKI J, and WILK S. Learning from imbalanced data in presence of noisy and borderline examples[C]. The 7th International Conference on Rough Sets and Current Trends in Computing, Warsaw, Poland, 2010: 158–167. doi: 10.1007/978-3-642-13529-3_18. [34] SÁEZ J A, LUENGO J, STEFANOWSKI J, et al. SMOTE-IPF: Addressing the noisy and borderline examples problem in imbalanced classification by a re-sampling method with filtering[J]. Information Sciences, 2015, 291: 184–203. doi: 10.1016/j.ins.2014.08.051. [35] LI Junnan, ZHU Qingsheng, WU Quanwang, et al. SMOTE-NaN-DE: Addressing the noisy and borderline examples problem in imbalanced classification by natural neighbors and differential evolution[J]. Knowledge-Based Systems, 2021, 223: 107056. doi: 10.1016/J.KNOSYS.2021.107056. [36] SHI Hua, WU Chenjin, BAI Tao, et al. Identify essential genes based on clustering based synthetic minority oversampling technique[J]. Computers in Biology and Medicine, 2023, 153: 106523. doi: 10.1016/J.COMPBIOMED.2022.106523. [37] DOUZAS G, BACAO F, and LAST F. Improving imbalanced learning through a heuristic oversampling method based on k-means and SMOTE[J]. Information Sciences, 2018, 465: 1–20. doi: 10.1016/j.ins.2018.06.056. [38] SONG Jia, HUANG Xianglin, QIN Sijun, et al. A bi-directional sampling based on K-means method for imbalance text classification[C]. 2016 IEEE/ACIS 15th International Conference on Computer and Information Science, Okayama, Japan, 2016: 1–5. doi: 10.1109/ICIS.2016.7550920. [39] NEKOOEIMEHR I and LAI-YUEN S K. Adaptive semi-unsupervised weighted oversampling (A-SUWO) for imbalanced datasets[J]. Expert Systems with Applications, 2016, 46: 405–416. doi: 10.1016/j.eswa.2015.10.031. [40] WEI Jianan, HUANG Haisong, YAO Liguo, et al. IA-SUWO: An improving adaptive semi-unsupervised weighted oversampling for imbalanced classification problems[J]. Knowledge-Based Systems, 2020, 203: 106116. doi: 10.1016/j.knosys.2020.106116. [41] RODRIGUEZ A and LAIO A. Clustering by fast search and find of density peaks[J]. Science, 2014, 344(6191): 1492–1496. doi: 10.1126/science.1242072. [42] Machine learning repository UCI[EB/OL]. http://archive.ics.uci.edu/ml/datasets.html. -





 下载:
下载:


 下载:
下载:
