Gas Station Inspection Task Allocation Algorithm in Digital Twin-assisted Reinforcement Learning
-
摘要: 针对燃气站场机器人智能巡检过程中由于突发任务导致的巡检效率下降、任务延迟和能耗增加问题,该文提出基于数字孪生辅助强化学习的燃气站场巡检任务分配算法。首先基于多机器人、差异化任务的执行状况,建立面向能耗、任务延迟的多目标联合优化巡检任务分配模型;其次利用李雅普诺夫理论对时间-能耗耦合下的巡检目标进行解耦,简化多目标联合优化问题;最后通过结合数字孪生技术和PPO(Proximal Policy Optimization)算法,对解耦后的优化目标进行求解来构建多机器人巡检任务分配策略。仿真结果表明,与现有方法相比,所提方法具有较高的任务完成率,有效地提高了多机器人系统的巡检效率。Abstract:
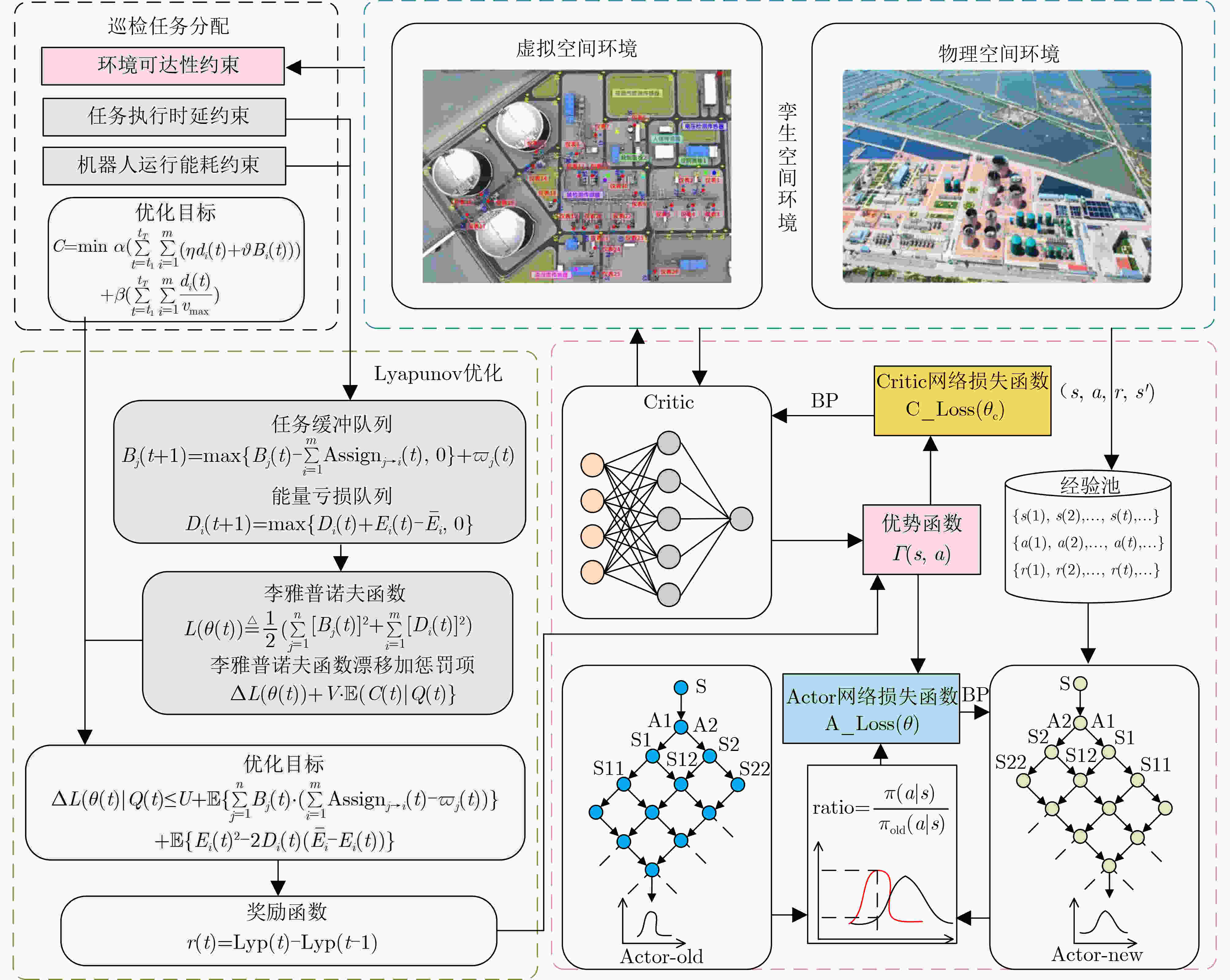
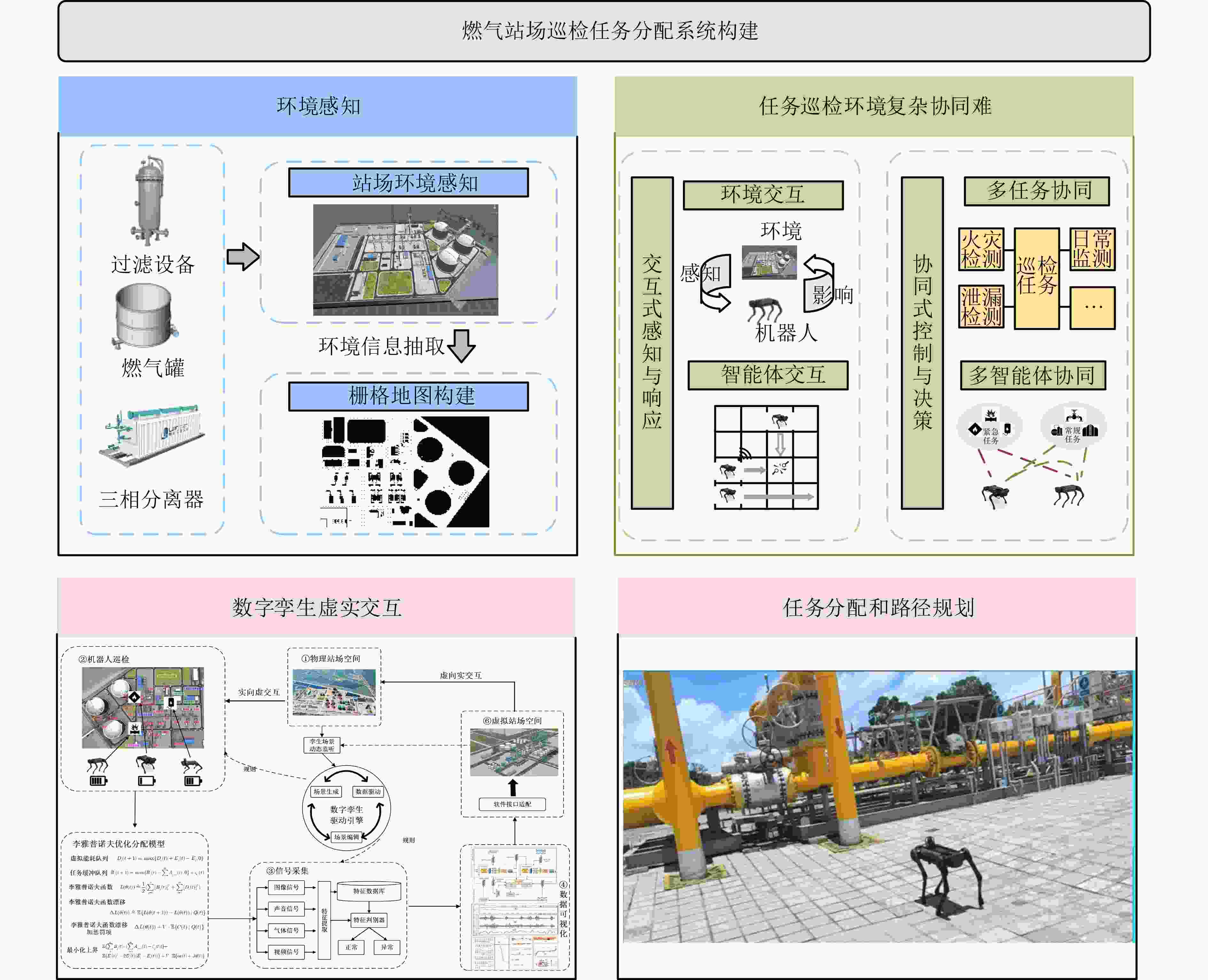
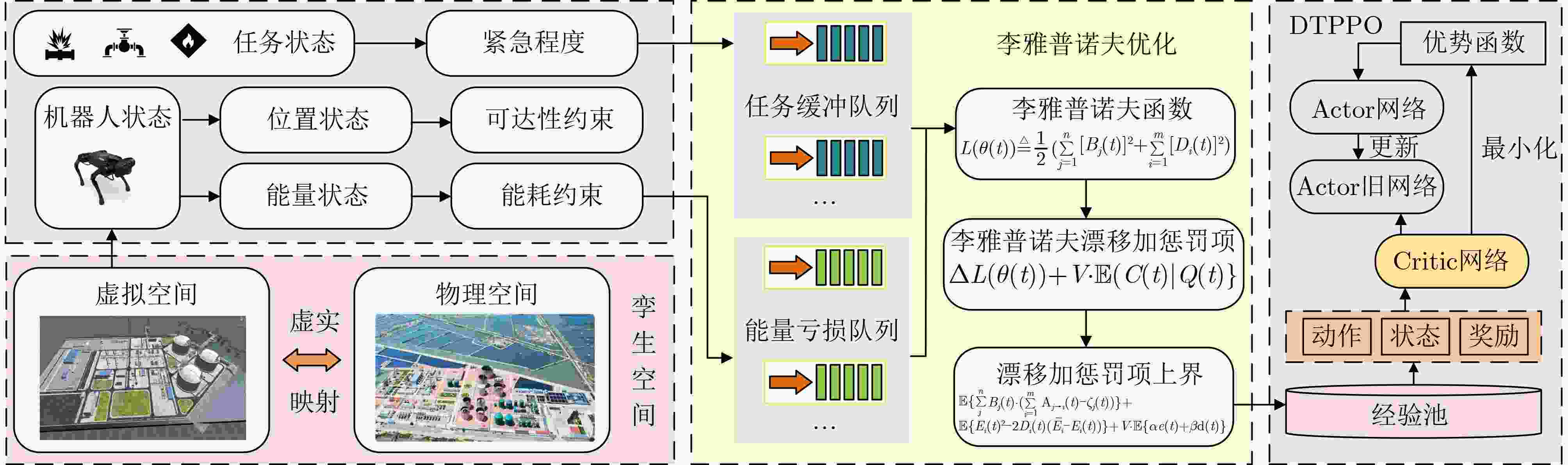
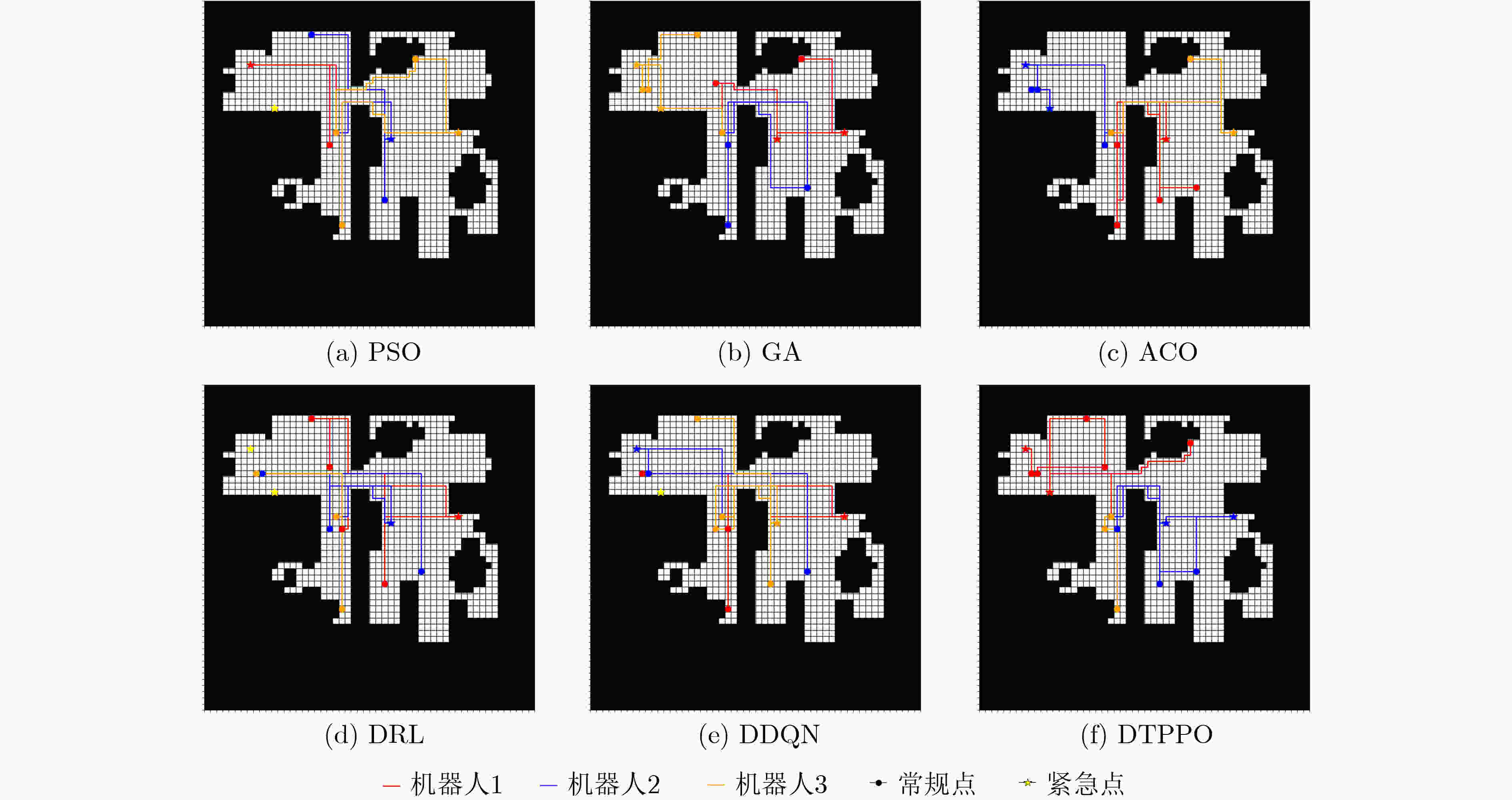
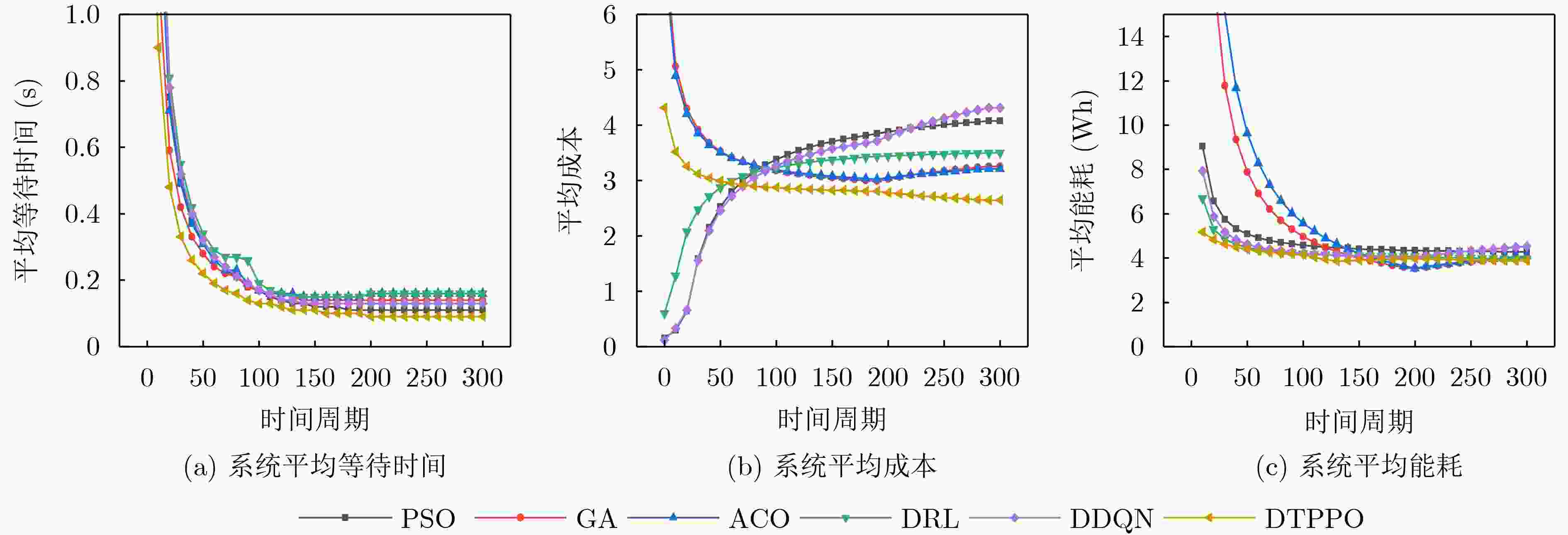
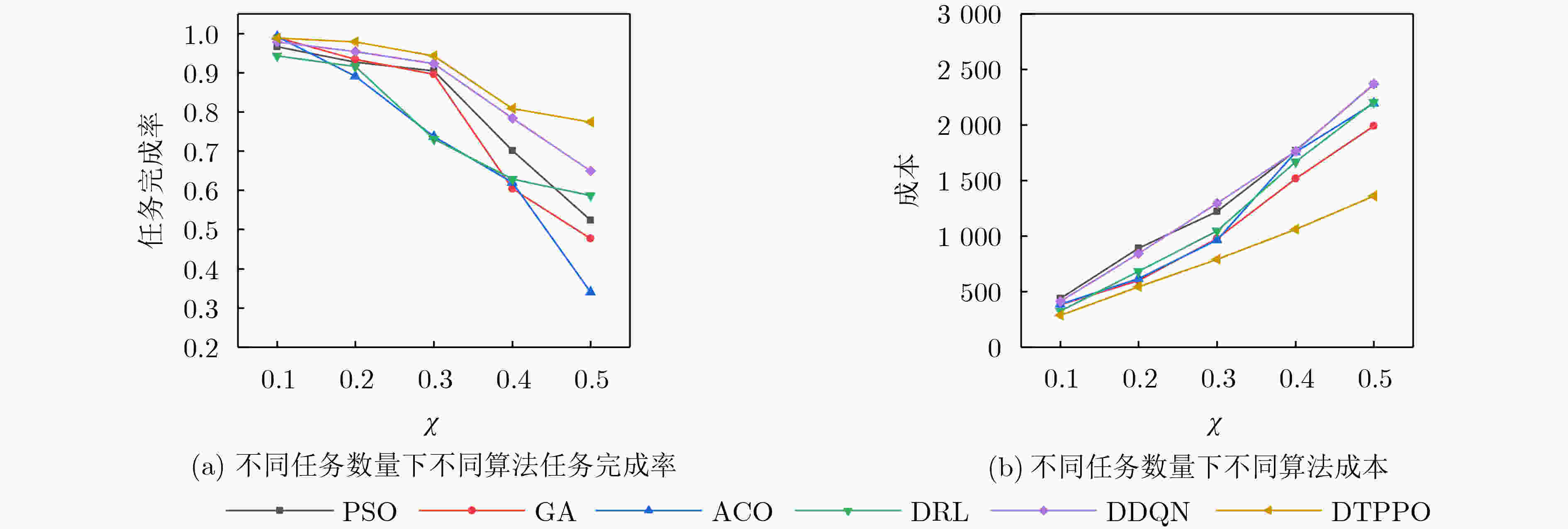
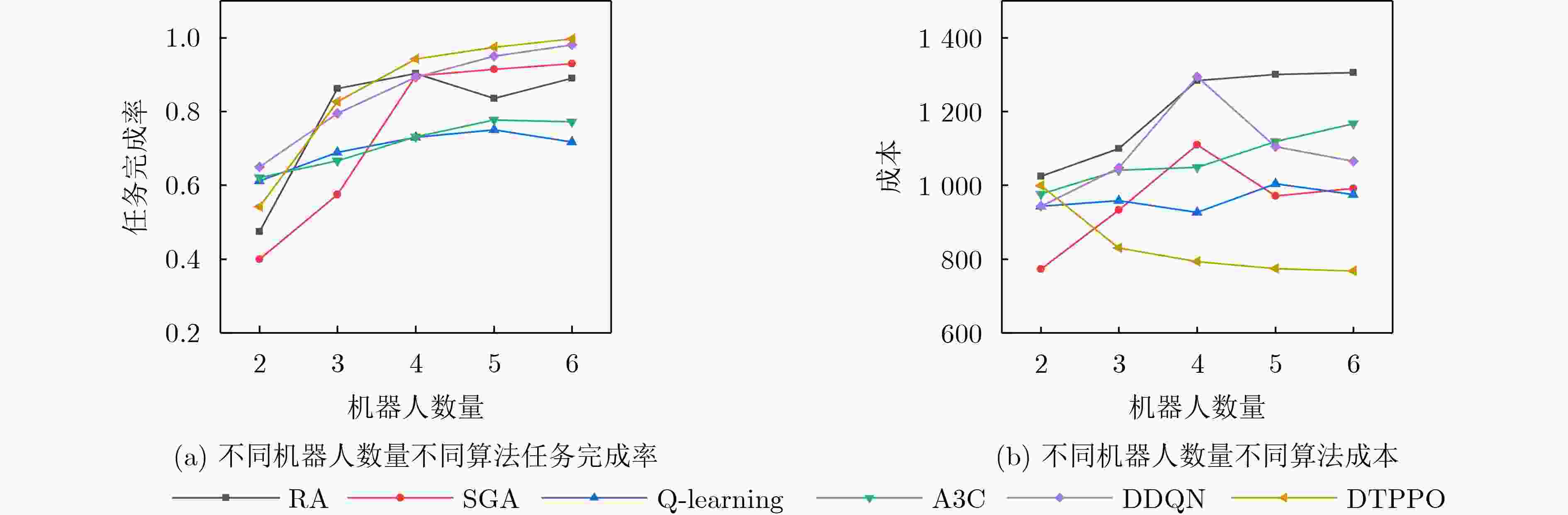
Objective With the increasing quantity of equipment in gas stations and the growing demand for safety, Multi-Robot Task Allocation (MRTA) has become essential for improving inspection efficiency. Although existing MRTA algorithms offer basic allocation strategies, they have limited capacity to respond to emergent tasks and to manage energy consumption effectively. To address these limitations, this study integrates digital twin technology with a reinforcement learning framework. By incorporating Lyapunov optimization and decoupling the optimization objectives, the proposed method improves inspection efficiency while maintaining a balance between robot energy use and task delay. This approach enhances task allocation in complex gas station scenarios and provides theoretical support for intelligent unmanned management systems in such environments. Methods The DTPPO algorithm constructs a multi-objective joint optimization model for inspection task allocation, with energy consumption and task delay as the primary criteria. The model considers the execution performance of multiple robots and the characteristics of heterogeneous tasks. Lyapunov optimization theory is then applied to decouple the time-energy coupling constraints of the inspection objectives. Using the Lyapunov drift-plus-penalty framework, the algorithm balances task delay and energy consumption, which simplifies the original joint optimization problem. The decoupled objectives are solved using a strategy that combines digital twin technology with the Proximal Policy Optimization (PPO) algorithm, resulting in a task allocation policy for multi-robot inspection in gas station environments. Results and Discussions The DTPPO algorithm decouples long-term energy consumption and time constraints using Lyapunov optimization, incorporating their variations into the reward function of the reinforcement learning model. Simulation results show that the Pathfinding inspection path ( Fig. 4 ) generated by the DTPPO algorithm improves the task completion rate by 1.94% compared to benchmark experiments. In complex gas station environments (Fig. 5 ), the algorithm achieves a 1.92% improvement. When the task quantity parameter is set between 0.1 and 0.5 (Fig. 8 ), the algorithm maintains a high task completion rate even under heavy load. With 2 to 6 robots (Fig. 9 ), the algorithm demonstrates strong adaptability and effectiveness in resource-constrained scenarios.Conclusions This study addresses the coupling between energy consumption and time by decoupling the objective function constraints through Lyapunov optimization. By incorporating the variation of Lyapunov drift-plus-penalty terms into the reward function of reinforcement learning, a digital twin-assisted reinforcement learning algorithm, named DTPPO, is proposed. The method is evaluated in multiple simulated environments, and the results show the following: (1) The proposed approach achieves a 1.92% improvement in task completion rate compared to the DDQN algorithm; (2) Lyapunov optimization improves performance by 5.89% over algorithms that rely solely on reinforcement learning; (3) The algorithm demonstrates good adaptability and effectiveness under varying task quantities and robot numbers. However, this study focuses solely on Lyapunov theory, and future research should explore the integration of Lyapunov optimization with other algorithms to further enhance MRTA methods. -
Key words:
- Gas station /
- Digital twin(DT) /
- Task allocation /
- Lyapunov /
- Proximal Policy Optimization(PPO)
-
表 1 参数符号定义
参数 含义 参数 含义 $\tau = \{ {t_1},{t_2}, \cdots ,{t_T}\} $ 时隙集合 $Q$ 多级任务队列 $M$ 机器人数量 $N$ 巡检目标数量 ${\text{QR}} = \{ {q_1},{q_2}, \cdots {q_m}\} $ 机器人集合 $\varpi $ 任务接收速率 $ g(h,w) $ 站场栅格环境可达性 $\delta $ 任务产生速率 $ (h,w) $ 站场栅格位置坐标 $B$ 任务缓冲队列 $x$ 机器人在站场中位置横坐标 $D$ 能量亏损队列 $y$ 机器人在站场中位置纵坐标 ${E_{{\text{system}}}}$ 系统能耗 $\vartheta $ 单位巡检点的信息处理能耗 $\eta $ 机器人单位移动距离能耗 $v$ 机器人行动速度 ${F_{{\text{time}}}}$ 任务完成时间 $d$ 机器人在站场中累计移动距离 $C$ 目标函数 ${\text{direction}}$ 机器人运动方向 ${\text{Assig}}{{\text{n}}_{j \to i}}$ 任务分配策略 ${\text{track}}$ 机器人轨迹坐标集合 $L(\theta (t))$ 李雅普诺夫函数 ${\text{energy}}$ 机器人消耗能量 ${\text{ratio}}$ 裁剪比率 $P = \{ {p_1},{p_2}, \cdots ,{p_n}\} $ 巡检任务集合 ${\text{clip}}$ 裁剪函数 ${\text{type}}$ 巡检任务类型 $\varepsilon $ 裁剪因子 $ {\text{location}} $ 巡检任务位置 $\pi $ 采取动作的概率 ${\text{last}}$ 巡检任务持续时间 $\varphi $ 时间缩放因子 1 DTPPO算法
输入:权重系数$V$,比例系数$\alpha $ 输出:分配策略$A$ (1)初始化${\mathrm{QR}}$, $P$, $Q$, $D$, $\pi $ (2)for big_episode=0,1,2,···,m do (3) for small_episode=0,1,2,···,n do (4) 从虚拟状态空间中获取${s^t}$,根据$\pi (\theta )$选择动作 (5) 由式(30) 计算孪生空间奖励$r$,存储$[(s,a,r),].s\_$ (6) 根据$r$,${s^{t + 1}}$,$\gamma $更新 Actor网络 (7) 从物理状态空间中获取${s^t}$,根据$\pi (\theta )$选择动作 (8) 计算物理空间奖励$r$,存储 $[(s,a,r),].s\_$ (9) 根据$r$,${s^{t + 1}}$更新Critic网络 (10) end for (11) 根据${\hat A_{{\pi _{{\text{old}}}}}}({s_t},{a_t}) =\displaystyle\sum\nolimits_{t' > t} {{\gamma ^{t' - t}}} {r_{t'}} - {V_{{\pi _{{\text{old}}}}}}({s_t})$更新
Critic,优化值函数(12) for l=0,1,2,···,o do (13) 由式(25)更新Actor (14) 通过clip函数来控制更新的稳定性 (15) end for (16) ${\pi _{{\mathrm{old}}}} \leftarrow \pi $ (17)end 表 2 仿真参数及超参数设置
参数名称 参数设置 参数名称 参数设置 $\chi $ 0.3 ${\text{l}}{{\text{r}}_{{\text{policy}}}}$ 0.0003 $\alpha $ 0.5 ${\text{l}}{{\text{r}}_{{\text{value}}}}$ 0.0003 $\beta $ 0.5 $\gamma $ 0.99 $m$ 4 $\varepsilon $ 0.2 ${v_{\max }}$ 60 $\eta $ 0.001 ${G_{{\text{clip}}}}$ 0.5 ${\beta _H}$ 0.01 $ B $ 256 ${\beta _V}$ 0.5 表 3 Pathfinding数据集任务分配算法分析结果
方法 任务完成率(%)↑ 系统能耗(Wh)↓ 任务平均等待时间(min)↓ 成本C↓ 移动距离(m)↓ PSO 92.85 118.47 2.08 68.23 226.30 GA 91.74 109.23 5.88 70.99 239.42 ACO 93.24 106.68 7.97 85.04 185.15 DRL 95.52 124.86 10.16 72.59 216.89 DDQN 95.97 123.04 8.31 61.69 233.20 DTPPO 97.91 92.11 1.50 58.49 205.58 表 4 燃气站场任务分配算法分析结果
方法 时间周期 任务完成率(%)↑ 系统能耗(Wh)↓ 任务平均等待时间(min)↓ 成本C↓ 移动距离(m)↓ PSO 100 83.57 458.09 14.15 328.09 8303.40 200 79.62 866.55 24.87 769.07 18767.80 300 90.25 1283.96 29.08 1223.68 29949.30 GA 100 92.85 496.68 10.54 322.14 5858.70 200 85.55 701.39 18.33 598.24 14039.60 300 89.62 1209.99 21.07 976.45 25038.59 ACO 100 87.14 557.60 13.50 323.30 5343.00 200 71.11 709.01 22.27 605.15 12725.80 300 73.75 1226.27 25.03 963.73 20456.80 DRL 100 76.57 419.71 15.64 319.36 7892.35 200 70.70 811.68 20.80 686.65 18238.97 300 73.15 1185.61 22.81 1049.13 27796.10 DDQN 100 94.68 421.49 15.19 317.08 7802.36 200 93.52 801.84 25.23 741.58 17827.04 300 92.34 1359.78 35.69 1293.77 27843.77 DTPPO 100 96.13 376.86 8.55 288.36 5186.44 200 94.57 794.05 16.76 560.86 10777.12 300 94.26 1161.20 22.30 793.19 15663.63 表 5 消融实验结果
方法 任务完成率(%) 系统能耗 等待时间 成本 移动距离 RA 77.60 2238.04 576.23 1407.13 33703.72 Ly 77.45 1230.86 643.06 468.48 17230.30 DTPPO 88.37 1289.24 486.71 887.97 17786.83 Ly+DTPPO 94.26 1161.20 425.18 793.19 15663.63 -
[1] SHUKLA A and KARKI H. A review of robotics in onshore oil-gas industry[C]. 2013 IEEE International Conference on Mechatronics and Automation, Takamatsu, Japan, 2013: 1153–1160. doi: 10.1109/ICMA.2013.6618077. [2] GERKEY B P and MATARIĆ M J. A formal analysis and taxonomy of task allocation in multi-robot systems[J]. The International Journal of Robotics Research, 2004, 23(9): 939–954. doi: 10.1177/0278364904045564. [3] GAO Jianqi, LI Yanjie, XU Yunhong, et al. A two-objective ILP model of OP-MATSP for the multi-robot task assignment in an intelligent warehouse[J]. Applied Sciences, 2022, 12(10): 4843. doi: 10.3390/app12104843. [4] TOTH P and VIGO D. Vehicle Routing: Problems, Methods, and Applications[M]. 2nd ed. Philadelphia: Society for Industrial and Applied Mathematics, 2014. [5] DIAS M B, ZLOT R, KALRA N, et al. Market-based multirobot coordination: A survey and analysis[J]. Proceedings of the IEEE, 2006, 94(7): 1257–1270. doi: 10.1109/JPROC.2006.876939. [6] SCHNEIDER E, SKLAR E I, PARSONS S, et al. Auction-based task allocation for multi-robot teams in dynamic environments[C]. The 16th Annual Conference on Towards Autonomous Robotic Systems, Liverpool, UK, 2015: 246–257. doi: 10.1007/978-3-319-22416-9_29. [7] GHASSEMI P and CHOWDHURY S. Decentralized task allocation in multi-robot systems via bipartite graph matching augmented with fuzzy clustering[C]. International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Quebec, Canada, 2018: V02AT03A014. doi: 10.1115/DETC2018-86161. [8] GHASSEMI P, DEPAUW D, and CHOWDHURY S. Decentralized dynamic task allocation in swarm robotic systems for disaster response: Extended abstract[C]. 2019 International Symposium on Multi-Robot and Multi-Agent Systems (MRS), New Brunswick, USA, 2019: 83–85. doi: 10.1109/MRS.2019.8901062. [9] XIAO Kun, LU Junqi, NIE Ying, et al. A benchmark for multi-UAV task assignment of an extended team orienteering problem[C]. 2022 China Automation Congress (CAC), Xiamen, China, 2022: 6966–6970. doi: 10.1109/CAC57257.2022.10054991. [10] KOENIG S, TOVEY C, LAGOUDAKIS M, et al. The power of sequential single-item auctions for agent coordination[C]. Proceedings of the 21st National Conference on Artificial Intelligence-Volume 2, Boston Massachusetts, USA, 2006: 1625–1629. [11] GAUTIER P, LAURENT J, and DIGUET J P. DQN as an alternative to Market-based approaches for Multi-Robot processing Task Allocation (MRpTA)[J]. International Journal of Robotic Computing, 2021, 3(1): 69–98. doi: 10.35708/rc1870-126266. [12] AGRAWAL A, BEDI A S, and MANOCHA D. RTAW: An attention inspired reinforcement learning method for multi-robot task allocation in warehouse environments[C]. 2023 IEEE International Conference on Robotics and Automation (ICRA), London, United Kingdom, 2023: 1393–1399. doi: 10.1109/ICRA48891.2023.10161310. [13] STRENS M and WINDELINCKX N. Combining planning with reinforcement learning for multi-robot task allocation[M]. KUDENKO D, KAZAKOV D, and ALONSO E. Adaptive Agents and Multi-Agent Systems II: Adaptation and Multi-Agent Learning. Berlin, Heidelberg: Springer, 2005: 260–274. doi: 10.1007/978-3-540-32274-0_17. [14] HERSI A H and UDAYAN J D. Efficient and robust multirobot navigation and task allocation using soft actor critic[J]. Procedia Computer Science, 2024, 235: 484–495. doi: 10.1016/j.procs.2024.04.048. [15] AZIZ H, PAL A, POURMIRI A, et al. Task allocation using a team of robots[J]. Current Robotics Reports, 2022, 3(4): 227–238. doi: 10.1007/s43154-022-00087-4. [16] TAO Fei, XIAO Bin, QI Qinglin, et al. Digital twin modeling[J]. Journal of Manufacturing Systems, 2022, 64: 372–389. doi: 10.1016/j.jmsy.2022.06.015. [17] LEE D, LEE S, MASOUD N, et al. Digital twin-driven deep reinforcement learning for adaptive task allocation in robotic construction[J]. Advanced Engineering Informatics, 2022, 53: 101710. doi: 10.1016/j.aei.2022.101710. [18] SHEN Gaoqing, LEI Lei, LI Zhilin, et al. Deep reinforcement learning for flocking motion of multi-UAV systems: Learn from a digital twin[J]. IEEE Internet of Things Journal, 2022, 9(13): 11141–11153. doi: 10.1109/jiot.2021.3127873. [19] TANG Xin, LI Xiaohuan, YU Rong, et al. Digital-twin-assisted task assignment in multi-UAV systems: A deep reinforcement learning approach[J]. IEEE Internet of Things Journal, 2023, 10(17): 15362–15375. doi: 10.1109/jiot.2023.3263574. [20] SHEN Xingwang, LIU Shimin, ZHOU Bin, et al. Digital twin-driven reinforcement learning method for marine equipment vehicles scheduling problem[J]. IEEE Transactions on Automation Science and Engineering, 2024, 21(3): 2173–2183. doi: 10.1109/tase.2023.3289915. [21] XU Zhenyu, CHANG Daofang, SUN Miaomiao, et al. Dynamic scheduling of crane by embedding deep reinforcement learning into a digital twin framework[J]. Information, 2022, 13(6): 286. doi: 10.3390/info13060286. [22] SHEVITZ D and PADEN B. Lyapunov stability theory of nonsmooth systems[J]. IEEE Transactions on Automatic Control, 1994, 39(9): 1910–1914. doi: 10.1109/9.317122. [23] SCHULMAN J, WOLSKI F, DHARIWAL P, et al. Proximal policy optimization algorithms[J]. arXiv preprint arXiv: 1707.06347, 2017. doi: 10.48550/arXiv.1707.06347. [24] STURTEVANT N R. Benchmarks for grid-based pathfinding[J]. IEEE Transactions on Computational Intelligence and AI in Games, 2012, 4(2): 144–148. doi: 10.1109/tciaig.2012.2197681. -





 下载:
下载:




 下载:
下载:
