A Black-Box Query Adversarial Attack Method for Signal Detection Networks Based on Sparse Subspace Sampling
-
摘要: 随着深度神经网络在信号检测任务的应用,神经网络易受到对抗样本攻击的脆弱性也受到了广泛关注。针对无法获取模型内部信息的信号检测网络黑盒攻击场景,该文提出一种基于稀疏子空间采样的黑盒查询对抗攻击方法。该方法将信号样本检测数量消失比例作为判断攻击是否成功的约束条件,构造信号检测网络对抗样本攻击模型,参考跳步跳跃攻击(HSJA)算法设计基于决策边界的信号检测网络黑盒查询对抗攻击方法求解该模型,以生成信号对抗样本。为了进一步改善查询效率,该文根据信号对抗扰动特点构建稀疏子空间采样进行查询攻击,即在生成对抗样本时,按照一定比例选择具有较大幅度的信号分量,并仅在这些选定的分量上添加扰动。实验结果表明,在信号目标消失数量比例0.3的决策边界下,稀疏子空间采样黑盒对抗攻击方法使得信号检测网络mAP值降低了43.6%、召回率降低了41.2%。与全空间采样方法相比,稀疏子空间采样方法攻击成功率提升了2.5%,且对抗扰动平均能量比降低了3.47%。稀疏子空间采样攻击方法可以使得信号检测网络性能明显下降,相较于全空间采样具有攻击成功率更高、扰动强度更小等优势。Abstract:
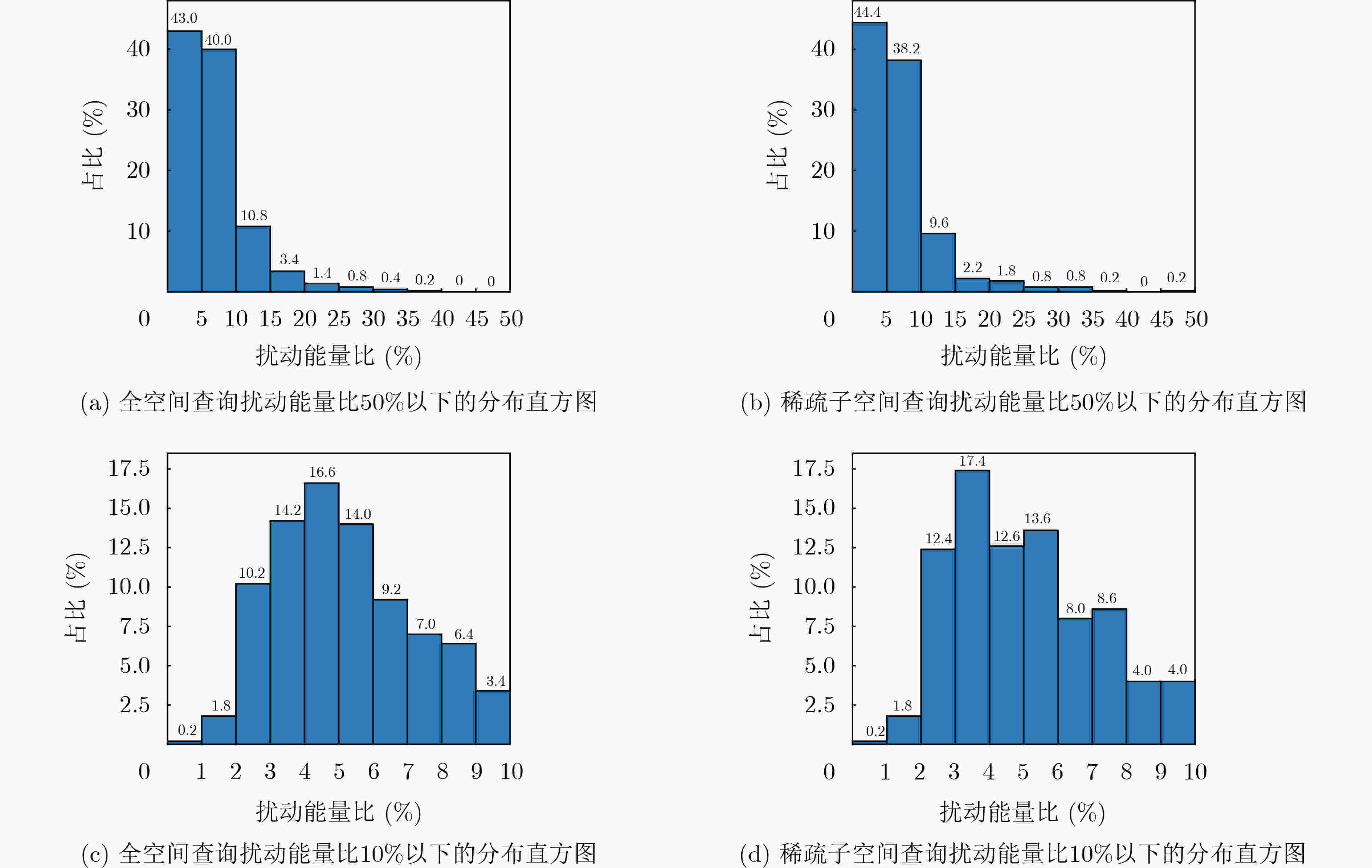
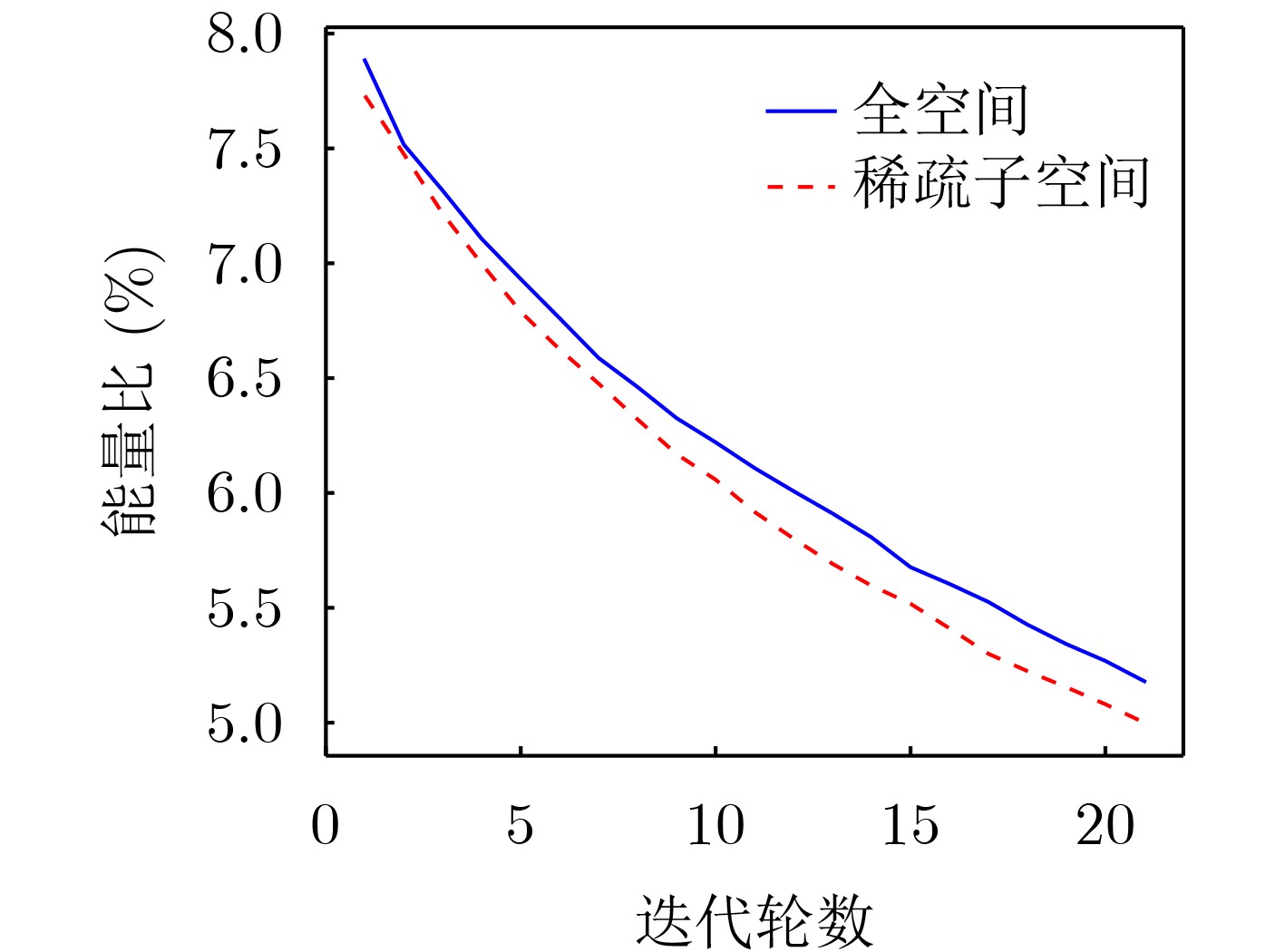
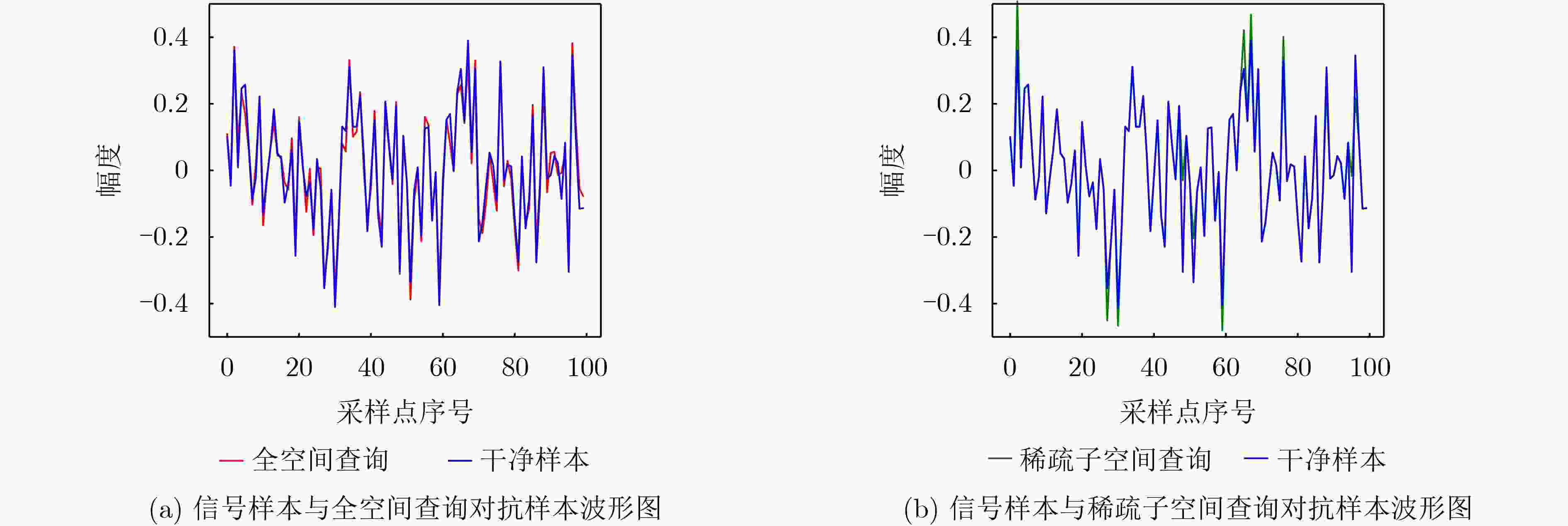
Objective The application of deep neural networks to signal detection has raised concerns regarding their vulnerability to adversarial example attacks. In black-box attack scenarios, where internal model information is inaccessible, this paper proposes a black-box query adversarial attack method based on sparse subspace sampling. The method offers an approach to evaluate the robustness of signal detection networks under black-box conditions, providing theoretical support and practical guidance for improving the reliability and robustness of these networks. Methods This study combines the characteristics of signal detection networks with the attack objective of reducing the recall rate of signal targets. The disappearance ratio of detected signal targets is used as the constraint for determining attack success, forming an adversarial attack model for signal detection networks. Based on the HopSkipJumpAttack (HSJA) algorithm, a black-box query adversarial attack method for signal detection networks is designed, which generates adversarial examples by approaching the model’s decision boundary. To further improve query efficiency, a sparse subspace query adversarial attack method is proposed. This approach constructs sparse subspace sampling based on the characteristics of signal adversarial perturbations. Specifically, during the generation of adversarial examples, signal components with large amplitudes are selected in proportion, and only these components are perturbed. Results and Discussions Experimental results show that under a decision boundary condition with a signal target disappearance ratio of 0.3, the proposed sparse subspace sampling black-box adversarial attack method reduces the mean Average Precision (mAP) by 43.6% and the recall rate by 41.2%. Under the same number of queries, all performance metrics for the sparse subspace sampling method exceed those of the full-space sampling approach, demonstrating improved attack effectiveness, with the success rate increasing by 2.5% ( Table 2 ). In terms of signal perturbation intensity, the proposed method effectively reduces perturbation intensity through iterative optimization under both sampling spaces. At the beginning of the iterations, the perturbation energies for the two spaces are similar. As the number of query rounds increases, the perturbation energy required for sparse subspace sampling becomes slightly lower than that of full-space sampling, and the difference continues to widen. The average adversarial perturbation energy ratio for full-space sampling is 5.18%, whereas sparse subspace sampling achieves 5.00%, reflecting a 3.47% reduction relative to full-space sampling (Fig. 4 ). For waveform perturbations, both sampling strategies proposed in this study can generate effective adversarial examples while preserving the primary waveform characteristics of the original signal. Specifically, the full-space query method applies perturbations to every sampling point, whereas the sparse subspace query method selectively perturbs only the large-amplitude signal components, leaving other components unchanged (Fig. 5 ). This selective approach provides the sparse subspace method with a notable l0-norm control property for adversarial perturbations, minimizing the number of perturbed components without compromising attack performance. In contrast, the full-space sampling method focuses on optimizing the l2-norm of perturbations, without achieving this selective control.Conclusions This study proposes a black-box query adversarial attack method for signal detection networks based on sparse subspace sampling. The disappearance ratio of detected signal targets is used as the success criterion for attacks, and an adversarial example generation model for signal detection networks is established. Drawing on the HSJA algorithm, a decision-boundary-based black-box query attack method is designed to generate adversarial signal examples. To further enhance query efficiency, a sparse subspace sampling strategy is constructed based on the characteristics of signal adversarial perturbations. Experimental results show that under a decision boundary with a target disappearance ratio of 0.3, the proposed sparse subspace sampling black-box attack method reduces the mAP of the signal detection network by 43.6% and the recall rate by 41.2%. Compared with full-space sampling, sparse subspace sampling increases the attack success rate by 2.5% and reduces the average perturbation energy ratio by 3.47%. The sparse subspace method significantly degrades signal detection network performance while achieving superior attack efficiency and lower perturbation intensity relative to full-space sampling. Furthermore, the full-space query method introduces perturbations at all sampling points, whereas the sparse subspace method selectively perturbs only the high-amplitude signal components, leaving other components unchanged. This approach enforces l0-norm sparsity constraints, minimizing the number of perturbed components without compromising attack effectiveness. The proposed method provides a practical solution for evaluating the robustness of signal detection networks under black-box conditions and offers theoretical support for improving the reliability of these networks against adversarial threats. -
表 1 不同攻击方法下对抗扰动幅度与信号幅度对应位置比例
对抗攻击方法 p Max Min Avg Avg/p FGM 0.02 0.50 0.06 0.35 17.50 0.04 0.55 0.20 0.43 10.75 0.10 0.62 0.40 0.54 5.40 PGD 0.02 0.49 0.07 0.35 17.50 0.04 0.54 0.24 0.43 10.75 0.10 0.61 0.39 0.53 5.30 1 基于稀疏子空间采样查询的梯度方向估计
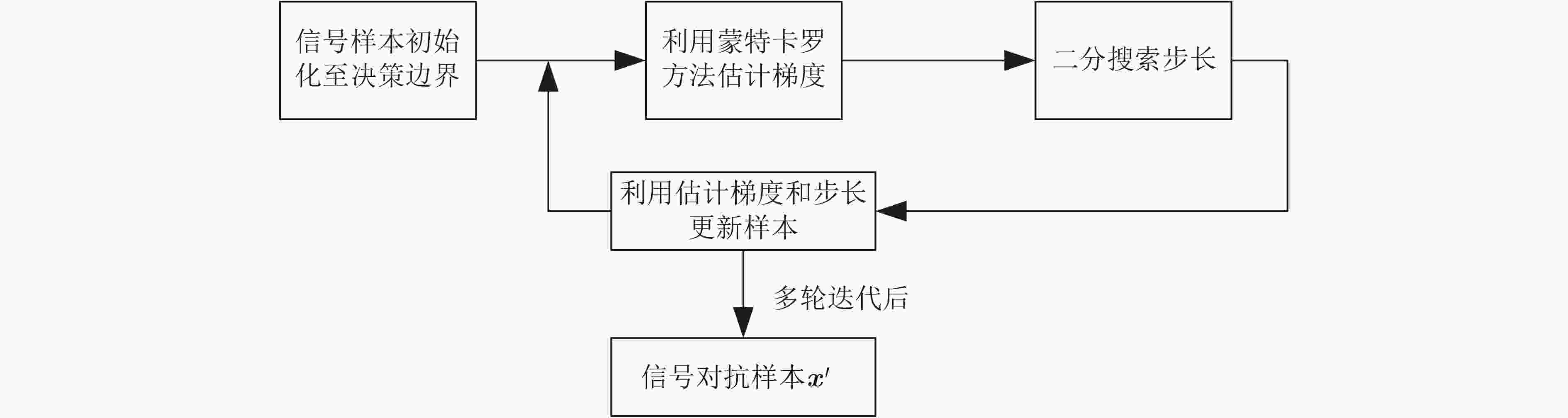
输入:信号长度$n$,信号采样分量比例$p$,决策边界附近的信号数据$ {{\boldsymbol{x}}_0} \in {\mathbb{R}^{{\text{ }}1 \times n}} $,信号采样稀疏子空间${\boldsymbol{W}} \in {\mathbb{R}^{{\text{ 1}} \times np}}$,稀疏采样的数量
$B$,符号函数${\phi _{\boldsymbol{x}}}(\cdot)$输出:估计梯度$ \hat \nabla {S_{\boldsymbol{x}}} $ (1) 从信号采样稀疏子空间${\boldsymbol{W}}$中采样$B$个随机均匀分布噪声,组成向量组${\boldsymbol{V}} \in {\mathbb{R}^{{\text{ }}B \times np}}$。 (2) 在信号幅度较小的$1 - p$个位置上补0,将向量组${\boldsymbol{V}}$扩充为稀疏采样扰动向量组$ {\boldsymbol{U}} \in {\mathbb{R}^{{\text{ }}B \times n}} $。 (3) 将稀疏采样扰动向量${{\mathbf{u}}_b}^{1 \times n} \in {\boldsymbol{U}}$与信号数据$ {{\boldsymbol{x}}_0} $相叠加,利用蒙特卡罗方法估计梯度:
$ \hat \nabla {S_{\boldsymbol{x}}}({{\boldsymbol{x}}_t},\varepsilon ): = \dfrac{1}{{B - 1}}\displaystyle\sum\nolimits_{b = 1}^B {({\phi _{\boldsymbol{x}}}({{\boldsymbol{x}}_t} + \varepsilon {{\mathbf{u}}_b}) - {{\bar \phi }_{\boldsymbol{x}}})} {{\mathbf{u}}_b} $。(4) 返回估计梯度$ \hat \nabla {S_{\boldsymbol{x}}} $。 2 基于稀疏子空间采样的信号检测网络黑盒查询对抗攻击方法
输入:信号检测网络$ C( \cdot ) $,信号样本${\boldsymbol{x}}$,迭代轮数$T$。 输出:信号对抗样本$ {\boldsymbol{x}}' $。 (1) 定义决策函数${S_{\boldsymbol{x}}}({\boldsymbol{x}}'): = C({\boldsymbol{x}})\times\alpha - C({\boldsymbol{x}}')$、决策边界${{\mathrm{bd}}} ({S_{\boldsymbol{x}}}): = {{\mathrm{bd}}} \left\{ {{\boldsymbol{x}}'\left| {{S_{\boldsymbol{x}}}({\boldsymbol{x}}') = 0} \right.} \right\}$和查询符号函数
$ {\phi }_{{\boldsymbol{x}}}({{\boldsymbol{x}}}^{\prime }):=\text{sign}({S}_{{\boldsymbol{x}}}({{\boldsymbol{x}}}^{\prime }))=\left\{\begin{aligned} & 1,\text{ }{S}_{{\boldsymbol{x}}}({{\boldsymbol{x}}}^{\prime })\ge 0\\& {-1,\text{ }其他}\end{aligned}\right. $。(2) 对信号样本${\boldsymbol{x}}$进行初始化操作,得到信号样本$ {{\boldsymbol{x}}_0} $在决策边界${{\boldsymbol{S}}_x}$附近且满足$ {\phi _{\boldsymbol{x}}}({{\boldsymbol{x}}_0}) = 1 $。 (3) ${\text{for}}$ $t$ 从 $0$~$T - 1$: 使用算法1,估计梯度方向$ \hat \nabla {S_{\boldsymbol{x}}}({{\boldsymbol{x}}_t}) $; 搜索步长$ {\xi _t} $,并更新信号样本$ {\tilde {\boldsymbol{x}}_{t + 1}} = {{\boldsymbol{x}}_t} + {\xi _t}\dfrac{{\hat \nabla S({{\boldsymbol{x}}_t},{\boldsymbol{\delta}} )}}{{{{\left\| {\hat \nabla S({{\boldsymbol{x}}_t},{\boldsymbol{\delta}} )} \right\|}_2}}} $; 搜索投影比例$ {\beta _t} $,将$ {\tilde {\boldsymbol{x}}_{t + 1}} $投影到决策边界得到$ {{\boldsymbol{x}}_{t + 1}} = {\beta _t}{\boldsymbol{x}} + (1 - {\beta _t}){\tilde {\boldsymbol{x}}_{t + 1}} $,$ {{\boldsymbol{x}}_{t + 1}} $满足$ {\phi _{\boldsymbol{x}}}({{\boldsymbol{x}}_{t + 1}}) = 1 $; ${\text{end for}}$ (4) 返回信号对抗样本$ {\boldsymbol{x}}' = {{\boldsymbol{x}}_T} $。 表 2 0.3决策边界下不同样本攻击结果
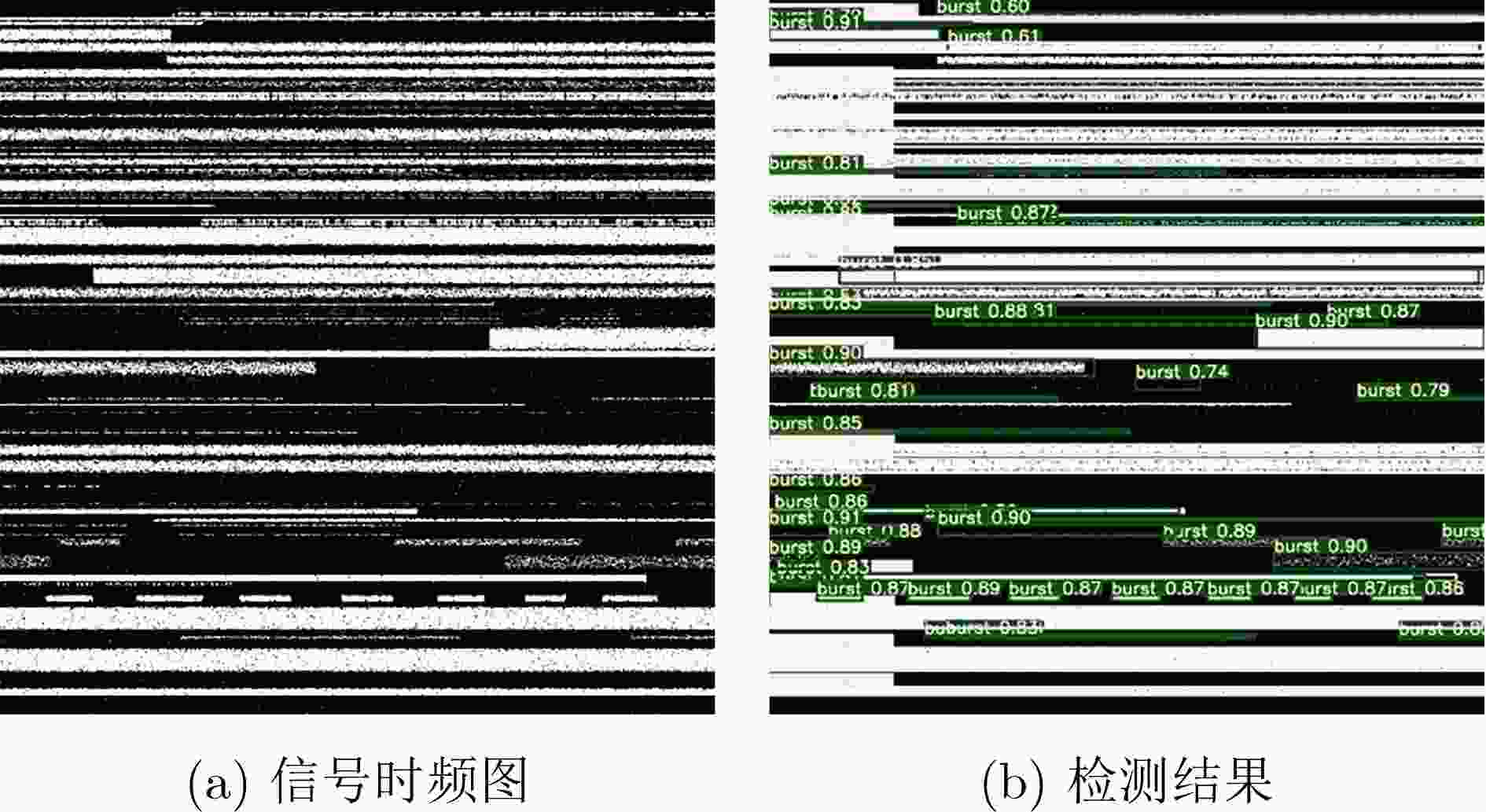
样本类别 mAP P R 攻击成功率(%) 干净样本 0.872 0.953 0.813 / 全空间采样对抗样本 0.519 0.708 0.508 48.0 全空间采样下同等强度随机噪声干扰样本 0.549 0.736 0.539 40.8 稀疏子空间采样对抗样本 0.492 0.664 0.478 49.2 稀疏子空间采样下同等强度随机噪声干扰样本 0.555 0.73 0.55 36.6 -
[1] REN Shaoqing, HE Kaiming, GIRSHICK R, et al. Faster R-CNN: Towards real-time object detection with region proposal networks[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2017, 39(6): 1137–1149. doi: 10.1109/TPAMI.2016.2577031. [2] REDMON J, DIVVALA S, GIRSHICK R, et al. You only look once: Unified, real-time object detection[C]. 2016 IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, USA, 2016: 779–788. doi: 10.1109/CVPR.2016.91. [3] WANG C Y, BOCHKOVSKIY A, and LIAO H Y M. YOLOv7: Trainable bag-of-freebies sets new state-of-the-art for real-time object detectors[C]. 2023 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, Canada, 2023: 7464–7475. doi: 10.1109/CVPR52729.2023.00721. [4] ZHA Xiong, PENG Hua, QIN Xin, et al. A deep learning framework for signal detection and modulation classification[J]. Sensors, 2019, 19(18): 4042. doi: 10.3390/s19184042. [5] VAGOLLARI A, HIRSCHBECK M, and GERSTACKER W. An end-to-end deep learning framework for wideband signal recognition[J]. IEEE Access, 2023, 11: 52899–52922. doi: 10.1109/ACCESS.2023.3280454. [6] LI Qing, ZHOU Xin, MENG Xiandong, et al. Lightweight RadioYOLO for radio signal detection[C]. 2022 International Conference on Algorithms, Data Mining, and Information Technology, Xi'an, China, 2022: 117–123. doi: 10.1109/ADMIT57209.2022.00027. [7] 耿频永, 曹叶文, 赵晓蕾, 等. 基于频率敏感注意力的短波宽带特定信号检测[J]. 数据采集与处理, 2023, 38(1): 63–73. doi: 10.16337/j.1004-9037.2023.01.004.GENG Pinyong, CAO Yewen, ZHAO Xiaolei, et al. Shortwave wideband specific signal detection based on frequency-sensitive attention[J]. Journal of Data Acquisition and Processing, 2023, 38(1): 63–73. doi: 10.16337/j.1004-9037.2023.01.004. [8] 李润东. 基于深度学习的通信信号智能盲检测与识别技术研究[D]. [博士论文], 电子科技大学, 2021.LI Rundong. Research on intelligent blind detection and recognition of communication signals based on deep learning[D]. [Ph. D. dissertation], University of Electronic Science and Technology of China, 2021. [9] XIE Cihang, WANG Jianyu, ZHANG Zhishuai, et al. Adversarial examples for semantic segmentation and object detection[C]. 2017 IEEE International Conference on Computer Vision, Venice, Italy, 2017: 1378–1387. doi: 10.1109/ICCV.2017.153. [10] WANG Derui, LI Chaoran, WEN Sheng, et al. Daedalus: Breaking nonmaximum suppression in object detection via adversarial examples[J]. IEEE Transactions on Cybernetics, 2022, 52(8): 7427–7440. doi: 10.1109/TCYB.2020.3041481. [11] ZHU Hegui, SUI Xiaoyan, REN Yuchen, et al. Boosting transferability of targeted adversarial examples with non-robust feature alignment[J]. Expert Systems with Applications, 2023, 227: 120248. doi: 10.1016/j.eswa.2023.120248. [12] CHOW K H, LIU Ling, LOPER M, et al. Adversarial objectness gradient attacks in real-time object detection systems[C]. 2020 Second IEEE International Conference on Trust, Privacy and Security in Intelligent Systems and Applications, Atlanta, USA, 2020: 263–272. doi: 10.1109/TPS-ISA50397.2020.00042. [13] SADEGHI M and LARSSON E G. Adversarial attacks on deep-learning based radio signal classification[J]. IEEE Wireless Communications Letters, 2019, 8(1): 213–216. doi: 10.1109/LWC.2018.2867459. [14] ZHANG Sicheng, FU Jiangzhi, YU Jiarun, et al. Channel-robust class-universal spectrum-focused frequency adversarial attacks on modulated classification models[J]. IEEE Transactions on Cognitive Communications and Networking, 2024, 10(4): 1280–1293. doi: 10.1109/TCCN.2024.3382126. [15] TIAN Qiao, ZHANG Sicheng, MAO Shiwen, et al. Adversarial attacks and defenses for digital communication signals identification[J]. Digital Communications and Networks, 2024, 10(3): 756–764. doi: 10.1016/j.dcan.2022.10.010. [16] LI Dongyang, WANG Linyuan, XIONG Guangwei, et al. Signal adversarial examples generation for signal detection network via white-box attack[J]. Electronics Letters, 2025, 61(1): e70348. doi: 10.1049.ell2.70348. [17] SHIN Y, NAM S W, AN C K, et al. Design of a time-frequency domain matched filter for detection of non-stationary signals[C]. 2001 IEEE International Conference on Acoustics, Speech, and Signal Processing, Salt Lake City, USA, 2001: 3585–3588. doi: 10.1109/ICASSP.2001.940617. [18] DIAMANT R. Closed form analysis of the normalized matched filter with a test case for detection of underwater acoustic signals[J]. IEEE Access, 2016, 4: 8225–8235. doi: 10.1109/ACCESS.2016.2630498. [19] GARDNER W A. Exploitation of spectral redundancy in cyclostationary signals[J]. IEEE Signal Processing Magazine, 1991, 8(2): 14–36. doi: 10.1109/79.81007. [20] ZENG Yonghong and LIANG Yingchang. Maximum-minimum eigenvalue detection for cognitive radio[C]. The 18th International Symposium on Personal, Indoor and Mobile Radio Communications, Athens, Greece, 2007: 1–5. doi: 10.1109/PIMRC.2007.4394211. [21] URKOWITZ H. Energy detection of unknown deterministic signals[J]. Proceedings of the IEEE, 1967, 55(4): 523–531. doi: 10.1109/PROC.1967.5573. [22] PAPERNOT N, MCDANIEL P, and GOODFELLOW I. Transferability in machine learning: From phenomena to black-box attacks using adversarial samples[EB/OL]. https://arxiv.org/abs/1605.07277, 2016. [23] LIU Yanpei, CHEN Xinyun, LIU Chang, et al. Delving into transferable adversarial examples and black-box attacks[C]. The 5th International Conference on Learning Representations, Toulon, France, 2017. [24] WANG Zhibo, YANG Hongshan, FENG Yunhe, et al. Towards transferable targeted adversarial examples[C]. 2023 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, Canada, 2023: 20534–20543. doi: 10.1109/CVPR52729.2023.01967. [25] CHEN Pinyun, ZHANG Huan, SHARMA Y, et al. ZOO: Zeroth order optimization based black-box attacks to deep neural networks without training substitute models[C]. The 10th ACM Workshop on Artificial Intelligence and Security, Dallas, USA, 2017: 15–26. doi: 10.1145/3128572.3140448. [26] GUO Chuan, GARDNER J R, YOU Yurong, et al. Simple black-box adversarial attacks[C]. The 36th International Conference on Machine Learning, Long Beach, USA, 2019: 2484–2493. [27] ANDRIUSHCHENKO M, CROCE F, FLAMMARION N, et al. Square attack: A query-efficient black-box adversarial attack via random search[C]. The 16th European Conference on Computer Vision, Glasgow, UK, 2020: 484–501. doi: 10.1007/978-3-030-58592-1_29. [28] BRENDEL W, RAUBER J, and BETHGE M. Decision-based adversarial attacks: Reliable attacks against black-box machine learning models[C]. The 6th International Conference on Learning Representations, Vancouver, Canada, 2018. [29] CHENG Minhao, SINGH S, CHEN P H, et al. Sign-OPT: A query-efficient hard-label adversarial attack[C]. The 8th International Conference on Learning Representations, Addis Ababa, Ethiopia, 2020. [30] CHEN Jianbo, JORDAN M I, and WAINWRIGHT M J. HopSkipJumpAttack: A query-efficient decision-based attack[C]. Proceedings of 2020 IEEE Symposium on Security and Privacy, San Francisco, USA, 2020: 1277–1294. doi: 10.1109/SP40000.2020.00045. [31] LI Huichen, XU Xiaojun, ZHANG Xiaolu, et al. QEBA: Query-efficient boundary-based blackbox attack[C]. 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, USA, 2020: 1221–1230. doi: 10.1109/CVPR42600.2020.00130. [32] SHAMIR A, SAFRAN I, RONEN E, et al. A simple explanation for the existence of adversarial examples with small hamming distance[EB/OL]. https://arxiv.org/abs/1901.10861, 2019. [33] CAI Hanqin, LOU Yuchen, MCKENZIE D, et al. A zeroth-order block coordinate descent algorithm for huge-scale black-box optimization[C]. The 38th International Conference on Machine Learning, Graz, Austria, 2021: 1193–1203. [34] CAI Hanqin, MCKENZIE D, YIN Wotao, et al. A one-bit, comparison-based gradient estimator[J]. Applied and Computational Harmonic Analysis, 2022, 60: 242–266. doi: 10.1016/j.acha.2022.03.003. [35] 武越, 苑咏哲, 岳铭煜, 等. 点云配准中多维度信息融合的特征挖掘方法[J]. 计算机研究与发展, 2022, 59(8): 1732–1741. doi: 10.7544/issn1000-1239.20220042.WU Yue, YUAN Yongzhe, YUE Mingyu, et al. Feature mining method of multi-dimensional information fusion in point cloud registration[J]. Journal of Computer Research and Development, 2022, 59(8): 1732–1741. doi: 10.7544/issn1000-1239.20220042. [36] 郭宇琦, 李东阳, 尹志宁, 等. 采用1-bit压缩感知的信号识别网络黑盒对抗攻击方法[J]. 信息工程大学学报, 2024, 25(5): 593–600. doi: 10.3969/j.issn.1671-0673.2024.05.014.GUO Yuqi, LI Dongyang, YIN Zhining, et al. Black-box adversarial attacks on signal recognition networks using 1-bit compressed sensing[J]. Journal of Information Engineering University, 2024, 25(5): 593–600. doi: 10.3969/j.issn.1671-0673.2024.05.014. [37] 郭宇琦. 无线I/Q信号调制识别神经网络对抗样本生成方法[D]. [硕士论文], 战略支援部队信息工程大学, 2023.GUO Yuqi. Research on wireless I/Q signal adversarial examples in modulation recognition neural networks[D]. [Master dissertation], PLA Strategy Support Force Information Engineering University, 2023. -






 下载:
下载:


 下载:
下载:
