Regularized Neural Network-Based Normalized Min-Sum Decoding for LDPC Codes
-
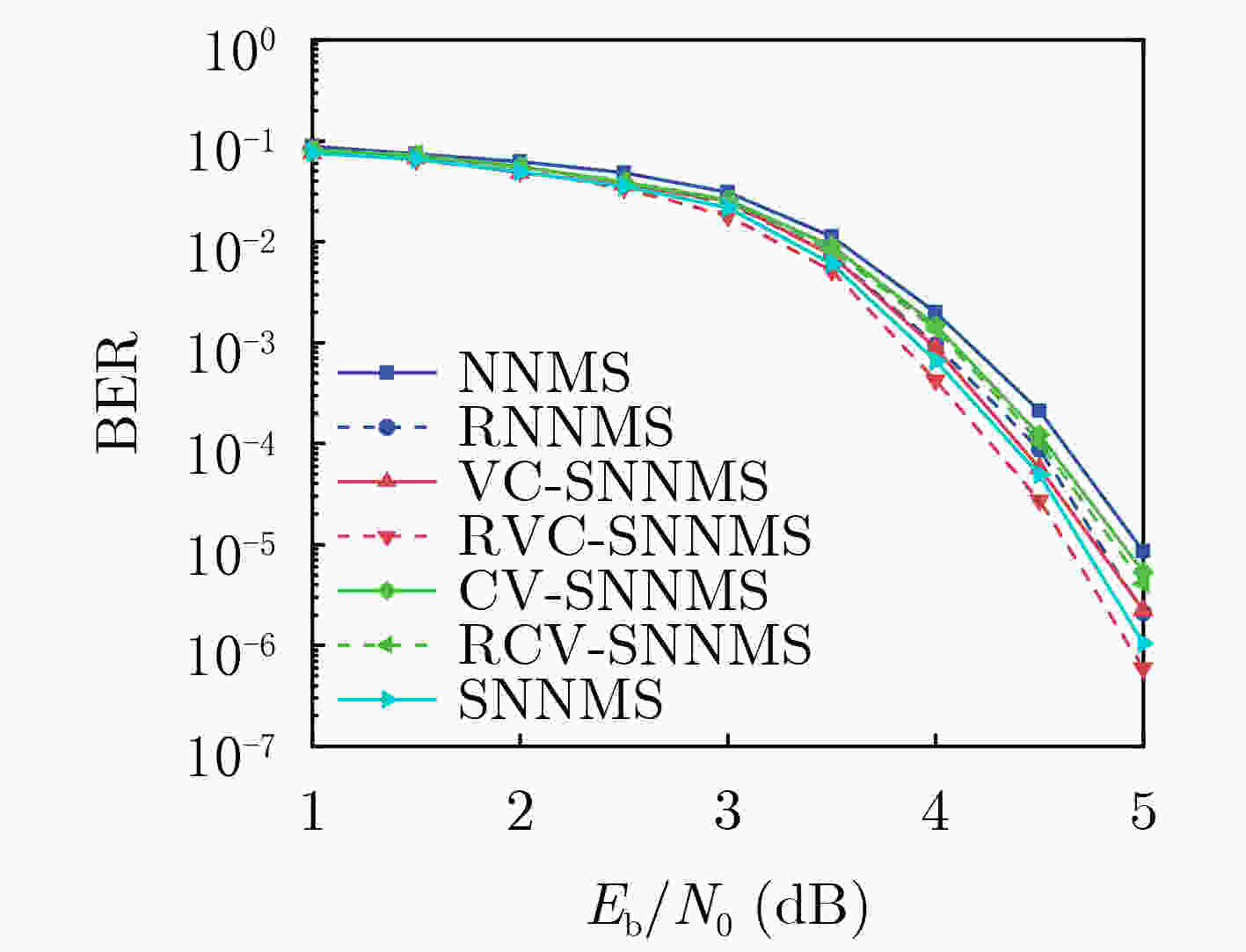
摘要: 低密度奇偶校验(LDPC)码基于神经网络的归一化最小和(NNMS)译码算法按照网络中权重的共享方式可分为不共享(NNMS)、全共享(SNNMS)、部分共享(VC-SNNMS和CV-SNNMS)等。该文针对LDPC码在使用NNMS, VC-SNNMS和CV-SNNMS译码时因高复杂度导致的过拟合问题,引入正则化(Regularization)优化了神经网络中边信息的权重训练,抑制了基于神经网络译码的过拟合问题,分别得到 RNNMS, RVC-SNNMS和RCV-SNNMS算法。仿真结果表明:采用共享权重可以减轻神经网络训练负担,降低LDPC 码基于神经网络译码的误比特率(BER);正则化能有效缓解过拟合现象提升神经网络的译码性能。针对码长为576,码率为0.75的LDPC码,当误码率BER=10–6时,RNNMS, RVC-SNNMS和RCV-SNNMS算法相较于NNMS, VC-SNNMS和CV-SNNMS算法分别得到了0.18 dB, 0.22 dB和0.27 dB的信噪比(SNR)增益,其中最佳的RVC-SNNMS算法相较于BP算法、NNMS算法和SNNMS算法,分别获得了0.55 dB, 0.51 dB和0.22 dB的信噪比增益。Abstract:
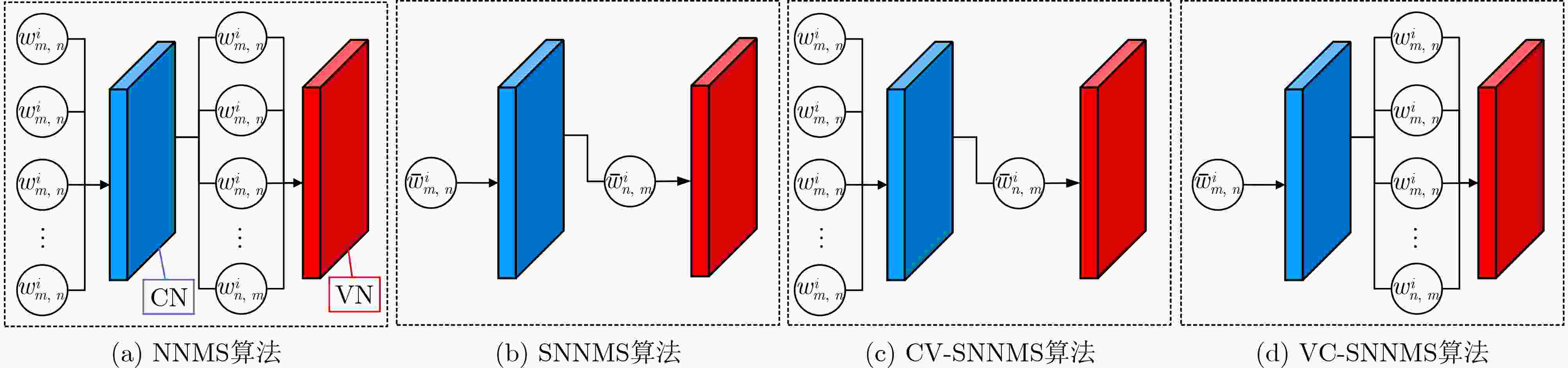
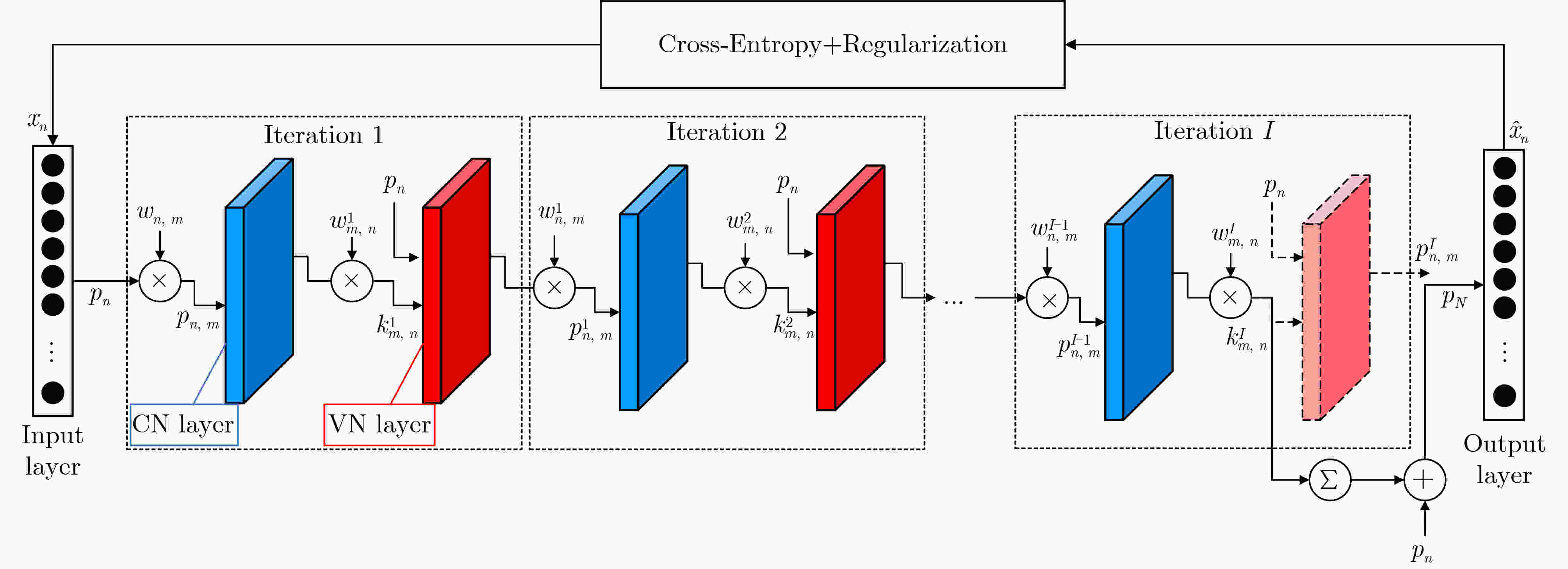
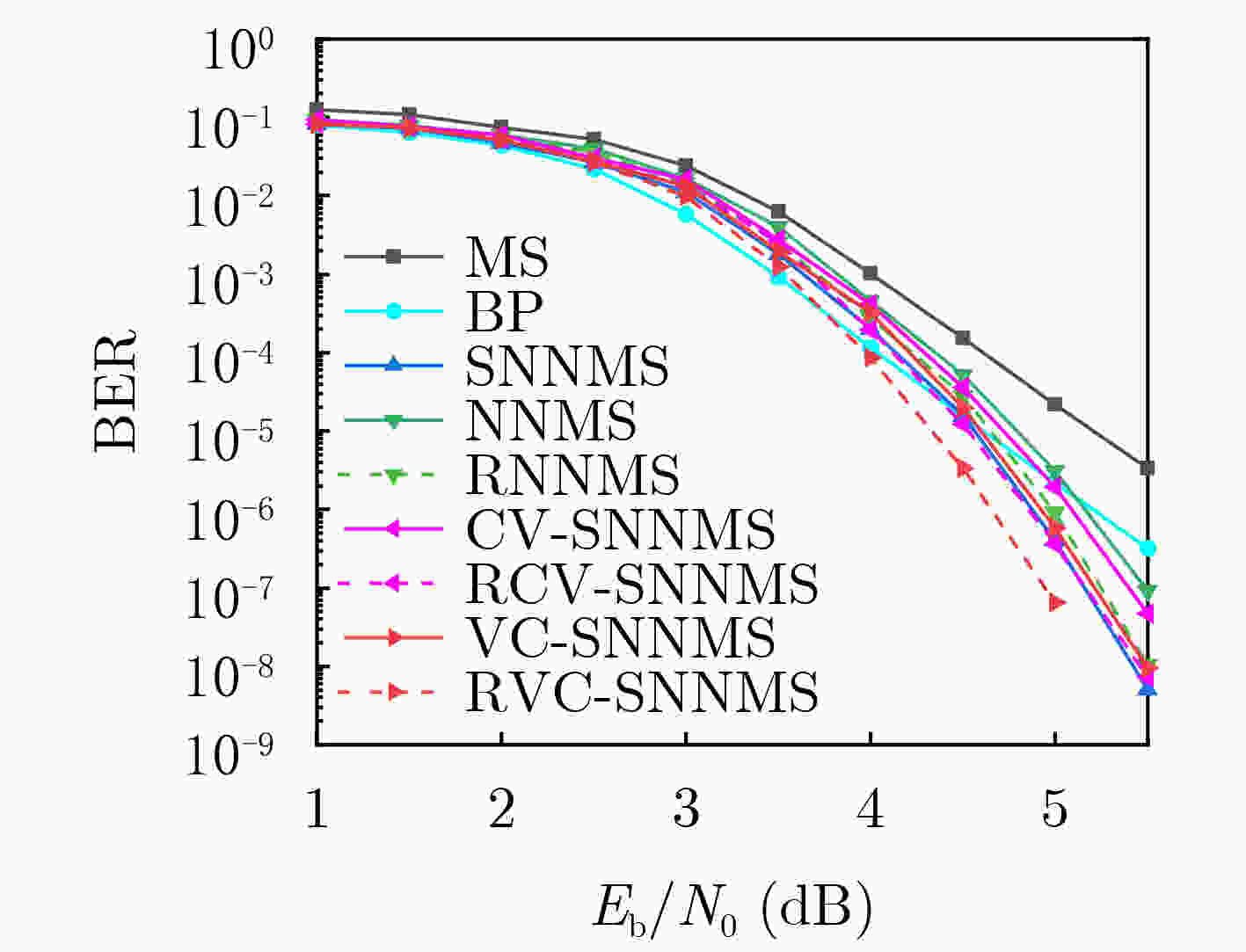
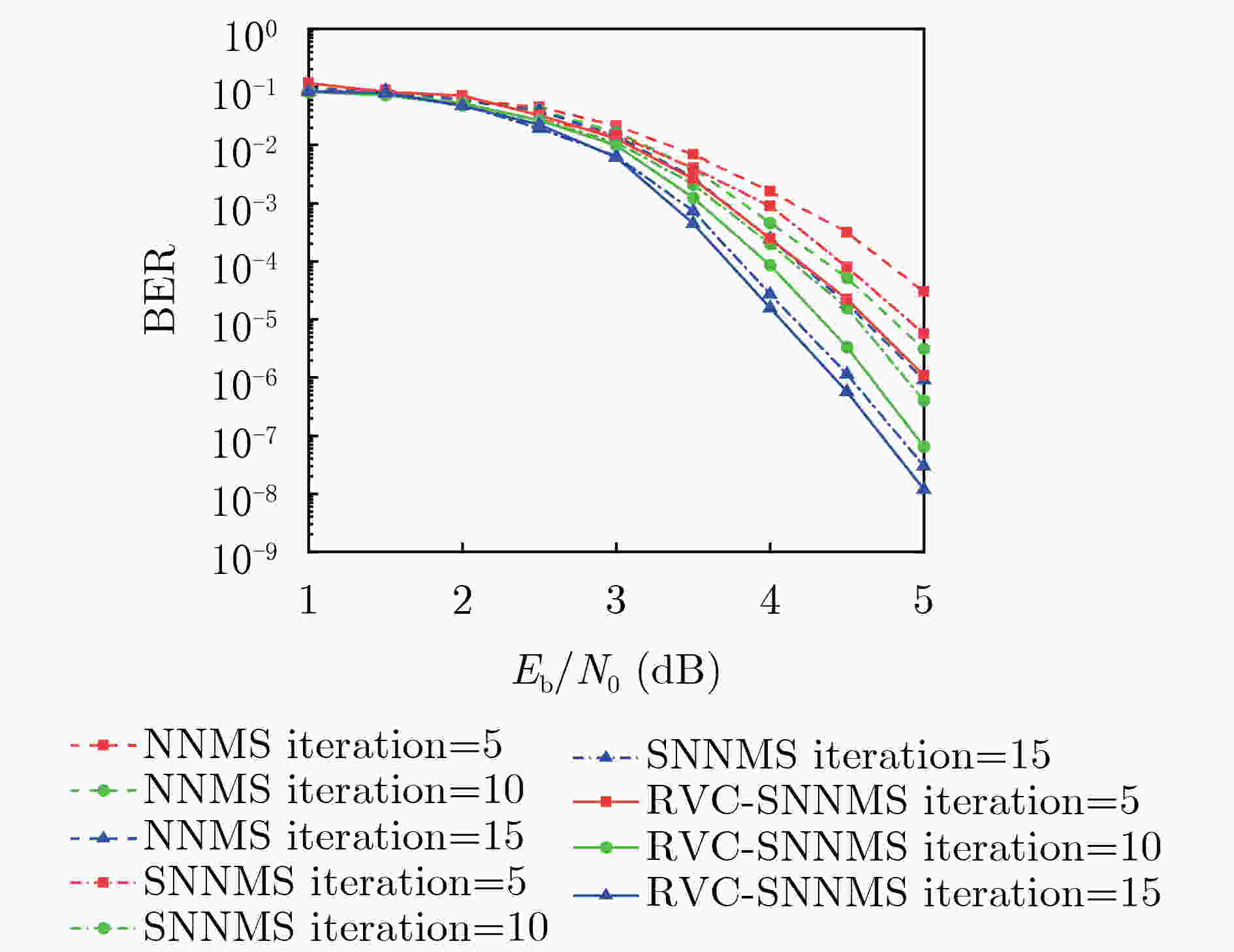
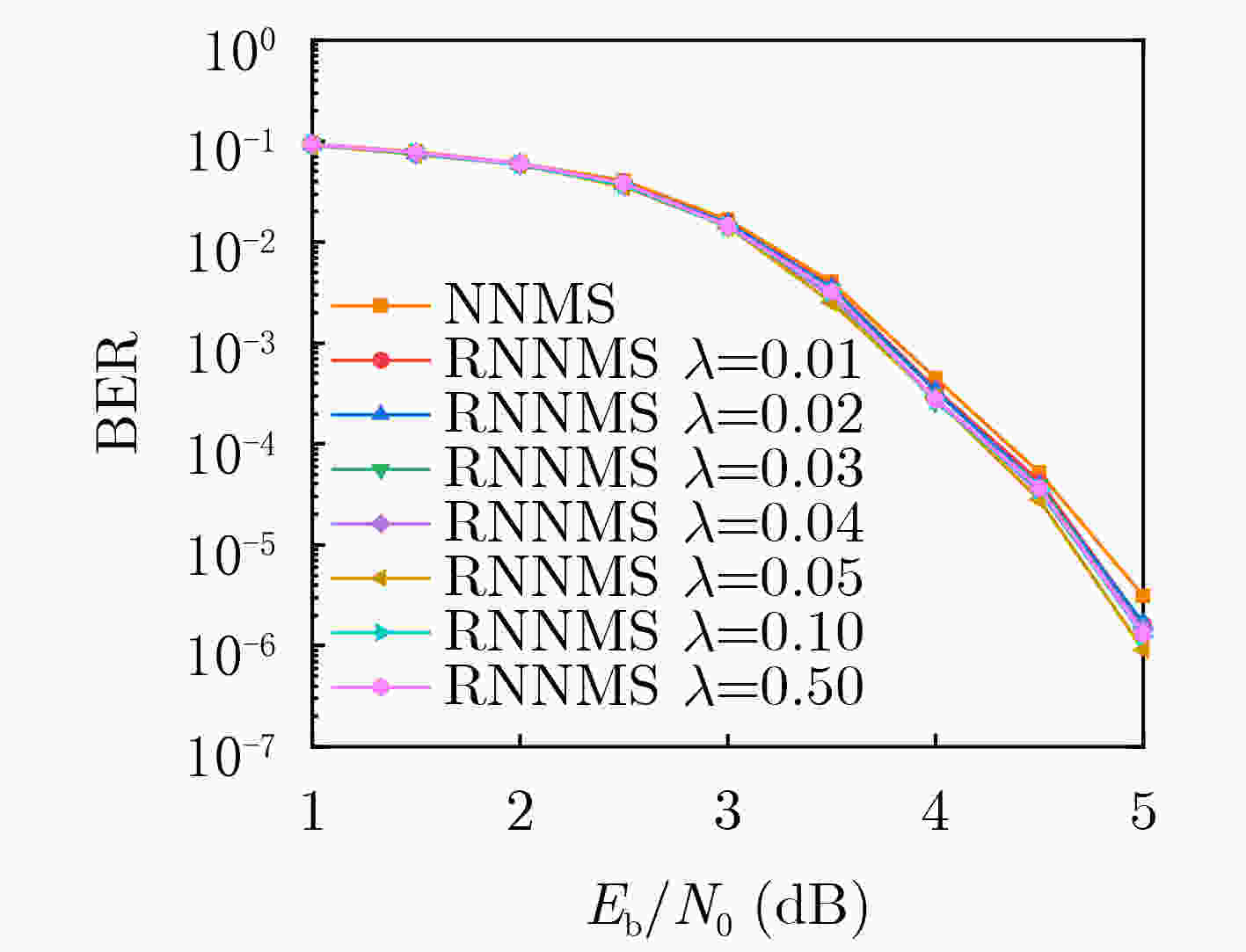
Objective The application of deep learning in communications has demonstrated significant potential, particularly in Low Density Parity Check (LDPC) code decoding. As a rapidly evolving branch of artificial intelligence, deep learning effectively addresses complex optimization problems, making it suitable for enhancing traditional decoding techniques in modern communication systems. The Neural-network Normalized Min-Sum (NNMS) algorithm has shown improved performance over the Min-Sum (MS) algorithm by incorporating trainable neural network models. However, NNMS decoding assigns independent training weights to each edge in the Tanner graph, leading to excessive training complexity and high storage overhead due to the large number of weight parameters. This significantly increases computational demands, posing challenges for implementation in resource-limited hardware. Moreover, the excessive number of weights leads to overfitting, where the model memorizes training data rather than learning generalizable features, degrading decoding performance on unseen codewords. This issue limits the practical applicability of NNMS-based decoders and necessitates advanced regularization techniques. Therefore, this study explores methods to reduce NNMS decoding complexity, mitigate overfitting, and enhance the decoding performance of LDPC codes. Methods Building on the traditional NNMS decoding algorithm, this paper proposes two partially weight-sharing models: VC-SNNMS (sharing weights for edges from variable nodes to check nodes) and CV-SNNMS (sharing weights for edges from check nodes to variable nodes). These models apply a weight-sharing strategy to specific edge types in the bipartite graph, reducing the number of training weights and computational complexity. To mitigate neural network overfitting caused by the high complexity of NNMS and its variants, a regularization technique is proposed. This leads to the development of the Regularized NNMS (RNNMS), Regularized VC-SNNMS (RVC-SNNMS), and Regularized CV-SNNMS (RCV-SNNMS) algorithms. Regularization refines network parameters by modifying the loss function and gradients, penalizing excessively large weights or redundant features. By reducing model complexity, this approach enhances the generalization ability of the decoding neural network, ensuring robust performance on both training and test data. Results and Discussions To evaluate the effectiveness of the proposed algorithms, extensive simulations are conducted under various Signal-to-Noise Ratio (SNR) conditions. The performance is assessed in terms of Bit Error Rate (BER), decoding complexity, and convergence speed. Additionally, a comparative analysis of NNMS, SNNMS, VC-SNNMS, and CV-SNNMS, and their regularized variants systematically examines the effects of weight-sharing and regularization on neural network-based decoding. Simulation results show that for an LDPC code with a block length of 576 and a code rate of 0.75, when BER = 10–6, the RNNMS, RVC-SNNMS, and RCV-SNNMS algorithms achieve SNR gains of 0.18 dB, 0.22 dB, and 0.27 dB, respectively, compared to their corresponding NNMS, VC-SNNMS, and CV-SNNMS algorithms. Notably, the RVC-SNNMS algorithm demonstrates the best performance, with SNR gains of 0.55 dB, 0.51 dB, and 0.22 dB compared to the BP, NNMS, and SNNMS algorithms, respectively ( Fig. 3 ). Furthermore, under different numbers of decoding iterations, the RVC-SNNMS algorithm consistently outperforms the others in BER performance. Specifically, at BER = 10–6 with 15 decoding iterations, it achieves SNR gains of 0.57 dB and 0.1 dB compared to the NNMS and SNNMS algorithms, respectively (Fig. 4 ). Similarly, for an LDPC code with a block length of1056 , when BER = 10–5 and 10 decoding iterations are used, the RVC-SNNMS algorithm attains SNR gains of 0.34 dB and 0.08 dB compared to the NNMS and SNNMS algorithms, respectively (Fig. 5 ).Conclusions This study investigates the performance of NNMS and SNNMS for LDPC code decoding and proposes two partially weight-sharing algorithms, VC-SNNMS and CV-SNNMS. Simulation results show that weight-sharing strategies effectively reduce training complexity while maintaining competitive BER performance. To address the overfitting issue associated with the high complexity of NNMS-based algorithms, regularization is incorporated, leading to the development of RNNMS, RVC-SNNMS, and RCV-SNNMS. Regularization effectively mitigates overfitting, enhances network generalization, and improves error-correcting performance for various LDPC codes. Simulation results indicate that the RVC-SNNMS algorithm achieves the best decoding performance due to its reduced complexity and the improved generalization provided by regularization. -
表 1 复杂度分析
序号 NNMS SNNMS CV-SNNMS VC-SNNMS CMP $ \displaystyle\sum\limits _{u=1}^{N-k}{a}_{u}\left({a}_{u}-2\right)I $ $ \displaystyle\sum\limits _{u=1}^{N-k}{a}_{u}\left({a}_{u}-2\right)I $ $ \displaystyle\sum\limits _{u=1}^{N-k}{a}_{u}\left({a}_{u}-2\right)I $ $ \displaystyle\sum\limits _{u=1}^{N-k}{a}_{u}\left({a}_{u}-2\right)I $ XOR $ \displaystyle\sum\limits _{u=1}^{N-k}{a}_{u}\left({a}_{u}-2\right)I $ $ \displaystyle\sum\limits _{u=1}^{N-k}{a}_{u}\left({a}_{u}-2\right)I $ $ \displaystyle\sum\limits _{u=1}^{N-k}{a}_{u}\left({a}_{u}-2\right)I $ $ \displaystyle\sum\limits _{u=1}^{N-k}{a}_{u}\left({a}_{u}-2\right)I $ ADD $ \displaystyle\sum\limits _{v=1}^{N}\left({b}_{v}\left({b}_{v}-1\right)+1\right)I $ $ \displaystyle\sum\limits _{v=1}^{N}\left({b}_{v}\left({b}_{v}-1\right)+1\right)I $ $ \displaystyle\sum\limits _{v=1}^{N}\left({b}_{v}\left({b}_{v}-1\right)+1\right)I $ $ \displaystyle\sum\limits _{v=1}^{N}\left({b}_{v}\left({b}_{v}-1\right)+1\right)I $ MUL $ \displaystyle\sum\limits _{u=1}^{N-k}{a}_{u}\left({a}_{u}-2\right)I+\displaystyle\sum\limits _{v=1}^{N}{b}_{v}\left({b}_{v}-2\right)I $ $ 2I $ $ \displaystyle\sum\limits _{u=1}^{N-k}{a}_{u}\left({a}_{u}-2\right)I+I $ $ I+\displaystyle\sum\limits _{v=1}^{N}{b}_{v}\left({b}_{v}-2\right)I $ 表 2 训练数据集参数设置
参数 值 学习率$ \eta $ 0.001 优化器 Adam 批处理大小 100 SNR步长(dB) 0.5 每轮训练每个SNR码字数 20 每个信噪比训练数据量 2 000 正则化方法 L2 正则化参数$ \lambda $ 0.05 -
[1] MACKAY D J C. Good error-correcting codes based on very sparse matrices[J]. IEEE Transactions on Information Theory, 1999, 45(2): 399–431. doi: 10.1109/18.748992. [2] FOSSORIER M P C, MIHALJEVIC M, and IMAI H. Reduced complexity iterative decoding of low-density parity check codes based on belief propagation[J]. IEEE Transactions on Communications, 1999, 47(5): 673–680. doi: 10.1109/26.768759. [3] CHEN Jinghu, DHOLAKIA A, ELEFTHERIOU E, et al. Reduced-complexity decoding of LDPC codes[J]. IEEE Transactions on Communications, 2005, 53(8): 1288–1299. doi: 10.1109/TCOMM.2005.852852. [4] SILVER D, HUANG A, MADDISON C J, et al. Mastering the game of go with deep neural networks and tree search[J]. Nature, 2016, 529(7587): 484–489. doi: 10.1038/nature16961. [5] HINTON G, DENG Li, YU Dong, et al. Deep neural networks for acoustic modeling in speech recognition: The shared views of four research groups[J]. IEEE Signal Processing Magazine, 2012, 29(6): 82–97. doi: 10.1109/MSP.2012.2205597. [6] TERA S P, CHINTHAGINJALA R, NATHA P, et al. CNN-based approach for enhancing 5G LDPC code decoding performance[J]. IEEE Access, 2024, 12: 89873–89886. doi: 10.1109/ACCESS.2024.3420106. [7] 郝崇正, 党小宇, 李赛, 等. 基于稀疏自编码器的混合信号符号检测研究[J]. 电子与信息学报, 2022, 44(12): 4204–4210. doi: 10.11999/JEIT211074.HAO Chongzheng, DANG Xiaoyu, LI Sai, et al. Research on symbol detection of mixed signals based on sparse AutoEncoder detector[J]. Journal of Electronics & Information Technology, 2022, 44(12): 4204–4210. doi: 10.11999/JEIT211074. [8] LIANG Fei, SHEN Cong, and WU Feng. An iterative BP-CNN architecture for channel decoding[J]. IEEE Journal of Selected Topics in Signal Processing, 2018, 12(1): 144–159. doi: 10.1109/JSTSP.2018.2794062. [9] NACHMANI E, BE'ERY Y, and BURSHTEIN D. Learning to decode linear codes using deep learning[C]. 2016 54th Annual Allerton Conference on Communication, Control, and Computing (Allerton), Monticello, USA, 2016: 341–346. doi: 10.1109/ALLERTON.2016.7852251. [10] MA Liangsi, LIU Bei, SU Xibin, et al. A model-driven quasi-ResNet belief propagation neural network decoder for LDPC codes[C]. 2023 IEEE Symposium on Computers and Communications (ISCC), Gammarth, Tunisia, 2023: 643–648. doi: 10.1109/ISCC58397.2023.10217911. [11] LI Ying, ZHANG Baoye, TAN Bin, et al. A neural network-based compressive LDPC decoder design over correlated noise channel[J]. IEEE Transactions on Cognitive Communications and Networking, 2024, 10(4): 1317–1326. doi: 10.1109/TCCN.2024.3364234. [12] NACHMANI E, MARCIANO E, LUGOSCH L, et al. Deep learning methods for improved decoding of linear codes[J]. IEEE Journal of Selected Topics in Signal Processing, 2018, 12(1): 119–131. doi: 10.1109/JSTSP.2017.2788405. [13] 贺文武, 夏巧桥, 邹炼. 基于变量节点更新的交替方向乘子法LDPC惩罚译码算法[J]. 电子与信息学报, 2018, 40(1): 95–101. doi: 10.11999/JEIT170358.HE Wenwu, XIA Qiaoqiao, and ZOU Lian. Alternating direction method of multipliers LDPC penalized decoding algorithm based on variable node update[J]. Journal of Electronics & Information Technology, 2018, 40(1): 95–101. doi: 10.11999/JEIT170358. [14] KIM T and PARK J S. Neural self-corrected min-sum decoder for NR LDPC codes[J]. IEEE Communications Letters, 2024, 28(7): 1504–1508. doi: 10.1109/LCOMM.2024.3404110. [15] DAI Jincheng, TAN Kailin, SI Zhongwei, et al. Learning to decode protograph LDPC codes[J]. IEEE Journal on Selected Areas in Communications, 2021, 39(7): 1983–1999. doi: 10.1109/JSAC.2021.3078488. [16] WANG Qing, LIU Qing, WANG Shunfu, et al. Normalized min-sum neural network for LDPC decoding[J]. IEEE Transactions on Cognitive Communications and Networking, 2023, 9(1): 70–81. doi: 10.1109/TCCN.2022.3212438. [17] LIANG Yuanhui, LAM C T, and NG B K. A low-complexity neural normalized min-sum LDPC decoding algorithm using tensor-train decomposition[J]. IEEE Communications Letters, 2022, 26(12): 2914–2918. doi: 10.1109/LCOMM.2022.3207506. [18] YU Haochen, ZHAO Mingmin, LEI Ming, et al. Neural adjusted min-sum decoding for LDPC codes[C]. 2023 IEEE 98th Vehicular Technology Conference (VTC2023-Fall), Hong Kong, China, 2023: 1–5. doi: 10.1109/VTC2023-Fall60731.2023.10333372. [19] LIANG Shuo, LIU Xingcheng, and ZHANG Lin. Low complexity deep learning method for base graph of protograph LDPC decoding[C]. 2023 9th International Conference on Computer and Communications (ICCC), Chengdu, China, 2023: 730–736. doi: 10.1109/ICCC59590.2023.10507610. [20] BADOLA A, NAIR V P, and LAL R P. An analysis of regularization methods in deep neural networks[C]. 2020 IEEE 17th India Council International Conference (INDICON), New Delhi, India, 2020: 1–6. doi: 10.1109/INDICON49873.2020.9342192. -





 下载:
下载:


 下载:
下载:
