高速网络中优先级敏感的每流大小测量

高国举; 周少龙; 孙玉娥; 黄河

doi:10.11999/JEIT240834

高速网络中优先级敏感的每流大小测量

doi: 10.11999/JEIT240834 cstr: 32379.14.JEIT240834

1.
苏州大学计算机科学与技术学院苏州 215006
2.
苏州大学轨道交通学院苏州 215131

基金项目: 国家自然科学基金(62332013, 62472298),中国博士后基金(2023M732537)

详细信息

作者简介:
高国举：男，副教授，研究方向为网络流量测量、Sketch结构设计、智能感知计算等

周少龙：男，硕士，研究方向为网络流量测量

孙玉娥：女，教授，研究方向为交通及网络流量统计、物联网、智能交通等

黄河：男，教授，研究方向为网络流量测量与大数据可信分析、智能物联网、信息安全与隐私保护等

通讯作者:
孙玉娥　sunye12@suda.edu.cn

中图分类号: TP393
计量
- 文章访问数: 195
- HTML全文浏览量: 103
- PDF下载量: 35
- 被引次数: 0
出版历程
- 收稿日期: 2024-10-08
- 修回日期: 2025-05-02
- 网络出版日期: 2025-05-24
- 刊出日期: 2025-06-30

Priority-aware Per-flow Size Measurement in High-speed Networks

1.
School of Computer Science and Technology, Soochow University, Suzhou 215006, China
2.
School of Rail Transportation, Soochow University, Suzhou 215131, China

Funds: The National Natural Science Foundation of China (62332013, 62472298), China Postdoctoral Science Foundation (2023M732537)

摘要

摘要: 高速网络中的流量测量在许多实际应用中起着至关重要的作用。在有限的内存资源下，Sketch能够保持良好的精度和较高的吞吐量，因此在流量测量中得到了广泛应用。然而，大多数现有的Sketch忽略了流之间的优先级差异。优先级敏感Sketch是一种新兴的Sketch，旨在为不同优先级的流量提供不同的测量精度。目前已有的优先级敏感Sketch很难在处理速度与高优先级测量精度之间取得良好平衡。为此，该文提出EssentialKeeper算法，该算法结合优先级敏感哈希与布谷鸟哈希的优势。优先级敏感哈希通过差异化处理不同优先级的流，确保大量低优先级流能够得到快速处理；布谷鸟哈希则最大限度地将高优先级流信息记录在高优先级部分，从而在保持高优先级流的高测量精度的同时，维持较高的吞吐量。在真实数据集上进行了大量的实验，实验结果表明，与最先进的优先级敏感Sketch相比，EssentialKeeper在高优先级流上的准确率平均提高58.5%，F1分数平均提高13.3%，同时可保证较高的吞吐量。
- 流量测量 /
- 优先级敏感 /
- 每流大小测量 /
- Sketch /
- 布谷鸟哈希
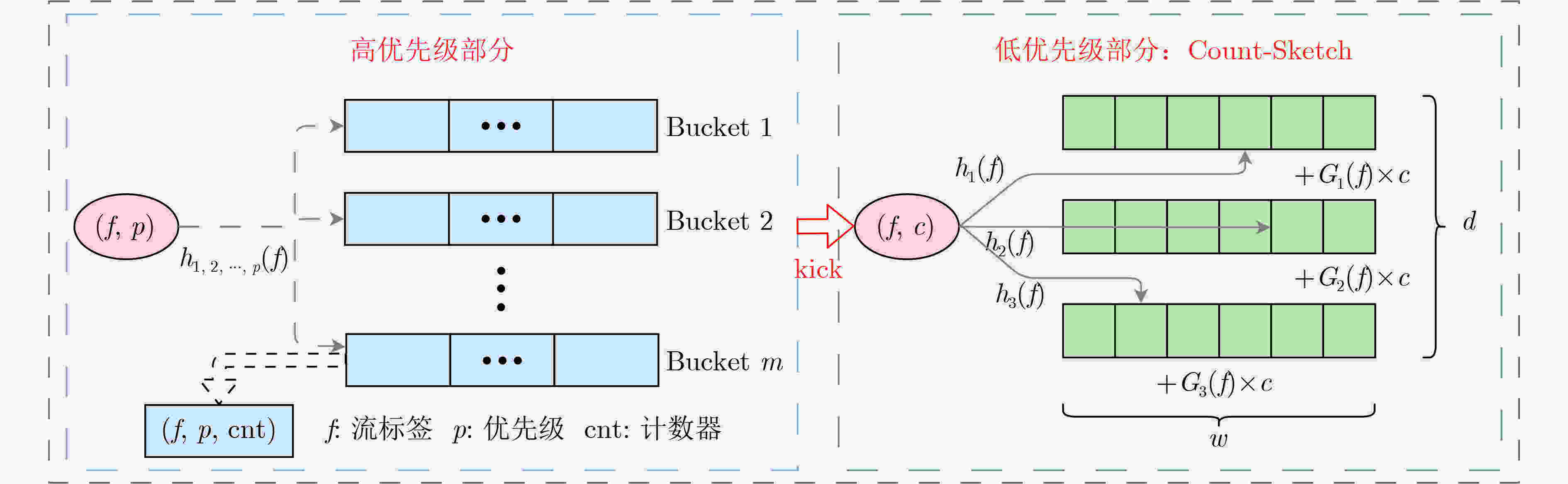
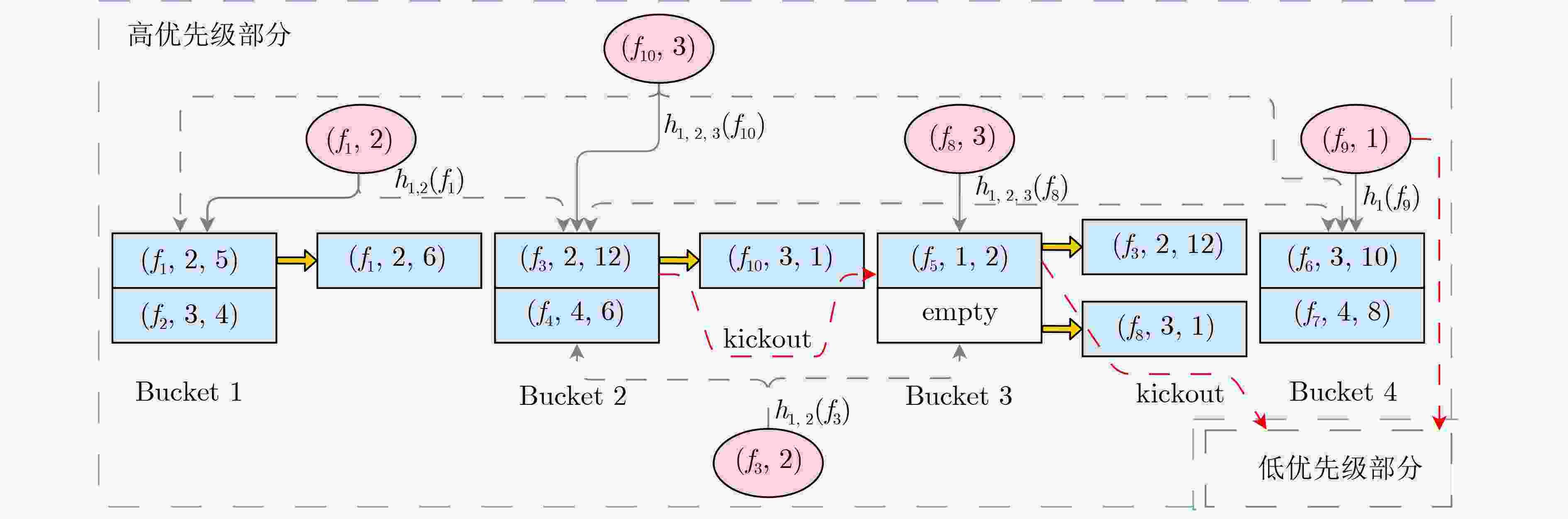
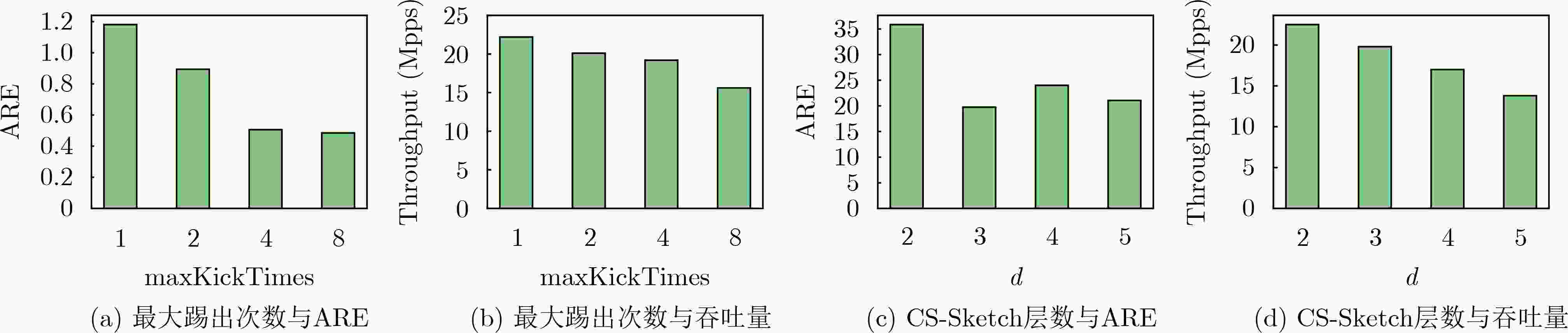
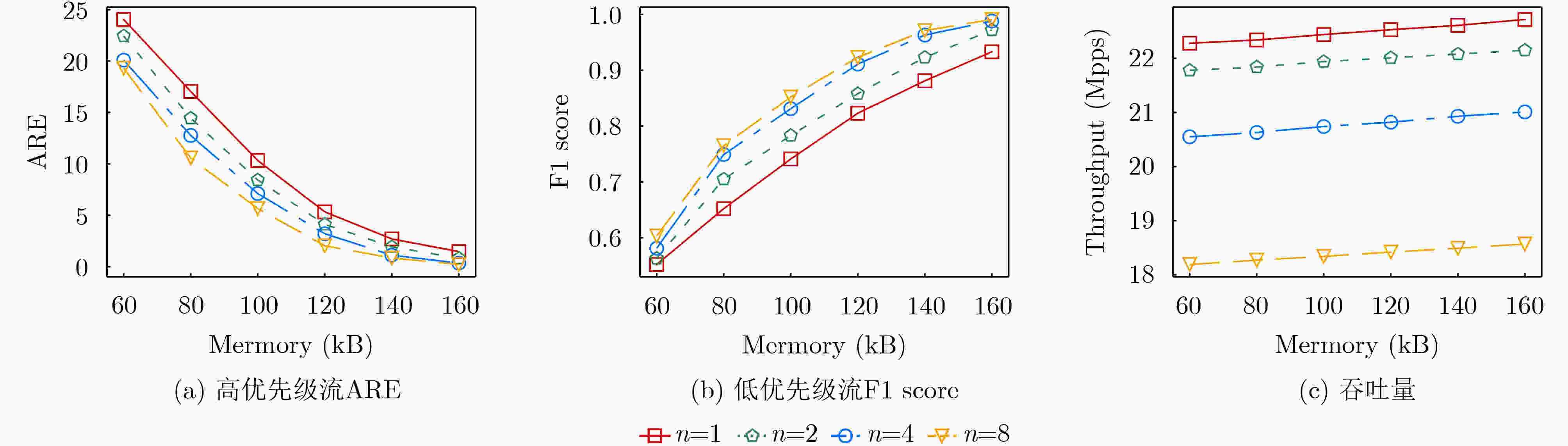
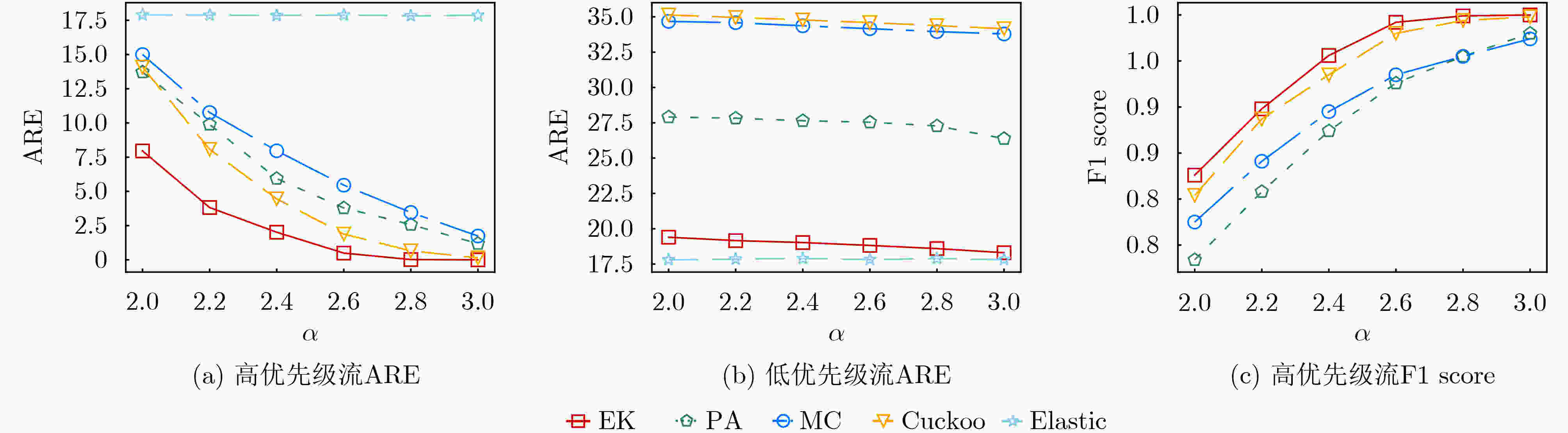
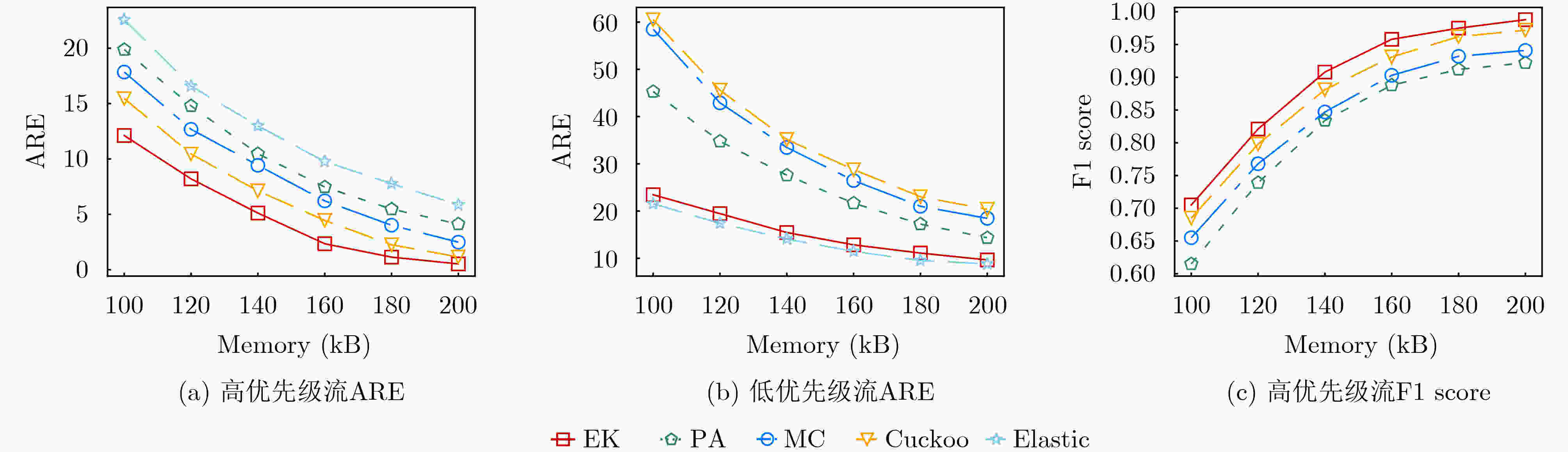
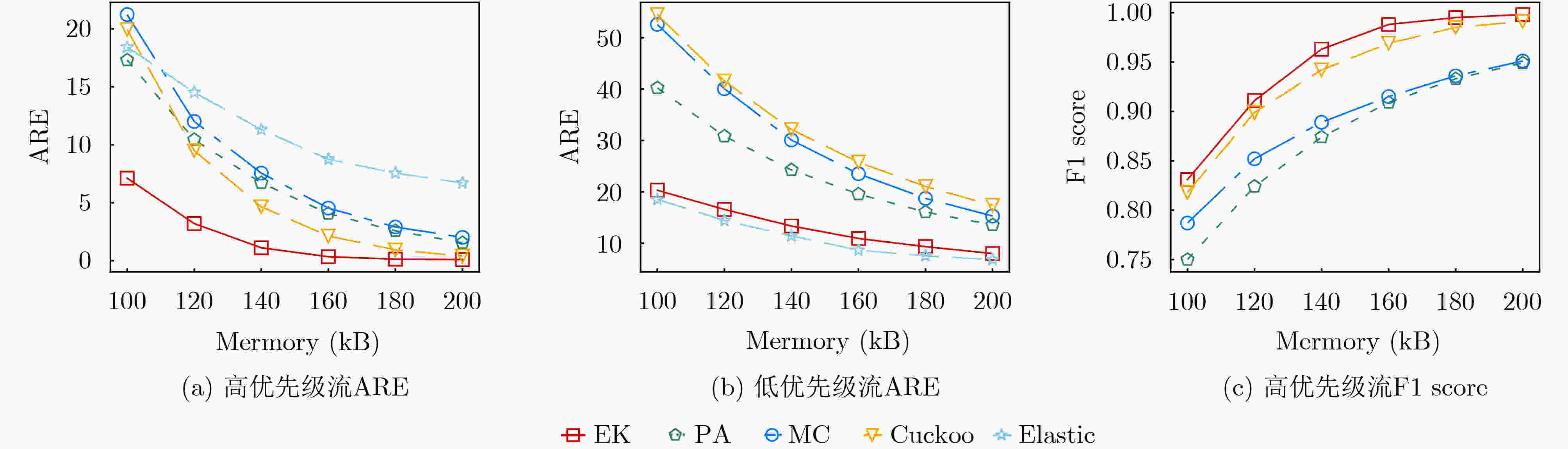
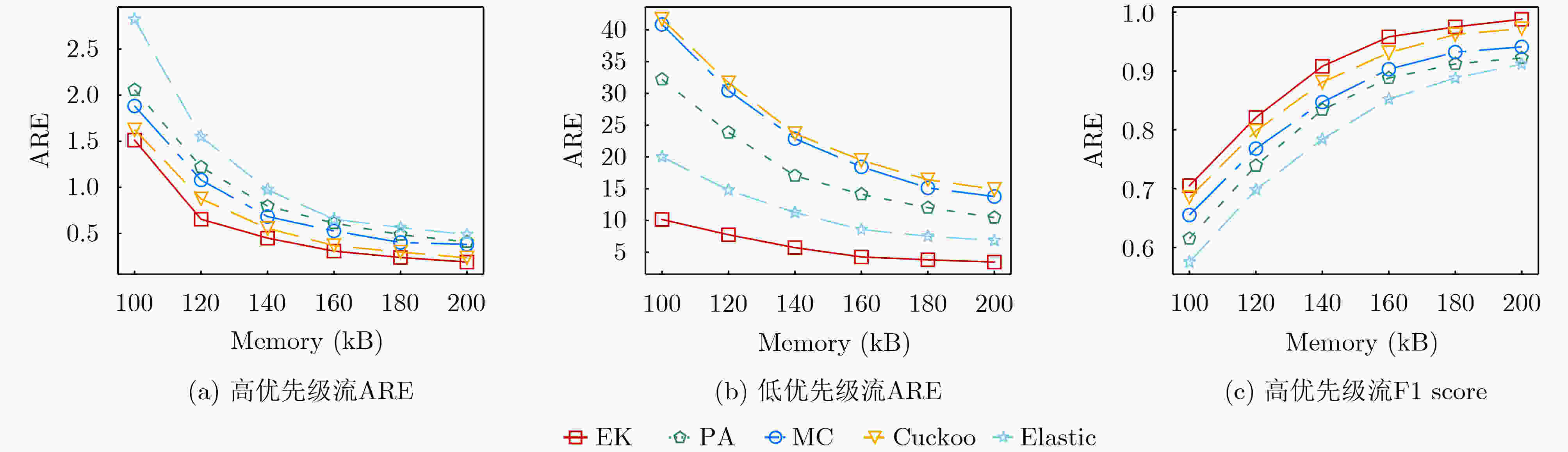
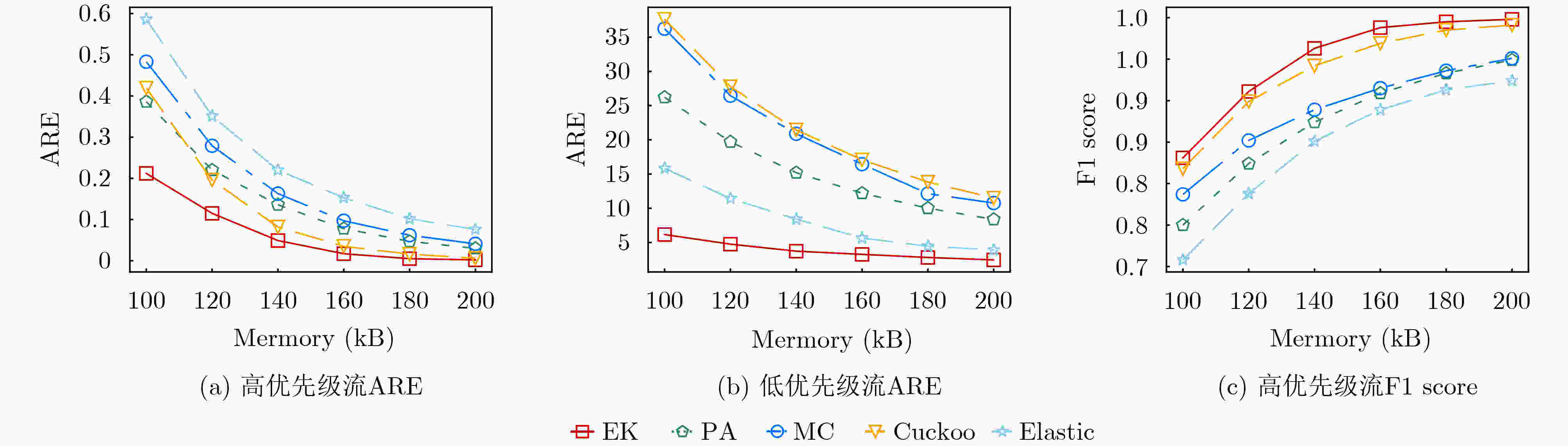
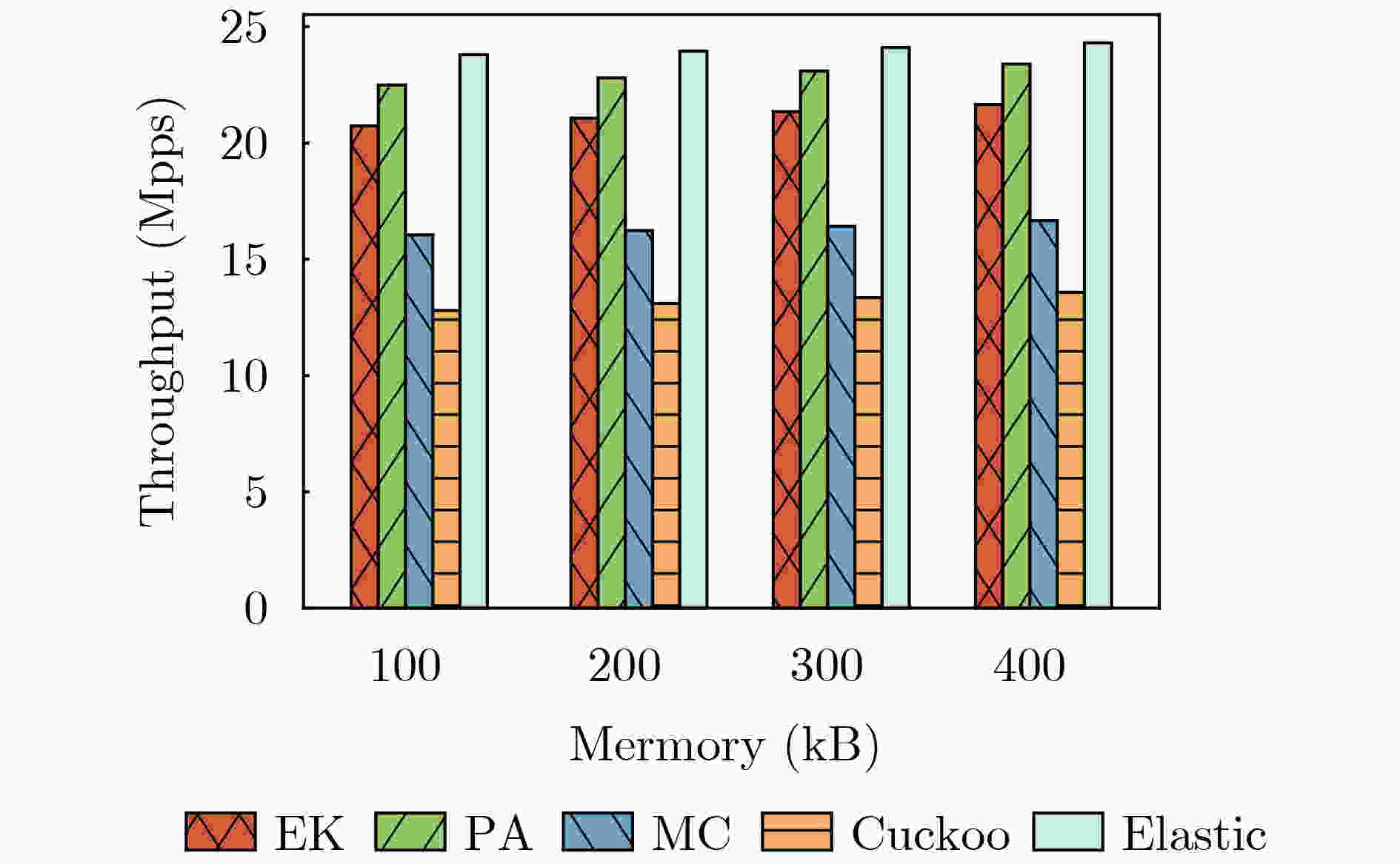
Abstract: Objective Network traffic measurement is essential for supporting applications such as anomaly detection and capacity planning. With growing demand for flow-level analysis, traffic measurement technologies are facing increasing performance requirements. In typical network environments, a flow comprises packets sharing a common five-tuple (including source/destination IP address, source/destination port, and protocol). Measuring per-flow size presents three core challenges: high data volume, fast transmission rates, and limited on-chip memory. Sketch-based data structures offer an effective trade-off among memory efficiency, query speed, and measurement accuracy, and have been widely adopted for tasks such as per-flow size estimation, cardinality estimation, persistent flow detection, and burst detection. However, the rising need for differentiated traffic handling has highlighted the limitations of traditional Sketches, which treat all flows uniformly. Existing priority-aware Sketches often fail to maintain both high accuracy for high-priority flows and overall system throughput. To address this gap, this study proposes EssentialKeeper, a priority-aware algorithm that combines priority-sensitive hashing with Cuckoo Hashing. The proposed method ensures accurate measurement for high-priority flows while maintaining efficient system-wide performance. This approach supports differentiated traffic measurement in high-speed networks and contributes both theoretical insights and practical value. Methods In practical networks, different traffic types have distinct requirements for measurement accuracy. For example, suspicious or malicious flows require high-precision measurement for security monitoring, whereas latency-sensitive services such as real-time video streaming demand continuous tracking to maintain service quality. To accommodate these varying demands, several priority-aware Sketch algorithms have been proposed. These typically partition memory into high- and low-priority regions, assigning different levels of accuracy according to flow priority. All incoming traffic first passes through the high-priority region, where high-priority flows are retained, whereas others are redirected with degraded measurement accuracy. This architecture, however, presents performance challenges. Because low-priority flows constitute the majority of network traffic, they still traverse the high-priority region, incurring additional hash computations and memory access overhead. This overhead substantially lowers throughput. Algorithms such as MC-Sketch and Cuckoo Sketch are particularly affected. Although PA-Sketch introduces priority-aware hashing to reduce the processing load for low-priority flows, it compromises measurement accuracy for medium-priority flows, limiting its practical utility. To address these limitations, this study proposes EssentialKeeper, a new Sketch algorithm for efficient priority-aware traffic measurement under constrained memory conditions. The algorithm combines priority-aware hashing with Cuckoo Hashing. For high-priority flows, it dynamically allocates more hash functions and candidate buckets, using Cuckoo hashing’s "kick-out and relocate" mechanism to enhance measurement precision. For low-priority flows, it employs an optimized Count-Sketch (CS-Sketch) structure to ensure fast processing. This hybrid design sustains high throughput while ensuring accurate tracking of high-priority traffic, thereby resolving the speed-accuracy trade-off that limits existing approaches. Results and Discussions This study evaluates EssentialKeeper using the real-world CAIDA-2019 traffic dataset and a network interaction dataset derived from Stack Overflow. Performance is assessed under different priority allocation strategies—random and size-based—and across a range of memory configurations. Optimal algorithm parameters are determined through systematic tuning (Fig. 3–5). Compared with existing priority-aware Sketches, EssentialKeeper demonstrates substantial improvements across three key metrics. Under the random priority allocation strategy, the average relative error for high-priority flows decreases by 63.2%, while the F1-score increases by 14.8% (Fig. 6, Fig. 7). With size-based priority allocation, the error is reduced by 53.8%, and the F1-score improves by 11.8% (Fig. 8, Fig. 9). Additionally, EssentialKeeper achieves a 10.8% increase in throughput (Fig. 10), while maintaining lower memory overhead. These results highlight the effectiveness of EssentialKeeper in supporting accurate and efficient priority-aware traffic measurement in high-speed network environments. Conclusions This study proposes EssentialKeeper, a novel algorithm for priority-aware traffic measurement in high-speed networks. By enhancing the structure of existing priority-aware Sketches, the algorithm enables accurate, differentiated measurement based on flow priority. It combines the efficient conflict resolution of Cuckoo Hashing with the adaptive precision of priority-aware hashing, thereby improving measurement accuracy for high-priority flows while sustaining high throughput for low-priority traffic. Experimental results demonstrate that EssentialKeeper reduces the average relative error of high-priority flows by 58.5%, increases the F1-score by 13.3%, and improves overall system throughput by 10.8% compared to the best existing approaches, achieving a favorable trade-off between speed and accuracy. Despite these advances, several challenges remain. One is the integration with sampling algorithms. Since high-priority flows often carry more critical information, future work could explore dynamic sampling strategies that retain high-priority packets while selectively discarding lower-priority traffic. This hybrid approach may further reduce system overhead without compromising measurement precision. Another direction is task generalization. Beyond per-flow size and cardinality estimation, other core measurement tasks—such as persistent flow detection and burst detection—may benefit from priority-aware techniques. Extending EssentialKeeper to support these applications would broaden its utility. Finally, current experiments are conducted in a CPU-based environment. However, practical deployment in production networks may require adaptation to hardware platforms such as P4 switches or FPGAs, which impose tighter resource constraints. Future research should focus on implementing and optimizing priority-aware Sketch algorithms for hardware deployment to assess feasibility and facilitate real-world adoption.
- Traffic measurement /
- Priority-aware /
- Per-flow size measurement /
- Sketch /
- Cuckoo hash

HTML全文

图 1 Essentialkeeper结构图

下载: 全尺寸图片幻灯片

图 2 Essentialkeeper处理流过程的示例

下载: 全尺寸图片幻灯片

图 3 参数调节实验图

下载: 全尺寸图片幻灯片

图 4 调节参数n实验图

下载: 全尺寸图片幻灯片

图 5 Zipf分布偏度参数调节实验图

下载: 全尺寸图片幻灯片

图 6 采用随机优先级分配策略(Stack Overflow数据集)

下载: 全尺寸图片幻灯片

图 7 采用随机优先级分配策略(CAIDA2019数据集)

下载: 全尺寸图片幻灯片

图 8 基于流大小分配优先级策略(Stack Overflow数据集)

下载: 全尺寸图片幻灯片

图 9 基于大小分配优先级策略(CAIDA 2019数据集)

下载: 全尺寸图片幻灯片

图 10 吞吐量实验图

下载: 全尺寸图片幻灯片

表 1 相关算法性能对比表

Sketch	优先级敏感性	可逆性	空间高效性	哈希次数
CM	×	×	×	d
CU	×	×	×	d
CS	×	×	×	2d
Elastic	×	√	√	1～1+d
PA	√	√	×	p～p+d
MC	√	√	√	1～L+d
Cuckoo	√	√	√	1～2K+d
EK (Ours)	√	√	√	1～p·K+d

下载: 导出CSV

1 EssentialKeeper插入算法

输入：流标签为f，优先级为p的数据包
输出：无输出
初始化：
所有数组置为空，计数器置为0；
p_min ← ∞; // 所有候选桶中流的最小优先级
idx_min ← -1; // 所有候选桶中优先级最小的流所在桶的索引
1. for i = 0 to gen(p) do:
2.　 idx = h_i(f) % m;
3. 　if BucketArray[idx]已存储流f:
4. 　　BucketArray[idx][pos].cnt++;
5. 　　return;
6. 　else if BucketArray[idx] 有空余单元格:
7. 　　将(f, p, 1)插入BucketArray[idx]中;
8. 　　return;
9. 　else if BucketArray[idx][0].p < p_min:
10. 　 p_min = BucketArray[idx][0].p;
11. 　 idx_min = idx;
12. if p > p_min :
13. temp = BucketArray[idx_min][0];
14. BucketArray[idx_min][0] → (f, p, 1);
15. 将BucketArray[idx_min]中的单元格按优先级排序;
16. 　 kickout(temp.f, temp.p, temp.cnt, 0);
17. else:
当前插入数据包的优先级小于候选桶中的任意一条流，故将(f, 1)插入低优先级部分；

下载: 导出CSV

2 kickout算法

输入：流标签f，优先级p，计数器值cnt，踢出次数kickTimes
输出：无输出
1. /* 踢出次数达到最大踢出次数maxKickTimes，则终止递归踢　出过程 */
2. if kickTimes == maxKickTimes:
3. 　将(f, cnt)插入低优先级部分;
4. 　return;
5. for i = 0 to gen(p) do:
6. 　idx = h_i(f) % m;
7. 　if BucketArray[idx]有空余单元格:
8. 　　将(f,p,cnt)插入BucketArray[idx]中;
9. 　　return;
10. else if BucketArray[idx][0].p < p_min:11. p_min = 　　　 BucketArray[idx][0].p;
12. 　 idx_min = idx;
13. if p <= p_min:
14. 将(f, cnt)插入低优先级部分;
15. else:
16. temp = BucketArray[idx_min][0];
17. BucketArray[idx_min][0] → (f, p, cnt);
18. 将BucketArray[idx_min]中的单元格按优先级排序;
19. kickout(temp.f, temp.p, temp.cnt, kickTimes + 1);

下载: 导出CSV

3 低优先级部分插入算法

输入：流标签f，流大小c
输出：无输出
1. for i = 0 to d do:
2. 　j = h_i(f) % w;
3. 　G_i(f) = 1 – 2 × (g_i(f) % 2);
4. 　CS[i][j] ← CS[i][j] + G_i(f) × c;

下载: 导出CSV

4 EssentialKeeper查询算法

输入：流标签f，优先级p
输出：流f的流大小估计值
1. /* 查询高优先级部分中是否存储流f */
2. for i = 0 to gen(p) do：
3. 　idx = h_i(f) % m;
4. 　if BucketArray[idx]已存储流f:
5. 　　return BucketArray[idx][pos].cnt;
6. /* 高优先级部分中没有存储流f，则在低优先级部分查询 */
7. for i = 0 to d do:
8. 　j = h_i(f) % w;
9. 　G_i(f) = 1 – 2 × (g_i(f) % 2);
10. $\varGamma_i $ ← G_i(f) × CS[i][j];
11. return max{0,median({$\varGamma_i $ \|0≤i≤d})};

下载: 导出CSV

参考文献(17)

[1]	CISCO. Cisco annual internet report (2018–2023) white paper[EB/OL]. https://www.cisco.com/c/en/us/solutions/collateral/executive-perspectives/annual-internet-report/white-paper-c11-741490.html, 2020.
[2]	ZHAO Yikai, ZHOU Wei, HAN Wenchen, et al. Achieving top-K K-fairness for finding global top-K K frequent items[J]. IEEE Transactions on Knowledge and Data Engineering, 2025, 37(4): 1508–1526. doi: 10.1109/TKDE.2024.3523033.
[3]	LI Yuanpeng, WANG Feiyu, YU Xiang, et al. LadderFilter: Filtering infrequent items with small memory and time overhead[J]. Proceedings of the ACM on Management of Data, 2023, 1(1): 10. doi: 10.1145/3588690.
[4]	YANG Tong, JIANG Jie, LIU Peng, et al. Elastic sketch: Adaptive and fast network-wide measurements[C]. The 2018 Conference of the ACM Special Interest Group on Data Communication, Budapest, Hungary, 2018: 561–575. doi: 10.1145/3230543.3230544.
[5]	YANG Tong, ZHANG Haowei, LI Jinyang, et al. HeavyKeeper: An accurate algorithm for finding top-k elephant flows[J]. IEEE/ACM Transactions on Networking, 2019, 27(5): 1845–1858. doi: 10.1109/TNET.2019.2933868.
[6]	CHENG Shiyu, YANG Dongsheng, YANG Tong, et al. LTC: A fast algorithm to accurately find significant items in data streams[J]. IEEE Transactions on Knowledge and Data Engineering, 2022, 34(9): 4342–4356. doi: 10.1109/TKDE.2020.3038911.
[7]	DU Yang, HUANG He, SUN Y E, et al. Self-adaptive sampling based per-flow traffic measurement[J]. IEEE/ACM Transactions on Networking, 2023, 31(3): 1010–1025. doi: 10.1109/TNET.2022.3212066.
[8]	ZHANG Yinda, LI Jinyang, LEI Yutian, et al. On-off sketch: A fast and accurate sketch on persistence[J]. Proceedings of the VLDB Endowment, 2020, 14(2): 128–140. doi: 10.14778/3425879.3425884.
[9]	WANG Haibo, MELISSOURGOS D, MA Chaoyi, et al. Real-time spread burst detection in data streaming[J]. Proceedings of the ACM on Measurement and Analysis of Computing Systems, 2023, 7(2): 35. doi: 10.1145/3589979.
[10]	LIN K C J and LAI Weilun. MC-sketch: Enabling heterogeneous network monitoring resolutions with multi-class sketch[C]. IEEE INFOCOM 2022 - IEEE Conference on Computer Communications, London, United Kingdom, 2022: 220–229. doi: 10.1109/INFOCOM48880.2022.9796955.
[11]	YAN Yibo, CHEN Cheng, LIN Huiping, et al. Priority-aware per-flow measurement using cuckoo Sketch[C]. 2020 IFIP Networking Conference (Networking), Paris, France, 2020: 622–624.
[12]	LI Sitan, HUANG Jiawei, ZHANG Wenlu, et al. PA-sketch: A fast and accurate sketch for differentiated flow estimation[C]. 2023 IEEE 31st International Conference on Network Protocols (ICNP), Reykjavik, Iceland, 2023: 1–11. doi: 10.1109/ICNP59255.2023.10355581.
[13]	MINTON G T and PRICE E. Improved concentration bounds for count-sketch[C]. The Twenty-Fifth Annual ACM-SIAM Symposium on Discrete Algorithms, Portland, Oregon, 2014: 669–686. doi: 10.5555/2634074.2634125.
[14]	TING D. Count-min: Optimal estimation and tight error bounds using empirical error distributions[C]. The 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, London, United Kingdom, 2018: 2319–2328. doi: 10.1145/3219819.3219975.
[15]	ESTAN C and VARGHESE G. New directions in traffic measurement and accounting: Focusing on the elephants, ignoring the mice[J]. ACM Transactions on Computer Systems, 2003, 21(3): 270–313. doi: 10.1145/859716.859719.
[16]	ZHAO Xiaolei, WEN Mei, TANG Minjin, et al. HybridSketch: A memory-centric precise approach for flow measurement[C]. ICC 2020 - 2020 IEEE International Conference on Communications (ICC), Dublin, Ireland, 2020: 1–7. doi: 10.1109/ICC40277.2020.9149374.
[17]	CAIDA. Anonymized internet traces 2019[EB/OL]. https://catalog.caida.org/dataset/passive_2019_pcap, 2019.