Radar Emitter Individual Identification Based on Information Sidebands of Unintentional Phase Modulation on Pulses
-
摘要: 无意调相是雷达辐射源个体识别中的关键信息,能够提供细微的相位变化信息,捕捉到不同辐射源的微小差异,在区分具有相似硬件结构的雷达辐射源时具有显著优势。针对同一厂家生产的同型号辐射源无意调相特性区分性不明显的问题,该文提出一种基于无意调相边带信息与深度学习相结合的个体识别方法。通过深入挖掘无意调相特性中的边带信息,增强不同辐射源个体间的差异性,并引入双路循环膨胀卷积网络增加神经网络感受野。实验实测数据显示,该方法在信噪比为5 dB的条件下,仍能对10台同型号的辐射源实现87.58%的平均识别准确率,对比1维残差网络,识别精度提高了21.41%。Abstract:
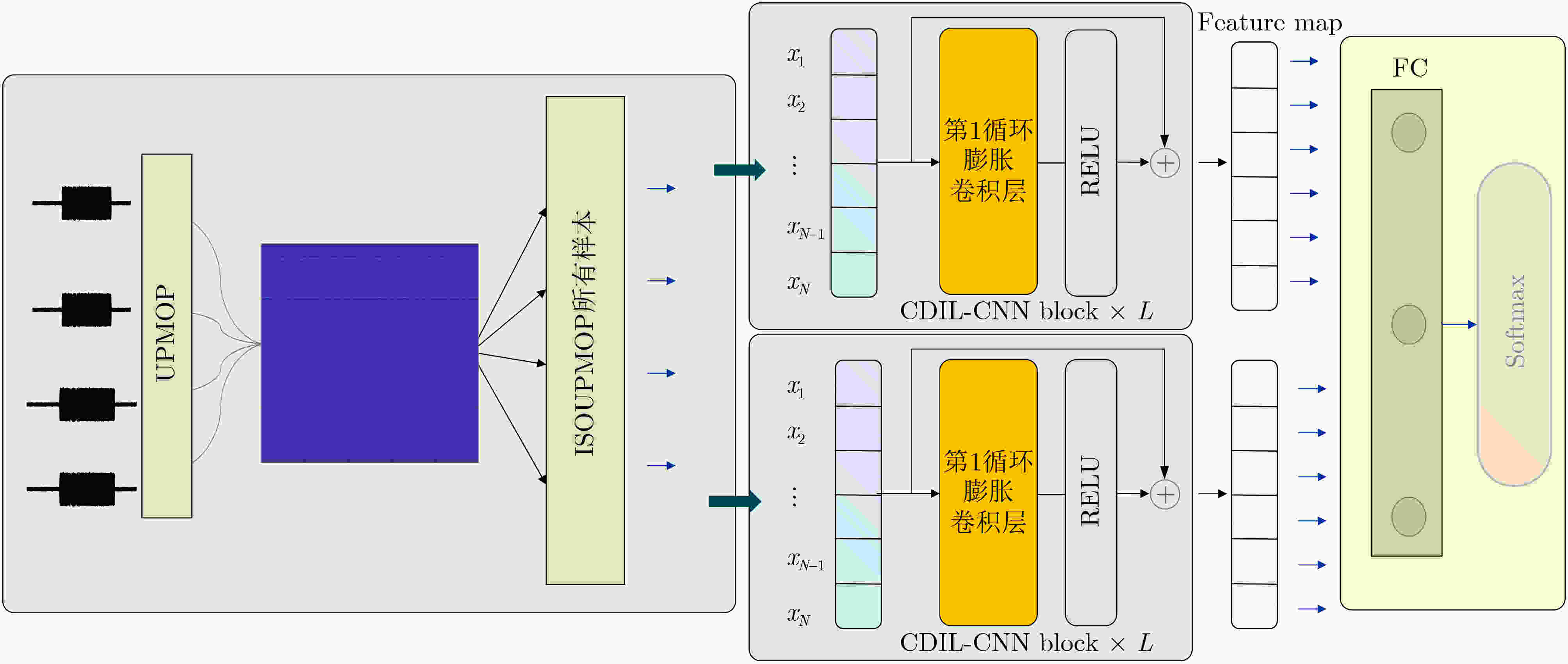
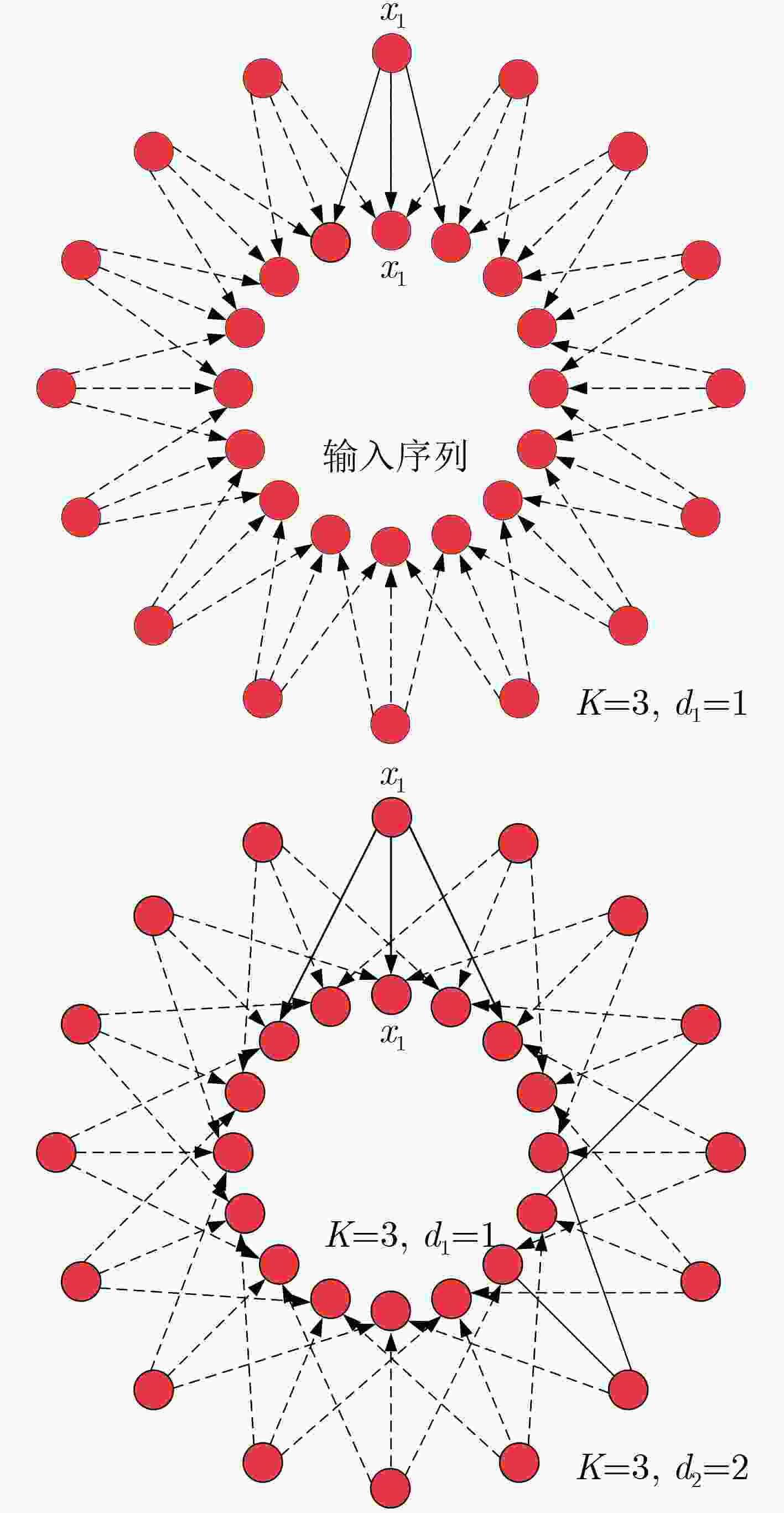
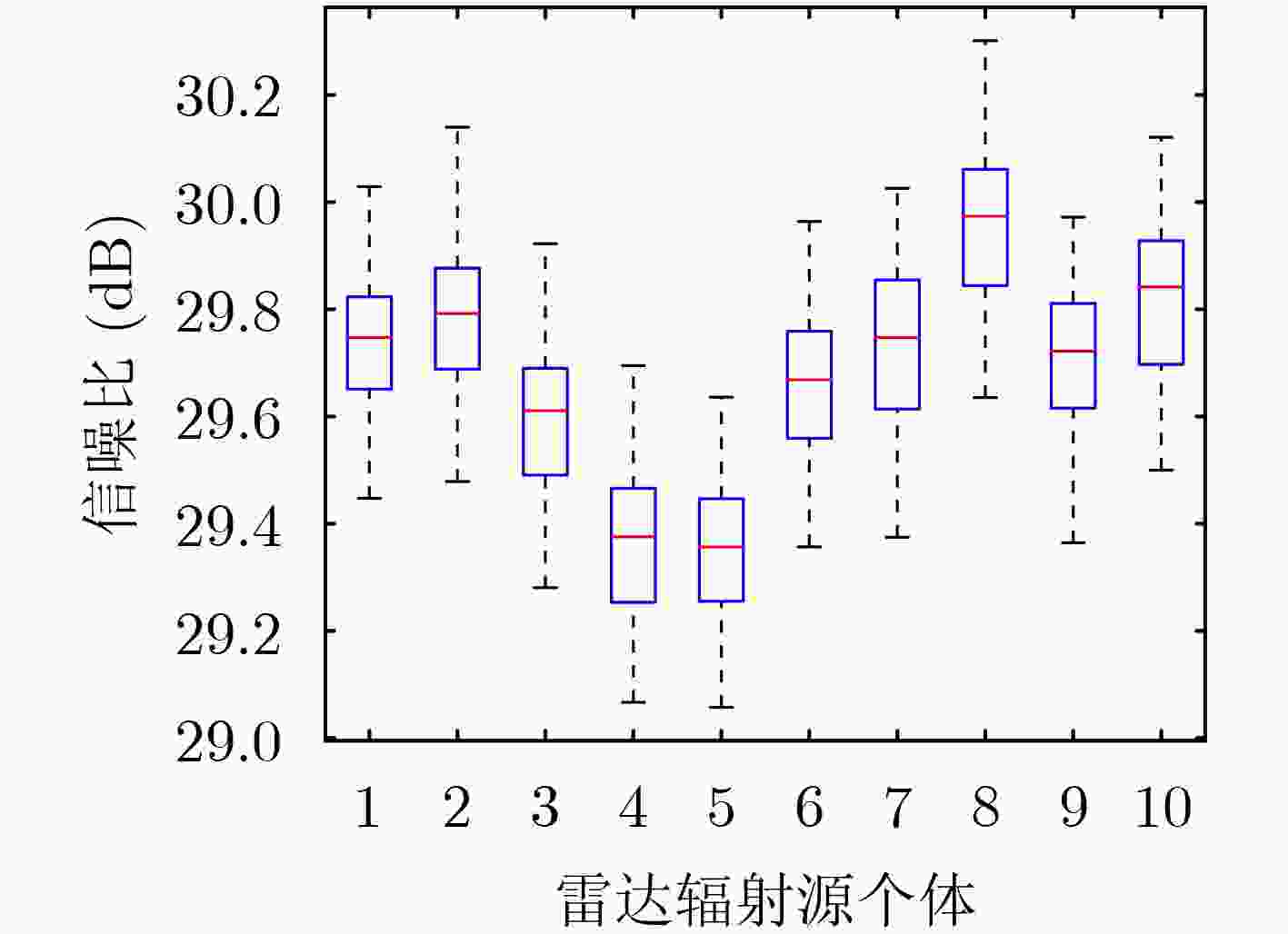
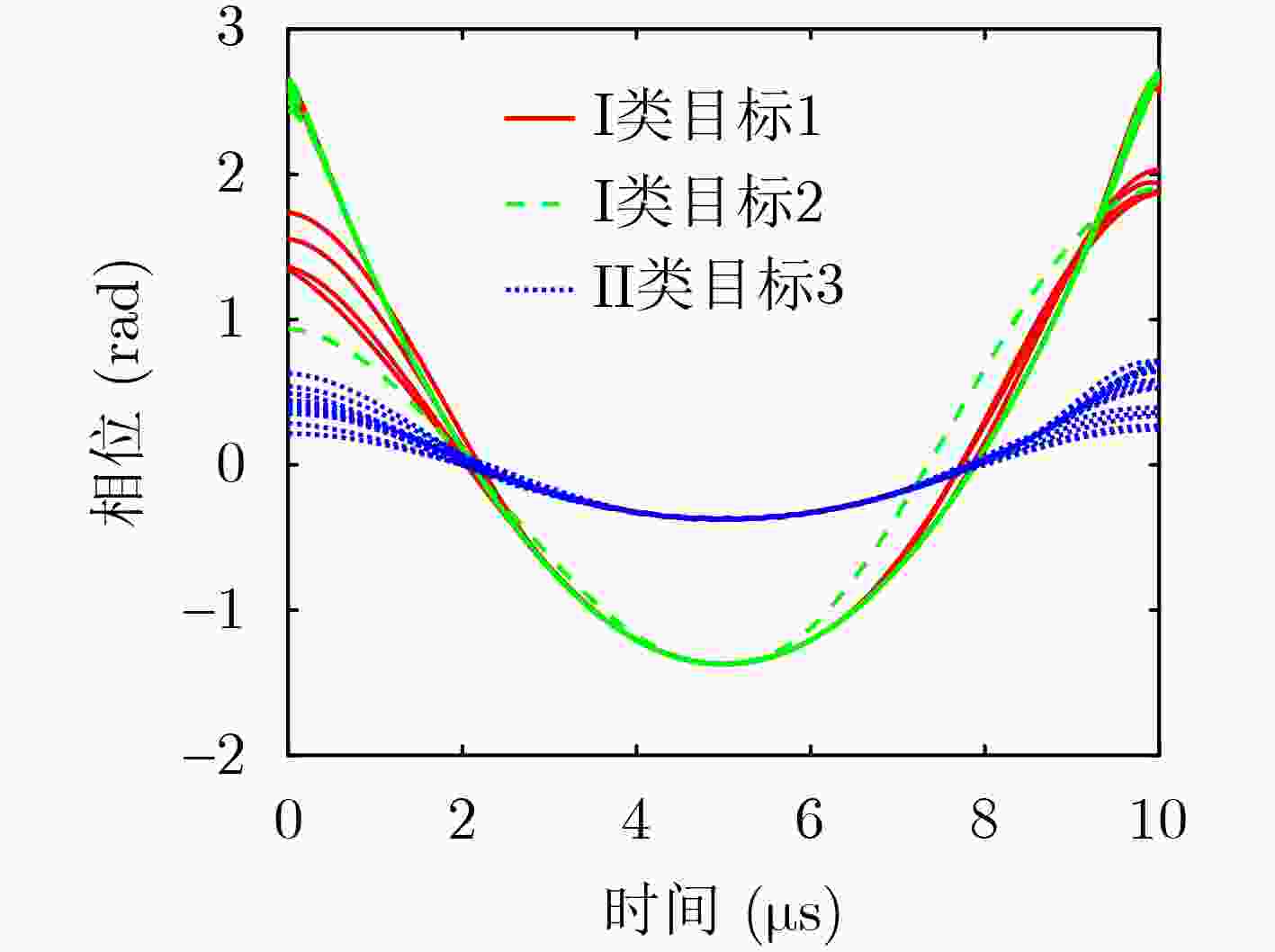
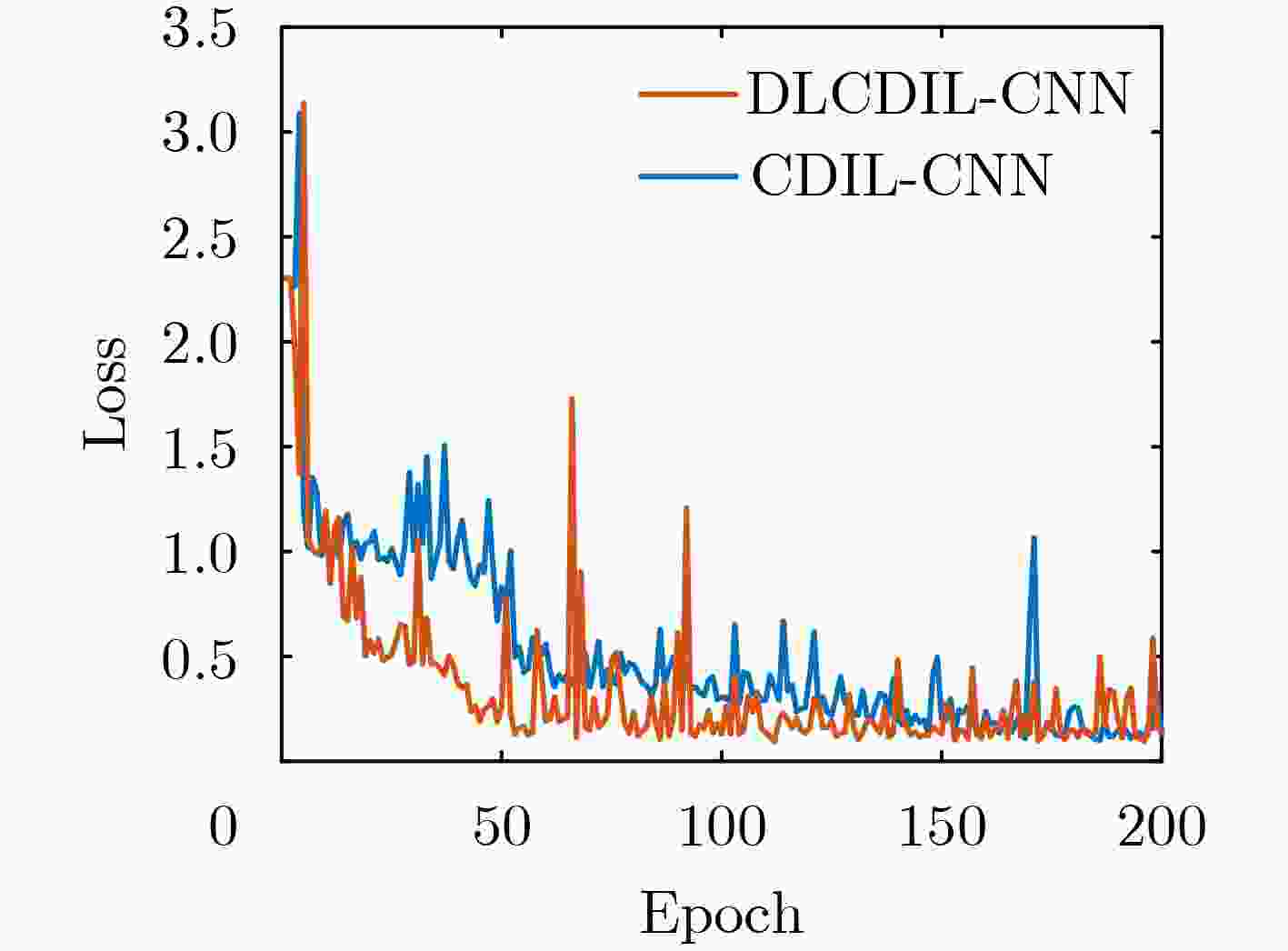
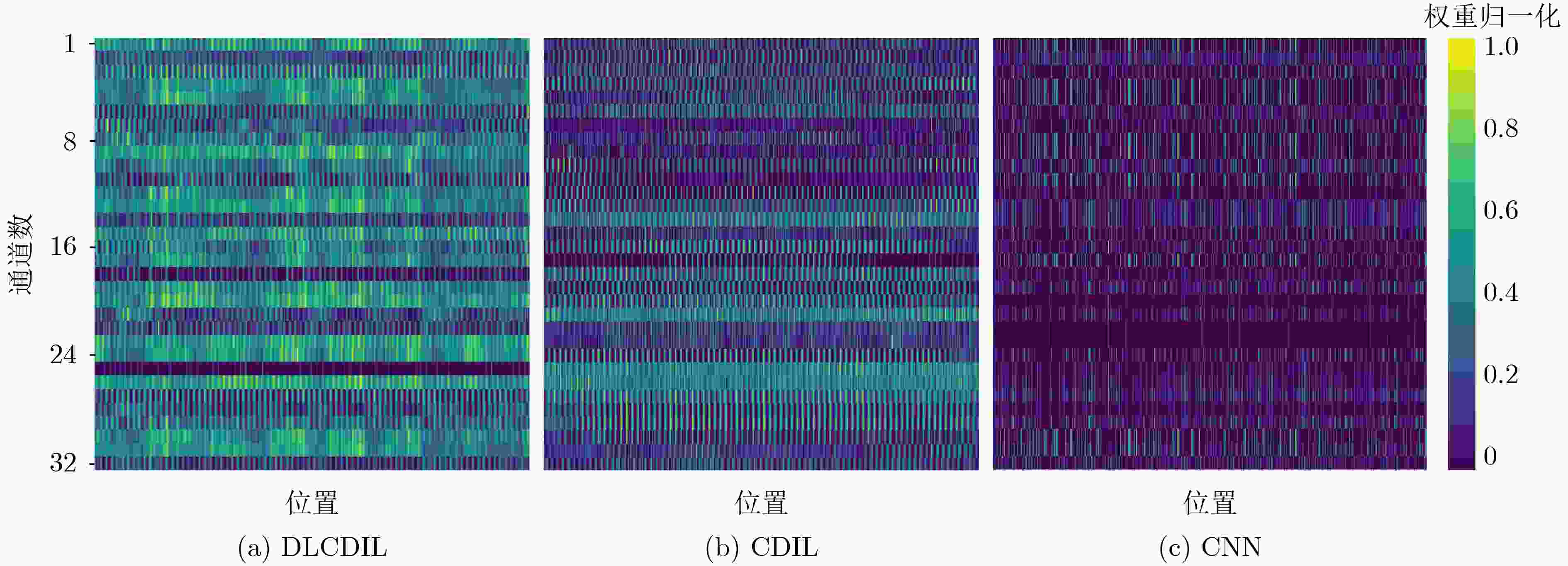
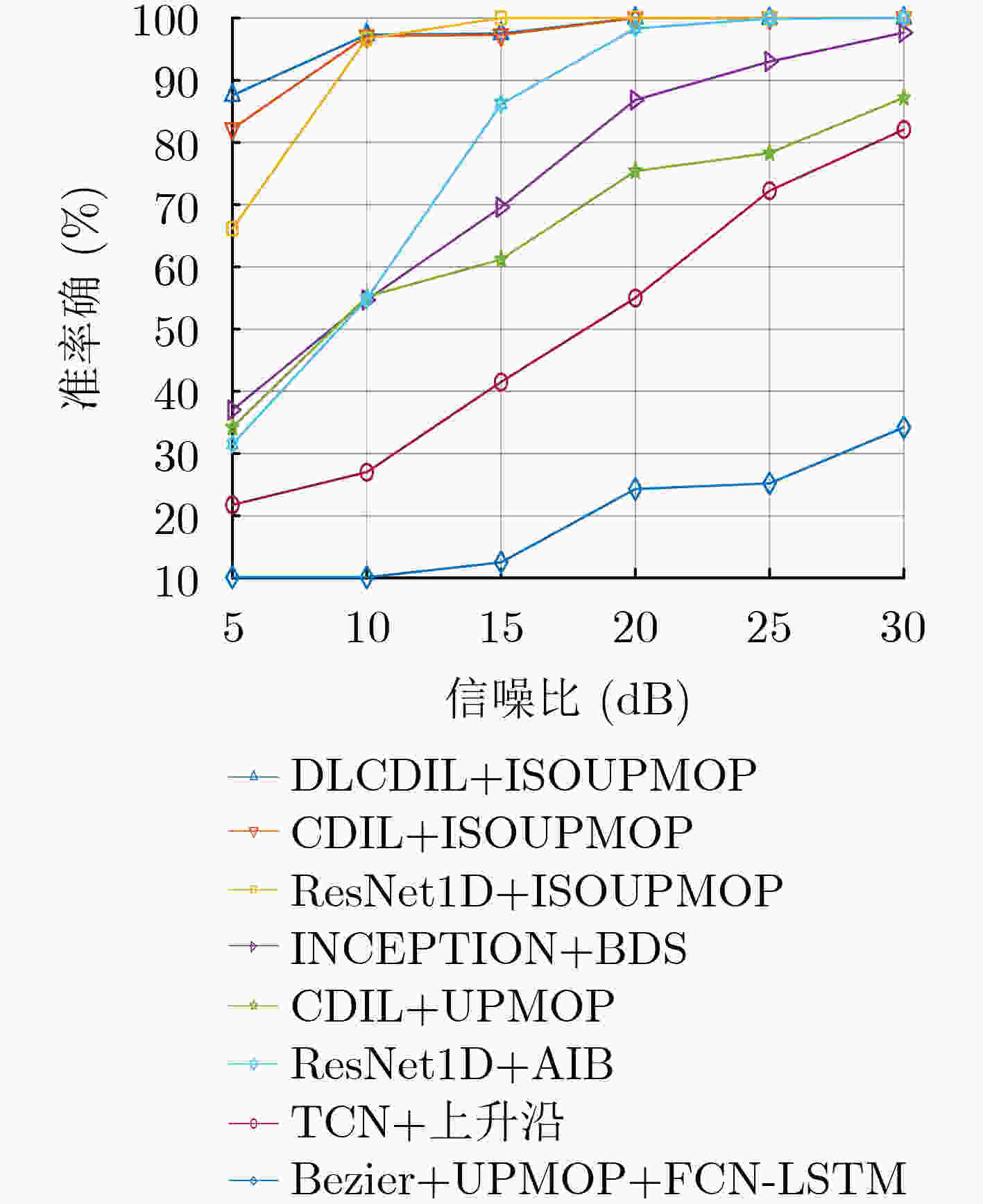
Objective Radar Emitter Identification (REI) plays a critical role in complex battlefield environments and electronic warfare. Conventional methods for extracting Unintentional Phase Modulation On Pulse (UPMOP) features are often ineffective at distinguishing emitters of the same model and manufacturer, due to hardware similarities. This limitation hinders the ability to accurately identify individual emitters. To overcome this challenge, a new method is proposed that integrates Information Sidebands Of Unintentional Phase Modulation On Pulses (ISOUPMOP) with deep learning techniques. This approach mitigates phase ambiguity and noise, thereby enhancing the ability to discriminate between emitters of the same type. A Dual-Loop Circular DILated Convolutional Neural Network (DLCDIL-CNN) is used to expand the receptive field, improving the processing of long-sequence data. This design results in a more accurate identification of radar radiation sources with similar hardware characteristics. Methods Unintentional phase modulation refers to subtle fluctuations in the phase of radar signals, primarily caused by hardware instability and nonlinear characteristics of radar transmitters. This study first applies Variational Mode Decomposition (VMD) to denoise the UPMOP features by decomposing them into signal components at different frequency bands. These components are then analyzed using the Wavelet SynchroSqueezed Transform (WSST) to perform high-resolution time-frequency analysis and extract phase information from multiple time-frequency components. The mean of the time-frequency ridge line is used for discriminative analysis, and components containing ISOUPMOP are reconstructed as identification features. For individual identification, a DLCDIL-CNN is employed. The input data are split into two branches, each processed using Circular Dilated Convolution (CDC) layers with ring padding. This architecture expands the receptive field without introducing boundary effects, enabling the model to capture long-range dependencies and maintain robustness to data shifts. Results and Discussions Visualization experiments reveal that traditional UPMOP features are strongly influenced by the emitter model, resulting in poor differentiation among sources of the same type ( Figure 9 ). Feature map analysis and model performance comparisons show that HeatMap visualizations of the fully connected layers highlight higher Activation Values (AV) in the final layer of the DLCDIL-CNN compared to those of CDIL-CNN and conventional CNNs (Figure 11 ). This indicates that the CDC used in DLCDIL-CNN is more effective at capturing global features. Robustness validation is conducted under varying Signal-to-Noise Ratio (SNR) conditions, comparing the proposed method with several other identification approaches. At 5 dB SNR, the ISOUPMOP feature extraction method combined with ResNet1D achieves an average identification accuracy of 66.17%, outperforming other methods. When paired with the DLCDIL-CNN, average accuracy increases to 87.58%, representing a 21.42% improvement over ResNet1D (Figure 12 ). Although DLCDIL-based identification using noisy UPMOP features remains functional, its accuracy is lower than that of the proposed approach. Moreover, smoothed UPMOP features fail to support accurate recognition, even under high SNR conditions. These results suggest that although noisy UPMOP retains individual information, emitters of the same model exhibit similar circuit behavior, and denoising may remove critical nonlinear characteristics. As the number of individual emitters increases, the smoothed UPMOP feature curve leads to feature aliasing, reducing recognition performance. In contrast, the ISOUPMOP method retains unintentional signal characteristics while eliminating trend components, thereby enhancing model generalizability and mitigating overfitting.Conclusions To improve individual differentiation among radar sources of the same model, this study proposes a method that combines ISOUPMOP feature extraction with a DLCDIL-CNN architecture. The approach enhances feature discriminability by preserving subtle individual variations and improves identification accuracy through expanded receptive fields and reduced boundary effects. Experimental results confirm that the proposed method achieves an average accuracy of 87.58% under 5 dB SNR for 10 emitters of the same model. These findings indicate that the method effectively resolves the challenge of limited individual differentiation in traditional UPMOP-based techniques and provides a reliable framework for radar emitter individual identification. -
1 ISOUPMOP提取流程
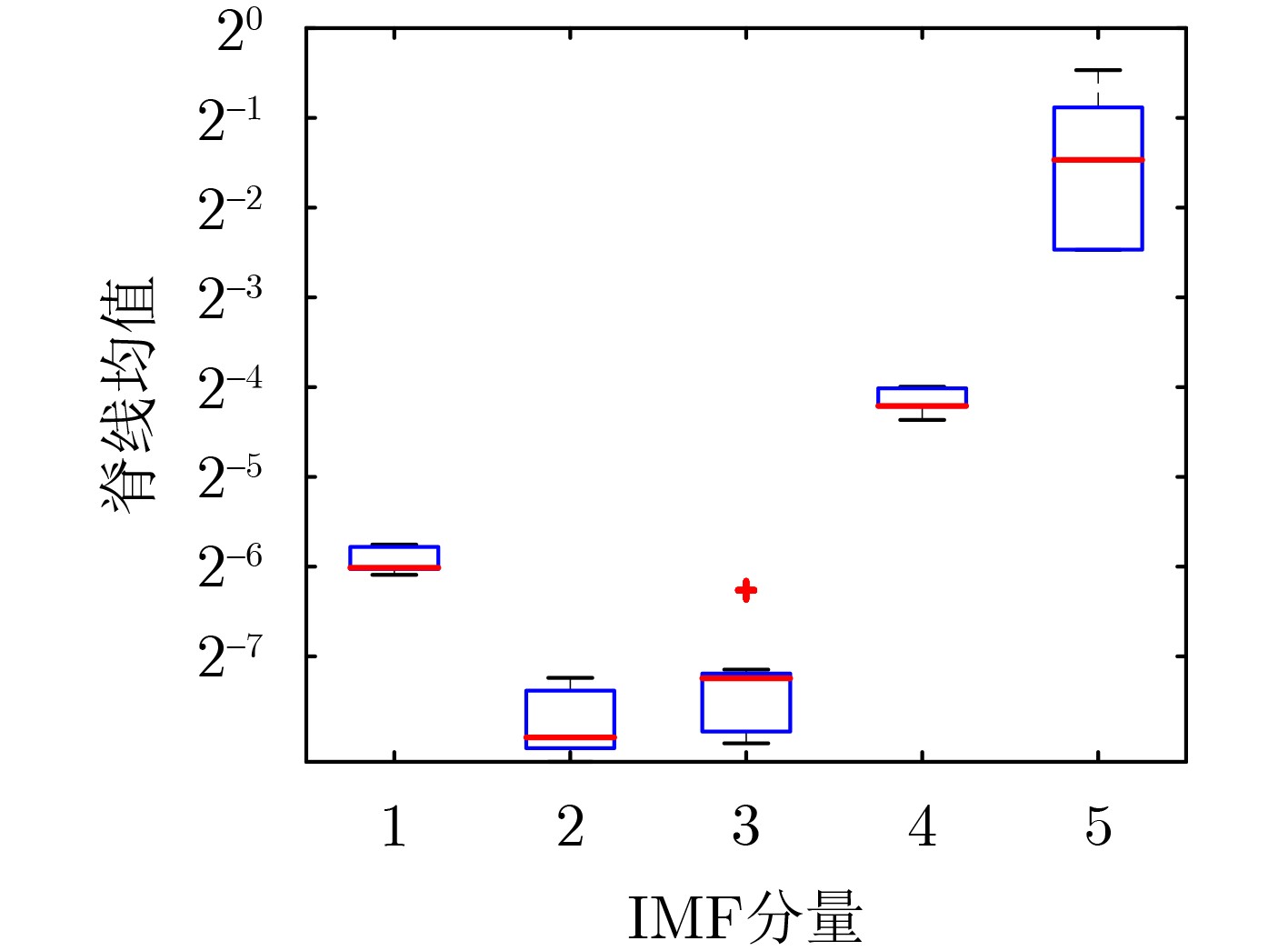
初始化:UPMOP序列$ {\boldsymbol{u}} $,阈值$ \tau $,$ {\text{IM}}{{\text{F}}_{{\text{keep}}}} = [\;] $ 分解$ {u} = \displaystyle\sum\nolimits_{k = 1}^{K - 1} {{u_k}(n)} $得到不同本征模函数$ {\text{IM}}{{\text{F}}k} = {u_k}(n) $ For $ k $=1: $ K{{ - 1}} $ 计算得到时频矩阵 $ {{\boldsymbol{T}}_k}(n,f) = {\text{WSST(}}{u_k}{{(n))}} $ 提取脊线$ {R_k}(n) = \arg \mathop {\max }\limits_f {{\boldsymbol{T}}_k}(n,f) $ 计算脊线均值$ {\gamma _k} = \dfrac{1}{N}\displaystyle\sum\nolimits_{n = 0}^N {{R_k}(n)} $ If $ {\gamma _k} > \tau $,则$ {\text{IM}}{{\text{F}}_{{\text{keep}}}} \leftarrow {\text{IM}}{{\text{F}}_{{\text{keep}}}} \cup \left\{ {{u_k}(n)} \right\} $ Return $ {\text{IM}}{{\text{F}}_{{\text{keep}}}} $ 输出:$ {x} = \displaystyle\sum\nolimits_{{{\boldsymbol{u}}_k} \in {\text{IM}}{{\text{F}}_{{\text{keep}}}}} {{u_k}(n)} $ 表 1 信号参数设置
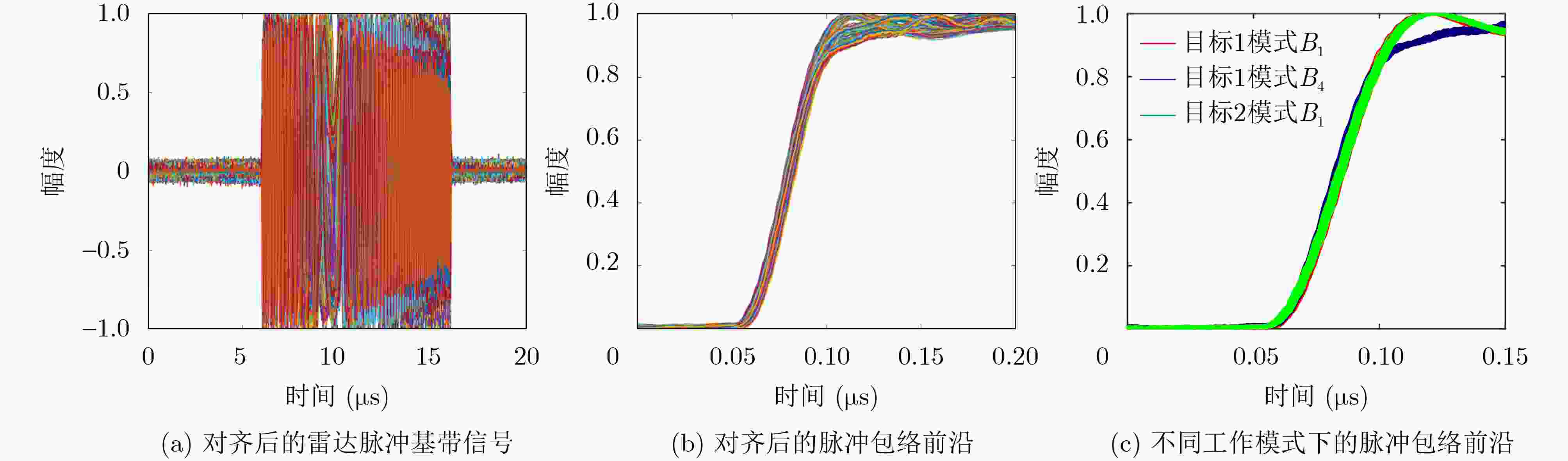
调制方式 参数 取值 LFM 中心频率(GHz) 1.5 调制带宽(MHz) $ {B_1} \text{~} {B_4} $ 脉冲宽度(μs) 10 -
[1] PENG Heli, XIE Kai, and ZOU Wenxu. Research on an enhanced multimodal network for specific emitter identification[J]. Electronics, 2024, 13(3): 651. doi: 10.3390/electronics13030651. [2] 张立民, 谭凯文, 闫文君, 等. 基于持续学习和联合特征提取的特定辐射源识别[J]. 电子与信息学报, 2023, 45(1): 308–316. doi: 10.11999/JEIT211176.ZHANG Limin, TAN Kaiwen, YAN Wenjun, et al. Specific emitter identification based on continuous learning and joint feature extraction[J]. Journal of Electronics & Information Technology, 2023, 45(1): 308–316. doi: 10.11999/JEIT211176. [3] GUO Shanzeng, AKHTAR S, and MELLA A. A method for radar model identification using time-domain transient signals[J]. IEEE Transactions on Aerospace and Electronic Systems, 2021, 57(5): 3132–3149. doi: 10.1109/TAES.2021.3074129. [4] LI Haozhe, LIAO Yilin, WANG Wenhai, et al. A novel time-domain graph tensor attention network for specific emitter identification[J]. IEEE Transactions on Instrumentation and Measurement, 2023, 72: 5501414. doi: 10.1109/TIM.2023.3241976. [5] 肖易寒, 王博煜, 于祥祯, 等. 基于双路射频指纹卷积神经网络与特征融合的雷达辐射源个体识别[J]. 电子与信息学报, 2024, 46(8): 3238–3245. doi: 10.11999/JEIT231236.XIAO Yihan, WANG Boyu, YU Xiangzhen, et al. Radar emitter identification based on dual radio frequency fingerprint convolutional neural network and feature fusion[J]. Journal of Electronics & Information Technology, 2024, 46(8): 3238–3245. doi: 10.11999/JEIT231236. [6] 刘钊, 马爽, 张梦杰, 等. 多径条件下的雷达辐射源个体识别方法[J]. 电子学报, 2023, 51(6): 1654–1665. doi: 10.12263/DZXB.20220990.LIU Zhao, MA Shuang, ZHANG Mengjie, et al. Radar specific emitter identification method under multipath conditions[J]. Acta Electronica Sinica, 2023, 51(6): 1654–1665. doi: 10.12263/DZXB.20220990. [7] 叶浩欢, 柳征, 姜文利. 考虑多普勒效应的脉冲无意调制特征比较[J]. 电子与信息学报, 2012, 34(11): 2654–2659.YE Haohuan, LIU Zheng, and JIANG Wenli. A comparison of unintentional modulation on pulse features with the consideration of Doppler effect[J]. Journal of Electronics & Information Technology, 2012, 34(11): 2654–2659. [8] 秦鑫, 黄洁, 王建涛, 等. 基于无意调相特性的雷达辐射源个体识别[J]. 通信学报, 2020, 41(5): 104–111. doi: 10.11959/j.issn.1000-436x.2020084.QIN Xin, HUANG Jie, WANG Jiantao, et al. Radar emitter identification based on unintentional phase modulation on pulse characteristic[J]. Journal on Communications, 2020, 41(5): 104–111. doi: 10.11959/j.issn.1000-436x.2020084. [9] ZHANG Wenxu, ZHANG Fosheng, ZHAO Zhongkai, et al. Radar specific emitter identification via the Attention-GRU model[J]. Digital Signal Processing, 2023, 142: 104198. doi: 10.1016/j.dsp.2023.104198. [10] TRIBOLET J. A new phase unwrapping algorithm[J]. IEEE Transactions on Acoustics, Speech, and Signal Processing, 1977, 25(2): 170–177. doi: 10.1109/TASSP.1977.1162923. [11] RU Xiaohu, LIU Zheng, JIANG Wenli, et al. Recognition performance analysis of instantaneous phase and its transformed features for radar emitter identification[J]. IET Radar, Sonar & Navigation, 2016, 10(5): 945–952. doi: 10.1049/iet-rsn.2014.0512. [12] MORALES S and BOWERS M E. Time-frequency analysis methods and their application in developmental EEG data[J]. Developmental Cognitive Neuroscience, 2022, 54: 101067. doi: 10.1016/j.dcn.2022.101067. [13] YU Xiao, LIANG Zhongting, WANG Youjie, et al. A wavelet packet transform-based deep feature transfer learning method for bearing fault diagnosis under different working conditions[J]. Measurement, 2022, 201: 111597. doi: 10.1016/j.measurement.2022.111597. [14] DAUBECHIES I, LU Jianfeng, and WU H T. Synchrosqueezed wavelet transforms: An empirical mode decomposition-like tool[J]. Applied and Computational Harmonic Analysis, 2011, 30(2): 243–261. doi: 10.1016/j.acha.2010.08.002. [15] LI Shuai, LI Wanqing, COOK C, et al. Independently recurrent neural network (IndRNN): Building a longer and deeper RNN[C]. 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, USA, 2018: 5457–5466. doi: 10.1109/CVPR.2018.00572. [16] TAY Y, DEHGHANI M, BAHRI D, et al. Efficient transformers: A survey[J]. ACM Computing Surveys, 2022, 55(6): 109. doi: 10.1145/3530811. [17] HEWAGE P, BEHERA A, TROVATI M, et al. Temporal convolutional neural (TCN) network for an effective weather forecasting using time-series data from the local weather station[J]. Soft Computing, 2020, 24(21): 16453–16482. doi: 10.1007/s00500-020-04954-0. [18] CHENG Lei, KHALITOV R, YU Tong, et al. Classification of long sequential data using circular dilated convolutional neural networks[J]. Neurocomputing, 2023, 518: 50–59. doi: 10.1016/j.neucom.2022.10.054. [19] ZHANG Jinglu, NIE Yinyu, LYU Yao, et al. Symmetric dilated convolution for surgical gesture recognition[C]. The 23rd International Conference on Medical Image Computing and Computer Assisted Intervention – MICCAI 2020, Lima, Peru, 2020: 409–418. doi: 10.1007/978-3-030-59716-0_39. [20] 唱亮, 汪芙平. 非协作通信中的盲信噪比估计算法[J]. 通信学报, 2008, 29(3): 76–81. doi: 10.3321/j.issn:1000-436X.2008.03.012.CHANG Liang and WANG Fuping. Blind SNR estimation in non-cooperative communications[J]. Journal on Communications, 2008, 29(3): 76–81. doi: 10.3321/j.issn:1000-436X.2008.03.012. -





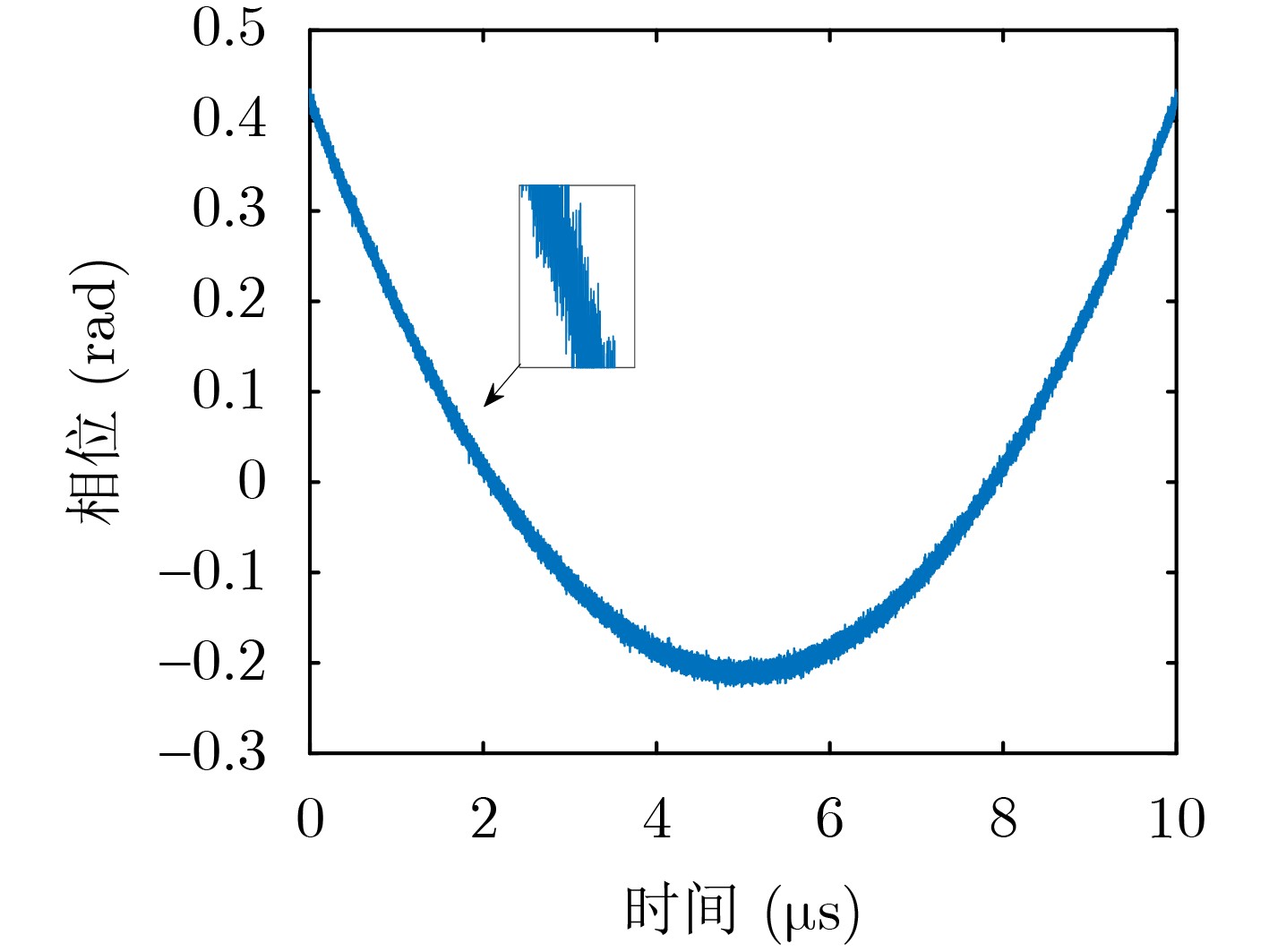
 下载:
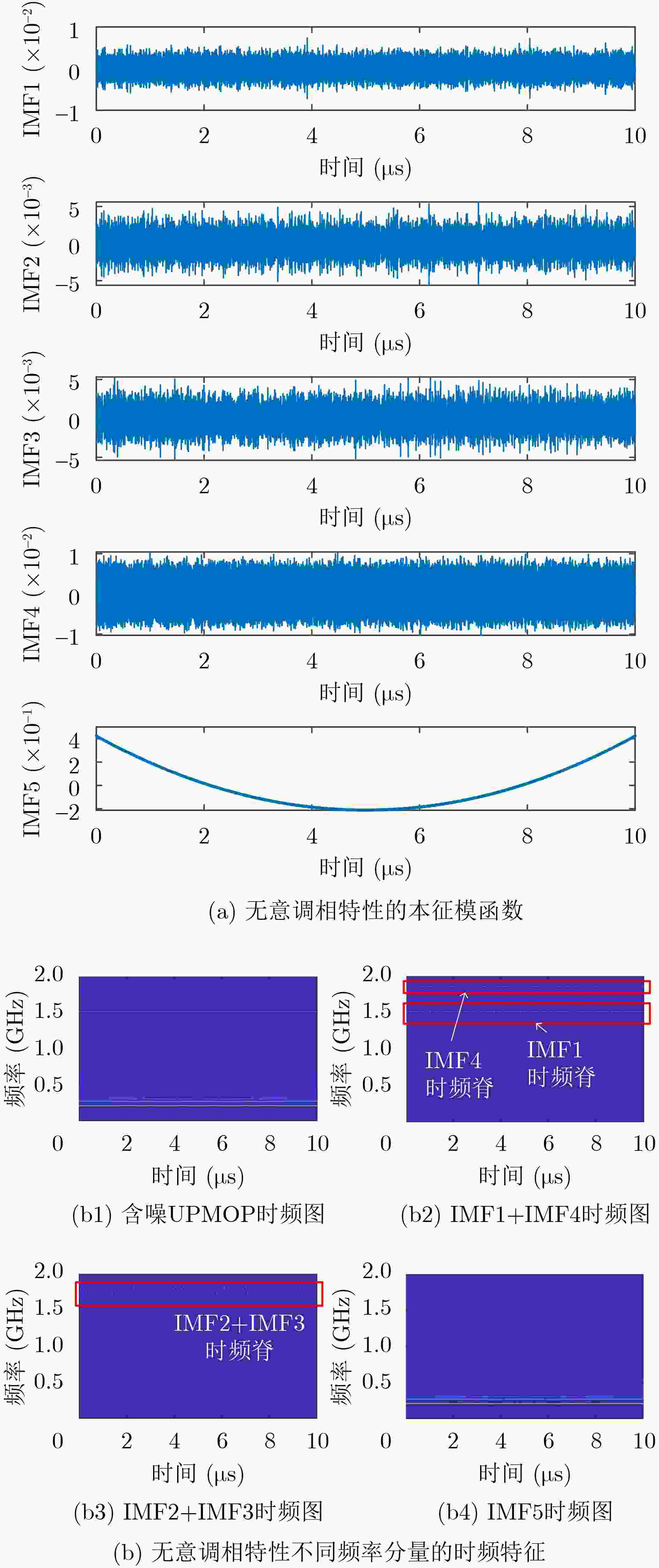
下载:
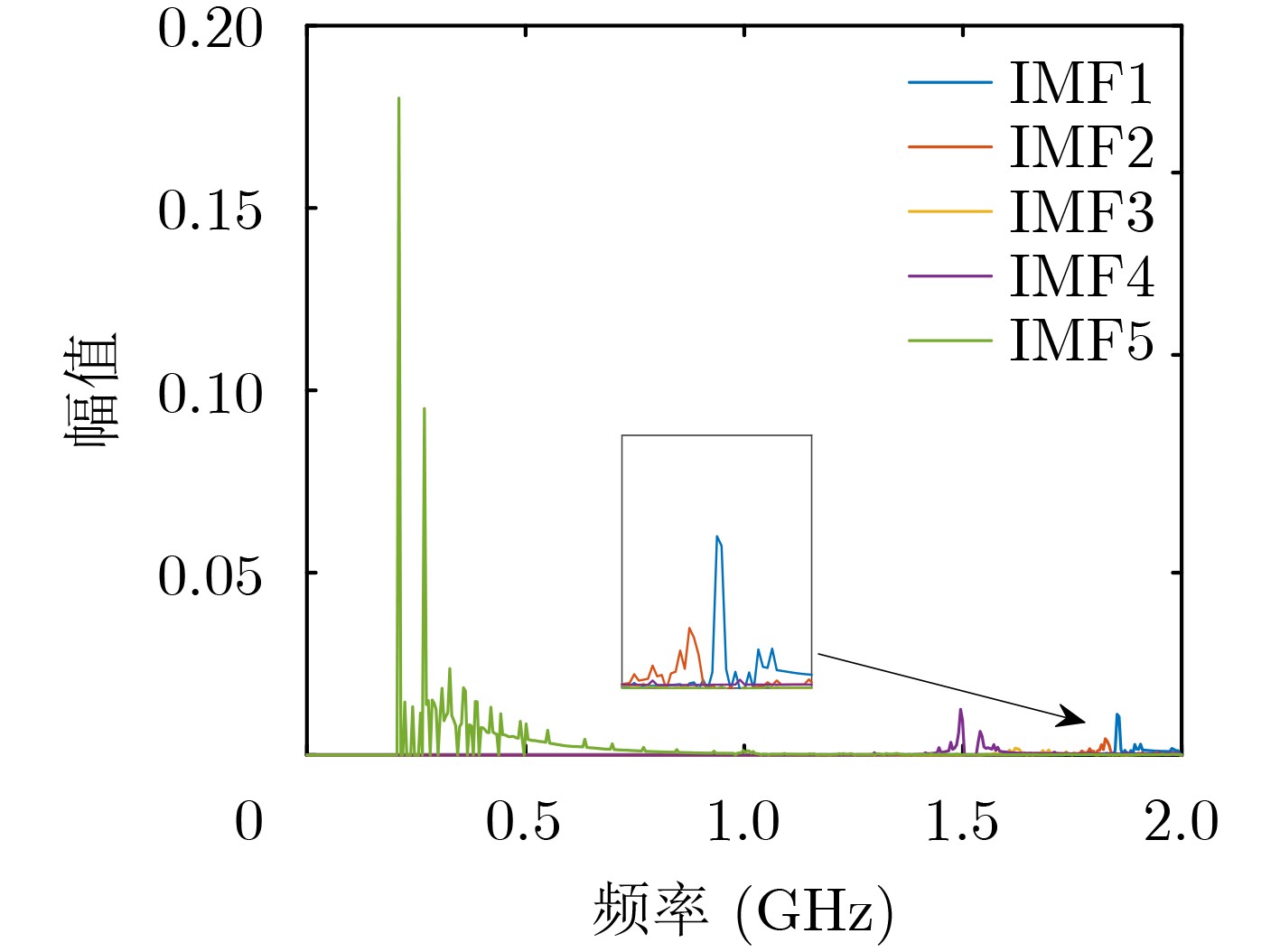


 下载:
下载:
