Federated Slicing Resource Management in Edge Computing Networks based on GAN-assisted Multi-Agent Reinforcement Learning
-
摘要: 为满足动态边缘计算网络场景下用户差异化服务需求,该文提出一种基于生成对抗网络(GAN)辅助多智能体强化学习(RL)的联邦切片资源管理方案。首先,考虑未知时变信道和随机用户流量到达的场景,以同时优化长期平均服务等待时延和服务满意率为目标,构建联合带宽和计算切片资源管理优化问题,并进一步建模为分布式部分可观测马尔可夫决策过程 (Dec-POMDP)。其次,运用多智能体竞争双深度Q网络(D3QN)方法,结合GAN算法对状态值分布多模态学习的优势,以及利用联邦学习框架促使智能体合作学习,最终实现仅需共享各智能体生成网络加权参数即可完成切片资源管理协同决策。仿真结果表明,所提方案相较于基准方案能够在保护用户隐私的前提下,降低用户平均服务等待时延28%以上,且同时提升用户平均服务满意率8%以上。Abstract:
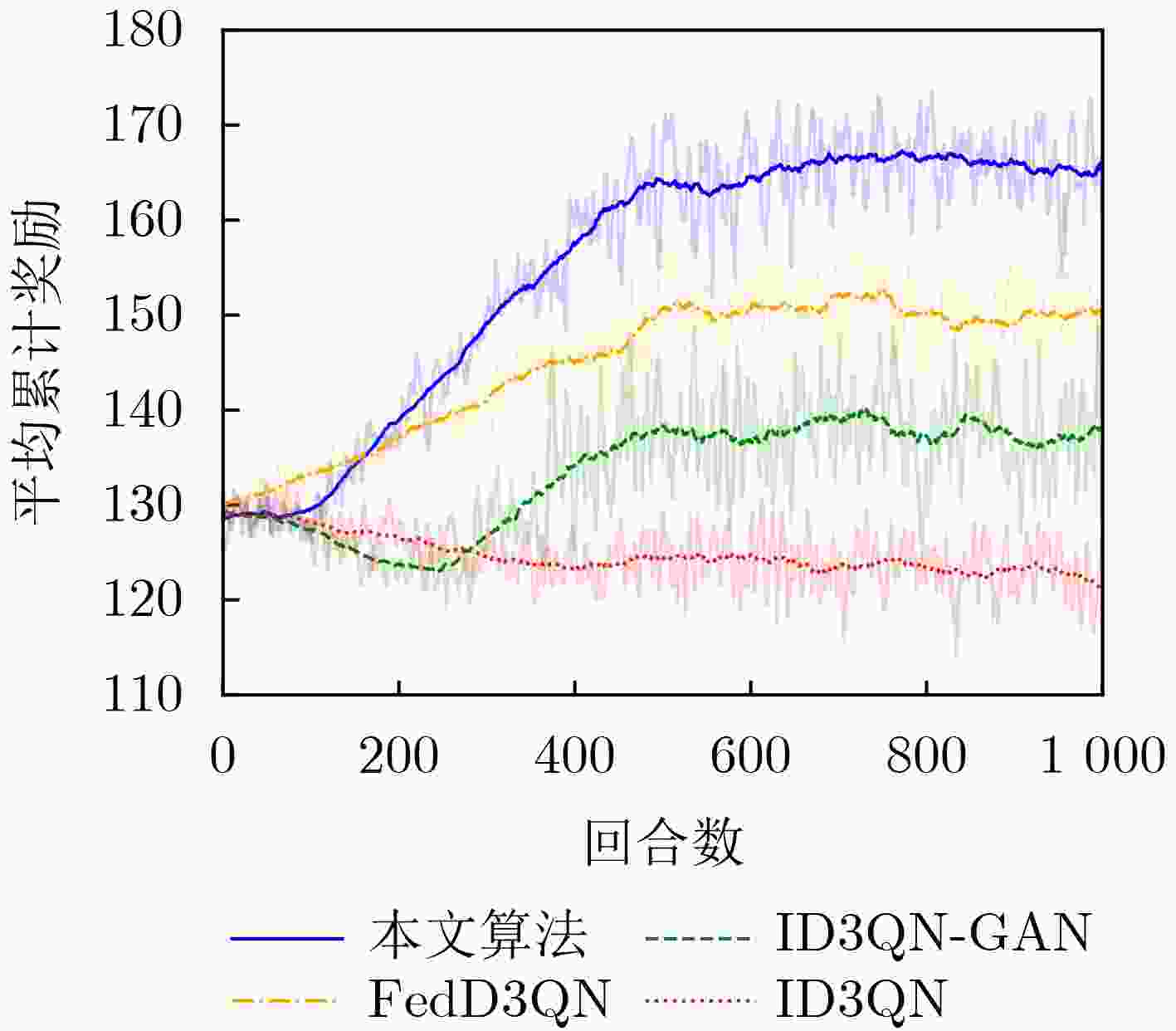
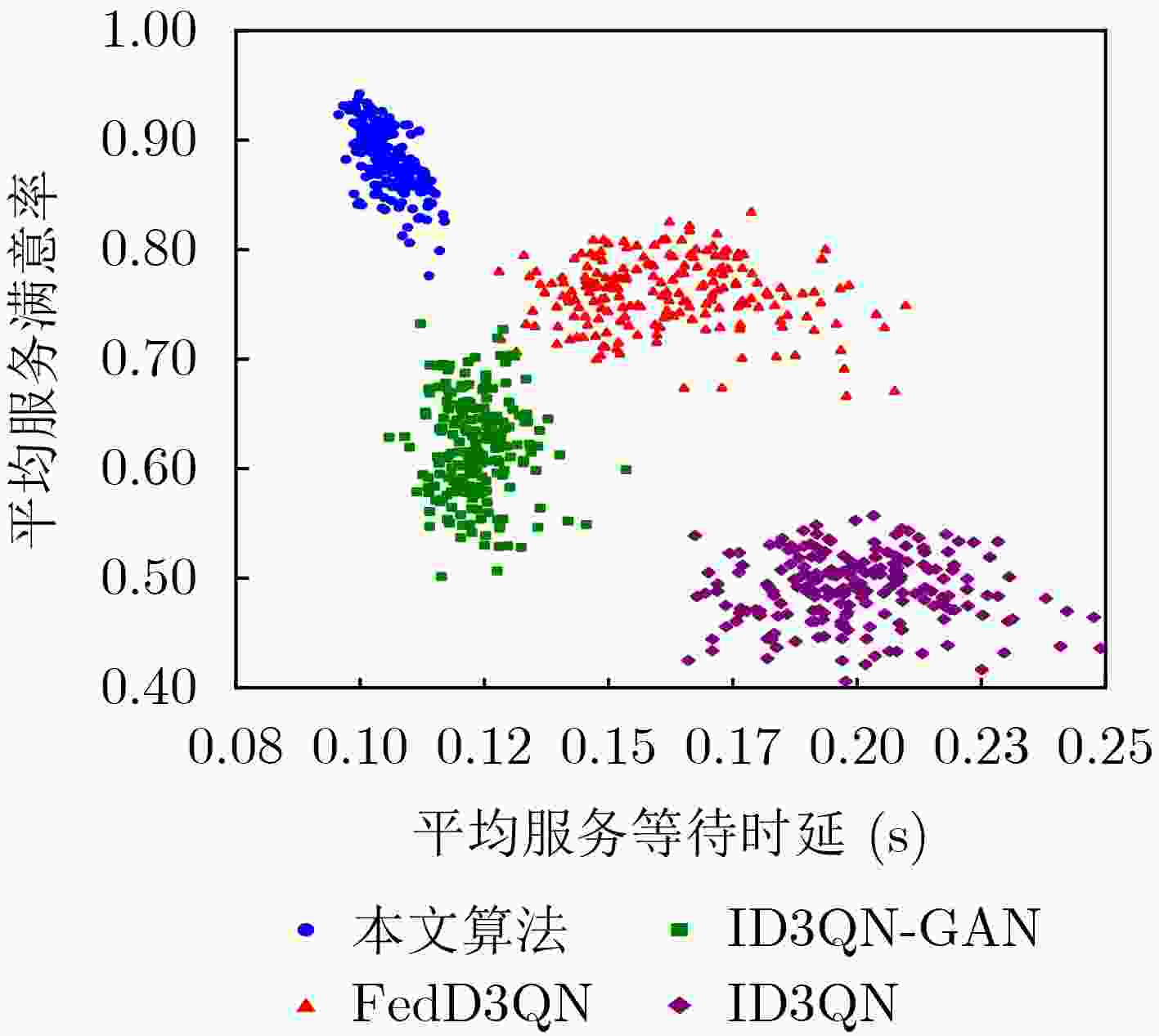
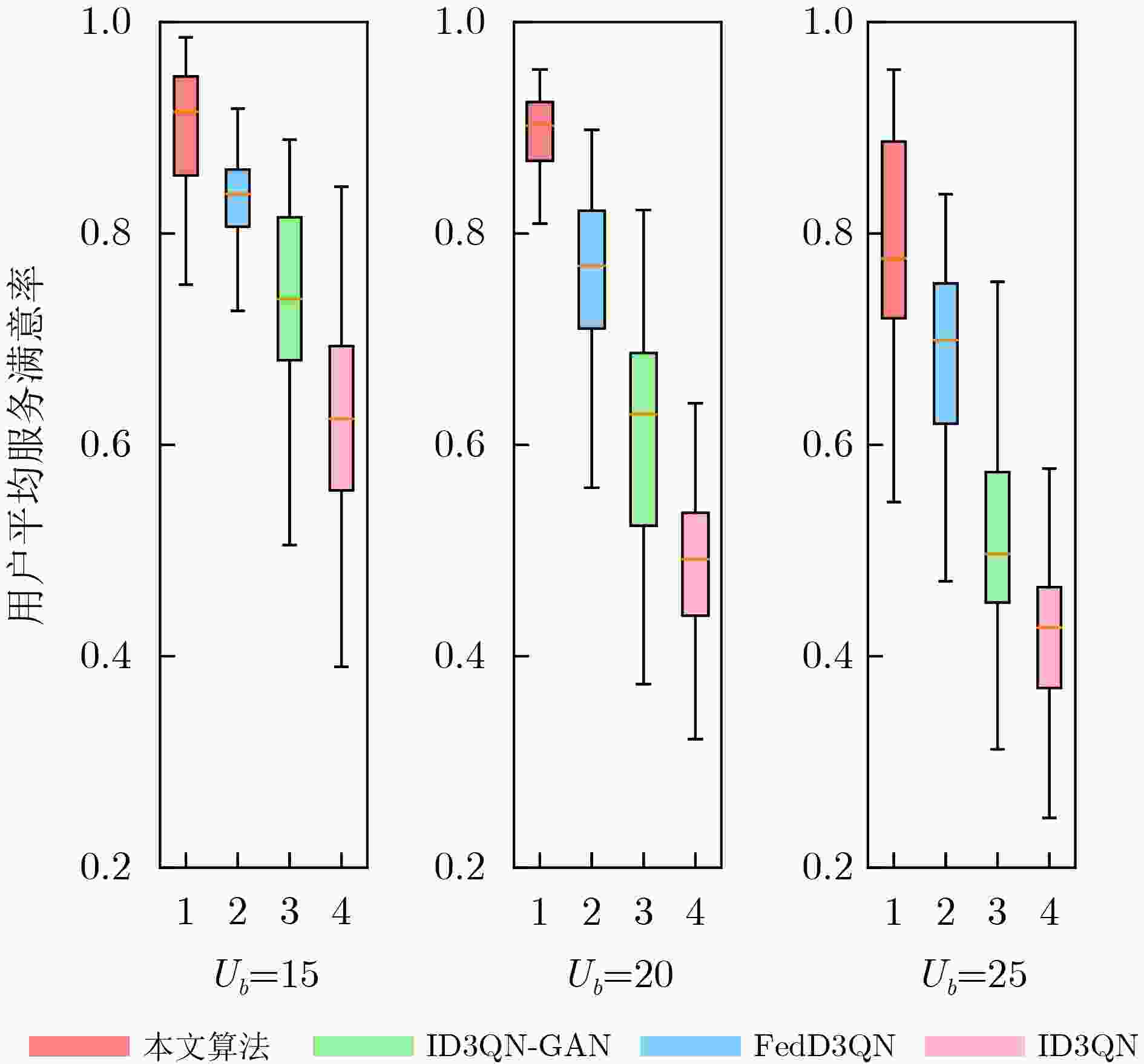
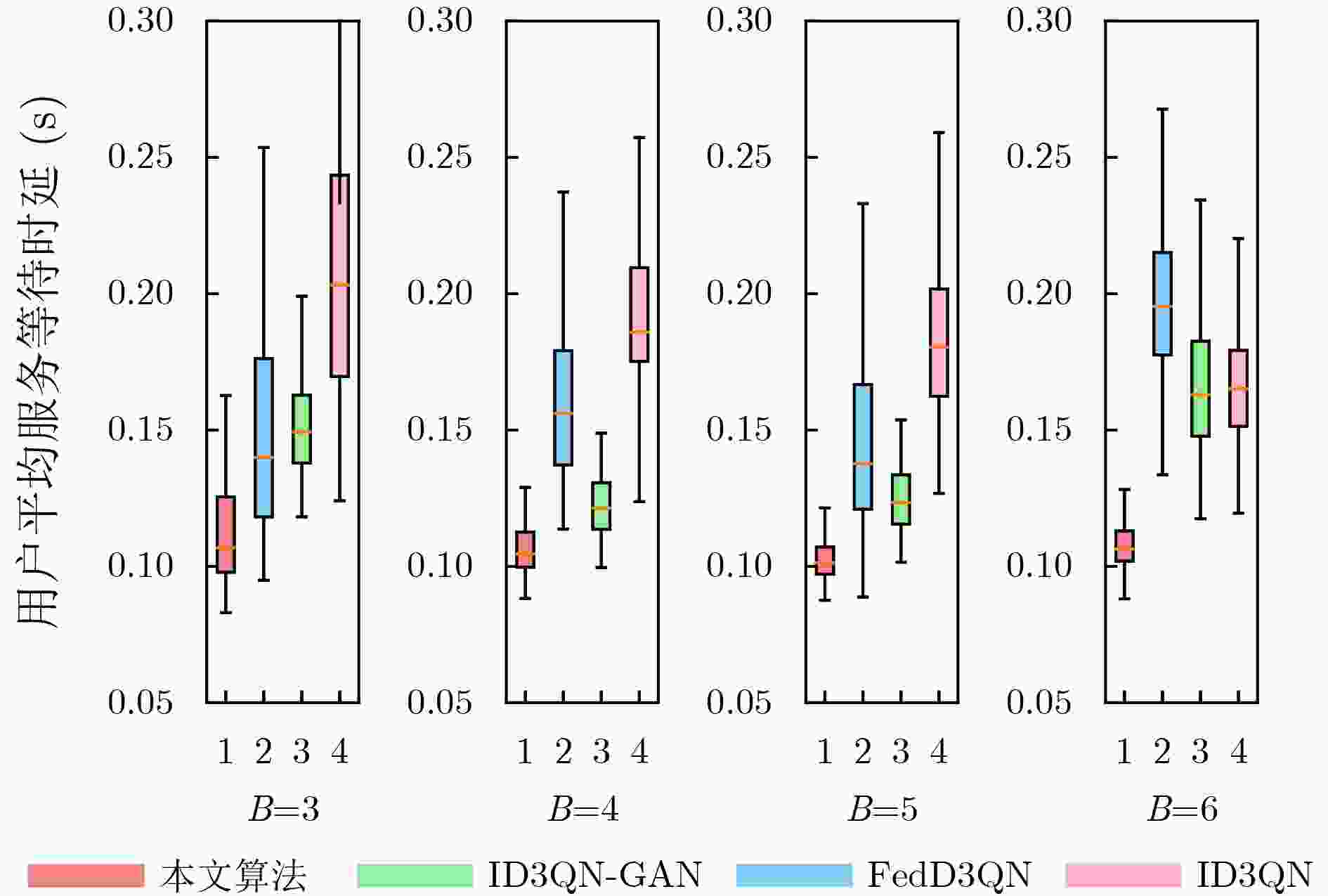
Objective To meet the differentiated service requirements of users in dynamic Edge Computing (EC) network scenarios, network slicing technology has become a crucial enabling approach for EC networks to offer differentiated edge services. It facilitates flexible allocation and customized management of communication and computation resources by dividing network resources into multiple independent sub-slices. However, traditional slicing resource management methods cannot handle the time-varying wireless channel conditions and the randomness of service arrivals in EC networks. Additionally, existing intelligent slicing resource management schemes based on deep reinforcement learning face challenges, including the need for extensive information sharing, privacy leakage, and unstable training convergence. To address these challenges, the integration of Multi-Agent Reinforcement Learning (MARL) and Federated Learning (FL) allows for experience sharing among agents while protecting users’ privacy. Furthermore, Generative Adversarial Network (GAN) is used to generate state-action value distributions, improving the ability of traditional MARL methods to learn state-value information. By modeling the joint bandwidth and computing slicing resource management optimization problem as a Decentralized Partially Observable Markov Decision Process (Dec-POMDP), collaborative decision-making for slicing resource management is achieved by sharing only the generator network parameters of each agent through the combination of FL and GAN. This study provides a federated collaborative decision-making framework for addressing the slicing resource management problem in EC scenarios and offers theoretical support for enhancing the utilization efficiency of edge slicing resources while preserving users’ privacy. Methods The core concept of the proposed federated slicing resource management scheme is to first employ both GAN technology and the D3QN algorithm for local training within a multi-agent framework. The FL architecture is then used to share the generator network parameters of each agent, facilitating collaborative decision-making for joint bandwidth and computing slicing resource management. In this approach, each Access Point (AP) agent collects data on the total number of tasks to be transmitted and the number of Central Processing Unit (CPU) cycles required for computing tasks in each associated slice as local observations during each training time slot. Each agent subsequently selects the optimal local bandwidth and computing resource management action, obtaining the system reward, which consists of the average service waiting delay and service satisfaction rate, as well as the observation for the next time slot to train the local network. During the training process, each AP agent maintains its own main generator network, target generator network, and discriminator network. In each training episode, the D3QN algorithm is applied to decompose the state-action values, and GAN is used to perform multi-modal learning of the state value distribution, thus completing the local training. After each training episode, the AP agents upload their main generator network parameters for federated aggregation and receive the global main generator network parameters for the next training episode. Results and Discussions By employing the D3QN algorithm and integrating the advantages of GAN within the MARL framework, alongside leveraging FL to share learning experiences among agents while protecting users’ privacy, the proposed scheme reduces the long-term service waiting delay and improves the long-term average service satisfaction rate. Simulation results demonstrate that the proposed scheme achieves the highest average cumulative reward after approximately 500 episodes ( Fig. 3 ), with a notable improvement of at least 10% in convergence performance compared to the baselines. Furthermore, the scheme strikes a better balance between average service waiting delay and average service satisfaction rate (Fig. 4 ). Additionally, it delivers superior performance in terms of user average service satisfaction rate, with at least an 8% improvement under varying user numbers (Fig. 5 ), highlighting its effectiveness in resource management under different task loads. Moreover, the proposed scheme reduces the average service waiting delay by at least 28% (Fig. 6 ) under varying numbers of agents.Conclusions This paper investigates the joint bandwidth and computing slicing resource management problem in dynamic, unknown EC network scenarios and proposes a federated slicing resource management scheme based on GAN-assisted MARL. The proposed scheme enhances the agents’ ability to learn state-value information and promotes collaborative learning by sharing the training network parameters of agents, which ultimately reduces long-term service waiting delays and improves long-term average service satisfaction rates, while protecting users’ privacy. Simulation results show that: (1) The cumulative reward convergence performance of the proposed scheme improves by at least 10% compared to the baselines; (2) The average service satisfaction rate of the proposed scheme is more than 8% higher than that of the baselines under varying user numbers; (3) The average service waiting delay of the proposed scheme is reduced by at least 28% compared to the baselines under varying agent numbers. However, this study only considers ideal, static user scenarios and interference-free communication conditions. Future work should incorporate more real-world dynamics, such as time-varying user mobility and complex multi-user interference. -
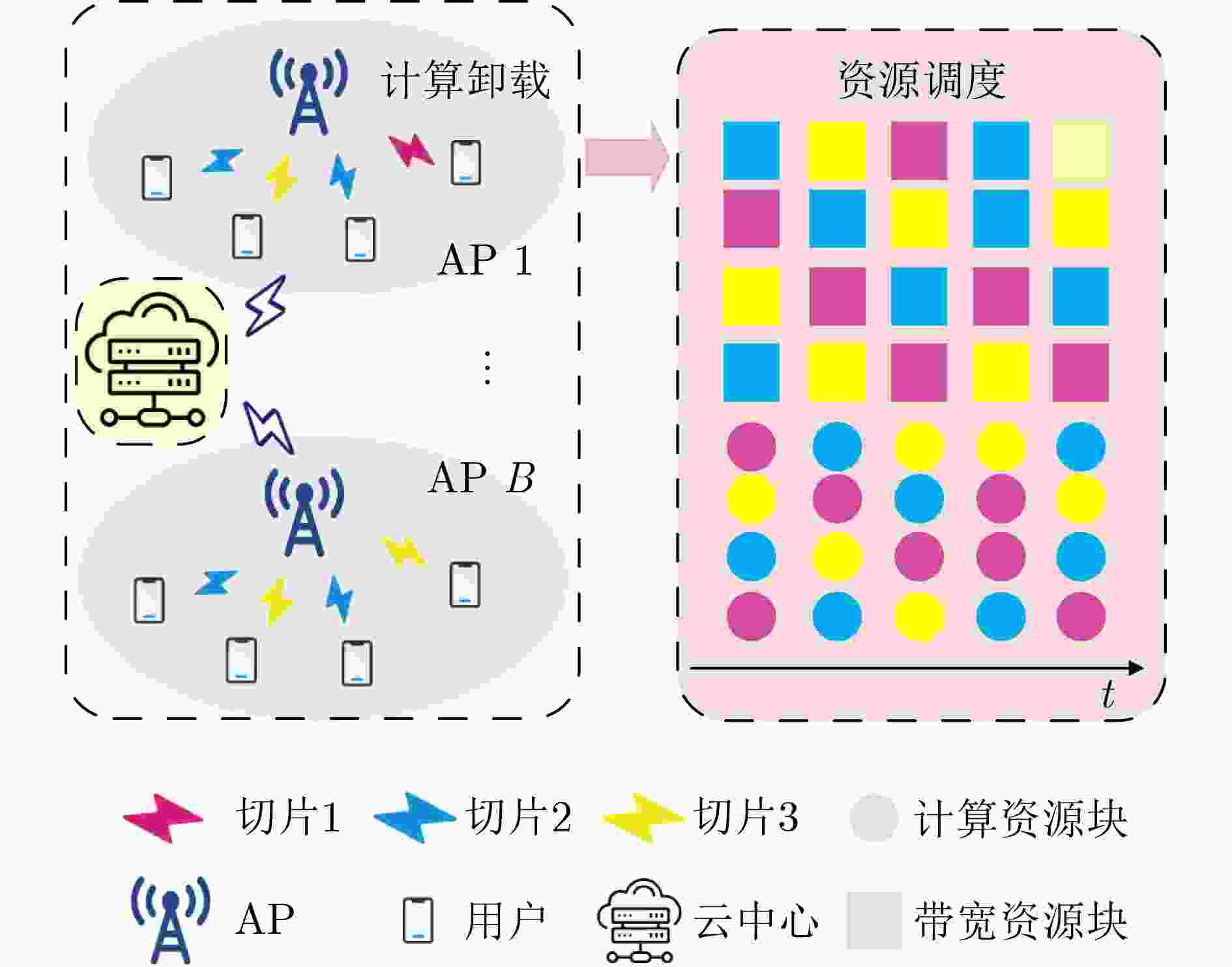
1 基于GAN辅助多智能体强化学习的边缘计算网络联邦切片资源管理算法
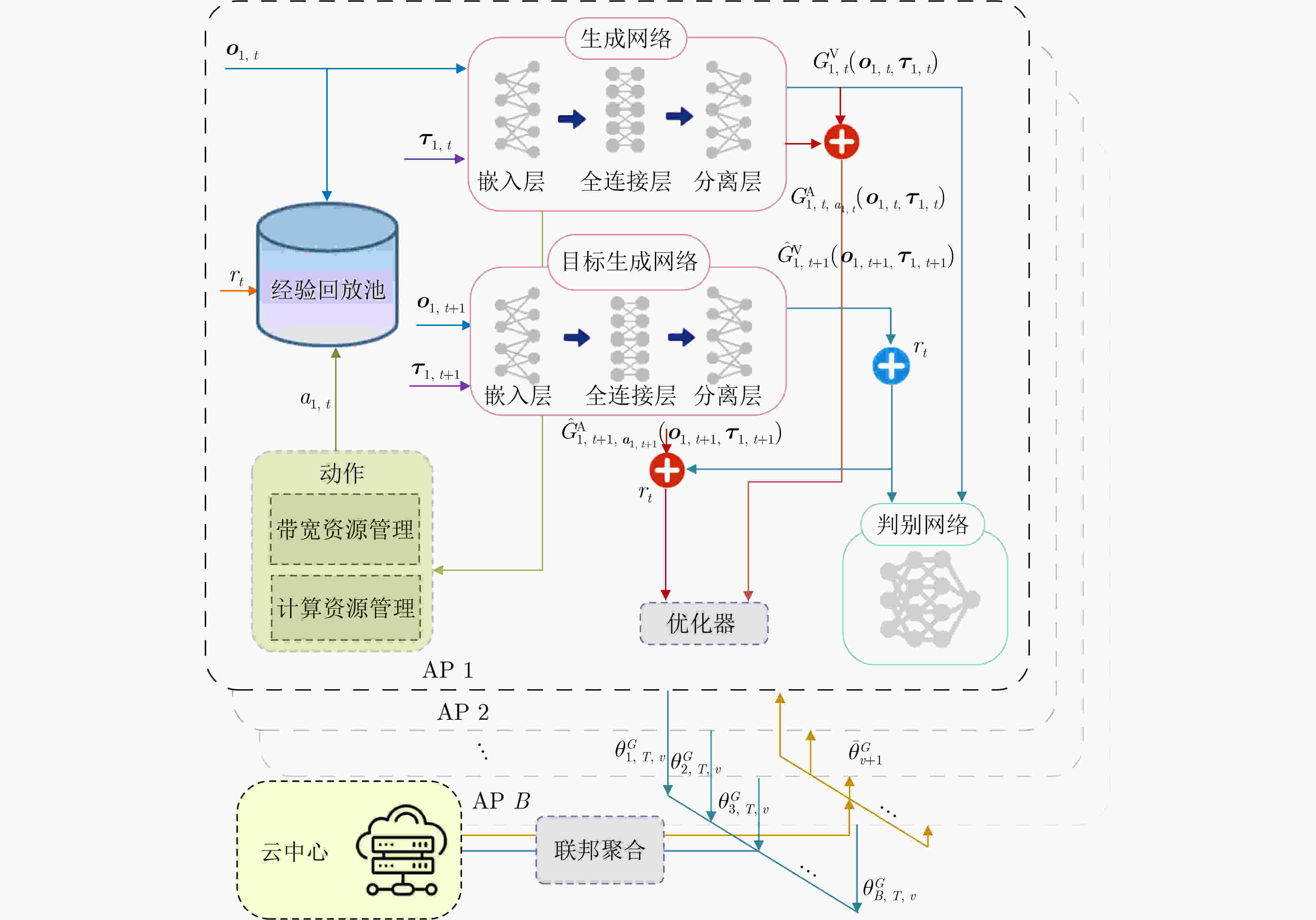
(1) 每个AP智能体初始化的生成网络${G_b}$和判别网络${D_b}$; (2) 每个AP智能体初始化目标生成网络${\hat G_b}$,本地经验回放池
${\mathcal{M}_b}$,粒子个数$N$;(3) ${T^{{\text{train}}}} \leftarrow 0$; (4) for Episode $v = 1,2, \cdots ,V$ do: (5) 重置环境 (6) for TS $t = 1,2, \cdots ,T$ do: (7) for AP智能体 $b = 1,2, \cdots ,B$ do: (8) 采样噪声${{\boldsymbol{\tau}} _{b,t}}{\text{~}}U\left( {0,1} \right)$,获取本地观测${{\boldsymbol{o}}_{b,t}}$,同时输
入生成网络${G_b}$;(9) 得到状态值粒子$\left\{ {G_{b,t}^{\text{V}}\left( {{{\boldsymbol{o}}_{b,t}},{{\boldsymbol{\tau}} _{b,t}}} \right)} \right\}$和动作优势值
$G_{b,t,{{\boldsymbol{a}}_{b,t}}}^{\text{A}}\left( {{{\boldsymbol{o}}_{b,t}},{{\boldsymbol{\tau}} _{b,t}}} \right)$(10) 根据式(10)计算状态动作价值函数${Q_{b,t}}\left( {{{\boldsymbol{o}}_{b,t}},{{\boldsymbol{a}}_{b,t}}} \right)$; (11) 执行动作${\boldsymbol{a}}_{b,t}^* \leftarrow {\text{argmax}}{Q_{b,t}}\left( {{{\boldsymbol{o}}_{b,t}},{{\boldsymbol{a}}_{b,t}}} \right)$; (12) 获取环境奖励${r_t}$和下一时隙观测${{\boldsymbol{o}}_{b,t + 1}}$; (13) 储存训练信息$\left\{ {{{\boldsymbol{o}}_{b,t}},{{\boldsymbol{a}}_{b,t}},{{\boldsymbol{o}}_{b,t + 1}},{r_t}} \right\}$至本地经验回放
池${\mathcal{M}_b}$;(14) end for; (15) if ${T^{{\text{train}}}} \ge {T^{{\text{update}}}}$: (16) for AP智能体 $b = 1,2, \cdots ,B$ do: (17) 随机抽取 $\left\{ {{{\boldsymbol o}_{b,k}},{{\boldsymbol{a}}_{b,k}},{{\boldsymbol{o}}_{b,k + 1}},{r_k}} \right\}_{k = 1}^K{\text{~}}{\mathcal{M}_b}$,采样
噪声$\left\{ {{{\boldsymbol{\tau}} _{b,k}}} \right\}_{k = 1}^K$和$ {\left\{{\varepsilon }_{b,k}\right\}}_{k=1}^{K} $;(18) 根据式(14)–式(16)计算损失函数$J_{b,k}^D$并根据式
$\begin{array}{*{20}{c}} {\theta _{b,t + 1}^D \leftarrow \theta _{b,t}^D - {\eta ^D}{\nabla _\theta }J_{b,t}^D} \end{array}$更新网络${D_b}$;(19) 计算${Q_{b,k}}\left( {{{\boldsymbol o}_{b,k}},{{\boldsymbol{a}}_{b,k}}} \right)$和${\hat Q_{b,k}}\left( {{{\boldsymbol o}_{b,k}},{{\boldsymbol{a}}_{b,k}}} \right)$; (20) 根据式(12)–式(13)计算损失函数$J_{b,k}^G$更新网络${G_b}$,
和网络${\hat G_b}$;(21) 根据式$ {\theta _{b,t + 1}^G \leftarrow \theta _{b,t}^G - {\eta ^G}{\nabla _\theta }J_{b,t}^G} $更新主网络
${G_b}$,根据式$\hat \theta _{b,t}^G \leftarrow \theta _{b,t}^G\hat \theta _{b,t}^G \leftarrow \theta _{b,t}^G$更新目标网络
${\hat G_b}$;(22) end for; (23) end if; (24) end for; (25) 根据式(17)–式(18)执行联邦聚合并向所有智能体广播生成
网络参数$\theta _{b,1,v + 1}^G$;(26) ${T^{{\text{train}}}} \leftarrow {T^{{\text{train}}}} + 1$; (27) end for; 表 1 仿真参数设置
系统参数 值 AP传输功率${P^{\text{A}}}$ 46 dBm 用户传输功率${P^{\text{U}}}$ 23 dBm 时隙持续时间$\tau $ 10 ms 最大可容忍时延$l_i^{{\text{max}}}$ {5,8,9} ms 上行任务包大小${x_{{u_b},t}}$ {2.4,12,30} kbit 处理前后数据包之比$\beta $ 0.25 计算任务量${s_{{u_b},t}}$ {0.1,0.2,1} kMc 用户数${U_b}$ 20 切片数量$I$ 3 AP覆盖半径 40 m AP数$B$ 4 AP总带宽${W_b}$ 36 MHz AP总计算资源${C_b}$ 900 kMc/s 带宽资源块大小${\rho ^{\text{B}}}$ 2 MHz 计算资源块大小${\rho ^{\text{C}}}$ 50 kMc 训练参数 值 生成网络学习率${\eta ^G}$ 1e–3 判别网络学习率${\eta ^D}$ 1e–3 奖励折扣系数 $\gamma $ 0.8 每回合步数 100 状态值粒子个数$N$ 30 权重系数$\alpha $ 0.5 批大小 32 经验回放池大小 50 000 目标网络更新频率 10$ \tau $ 输入噪声维度 10 -
[1] GHONGE M, MANGRULKAR R S, JAWANDHIYA P M, et al. Future Trends in 5G and 6G: Challenges, Architecture, and Applications[M]. Boca Raton: CRC Press, 2022. [2] DEBBABI F, JMAL R, FOURATI L C, et al. Algorithmics and modeling aspects of network slicing in 5G and Beyonds network: Survey[J]. IEEE Access, 2020, 8: 162748–162762. doi: 10.1109/ACCESS.2020.3022162. [3] MATENCIO-ESCOLAR A, WANG Qi, and CALERO J M A. SliceNetVSwitch: Definition, design and implementation of 5G multi-tenant network slicing in software data paths[J]. IEEE Transactions on Network and Service Management, 2020, 17(4): 2212–2225. doi: 10.1109/TNSM.2020.3029653. [4] 吴大鹏, 郑豪, 崔亚平. 面向服务的车辆网络切片协调智能体设计[J]. 电子与信息学报, 2020, 42(8): 1910–1917. doi: 10.11999/JEIT190635.WU Dapeng, ZHENG Hao, and CUI Yaping. Service-oriented coordination agent design for network slicing in vehicular networks[J]. Journal of Electronics & Information Technology, 2020, 42(8): 1910–1917. doi: 10.11999/JEIT190635. [5] 唐伦, 魏延南, 谭颀, 等. H-CRAN网络下联合拥塞控制和资源分配的网络切片动态资源调度策略[J]. 电子与信息学报, 2020, 42(5): 1244–1252. doi: 10.11999/JEIT190439.TANG Lun, WEI Yannan, TAN Qi, et al. Joint congestion control and resource allocation dynamic scheduling strategy for network slices in heterogeneous cloud raido access network[J]. Journal of Electronics & Information Technology, 2020, 42(5): 1244–1252. doi: 10.11999/JEIT190439. [6] SHAH S D A, GREGORY M A, and LI Shuo. Cloud-native network slicing using software defined networking based multi-access edge computing: A survey[J]. IEEE Access, 2021, 9: 10903–10924. doi: 10.1109/ACCESS.2021.3050155. [7] SHAH S D A, GREGORY M A, and LI Shuo. Toward network-slicing-enabled edge computing: A cloud-native approach for slice mobility[J]. IEEE Internet of Things Journal, 2024, 11(2): 2684–2700. doi: 10.1109/JIOT.2023.3292520. [8] FAN Wenhao, LI Xuewei, TANG Bihua, et al. MEC network slicing: Stackelberg-game-based slice pricing and resource allocation with QoS guarantee[J]. IEEE Transactions on Network and Service Management, 2024, 21(4): 4494–4509. doi: 10.1109/TNSM.2024.3409277. [9] JOŠILO S and DÁN G. Joint wireless and edge computing resource management with dynamic network slice selection[J]. IEEE/ACM Transactions on Networking, 2022, 30(4): 1865–1878. doi: 10.1109/TNET.2022.3156178. [10] HUSAIN S, KUNZ A, PRASAD A, et al. Mobile edge computing with network resource slicing for internet-of-things[C]. The 2018 IEEE 4th World Forum on Internet of Things, Singapore, 2018: 1–6. doi: 10.1109/WF-IoT.2018.8355232. [11] SHEN Xuemin, GAO Jie, WU Wen, et al. AI-assisted network-slicing based next-generation wireless networks[J]. IEEE Open Journal of Vehicular Technology, 2020, 1: 45–66. doi: 10.1109/OJVT.2020.2965100. [12] ELSAYED M and EROL-KANTARCI M. Reinforcement learning-based joint power and resource allocation for URLLC in 5G[C]. 2019 IEEE Global Communications Conference, Waikoloa, USA, 2019: 1–6. doi: 10.1109/GLOBECOM38437.2019.9014032. [13] AZIMI Y, YOUSEFI S, KALBKHANI H, et al. Energy-efficient deep reinforcement learning assisted resource allocation for 5G-RAN slicing[J]. IEEE Transactions on Vehicular Technology, 2022, 71(1): 856–871. doi: 10.1109/TVT.2021.3128513. [14] HUA Yuxiu, LI Rongpeng, ZHAO Zhifeng, et al. GAN-powered deep distributional reinforcement learning for resource management in network slicing[J]. IEEE Journal on Selected Areas in Communications, 2020, 38(2): 334–349. doi: 10.1109/JSAC.2019.2959185. [15] ADDAD R A, DUTRA D L C, TALEB T, et al. Toward using reinforcement learning for trigger selection in network slice mobility[J]. IEEE Journal on Selected Areas in Communications, 2021, 39(7): 2241–2253. doi: 10.1109/JSAC.2021.3078501. [16] LI Xuanheng, JIAO Kajia, CHEN Xingyun, et al. Demand-oriented Fog-RAN slicing with self-adaptation via deep reinforcement learning[J]. IEEE Transactions on Vehicular Technology, 2023, 72(11): 14704–14716. doi: 10.1109/TVT.2023.3280242. [17] ZHOU Hao, ELSAYED M, and EROL-KANTARCI M. RAN resource slicing in 5G using multi-agent correlated Q-learning[C]. The 2021 IEEE 32nd Annual International Symposium on Personal, Indoor and Mobile Radio Communications, Helsinki, Finland, 2021: 1179–1184. doi: 10.1109/PIMRC50174.2021.9569358. [18] AKYILDIZ H A, GEMICI Ö F, HÖKELEK I, et al. Hierarchical reinforcement learning based resource allocation for RAN slicing[J]. IEEE Access, 2024, 12: 75818–75831. doi: 10.1109/ACCESS.2024.3406949. [19] CUI Yaping, SHI Hongji, WANG Ruyan, et al. Multi-agent reinforcement learning for slicing resource allocation in vehicular networks[J]. IEEE Transactions on Intelligent Transportation Systems, 2024, 25(2): 2005–2016. doi: 10.1109/TITS.2023.3314929. [20] HUANG Chen, CAO Jiannong, WANG Shihui, et al. Dynamic resource scheduling optimization with network coding for multi-user services in the internet of vehicles[J]. IEEE Access, 2020, 8: 126988–127003. doi: 10.1109/ACCESS.2020.3001140. [21] LIN Yan, BAO Jinming, ZHANG Yijin, et al. Privacy-preserving joint edge association and power optimization for the internet of vehicles via federated multi-agent reinforcement learning[J]. IEEE Transactions on Vehicular Technology, 2023, 72(6): 8256–8261. doi: 10.1109/TVT.2023.3240682. [22] GUPTA A, MAURYA M K, DHERE K, et al. Privacy-preserving hybrid federated learning framework for mental healthcare applications: Clustered and quantum approaches[J]. IEEE Access, 2024, 12: 145054–145068. doi: 10.1109/ACCESS.2024.3464240. [23] GULRAJANI I, AHMED F, ARJOVSKY M, et al. Improved training of Wasserstein GANs[C]. The 31st International Conference on Neural Information Processing Systems, Long Beach, USA, 2017: 5769–5779. -





 下载:
下载:


 下载:
下载:
