MIMO Dual-functional Radar-communication: Beampattern Gain Maximization Beamforming Design
-
摘要: 无线通信设备数量的骤增造成频谱资源日益稀缺,通信用频逐渐向更高频段扩展,从而导致通信与雷达频段出现越来越多的重叠,雷达通信一体化被视为解决频谱拥挤实现高效共生的潜在技术。该文考虑一个多输入多输出(MIMO)雷达通信一体化系统,在实现目标探测的同时进行多用户通信。首先,在满足多用户信干噪比和总功率约束的条件下,最大化目标方向的波束图增益。然后,针对一体化发射波束成形设计问题,提出基于半正定松弛(SDR)和优化最小化(MM)的两种波束成形设计方案,求解得到发射波束成形矢量。最后,仿真结果表明基于MM的方案复杂度更低,并且能够实现与基于SDR的方案几乎相同的波束图增益。此外,随着发射天线数量的增加,基于MM的方案相比于基于SDR的方案复杂度的降低程度变得更为显著。Abstract:
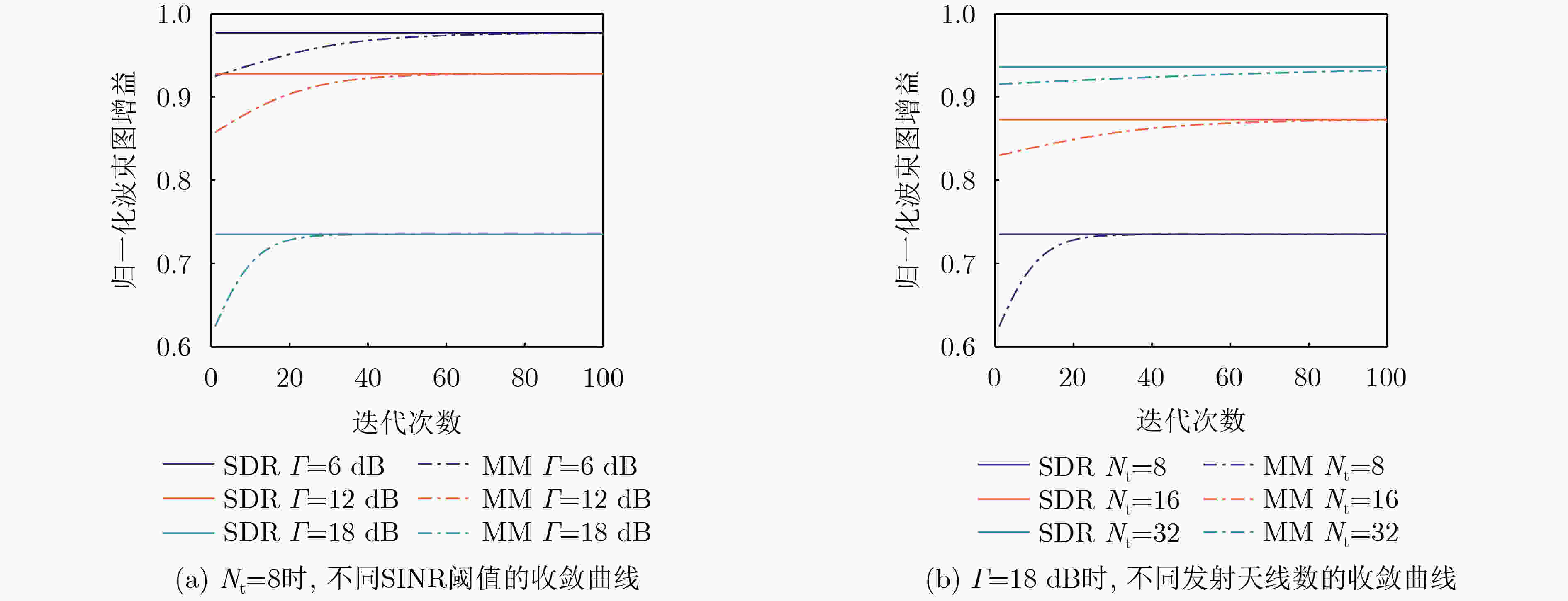
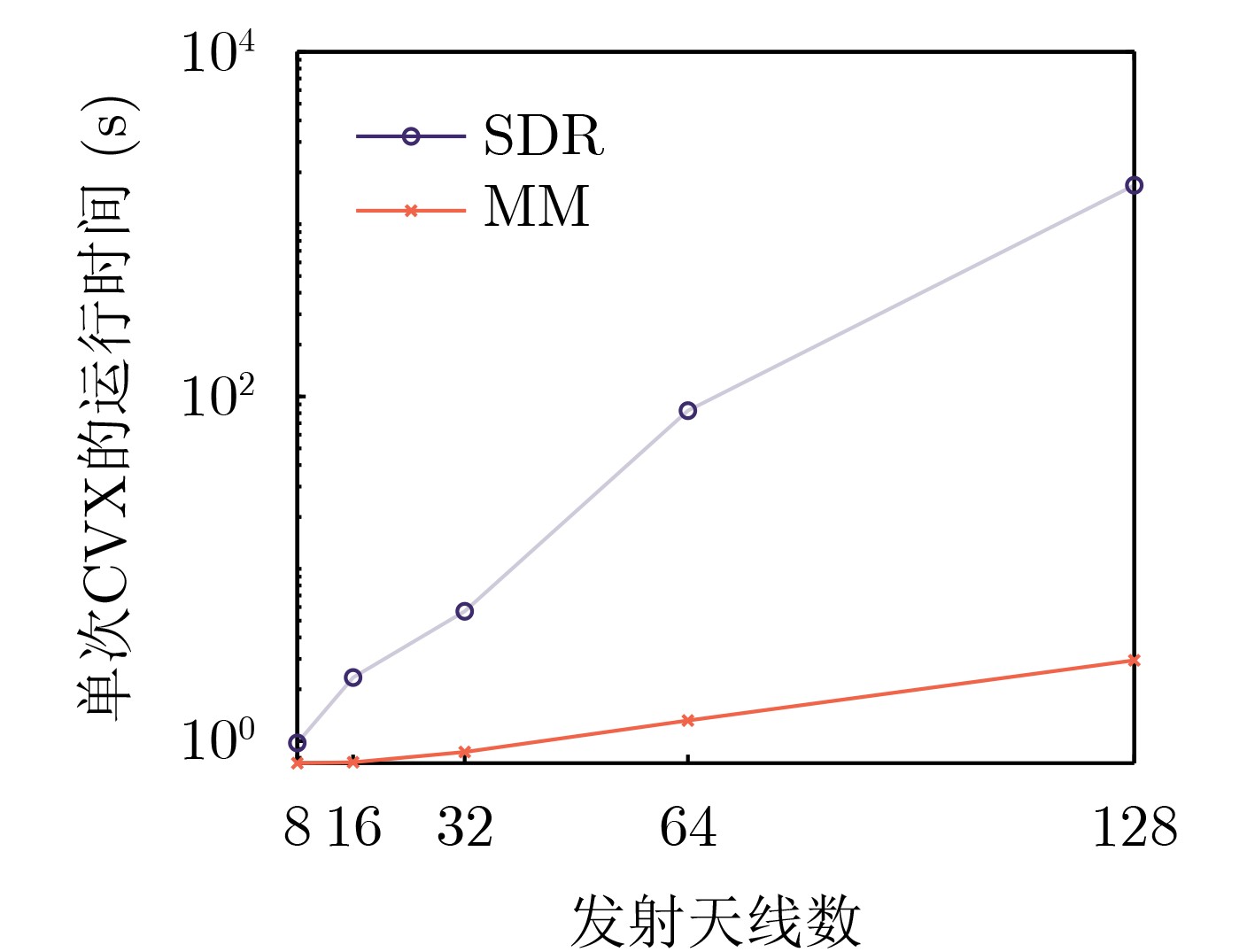
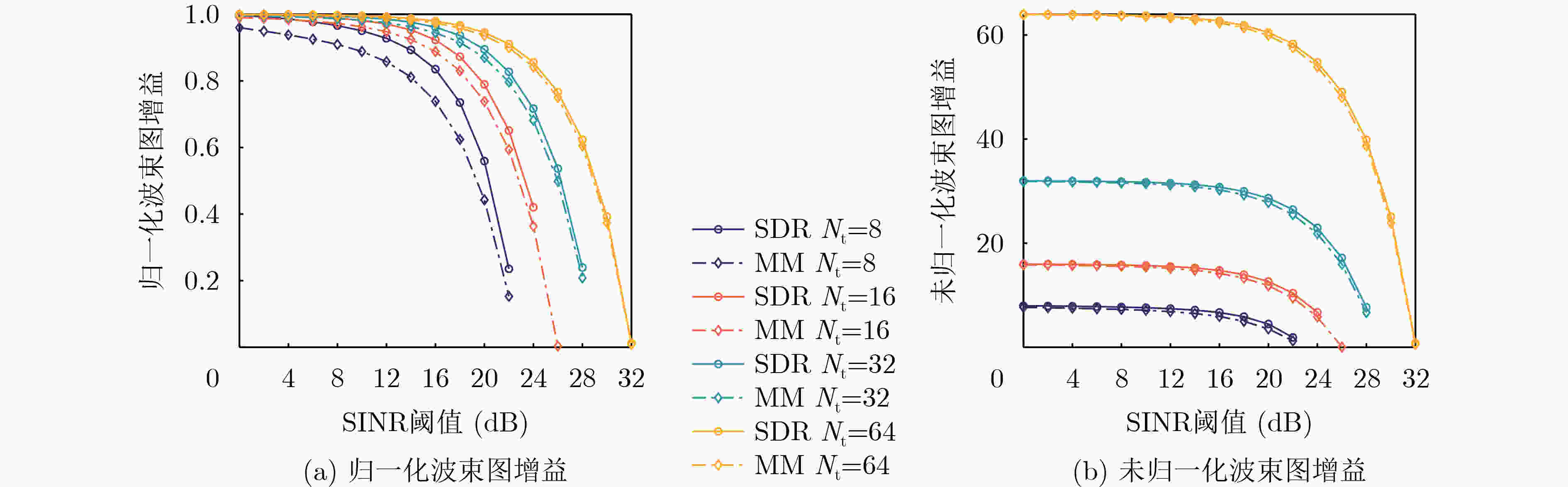
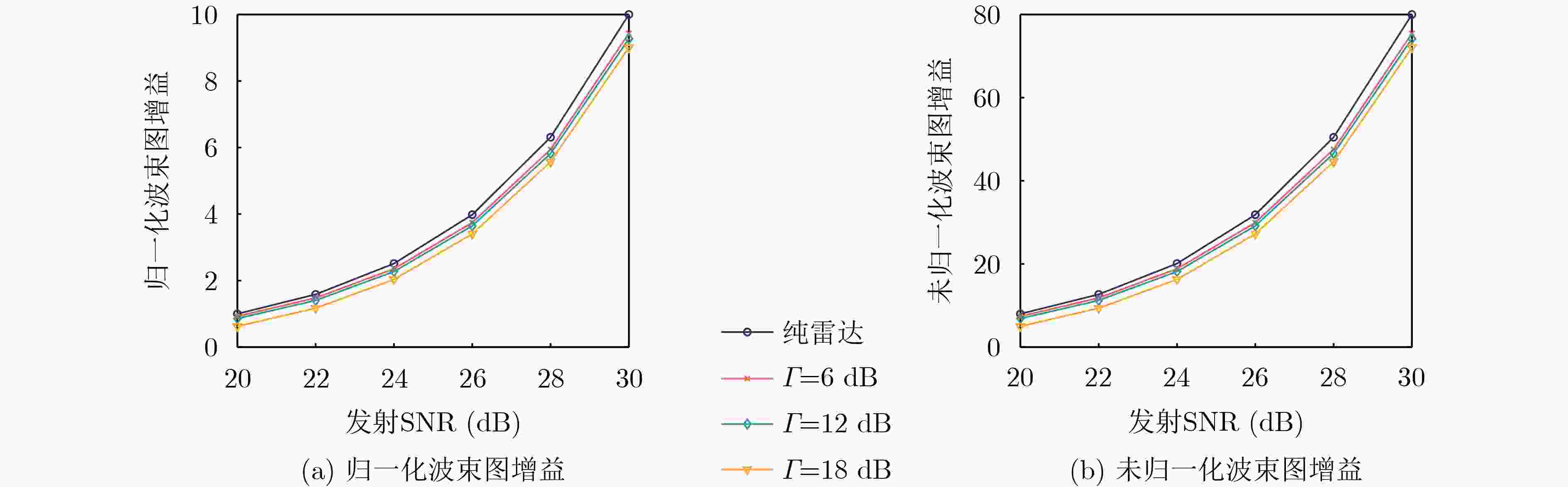
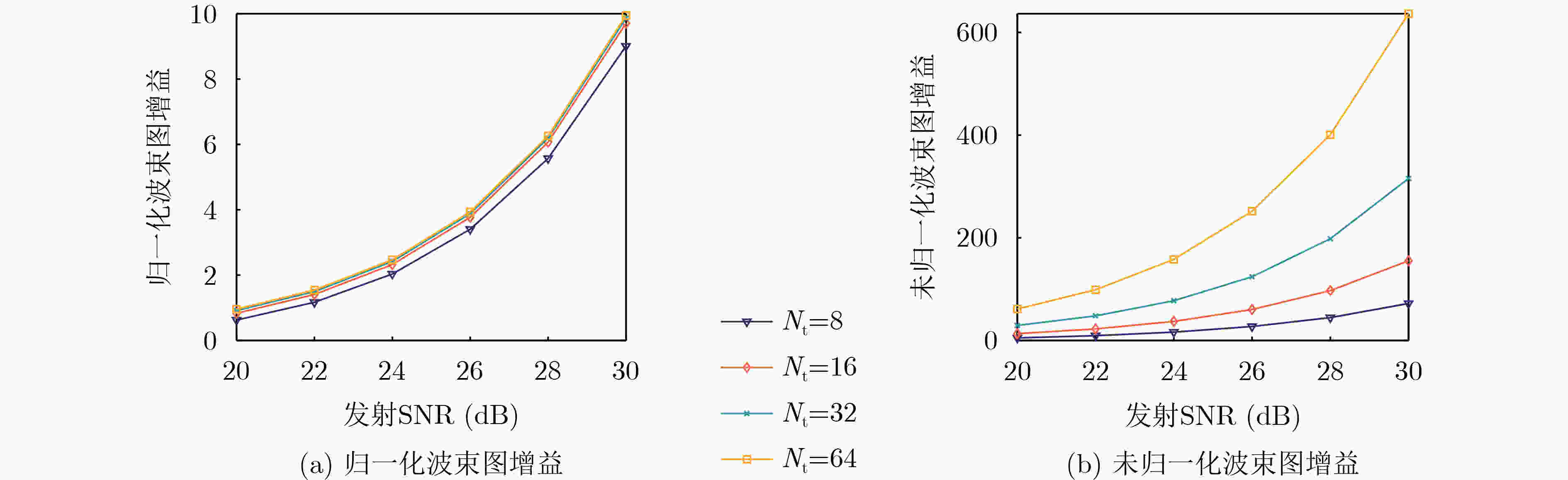
Objective The rapid growth in the number of wireless communication devices has led to the expansion of frequency bands to higher frequencies, resulting in increased overlap between communication and radar systems. Dual-Functional Radar-Communication (DFRC), which shares spectrum resources on the same hardware platform, is an effective solution to address spectrum congestion. The integration of Multiple-Input Multiple-Output (MIMO) technology, which employs multi-antenna techniques, with DFRC is crucial for achieving both high-precision detection and large-capacity communication. Beamforming technology plays a key role in efficiently allocating resources between these two requirements, further enhancing the collaborative gain of DFRC systems. Beampattern gain, a critical performance metric for target detection, makes it essential to investigate beamforming designs that maximize this gain in MIMO DFRC systems. Methods An MIMO DFRC system is considered, which simultaneously achieves target detection and Multi-User (MU) communication. First, a beamforming problem is formulated to maximize the beampattern gain in the target direction, while satisfying MU Signal-to-Interference-plus-Noise Ratio (SINR) and total power constraints. To address this beamforming design problem, two methods based on Semidefinite Relaxation (SDR) and Majorization Minimization (MM) are proposed to solve for the transmit beamforming vectors. Specifically, the SDR-based method transforms the beamforming problem into a semidefinite programming problem by introducing auxiliary variables and relaxing the rank-one constraint. The MM-based method, on the other hand, uses the first-order Taylor expansion to construct a cost function from the objective function, transforms the SINR constraint into a second-order cone constraint, and iteratively solves the simplified problem. Results and Discussions The convergence curves of the SDR-based and MM-based beamforming design schemes are shown ( Figure 2 ). The results indicate that the MM-based method can achieve almost the same beampattern gain as the SDR-based method. Under the same number of transmit antennas, a higher SINR threshold results in a smaller beampattern gain. This phenomenon reflects the performance trade-off between communication and radar in MIMO DFRC systems. Under the same SINR threshold, increasing the number of transmit antennas leads to a greater beampattern gain. This is because an increase in the number of transmit antennas provides additional degrees of freedom for the radar. The comparison of the single CVX running time of the SDR-based and MM-based methods under different numbers of transmit antennas is shown (Figure 3 ). The results demonstrate that the single CVX running time of the MM-based method is shorter than that of the SDR-based method for the same number of transmit antennas, and as the number of transmit antennas increases, the complexity reduction of the MM-based method becomes more significant than that of the SDR-based method. The variation curves of beampattern gain with SINR threshold for different numbers of transmit antennas in the MM-based and SDR-based methods are shown (Figure 4 ). The beampattern gain obtained by the MM-based method is slightly lower than that obtained by the SDR-based method. However, as the number of transmit antennas increases, the difference between the two methods gradually decreases. Moreover, the more transmit antennas there are, the greater the SINR achievable by the communication user. When the number of antennas is fixed, the relationship between beampattern gain and transmit SNR obtained by the radar using the MM-based method is presented (Figure 5 ). When the SINR threshold remains unchanged, the relationship between them is shown (Figure 6 ). The results illustrate that, compared with the radar-only scenario, the beampattern gain performance of MIMO DFRC systems is lower, and a larger SINR threshold results in a smaller beampattern gain. Additionally, within a certain range, when the transmit SNR is constant, beampattern gain is directly proportional to the number of transmit antennas.Conclusions This paper addresses the beamforming design problem for MIMO DFRC systems with the objective of maximizing beampattern gain. By jointly optimizing the communication and radar transmit beamforming vectors, the beampattern gain in the target direction is maximized while satisfying the SINR constraint for communication users and the total transmit power constraint. To solve this problem, the SDR-based and MM-based beamforming design methods are proposed. Simulation results demonstrate that the MM-based method offers lower complexity and achieves nearly the same beampattern gain as the SDR-based method. Moreover, as the number of transmit antennas increases, the complexity reduction of the MM-based method is more significant compared to the SDR-based method. -
1 基于SDR的波形设计方案
输入:初始化${P_{\rm t}}$, ${{{\boldsymbol{h}}}_k}$, ${{\boldsymbol{f}}}({\theta _0})$, ${\sigma ^2}$, $\varGamma $。 输出:总发射波束成形矢量$ {\bar {\boldsymbol{w}}} $。 步骤: 1:使用MATLAB的CVX工具箱求解问题式(12)得到
${\tilde {\boldsymbol{R}}},{{\tilde {\boldsymbol{R}}}_1},{{\tilde {\boldsymbol{R}}}_2}, \cdots ,{{\tilde {\boldsymbol{R}}}_K}$;2:根据式(13)求解通信发射波束成形矢量$ {{\bar {\boldsymbol{w}}}_k} $; 3:根据式(14)和式(15)求解雷达发射波束成形矩阵$ {{\bar {\boldsymbol{W}}}_{\mathrm{r}}} $; 4:将$ K $个$ {{\bar {\boldsymbol{w}}}_k} $与$ {{\bar {\boldsymbol{W}}}_{\mathrm{r}}} $的各列按列堆叠得到总发射波束成形矢量$ {\bar {\boldsymbol{w}}} $。 2 基于MM的波形设计方案
输入:初始化${{{\boldsymbol{w}}}_0}$, ${P_{\rm t}}$, ${{{\boldsymbol{h}}}_k}$, ${{\boldsymbol{f}}}({\theta _0})$, ${\sigma ^2}$, $\varGamma $, $\varepsilon $。 输出:总发射波束成形矩阵的向量化形式$ {\bar {\boldsymbol{w}}} $。 步骤: 1:$t = 0$,随机初始化${{{\boldsymbol{w}}}_{\rm t}}$; 2:$t = t + 1$; 3:使用MATLAB的CVX工具箱求解问题式(20)得到${{\boldsymbol{w}}}$; 4:计算${\text{res}} = {{\left| {\mathcal{P}({\theta _0},{{\boldsymbol{w}}}) - \mathcal{P}({\theta _0},{{{\boldsymbol{w}}}_{\rm t}})} \right|} \mathord{\left/ {\vphantom {{\left| {\mathcal{P}({\theta _0},{w}) - \mathcal{P}({\theta _0},{{w}_{\rm t}})} \right|} {\mathcal{P}({\theta _0},{{w}_{\rm t}})}}} \right. } {\mathcal{P}({\theta _0},{{{\boldsymbol{w}}}_{\rm t}})}}$; 5:若${\text{res}} \gt \varepsilon $,则${{{\boldsymbol{w}}}_{\rm t}} = {{\boldsymbol{w}}}$并返回第2步;否则$ {\bar {\boldsymbol{w}}} = {{\boldsymbol{w}}} $。 -
[1] IMT-2030(6G)推进组. 6G总体愿景与潜在关键技术白皮书[R]. 2020.IMT-2030(6G) Promotion Group. 6G vision and candidate technologies[R]. 2020. [2] 刘凡, 袁伟杰, 原进宏, 等. 雷达通信频谱共享及一体化: 综述与展望[J]. 雷达学报, 2021, 10(3): 467–484. doi: 10.12000/JR20113.LIU Fan, YUAN Weijie, YUAN Jinhong, et al. Radar-communication spectrum sharing and integration: Overview and prospect[J]. Journal of Radars, 2021, 10(3): 467–484. doi: 10.12000/JR20113. [3] LIU Fan, ZHOU Longfei, MASOUROS C, et al. Toward dual-functional radar-communication systems: Optimal waveform design[J]. IEEE Transactions on Signal Processing, 2018, 66(16): 4264–4279. doi: 10.1109/TSP.2018.2847648. [4] CHEN Guangyi, ZHANG Ruoyu, REN Hong, et al. Hybrid beamforming design with overlapped subarrays for massive MIMO-ISAC systems[C]. Proceedings of GLOBECOM 2023 - 2023 IEEE Global Communications Conference, Kuala Lumpur, Malaysia, 2023: 528–533. doi: 10.1109/GLOBECOM54140.2023.10437590. [5] ZHOU Wenxing, ZHANG Ruoyu, CHEN Guangyi, et al. Integrated sensing and communication waveform design: A survey[J]. IEEE Open Journal of the Communications Society, 2022, 3: 1930–1949. doi: 10.1109/OJCOMS.2022.3215683. [6] 肖博, 霍凯, 刘永祥. 雷达通信一体化研究现状与发展趋势[J]. 电子与信息学报, 2019, 41(3): 739–750. doi: 10.11999/JEIT180515.XIAO Bo, HUO Kai, and LIU Yongxiang. Development and prospect of radar and communication integration[J]. Journal of Electronics & Information Technology, 2019, 41(3): 739–750. doi: 10.11999/JEIT180515. [7] 张若愚, 袁伟杰, 崔原豪, 等. 面向6G的大规模MIMO通信感知一体化: 现状与展望[J]. 移动通信, 2022, 46(6): 17–23. doi: 10.3969/j.issn.1006-1010.2022.06.003.ZHANG Ruoyu, YUAN Weijie, CUI Yuanhao, et al. Integrated sensing and communications with massive MIMO for 6G: Status and prospect[J]. Mobile Communications, 2022, 46(6): 17–23. doi: 10.3969/j.issn.1006-1010.2022.06.003. [8] ZHANG J A, RAHMAN M L, WU Kai, et al. Enabling joint communication and radar sensing in mobile networks—a survey[J]. IEEE Communications Surveys & Tutorials, 2022, 24(1): 306–345. doi: 10.1109/COMST.2021.3122519. [9] HASSANIEN A, AMIN M G, ZHANG Y D, et al. Dual-function radar-communications: Information embedding using sidelobe control and waveform diversity[J]. IEEE Transactions on Signal Processing, 2016, 64(8): 2168–2181. doi: 10.1109/TSP.2015.2505667. [10] WANG Xiangrong, HASSANIEN A, and AMIN M G. Dual-function MIMO radar communications system design via sparse array optimization[J]. IEEE Transactions on Aerospace and Electronic Systems, 2019, 55(3): 1213–1226. doi: 10.1109/TAES.2018.2866038. [11] LIU Yongjun, LIAO Guisheng, XU Jingwei, et al. Adaptive OFDM integrated radar and communications waveform design based on information theory[J]. IEEE Communications Letters, 2017, 21(10): 2174–2177. doi: 10.1109/LCOMM.2017.2723890. [12] KUMARI P, CHOI J, GONZÁLEZ-PRELCIC N, et al. IEEE 802.11ad-based radar: An approach to joint vehicular communication-radar system[J]. IEEE Transactions on Vehicular Technology, 2018, 67(4): 3012–3027. doi: 10.1109/TVT.2017.2774762. [13] CUI Yuanhao, LIU Fan, JING Xiaojun, et al. Integrating sensing and communications for ubiquitous IoT: Applications, trends, and challenges[J]. IEEE Network, 2021, 35(5): 158–167. doi: 10.1109/MNET.010.2100152. [14] LIU Fan, MASOUROS C, LI Ang, et al. MU-MIMO communications with MIMO radar: From co-existence to joint transmission[J]. IEEE Transactions on Wireless Communications, 2018, 17(4): 2755–2770. doi: 10.1109/TWC.2018.2803045. [15] LIU Xiang, HUANG Tianyao, SHLEZINGER N, et al. Joint transmit beamforming for multiuser MIMO communications and MIMO radar[J]. IEEE Transactions on Signal Processing, 2020, 68: 3929–3944. doi: 10.1109/TSP.2020.3004739. [16] LIU Fan, LIU Yafeng, LI Ang, et al. Cramér-Rao bound optimization for joint radar-communication beamforming[J]. IEEE Transactions on Signal Processing, 2022, 70: 240–253. doi: 10.1109/TSP.2021.3135692. [17] HUA Haocheng, SONG Xianxin, FANG Yuan, et al. MIMO integrated sensing and communication with extended target: CRB-Rate tradeoff[C]. Proceedings of GLOBECOM 2022 - 2022 IEEE Global Communications Conference, Rio de Janeiro, Brazil, 2022: 4075–4080. doi: 10.1109/GLOBECOM48099.2022.10000676. [18] CHEN Li, WANG Zhiqin, DU Ying, et al. Generalized transceiver beamforming for DFRC with MIMO radar and MU-MIMO communication[J]. IEEE Journal on Selected Areas in Communications, 2022, 40(6): 1795–1808. doi: 10.1109/JSAC.2022.3155515. [19] DU Ying, LIU Yao, HAN Kaifeng, et al. Multi-user and multi-target dual-function radar-communication waveform design: Multi-fold performance tradeoffs[J]. IEEE Transactions on Green Communications and Networking, 2023, 7(1): 483–496. doi: 10.1109/TGCN.2023.3234275. [20] HUA Haocheng, XU Jie, and HAN T X. Optimal transmit beamforming for integrated sensing and communication[J]. IEEE Transactions on Vehicular Technology, 2023, 72(8): 10588–10603. doi: 10.1109/TVT.2023.3262513. [21] ZHANG Ruoyu, CHENG Lei, WANG Shuai, et al. Tensor decomposition-based channel estimation for hybrid mmWave massive MIMO in high-mobility scenarios[J]. IEEE Transactions on Communications, 2022, 70(9): 6325–6340. doi: 10.1109/TCOMM.2022.3187780. [22] ZHANG Ruoyu, CHENG Lei, WANG Shuai, et al. Integrated sensing and communication with massive MIMO: A unified tensor approach for channel and target parameter estimation[J]. IEEE Transactions on Wireless Communications, 2024, 23(8): 8571–8587. doi: 10.1109/TWC.2024.3351856. [23] LUO Zhiquan and YU Wei. An introduction to convex optimization for communications and signal processing[J]. IEEE Journal on Selected Areas in Communications, 2006, 24(8): 1426–1438. doi: 10.1109/JSAC.2006.879347. [24] TRAN L N, HANIF M F, TOLLI A, et al. Fast converging algorithm for weighted sum rate maximization in multicell MISO downlink[J]. IEEE Signal Processing Letters, 2012, 19(12): 872–875. doi: 10.1109/LSP.2012.2223211. [25] SUN Ying, BABU P, and PALOMAR D P. Majorization-minimization algorithms in signal processing, communications, and machine learning[J]. IEEE Transactions on Signal Processing, 2017, 65(3): 794–816. doi: 10.1109/TSP.2016.2601299. [26] MOSEK ApS. Mosek optimization toolbox for matlab[R]. 2025. [27] WANG Kunyu, SO A M C, CHANG T H, et al. Outage constrained robust transmit optimization for multiuser MISO downlinks: Tractable approximations by conic optimization[J]. IEEE Transactions on Signal Processing, 2014, 62(21): 5690–5705. doi: 10.1109/TSP.2014.2354312. [28] BEN-TAL A and NEMIROVSKI A. Lectures on Modern Convex Optimization: Analysis, Algorithms, and Engineering Applications[M]. Philadelphia: Society for Industrial and Applied Mathematics, 2001. doi: 10.1137/1.9780898718829. -





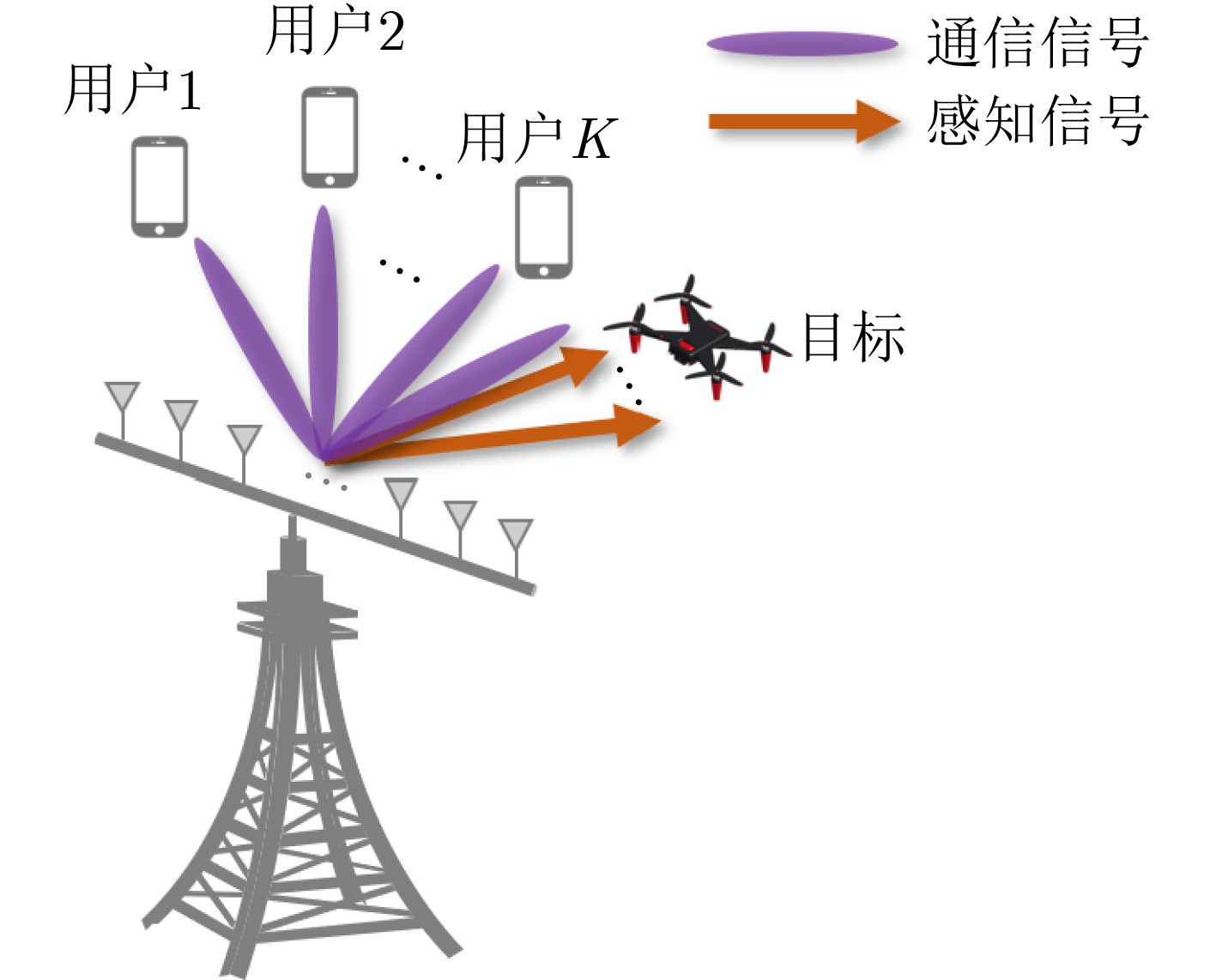
 下载:
下载:


 下载:
下载:
