Improved Extended Kalman Filter Tracking Method Based On Active Waveguide Invariant Distribution
-
摘要: 在复杂的海洋环境中,目标的可知信息受环境噪声、混响等的干扰严重,导致目标跟踪效果较差,而从这些干扰中提取目标的可利用特征及其困难。该文将目标与环境的耦合特征融入目标跟踪算法中,提出了一种基于主动波导不变量分布的改进扩展卡尔曼滤波跟踪方法。首先基于浅海波导中目标散射特性基本理论,推导了收发分置条件下的主动波导不变量表征的数学模型,获得了距离、频率以及主动波导不变量分布的约束关系;然后将该约束加入到扩展卡尔曼滤波的状态向量中,通过增加新的约束来提高目标运动模型与真实目标运动轨迹的契合度进而提高目标跟踪的精度;最后通过仿真实验和实测数据验证了该方法的跟踪性能,结果显示:该方法较常规扩展卡尔曼滤波跟踪方法能够更好地提高目标跟踪精度,仿真中结果的优化率约能达到50%,实测数据处理结果的优化率约在60%左右。Abstract:
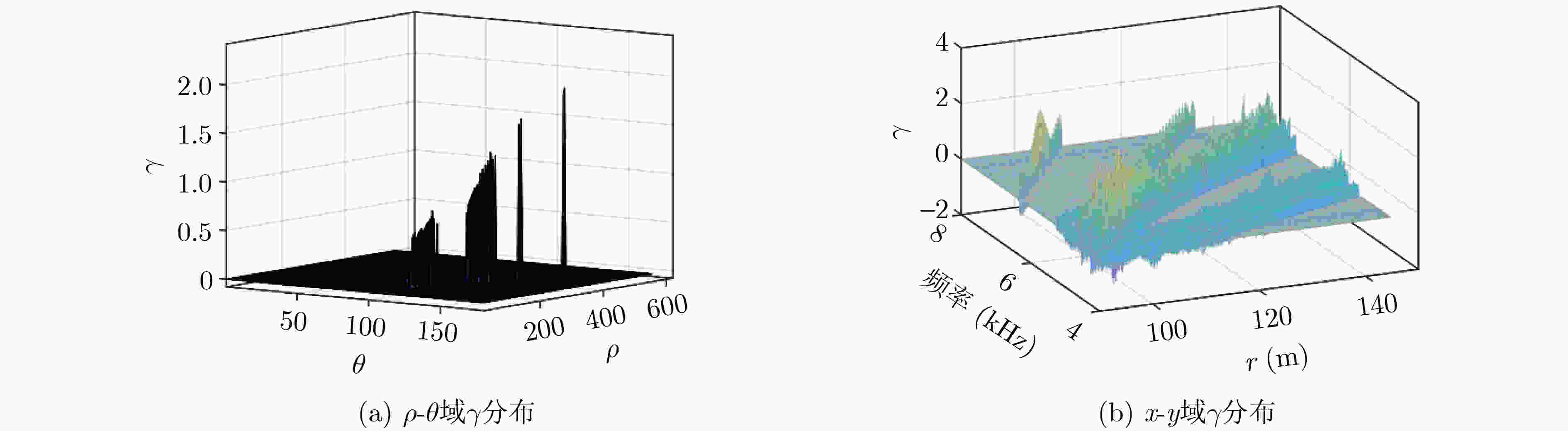
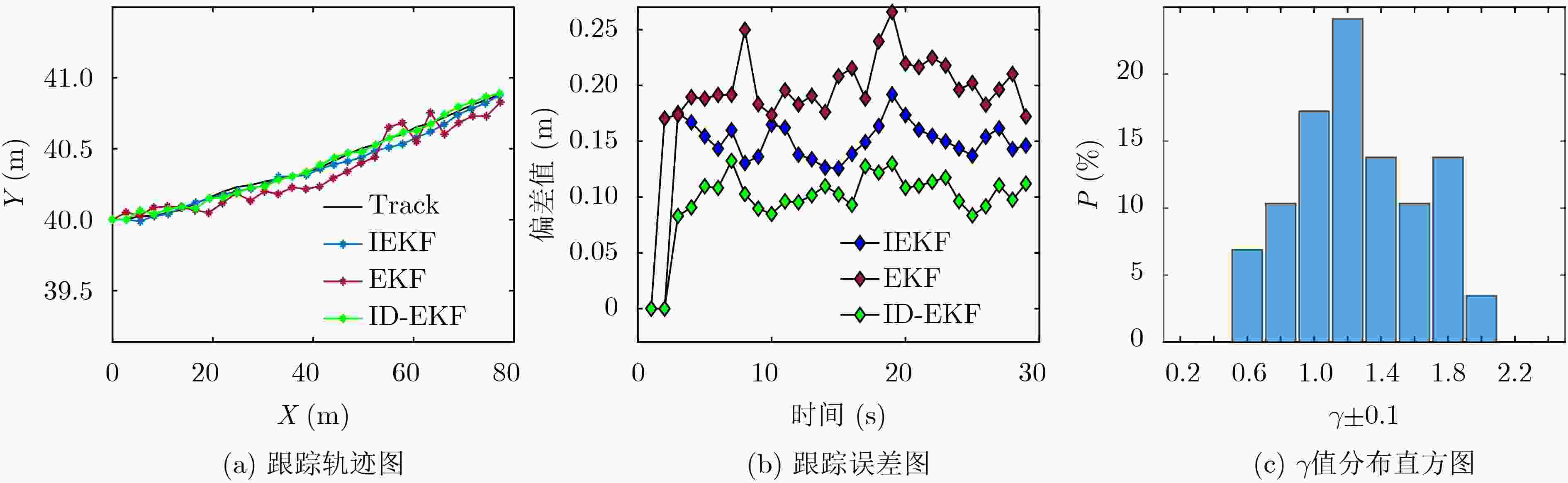
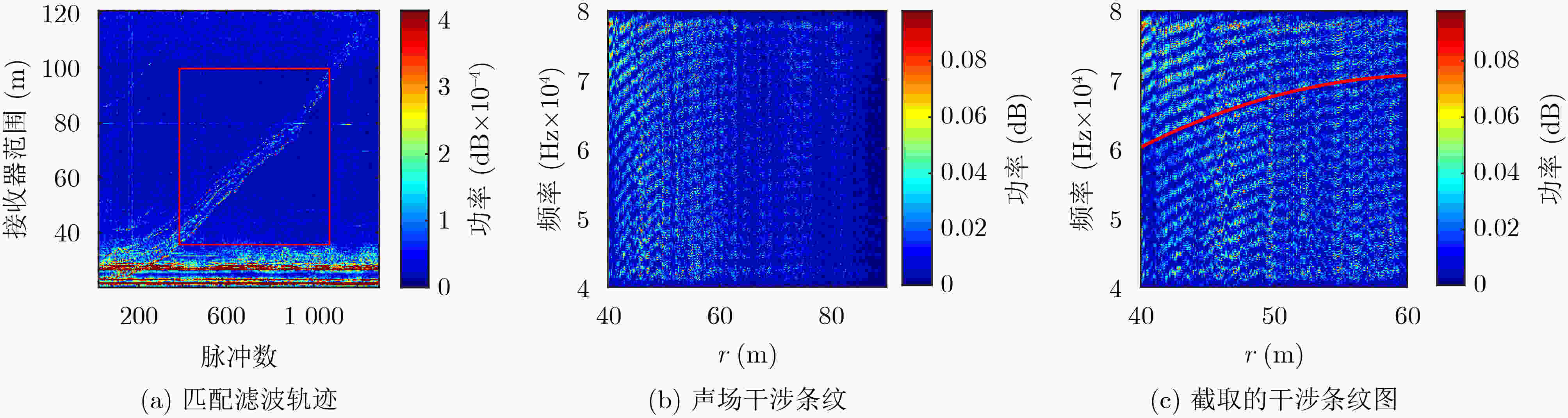
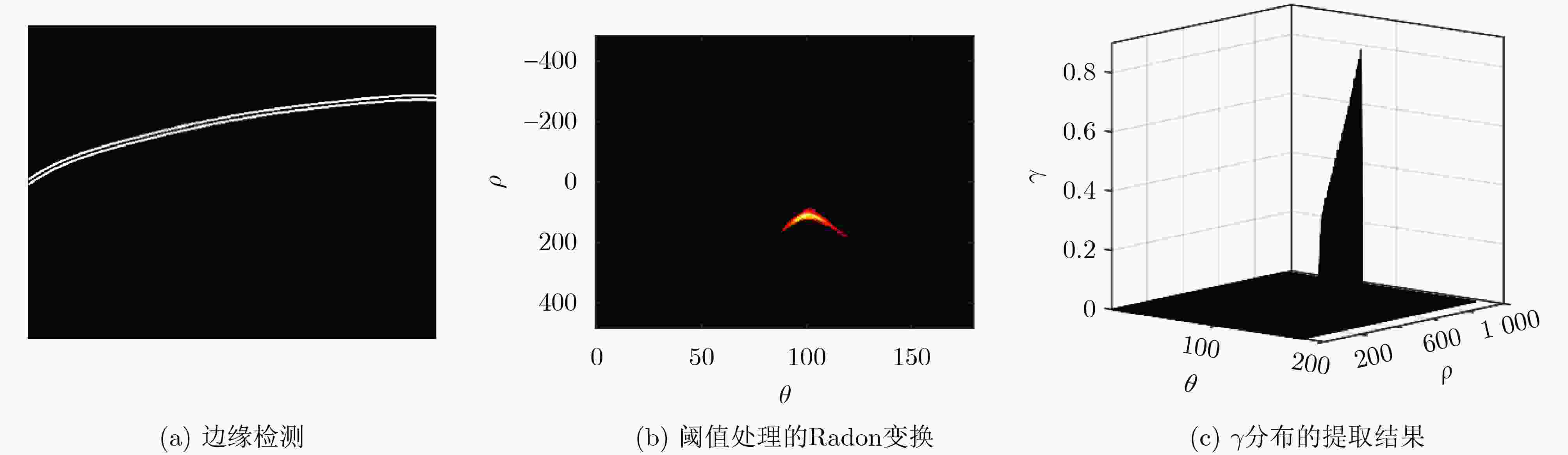
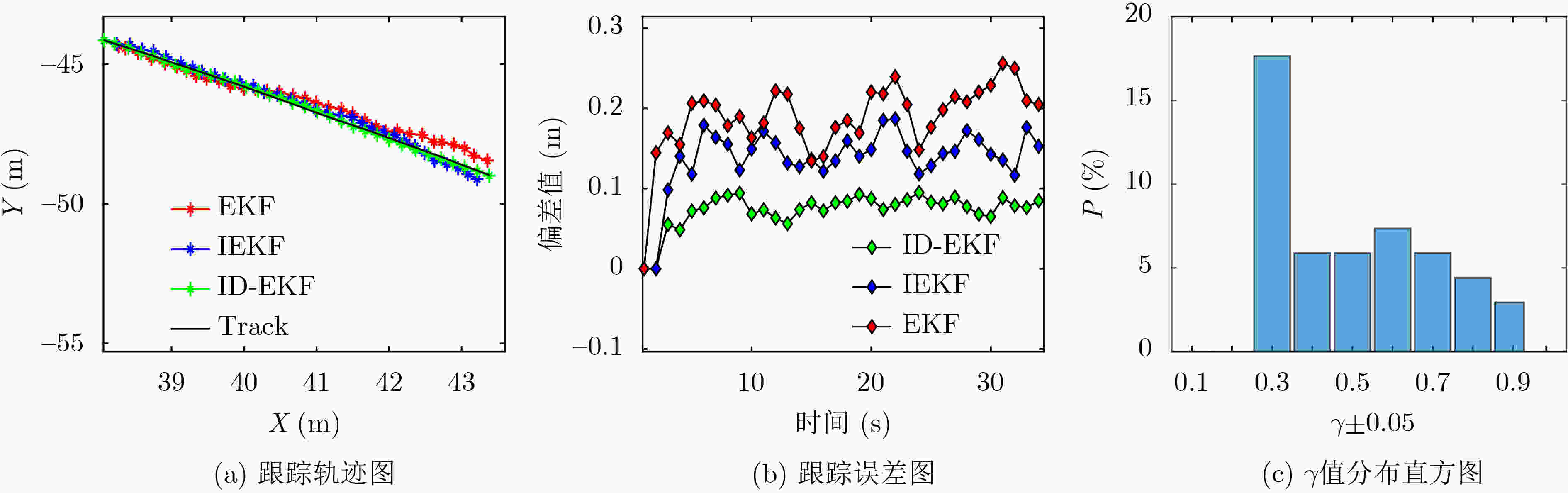
Objective The complex and variable nature of the underwater environment presents significant challenges for the field of underwater target tracking. Factors such as environmental noise, interference, and reverberation can severely distort and obscure the signals emitted or reflected by underwater targets, complicating accurate detection and tracking efforts. Additionally, advancements in weak target signal technology add further complexity, as they necessitate sophisticated methods to enhance and interpret signals that may be lost amidst background noise. The challenges associated with underwater target tracking are multifaceted. One major issue is the interference that can compromise the integrity and reliability of target information. Another critical challenge lies in the difficulty of extracting useful feature information from the often chaotic underwater environment. Traditional tracking methods, which typically rely on basic signal processing techniques, frequently fall short in addressing these complexities. Underwater tracking technology serves as a cornerstone in several key fields, including marine science, military strategy, and marine resource development. Notably, effective underwater tracking is essential for monitoring, sonar detection, and the deployment of underwater weapons within the military sector. Considering the significance of underwater tracking technology, there is an urgent need for innovative methods to address the existing challenges. Therefore, this paper proposes a unified approach that views the target and environment as an integrated system, extracting coupled features—specifically, active waveguide invariants—and fusing these features into the motion model to enhance underwater tracking capabilities. Methods: This paper presents an enhanced extended Kalman filter tracking method, which is built upon the active waveguide invariant distribution. The mathematical model for active waveguide invariant representation is derived based on the foundational theory of target scattering characteristics in shallow water waveguides, with specific consideration of transmitter-receiver separation. This derivation establishes the constraint relationships among distance, frequency, and the active waveguide invariant distribution. These constraints are subsequently incorporated into the state vector of the extended Kalman filter to enhance the alignment between the target motion model and the actual trajectory, thereby improving tracking accuracy. The method includes image preprocessing steps such as filtering, edge detection, and edge smoothing, followed by the application of the Radon transform to extract essential parameters, including distance and frequency. The Radon transform is refined using threshold filtering to improve parameter extraction. The active waveguide invariant distribution is then computed, and the tracking performance of the method is validated through simulation experiments and real measurement data. The simulation setup involves a rigid ball as the target in a shallow water environment, modeled using a constant velocity assumption. Real measurement data is collected under similar conditions at the Xin’An River experimental site. For both simulations and real measurements, a steel ball model target and constant velocity model are employed, with equipment deployed on the same horizontal plane. Results and Discussions: First, the distribution of the constant of propagation within the active waveguide was obtained through simulation experiments. A comparison was made between the Invariant Distribution-Extended Kalman Filter (ID-EKF), the Extended Kalman Filter (EKF), and the Invariance Extended Kalman Filter (IEKF). In trajectory tracking, the ID-EKF demonstrated closer alignment to the true trajectory compared to both the EKF and IEKF. Additionally, in terms of the mean square error of the predicted posterior position, the ID-EKF exhibited a lower error rate. As indicated by the overall estimation accuracy, the ID-EKF achieved approximately 50% greater accuracy than the EKF and about 30% higher accuracy than the IEKF. Subsequently, the ID-EKF algorithm was validated in a real-world scenario using actual measurement data. The acoustic field interference stripes were obtained through the processing of received echo signals, and the distribution of the constant of propagation was extracted by manually selecting points and conducting a maximum search, followed by curve fitting using the joint edge curve fitting method. Results from Monte Carlo simulation experiments demonstrated a decreasing order of tracking accuracy for the ID-EKF, IEKF, and EKF, consistent with the simulation results. The overall estimation accuracy of the ID-EKF was approximately 60% higher than that of the EKF and about 40% superior to that of the IEKF. Conclusions: This paper presents a novel tracking method based on the extended Kalman filter, informed by the interference characteristics of target and environmental coupling in shallow water waveguides. The effectiveness of this method is substantiated through both theoretical simulation data and empirical lake measurement data. The active waveguide invariant distribution was derived using the Radon transform, which facilitated the implementation of the ID-EKF tracking. Results from both simulations and experiments reveal that the extracted active invariant value distribution manifests in two scenarios: either coinciding with 1 or exhibiting significant deviation from 1. When the extracted invariant value is markedly different from 1, the ID-EKF demonstrates a reduced tracking error and a more pronounced convergence relative to other tracking algorithms, highlighting the importance of precisely extracting this value to enhance the ID-EKF’s performance. Conversely, when the extracted value is close to 1, the tracking error of the ID-EKF aligns more closely with that of the IEKF algorithm. In both cases, it is evident that the extracted invariant value is pivotal in enhancing the accuracy of the tracking algorithm. Future research will prioritize the extraction of more accurate invariant values to facilitate the development of higher-precision tracking algorithms. -
表 1 3种算法仿真的估计位置与真值误差表(m)
算法 估计位置和真值偏差-均值 估计位置和真值偏差-峰值 EKF 0.19 0.25 IEKF 0.13 0.19 ID-EKF 0.09 0.13 表 2 算法仿真对比优化表(%)
对比算法 均值优化率 峰值优化率 IEKF相对EKF 31.58 24.00 ID-EKF相对EKF 52.63 48.00 ID-EKF相对IEKF 30.77 31.58 表 3 测试参数及目标
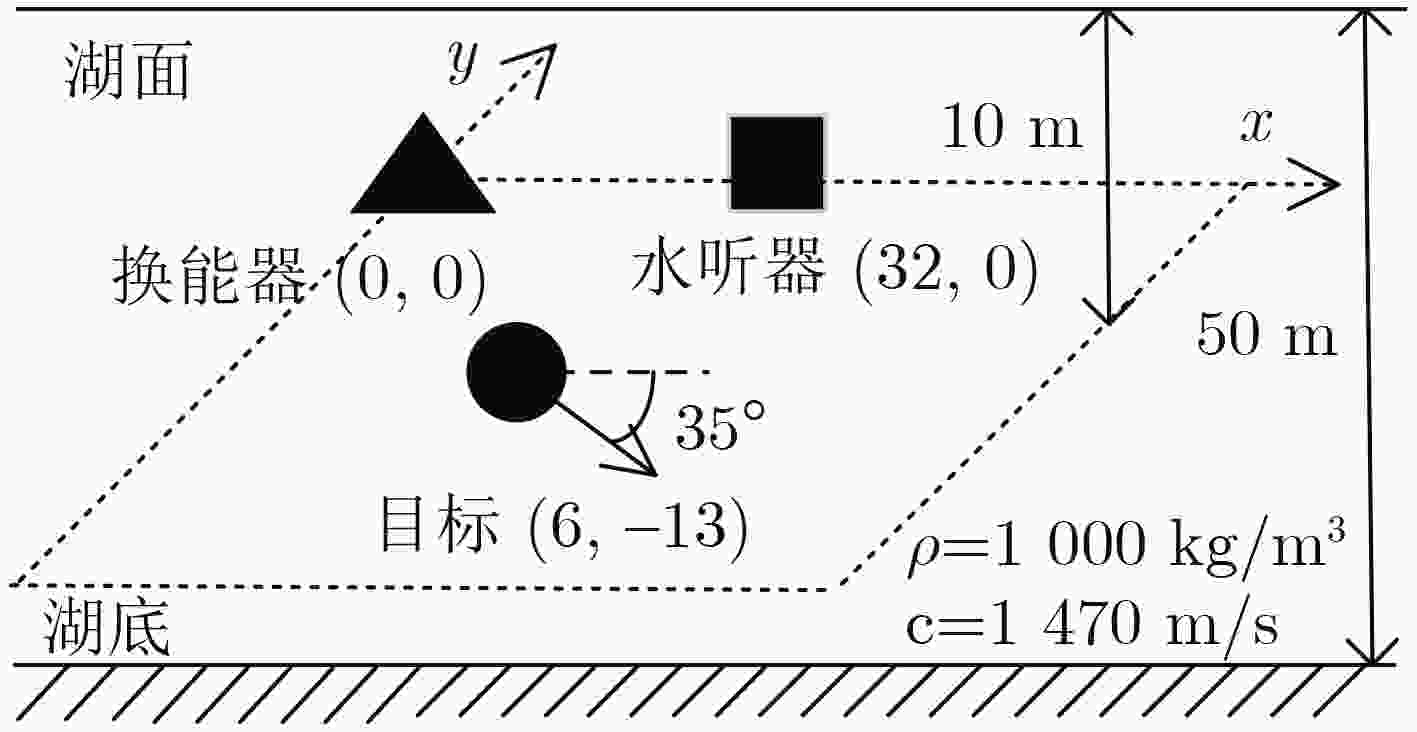
信号参数 目标及其运动状态 信号形式 频率(kHz) 脉冲间隔(ms) 脉宽(ms) 采样率(kHz) 球体目标模型(1.2 m直径),由近及远运动 LFM 40~80 400 5 512 表 4 3种算法试验的估计位置与真值误差表(m)
算法 估计位置和真值偏差-均值 估计位置和真值偏差-峰值 EKF 0.195 0.256 IEKF 0.142 0.187 ID-EKF 0.079 0.095 表 5 算法试验对比优化表(%)
算法对比 均值优化率 峰值优化率 IEKF相对EKF 27.179 26.953 ID-EKF相对EKF 59.487 62.891 ID-EKF相对IEKF 44.366 49.197 -
[1] 郭戈, 王兴凯, 徐慧朴. 基于声呐图像的水下目标检测、识别与跟踪研究综述[J]. 控制与决策, 2018, 33(5): 906–922. doi: 10.13195/j.kzyjc.2017.1678.GUO Ge, WANG Xingkai, and XU Huipu. Review on underwater target detection, recognition and tracking based on sonar image[J]. Control and Decision, 2018, 33(5): 906–922. doi: 10.13195/j.kzyjc.2017.1678. [2] KALMAN R E and BUCY R S. New results in linear filtering and prediction theory[J]. Journal of Basic Engineering, 1961, 83(1): 95–108. doi: 10.1115/1.3658902. [3] KALMAN R E. A new approach to linear filtering and prediction problems[J]. Journal of Basic Engineering, 1960, 82(1): 35–45. doi: 10.1115/1.3662552. [4] LI Tiancheng, SU Jinya, LIU Wei, et al. Approximate Gaussian conjugacy: Parametric recursive filtering under nonlinearity, multimodality, uncertainty, and constraint, and beyond[J]. Frontiers of Information Technology & Electronic Engineering, 2017, 18(12): 1913–1939. doi: 10.1631/FITEE.1700379. [5] 周云, 胡锦楠, 赵瑜, 等. 基于卡尔曼滤波改进压缩感知算法的车辆目标跟踪[J]. 湖南大学学报: 自然科学版, 2023, 50(1): 11–21. doi: 10.16339/j.cnki.hdxbzkb.2023002.ZHOU Yun, HU Jinnan, ZHAO Yu, et al. Vehicle target tracking based on Kalman filtering improved compressed sensing algorithm[J]. Journal of Hunan University: Natural Sciences, 2023, 50(1): 11–21. doi: 10.16339/j.cnki.hdxbzkb.2023002. [6] 白冬杰. 车载毫米波雷达多目标跟踪算法研究[D]. [硕士论文], 北京交通大学, 2019.BAI Dongjie. Research on multi-target tracking algorithm of vehicle-mounted millimeter-wave radar[D]. [Master dissertation], Beijing Jiaotong University, 2019. [7] 吴叶丽, 行鸿彦, 侯天浩, 等. 基于改进自适应扩展卡尔曼滤波的高精度姿态解算[J]. 探测与控制学报, 2023, 45(6): 69–76.WU Yeli, XiNG Hongyan, HOU Tianhao, et al. An improved adaptive extended Kalman filter for high precision attitude solution[J]. Journal of Detection & Control, 2023, 45(6): 69–76. [8] 成春彦, 李亚安. EKF和UKF算法在双观测站纯方位目标跟踪中的应用[J]. 水下无人系统学报, 2023, 31(3): 388–397. doi: 10.11993/j.issn.2096-3920.202203014.CHENG Chunyan and LI Yaan. Applications of EKF and UKF algorithms in bearings-only target tracking with a double observation stations[J]. Journal of Unmanned Undersea Systems, 2023, 31(3): 388–397. doi: 10.11993/j.issn.2096-3920.202203014. [9] 丁凯. 基于前视声纳的水下目标跟踪技术研究[D]. [硕士论文], 哈尔滨工程大学, 2006. doi: 10.7666/d.y936424.DING Kai. Research on tracking of underwater object based on forward-looking sonar[D]. [Master dissertation], Harbin Engineering University, 2006. doi: 10.7666/d.y936424. [10] CHUPROV S D. Interference structure of a sound field in a layered ocean[M]. BREKHOVSKIKH L M and ANDREEVOI L B. Ocean Acoustics: Current State. Moscow: Nauka, 1982: 71–91. [11] BROOKS L A, KIDNER M R F, ZANDER A C, et al. Techniques for extraction of the waveguide invariant from interference patterns in spectrograms[C]. ACOUSTICS 2006, Christchurch, New Zealand, 2006: 445. [12] SELL A W and LEE CULVER R. Waveguide invariant analysis for modeling time-frequency striations in a range-dependent environment[J]. The Journal of the Acoustical Society of America, 2011, 129(S4): 2509. doi: 10.1121/1.3588287. [13] TURGUT A, ORR M, and ROUSEFF D. Broadband source localization using horizontal-beam acoustic intensity striations[J]. The Journal of the Acoustical Society of America, 2010, 127(1): 73–83. doi: 10.1121/1.3257211. [14] 李永飞, 郭瑞明, 赵航芳. 浅海内波环境下声场干涉条纹的稀疏重建[J]. 物理学报, 2023, 72(7): 074301. doi: 10.7498/aps.72.20221932.LI Yongfei, GUO Ruiming, and ZHAO Hangfang. Sparse reconstruction of acoustic interference fringes in shallow water and internal wave environment[J]. Acta Physica Sinica, 2023, 72(7): 074301. doi: 10.7498/aps.72.20221932. [15] 余赟, 惠俊英, 殷敬伟, 等. 基于波导不变量的目标运动参数估计及被动测距[J]. 声学学报, 2011, 36(3): 258–264. doi: 10.15949/j.cnki.0371-0025.2011.03.015.YU Yun, HUI Junying, YIN Jingwei, et al. Moving target parameter estimation and passive ranging based on waveguide invariant theory[J]. Acta Acustica, 2011, 36(3): 258–264. doi: 10.15949/j.cnki.0371-0025.2011.03.015. [16] 宋雪晶. 基于声场干涉结构的水声目标被动定位技术[D]. [博士论文], 哈尔滨工程大学, 2017.SONG Xuejing. Underwater acoustic target passive localization techniques based on acoustic field interference structure[D]. [Ph. D. dissertation], Harbin Engineering University, 2017. [17] QUIJANO J E, ZURK L M, and ROUSEFF D. Demonstration of the invariance principle for active sonar[J]. The Journal of the Acoustical Society of America, 2008, 123(3): 1329–1337. doi: 10.1121/1.2836763. [18] QUIJANO J E, CAMPBELL R L JR, OESTERLEIN T G, et al. Experimental observations of active invariance striations in a tank environment[J]. The Journal of the Acoustical Society of America, 2010, 128(2): 611–618. doi: 10.1121/1.3455813. [19] ZURK L M and ROUSEFF D. Striation-based beamforming for active sonar with a horizontal line array[J]. The Journal of the Acoustical Society of America, 2012, 132(4): EL264–EL270. doi: 10.1121/1.4748281. [20] HE Chensong, QUIJANO J E, and ZURK L M. Enhanced Kalman filter algorithm using the invariance principle[J]. IEEE Journal of Oceanic Engineering, 2009, 34(4): 575–585. doi: 10.1109/joe.2009.2028058. [21] 芬恩·B·延森, 威廉·A·库珀曼, 米切尔·B·波特, 等, 周利生, 王鲁军, 杜栓平, 译. 计算海洋声学[M]. 2版. 北京: 国防工业出版社, 2018: 54–57, 267–269.JENSEN F B, KUPERMAN W A, POTER M B, et al, ZHOU Lisheng, WANG Lujun, and DU Shuanping. translation. Computational Ocean Acoustics[M]. 2nd ed. Beijing: National Defense Industry Press, 2018: 54–57, 267–269. [22] 林萌, 李翠华, 黄剑航. 基于Radon变换的运动模糊图像参数估计[J]. 计算机技术与发展, 2008, 18(1): 33–36. doi: 10.3969/j.issn.1673-629X.2008.01.009.LIN Meng, LI Cuihua, and HUANG Jianhang. Parameters estimation of motion blurred images based on radon transform[J]. Computer Technology and Development, 2008, 18(1): 33–36. doi: 10.3969/j.issn.1673-629X.2008.01.009. -





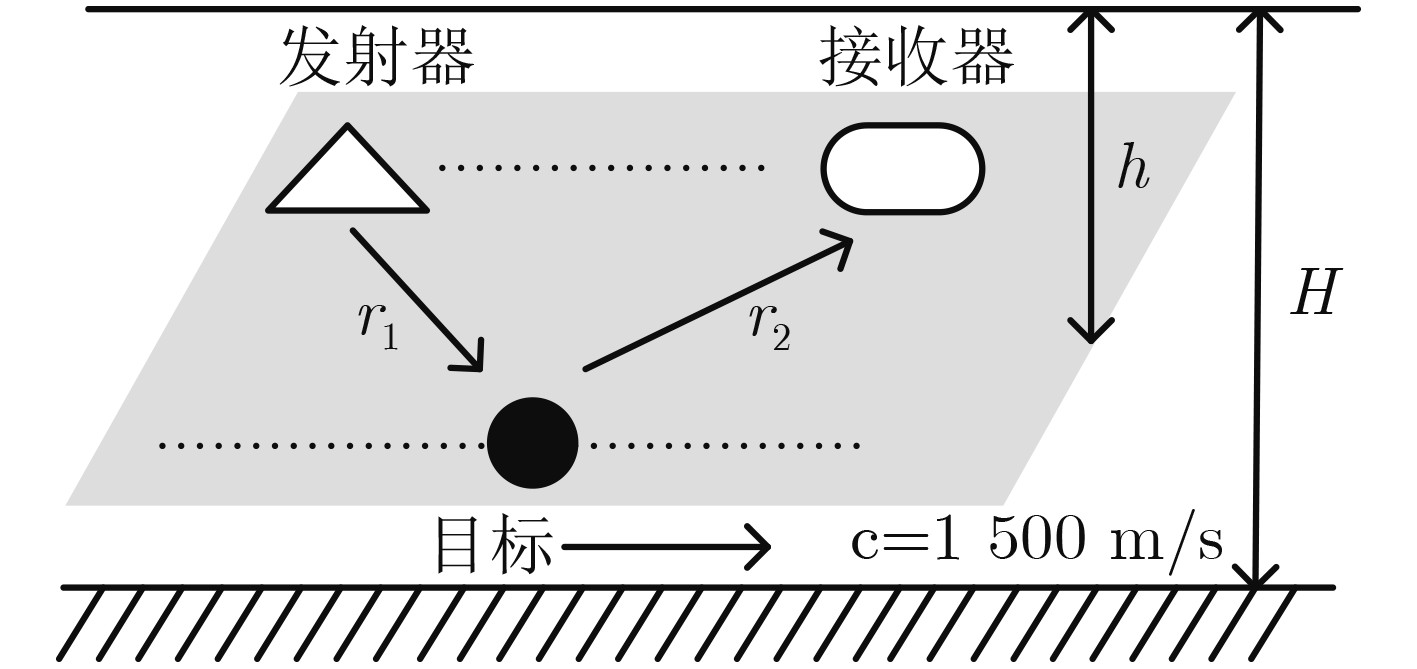
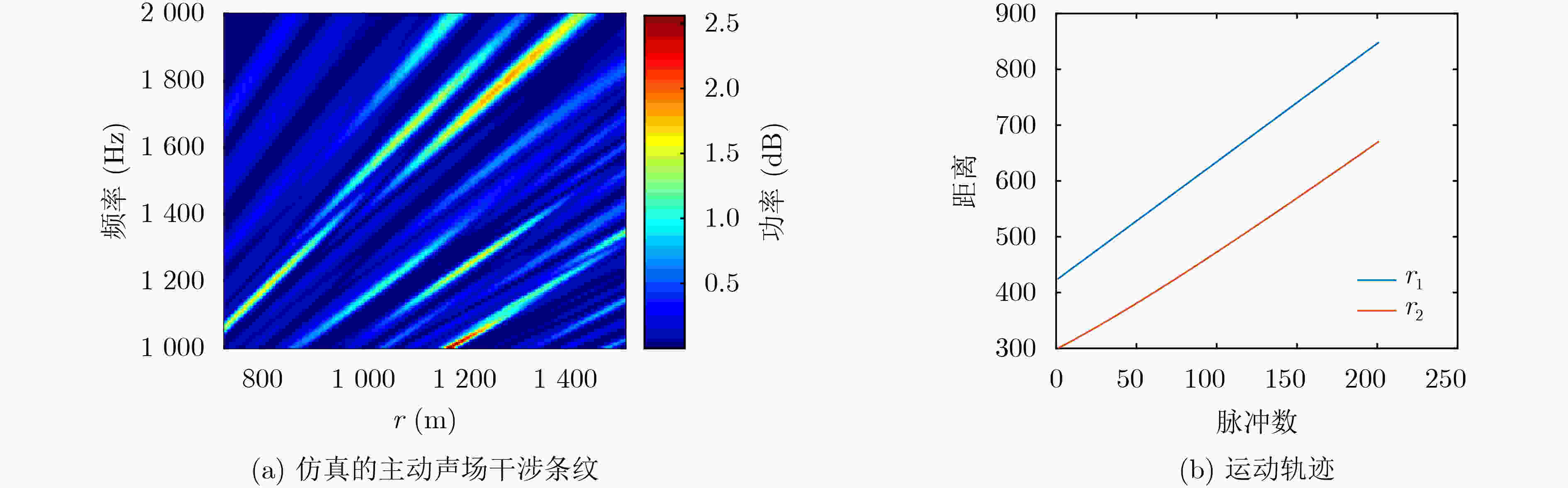
 下载:
下载:
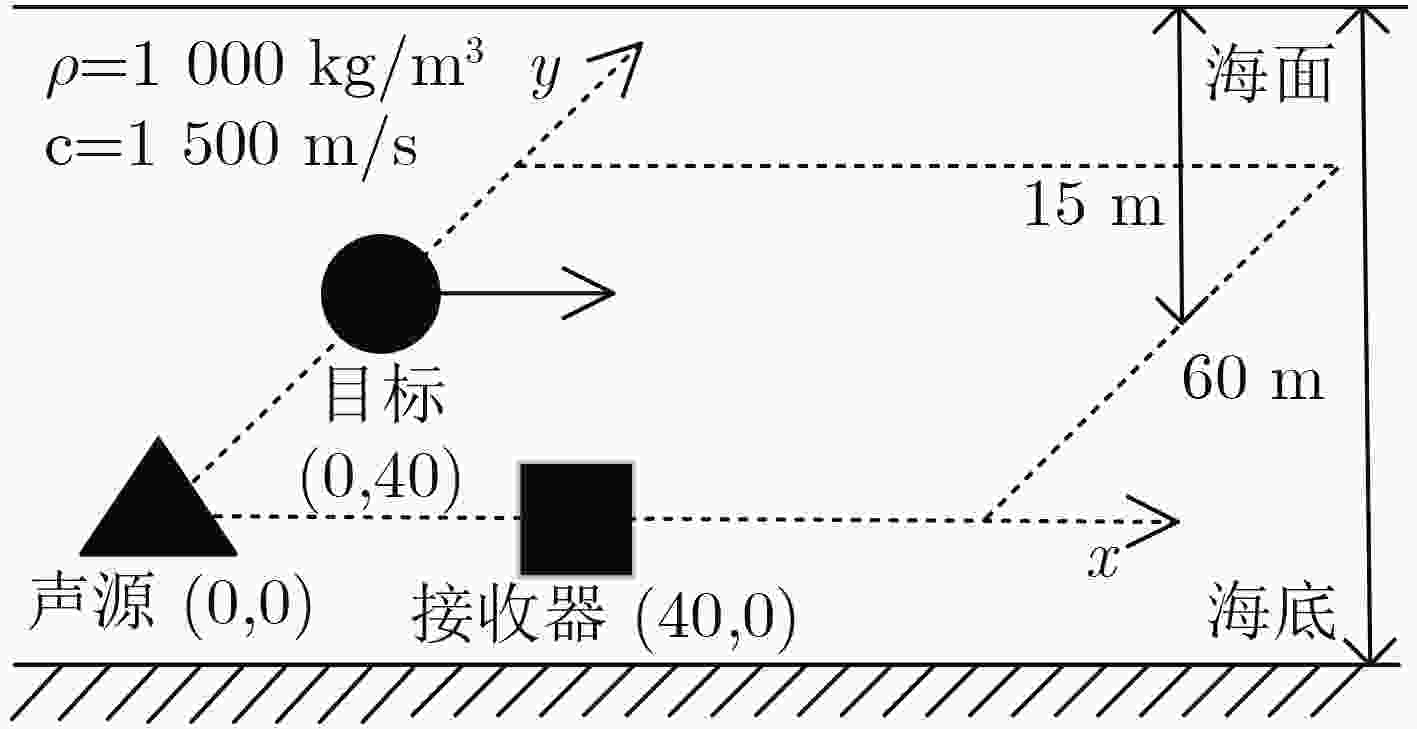


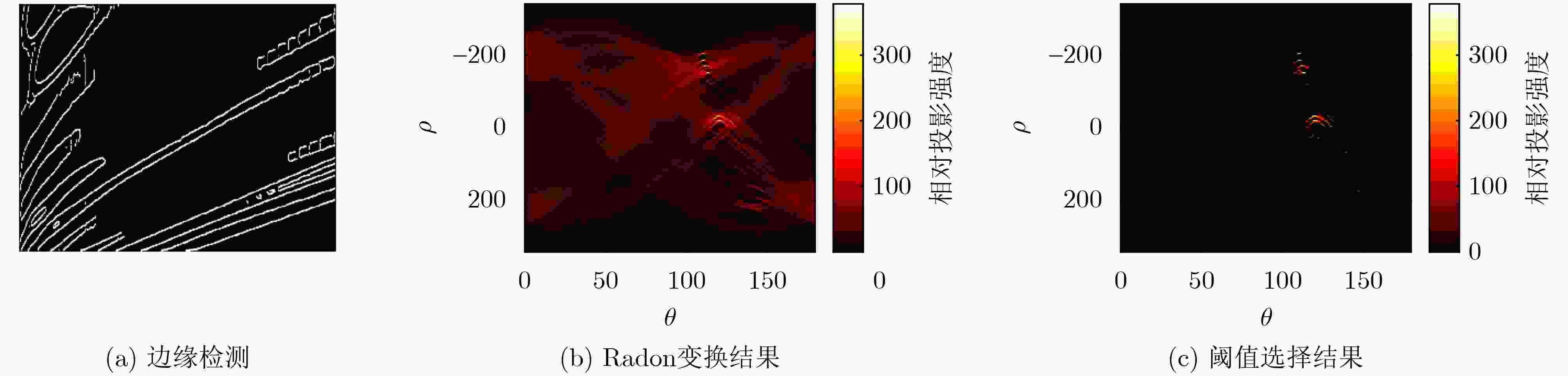


 下载:
下载:
