A Decision-making Method for UAV Conflict Detection and Avoidance System
-
摘要: 针对无人机探测与避让(DAA)系统中无人机飞行碰撞避免的决策问题,该文提出一种将无人机系统检测和避免警报逻辑(DAIDALUS)和马尔可夫决策过程(MDP)相结合的方法。DAIDALUS算法的引导逻辑可以根据当前状态空间计算无人机避撞策略,将这些策略作为MDP的动作空间,并设置合适的奖励函数和状态转移概率,建立MDP模型,探究不同折扣因子对无人机飞行避撞过程的影响。仿真结果表明:相比于DAIDALUS,本方法的效率提升27.2%;当折扣因子设置为0.99时,可以平衡长期与短期收益;净空入侵率为5.8%,威胁机与本机最近距离为343 m,该方法可以满足无人机飞行过程中避撞的要求。Abstract:
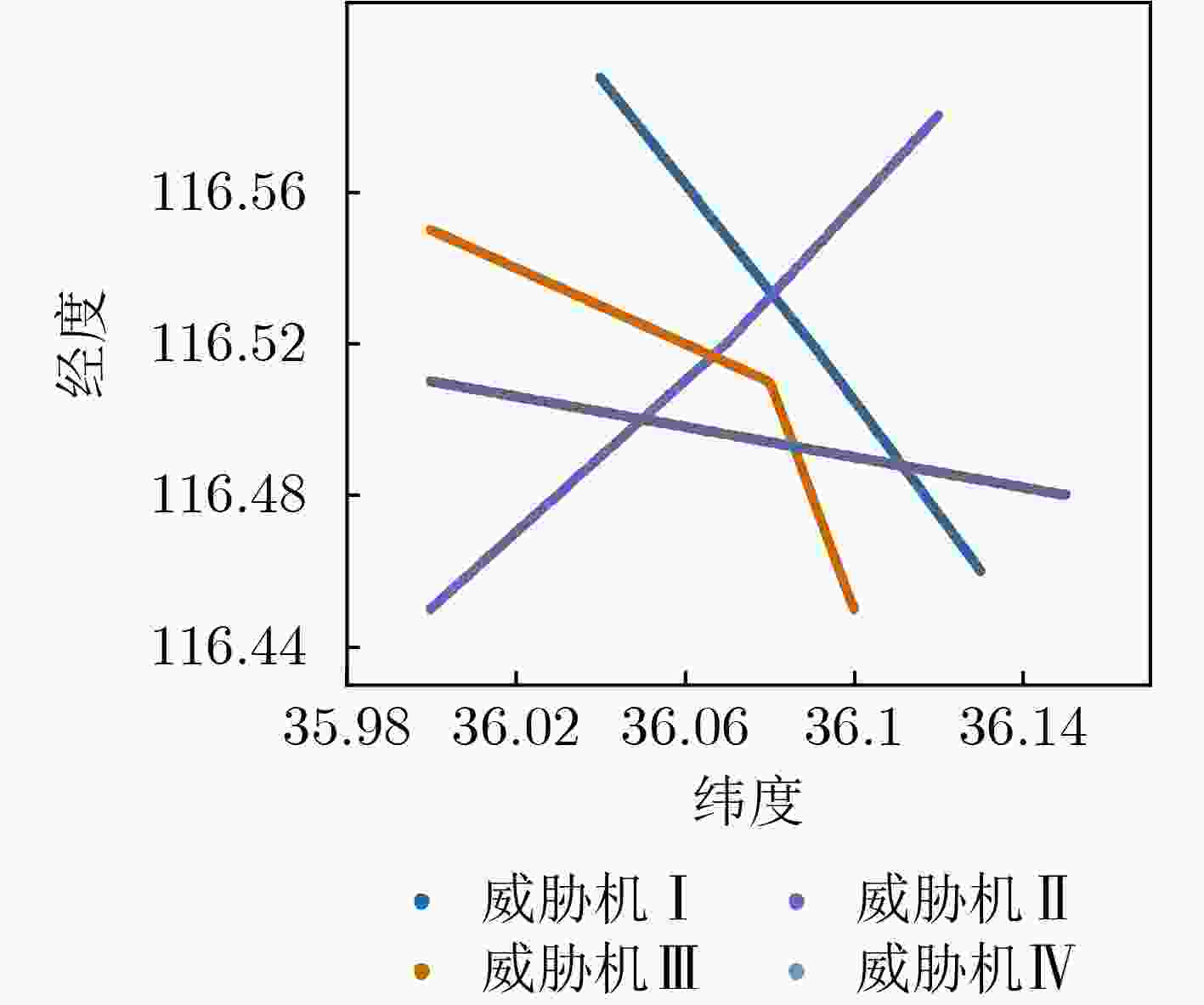
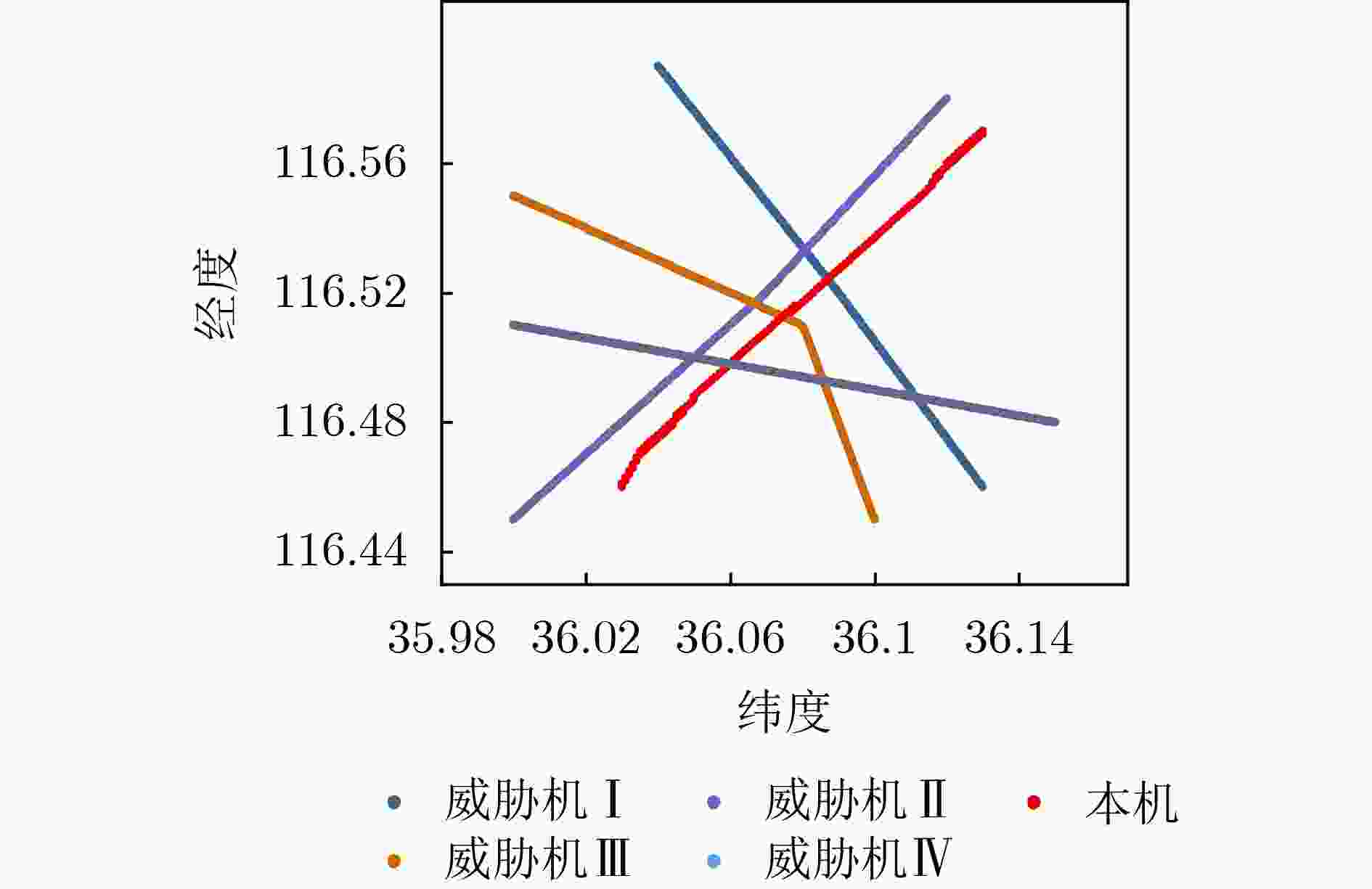
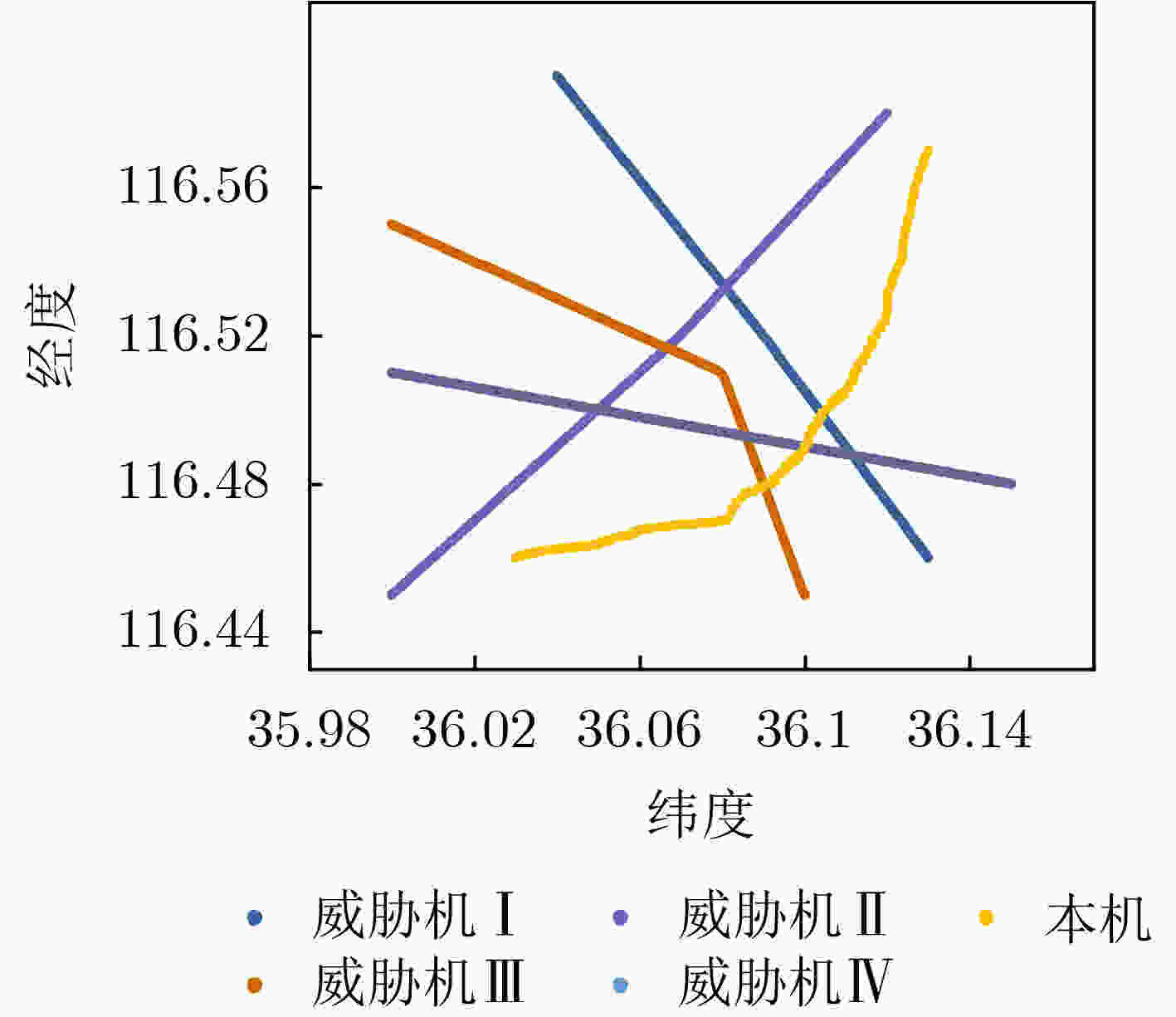
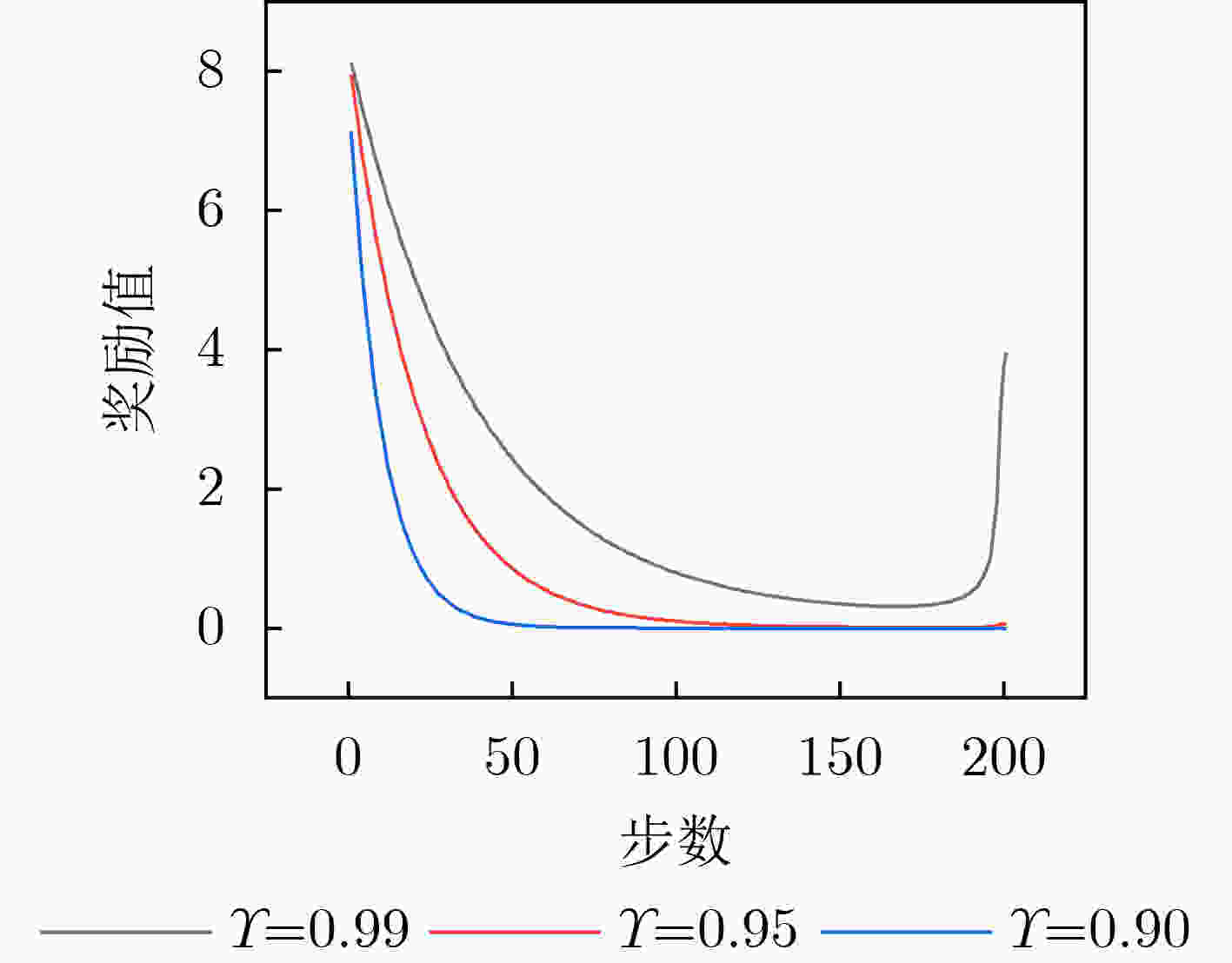
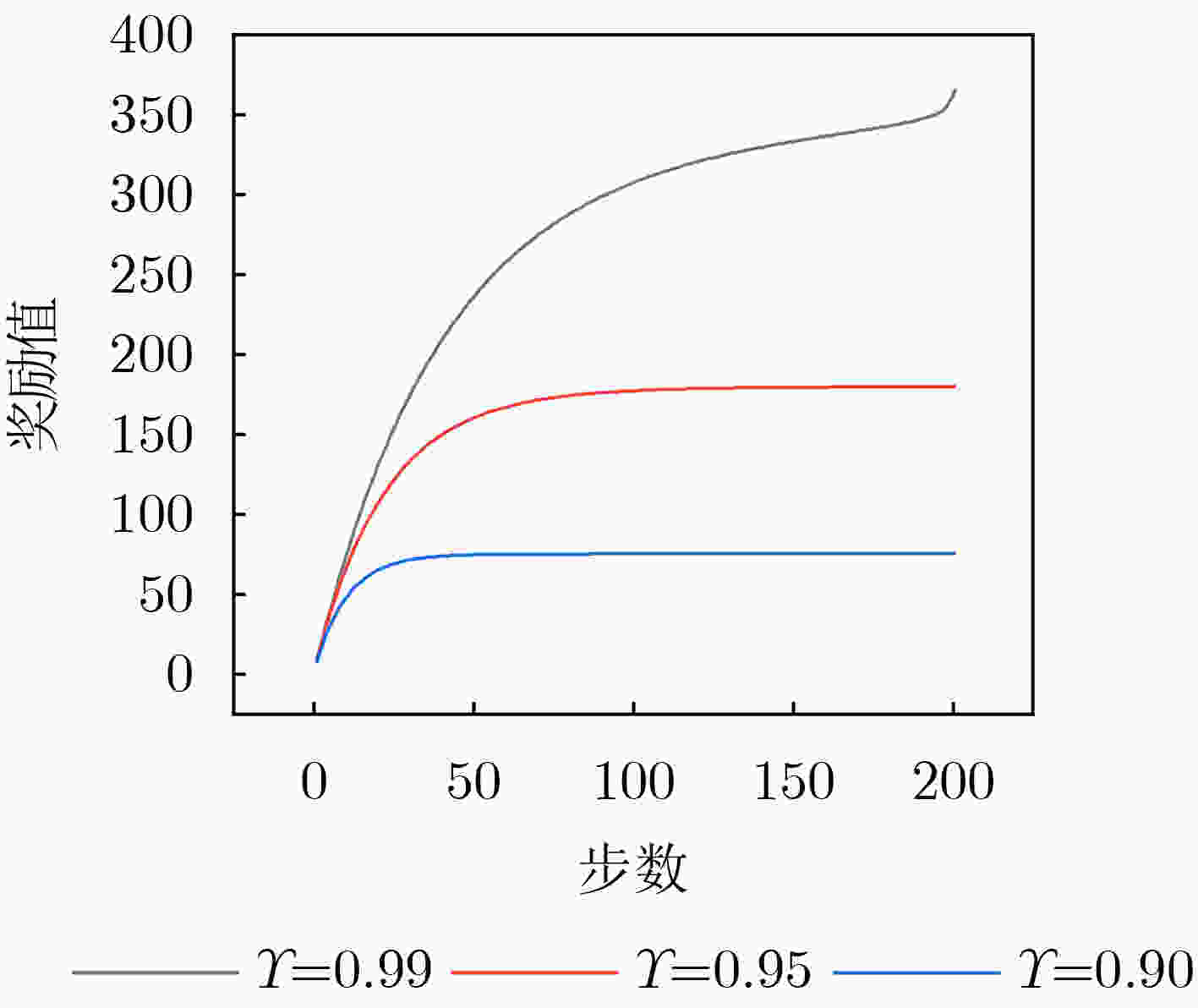
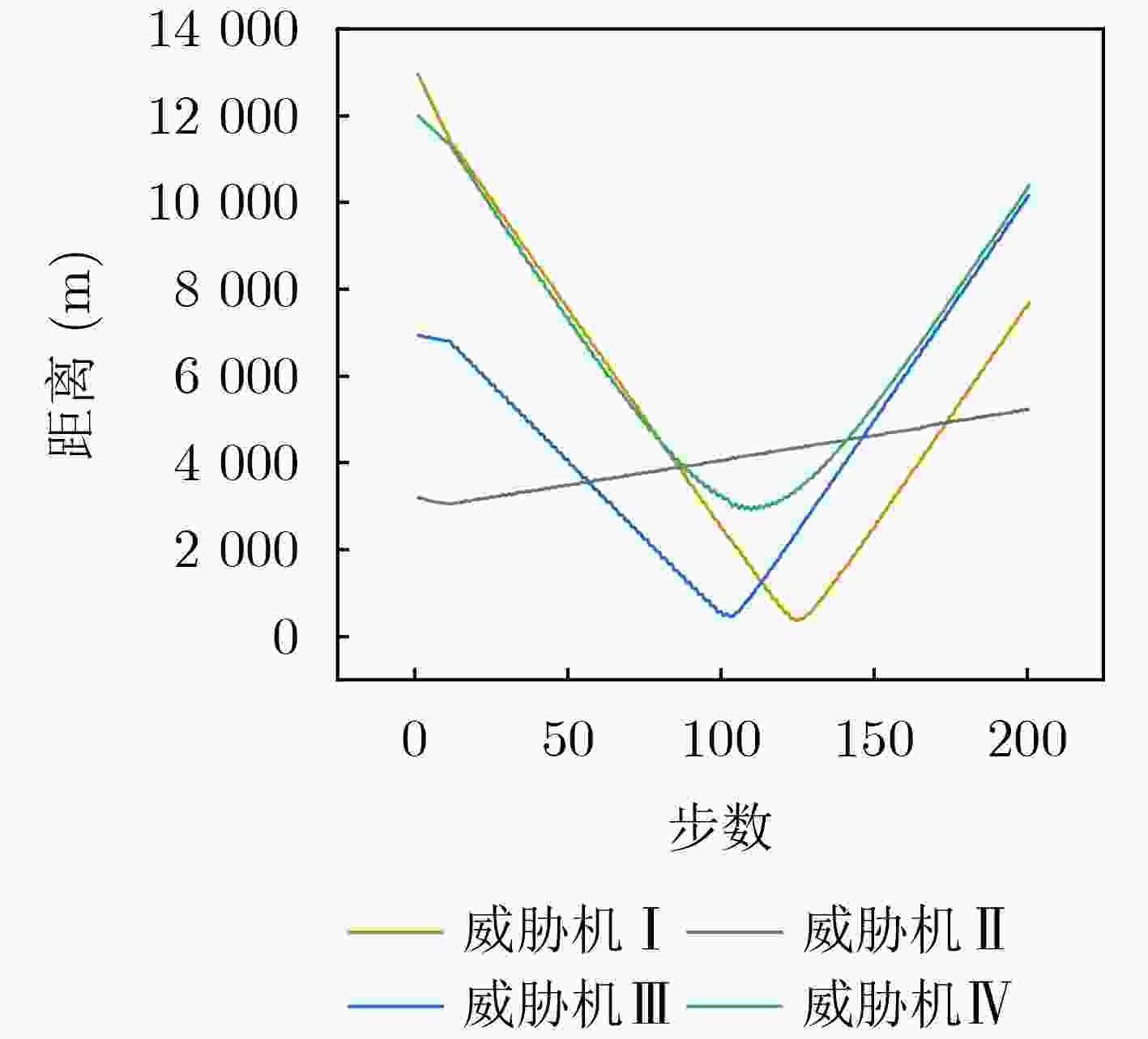
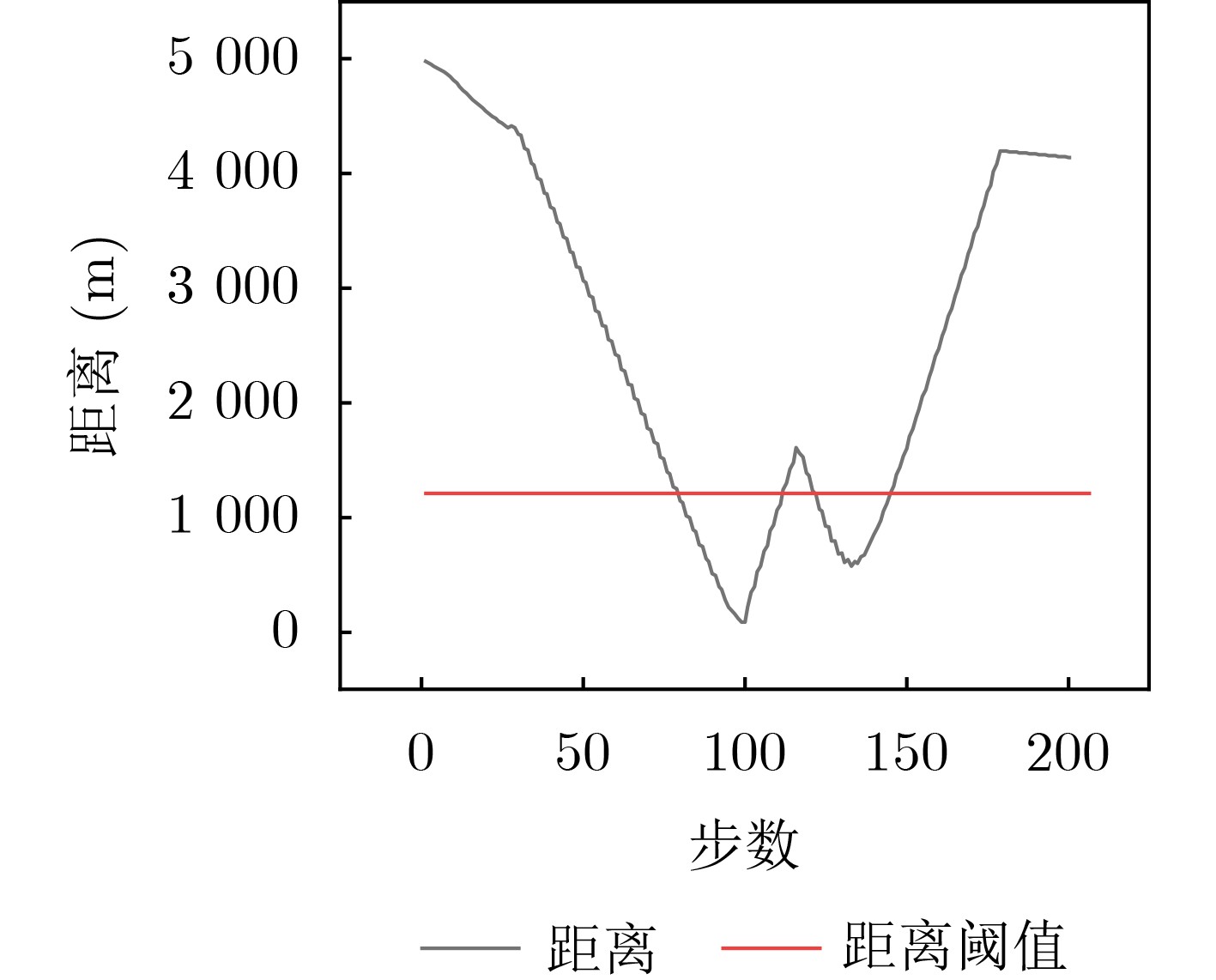
Objective With the rapid increase in UAV numbers and the growing complexity of airspace environments, Detect-and-Avoid (DAA) technology has become essential for ensuring airspace safety. However, the existing Detection and Avoidance Alerting Logic for Unmanned Aircraft Systems (DAIDALUS) algorithm, while capable of providing basic avoidance strategies, has limitations in handling multi-aircraft conflicts and adapting to dynamic, complex environments. To address these challenges, integrating the DAIDALUS output strategies into the action space of a Markov Decision Process (MDP) model has emerged as a promising approach. By incorporating an MDP framework and designing effective reward functions, it is possible to enhance the efficiency and cost-effectiveness of avoidance strategies while maintaining airspace safety, thereby better meeting the needs of complex airspaces. This research offers an intelligent solution for UAV avoidance in multi-aircraft cooperative environments and provides theoretical support for the coordinated management of shared airspace between UAVs and manned aircraft. Methods The guidance logic of the DAIDALUS algorithm dynamically calculates the UAV’s collision avoidance strategy based on the current state space. These strategies are then used as the action space in an MDP model to achieve autonomous collision avoidance in complex flight environments. The state space in the MDP model includes parameters such as the UAV's position, speed, and heading angle, along with dynamic factors like the relative position and speed of other aircraft or potential threats. The reward function is crucial for ensuring the UAV balances flight efficiency and safety during collision avoidance. It accounts for factors such as success rewards, collision penalties, proximity to target point rewards, and distance penalties to optimize decision-making. Additionally, the discount factor determines the weight of future rewards, balancing the importance of immediate versus future rewards. A lower discount factor typically emphasizes immediate rewards, leading to faster avoidance actions, while a higher discount factor encourages long-term flight safety and resource consumption. Results and Discussions The DAIDALUS algorithm calculates the UAV’s collision avoidance strategy based on the current state space, which then serves as the action space in the MDP model. By defining an appropriate reward function and state transition probabilities, the MDP model is established to explore the impact of different discount factors on collision avoidance. Simulation results show that the optimal flight strategy, calculated through value iteration, is represented by the red trajectory ( Fig. 7 ). The UAV completes its flight in 203 steps, while the comparative experiment trajectory (Fig. 8 ) consists of 279 steps, demonstrating a 27.2% improvement in efficiency. When the discount factor is set to 0.99 (Fig. 9 ,Fig. 10 ), the UAV selects a path that balances immediate and long-term safety, effectively avoiding potential collision risks. The airspace intrusion rate is 5.8% (Fig. 11 ,Fig. 12 ), with the closest distance between the threat aircraft and the UAV being 343 meters, which meets the safety requirements for UAV operations.Conclusions This paper addresses the challenge of UAV collision avoidance in complex environments by integrating the DAIDALUS algorithm with a Markov Decision Process model. The proposed decision-making method enhances the DAIDALUS algorithm by using its guidance strategies as the action space in the MDP. The method is evaluated through multi-aircraft conflict simulations, and the results show that: (1) The proposed method improves efficiency by 27.2% over the DAIDALUS algorithm; (2) Long-term and short-term rewards are considered by selecting a discount factor of 0.99 based on the relationship between the discount factor and reward values at each time step; (3) In multi-aircraft conflict scenarios, the UAV effectively handles various conflicts and maintains a safe distance from threat aircraft, with a clear airspace intrusion rate of only 5.8%. However, this study only considers ideal perception capabilities, and real-world flight conditions, including sensor noise and environmental variability, should be accounted for in future work. -
Key words:
- UAV systems /
- Detect and Avoid (DAA) /
- Markov Decision Process (MDP) /
- Reward function
-
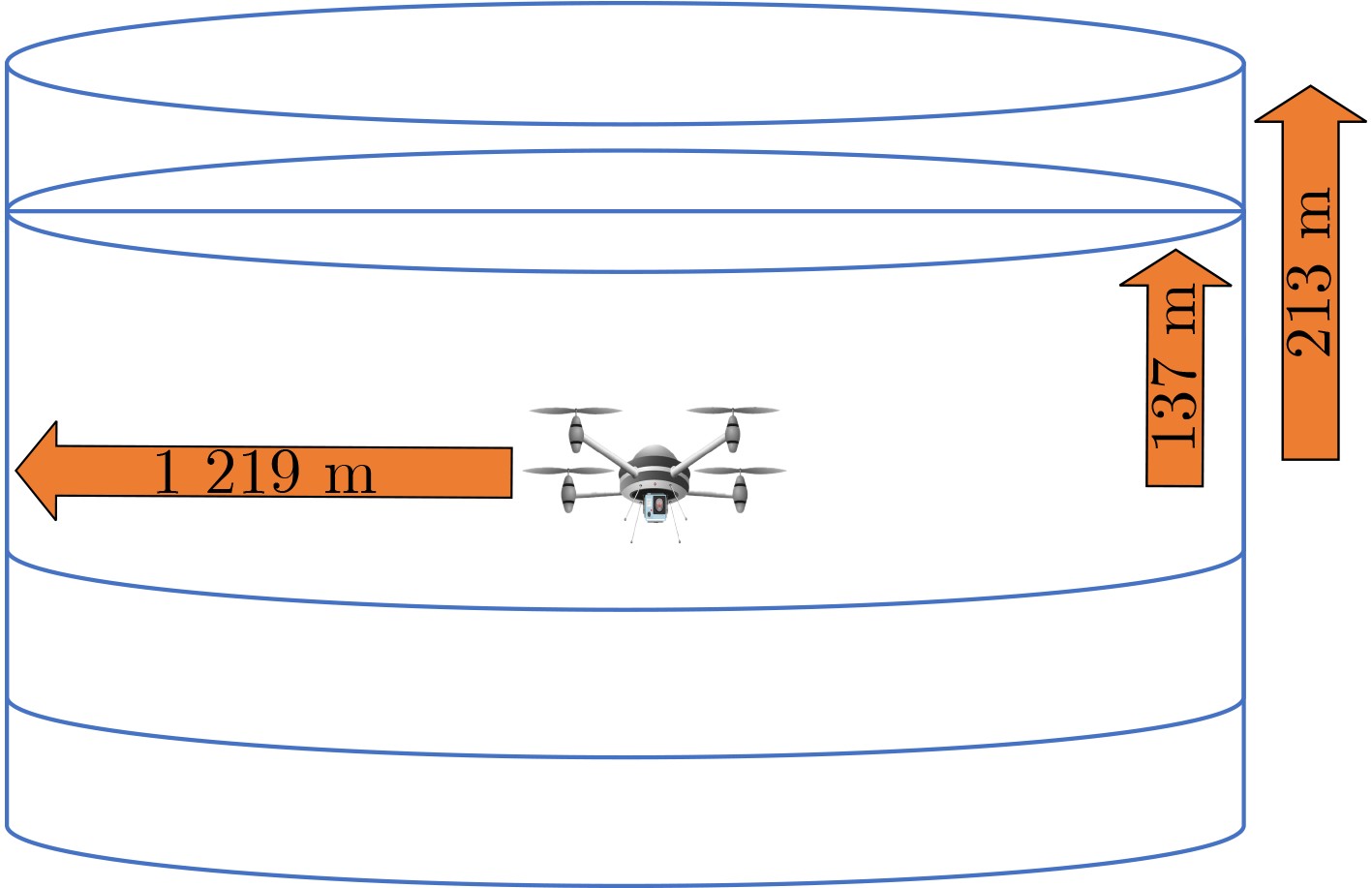
表 1 警报参数表
警报级别 水平分离距离(m) 垂直分离距离(m) 平均警报时间(s) 无告警 > 1219 >213 >55 预防级 1219 213 55 纠正级 1219 137 55 警报级 1219 137 25 表 2 规避策略-无人机动作集合映射表
DAIDALUS规避策略 无人机动作 改变航向 - 向左转 左移 改变航向 - 向右转 右移 改变高度 - 上升 上升 改变高度 - 下降 下降 改变速度 – 加速 前进加速 改变速度 – 减速 前进减速 表 3 飞行轨迹设计表
无人机 飞行航路点 飞行高度(m) UAV0 36.03,116.46;36.13,116.57 UAV1 36.04,116.59;36.09,116.52; 36.13,116.46; 200 UAV2 36,116.45;36.07,116.5; 36.12,116.58; 180 UAV3 36.10,116.45;36.08,116.51; 36,116.55; 220 UAV4 36.15,116.48;36.05,116.5; 36.00,116.51; 200 表 4 参数设计表
参数名称 参数值 3维状态空间离散化宽度 100 m, 100 m, 100 m 状态转移概率 0.05, 1–0.05($k$–1) 训练成功奖励系数 20 碰撞惩罚系数 20 距离惩罚系数 0.1 靠近目标点奖励系数 1 折扣因子 0.98, 0.95, 0.9 -
[1] DIEZ-TOMILLO J, ALCARAZ-CALERO J M, and WANG Qi. Face verification algorithms for UAV applications: An empirical comparative analysis[J]. Journal of Communications Software and Systems, 2024, 20(1): 1–12. doi: 10.24138/JCOMSS-2023-0165. [2] OMERI M, ISUFAJ R, and ORTIZ R M. Quantifying well clear for autonomous small UAS[J]. IEEE Access, 2022, 10: 68365–68383. doi: 10.1109/ACCESS.2022.3186025. [3] KURU K, PINDER J M, JON WATKINSON B, et al. Toward mid-air collision-free trajectory for autonomous and pilot-controlled unmanned aerial vehicles[J]. IEEE Access, 2023, 11: 100323–100342. doi: 10.1109/ACCESS.2023.3314504. [4] INCE B, MARTINEZ V C, SELVAM P K, et al. Sense and avoid considerations for safe sUAS operations in urban environments[J]. IEEE Aerospace and Electronic Systems Magazine, 2024, 5(7): 1–16. doi: 10.1109/MAES.2024.3397269. [5] LEE S, WU M G, and CONE A C. Evaluating noncooperative detect-and-avoid well clear definitions with alerting performance and surveillance requirement[J]. Journal of Air Transportation, 2021, 29(4): 171–183. doi: 10.2514/1.D0246. [6] RTCA. RTCA DO-365B Minimum Operational Performance Standards (MOPS) for detect and avoid (DAA) systems[S]. Washington: RTCA, 2021. [7] BERNARDES FERNANDES FERREIRA N, MOSCATO M, TITOLO L, et al. A provably correct floating-point implementation of well clear avionics concepts[C]. The 23rd Conference on Formal Methods in Computer-Aided Design, Wien, Austria, 2023: 37–46. doi: 10.34727/2023/isbn.978-3-85448-060-0_32. [8] RYU J Y, LEE H, and LEE H T. Detect and avoid AI system model using a deep neural network[C]. 2022 IEEE/AIAA 41st Digital Avionics Systems Conference, Portsmouth, USA, 2022: 1–8. doi: 10.1109/DASC55683.2022.9925767. [9] 高雅琪. 无人机系统中DAA模块的研究和设计实现[D]. [硕士论文], 电子科技大学, 2022. doi: 10.27005/d.cnki.gdzku.2022.003399.GAO Yaqi. Research design and implementation on DAA module of UAV system[D]. [Master dissertation], University of Electronic Science and Technology of China, 2022. doi: 10.27005/d.cnki.gdzku.2022.003399. [10] DE OLIVEIRA Í R, MATSUMOTO T, MAYNE A, et al. Analyzing the closed-loop performance of detect-and-avoid systems[C]. 2023 IEEE 26th International Conference on Intelligent Transportation Systems, Bilbao, Spain, 2023: 4947–4952. doi: 10.1109/ITSC57777.2023.10422365. [11] 赵柠霄. 无人机探测与避撞系统告警和引导逻辑的研究[D]. [硕士论文], 电子科技大学, 2023. doi: 10.27005/d.cnki.gdzku.2023.005879.ZHAO Ningxiao. Research on warning and guidance logic in detect and avoid of UAV[D]. [Master dissertation], University of Electronic Science and Technology of China, 2023. doi: 10.27005/d.cnki.gdzku.2023.005879. [12] LIU Haotian, JIN Jiangfeng, LIU Kun, et al. Research on UAV air combat maneuver decision based on decision tree CART algorithm[M]. FU Wenxing, GU Mancang, and NIU Yifeng. Proceedings of 2022 International Conference on Autonomous Unmanned Systems (ICAUS 2022). Singapore, Singapore: Springer, 2023: 2638–2650. doi: 10.1007/978-981-99-0479-2_243. [13] HU Shiguang, RU Le, LV Maolong, et al. Evolutionary game analysis of behaviour strategy for UAV swarm in communication-constrained environments[J]. IET Control Theory & Applications, 2024, 18(3): 350–363. doi: 10.1049/cth2.12602. [14] CHANG Zheng, DENG Hengwei, YOU Li, et al. Trajectory design and resource allocation for multi-UAV networks: Deep reinforcement learning approaches[J]. IEEE Transactions on Network Science and Engineering, 2023, 10(5): 2940–2951. doi: 10.1109/TNSE.2022.3171600. [15] SHEN Yang, WANG Xianbing, WANG Huajun, et al. A dynamic task assignment model for aviation emergency rescue based on multi-agent reinforcement learning[J]. Journal of Safety Science and Resilience, 2023, 4(3): 284–293. doi: 10.1016/J.JNLSSR.2023.06.001. [16] KATZ S M, ALVAREZ L E, OWEN M, et al. Collision risk and operational impact of speed change advisories as aircraft collision avoidance maneuvers[C]. The AIAA AVIATION 2022 Forum, Chicago, USA, 2022: 3824. doi: 10.2514/6.2022-3824. [17] 王允钊. 机载防撞系统ACAS X中TRM模块的设计与实现[D]. [硕士论文], 电子科技大学, 2021.WANG Yunzhao. Design and implementation of TRM module in airborne collision avoidance system X[D]. [Master dissertation], University of Electronic Science and Technology of China, 2021. [18] HE Donglin, YANG Youzhi, DENG Shengji, et al. Comparison of collision avoidance logic between ACAS X and TCAS II in general aviation flight[C]. 2023 IEEE 5th International Conference on Civil Aviation Safety and Information Technology, Dali, China, 2023: 568–573. doi: 10.1109/ICCASIT58768.2023.10351533. [19] RUBÍ B, MORCEGO B, and PÉREZ R. Quadrotor path following and reactive obstacle avoidance with deep reinforcement learning[J]. Journal of Intelligent & Robotic Systems, 2021, 103(4): 62. doi: 10.1007/s10846-021-01491-2. [20] KATZ S M, JULIAN K D, STRONG C A, et al. Generating probabilistic safety guarantees for neural network controllers[J]. Machine Learning, 2023, 112(8): 2903–2931. doi: 10.1007/s10994-021-06065-9. [21] MOON C and AHN J. Markov decision process-based potential field technique for UAV planning[J]. Journal of the Korean Society for Industrial and Applied Mathematics, 2021, 25(4): 149–161. doi: 10.12941/jksiam.2021.25.149. [22] LI Ming, BAI He, and KRISHNAMURTHI N. A Markov decision process for the interaction between autonomous collision avoidance and delayed pilot commands[J]. IFAC-PapersOnLine, 2019, 51(34): 378–383. doi: 10.1016/j.ifacol.2019.01.012. -





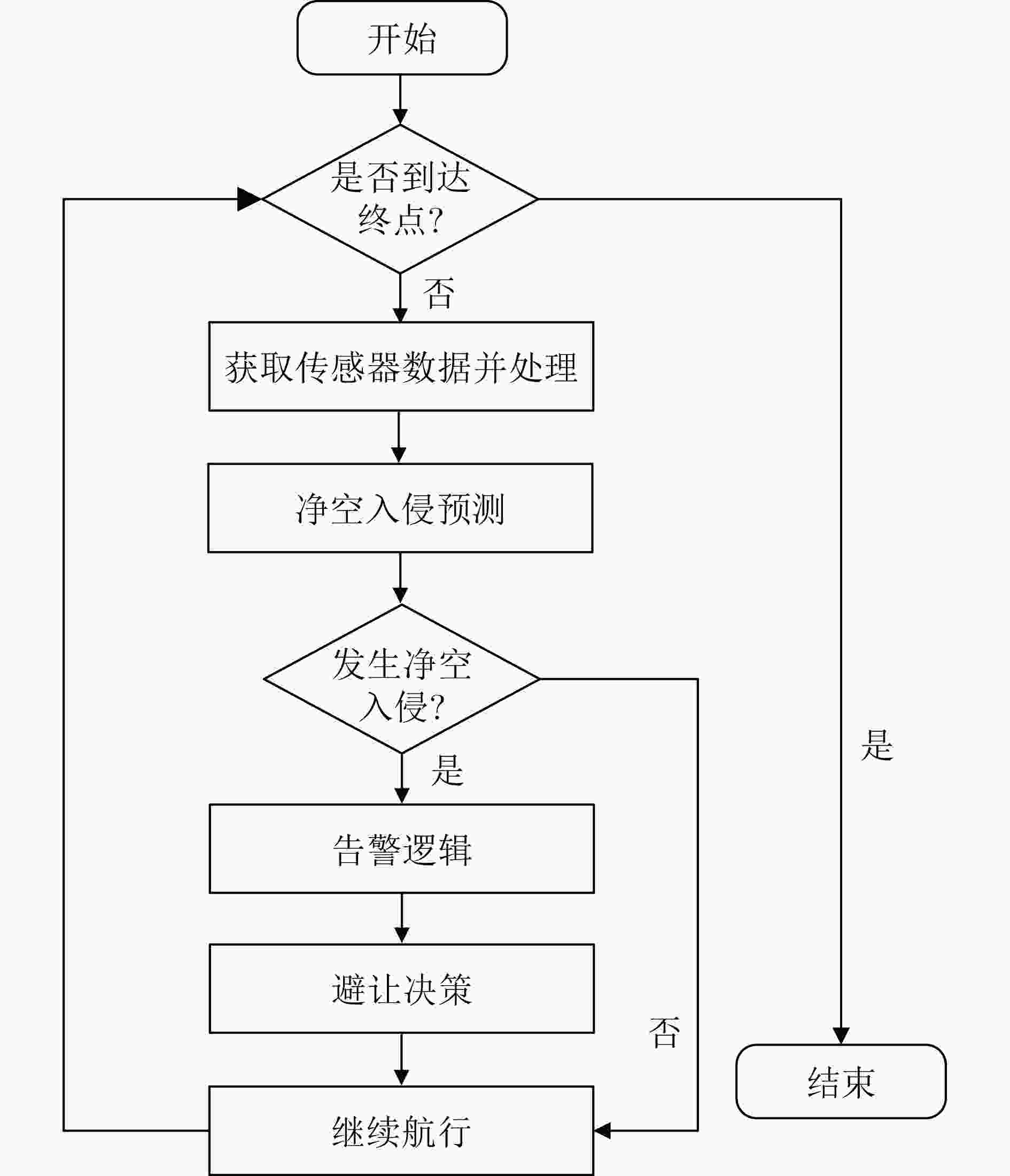
 下载:
下载:
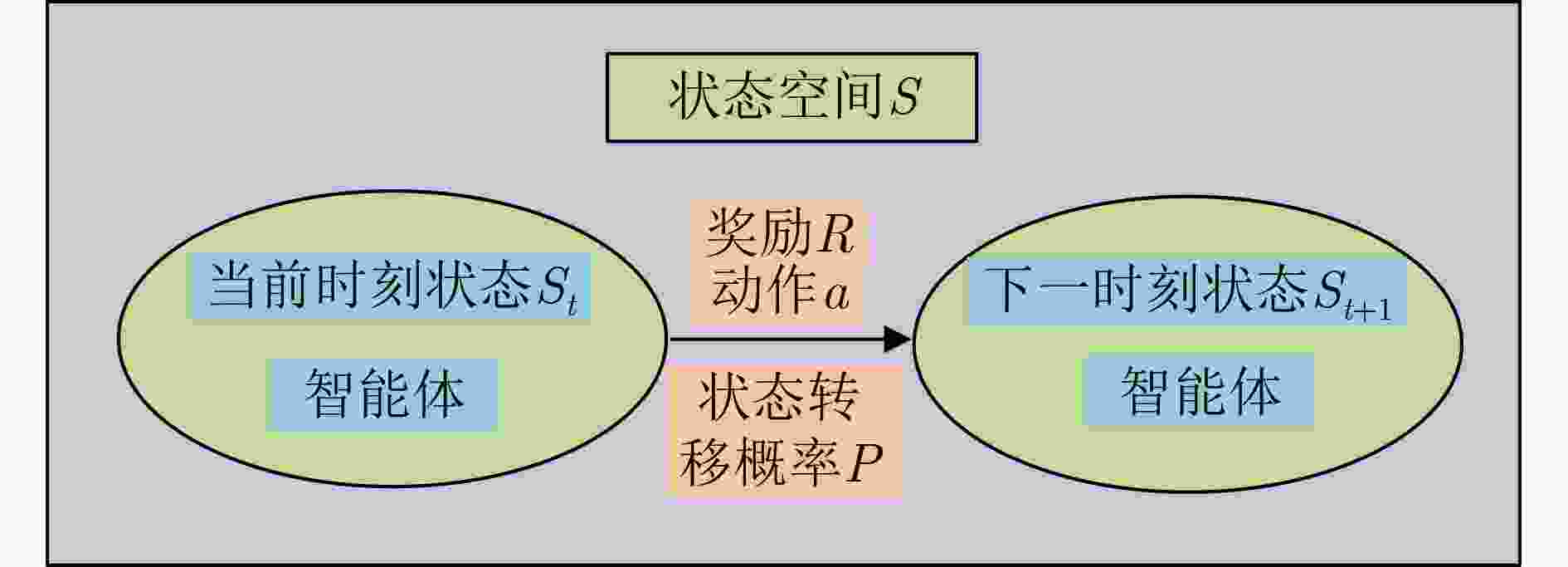

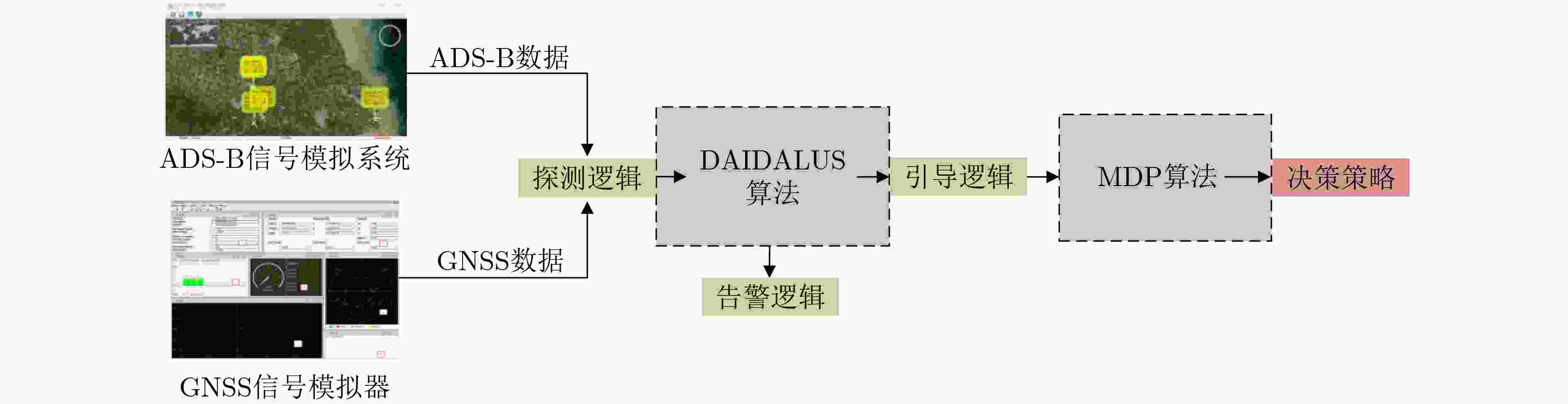


 下载:
下载:
