频移Chirp信号短包的自适应分数傅里叶变换检测方法

修梦雷; 窦高奇; 冯士民

doi:10.11999/JEIT240370

频移Chirp信号短包的自适应分数傅里叶变换检测方法

doi: 10.11999/JEIT240370

海军工程大学电子工程学院武汉 430033

基金项目: 国家自然科学基金(61871473)，海军工程大学自主研发计划(2023503090)

详细信息

作者简介:
修梦雷：男，博士生，研究方向为无线通信系统

窦高奇：男，教授，研究方向为无线通信理论与技术

冯士民：男，副教授，研究方向为无线通信系统

通讯作者:
窦高奇　hjgcqq@163.com

中图分类号: TN92
计量
- 文章访问数: 83
- HTML全文浏览量: 21
- PDF下载量: 12
- 被引次数: 0
出版历程
- 收稿日期: 2024-05-09
- 修回日期: 2024-11-26
- 网络出版日期: 2024-11-30

Adaptive Fractional Fourier Transform Detection Method for Short Packets of Frequency-shifted Chirp Signal

School of Electronic Engineering, Naval University of Engineering, Wuhan 430033, China

Funds: The National Natural Science Foundation of China (61871473), The Naval Engineering University’s Independent Research and Development Program Project (2023503090)

摘要

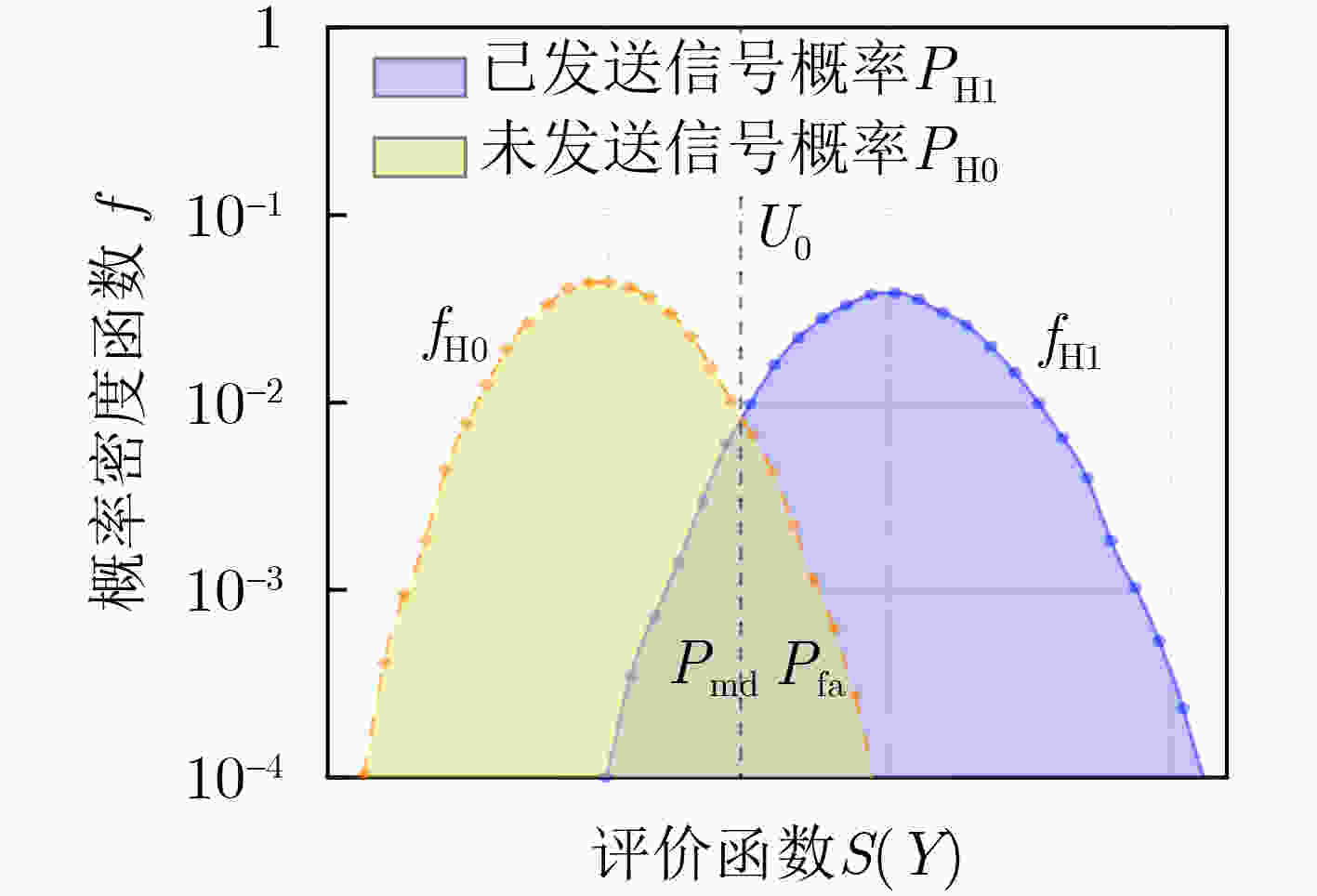
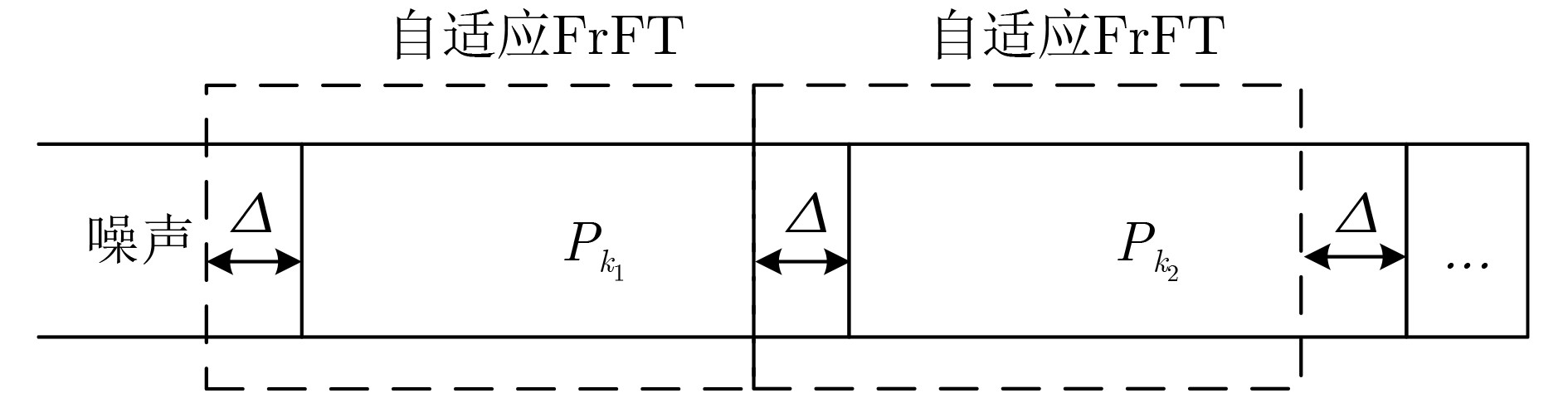
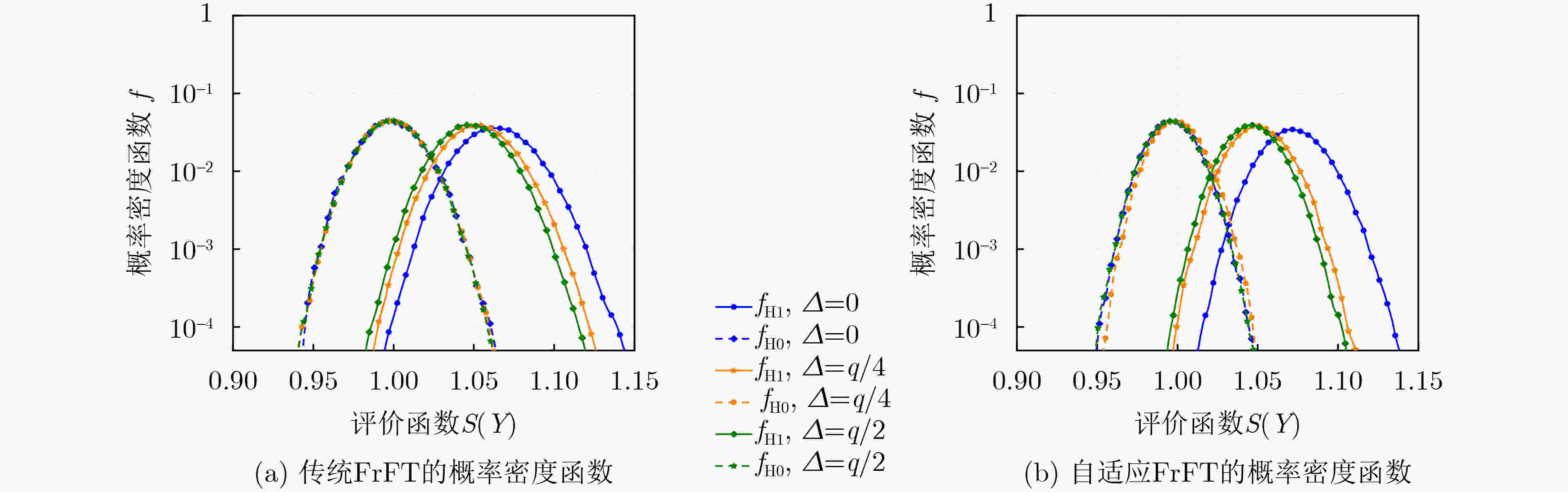
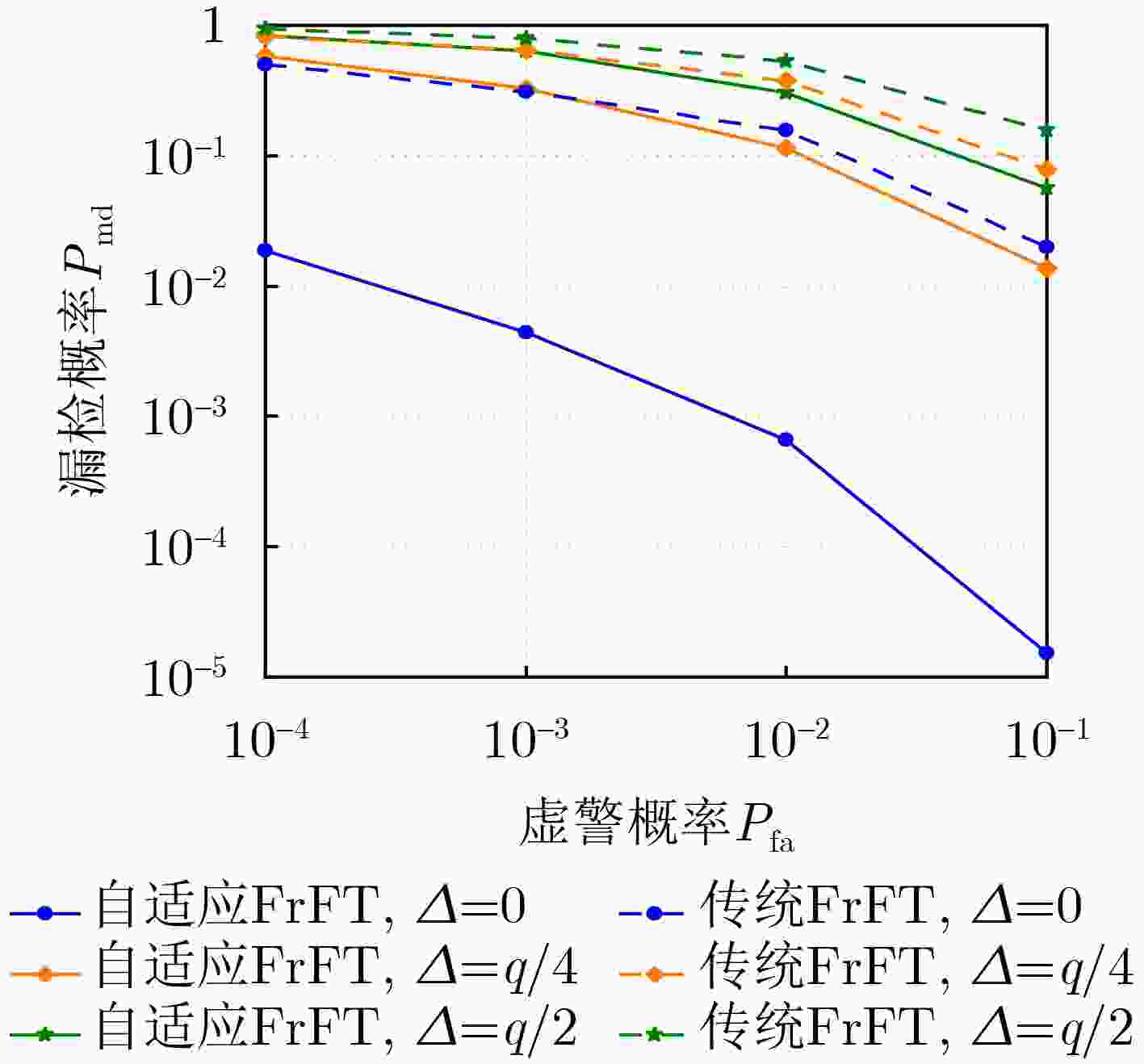
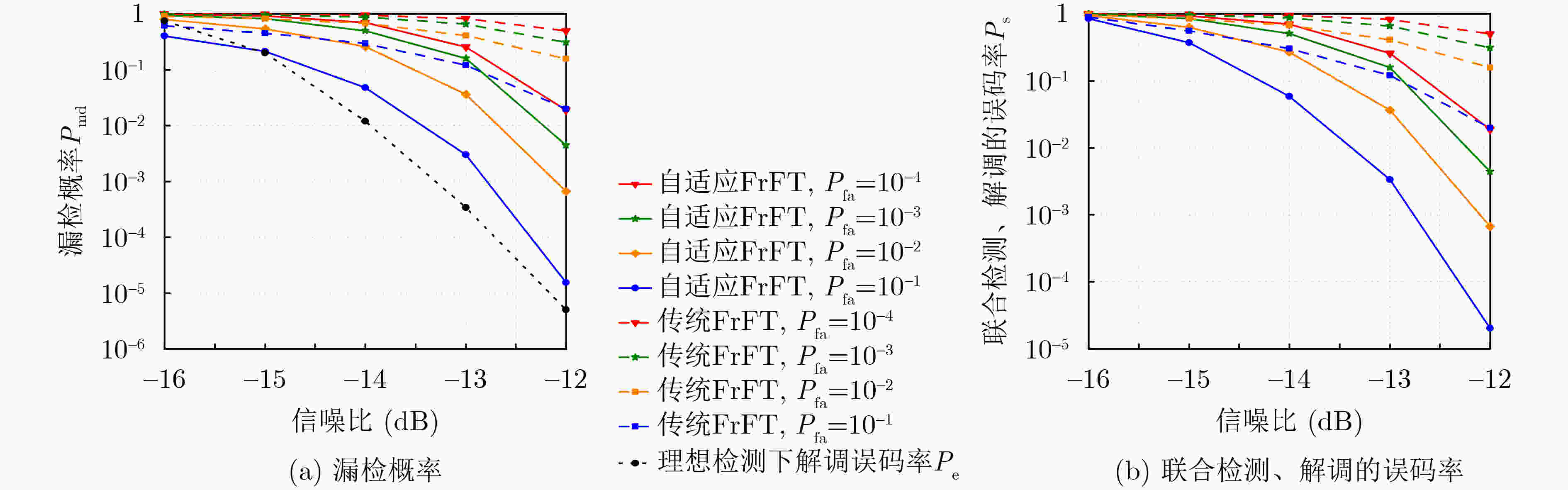
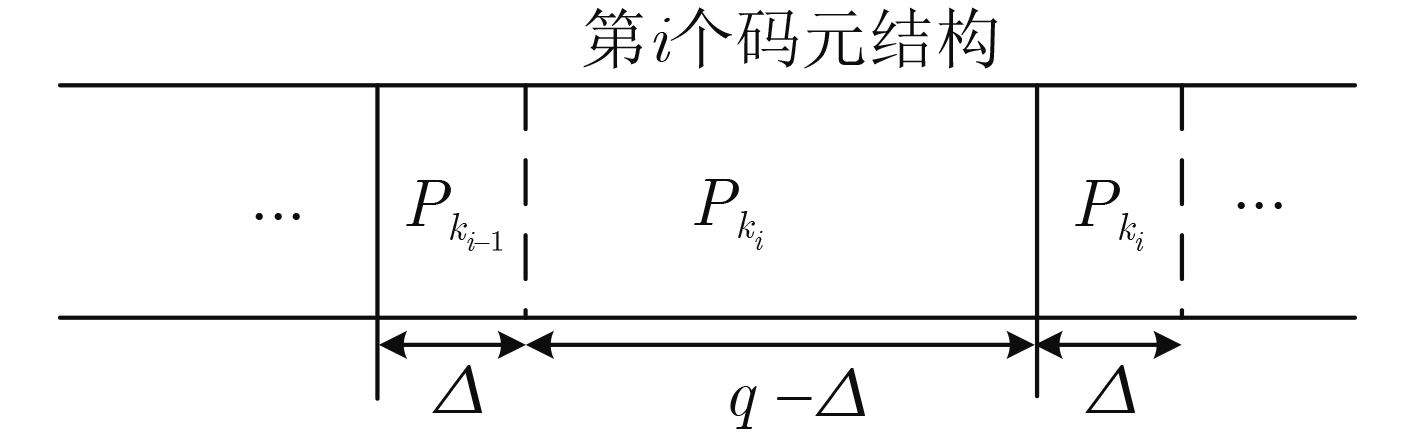
摘要: 为解决传统分数傅里叶变换(FrFT)在检测频移Chirp信号时脉冲分散问题，该文提出一种自适应FrFT的检测方法。该方法基于短包的结构模型以及Neyman-Pearson检测模型，引出了借助评价函数和判定阈值对信号帧检测的虚警概率和漏检概率的分析方法。结合传统FrFT对完整Chirp信号的脉冲特性，给出了对分数傅里叶积分算子的修正方案，推导出自适应FrFT对频移Chirp码元的峰值分布函数。针对自适应FrFT检测过程存在搜索时移问题，分析了该情况下频移Chirp码元峰值大小及分布情况，证明了相比于传统FrFT，自适应FrFT检测捕获无前导短数据包的性能更加优越。
- 短包 /
- 频移Chirp信号 /
- 自适应分数傅里叶变换 /
- 帧检测性能
Abstract: To address the pulse dispersion issue in detecting frequency-shifted chirp signals with traditional Fractional Fourier Transform (FrFT), an adaptive FrFT detection method is proposed in this paper. Leveraging the structural model of short packets and the Neyman-Pearson detection model, an analytical method is derived to evaluate the false alarm probability and missed detection probability of signal frame detection using an evaluation function and a decision threshold. Incorporating the pulse characteristics of traditional FrFT for complete chirp signals, a correction scheme for the fractional Fourier integral operator is proposed, and the peak distribution function of the frequency-shifted chirp symbol is derived for the adaptive FrFT. Addressing the search time shift issue in the adaptive FrFT detection process, the peak size and distribution of the frequency-shifted chirp symbol are analyzed, and the superiority of the adaptive FrFT detection compared to traditional FrFT is demonstrated.
- Short packet /
- Frequency-shifted chirp signal /
- Adaptive Fractional Fourier Transform (FrFT) /
- Frame detection performance

HTML全文

图 1 短数据包构成及Chirp码元频率移位示意图

下载: 全尺寸图片幻灯片

图 2 虚警概率和漏检概率、概率密度函数与判断阈值的关系

下载: 全尺寸图片幻灯片

图 3 时间偏移$ \varDelta $时自适应FrFT的检测示意图

下载: 全尺寸图片幻灯片

图 4 传统FrFT及自适应FrFT对频移Chirp信号帧检测性能对比

下载: 全尺寸图片幻灯片

图 5 –12 dB下漏检概率随虚警概率的变化曲线

下载: 全尺寸图片幻灯片

图 6 给定虚警概率时低信噪比下[–16 dB，–12 dB]的错误概率

下载: 全尺寸图片幻灯片

图 7 第2～N个码元结构分布

下载: 全尺寸图片幻灯片

表 1 频移调制技术调制原理

频移量	码元表示	频移段排列状态
0	P₀	{s₁, s₂, s₃,···, s_q–2, s_q–1, s_q}
1	P₁	{s_q, s₁, s₂, s₃,···, s_q–2, s_q–1}
2	P₂	{s_q–1, s_q, s₁, s₂, s₃,···, s_q–2}
$\vdots $	$\vdots $	$\vdots $
q–2	P_q–2	{s₃,…, s_q–2, s_q–1, s_q, s₁, s₂}
q–1	P_q–1	{s₂, s₃,···, s_q–2, s_q–1, s_q, s₁}

下载: 导出CSV

表 2 系统仿真参数设定

参数名称	符号表示	参数取值
信号帧长度	N	64
扩频因子	SF	6
循环段数	q	64
循环段数持续时间	T_c	10 ms
Chirp码元持续时间	T_s	640 ms
初始频率	f₀	50 Hz
离散调频率	$\mu $	1
带宽	B_s	100 Hz
采样率	f_s	100 Hz

下载: 导出CSV

参考文献(23)

[1]	NOURA M, ATIQUZZAMAN M, and GAEDKE M. Interoperability in internet of things: Taxonomies and open challenges[J]. Mobile Networks and Applications, 2019, 24(3): 796–809. doi: 10.1007/s11036-018-1089-9.
[2]	SOBIN C C. A survey on architecture, protocols and challenges in IoT[J]. Wireless Personal Communications, 2020, 112(3): 1383–1429. doi: 10.1007/s11277-020-07108-5.
[3]	SON P N, DUY T T, TUAN P V, et al. Short packet communication in underlay cognitive network assisted by an intelligent reflecting surface[J]. ETRI Journal, 2023, 45(1): 28–44. doi: 10.4218/ETRIJ.2021-0435.
[4]	HUANG Lei, ZHAO Xiaoyu, CHEN Wei, et al. Low-latency short-packet transmission over a large spatial scale[J]. Entropy, 2021, 23(7): 916. doi: 10.3390/E23070916.
[5]	LU Xingbo, YANG Weiwei, and YAN Shihao. Short-packet covert communication with transmission time uncertainty[C]. 2022 7th International Conference on Computer and Communication Systems (ICCCS), Wuhan, China, 2022: 628–632. doi: 10.1109/ICCCS55155.2022.9846514.
[6]	ZHANG Yanfeng, ZHU Xu, LIU Yujie, et al. Sparse superimposed vector transmission for short-packet high-mobility communication[J]. IEEE Wireless Communications Letters, 2023, 12(11): 1961–1965. doi: 10.1109/LWC.2023.3303234.
[7]	韩书君, 吕素玉, 许晓东, 等. RIS辅助的短包通信系统时延与安全性能分析[J]. 北京邮电大学学报, 2022, 45(6): 68–74. doi: 10.13190/j.jbupt.2022-131. HAN Shujun, LYU Suyu, XU Xiaodong, et al. Delay and security performance analysis in RIS assisted short packet communication system[J]. Journal of Beijing University of Posts and Telecommunications, 2022, 45(6): 68–74. doi: 10.13190/j.jbupt.2022-131.
[8]	DURISI G, KOCH T, and POPOVSKI P. Toward massive, ultrareliable, and low-latency wireless communication with short packets[J]. Proceedings of the IEEE, 2016, 104(9): 1711–1726. doi: 10.1109/JPROC.2016.2537298.
[9]	MOOUSAEI M and SMIDA B. Optimizing pilot overhead for ultra-reliable short-packet transmission[C]. 2017 IEEE International Conference on Communications (ICC), Paris, France, 2017: 1–5. doi: 10.1109/ICC.2017.7996416.
[10]	甘泉. LoRa物联网通信技术[M]. 北京: 清华大学出版社, 2021: 95–96. GAN Quan. LoRa IoT Communication Technology[M]. Beijing, China: Tsinghua University Press, 2021: 95–96.
[11]	KOÇ A. Operator theory-based discrete fractional Fourier transform[J]. Signal, Image and Video Processing, 2019, 13(7): 1461–1468. doi: 10.1007/s11760-019-01553-x.
[12]	ALMEIDA L B. The fractional Fourier transform and time-frequency representations[J]. IEEE Transactions on Signal Processing, 1994, 42(11): 3084–3091. doi: 10.1109/78.330368.
[13]	GRETINGER M, SECARA M, FESTILA C, et al. “Chirp” signal generators for frequency response experiments[C]. 2014 IEEE International Conference on Automation, Quality and Testing, Robotics, Cluj-Napoca, Romania, 2014: 1–4. doi: 10.1109/AQTR.2014.6857860.
[14]	李诗铭. Chirp-BOK及多址通信技术研究[D]. [硕士论文], 哈尔滨工程大学, 2019. LI Shiming. The study of Chirp-BOK and its multiple access communication technologies[D]. [Master dissertation], Harbin Engineering University, 2019.
[15]	王明. 基于Chirp超宽带通信技术的研究与实现[D]. [硕士论文], 电子科技大学, 2010. WANG Ming. Research and implementation of Chirp ultra-wideband communication technology[D]. [Master dissertation], University of Electronic Science and Technology of China, 2010.
[16]	YU Linchen, CAO Jigang, CHEN Mianlong, et al. Key frame extraction scheme based on sliding window and features[J]. Peer-to-Peer Networking and Applications, 2018, 11(5): 1141–1152. doi: 10.1007/s12083-017-0567-3.
[17]	CHAUVAT R, GARCIA-PENA A, and PAONNI M. Efficient LDPC-coded CCSK links for robust high data rates GNSS[J]. IEEE Transactions on Aerospace and Electronic Systems, 2023, 59(1): 404–417. doi: 10.1109/TAES.2022.3190819.
[18]	SAIED K, GHOUWAYEL A C A, and BOUTILLON E. Short frame transmission at very low SNR by associating CCSK modulation with NB-Code[J]. IEEE Transactions on Wireless Communications, 2022, 21(9): 7194–7206. doi: 10.1109/TWC.2022.3156628.
[19]	DILLARD G M, REUTER M, ZEIDDLER J, et al. Cyclic code shift keying: a low probability of intercept communication technique[J]. IEEE Transactions on Aerospace and Electronic Systems, 2003, 39(3): 786–798. doi: 10.1109/TAES.2003.1238736.
[20]	KASSEM S. Quasi-cyclic short packet (QCSP) transmission for IoT[D]. Université Bretagne Sud, 2022.
[21]	岳佳. 基于频移Chirp调制的通信信号抗截获波形设计[D]. [硕士论文], 哈尔滨工业大学, 2021. YUE Jia. Anti-interception waveform design of communication signal based on frequency shift chirp modulation[D]. [Master dissertation], Harbin Institute of Technology, 2021.
[22]	东锦鹏, 陈世文, 杨锦程, 等. 基于FRFT的低信噪比LFM信号参数快速估计算法[J]. 指挥控制与仿真, 2024, 46(1): 71–77. doi: 10.3969/j.issn.1673-3819.2024.01.009. DONG Jinpeng, CHEN Shiwen, YANG Jincheng, et al. A fast parameter estimation algorithm for LFM signal under low SNR based on FRFT[J]. Command, Control & Simulation, 2024, 46(1): 71–77. doi: 10.3969/j.issn.1673-3819.2024.01.009.
[23]	杜欣宜. 基于FRFT频移Chirp调制的物理层安全信号设计[D]. [硕士论文], 哈尔滨工业大学, 2023. DU Xinyi. Physical layer security signal design of frequency shift Chirp modulation based on FRFT[D]. [Master dissertation], Harbin Institute of Technology, 2023.