Adversarial Autoencoders Oversampling Algorithm for Imbalanced Image Data
-
摘要: 许多适用于低维数据的传统不平衡学习算法在图像数据上的效果并不理想。基于生成对抗网络(GAN)的过采样算法虽然可以生成高质量图像,但在类不平衡情况下容易产生模式崩溃问题。基于自编码器(AE)的过采样算法容易训练,但生成的图像质量较低。为进一步提高过采样算法在不平衡图像中生成样本的质量和训练的稳定性,该文基于生成对抗网络和自编码器的思想提出一种融合自编码器和生成对抗网络的过采样算法(BAEGAN)。首先在自编码器中引入一个条件嵌入层,使用预训练的条件自编码器初始化GAN以稳定模型训练;然后改进判别器的输出结构,引入一种融合焦点损失和梯度惩罚的损失函数以减轻类不平衡的影响;最后从潜在向量的分布映射中使用合成少数类过采样技术(SMOTE)来生成高质量的图像。在4个图像数据集上的实验结果表明该算法在生成图像质量和过采样后的分类性能上优于具有辅助分类器的条件生成对抗网络(ACGAN)、平衡生成对抗网络 (BAGAN)等过采样算法,能有效解决图像数据中的类不平衡问题。
-
关键词:
- 不平衡图像数据 /
- 过采样 /
- 生成对抗网络 /
- 对抗自编码器 /
- 合成少数类过采样技术
Abstract: Many traditional imbalanced learning algorithms suitable for low-dimensional data do not perform well on image data. Although the oversampling algorithm based on Generative Adversarial Networks (GAN) can generate high-quality images, it is prone to mode collapse in the case of class imbalance. Oversampling algorithms based on AutoEncoders (AE) are easy to train, but the generated images are of lower quality. In order to improve the quality of samples generated by the oversampling algorithm in imbalanced images and the stability of training, a Balanced oversampling method with AutoEncoders and Generative Adversarial Networks (BAEGAN) is proposed in this paper, which is based on the idea of GAN and AE. First, a conditional embedding layer is introduced in the Autoencoder, and the pre-trained conditional Autoencoder is used to initialize the GAN to stabilize the model training; then the output structure of the discriminator is improved, and a loss function that combines Focal Loss and gradient penalty is proposed to alleviate the impact of class imbalance; and finally the Synthetic Minority Oversampling TEchnique (SMOTE) is used to generate high-quality images from the distribution map of latent vectors. Experimental results on four image data sets show that the proposed algorithm is superior to oversampling methods such as Auxiliary Classifier Generative Adversarial Networks (ACGAN) and BAlancing Generative Adversarial Networks (BAGAN) in terms of image quality and classification performance after oversampling and can effectively solve the class imbalance problem in image data. -
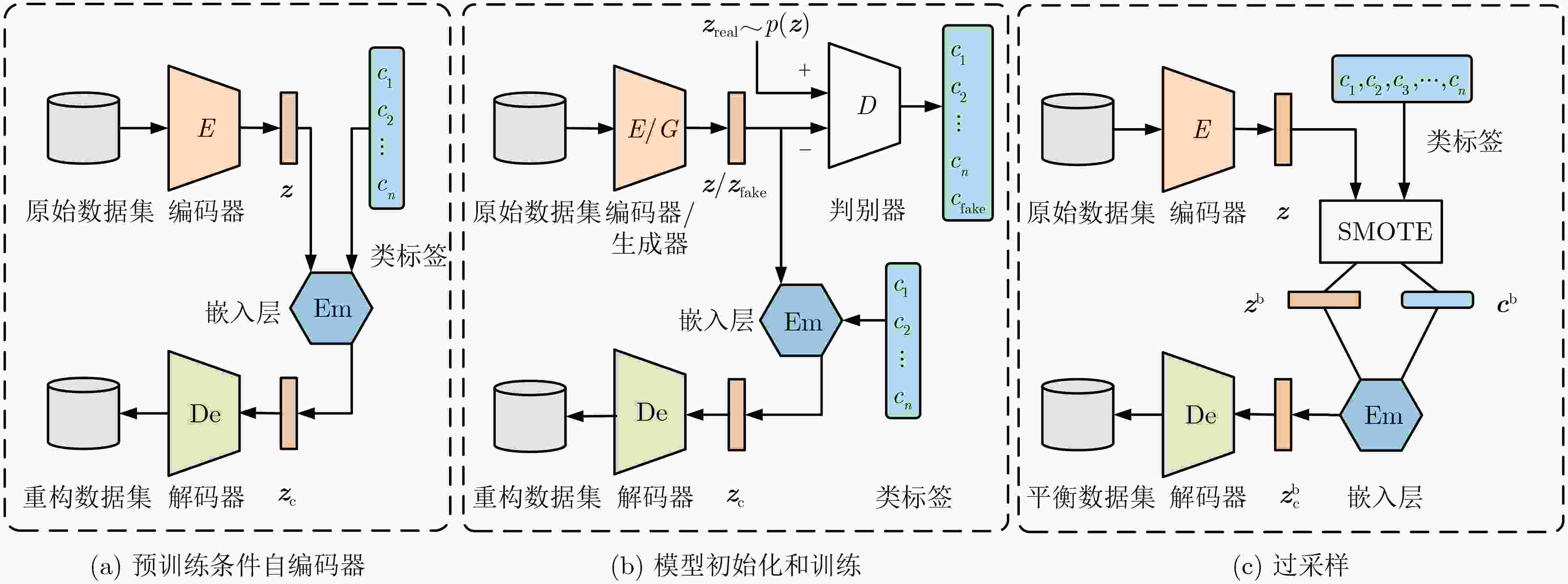
1 BAEGAN算法描述
输入:从不平衡的训练集$X$中划分一批数据$B = \{ {b_1},{b_2},\cdots,$
${b_{|X|/m}}\} $;批量大小$m$;类别数量$n$;预先设定的模型超参数;
先验分布$p({\boldsymbol{z}})$;输出:平衡后的数据集${X_{\text{b}}}$ (1) (a) 初始化所有网络参数(编码器${\theta _E}$、解码器${\theta _{{\text{De}}}}$、生成器
${\theta _G}$、判别器${\theta _D}$),预训练条件自编码器:(2) WHILE预训练轮数 DO: (3) FOR 从$B$中选取一组数据$({\boldsymbol{x}},{\boldsymbol{c}})$ DO: (4) 将数据${\boldsymbol{x}}$送入编码器$E$,获得${\boldsymbol{z}}$; (5) 将${\boldsymbol{z}}$和${\boldsymbol{c}}$输入嵌入层,获得${{\boldsymbol{z}}_{\text{c}}}$; (6) 将${{\boldsymbol{z}}_{\text{c}}}$送入解码器${\text{De}}$,获得重构图像$\hat {\boldsymbol{x}}$; (7) 由式(2)计算损失,更新${\theta _E}$和${\theta _{{\text{De}}}}$。 (8) END (9) END (10) (b) 预训练的条件自编码器初始化${\theta _G}$和${\theta _{{\text{De}}}}$,训练模型: (11) WHILE 模型未收敛或未达到训练轮数 DO: (12) FOR 从$B$中选取一组数据$({\boldsymbol{x}},{\boldsymbol{c}})$ DO: (13) 将数据${\boldsymbol{x}}$送入编码器$E$中,获得${\boldsymbol{z}}$; (14) 将${\boldsymbol{z}}$和${\boldsymbol{c}}$输入嵌入层中,获得${{\boldsymbol{z}}_{\text{c}}}$; (15) 将${{\boldsymbol{z}}_{\text{c}}}$送入解码器${\text{De}}$,获得重构图像$\hat {\boldsymbol{x}}$; (16) 根据式(2)计算损失,更新${\theta _E}$和${\theta _{{\text{De}}}}$。 (17) 将${\boldsymbol{x}}$送入$G$,获得${{\boldsymbol{z}}_{{\text{fake}}}}$ ,从$p({\boldsymbol{z}})$中获得${{\boldsymbol{z}}_{{\text{real}}}}$; (18) 将${{\boldsymbol{z}}_{{\text{fake}}}}$和${{\boldsymbol{z}}_{{\text{real}}}}$输入判别器$D$,由式(4)计算判别器损失,
更新${\theta _D}$;(19) ${{\boldsymbol{z}}_{{\text{fake}}}}$送入$D$,由式(5)计算生成器损失,更新${\theta _G}$; (20) END (21) END (22) (c) 生成样本,平衡数据集: (23) WHILE 选取少数类${{c}}$中的所有样本$({{\boldsymbol{x}}_{\text{c}}},{\boldsymbol{c}})$ ,直至所有少数
类选取完毕DO:(24) 将数据${{\boldsymbol{x}}_{\mathrm{c}}}$送入$E$中,获得潜在向量${\boldsymbol{z}}$; (25) 将${\boldsymbol{z}}$和${\boldsymbol{c}}$送入SMOTE中,获得平衡后的潜在向量${{\boldsymbol{z}}^{\text{b}}}$和类
标签${{\boldsymbol{c}}^{\text{b}}}$;(26) 将${{\boldsymbol{z}}^{\text{b}}}$和${{\boldsymbol{c}}^{\text{b}}}$输入嵌入层中,获得嵌入条件的向量$ {\boldsymbol{z}}_{\text{c}}^{\text{b}} $; (27) 将$ {\boldsymbol{z}}_{\text{c}}^{\text{b}} $送入解码器${\text{De}}$,获得平衡后属于类${\text{c}}$的样本集; (28) END (29) 获得平衡数据集${X_{\text{b}}}$。 表 1 网络结构设置
层数 卷积核数量 卷积核大小 步长 填充 判别器或编码器 1 64 4 2 1 2 128 4 2 1 3 256 4 2 1 4 512 4 2 1 生成器或解码器 1 512 4 1 0 2 256 4 2 1 3 128 4 2 1 4 64 4 2 1 5 图像通道数 4 2 1 表 2 不同过采样算法在各不平衡数据集上的FID分数
表 3 不同过采样算法在各不平衡数据集上的分类性能
算法 MNIST FMNIST SVHN CIFAR-10 ACSA F1 GM ACSA F1 GM ACSA F1 GM ACSA F1 GM CGAN[12] 0.8792 0.8544 0.9057 0.6528 0.6362 0.7263 0.7259 0.6908 0.7936 0.3319 0.3088 0.5302 ACGAN[13] 0.9212 0.9123 0.9492 0.8144 0.7895 0.8606 0.7720 0.7403 0.8239 0.4006 0.3410 0.5918 BAGAN[16] 0.9306 0.9277 0.9598 0.8148 0.8093 0.8931 0.8023 0.7775 0.8677 0.4338 0.4025 0.6373 DeepSMOTE[11] 0.9609 0.9603 0.9780 0.8363 0.8327 0.9061 0.8094 0.7873 0.8739 0.4538 0.4335 0.6530 BAEGAN 0.9807 0.9715 0.9842 0.8799 0.8156 0.9133 0.8357 0.7769 0.8942 0.5443 0.5254 0.7301 表 4 在CIFAR-10上消融实验分类结果
算法 ACSA F1 GM BAEGAN-AE 0.4226 0.3946 0.5802 BAEGAN-L 0.3584 0.3142 0.4098 BAEGAN-S 0.2732 0.2233 0.3083 BAEGAN 0.5443 0.5254 0.7301 -
[1] FAN Xi, GUO Xin, CHEN Qi, et al. Data augmentation of credit default swap transactions based on a sequence GAN[J]. Information Processing & Management, 2022, 59(3): 102889. doi: 10.1016/j.ipm.2022.102889. [2] 刘侠, 吕志伟, 李博, 等. 基于多尺度残差双域注意力网络的乳腺动态对比度增强磁共振成像肿瘤分割方法[J]. 电子与信息学报, 2023, 45(5): 1774–1785. doi: 10.11999/JEIT220362.LIU Xia, LÜ Zhiwei, LI Bo, et al. Segmentation algorithm of breast tumor in dynamic contrast-enhanced magnetic resonance imaging based on network with multi-scale residuals and dual-domain attention[J]. Journal of Electronics & Information Technology, 2023, 45(5): 1774–1785. doi: 10.11999/JEIT220362. [3] 尹梓诺, 马海龙, 胡涛. 基于联合注意力机制和一维卷积神经网络-双向长短期记忆网络模型的流量异常检测方法[J]. 电子与信息学报, 2023, 45(10): 3719–3728. doi: 10.11999/JEIT220959.YIN Zinuo, MA Hailong, and HU Tao. A traffic anomaly detection method based on the joint model of attention mechanism and one-dimensional convolutional neural network-bidirectional long short term memory[J]. Journal of Electronics & Information Technology, 2023, 45(10): 3719–3728. doi: 10.11999/JEIT220959. [4] FERNÁNDEZ A, GARCÍA S, GALAR M, et al. Learning From Imbalanced Data Sets[M]. Cham: Springer, 2018: 327–349. doi: 10.1007/978-3-319-98074-4. [5] HUANG Zhan’ao, SANG Yongsheng, SUN Yanan, et al. A neural network learning algorithm for highly imbalanced data classification[J]. Information Sciences, 2022, 612: 496–513. doi: 10.1016/j.ins.2022.08.074. [6] FU Saiji, YU Xiaotong, and TIAN Yingjie. Cost sensitive ν-support vector machine with LINEX loss[J]. Information Processing & Management, 2022, 59(2): 102809. doi: 10.1016/j.ipm.2021.102809. [7] LIN T Y, GOYAL P, GIRSHICK R, et al. Focal loss for dense object detection[C]. The IEEE International Conference on Computer Vision, Venice, Italy, 2017: 2999–3007. doi: 10.1109/ICCV.2017.324. [8] LI Buyu, LIU Yu, and WANG Xiaogang. Gradient harmonized single-stage detector[C]. The 33rd AAAI Conference on Artificial Intelligence, Honolulu, USA, 2019: 8577–8584. doi: 10.1609/aaai.v33i01.33018577. [9] MICHELUCCI U. An introduction to autoencoders[J]. arXiv preprint arXiv: 2201.03898, 2022. doi: 10.48550/arXiv.2201.03898. [10] GOODFELLOW I J, POUGET-ABADIE J, MIRZA M, et al. Generative adversarial nets[C]. The 27th International Conference on Neural Information Processing Systems, Montreal, Canada, 2014: 2672–2680. [11] DABLAIN D, KRAWCZYK B, and CHAWLA N V. DeepSMOTE: Fusing deep learning and SMOTE for imbalanced data[J]. IEEE Transactions on Neural Networks and Learning Systems, 2023, 34(9): 6390–6404. doi: 10.1109/TNNLS.2021.3136503. [12] MIRZA M and OSINDERO S. Conditional generative adversarial nets[J]. arXiv preprint arXiv: 1411.1784, 2014. doi: 10.48550/arXiv.1411.1784. [13] ODENA A, OLAH C, and SHLENS J. Conditional image synthesis with auxiliary classifier GANs[C]. The 34th International Conference on Machine Learning, Sydney, Australia, 2017: 2642–2651. [14] GULRAJANI I, AHMED F, ARJOVSKY M, et al. Improved training of wasserstein GANs[C]. The 31st International Conference on Neural Information Processing Systems, Long Beach, USA, 2017: 5769–5779. [15] CHAWLA N V, BOWYER K W, HALL L O, et al. SMOTE: Synthetic minority over-sampling technique[J]. Journal of Artificial Intelligence Research, 2002, 16: 321–357. doi: 10.1613/jair.953. [16] MARIANI G, SCHEIDEGGER F, ISTRATE R, et al. BAGAN: Data augmentation with balancing GAN[J]. arXiv preprint arXiv: 1803.09655, 2018. doi: 10.48550/arXiv.1803.09655. [17] HUANG Gaofeng and JAFARI A H. Enhanced balancing GAN: Minority-class image generation[J]. Neural Computing and Applications, 2023, 35(7): 5145–5154. doi: 10.1007/s00521-021-06163-8. [18] BAO Jianmin, CHEN Dong, WEN Fang, et al. CVAE-GAN: Fine-grained image generation through asymmetric training[C]. The IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 2017: 2764–2773. doi: 10.1109/ICCV.2017.299. [19] MAKHZANI A, SHLENS J, JAITLY N, et al. Adversarial autoencoders[J]. arXiv preprint arXiv: 1511.05644, 2015. doi: 10.48550/arXiv.1511.05644. [20] CUI Yin, JIA Menglin, LIN T Y, et al. Class-balanced loss based on effective number of samples[C]. The IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, USA, 2019: 9260–9269. doi: 10.1109/CVPR.2019.00949. [21] DOWSON D C and LANDAU B V. The Fréchet distance between multivariate normal distributions[J]. Journal of Multivariate Analysis, 1982, 12(3): 450–455. doi: 10.1016/0047-259X(82)90077-X. [22] HUANG Chen, LI Yining, LOY C C, et al. Learning deep representation for imbalanced classification[C]. The IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, USA, 2016: 5375–5384. doi: 10.1109/CVPR.2016.580. [23] KUBAT M and MATWIN S. Addressing the curse of imbalanced training sets: One-sided selection[C]. 14th International Conference on Machine Learning, Nashville, USA, 1997: 179–186. [24] HRIPCSAK G and ROTHSCHILD A S. Agreement, the F-measure, and reliability in information retrieval[J]. Journal of the American Medical Informatics Association, 2005, 12(3): 296–298. doi: 10.1197/jamia.M1733. [25] SOKOLOVA M and LAPALME G. A systematic analysis of performance measures for classification tasks[J]. Information Processing & Management, 2009, 45(4): 427–437. doi: 10.1016/j.ipm.2009.03.002. [26] RADFORD A, METZ L, and CHINTALA S. Unsupervised representation learning with deep convolutional generative adversarial networks[C]. 4th International Conference on Learning Representations, San Juan, Puerto Rico, 2016. -






 下载:
下载:









 下载:
下载:
