SAR目标增量识别中基于最大化非重合体积的样例挑选方法

李斌; 崔宗勇; 汪浩瀚; 周正; 田宇; 曹宗杰

doi:10.11999/JEIT240217

SAR目标增量识别中基于最大化非重合体积的样例挑选方法

doi: 10.11999/JEIT240217

电子科技大学信息与通信工程学院成都 611731

基金项目: 国家自然科学基金(62271116)

详细信息

作者简介:
李斌：男，博士生，研究方向为SAR目标增量学习

崔宗勇：男，博士，研究方向为SAR目标检测

汪浩瀚：女，硕士生，研究方向为SAR目标增量学习

周正：男，博士生，研究方向为小样本SAR目标检测

田宇：男，博士生，研究方向为增量SAR目标检测

曹宗杰：男，博士，研究方向为SAR目标成像与识别

通讯作者:
曹宗杰　zjcao@uestc.edu.cn

中图分类号: TN957.52
计量
- 文章访问数: 91
- HTML全文浏览量: 37
- PDF下载量: 15
- 被引次数: 0
出版历程
- 收稿日期: 2024-03-28
- 修回日期: 2024-08-21
- 网络出版日期: 2024-08-30
- 刊出日期: 2024-10-30

Exemplar Selection Based on Maximizing Non-overlapping Volume in SAR Target Incremental Recognition

School of Information and Communication Engineering, University of Electronic Science and Technology of China, Chengdu, 611731, China

Funds: The National Natural Science Foundation of China (62271116)

摘要

摘要: 为了确保合成孔径雷达(SAR)自动目标识别(ATR)系统能够迅速适应新的应用环境，其必须具备快速学习新类的能力。目前的SAR ATR系统在学习新类时需要不断重复训练所有旧类样本，这会造成大量存储资源的浪费，同时识别模型无法快速更新。保留少量的旧类样例进行后续的增量训练是模型增量识别的关键。为了解决这个问题，该文提出基于最大化非重合体积的样例挑选方法(ESMNV)，一种侧重于分布非重合体积的样例选择算法。ESMNV将每个已知类的样例选择问题转化为分布非重合体积的渐近增长问题，旨在最大化所选样例的分布的非重合体积。ESMNV利用分布之间的相似性来表示体积之间的差异。首先，ESMNV使用核函数将目标类别的分布映射到重建核希尔伯特空间(RKHS)，并使用高阶矩来表示分布。然后，它使用最大均值差异(MMD)来计算目标类别与所选样例分布之间的差异。最后，结合贪心算法，ESMNV逐步选择使样例分布与目标类别分布差异最小的样例，确保在有限数量的样例情况下最大化所选样例的非重合体积。
- SAR目标增量识别 /
- 样例挑选 /
- 非重合体积 /
- 最大均值差异 /
- 贪心算法
Abstract: To ensure the Synthetic Aperture Radar (SAR) Automatic Target Recognition (ATR) system can quickly adapt to new application environments, it must possess the ability to rapidly learn new classes. Currently, SAR ATR systems require repetitive training of all old class samples when learning new classes, leading to significant waste of storage resources and preventing the recognition model from updating quickly. Preserving a small number of old class examples for subsequent incremental training is crucial for model incremental recognition. To address this issue, Exemplar Selection based on Maximizing Non-overlapping Volume (ESMNV) is proposed in this paper, an exemplar selection algorithm that emphasizes the non-overlapping volume of the distribution. ESMNV transforms the exemplar selection problem for each known class into an asymptotic growth problem of the Non-overlapping volume of the distribution, aiming to maximize the Non-overlapping volume of the distribution of the selected exemplars. ESMNV utilizes the similarity between distributions to represent differences in volume. Firstly, ESMNV uses a kernel function to map the distribution of the target class into a Reconstructed Kernel Hilbert Space (RKHS) and employs higher-order moments to represent the distribution. Then, it uses the Maximum Mean Discrepancy (MMD) to compute the difference between the distribution of the target class and the selected exemplars. Combined with a greedy algorithm, ESMNV progressively selects exemplars that minimize the difference in distribution between the selected exemplars and the target class, ensuring the maximum Non-overlapping volume of the selected exemplars with a limited number.
- SAR target incremental recognition /
- Exemplar selection /
- Non-overlapping volume /
- Maximum Mean Discrepancy (MMD) /
- Greedy algorithm.

HTML全文

图 1 所选样例分布q与候选样本分布$ e $之间的3种关系类型

下载: 全尺寸图片幻灯片

图 2 所选样例非重合体积的示意图

下载: 全尺寸图片幻灯片

图 3 ESMNV在MSTAR数据集类2S1上的示例性选择可视化结果

下载: 全尺寸图片幻灯片

图 4 所选样例分布的进一步分析

下载: 全尺寸图片幻灯片

图 5 各方法在不同初始训练类数N下的平均增量准确度

下载: 全尺寸图片幻灯片

图 6 各方法在不同增量步长T条件下的平均增量准确率

下载: 全尺寸图片幻灯片

图 7 各方法在SAR-AIRcraft-1.0上不同保存样例m条件下的平均增量准确度

下载: 全尺寸图片幻灯片

图 8 各方法在OpenSARShip上不同保存样例m条件下的平均增量准确率

下载: 全尺寸图片幻灯片

表 1 保留样例数量为5时的增量识别准确率(%)

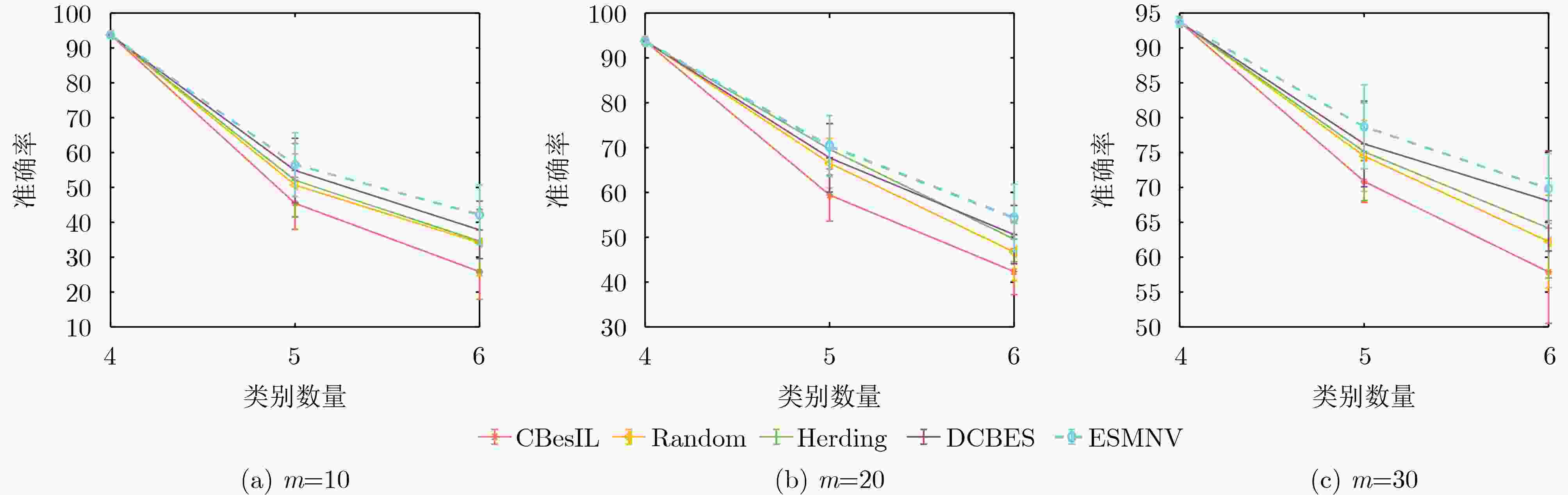
模型	4	5	6	7	8	9	10
CBesIL	99.62	79.96	67.23	58.44	53.88	47.93	41.88
Random	99.62	83.32	69.98	61.56	56.73	49.96	47.21
Herding	99.62	83.92	71.77	61.95	58.67	52.16	51.04
DCBES	99.62	83.09	71.90	65.07	59.54	55.27	54.42
ESMNV	99.62	87.15	75.60	69.32	66.95	61.90	60.49

下载: 导出CSV

表 2 保留样例数量为10时的增量识别准确率(%)

模型	4	5	6	7	8	9	10
CBesIL	99.62	89.13	80.10	74.44	70.58	68.63	65.31
Random	99.62	90.09	80.46	78.05	73.25	70.38	68.68
Herding	99.62	89.68	83.64	79.08	76.20	74.33	71.10
DCBES	99.62	91.33	85.08	81.67	79.12	77.69	75.97
ESMNV	99.62	92.87	86.03	85.40	83.53	81.62	81.05

下载: 导出CSV

表 3 保留样例数量为15时的增量识别准确率(%)

模型	4	5	6	7	8	9	10
CBesIL	99.62	92.25	85.76	83.21	80.51	79.04	75.35
Random	99.62	93.00	87.06	86.28	84.19	80.64	79.70
Herding	99.62	93.48	88.24	86.37	85.70	83.01	81.10
DCBES	99.62	93.63	89.42	88.65	87.02	85.09	83.70
ESMNV	99.62	95.53	92.15	90.59	89.73	89.28	87.31

下载: 导出CSV

参考文献(19)

[1]	LI Jianwei, YU Zhentao, YU Lu, et al. A comprehensive survey on SAR ATR in deep-learning era[J]. Remote Sensing, 2023, 15(5): 1454. doi: 10.3390/rs15051454.
[2]	WANG Chengwei, LUO Siyi, PEI Jifang, et al. Crucial feature capture and discrimination for limited training data SAR ATR[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2023, 204: 291–305. doi: 10.1016/j.isprsjprs.2023.09.014.
[3]	徐丰, 王海鹏, 金亚秋. 深度学习在SAR目标识别与地物分类中的应用[J]. 雷达学报, 2017, 6(2): 136–148. doi: 10.12000/JR16130. XU Feng, WANG Haipeng, and JIN Yaqiu. Deep learning as applied in SAR target recognition and terrain classification[J]. Journal of Radars, 2017, 6(2): 136–148. doi: 10.12000/JR16130.
[4]	CARUANA R. Multitask learning[J]. Machine Learning, 1997, 28(1): 41–75. doi: 10.1023/A:1007379606734.
[5]	MCCLOSKEY M and COHEN N J. Catastrophic interference in connectionist networks: The sequential learning problem[J]. Psychology of Learning and Motivation, 1989, 24: 109–165. doi: 10.1016/S0079-7421(08)60536-8.
[6]	CHAUDHRY A, DOKANIA P K, AJANTHAN T, et al. Riemannian walk for incremental learning: Understanding forgetting and intransigence[C]. Proceedings of the 15th European Conference on Computer Vision (ECCV), Munich, Germany, 2018: 556–572. doi: 10.1007/978-3-030-01252-6_33.
[7]	DANG Sihang, CAO Zongjie, CUI Zongyong, et al. Class boundary exemplar selection based incremental learning for automatic target recognition[J]. IEEE Transactions on Geoscience and Remote Sensing, 2020, 58(8): 5782–5792. doi: 10.1109/TGRS.2020.2970076.
[8]	MITTAL S, GALESSO S, and BROX T. Essentials for class incremental learning[C]. Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, USA, 2021: 3528–3517. doi: 10.1109/CVPRW53098.2021.00390.
[9]	REBUFFI S A, KOLESNIKOV A, SPERL G, et al. iCaRL: Incremental classifier and representation learning[C]. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, USA, 2017: 5533–5542. doi: 10.1109/CVPR.2017.587.
[10]	DE LANGE M, ALJUNDI R, MASANA M, et al. A continual learning survey: Defying forgetting in classification tasks[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2022, 44(7): 3366–3385. doi: 10.1109/TPAMI.2021.3057446.
[11]	LI Zhizhong and HOIEM D. Learning without forgetting[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2018, 40(12): 2935–2947. doi: 10.1109/TPAMI.2017.2773081.
[12]	RUSU A A, RABINOWITZ N C, DESJARDINS G, et al. Progressive neural networks[J]. arXiv: 1606.04671, 2016. doi: 10.48550/arXiv.1606.04671.
[13]	RUDD E M, JAIN L P, SCHEIRER W J, et al. The extreme value machine[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2018, 40(3): 762–768. doi: 10.1109/TPAMI.2017.2707495.
[14]	SHAO Junming, HUANG Feng, YANG Qinli, et al. Robust prototype-based learning on data streams[J]. IEEE Transactions on Knowledge and Data Engineering, 2018, 30(5): 978–991. doi: 10.1109/TKDE.2017.2772239.
[15]	LI Bin, CUI Zongyong, CAO Zongjie, et al. Incremental learning based on anchored class centers for SAR automatic target recognition[J]. IEEE Transactions on Geoscience and Remote Sensing, 2022, 60: 5235313. doi: 10.1109/TGRS.2022.3208346.
[16]	BORGWARDT K M, GRETTON A, RASCH M J, et al. Integrating structured biological data by kernel maximum mean discrepancy[J]. Bioinformatics, 2006, 22(14): e49–e57. doi: 10.1093/bioinformatics/btl242.
[17]	王智睿, 康玉卓, 曾璇, 等. SAR-AIRcraft-1.0: 高分辨率SAR飞机检测识别数据集[J]. 雷达学报, 2023, 12(4): 906–922. doi: 10.12000/JR23043. WANG Zhirui, KANG Yuzhuo, ZENG Xuan, et al. SAR-AIRcraft-1.0: High-resolution SAR aircraft detection and recognition dataset[J]. Journal of Radars, 2023, 12(4): 906–922. doi: 10.12000/JR23043.
[18]	HUANG Lanqing, LIU Bin, LI Boying, et al. OpenSARShip: A dataset dedicated to Sentinel-1 ship interpretation[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2018, 11(1): 195–208. doi: 10.1109/JSTARS.2017.2755672.
[19]	LI Bin, CUI Zongyong, SUN Yuxuan, et al. Density coverage-based exemplar selection for incremental SAR automatic target recognition[J]. IEEE Transactions on Geoscience and Remote Sensing, 2023, 61: 5211713. doi: 10.1109/TGRS.2023.3293509.