An Open Set Recognition Method for SAR Targets Combining Unknown Feature Generation and Classification Score Modification
-
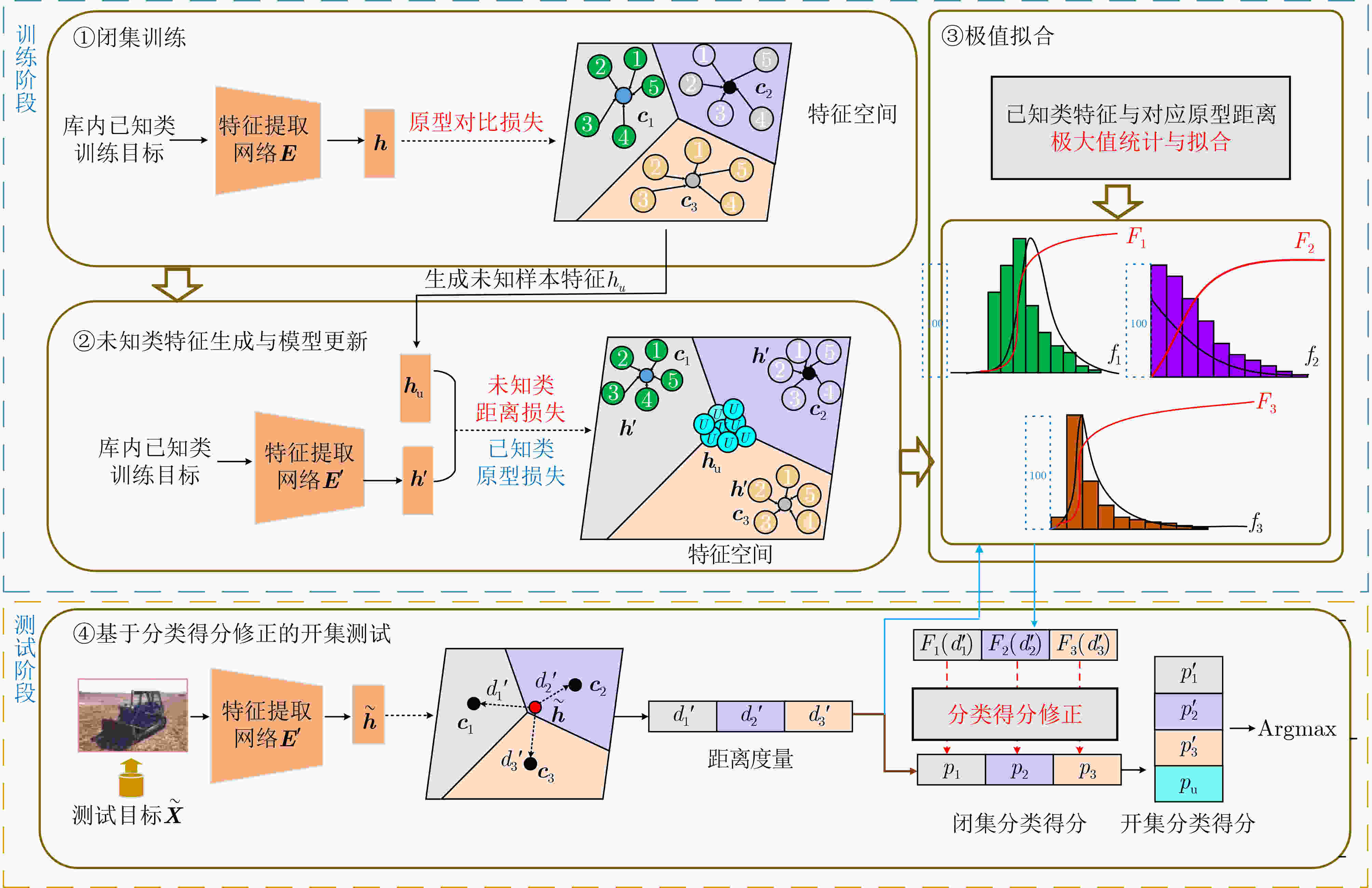
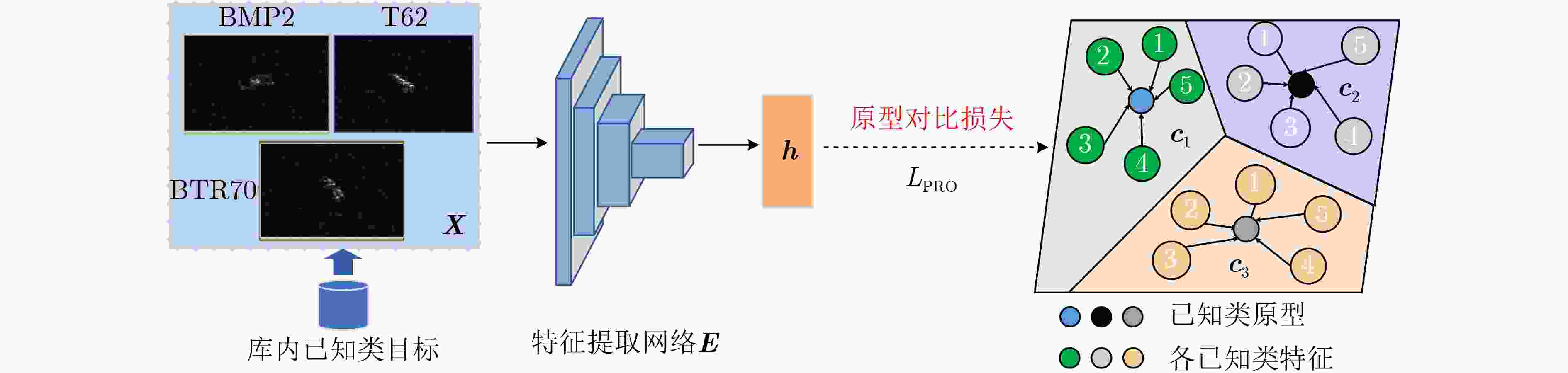
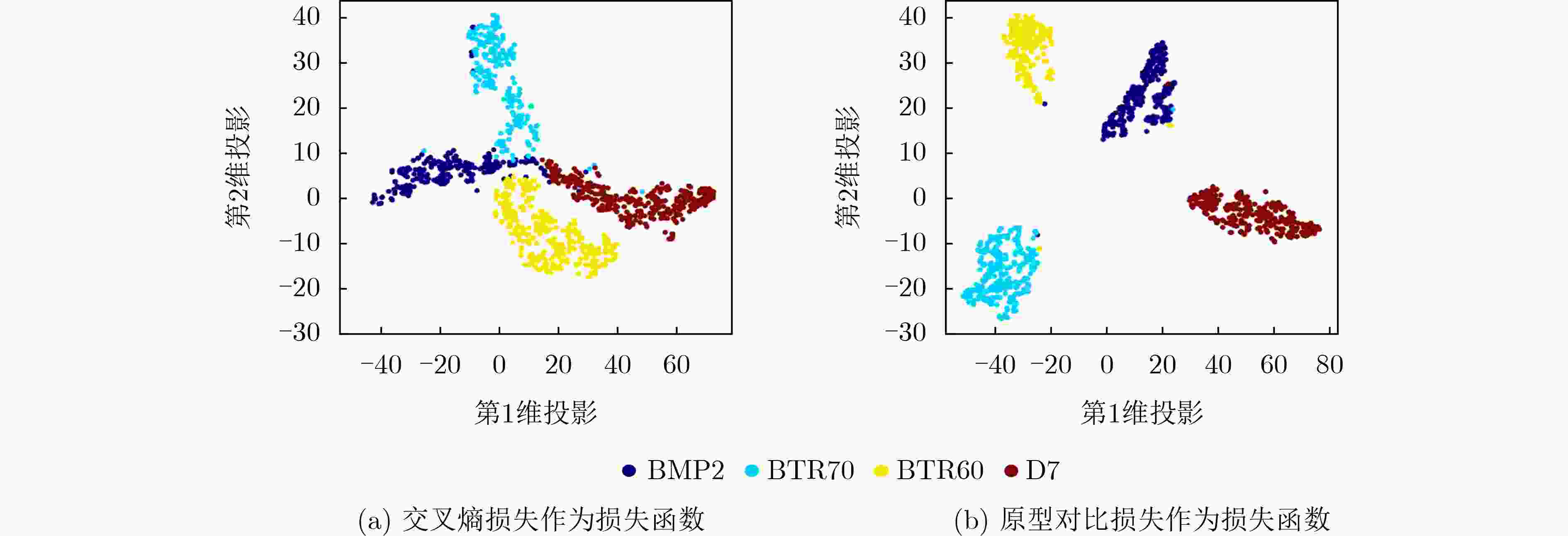
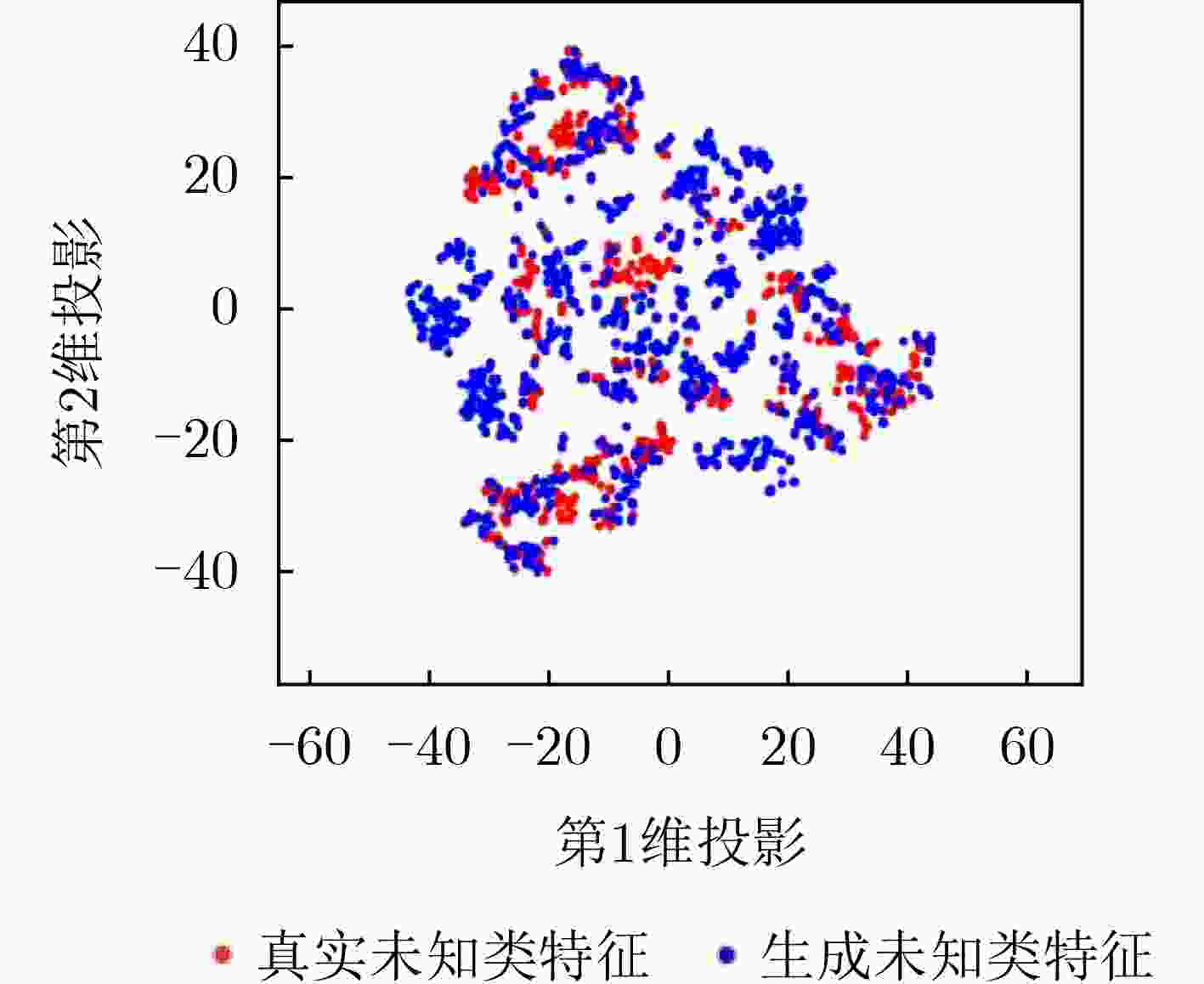
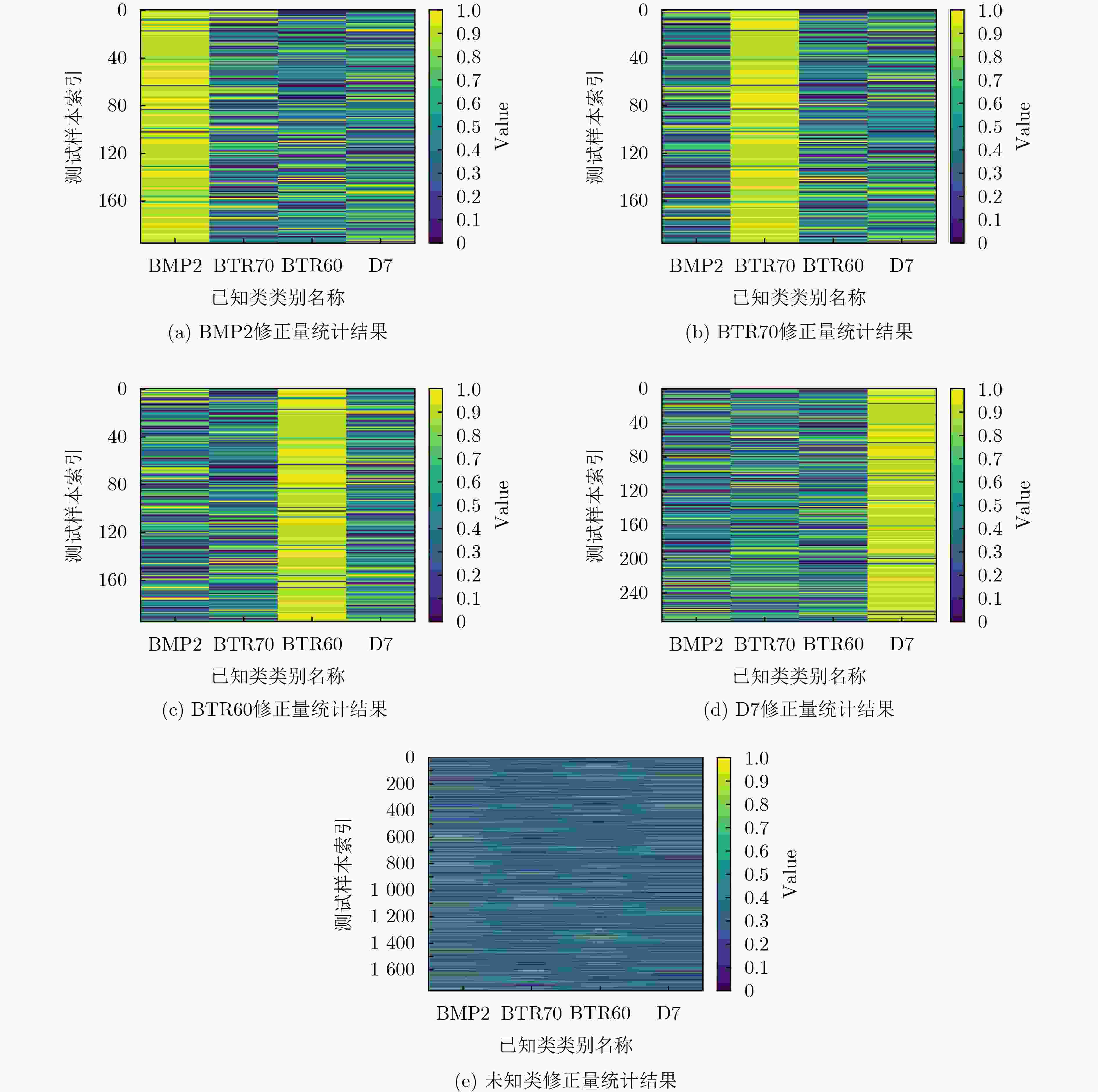
摘要: 现有合成孔径雷达(SAR)目标识别方法大多局限于闭集假定,即认为训练模板库内训练目标类别包含全部待测目标类别,不适用于库内已知类和库外未知新类目标共存的真实开放识别环境。针对训练模板库目标类别非完备情况下的SAR目标识别问题,该文提出一种结合未知类特征生成与分类得分修正的SAR目标开集识别方法。该方法在利用已知类学习原型网络保证已知类识别精度的基础上结合对潜在未知类特征分布的先验认知,生成未知类特征更新网络,进一步保证特征空间中已知类、未知类特征的鉴别性。原型网络更新完成后,所提方法挑选各已知类边界特征,并计算边界特征到各自类原型的距离(极大距离),通过极值理论对各已知类极大距离进行概率拟合确定了各已知类最大分布区域。测试阶段在度量待测样本特征与各已知类原型距离预测闭集分类得分的基础上,计算了各距离在对应已知类极大距离分布上的概率,并修正闭集分类得分,实现了拒判概率的自动确定。基于MSTAR实测数据集的实验结果表明,所提方法能够有效表征真实未知类特征分布并提升网络特征空间已知类与未知类特征的鉴别性,可同时实现对库内已知类目标的准确识别和对库外未知类新目标的准确拒判。Abstract: The existing Synthetic Aperture Radar (SAR) target recognition methods are mostly limited to the closed-set assumption, which considers that the training target categories in training template library cover all the categories to be tested and is not suitable for the open environment with the presence of both known and unknown classes. To solve the problem of SAR target recognition in the case of incomplete target categories in the training template library, an openset SAR target recognition method that combines unknown feature generation with classification score modification is proposed in this paper. Firstly, a prototype network is exploited to get high recognition accuracy of known classes, and then potential unknown features are generated based on prior knowledge to enhance the discrimination of known and unknown classes. After the prototype network being updated, the boundary features of each known class are selected and the distance of each boundary feature to the corresponding class prototype, i.e., maximum distance, is calculated, respectively. Subsequently the maximum distribution area for each known class is determined by the probability fitting of maximum distances for each known class by using extreme value theory. In the testing phase, on the basis of predicting closed-set classification scores by measuring the distance between the testing sample features and each known class prototype, the probability of each distance in the distribution of the corresponding known class’s maximum distance is calculated, and the closed-set classification scores are corrected to automatically determine the rejection probability. Experiments on measured MSTAR dataset show that the proposed method can effectively represent the distribution of unknown class features and enhance the discriminability of known and unknown class features in the feature space, thus achieving accurate recognition for both known class targets and unknown class targets.
-
1 未知类仿制与模型更新流程
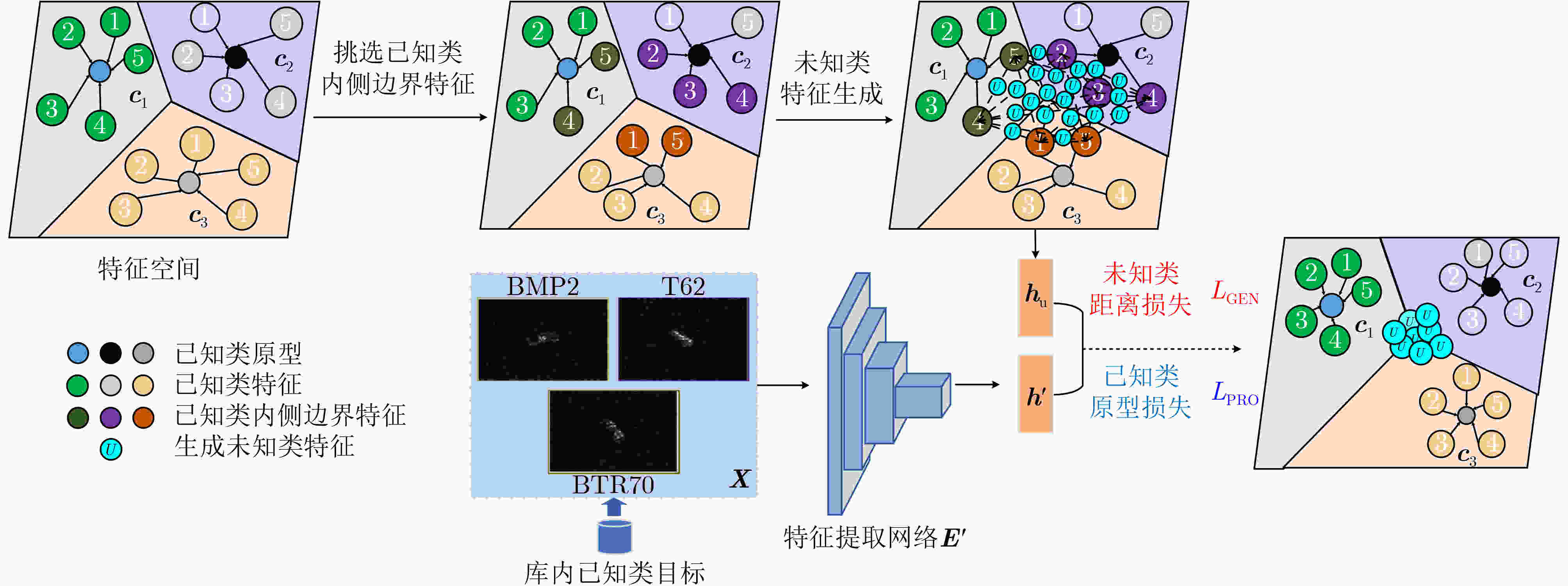
输入:训练数据$\left\{ {{{\boldsymbol{X}}_i}} \right\}_{i = 1}^{{N_{\mathrm{k}}}}$;特征空间中的各类初始化原型${{\boldsymbol{M}}_0}$;特征提取网络${\boldsymbol{E}}$的初始化参数${\theta _0}$;超参数$\lambda $;已知类类别数${N_k}$;已知类
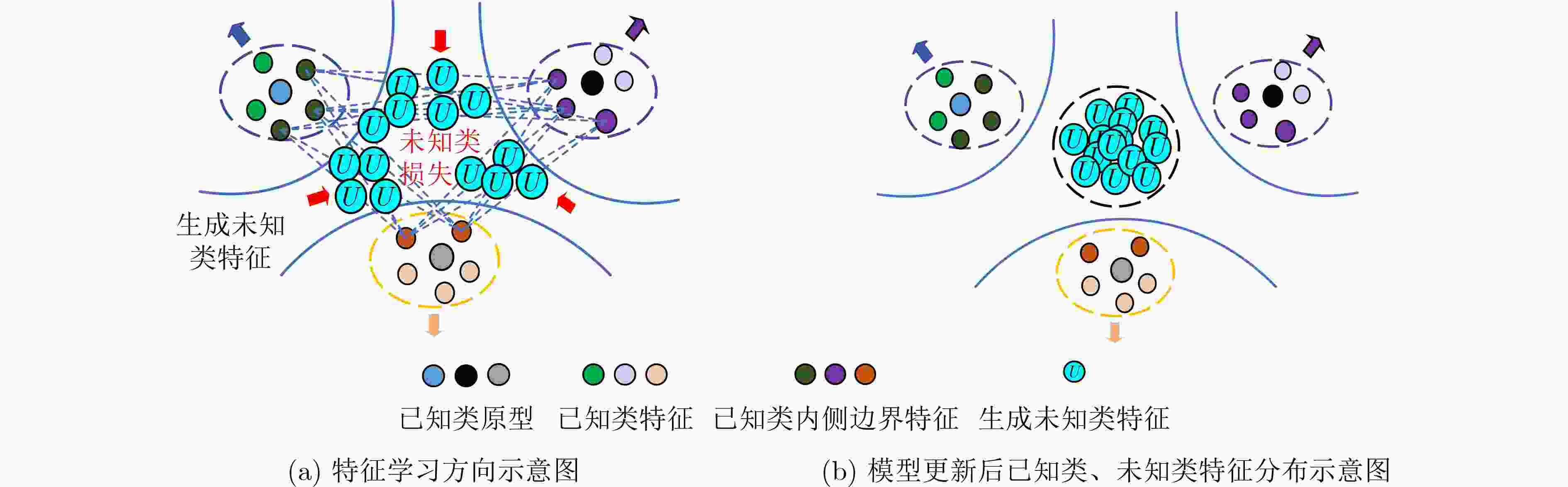
内侧边界特征挑选比例$K$;学习率$\mu $;Beta分布的参数$ \alpha $,$\beta $;迭代次数$t \leftarrow 0$。输出:原型参数${\boldsymbol{M}}$,更新后的网络参数$\theta $。 (1) while not converge do (2) $t \leftarrow t + 1$ (3) 按照比例$K$从各已知类中挑选较小模值的特征,记为$\left\{ {\left( {{{\boldsymbol{f}}_{{\theta ^t}}}\left( {{{\boldsymbol{X}}_{1,1}}} \right), \cdots ,{{\boldsymbol{f}}_{{\theta ^t}}}\left( {{{\boldsymbol{X}}_{1,k}}} \right), \cdots } \right), \cdots ,\left( {{{\boldsymbol{f}}_{{\theta ^t}}}\left( {{{\boldsymbol{X}}_{i,1}}} \right), \cdots ,{{\boldsymbol{f}}_{{\theta ^t}}}\left( {{{\boldsymbol{X}}_{i,m}}} \right), \cdots } \right)} \right\}$; (4) for i = 1: ${N_{\mathrm{k}}}$ do (5) for j = i + 1: ${N_{\mathrm{k}}}$ do (6) 任意挑选$k,m$ do (7) 利用已知类特征的凸组合,生成未知样本特征${{\boldsymbol{X}}_{\rm{GEN} }} = \lambda {{\boldsymbol{f}}_{{\theta ^t}}}\left( {{{\boldsymbol{X}}_{i,k}}} \right) + \left( {1 - \lambda } \right){{\boldsymbol{f}}_{{\theta ^t}}}\left( {{{\boldsymbol{X}}_{j,m}}} \right)$,其中$\lambda \sim {\text{Beta}}\left( {\alpha ,\beta } \right)$; (8) 计算已知类原型损失 $L_{{\text{pro}}}^t = {L_{{\text{pro}}}}\left( {{\boldsymbol{X}};\theta ,{\boldsymbol{M}}} \right)$; (9) 计算未知类距离损失 $L_{ {\text{GEN}}}^t = {{H}}\left( {{{\mathrm{softmax}}} \left( {d\left( {{{\boldsymbol{X}}_{{\text{GEN}}}},{\boldsymbol{M}}} \right)} \right),{{{U}}_{{N_{\mathrm{k}}}}}} \right)$; (10) 计算总损失${L^t} = L_{ {\text{PRO}}}^t + \lambda L_{ {\text{GEN}}}^t$ (11) 更新原型、网络参数$\left\{ {\theta ,{\boldsymbol{M}}} \right\}$:${\theta ^{t + 1}} = {\theta ^t} - \mu \dfrac{{\partial {L^t}}}{{\partial {\theta ^t}}}$, ${{\boldsymbol{M}}^{t + 1}} = {{\boldsymbol{M}}^t} - \mu \dfrac{{\partial {L^t}}}{{\partial {{\boldsymbol{M}}^t}}}$; (12) end while (13) end while 2 极值拟合流程
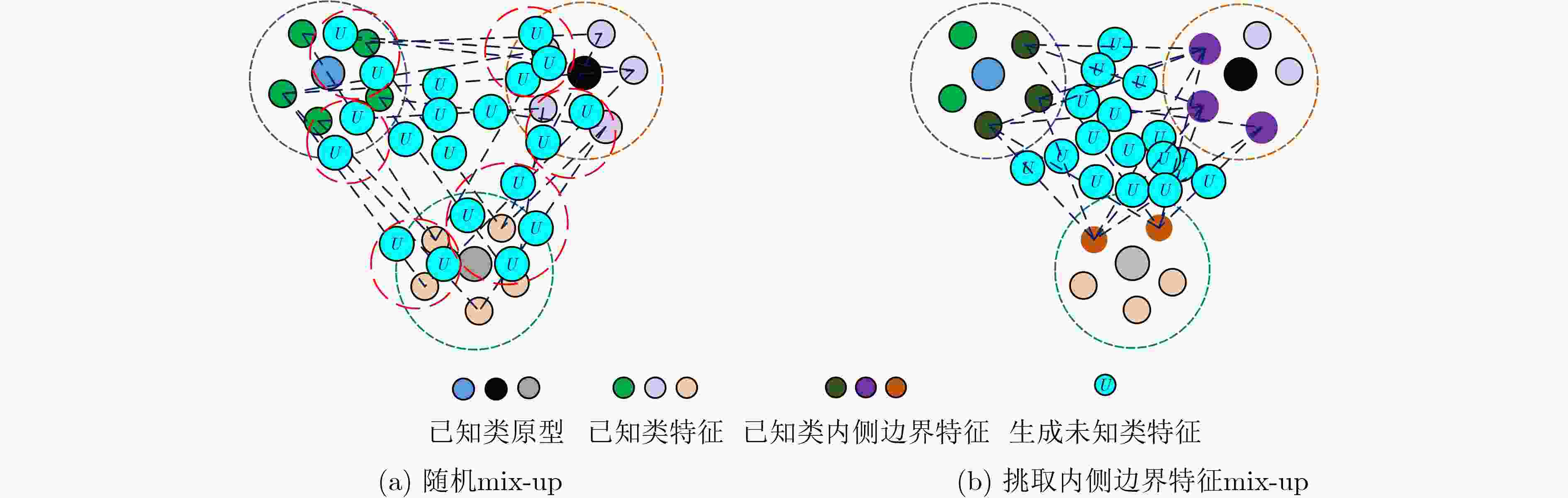
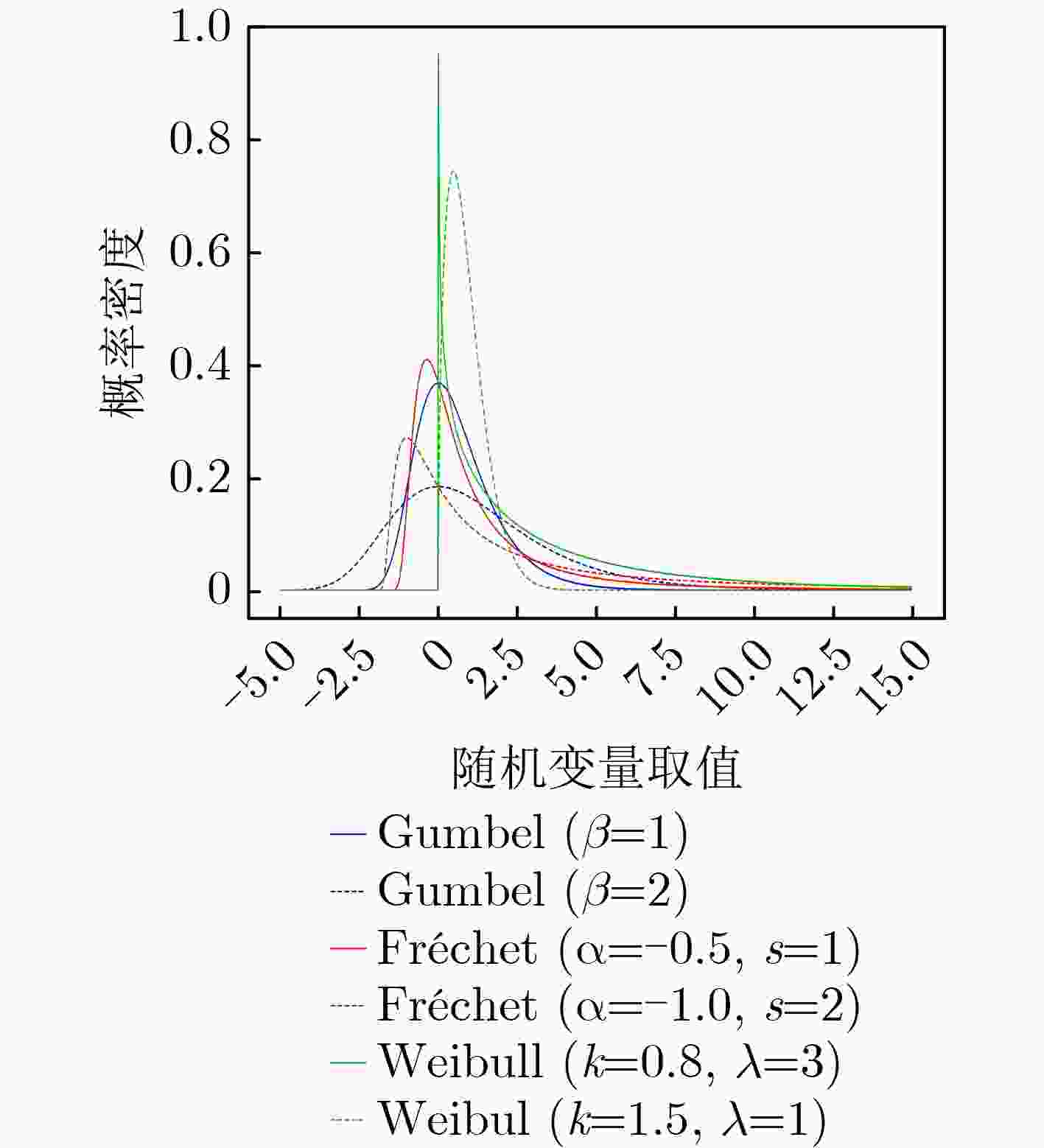
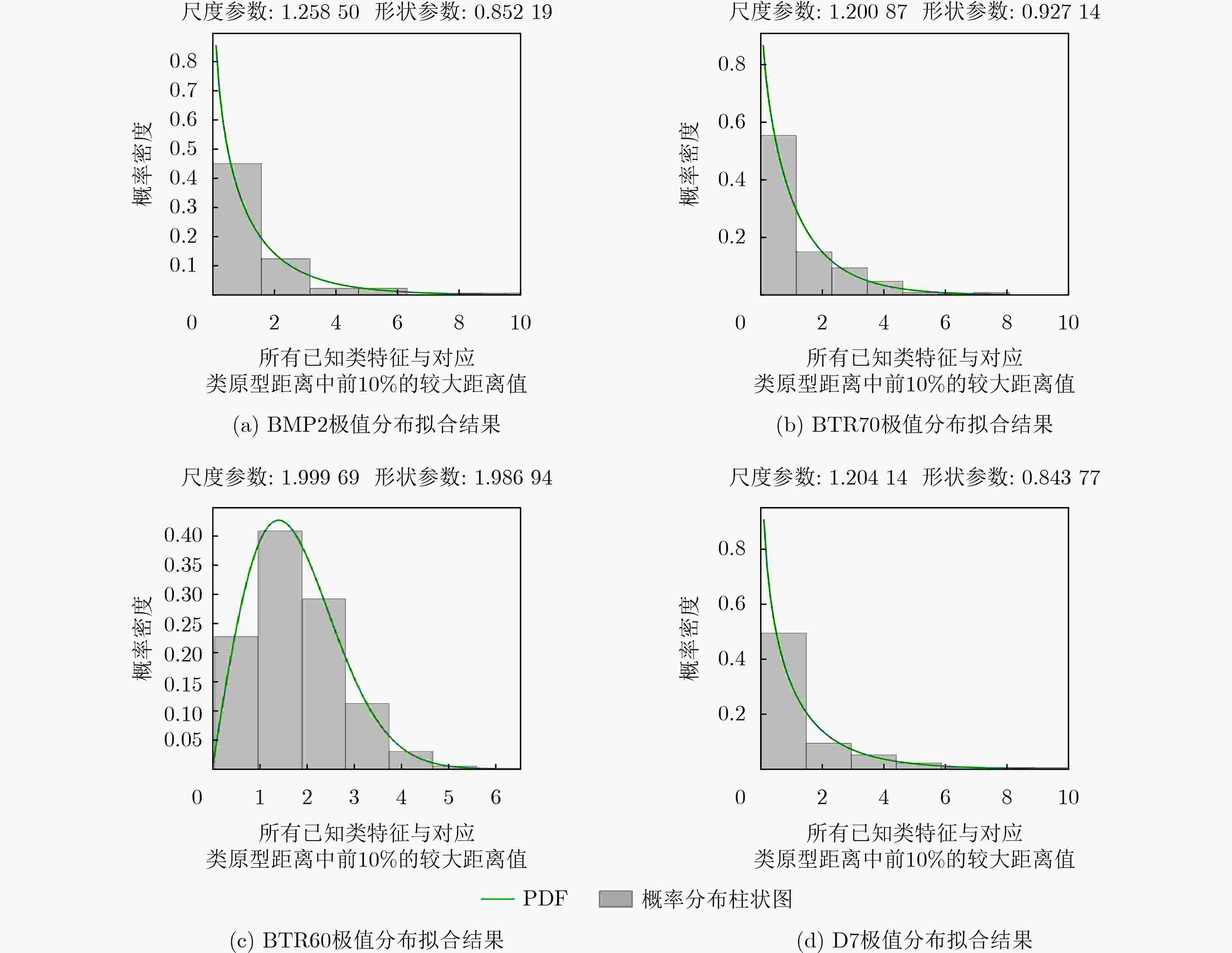
输入:训练数据$\left\{ {{{\boldsymbol{X}}_i}} \right\}_{i = 1}^{{N_{\mathrm{k}}}}$;特征空间中的各类已知类原型${\boldsymbol{M}}$;特征提取网络的参数$\theta $;用于拟合极值分布的极值个数挑选比例$L$; 输出:各已知类特征离类原型的极大距离所服从的威布尔分布函数参数$ \left\{ {{F_{{\text{Weibull}}}}\left( {{\boldsymbol{X}};{\lambda _i},{k_i}} \right)} \right\}_{i = 1}^{{N_{\mathrm{k}}}} $ (1) for $ i = 1:{N_{\mathrm{k}}} $ (2) 将训练数据${x_i}$通过特征提取网络,得到对应特征${{\boldsymbol{f}}_\theta }\left( {{{\boldsymbol{X}}_i}} \right)$; (3) 按类别计算样本特征与对应类原型的距离$ {d_i} = \left\| {\left. {{{\boldsymbol{f}}_\theta }\left( {{{\boldsymbol{X}}_i}} \right) - {{{\boldsymbol{m}}}'_i}} \right\|} \right._2^2 $,每类距离从小到大排序,按比例$L$选取取值较大的距离,构成
距离向量$ {{\boldsymbol{D}}_i} = \left[ {{d_{i1}},{d_{i2}},\cdots} \right] $,其中$ {d_{ik}} $表示第$i$个已知类的第$k$个极大值样本;(4) 采取极大似然估计的方法拟合各类的极值分布参数${\lambda _i}$, ${k_i}$。 (5) end 表 1 MSTAR数据集10类10型的训练测试集划分
2S1 BMP2 BRDM2 BTR70 BTR60 D7 T62 T72 ZIL131 ZSU234 训练样本数 299 233 298 233 256 299 299 232 299 299 测试样本数 274 196 274 196 195 274 273 196 274 274 表 2 不同开放度下的已知类与未知类划分
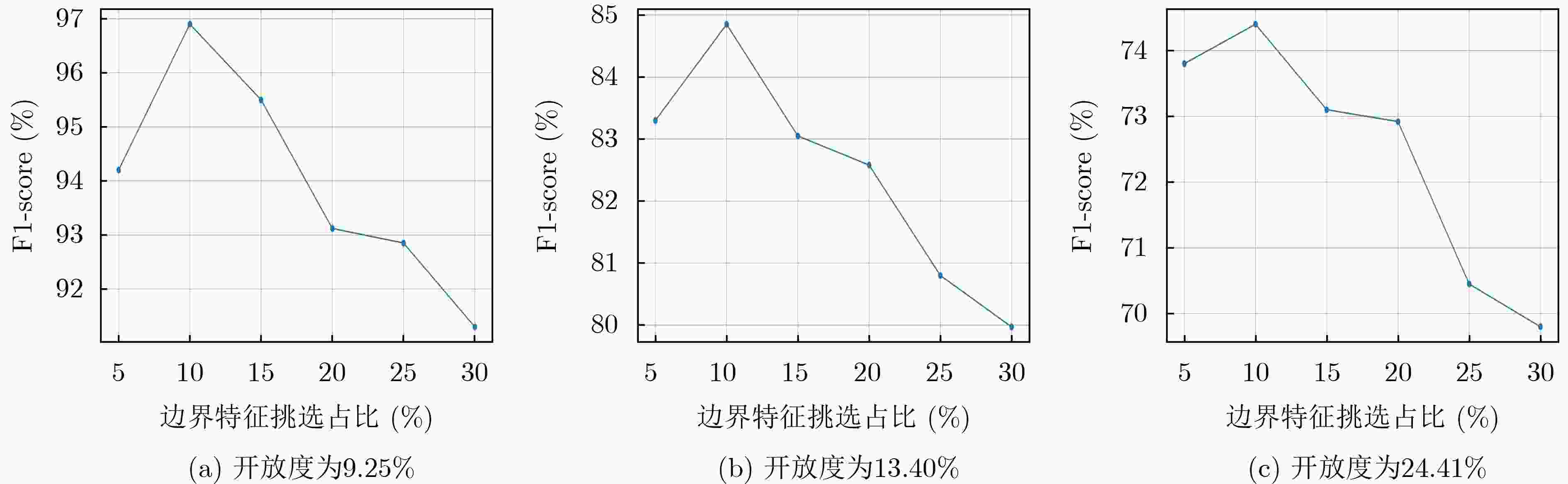
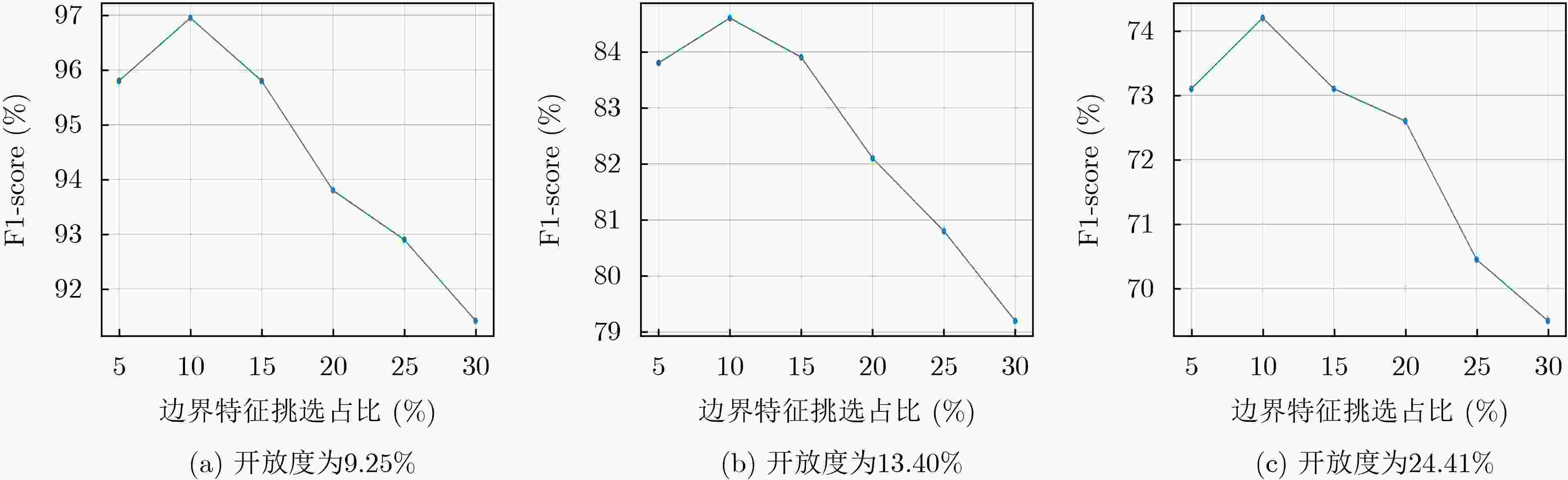
开放度(%) 随机实验 已知类 未知类 9.25 实验1 BMP2 BTR70 T72 2S1 BRDM2 BTR60 D7 T62 ZIL131 ZSU234 实验2 BMP2 BTR60 2S1 D7 T62 ZIL131 ZSU234 BMR70 T72 BRDM2 实验3 BTR70 T72 BRDM2 BTR60 D7 T62 ZIL131 BMP2 2S1 ZSU234 实验4 2S1 BRDM2 BTR60 D7 T62 ZIL131 ZSU234 BMP2 BTR70 T72 实验5 BTR70 2S1 T72 BTR60 T62 ZIL131 ZSU234 BMP2 BRDM2 D7 13.40 实验1 BMP2 BTR70 T72 2S1 BRDM2 BTR60 D7 T62 ZIL131 ZSU234 实验2 BMP2 BTR60 2S1 D7 T62 ZIL131 ZSU234 BMR70 T72 BRDM2 实验3 BTR70 T72 BRDM2 BTR60 D7 T62 ZIL131 BMP2 2S1 ZSU234 实验4 2S1 BRDM2 ZSU234 D7 T62 ZIL131 BMP2 BTR70 T72 BTR60 实验5 BTR70 2S1 T72 BTR60 T62 ZSU234 ZIL131 BMP2 BRDM2 D7 24.41 实验1 BMP2 BTR70 BTR60 D7 BRDM2 T62 ZIL131 ZSU234 2S1 T72 实验2 BMP2 BTR60 2S1 D7 T62 ZIL131 ZSU234 BMR70 T72 BRDM2 实验3 BTR70 T72 BRDM2 BTR60 D7 T62 ZIL131 BMP2 2S1 ZSU234 实验4 2S1 BRDM2 ZSU234 D7 T62 ZIL131 BMP2 BTR70 T72 BTR60 实验5 BTR70 2S1 T72 ZSU234 BTR60 T62 ZIL131 BMP2 BRDM2 D7 表 3 所提方法及对比方法开集实验结果(%)
开集识别方法 开放度 Accuracy Precision Recall F1-score Softmax+概率阈值 9.25 82.14 84.68 90.58 87.82 13.40 76.09 68.45 86.92 70.45 24.41 60.45 52.82 84.28 61.26 GCPL[8] 9.25 88.41 94.48 93.88 93.69 13.40 80.52 76.14 88.21 78.86 24.41 64.85 60.74 86.52 68.43 RPL[23] 9.25 88.83 94.82 93.97 94.02 13.40 82.76 77.29 89.65 79.74 24.41 65.25 63.48 85.02 68.48 DIAS[12] 9.25 93.08 95.90 96.03 96.01 13.40 84.25 82.36 89.42 82.14 24.41 70.99 68.17 88.90 72.43 所提方法 9.25 94.38 96.03 96.58 96.86 13.40 84.62 83.40 92.38 84.68 24.41 73.99 70.25 89.24 74.28 表 4 所提方法与现有SAR开集识别方法对比(%)
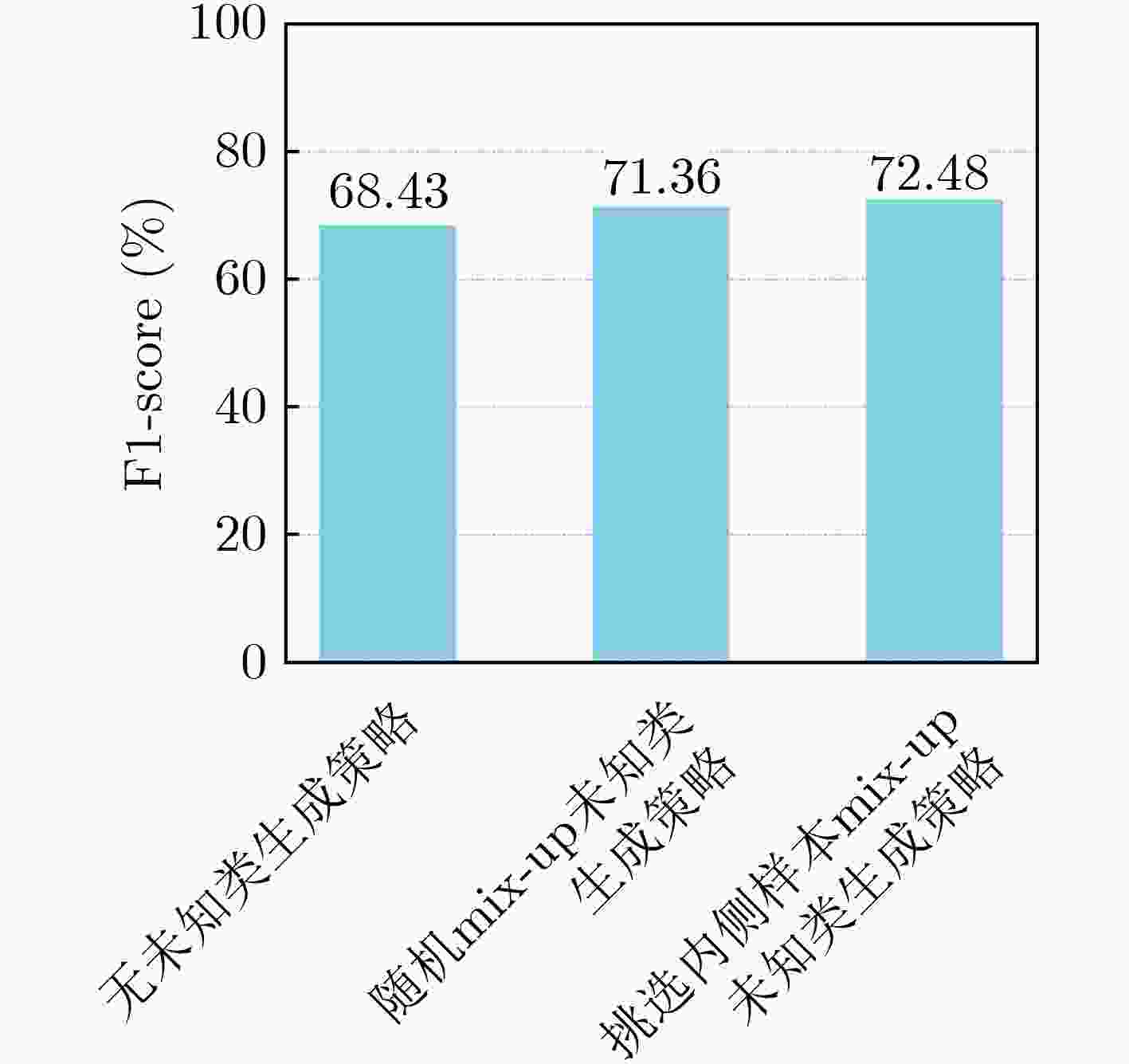
表 5 消融实验设置
实验编号 未知类特征生成 分类得分修正 F1-score(%) (1) √ × 72.48 (2) √ √ 74.28 -
[1] 金亚秋. 多模式遥感智能信息与目标识别: 微波视觉的物理智能[J]. 雷达学报, 2019, 8(6): 710–716. doi: 10.12000/JR19083.JIN Yaqiu. Multimode remote sensing intelligent information and target recognition: Physical intelligence of microwave vision[J]. Journal of Radars, 2019, 8(6): 710–716. doi: 10.12000/JR19083. [2] LOWE D G. Distinctive image features from scale-invariant keypoints[J]. International Journal of Computer Vision, 2004, 60(2): 91–110. doi: 10.1023/B:VISI.0000029664.99615.94. [3] 李璐, 杜兰, 何浩男, 等. 基于深度森林的多级特征融合SAR目标识别[J]. 电子与信息学报, 2021, 43(3): 606–614. doi: 10.11999/JEIT200685.LI Lu, DU Lan, HE Haonan, et al. Multi-level feature fusion SAR automatic target recognition based on deep forest[J]. Journal of Electronics & Information Technology, 2021, 43(3): 606–614. doi: 10.11999/JEIT200685. [4] LIN Huiping, WANG Haipeng, XU Feng, et al. Target recognition for SAR images enhanced by polarimetric information[J]. IEEE Transactions on Geoscience and Remote Sensing, 2024, 62: 5204516. doi: 10.1109/TGRS.2024.3361931. [5] ZENG Zhiqiang, SUN Jinping, YAO Xianxun, et al. SAR target recognition via information dissemination networks[C]. 2023 IEEE International Geoscience and Remote Sensing Symposium, Pasadena, USA, 2023: 7019–7022. doi: 10.1109/IGARSS52108.2023.10282727. [6] MENDES JÚNIOR P R, DE SOUZA R M, DE O. WERNECK R, et al. Nearest neighbors distance ratio open-set classifier[J]. Machine Learning, 2017, 106(3): 359–386. doi: 10.1007/s10994-016-5610-8. [7] XIA Ziheng, WANG Penghui, DONG Ganggang, et al. Radar HRRP open set recognition based on extreme value distribution[J]. IEEE Transactions on Geoscience and Remote Sensing, 2023, 61: 5102416. doi: 10.1109/TGRS.2023.3257879. [8] YANG Hongming, ZHANG Xuyao, YIN Fei, et al. Convolutional prototype network for open set recognition[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2022, 44(5): 2358–2370. doi: 10.1109/TPAMI.2020.3045079. [9] LU Jing, XU Yunlu, LI Hao, et al. PMAL: Open set recognition via robust prototype mining[C]. The 36th AAAI Conference on Artificial Intelligence, Vancouver, British Columbia Canada, 2022: 1872–1880. doi: 10.1609/aaai.v36i2.20081. [10] HUANG Hongzhi, WANG Yu, HU Qinghua, et al. Class-specific semantic reconstruction for open set recognition[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2023, 45(4): 4214–4228. doi: 10.1109/TPAMI.2022.3200384. [11] XIA Ziheng, WANG Penghui, DONG Ganggang, et al. Adversarial kinetic prototype framework for open set recognition[J]. IEEE Transactions on Neural Networks and Learning Systems, 2024, 35(7): 9238–9251. doi: 10.1109/TNNLS.2022.3231924. [12] MOON W J, PARK J, SEONG H S, et al. Difficulty-aware simulator for open set recognition[C]. The 17th European Conference on Computer Vision, Tel Aviv, Israel, 2022: 365–381. doi: 10.1007/978-3-031-19806-9_21. [13] ENGELBRECHT E R and DU PREEZ J A. On the link between generative semi-supervised learning and generative open-set recognition[J]. Scientific African, 2023, 22: e01903. doi: 10.1016/j.sciaf.2023.e01903. [14] DANG Sihang, CAO Zongjie, CUI Zongyong, et al. Open set SAR target recognition using class boundary extracting[C]. The 6th Asia-Pacific Conference on Synthetic Aperture Radar, Xiamen, China, 2019: 1–4. doi: 10.1109/APSAR46974.2019.9048316. [15] GENG Xiaojing, DONG Ganggang, XIA Ziheng, et al. SAR target recognition via random sampling combination in open-world environments[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2023, 16: 331–343. doi: 10.1109/JSTARS.2022.3225882. [16] LI Yue, REN Haohao, YU Xuelian, et al. Threshold-free open-set learning network for SAR automatic target recognition[J]. IEEE Sensors Journal, 2024, 24(5): 6700–6708. doi: 10.1109/JSEN.2024.3354966. [17] XIA Ziheng, WANG Penghui, DONG Ganggang, et al. Spatial location constraint prototype loss for open set recognition[J]. Computer Vision and Image Understanding, 2023, 229: 103651. doi: 10.1016/j.cviu.2023.103651. [18] HE Kaiming, ZHANG Xiangyu, REN Shaoping, et al. Deep residual learning for image recognition[C]. 2016 IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, USA, 2016: 770–778. doi: 10.1109/CVPR.2016.90. [19] ZHANG Hongyi, CISSÉ M, DAUPHIN Y N, et al. mixup: Beyond empirical risk minimization[C]. The 6th International Conference on Learning Representations, Vancouver, Canada, 2018. [20] FISHER R A and TIPPETT L H C. Limiting forms of the frequency distribution of the largest or smallest member of a sample[J]. Mathematical Proceedings of the Cambridge Philosophical Society, 1928, 24(2): 180–190. doi: 10.1017/S0305004100015681. [21] ROSS T D, WORRELL S W, VELTEN V J, et al. Standard SAR ATR evaluation experiments using the MSTAR public release data set[C]. SPIE 3370, Algorithms for Synthetic Aperture Radar Imagery V, Orlando, USA, 1998. doi: 10.1117/12.321859. [22] SCHEIRER W J, DE REZENDE ROCHA A, SAPKOTA A, et al. Toward open set recognition[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2013, 35(7): 1757–1772. doi: 10.1109/TPAMI.2012.256. [23] CHEN Guangyao, QIAO Limeng, SHI Yemin, et al. Learning open set network with discriminative reciprocal points[C]. The Computer Vision–ECCV 2020: 16th European Conference, Glasgow, UK, 2020: 507–522. doi: 10.1007/978-3-030-58580-8_30. -





 下载:
下载:






 下载:
下载:
