The Spoofing Detection Method of Navigation Terminal Using Partial Authenticated Signals
-
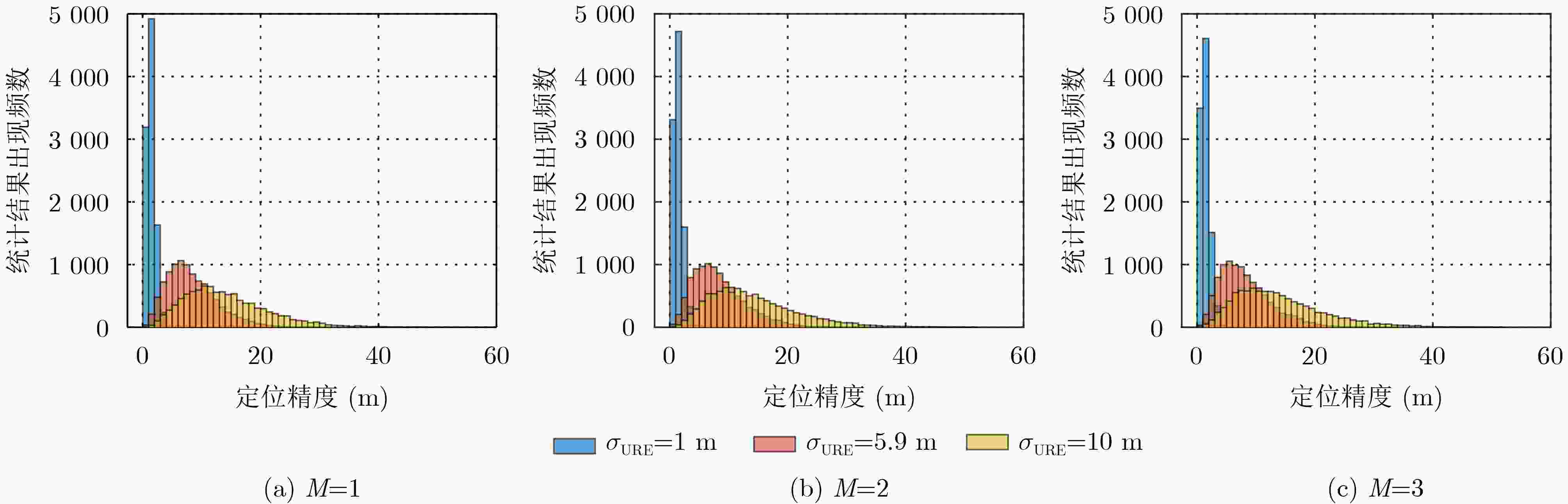
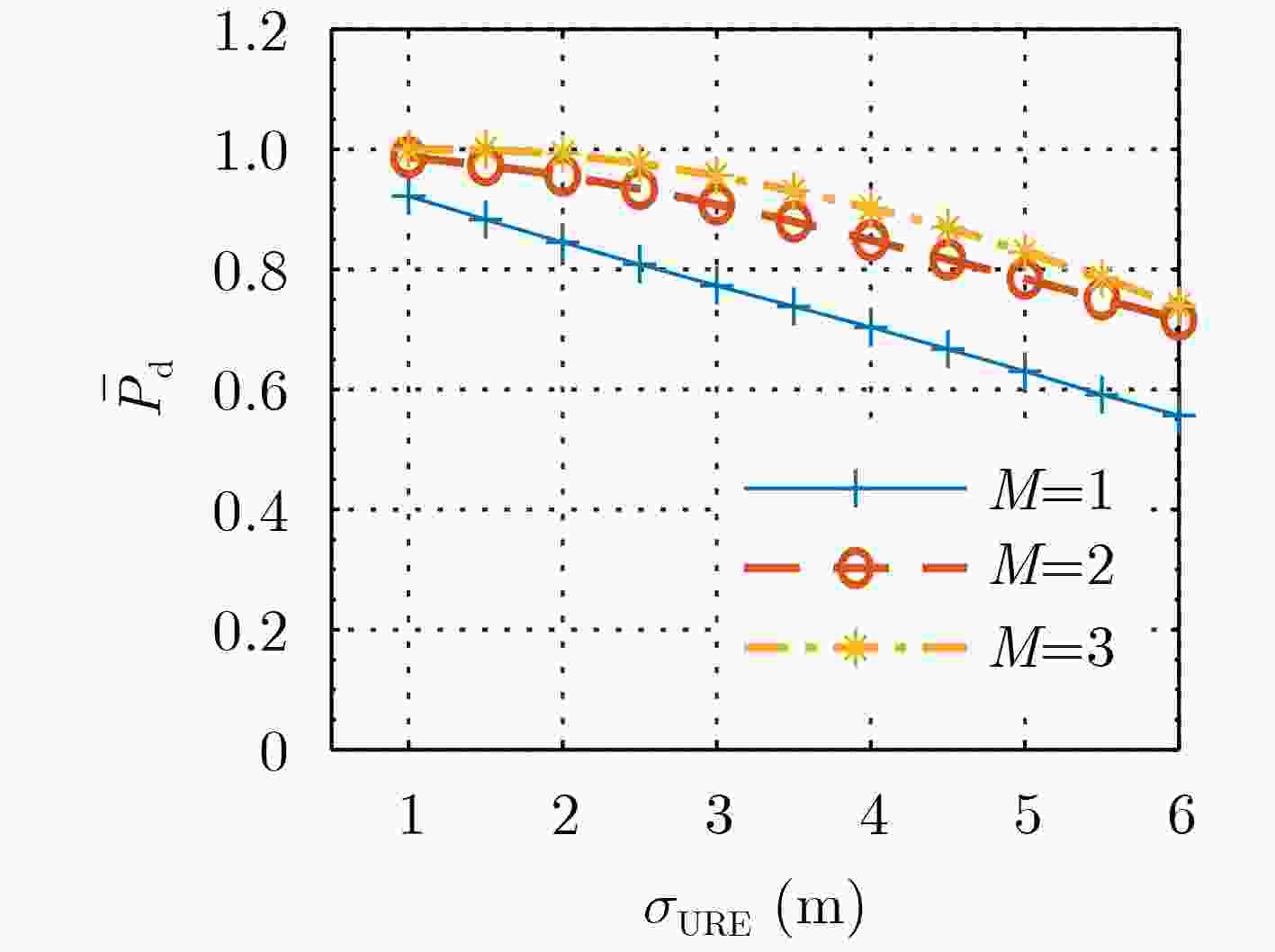
摘要: 导航信号认证服务处于初步部署阶段，认证信号对地覆盖重数无法满足独立定位授时需求，现有研究对这一阶段利用部分通过认证的信号，即可信信号，实现欺骗检测的方法关注度较低。针对这一现状，该文根据欺骗攻击原理，提出以可信信号为基准，基于可信信号伪距残差的欺骗检测方法，建立该场景下的欺骗检测模型，并分析影响所提方法检测性能的因素。经过仿真，在可信卫星数目为3颗、用户定位精度约10 m条件下，当欺骗导致的定位偏差为100 m时，该方法的平均欺骗检测概率可达0.96。此外，该文对算法欺骗检测盲区进行了分析，证明所提算法对于绝大部分欺骗导致的定位结果均有效。
-
关键词:
- 抗欺骗 /
- 导航认证信号 /
- 接收机自主完好性监测 /
- 伪距残差
Abstract: The navigation signal authentication service is in the initial stage. The coverage multiple numbers of the authentication signal to ground can not meet the requirement of independent positioning and timing. The existing research has paid little attention to the deception detection method based on partially trusted signals at this stage. Aiming at the status quo, according to the principle of spoofing attack, a spoofing detection method is proposed based on the pseudo-distance residual of the authentication signal, and the spoofing detection model is established in this scenario, and the factors that affect the detection performance of the proposed method are analyzed. After simulation, the average deception detection probability of the algorithm can reach 0.96 when the positioning deviation is 100 m, the positioning accuracy is about 10 m, and the number of trusted satellites is 3. In addition, the blind area of the algorithm is analyzed, and it is proved that the algorithm is effective for most of the deception positions. -
图 8 $ \Delta {d'^2} $与欺骗信号检测概率之间的曲线对比图(接收机位于北京，r=50 m, ${P_{{\text{fa}}}} = 0.01$, ${\sigma _{{\text{URE}}}} = 5.9{\text{ m}}$)
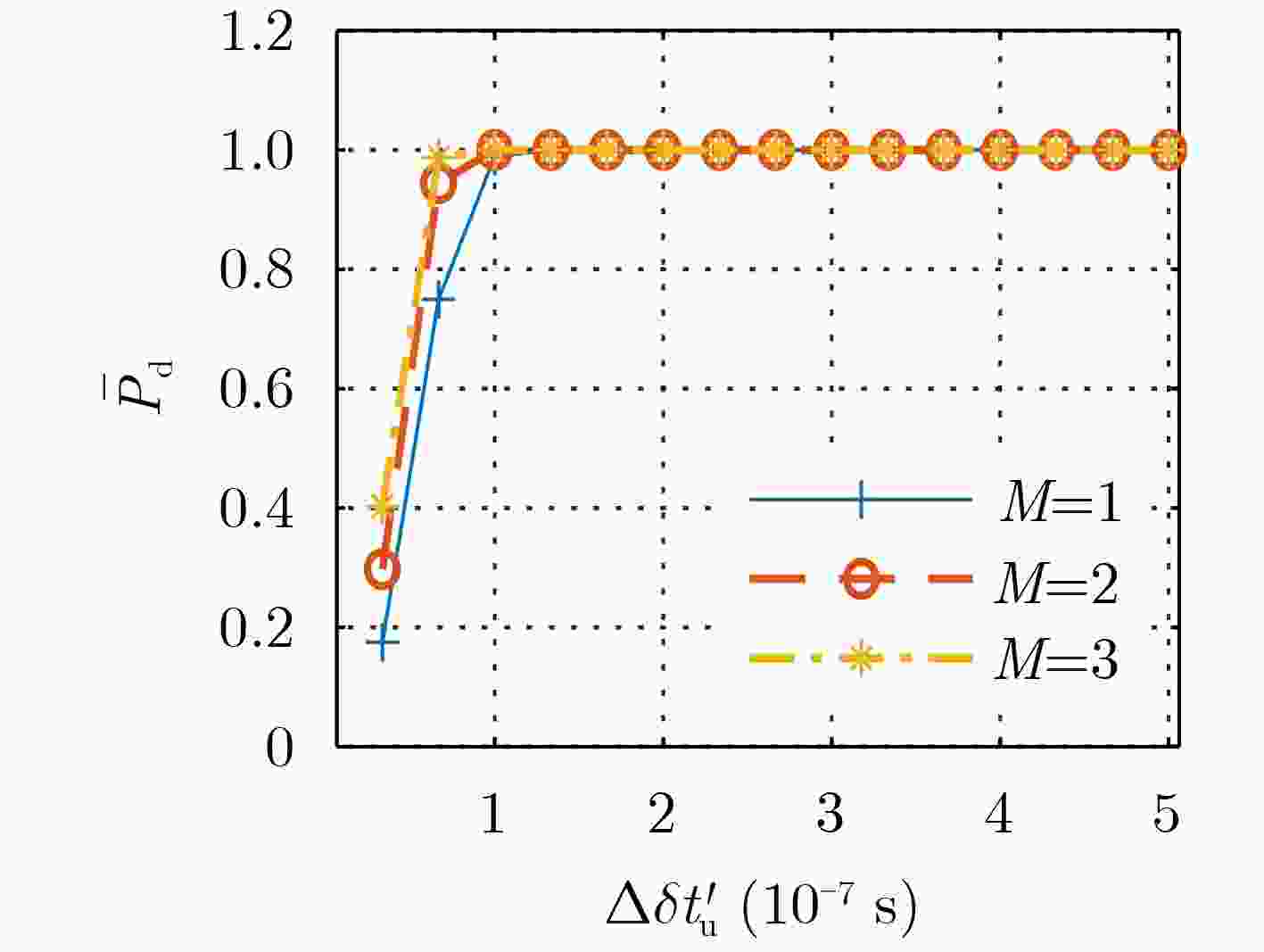
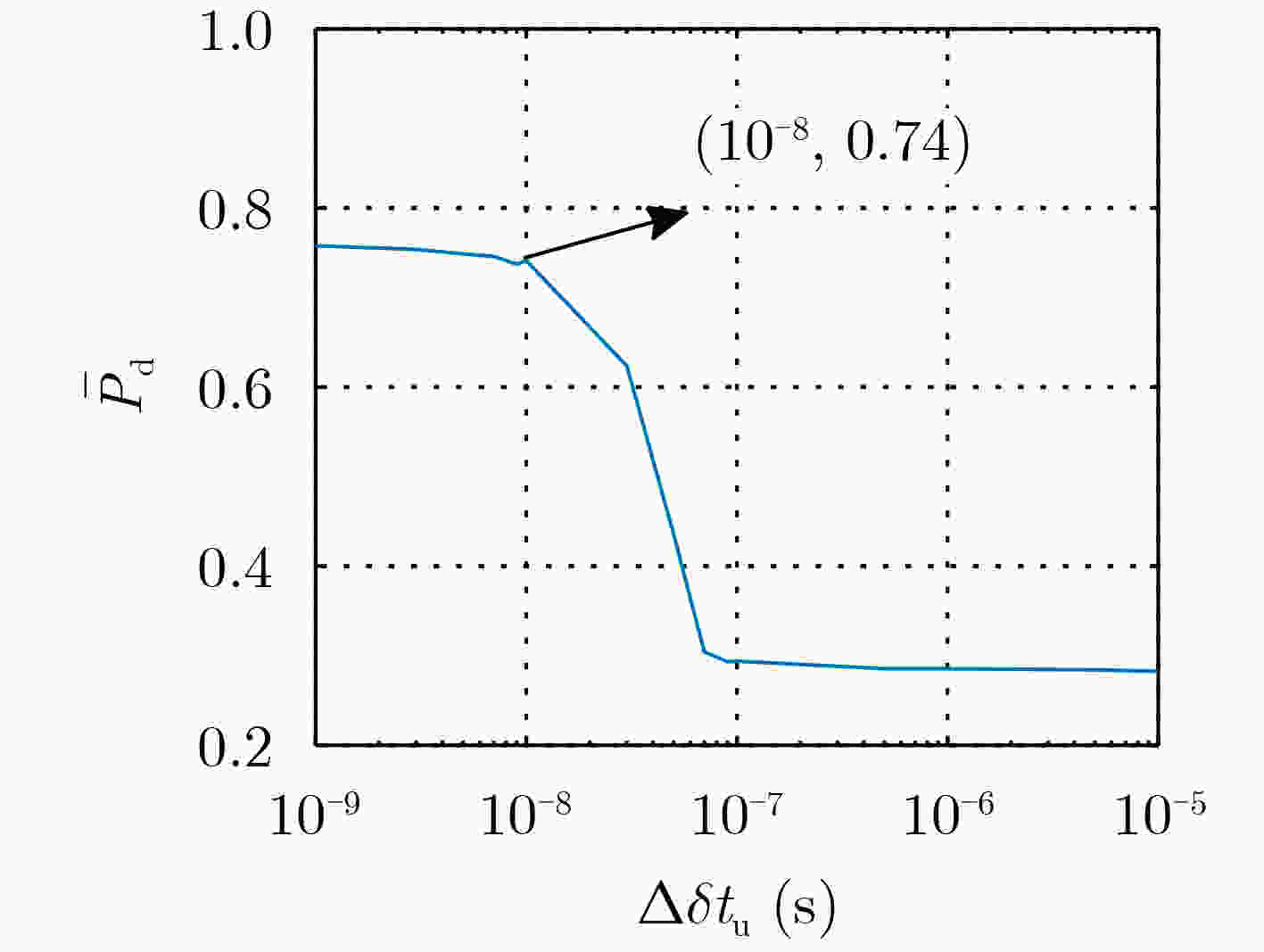
表 1 只存在时间欺骗时，不同可信卫星数目下，算法可检测出的接收机钟差欺骗距离的理论值(s)
可信卫星数目M 1 2 3 算法可检测出的接收机钟差欺骗 $ \ge 7.7 \times {10^{ - 8}}$ $ \ge 5.9 \times {10^{ - 8}}$ $ \ge 5.0 \times {10^{ - 8}}$ 
下载: 导出CSV
表 2 仿真场景参数
参数 描述 仿真时段 2023年9月2日16:00-2023年9月3日16:00，观测时间间隔为10 min，观测历元共144个 北斗星座 本文采用北斗三号卫星星座，包括：24颗MEO卫星，Walker24/3/1星座，卫星轨道高度为21 528 km，轨道倾角为55°；
3颗GEO卫星，轨道高度为35 786 km，分别定位于东经80°, 110.5°, 140°；3颗IGSO卫星，轨道高度35 786 km，
轨道倾角55°，相位间隔120°低轨星座 卫星播发认证信号，为近极地星座，为Walker类型，共有60颗卫星，6个轨道面，相位因子为1，轨道高度为1 175 km，
轨道倾角为86.5°接收机位置 随机选择国内5个城市作为接收机所在位置(地心地固坐标)，包括：
哈尔滨(–2661.32 ,3576.94 ,4546.01 ) km、北京(–2176.85 ,4387.47 ,4071.96 ) km、兰州(–1231 ,5014.65 ,3736.14 ) km、
成都(–1334.67 ,5326.66 ,3234.39 ) km、海口(–2083.66 ,5620.29 ,2172.46 ) km接收机天线 最低仰角为15°
下载: 导出CSV
-
[1] CARROLL J V, VAN DYKE K, KRAEMER J H, et al. Vulnerability assessment of the U. S. transportation infrastructure that relies on GPS[C]. Proceedings of the 14th International Technical Meeting of the Satellite Division of the Institute of Navigation, Salt Lake City, USA, 2001: 975–981. [2] WU Zhijun, ZHANG Yun, YANG Yiming, et al. Spoofing and anti-spoofing technologies of global navigation satellite system: A survey[J]. IEEE Access, 2020, 8: 165444–165496. doi: 10.1109/ACCESS.2020.3022294. [3] YUAN Muzi, TANG Xiaomei, and OU Gang. Authenticating GNSS civilian signals: A survey[J]. Satellite Navigation, 2023, 4(1): 6. doi: 10.1186/s43020-023-00094-6. [4] NICOLA M, MOTELLA B, PINI M, et al. Galileo OSNMA public observation phase: Signal testing and validation[J]. IEEE Access, 2022, 10: 27960–27969. doi: 10.1109/ACCESS.2022.3157337. [5] FERNÁNDEZ I, RIJMEN V, ASHUR T, et al. Galileo navigation message authentication specification for signal-in-space testing - v1.0[R]. European Commission, 2016. [6] ANDERSON J M, CARROLL K L, DEVILBISS N P, et al. Chips-message robust authentication (chimera) for GPS civilian signals[C]. Proceedings of the 30th International Technical Meeting of the Satellite Division of the Institute of Navigation, Portland, USA, 2017: 2388–2416. doi: 10.33012/2017.15206. [7] CHAPMAN D C. Chips message robust authentication (chimera) enhancement for the L1C signal: Space segment/user segment interface[R]. IS-AGT-100, 2019. [8] MANANDHAR D and SHIBASAKI R. Signal authentication for anti-spoofing based on L1S[C]. Proceedings of the ION 2017 Pacific PNT Meeting, Honolulu, USA, 2017: 938–947. doi: 10.33012/2017.15029. [9] MANANDHAR D and SHIBASAKI R. Authenticating GALILEO open signal using QZSS signal[C]. Proceedings of the 31st International Technical Meeting of the Satellite Division of the Institute of Navigation, Miami, USA, 2018: 3995–4003. doi: 10.33012/2018.15872. [10] 王磊, 李德仁, 陈锐志, 等. 低轨卫星导航增强技术——机遇与挑战[J]. 中国工程科学, 2020, 22(2): 144–152. doi: 10.15302/J-SSCAE-2020.02.018.WANG Lei, LI Deren, CHEN Ruizhi, et al. Low earth orbiter (LEO) navigation augmentation: Opportunities and challenges[J]. Strategic Study of CAE, 2020, 22(2): 144–152. doi: 10.15302/J-SSCAE-2020.02.018. [11] SUN Tianyu, HU Min, and YUN Chaoming. Low-orbit large-scale communication satellite constellation configuration performance assessment[J]. International Journal of Aerospace Engineering, 2022, 2022: 4918912. doi: 10.1155/2022/4918912. [12] S·柳辛. 使用PVT解估算来检测和消除GNSS欺骗信号[P]. 中国, 110114695A, 2019.S·LIUXIN. Detection and elimination of GNSS spoofing signals with PVT solution estimation[P]. CN, 110114695A, 2019. [13] 张超, 吕志伟, 张伦东, 等. 欺骗干扰对GNSS/INS系统定位性能的影响[J]. 导航定位学报, 2022, 10(4): 20–28. doi: 10.3969/j.issn.2095-4999.2022.04.003.ZHANG Cao, LYU Zhiwei, ZHANG Lundong, et al. Influence analysis of spoofing interference on positioning performance of GNSS/INS system[J]. Journal of Navigation and Positioning, 2022, 10(4): 20–28. doi: 10.3969/j.issn.2095-4999.2022.04.003. [14] 谢钢. GPS原理与接收机设计[M]. 北京: 电子工业出版社, 2009.XIE G. Principles of GPS and Receiver Design[M]. Beijing: Publishing House of Electronics Industry, 2009. [15] PARKINSON B W and AXELRAD P. Autonomous GPS integrity monitoring using the pseudorange residual[J]. Navigation, 1988, 35(2): 255–274. doi: 10.1002/j.2161-4296.1988.tb00955.x. [16] FU Dong, PENG Jing, GONG Hang, et al. Impact analysis of meaconing attack on timing receiver[M]. YANG Changfeng and XIE Jun. China Satellite Navigation Conference (CSNC 2021) Proceedings. Singapore: Springer, 2021: 423–434. doi: 10.1007/978-981-16-3146-7_39. -
图(9) / 表(2)
计量
- 文章访问数: 114
- HTML全文浏览量: 42
- PDF下载量: 21
- 被引次数: 0
下载:
