Specific Emitter Identification Based on Radio Environment Map Reconstruction
-
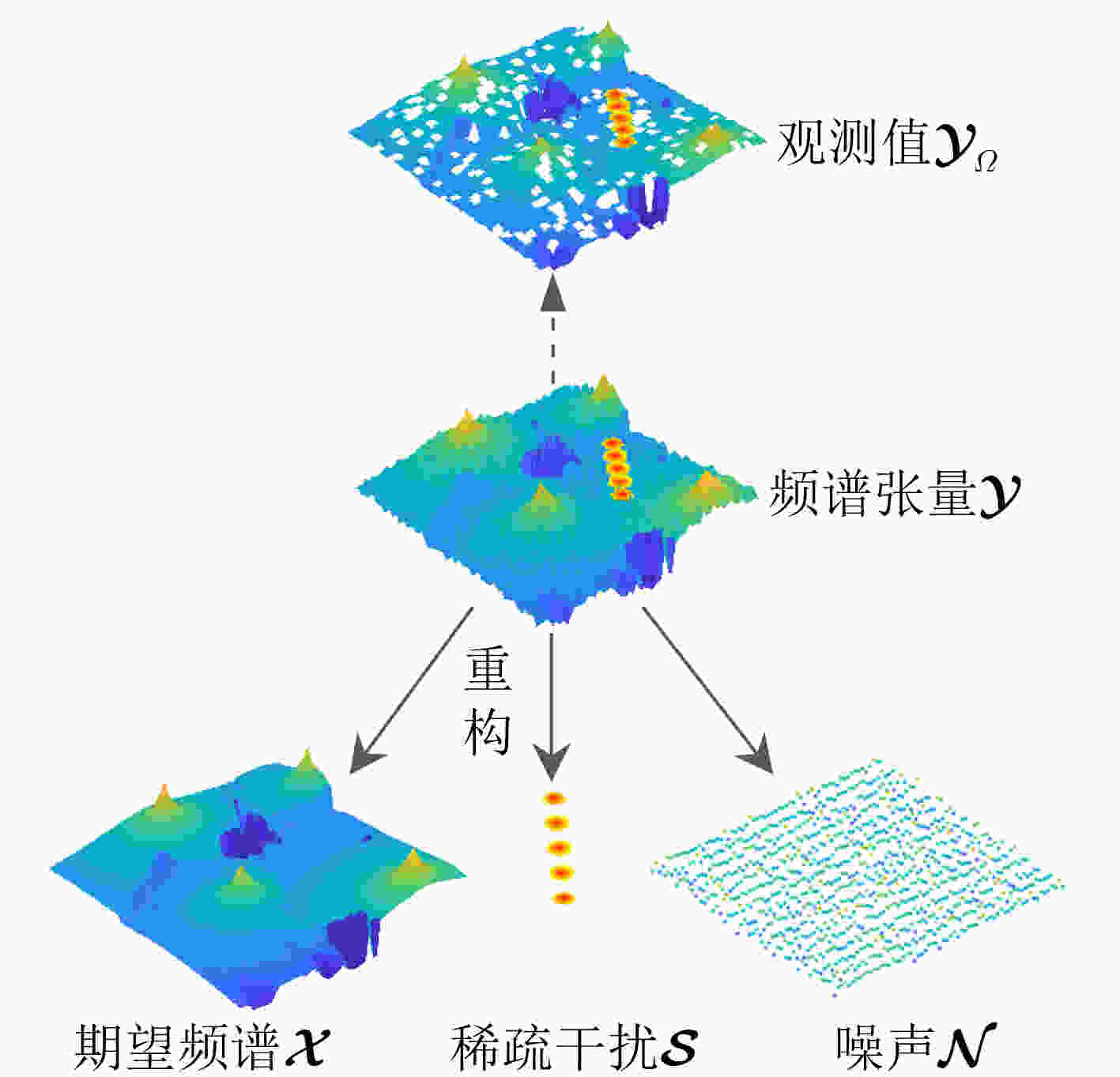
摘要: 无线环境地图(REM)是呈现电磁态势的一种有效形式,考虑实际观测的不完整频谱地图受到干扰和噪声污染的问题,该文对频谱地图进行重构,并在此基础上完成辐射源识别。首先,将复杂电磁环境下的频谱地图建模为高维张量,在预处理中通过线性插值对其初始化补全。然后,使用视觉Transformer模型解决语义分割问题以识别频谱语义区域,区域中仅单一辐射源功率占主导,每个语义张量的低秩性得以保留。提出了一种压缩式张量分解算法,并采用交替方向乘子法(ADMM)在语义区域中重构期望信号频谱和干扰;最后,在重构的频谱地图上检测未知辐射源的位置。该方法能够充分利用频谱数据的低秩性,适用于广域多辐射源个体的电磁场景。实验结果表明,所提方法比现有方法具有更优的重构性能,降低了达到相同频谱地图恢复精度时对观测样本比例的要求,并能够准确检测辐射源。Abstract: The Radio Environment Map (REM) is one of the effective ways to represent the electromagnetic situation. Considering the issue that the actual observed incomplete spectrum map is corrupted by the impulses and the noises, the incomplete radio environment map is reconstructed and the specific emitter identification is performed based on the reconstructed maps. First, the spectrum map in the complex electromagnetic environment is modeled as the high-dimensional spectrum tensor, and the incomplete spectrum tensor is initially completed by the linear interpolation in preprocessing. Then, the vision transformer model is employed to solve the semantic segmentation problem in order to identify the spectrum semantic regions, in which the power of only one emitter dominates and the low-rank property of each semantic tensor is further preserved. To reconstruct the REM, the compressed tensor decomposition algorithm is proposed, and the expected signal spectrum and impulses are recovered utilizing the Alternating Direction Method of Multipliers (ADMM) in the semantic regions. Finally, the locations of the unknown emitters are detected on the reconstructed spectrum map. The proposed approach leverages the low-rank property of spectrum data and works well in wide-area electromagnetic scenarios involving multiple emitters. The simulation results demonstrate that the proposed approach outperforms the comparative approach in terms of reconstruction performance. It requires fewer observation samples to achieve the same spectrum map recovery accuracy and can accurately detect emitters.
-
1 基于语义分割的频谱地图重构算法
输入:初始补全张量$ {{\tilde{ {\boldsymbol{\mathcal{Y}}}}}_m} $,语义标签$ {{{\boldsymbol{\mathcal{L}}}}_m} $, $ m \in {{\mathcal{I}}_M} $,迭代次数K; 输出:重构的期望频谱$ {\tilde {\boldsymbol{\mathcal{X}}}} $; 初始化:$ {\tilde{ {\boldsymbol{\mathcal{X}}}}}_m^{(1)} = {\bf{0}} $, $ {\tilde {{\boldsymbol{\mathcal{S}}}}}_m^{(1)} = 0 $, $ {\lambda ^{(1)}} = 0 $, $ {\beta ^{(1)}} = {10^{ - 6}} $,
$ {\beta _{\max }} = {10^{10}} $, $ \rho = 1.2 $,m = 1, $ k = 1 $;(1) 当$ ||{{\boldsymbol{\mathcal{X}}}_m}||_{{\mathrm{F}}} ^2 $未收敛且$ k < K $,重复步骤(2)~(7); (2) 使用式(22)更新$ {\boldsymbol{\mathcal{X}}}_m^{(k + 1)} $; (3) 使用式(24)更新$ {{\boldsymbol{\mathcal{S}}}}_m^{(k + 1)} $; (4) 使用式(25)更新$ \lambda _m^{(k + 1)} $; (5) 使用式(26)更新$ c_m^{(k + 1)} $; (6) $ {\beta ^{(k + 1)}} = \min \{ \rho {\beta ^{(k)}},{\beta _{{\text{max}}}}\} $; (7) k = k+1; (8) m = m+1; (9) 重复步骤(1)、步骤(8),直到m = M; (10) $ {\tilde {\boldsymbol{\mathcal{X}}}}{\text{ = }}\displaystyle\sum\nolimits_{m = 1}^M {{{\boldsymbol{\mathcal{X}}}_m} \odot } {{{\boldsymbol{\mathcal{L}}}}_m} $。 -
[1] HO K C and LE T K. Integrating AOA with TDOA for joint source and sensor localization[J]. IEEE Transactions on Signal Processing, 2023, 71: 2087–2102. doi: 10.1109/TSP.2023.3280417. [2] LIU Yan, SHEN Yuan, and WIN M Z. Single-anchor localization and synchronization of full-duplex agents[J]. IEEE Transactions on Communications, 2019, 67(3): 2355–2367. doi: 10.1109/TCOMM.2018.2878843. [3] YILMAZ H B and TUGCU T. Location estimation-based radio environment map construction in fading channels[J]. Wireless Communications and Mobile Computing, 2015, 15(3): 561–570. doi: 10.1002/wcm.2367. [4] SHIN B, LEE J H, KIM C, et al. LTE RSSI based vehicular localization system in long tunnel environment[J]. IEEE Transactions on Industrial Informatics, 2023, 19(11): 11102–11114. doi: 10.1109/TII.2023.3240690. [5] CHAUDHARI S and CABRIC D. Cyclic weighted centroid algorithm for transmitter localization in the presence of interference[J]. IEEE Transactions on Cognitive Communications and Networking, 2016, 2(2): 162–177. doi: 10.1109/TCCN.2016.2586078. [6] 张国勇, 王军, 陈霄南, 等. 基于空间稀疏采样的频谱态势生成: 模型与算法[J]. 中国科学: 信息科学, 2022, 52(11): 2011–2036. doi: 10.1360/SSI-2021-0382.ZHANG Guoyong, WANG Jun, CHEN Xiaonan, et al. Spectrum situation generation from sparse spatial sampling: Model and algorithm[J]. Scientia Sinica Informationis, 2022, 52(11): 2011–2036. doi: 10.1360/SSI-2021-0382. [7] DEBROY S, BHATTACHARJEE S, and CHATTERJEE M. Spectrum map and its application in resource management in cognitive radio networks[J]. IEEE Transactions on Cognitive Communications and Networking, 2015, 1(4): 406–419. doi: 10.1109/TCCN.2016.2517001. [8] SATO K, SUTO K, INAGE K, et al. Space-frequency-interpolated radio map[J]. IEEE Transactions on Vehicular Technology, 2021, 70(1): 714–725. doi: 10.1109/TVT.2021.3049894. [9] ZHANG Yongliang and MA Lin. Radio map crowdsourcing update method using sparse representation and low rank matrix recovery for WLAN indoor positioning system[J]. IEEE Wireless Communications Letters, 2021, 10(6): 1188–1191. doi: 10.1109/LWC.2021.3061539. [10] CAI Jianfeng, CANDÈS E J, and SHEN Zuowei. A singular value thresholding algorithm for matrix completion[J]. SIAM Journal on Optimization, 2010, 20(4): 1956–1982. doi: 10.1137/080738970. [11] SIDIROPOULOS N D, DE LATHAUWER L, FU Xiao, et al. Tensor decomposition for signal processing and machine learning[J]. IEEE Transactions on Signal Processing, 2017, 65(13): 3551–3582. doi: 10.1109/TSP.2017.2690524. [12] TANG Mengyun, DING Guoru, WU Qihui, et al. A joint tensor completion and prediction scheme for multi-dimensional spectrum map construction[J]. IEEE Access, 2016, 4: 8044–8052. doi: 10.1109/ACCESS.2016.2627243. [13] LIN Yun, TU Ya, DOU Zheng, et al. Contour Stella image and deep learning for signal recognition in the physical layer[J]. IEEE Transactions on Cognitive Communications and Networking, 2021, 7(1): 34–46. doi: 10.1109/TCCN.2020.3024610. [14] WANG Chenyue, WU Yuhang, ZHOU Fuhui, et al. Accurate spectrum map construction using an intelligent frequency-spatial reasoning approach[C]. 2022 IEEE Global Communications Conference, Rio de Janeiro, Brazil, 2022: 3460–3465. doi: 10.1109/GLOBECOM48099.2022.10001024. [15] SHRESTHA S, FU Xiao, and HONG Mingyi. Deep spectrum cartography: Completing radio map tensors using learned neural models[J]. IEEE Transactions on Signal Processing, 2022, 70: 1170–1184. doi: 10.1109/TSP.2022.3145190. [16] HU Tianyu, HUANG Yang, CHEN Junting, et al. 3D radio map reconstruction based on generative adversarial networks under constrained aircraft trajectories[J]. IEEE Transactions on Vehicular Technology, 2023, 72(6): 8250–8255. doi: 10.1109/TVT.2023.3239556. [17] LEVIE R, YAPAR Ç, KUTYNIOK G, et al. RadioUNet: Fast radio map estimation with convolutional neural networks[J]. IEEE Transactions on Wireless Communications, 2021, 20(6): 4001–4015. doi: 10.1109/TWC.2021.3054977. [18] LIN Yun, ZHAO Haojun, MA Xuefei, et al. Adversarial attacks in modulation recognition with convolutional neural networks[J]. IEEE Transactions on Reliability, 2021, 70(1): 389–401. doi: 10.1109/TR.2020.3032744. [19] MENG Lingchen, LI Hengduo, CHEN B C, et al. AdaViT: Adaptive vision transformers for efficient image recognition[C]. 2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, USA, 2022: 12299–12308. doi: 10.1109/CVPR52688.2022.01199. [20] LI Hongyu, LI Jie, SHEN Feng, et al. SOC algorithm-based framework for spectrum occupancy completion[J]. IEEE Transactions on Cognitive Communications and Networking, 2023, 9(5): 1155–1166. doi: 10.1109/TCCN.2023.3269763. -





 下载:
下载:





 下载:
下载:
