利用伯努利滤波的多目标机动雷达误差配准方法

邓洪高; 余润华; 纪元法; 吴孙勇; 孙希延

doi:10.11999/JEIT240013

利用伯努利滤波的多目标机动雷达误差配准方法

doi: 10.11999/JEIT240013

邓洪高^{1, 4},
余润华^{1, 2},
纪元法^{1, 2, 4},
吴孙勇^{2, 3, ,},
孙希延^{1, 2, 4, 5}

1.
桂林电子科技大学信息与通信学院桂林 541004
2.
桂林电子科技大学广西精密导航技术与应用重点实验室桂林 541004
3.
桂林电子科技大学数学与计算科学学院桂林 541004
4.
卫星导航定位与位置服务国家地方联合工程研究中心桂林 541004
5.
南宁桂电电子科技研究院有限公司南宁 530031

基金项目: 国家自然科学基金(U23A20280, 62061010, 62161007)，广西科技厅项目(AB23026120)

详细信息

作者简介:
邓洪高：男，研究员，研究方向为雷达信号处理和卫星导航

余润华：男，硕士生，研究方向为雷达多目标跟踪、空间误差配准和多源信息融合

纪元法：男，教授，研究方向为卫星导航和信号处理

吴孙勇：男，教授，研究方向为雷达信号处理、多目标检测与跟踪和多源信息融合

孙希延：女，研究员，研究方向为卫星导航和遥感

通讯作者:
吴孙勇　wusunyong121991@163.com

中图分类号: TN959.1; V243.2
计量
- 文章访问数: 84
- HTML全文浏览量: 30
- PDF下载量: 12
- 被引次数: 0
出版历程
- 收稿日期: 2024-01-16
- 修回日期: 2024-09-05
- 网络出版日期: 2024-09-11
- 刊出日期: 2024-10-30

Mobile Radar Registration with Multiple Targets Based on Bernoulli Filter

DENG Honggao^{1, 4},
YU Runhua^{1, 2},
JI Yuanfa^{1, 2, 4},
WU Sunyong^{2, 3
, ,},
SUN Xiyan^{1, 2, 4, 5}

1.
School of Information and Communication, Guilin University of Electronic Technology, Guilin 541004, China
2.
Guangxi Key Laboratory of Precision Navigation Technology and Application, Guilin University of Electronic Science and Technology, Guilin 541004, China
3.
School of Mathematics and Computing Science, Guilin University of Electronic Science and Technology, Guilin 541004, China
4.
National & Local Joint Engineering Research Center of Satellite Navigation Positioning and Location Service, Guilin 541004, China
5.
GUET-Nanning E-Tech Research Institute Co., Ltd., Nanning 530031, China

Funds: The National Natural Science Foundation of China (U23A20280, 62061010, 62161007), Guangxi Science and Technology Department Project (AB23026120)

摘要

摘要: 传统的组网雷达多目标误差配准方法通常假设数据关联关系已知，但在平台机动的情况下，系统同时存在雷达测量偏差和平台姿态角偏差，且雷达观测过程中会受到杂波干扰，导致数据关联尤为困难。针对这一问题，该文提出一种基于伯努利滤波的多目标机动雷达误差配准方法。首先建立系统偏差的量测与状态方程，然后将系统偏差建模成伯努利随机有限集，利用公共坐标系下的原始量测可实现系统偏差在伯努利滤波框架下的递推估计，有效避免了数据关联问题。同时，为了充分利用多目标量测信息，提出一种修正的贪婪量测划分方法，在每个滤波时刻挑选出系统偏差对应的最优量测子集，利用量测子集中的多量测信息实现系统偏差的集中式融合估计，提高了系统偏差的估计精度和收敛速度。仿真实验表明，所提方法能够在数据关联未知的多目标多杂波场景下对雷达测量偏差和平台姿态角偏差进行有效估计，在平台姿态角变化率较低时，所提方法具有较强的适应性。
- 误差配准 /
- 数据关联 /
- 伯努利滤波 /
- 集中式融合 /
- 量测划分
Abstract: Traditional methods for multi-target bias registration in networked radar system typically assume that the data association relationship is known. However, in the case of platform maneuvering, there are simultaneously radar measurement biases and platform attitude angle biases, and the radar observation process is prone to clutter interference, resulting in difficulties in data association. To address this issue, a multi-target mobile radar bias registration method based on Bernoulli filter is proposed. Firstly, the measurement and state equations for the system biases are established, and then the system biases are modeled as a Bernoulli random finite set. The recursive estimation of the system biases under the Bernoulli filtering framework is achieved using the original measurements in a common coordinate system, effectively avoiding the data association. Additionally, to fully utilize multi-target measurement information, a modified greedy measurement partitioning method is proposed to select the optimal measurement subset corresponding to the system biases at each filtering time step, and the centralized fusion estimation of the system biases is performed using the multi-measurement information in the measurement subset, improving the estimation accuracy and convergence speed of the system biases. Simulation experiments show that the proposed method can effectively estimate radar measurement biases and platform attitude angle biases in multi-target and cluttered scenarios with unknown data association. Moreover, this method demonstrates strong adaptability when the platform attitude angle variation rate is low.
- Registration /
- Data association /
- Bernoulli filter /
- Centralized fusion /
- Measurement partition

HTML全文

图 1 场景1中偏差估计均方根误差图

下载: 全尺寸图片幻灯片

图 2 场景2中偏差估计均方根误差图

下载: 全尺寸图片幻灯片

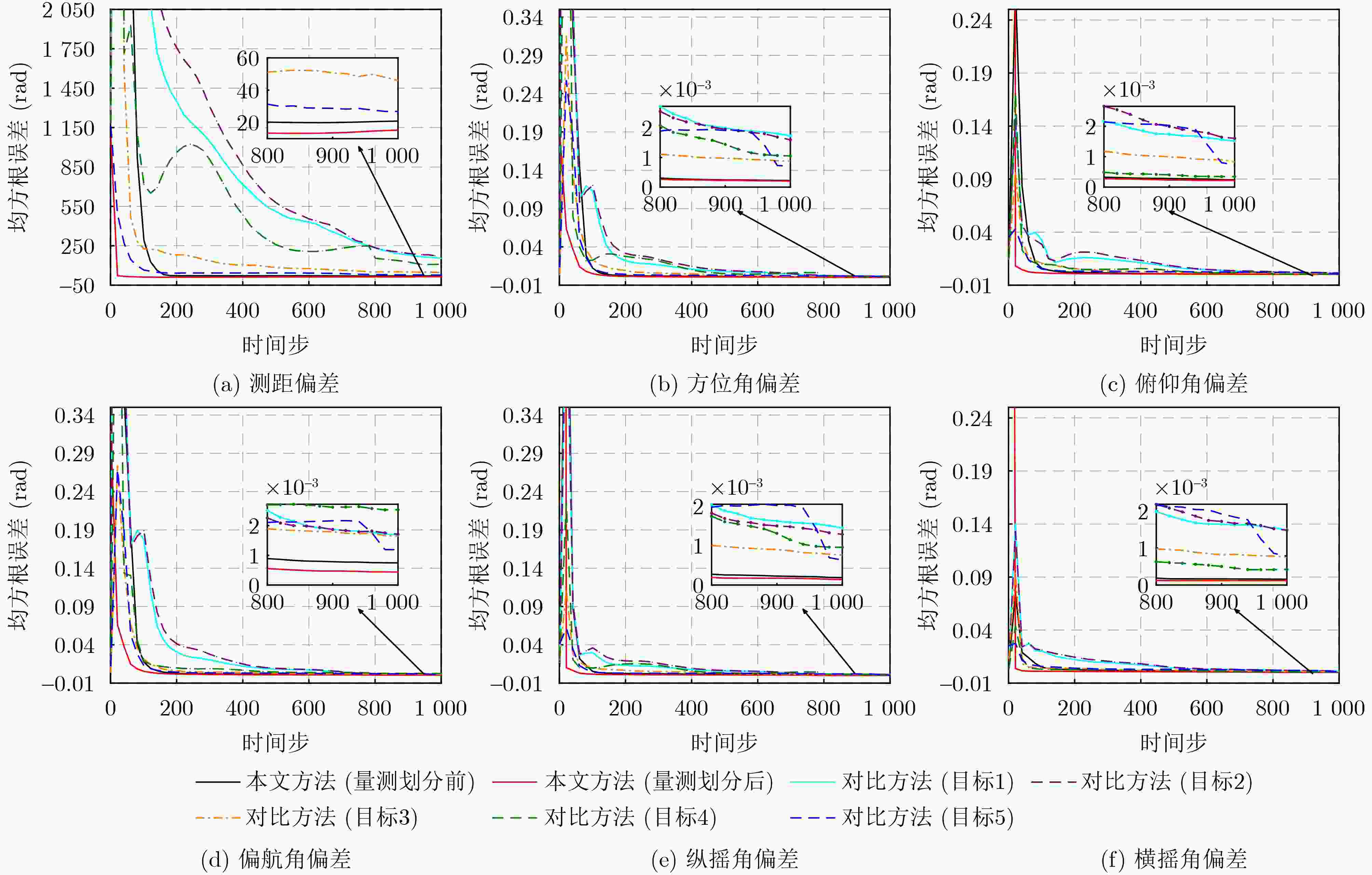
表 1 场景3中偏差收敛步数比较

量测划分前/后	偏差估计收敛步数
	雷达测量偏差			平台姿态角偏差
	径向距离	方位角	俯仰角	偏航角	纵摇角	横摇角
前	161	330	288	362	317	305
后	18	281	194	310	260	242

下载: 导出CSV

表 2 场景3中偏差估计精度比较(%)

量测划分前/后	偏差估计精度
	雷达测量偏差			平台姿态角偏差
	径向距离	方位角	俯仰角	偏航角	纵摇角	横摇角
前	98.43	96.52	90.33	93.25	93.34	92.14
后	98.66	98.18	95.04	97.31	96.71	96.53

下载: 导出CSV

参考文献(22)

[1]	何友, 修建娟, 关欣, 等. 雷达数据处理及应用[M]. 3版. 北京: 电子工业出版社, 2013: 335–340. HE You, XIU Jianjuan, GUAN Xin, et al. Radar Data Processing with Applications[M]. 3rd ed. Beijing: Publishing House of Electronics Industry, 2013: 335–340.
[2]	曾雅俊, 王俊, 魏少明, 等. 分布式多传感器多目标跟踪方法综述[J]. 雷达学报, 2023, 12(1): 197–213. doi: 10.12000/JR22111. ZENG Yajun, WANG Jun, WEI Shaoming, et al. Review of the method for distributed multi-sensor multi-target tracking[J]. Journal of Radars, 2023, 12(1): 197–213. doi: 10.12000/JR22111.
[3]	吴怡. 雷达组网误差配准与目标跟踪算法研究[D]. [硕士论文], 上海交通大学, 2020. doi: 10.27307/d.cnki.gsjtu.2020.001046. WU Yi. Research on radar network error registration and target tracking algorithm[D]. [Master dissertation], Shanghai Jiao Tong University, 2020. doi: 10.27307/d.cnki.gsjtu.2020.001046.
[4]	ZHOU Yifeng, LEUNG H, and BLANCHETTE M. Sensor alignment with Earth-centered Earth-fixed (ECEF) coordinate system[J]. IEEE Transactions on Aerospace and Electronic Systems, 1999, 35(2): 410–418. doi: 10.1109/7.766925.
[5]	董云龙, 何友, 王国宏, 等. 基于ECEF的广义最小二乘误差配准技术[J]. 航空学报, 2006, 27(3): 463–467. doi: 10.3321/j.issn:1000-6893.2006.03.023. DONG Yunlong, HE You, WANG Guohong, et al. Generalized least squares registration algorithm with Earth-Centered Earth-Fixed (ECEF) coordinate system[J]. Acta Aeronautica et Astronautica Sinica, 2006, 27(3): 463–467. doi: 10.3321/j.issn:1000-6893.2006.03.023.
[6]	董云龙, 张焱. 基于渐消因子的ECEF-GLS估计算法[J]. 系统工程与电子技术, 2024, 46(1): 137–142. doi: 10.12305/j.issn.1001-506X.2024.01.16. DONG Yunlong and ZHANG Yan. ECEF-GLS estimation algorithm based on fading factor[J]. Systems Engineering and Electronics, 2024, 46(1): 137–142. doi: 10.12305/j.issn.1001-506X.2024.01.16.
[7]	熊伟, 邢凤勇, 潘旭东, 等. 基于合作目标的动平台传感器偏差估计方法[J]. 系统工程与电子技术, 2011, 33(3): 544–547. doi: 10.3969/j.issn.1001-506X.2011.03.15. XIONG Wei, XING Fengyong, PAN Xudong, et al. Bias estimation for moving sensors network using cooperation targets[J]. Systems Engineering and Electronics, 2011, 33(3): 544–547. doi: 10.3969/j.issn.1001-506X.2011.03.15.
[8]	LU Chenyang, WANG Xiaorui, and KOUTSOUKOS X. Feedback utilization control in distributed real-time systems with end-to-end tasks[J]. IEEE Transactions on Parallel and Distributed Systems, 2005, 16(6): 550–561. doi: 10.1109/TPDS.2005.73.
[9]	OKELLO N and RISTIC B. Maximum likelihood registration for multiple dissimilar sensors[J]. IEEE Transactions on Aerospace and Electronic Systems, 2003, 39(3): 1074–1083. doi: 10.1109/TAES.2003.1238759.
[10]	崔亚奇, 熊伟, 何友. 基于MLR的机动平台传感器误差配准算法[J]. 航空学报, 2012, 33(1): 118–128. CUI Yaqi, XIONG Wei, and HE You. Mobile platform sensor registration algorithm based on MLR[J]. Acta Aeronautica et Astronautica Sinica, 2012, 33(1): 118–128.
[11]	WANG Jun, MA Shuheng, ZHANG Yuxi, et al. EMLR for multiple radars on a mobile platform[J]. The Journal of Engineering, 2019, 2019(20): 6494–6498. doi: 10.1049/joe.2019.0190.
[12]	WANG Jun, ZENG Yajun, WEI Shaoming, et al. Multi-sensor track-to-track association and spatial registration algorithm under incomplete measurements[J]. IEEE Transactions on Signal Processing, 2021, 69: 3337–3350. doi: 10.1109/TSP.2021.3084533.
[13]	LIN Xiangdong, BAR-SHALOM Y, and KIRUBARAJAN T. Exact multisensor dynamic bias estimation with local tracks[J]. IEEE Transactions on Aerospace and Electronic Systems, 2004, 40(2): 576–590. doi: 10.1109/TAES.2004.1310006.
[14]	LI W, LEUNG H, and ZHOU Yifeng. Space-time registration of radar and ESM using unscented Kalman filter[J]. IEEE Transactions on Aerospace and Electronic Systems, 2004, 40(3): 824–836. doi: 10.1109/TAES.2004.1337457.
[15]	CHEN Lei, WANG Guohong, HE You, et al. Analysis of mobile 3-D radar error registration when radar sways with platform[J]. Journal of Navigation, 2014, 67(3): 451–472. doi: 10.1017/s0373463313000799.
[16]	XIU Jianjuan, DONG Kai, and WANG Meng. System error real-time estimation of radar network based on iterative generalized least squares[C]. The 5th International Conference on Information Communication and Signal Processing, Shenzhen, China, 2022: 1–5. doi: 10.1109/ICICSP55539.2022.10050601.
[17]	LIAN Feng, HAN Cuiming, LIU Weifeng, et al. Joint spatial registration and multi-target tracking using an extended probability hypothesis density filter[J]. IET Radar, Sonar & Navigation, 2011, 5(4): 441–448. doi: 10.1049/iet-rsn.2010.0057.
[18]	LI Minzhe, JING Zhongliang, PAN Han, et al. Joint registration and multi-target tracking based on labelled random finite set and expectation maximisation[J]. IET Radar, Sonar & Navigation, 2018, 12(3): 312–322. doi: 10.1049/iet-rsn.2017.0137.
[19]	章涛, 李海, 吴仁彪. 基于概率假设密度滤波的多目标雷达空间误差配准算法[J]. 控制与决策, 2018, 33(8): 1429–1435. doi: 10.13195/j.kzyjc.2017.0506. ZHANG Tao, LI Hai, and WU Renbiao. Radar spatial registration with multiple targets based on probability hypothesis density filter[J]. Control and Decision, 2018, 33(8): 1429–1435. doi: 10.13195/j.kzyjc.2017.0506.
[20]	RISTIC B, VO B T, VO B N, et al. A tutorial on Bernoulli filters: Theory, implementation and applications[J]. IEEE Transactions on Signal Processing, 2013, 61(13): 3406–3430. doi: 10.1109/TSP.2013.2257765.
[21]	SAUCAN A A, COATES M J, and RABBAT M. A. A multisensor multi-Bernoulli filter[J]. IEEE Transactions on Signal Processing, 2017, 65(20): 5495–5509. doi: 10.1109/TSP.2017.2723348.
[22]	蔡如华, 樊向婷, 吴孙勇, 等. 基于交互式CPHD的多传感器多机动目标跟踪[J]. 控制与决策, 2022, 37(1): 47–57. doi: 10.13195/j.kzyjc.2020.0983. CAI Ruhua, FAN Xiangting, WU Sunyong, et al. Multi-sensor and multi-maneuver target tracking based on interactive CPHD[J]. Control and Decision, 2022, 37(1): 47–57. doi: 10.13195/j.kzyjc.2020.0983.