Robust Global Satellite Navigation System Positioning for Kernel Density Estimation in Non-Line-Of-Sight Environment
-
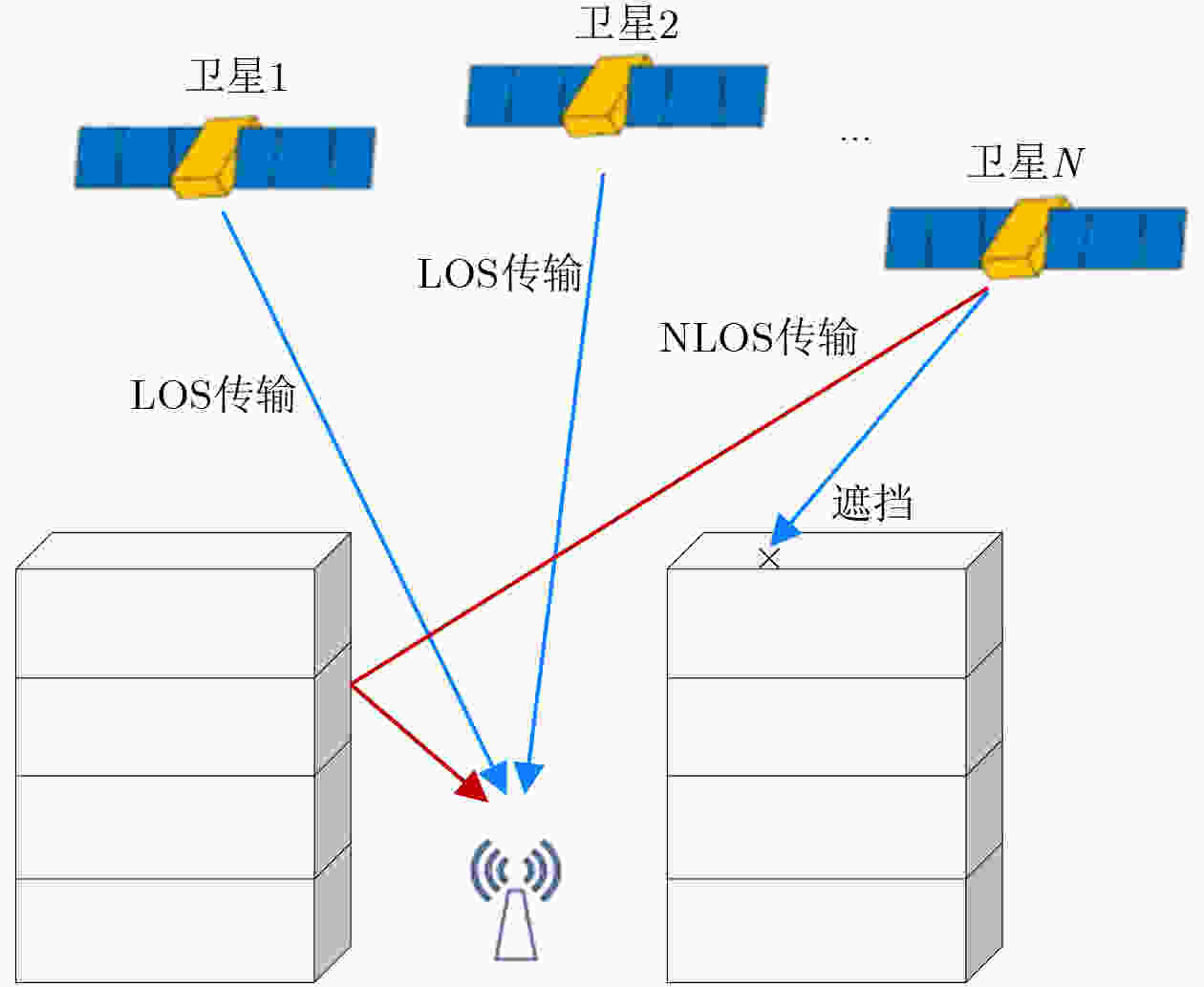
摘要: 非视距(NLOS)传输会引起全球卫星导航系统(GNSS)接收机的伪距测量误差,最终导致定位解出现较大误差,这一问题在城市峡谷等复杂环境下尤为突出。针对该问题,该文提出核密度估计的鲁棒定位方法,其核心思想是在定位解算中引入鲁棒估计来缓解NLOS的影响。考虑到NLOS引起的伪距观测误差偏离高斯分布,所提方法首先利用核密度估计(KDE)方法估计伪距观测误差的概率密度函数,并利用该概率密度函数来构造鲁棒代价函数用于导航解算,从而缓解NLOS引起的定位误差。实验结果表明所提方法在卫星存在NLOS传输时能够较好地减小GNSS的定位误差。Abstract: Non-Line-Of-Sight (NLOS) propagation will cause the pseudo-range measurement error of the Global Navigation Satellite System (GNSS) receivers, and eventually lead to a large positioning error, which is especially prominent in complex environments such as urban canyons. To solve this problem, a robust positioning method for Kernel Density Estimation (KDE) is proposed. The core idea is to introduce robust estimation theory into localization solution to alleviate the influence of NLOS. Considering that the pseudo-range observation error caused by NLOS deviates from the Gaussian distribution, the proposed method firstly uses the method based on KDE to estimate the probability density function of the observation error, and then uses the probability density function to construct a robust cost function for positioning solution, so as to alleviate the positioning error caused by NLOS. The experimental results show that the proposed method can effectively reduce GNSS positioning error in NLOS propagation environment.
-
1 核密度估计的鲁棒定位方法
步骤1 初始化设置,$l = 0$时利用传统LS得到接收机状态粗估
值${{\boldsymbol{\hat x}}_0}$;步骤2 根据式(12)确定观测量误差:
${\boldsymbol{\hat \varepsilon }} = {\boldsymbol{b}} - {\boldsymbol{G}}{[\Delta \hat x,\Delta \hat y,\Delta \hat z,\Delta \delta {\hat t_u}]^{\text{T}}}$;步骤3 应用核密度函数估计计算观测量误差的概率密度函数
$f(\hat {\boldsymbol{\varepsilon}} )$,并求其导函数$f'(\hat {\boldsymbol{\varepsilon}} )$;步骤4 用误差的概率密度函数及其导函数估计评分函数:
$\varphi ({\boldsymbol{\hat \varepsilon }}) = - {{f'({\boldsymbol{\hat \varepsilon }})} \mathord{\left/ {\vphantom {{f'({\boldsymbol{\hat \varepsilon }})} {f({\boldsymbol{\hat \varepsilon }})}}} \right. } {f({\boldsymbol{\hat \varepsilon }})}}$;步骤5 利用鲁棒代价函数迭代更新状态增量的估计值:
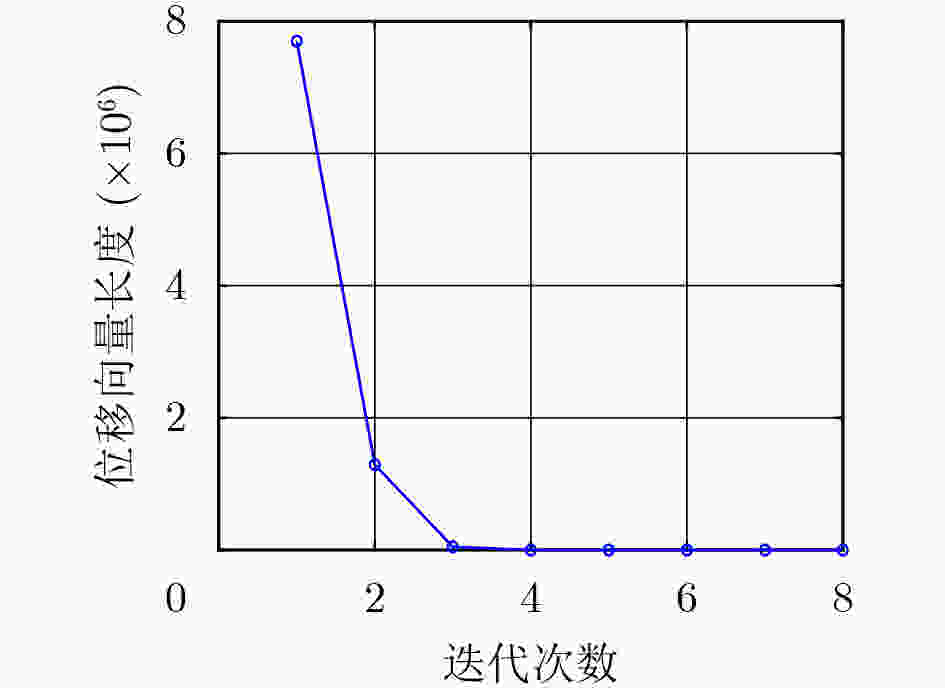
$\Delta {\boldsymbol{\hat x'}} = \Delta {\boldsymbol{\hat x}} + \mu {({{\boldsymbol{G}}^{\text{T}}}{\boldsymbol{G}})^{ - 1}}{{\boldsymbol{G}}^{\text{T}}}\hat \varphi ({\boldsymbol{\hat \varepsilon }})$步骤6 判断收敛性:若满足$\begin{array}{*{20}{c}} {\left\| {{{{\boldsymbol{\hat x}}}_l}} \right\| < \zeta ,}&{{\text{for}}} \end{array}\zeta \in {\boldsymbol{R}}$,则认
为导航解收敛,输出定位结果;否则返回至步骤2继续进行定
位解算。表 1 信号仿真参数
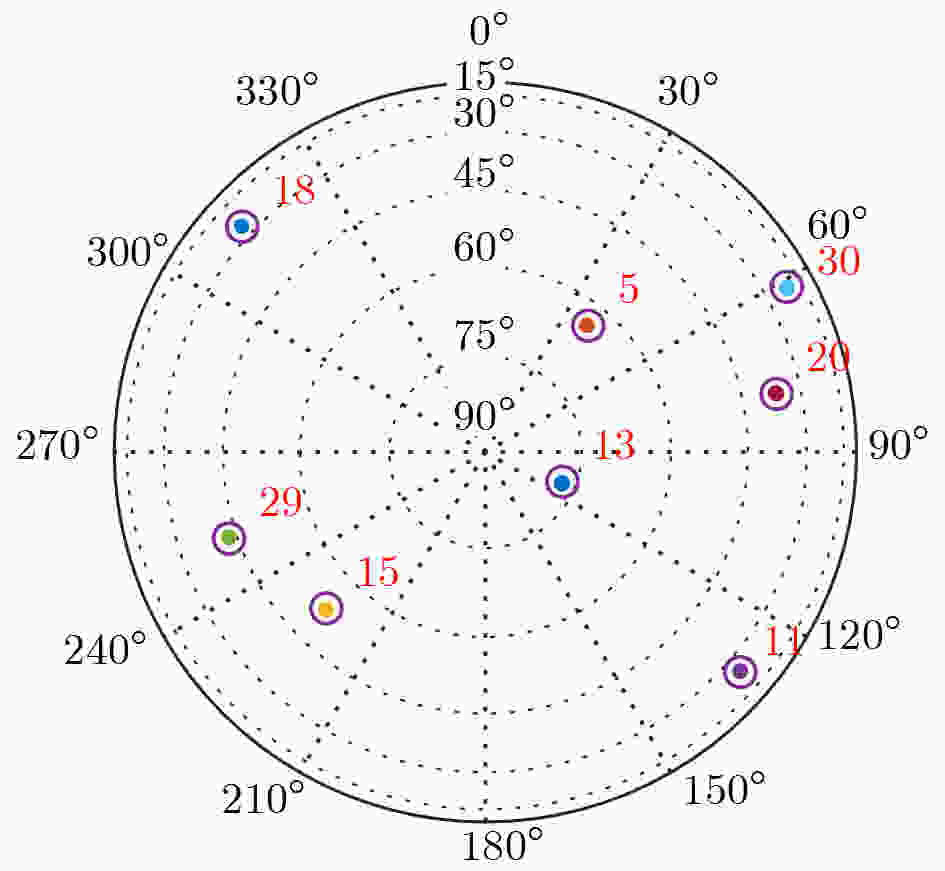
仿真信号参数 参数值 接收机中频(MHz) 1.364 接收机采样率(MHz) 5.45 定位周期(ms) 1 卫星PRN 5,11,13,15,18,20,29,30 卫星仰角(°) 64,25,77,52,26,37,43,22 载噪比(dB-Hz) 44.5,40.5,45.8,43.4,40.8,41.7,42.3,40.2 表 2 低仰角卫星存在NLOS时抑制前后的定位误差(m)
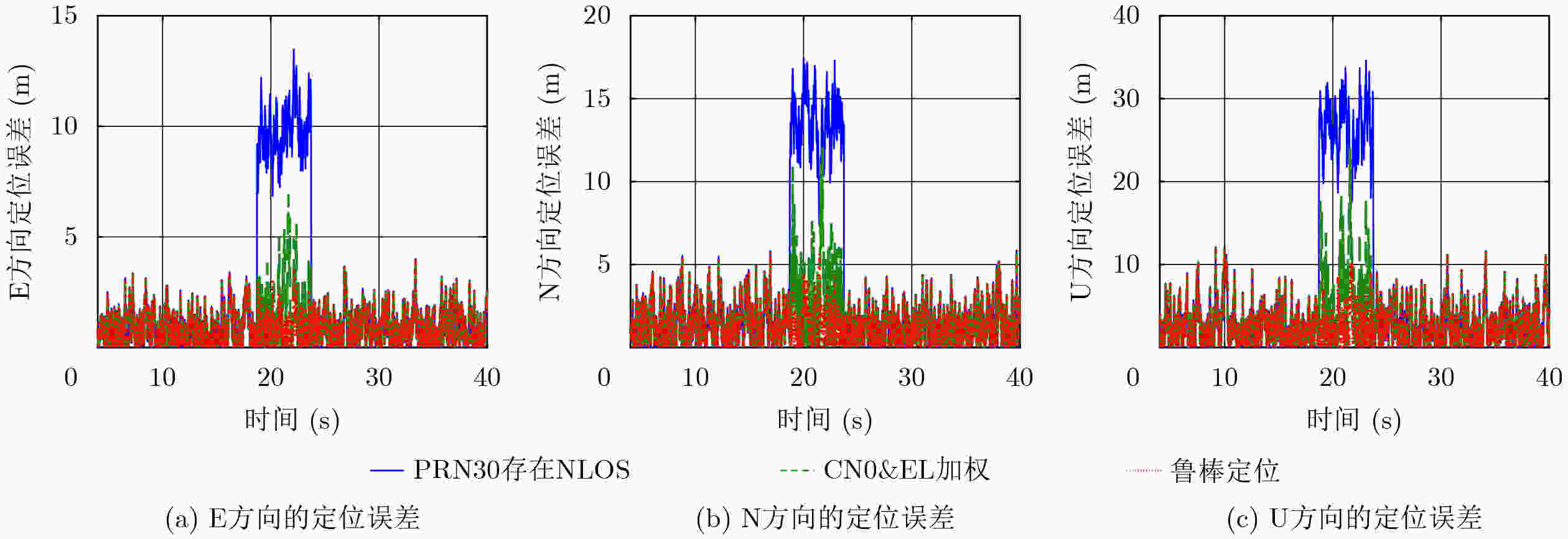
PRN30存在NLOS CN0&EI加权 鲁棒定位 平均值 E 9.8 1.6 1.2 N 13.5 3.1 2.7 U 26.4 6.1 9.8 均方根 E 9.9 2.1 1.1 N 13.6 3.8 1.8 U 26.6 7.6 3.5 最大值 E 13.5 6.9 3.6 N 17.4 12.1 5.6 U 34.6 24.4 10.2 表 3 高仰角卫星存在NLOS时抑制前后的定位误差(m)
PRN15存在NLOS CN0&EI加权 鲁棒定位 平均值 E 8.6 6.0 1.2 N 15.2 3.9 1.6 U 9.4 6.5 2.7 均方根 E 8.7 7.2 1.2 N 15.3 4.8 1.9 U 10.2 7.8 3.3 最大值 E 11.8 9.5 3.9 N 21.4 11.8 5.1 U 18.5 18.3 9.5 表 4 两颗卫星存在NLOS时抑制前后的定位误差(m)
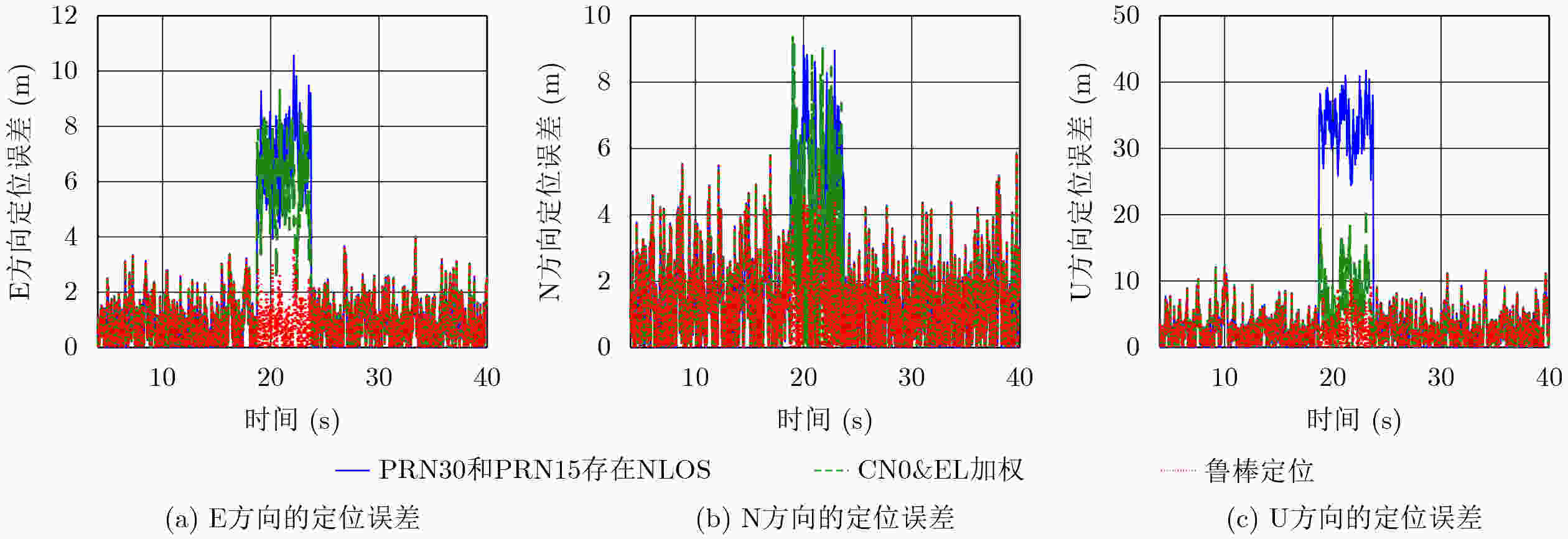
PRN30, PRN15存在NLOS CN0&EI加权 鲁棒定位 平均值 E 6.8 5.8 0.9 N 5.1 3.1 1.5 U 33.6 7.4 2.7 E 7.1 6.1 1.1 均方根 N 5.5 3.7 1.9 U 33.7 8.5 3.3 最大值 E 10.6 9.3 3.6 N 9.5 9.4 5.5 U 41.6 20.3 9.5 表 5 数据采集参数及可见卫星
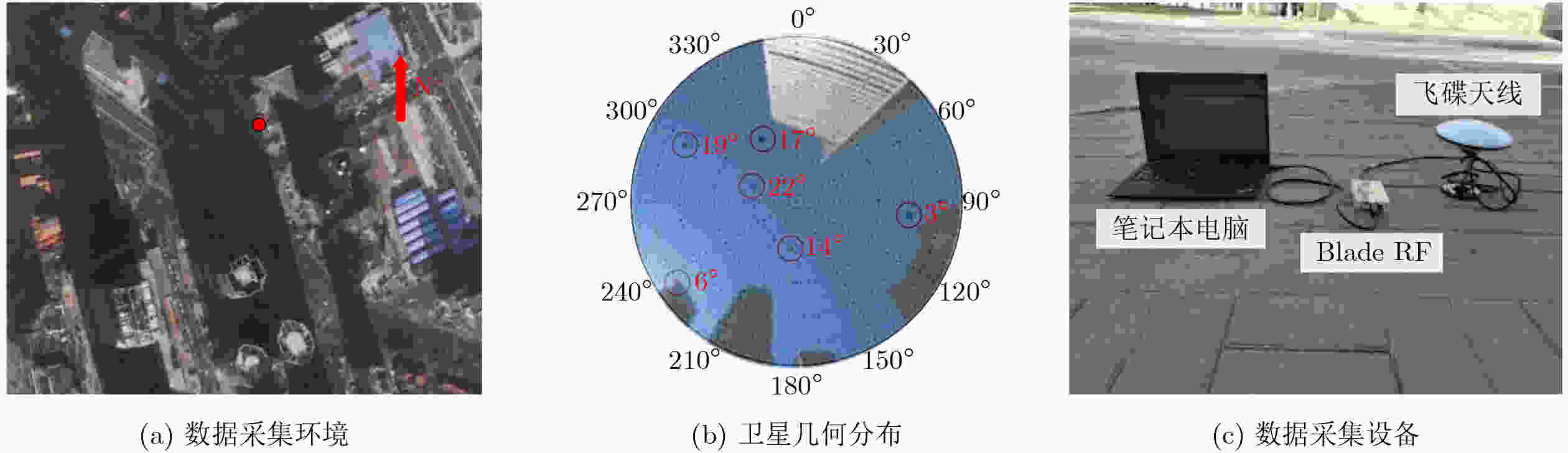
信号参数 参数值 接收机中频(MHz) 0 接收机采样率(MHz) 10 前端带宽(MHz) 2 信号采集时间(s) 50 卫星PRN 3,6,14,17,19,22 定位周期(s) 0.5 表 6 不同方法定位后的定位误差(m)
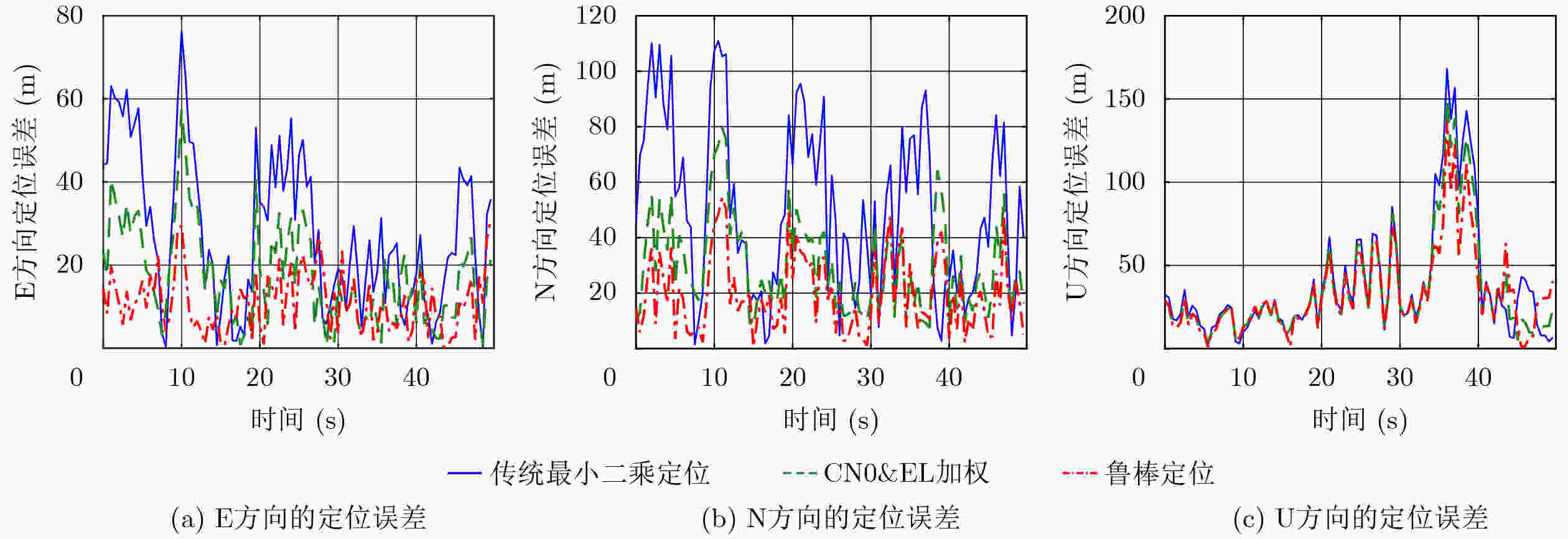
传统LS定位 CN0&EI加权 鲁棒定位 平均值 E 27.8 17.3 11.2 N 60.8 30.2 19.7 U 43.6 35.1 32.8 E 35.2 21.9 13.2 均方根 N 59.2 34.6 22.9 U 52.6 46.8 41.0 最大值 E 76.2 57.5 31.2 N 110.9 79.5 54.5 U 152.9 150.8 136.1 -
[1] 刘小汇, 王怡晨, 文超, 等. 复杂城市环境下的全球导航卫星系统/捷联惯性导航系统组合导航算法[J]. 电子与信息学报, 2023, 45(11): 4150–4160. doi: 10.11999/JEIT230834.LIU Xiaohui, WANG Yichen, WEN Chao, et al. Global navigation satellite system/strapdown inertial navigation system integrated navigation algorithm in complex urban environment[J]. Journal of Electronics & Information Technology, 2023, 45(11): 4150–4160. doi: 10.11999/JEIT230834. [2] 王巍, 邢朝洋, 冯文帅. 自主导航技术发展现状与趋势[J]. 航空学报, 2021, 42(11): 525049. doi: 10.7527/S1000-6893.2021.25049.WANG Wei, XING Chaoyang, and FENG Wenshuai. State of the art and perspectives of autonomous navigation technology[J]. Acta Aeronautica et Astronautica Sinica, 2021, 42(11): 525049. doi: 10.7527/S1000-6893.2021.25049. [3] ZHONG Qiming. Asymmetric positioning for NLOS mitigation[C]. The 36th International Technical Meeting of the Satellite Division of The Institute of Navigation, Denver, USA, 2023: 1905–1927. doi: 10.33012/2023.19336. [4] YE Xiaozhou, MA Pengcheng, LIU Wenxiang, et al. How NLOS signals affect GNSS relative positioning[J]. Journal of Physics: Conference Series, 2020, 1693(1): 012184. doi: 10.1088/1742-6596/1693/1/012184. [5] MOREAU J, AMBELLOUIS S, and RUICHEK Y. Fisheye-based method for GPS localization improvement in unknown semi-obstructed areas[J]. Sensors, 2017, 17(1): 119. doi: 10.3390/s17010119. [6] LIU Xikun, WEN Weisong, and HSU L T. 3D LiDAR aided GNSS NLOS correction with direction of arrival estimation using Doppler measurements[C]. The 36th International Technical Meeting of the Satellite Division of The Institute of Navigation, Denver, USA, 2023: 2206–2216. doi: 10.33012/2023.19447. [7] ZHONG Qiming and GROVES P. Optimizing LOS/NLOS modeling and solution determination for 3D-mapping-aided GNSS positioning[C]. The 36th International Technical Meeting of the Satellite Division of The Institute of Navigation, Denver, USA, 2023: 373–402. doi: 10.33012/2023.19406. [8] GROVES P D. Shadow matching: A new GNSS positioning technique for urban canyons[J]. Journal of Navigation, 2011, 64(3): 417–430. doi: 10.1017/S0373463311000087. [9] LV Xiang, DENG Zhongliang, and YE Nijun. Research on shadow matching algorithm based on consistency probability weighting[C]. China Satellite Navigation Conference (CSNC 2024) Proceedings, Singapore, 2024: 401–410. doi: 10.1007/978-981-99-6928-9_35. [10] NG H F, ZHANG Guohao, and HSU L T. Robust GNSS shadow matching for smartphones in urban canyons[J]. IEEE Sensors Journal, 2021, 21(16): 18307–18317. doi: 10.1109/JSEN.2021.3083801. [11] GROVES P D and JIANG Ziyi. Height aiding C/N0 weighting and consistency checking for GNSS NLOS and multipath mitigation in urban areas[J]. Journal of Navigation, 2013, 66(5): 653–669. doi: 10.1017/S0373463313000350. [12] HSU L T, TOKURA H, KUBO N, et al. Multiple faulty GNSS measurement exclusion based on consistency check in urban canyons[J]. IEEE Sensors Journal, 2017, 17(6): 1909–1917. doi: 10.1109/JSEN.2017.2654359. [13] SUZUKI T and AMANO Y. NLOS multipath classification of GNSS signal correlation output using machine learning[J]. Sensors, 2021, 21(7): 2503. doi: 10.3390/s21072503. [14] ZHANG Yilang, SUN Yuan, and DENG Zhongliang. Fuzzy C-mean clustering based NLOS signal identification method and localization model in urban canyon environment[C]. 2023 International Technical Meeting of The Institute of Navigation, Long Beach, USA, 2023: 844–858. doi: 10.33012/2023.18656. [15] YIN Naishu, HE Di, XIANG Yan, et al. Features effectiveness verification using machine-learning-based GNSS NLOS signal detection in urban canyon environment[C]. The 36th International Technical Meeting of the Satellite Division of The Institute of Navigation, Denver, USA, 2023: 3035–3048. doi: 10.33012/2023.19363. [16] COLLINS J P and LANGLEY R B. Possible weighting schemes for GPS carrier phase observations in the presence of multipath[R]. Contract No. DAAH04-96-C-0086, 1999. [17] BRUNNER F K, HARTINGER H, and TROYER L. GPS signal diffraction modelling: The stochastic SIGMA-Δ model[J]. Journal of Geodesy, 1999, 73(5): 259–267. doi: 10.1007/s001900050242. [18] REALINI E and REGUZZONI M. goGPS: Open source software for enhancing the accuracy of low-cost receivers by single-frequency relative kinematic positioning[J]. Measurement Science and Technology, 2013, 24(11): 115010. doi: 10.1088/0957-0233/24/11/115010. [19] LIM C H, ZOUBIR A M, SEE C M S, et al. A robust statistical approach to non-line-of-sight mitigation[C]. 2007 IEEE/SP 14th Workshop on Statistical Signal Processing, Madison, USA, 2007: 428–432. doi: 10.1109/SSP.2007.4301294. [20] HAMMES U, WOLSZTYNSKI E, and ZOUBIR A M. Semi-parametric geolocation estimation in NLOS environments[C]. 2008 16th European Signal Processing Conference, Lausanne, Switzerland, 2008: 1–5. [21] GHOSH S. Kernel Smoothing: Principles, Methods and Applications[M]. Switzerland: John Wiley and Sons Ltd., 2018. [22] MEDINA D, LI Haoqing, VILÀ-VALLS J, et al. Robust filtering techniques for RTK positioning in harsh propagation environments[J]. Sensors, 2021, 21(4): 1250. doi: 10.3390/s21041250. [23] YIN Feng and ZOUBIR A M. Robust positioning in NLOS environments using nonparametric adaptive kernel density estimation[C]. 2012 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Kyoto, Japan, 2012: 3517–3520. doi: 10.1109/ICASSP.2012.6288675. [24] DING Yi, FERIOL F, YOKO W, et al. Adaptive robust-statistics GNSS navigation based on environmental context detection[C]. 2023 International Technical Meeting of the Institute of Navigation, Long Beach, USA, 2023: 138–152. doi: 10.33012/2023.18636. [25] DANIELE B and PAU C. Complex Signum non-linearity for robust GNSS interference mitigation[J]. IET Radar, Sonar & Navigation, 2018, 12(8): 900–909. doi: 10.1049/iet-rsn.2017.0552. [26] GRAMACKI A. Nonparametric Kernel Density Estimation and its Computational Aspects[M]. Cham: Springer, 2018. doi: 10.1007/978-3-319-71688-6. [27] SILVERMAN B W. Density Estimation for Statistics and Data Analysis[M]. London: Chapman and Hall, 1986. [28] 谢钢. GPS原理与接收机设计[M]. 北京: 电子工业出版社, 2009: 103–106.XIE Gang. Principles of GPS and receiver design[M]. 1st ed. Bei jing: Publishing House of Electronics Industry, 2009: 103–106. -





 下载:
下载:




 下载:
下载:
