Off-grid DOA Estimation Algorithm Based on Taylor-expansion and Alternating Projection Maximum Likelihood
-
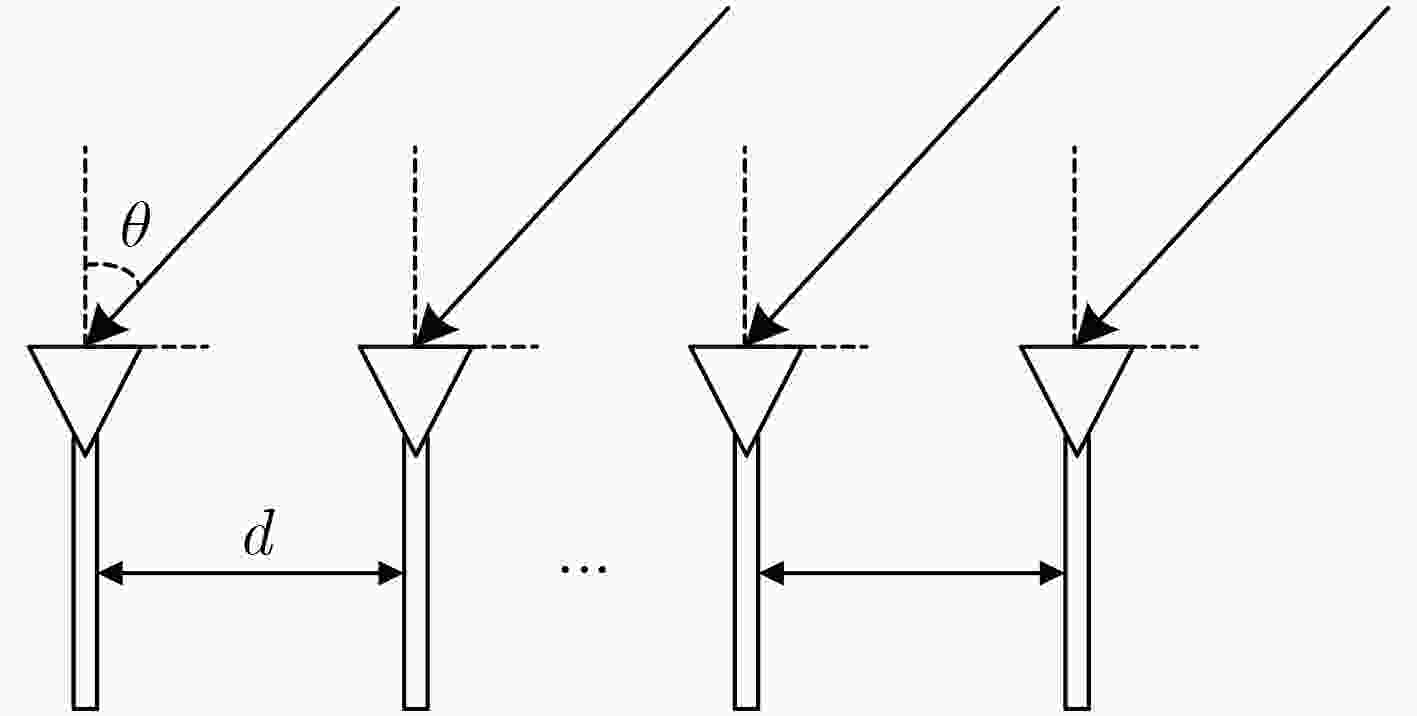
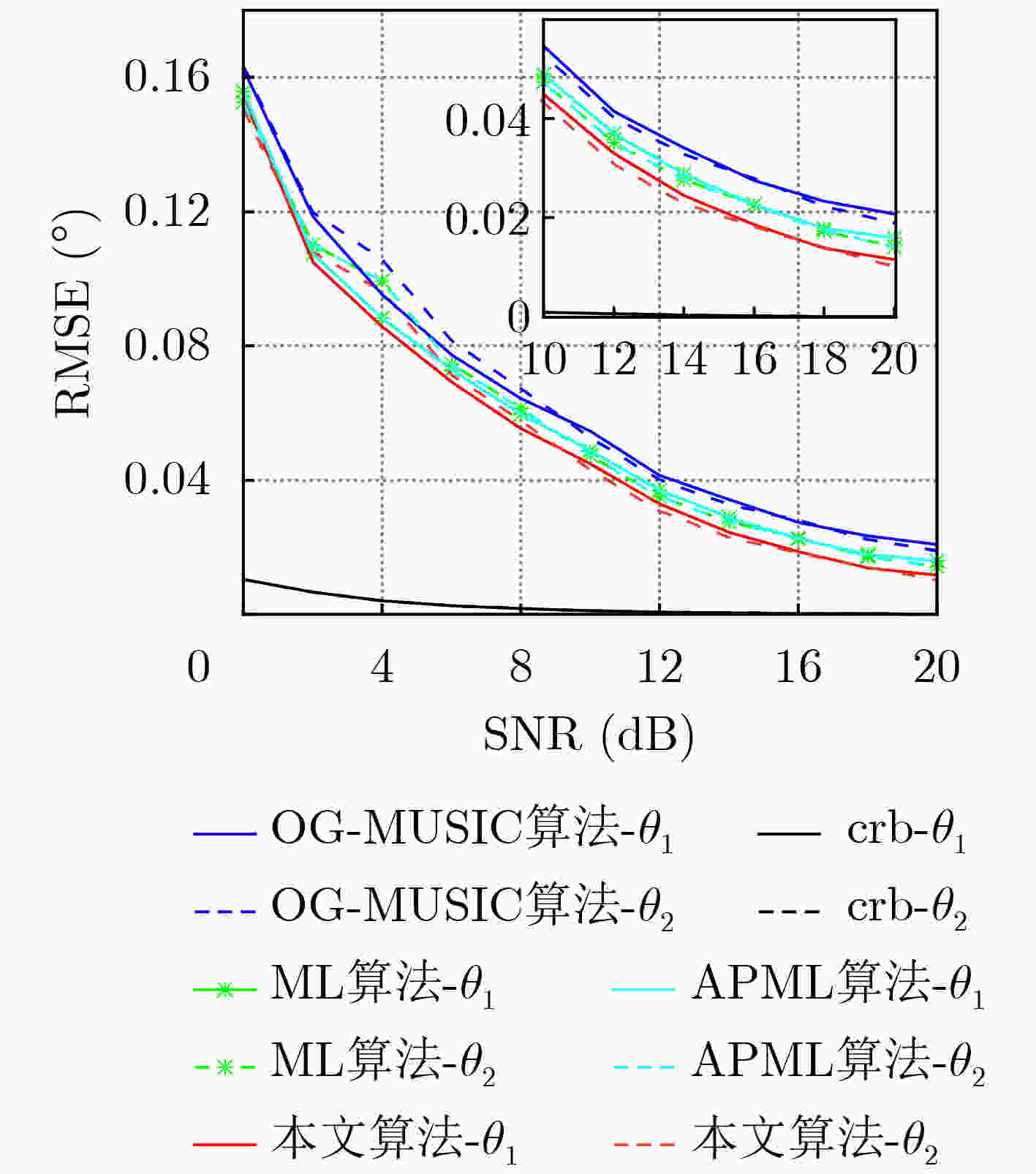
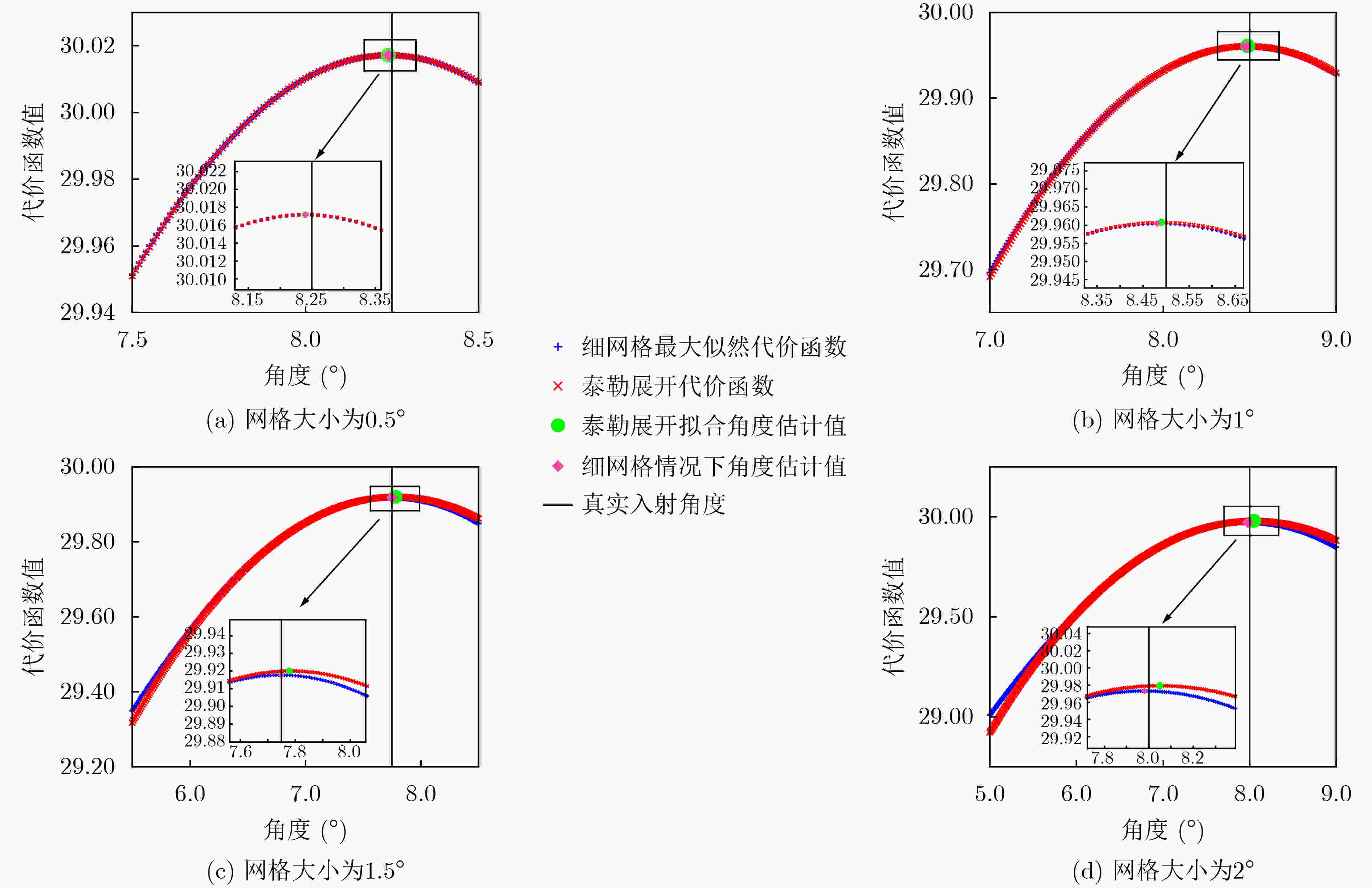
摘要: 针对最大似然DOA估计算法需要多维搜索、计算量大且面临着在网格估计的问题，该文提出一种基于泰勒展开的离网格交替投影最大似然算法。该方法首先利用交替投影将多维搜索转化为多个1维搜索，获得对应预设大网格的粗估计结果；再利用矩阵求导理论将1维代价函数在粗估计结果处进行2阶泰勒展开；最后通过对2阶泰勒展开求偏导并令导数等于零，求得离网参数的闭式解。与交替投影最大似然算法相比，该方法突破了搜索网格大小的限制，在保证算法精度的同时，有效减少了算法的在网格计算点数，提升了运算效率。仿真结果证明了该算法的有效性。Abstract: According to the problem that the maximum likelihood DOA estimation algorithm requires multi-dimensional search, is computationally intensive, and there is a problem in grid estimation, an Off-grid alternating projection maximum likelihood algorithm based on Taylor expansion is proposed. Firstly, the alternating projection method is used to transform the multi-dimensional search into multiple one-dimensional searches to obtain the rough estimation results corresponding to the preset large grid. Then, the second-order Taylor expansion of the one-dimensional cost function at the rough estimation results is carried out by using the matrix derivation theory. Finally, by calculating the partial derivative of the second-order Taylor expansion and making the derivative equal to zero, the closed-form solution of the off-grid parameters is obtained. Compared with the alternating projection maximum likelihood algorithm, the proposed algorithm breaks through the limitation of the search grid size. It effectively reduces the number of points in the grid calculation of the algorithm while ensuring the accuracy of itself, and improves the operation efficiency. Simulation results show the effectiveness of the algorithm.
-
Key words:
- Maximum likelihood algorithm /
- Alternating projection /
- Off-grid /
- Taylor expansion
-
[1] SHAMAEI K and KASSAS Z M. A joint TOA and DOA acquisition and tracking approach for positioning with LTE signals[J]. IEEE Transactions on Signal Processing, 2021, 69: 2689–2705. doi: 10.1109/TSP.2021.3068920. [2] LONMO T I B, AUSTENG A, and HANSEN R E. Data-driven autocalibration for swath sonars[J]. IEEE Journal of Oceanic Engineering, 2021, 46(3): 979–987. doi: 10.1109/JOE.2020.3036184. [3] SCHMID R. Multiple emitter location and signal parameter estimation[J]. IEEE Transactions on Antennas and Propagation, 1986, 34(3): 276–280. doi: 10.1109/TAP.1986.1143830. [4] ROY R and KAILATH T. ESPRIT — estimation of signal parameters via rotational invariance techniques[J]. IEEE Transactions on Acoustics, Speech, and Signal Processing, 1989, 37(7): 984–995. doi: 10.1109/29.32276. [5] WAX M and ADLER A. Direction of arrival estimation in the presence of model errors by signal subspace matching[J]. Signal Processing, 2021, 181: 107900. doi: 10.1016/j.sigpro.2020.107900. [6] SUN Meng, WANG Yide, and PAN Jingjing. Direction of arrival estimation by a modified orthogonal propagator method with spline interpolation[J]. IEEE Transactions on Vehicular Technology, 2019, 68(11): 11389–11393. doi: 10.1109/TVT.2019.2944516. [7] ASGHARI M, ZAREINEJAD, REZAEI S M, et al. DOA estimation of noncircular signals under impulsive noise using a novel empirical characteristic function-based MUSIC[J]. Circuits, Systems, and Signal Processing, 2023, 42(6): 3706–3743. doi: 10.1007/s00034-022-02289-9. [8] LIN Hongguang, JIN Longsheng, DING Ruixuan, et al. DOA estimation method for incoherently distributed sources based on spatial–temporal generalized ESPRIT[J]. AEU - International Journal of Electronics and Communications, 2023, 168: 154701. doi: 10.1016/j.aeue.2023.154701. [9] ZHANG Wei, HAN Yong, JIN Ming, et al. An improved ESPRIT-like algorithm for coherent signals DOA estimation[J]. IEEE Communications Letters, 2020, 24(2): 339–343. doi: 10.1109/LCOMM.2019.2953851. [10] YANG Zai, CHEN Xinyao, and WU Xunmeng. A robust and statistically efficient maximum-likelihood method for DOA estimation using sparse linear arrays[J]. IEEE Transactions on Aerospace and Electronic Systems, 2023, 59(5): 6798–6812. doi: 10.1109/TAES.2023.3280894. [11] GAO Yumeng, LI Jianghui, BAI Yechao, et al. An improved subspace weighting method using random matrix theory[J]. Frontiers of Information Technology & Electronic Engineering, 2020, 21(9): 1302–1307. doi: 10.1631/FITEE.1900463. [12] CADZOW J A. A high resolution direction-of-arrival algorithm for narrow-band coherent and incoherent sources[J]. IEEE Transactions on Acoustics, Speech, and Signal Processing, 1988, 36(7): 965–979. doi: 10.1109/29.1618. [13] SWINDLEHURST A. Alternative algorithm for maximum likelihood DOA estimation and detection[J]. IEE Proceedings –Radar, Sonar and Navigation, 1994, 141(6): 293–299. doi: 10.1049/ip-rsn:19941366. [14] VIBERG M, OTTERSTEN B, and KAILATH T. Detection and estimation in sensor arrays using weighted subspace fitting[J]. IEEE Transactions on Signal Processing, 1991, 39(11): 2436–2449. doi: 10.1109/78.97999. [15] ZISKIND I and WAX M. Maximum likelihood localization of multiple sources by alternating projection[J]. IEEE Transactions on Acoustics, Speech, and Signal Processing, 1988, 36(10): 1553–1560. doi: 10.1109/29.7543. [16] FU Haosheng, DAI Fengzhou, and HONG Ling. Off-grid error calibration for DOA estimation based on sparse Bayesian learning[J]. IEEE Transactions on Vehicular Technology, 2023, 72(12): 16293–16307. doi: 10.1109/TVT.2023.3298965. [17] GUO Qijia, XIN Zhinan, ZHOU Tian, et al. Off-grid space alternating sparse Bayesian learning[J]. IEEE Transactions on Instrumentation and Measurement, 2023, 72: 1002310. doi: 10.1109/TIM.2023.3243677. [18] YANG Zai, XIE Lihua, and ZHANG Cishen. Off-grid direction of arrival estimation using sparse Bayesian inference[J]. IEEE Transactions on Signal Processing, 2013, 61(1): 38–43. doi: 10.1109/TSP.2012.2222378. [19] MA Yanan, CAO Xianbin, and WANG Xiangrong. Efficient off-grid DOA estimation based on modified MUSIC for arbitrary linear arrays[C]. 2019 IEEE International Conference on Signal, Information and Data Processing (ICSIDP), Chongqing, China, 2019: 1–5. doi: 10.1109/ICSIDP47821.2019.9173323. [20] 曾富红, 彭占立, 司伟建, 等. 基于双平行互质极化敏感阵列的二维非网格DOA及极化参数估计[J]. 航空兵器, 2023, 30(3): 129–135. doi: 10.12132/ISSN.1673-5048.2022.0191.ZENG Fuhong, PENG Zhanli, SI Weijian, et al. Two-dimensional off-grid DOA and polarization parameter estimation for parallel coprime polarization sensitive array[J]. Aero Weaponry, 2023, 30(3): 129–135. doi: 10.12132/ISSN.1673-5048.2022.0191. [21] 揭允康, 张雯, 李想, 等. 一种基于迭代自适应的离网格DOA估计方法[J]. 电子与信息学报, 2023, 45(10): 3805–3811. doi: 10.11999/JEIT221061.JIE Yunkang, ZHANG Wen, LI Xiang, et al. An off-grid DOA estimation based on iterative adaptive approach[J]. Journal of Electronics & Information Technology, 2023, 45(10): 3805–3811. doi: 10.11999/JEIT221061. [22] 张贤达. 矩阵分析与应用[M]. 2版. 北京: 清华大学出版社, 2013: 50.ZHANG Xianda. Matrix Analysis and Applications[M]. 2nd ed. Beijing: Tsinghua University Press, 2013: 50. -
下载:
图(4) / 表(1)
计量
- 文章访问数: 221
- HTML全文浏览量: 66
- PDF下载量: 38
- 被引次数: 0
下载:
