3D Coordinate-coupled Variable Structure Multiple Model Estimator for Maneuvering Target Tracking
-
摘要: 在3维空间机动目标跟踪过程中,目标运动先验未知和坐标耦合误差会引起运动模型-模式失配,而模型-模式失配会引起状态估计有偏。该文根据目标运动速度正交条件修正状态转移矩阵,利用原始-对偶正则约束空间测量到球面可行域,结合自适应转弯率模型和无迹卡尔曼滤波(UKF),进行模型状态滤波并融合状态估计的一致输出,推导3维变结构多模型无迹卡尔曼滤波(VSMMUKF)算法。实验结果表明,相比多模重要性无迹卡尔曼滤波(MIUKF)算法,VSMMUKF计算量相当,能够更准确地拟合3维空间点目标机动运动。相比于交互多模型最大最小粒子滤波(IMM-MPF)算法,VSMMUKF跟踪固定翼无人机(UAV)的滤波精度提升了2.8%~59.9%,整体算法负担减小了1个数量级。Abstract: In the 3D maneuvering target tracking, unknown prior and coordinate coupling errors can cause model-mode mismatch and state estimation bias. In this paper, the state transition matrices are modified based on the target velocity-orthogonal condition, the spherical feasible domain is approximated by using the primal-dual regularization, and the adaptive turn rate model is combined in the frame of Unscented Kalman Filtering (UKF) to estimate the model-conditioned state, attaining the consistent output processing. 3D Variable Structure Multi-Model UKF (VSMMUKF) algorithm is derived. Simulation results show that, compared to the Multimode Importance UKF (MIUKF) algorithm, VSMMUKF can more accurately fit the maneuvering motion of 3D spatial point target with the comparable computational complexity; Compared to the Interactive Multi-model Maximum Minimum Particle Filtering (IMM-MPF) algorithm, the filtering accuracy of VSMMUKF for tracking a fixed-wing Unmanned Aerial Vehicle (UAV) has improved by 2.8%~59.9%, and the overall computation burden has reduced an order of magnitude.
-
表 1 表100轮蒙特卡罗实验统计滤波误差(均值、最大值及协方差)和实验运行时间
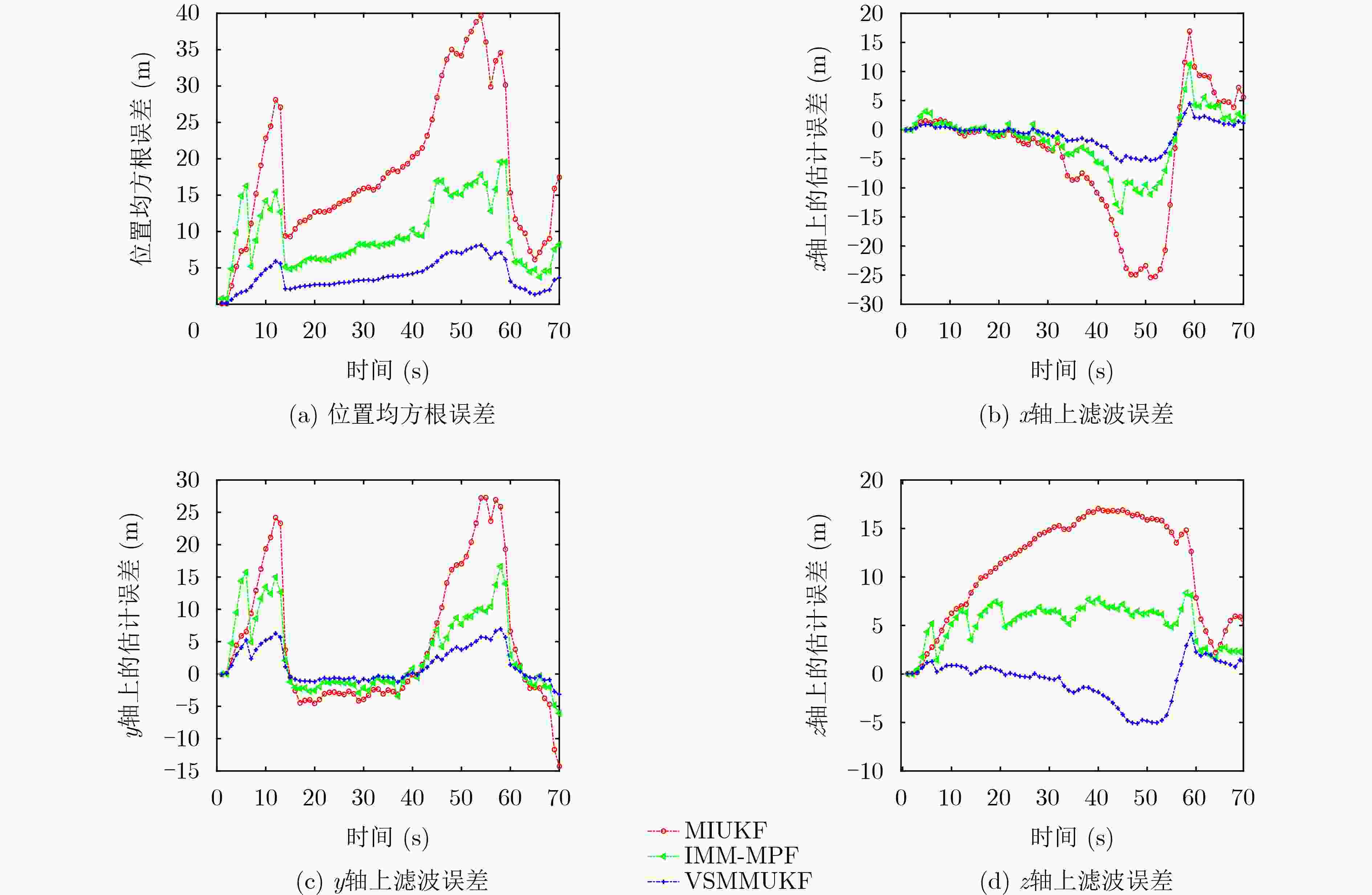
算法 位置均方根误差 $ x $轴上滤波误差 $ y $轴上滤波误差 $ z $轴上滤波误差 运行时间 (s) 均值 (m) 标准差 (m) 最大值 (m) 标准差 (m) 最大值 (m) 标准差 (m) 最大值 (m) 标准差 (m2) MIUKF 18.34 10.10 –25.41 10.19 27.28 10.70 17.04 5.42 1.36 IMM-MPF 9.69 4.68 –14.05 4.94 16.63 6.06 8.36 2.18 16.05 VSMUKF 3.88 2.05 –5.45 2.24 6.97 2.66 –5.11 2.12 5.93 -
[1] BAR-SHALOM Y, LI X R, and KIRUBARAJAN T. Estimation with Applications to Tracking and Navigation: Theory, Algorithms and Software[M]. New York: John Wiley & Sons, 2002. [2] LI X R and JILKOV V P. Survey of maneuvering target tracking. Part I. Dynamic models[J]. IEEE Transactions on Aerospace and Electronic Systems, 2003, 39(4): 1333–1364. doi: 10.1109/TAES.2003.1261132. [3] ZHANG Hongwei and LI Pengfei. Measurement-driven Gauss-Hermite particle filter with soft spatiotemporal constraints for multi-optical theodolites target tracking[J]. Chinese Journal of Aeronautics, 2023, 36(8): 313–330. doi: 10.1016/j.cja.2023.03.007. [4] 周宏仁. 机动目标跟踪[M]. 北京: 国防工业出版社, 1991.ZHOU Hongren. Tracking of Maneuvering Targets[M]. Beijing: National Defense Industry Press, 1991. [5] KIRUBARAJAN T and BAR-SHALOM Y. Kalman filter vs. IMM estimator: When do we need the latter?[C]. SPIE 4048, Signal and Data Processing of Small Targets 2000, Orlando, USA, 2000: 576–582. doi: 10.1117/12.392013. [6] 李盈萱, 王中训, 董云龙. 两种新的机动目标仿真模型[J]. 系统仿真学报, 2023, 35(7): 1581–1589. doi: 10.16182/j.issn1004731x.joss.22-0295.LI Yingxuan, WANG Zhongxun, and DONG Yunlong. Two new maneuvering target simulation methods[J]. Journal of System Simulation, 2023, 35(7): 1581–1589. doi: 10.16182/j.issn1004731x.joss.22-0295. [7] 滕康, 周勇. 基于当前统计模型改进的机动目标自适应跟踪算法[J/OL]. 现代雷达, 2023: 1–9. http://kns.cnki.net/kcms/detail/32.1353.TN.20231031.1535.002.html, 2024.TENG Kang and ZHOU Yong. Adaptive tracking algorithm of maneuvering target based on current statistical model[J]. Modern Radar, 2023: 1–9. http://kns.cnki.net/kcms/detail/32.1353.TN.20231031.1535.002.html, 2024. [8] 刘宗香, 谢维信, 黄敬雄. 一种用于三维空间杂波环境机动目标跟踪的数据互联方法[J]. 电子与信息学报, 2009, 31(4): 848–852. doi: 10.3724/SP.J.1146.2007.01880.LIU Zongxiang, XIE Weixin, and HUANG Jingxiong. A data association method for maneuvering target tracking in three-dimensional space under the circumstance of clutter[J]. Journal of Electronics & Information Technology, 2009, 31(4): 848–852. doi: 10.3724/SP.J.1146.2007.01880. [9] LI X R and JILKOV V P. Survey of maneuvering target tracking. Part V. Multiple-model methods[J]. IEEE Transactions on Aerospace and Electronic Systems, 2005, 41(4): 1255–1321. doi: 10.1109/TAES.2005.1561886. [10] LI X R, JILKOV V P, and RU J. Multiple-model estimation with variable structure-part VI: Expected-mode augmentation[J]. IEEE Transactions on Aerospace and Electronic Systems, 2005, 41(3): 853–867. doi: 10.1109/TAES.2005.1541435. [11] LI X R. Model-set sequence-conditioned estimation for variable-structure MM estimation[C]. SPIE 3373, Signal and Data Processing of Small Targets, Orlando, USA, 1998: 546−558. doi: 10.1117/12.324650. [12] LI X R. Multiple-model estimation with variable structure. II. Model-set adaptation[J]. IEEE Transactions on Automatic Control, 2000, 45(11): 2047–2060. doi: 10.1109/9.887626. [13] LI X R and ZHANG Youmin. Multiple-model estimation with variable structure. V. Likely-model set algorithm[J]. IEEE Transactions on Aerospace and Electronic Systems, 2000, 36(2): 448–466. doi: 10.1109/7.845222. [14] 孙照强, 王志贵, 孟飞, 等. 基于EKF及弹道方程的弹道目标跟踪滤波器设计[J]. 系统工程与电子技术, 2022, 44(10): 3207–3212. doi: 10.12305/j.issn.1001-506x.2022.10.25.SUN Zhaoqiang, WANG Zhigui, MENG Fei, et al. Ballistic target tracking filter design based on EKF and ballistic equations[J]. Systems Engineering and Electronics, 2022, 44(10): 3207–3212. doi: 10.12305/j.issn.1001-506x.2022.10.25. [15] ZHANG Hongwei and XIE Weixin. Constrained unscented Kalman filtering for bearings-only maneuvering target tracking[J]. Chinese Journal of Electronics, 2020, 29(3): 501–507. doi: 10.1049/cje.2020.02.006. [16] JULIER S J, UHLMANN J K, and DURRANT-WHYTE H F. A new approach for filtering nonlinear systems[C]. 1995 American Control Conference - ACC’95, Seattle, USA, 1995: 1628–1632. doi: 10.1109/ACC.1995.529783. [17] 王平波, 刘杨. 基于改进自适应IMM-UKF算法的水下目标跟踪[J]. 电子与信息学报, 2022, 44(6): 1999–2005. doi: 10.11999/jeit211128.WANG Pingbo and LIU Yang. Underwater target tracking algorithm based on improved adaptive IMM-UKF[J]. Journal of Electronics & Information Technology, 2022, 44(6): 1999–2005. doi: 10.11999/jeit211128. [18] LIM J, KIM H S, and PARK H M. Interactive-multiple-model algorithm based on Minimax particle filtering[J]. IEEE Signal Processing Letters, 2019, 27: 36–40. doi: 10.1109/LSP.2019.2954000. [19] JULIER S J and UHLMANN J K. Unscented filtering and nonlinear estimation[J]. Proceedings of the IEEE, 2004, 92(3): 401–422. doi: 10.1109/JPROC.2003.823141. [20] 张宏伟, 张小虎, 曹勇. 贝叶斯序贯重要性积分滤波器[J]. 电子学报, 2022, 50(4): 823–831. doi: 10.12263/DZXB.20210716.ZHANG Hongwei, ZHANG Xiaohu, and CAO Yong. Bayesian sequential importance quadrature filter[J]. Acta Electronica Sinica, 2022, 50(4): 823–831. doi: 10.12263/DZXB.20210716. [21] LIM J, KIM H S, and PARK H M. Minimax particle filtering for tracking a highly maneuvering target[J]. International Journal of Robust and Nonlinear Control, 2020, 30(2): 636–651. doi: 10.1002/rnc.4785. [22] 王昱淇, 卢宙, 蔡云泽. 基于一致性的分布式变结构多模型方法[J]. 自动化学报, 2021, 47(7): 1548–1557. doi: 10.16383/j.aas.c190091.WANG Yuqi, LU Zhou, and CAI Yunze. Consensus-based distributed variable structure multiple model[J]. Acta Automatica Sinica, 2021, 47(7): 1548–1557. doi: 10.16383/j.aas.c190091. [23] ROSSI F, VAN BEEK P, and WALSH T. Constraint programming[J]. Foundations of Artificial Intelligence, 2018, 3: 181–211. [24] XU Linfeng, LI X R, LIANG Yan, et al. Modeling and state estimation of linear destination-constrained dynamic systems[J]. IEEE Transactions on Signal Processing, 2022, 70: 2374–2387. doi: 10.1109/TSP.2022.3166113. [25] AFTAB W and MIHAYLOVA L. A learning gaussian process approach for maneuvering target tracking and smoothing[J]. IEEE Transactions on Aerospace and Electronic Systems, 2021, 57(1): 278–292. doi: 10.1109/TAES.2020.3021220. [26] ZHANG Hongwei, YE Xiaoyu, and HU Qi. Spatiotemporal learning via mixture importance Gaussian filtering with sparse regularization[J]. IEEE Signal Processing Letters, 2023, 30: 279–283. doi: 10.1109/LSP.2023.3258861. [27] FAN Xuxiang, WANG Gang, HAN Jiachen, et al. Interacting multiple model based on maximum correntropy Kalman filter[J]. IEEE Transactions on Circuits and Systems II: Express Briefs, 2021, 68(8): 3017–3021. doi: 10.1109/TCSII.2021.3068221. [28] ZHANG Hongwei. Multiple importance unscented Kalman filtering with soft spatiotemporal constraint for multi‐passive‐sensor target tracking[J]. International Journal of Robust and Nonlinear Control, 2023, 33(1): 264–281. doi: 10.1002/rnc.5977. [29] SÄRKKÄ S. Bayesian Filtering and Smoothing[M]. Cambridge: Cambridge University Press, 2013. doi: 10.1017/CBO9781139344203. [30] SILVESTRE D. Constrained convex generators: A tool suitable for set-based estimation with range and bearing measurements[J]. IEEE Control Systems Letters, 2021, 6: 1610–1615. doi: 10.1109/LCSYS.2021.3129729. [31] BOYD S, BOYD S P, and VANDENBERGHE L. Convex Optimization[M]. Cambridge, U. K. : Cambridge University Press, 2004. -






 下载:
下载:


 下载:
下载:
