Cost-Effective TMR Soft Error Tolerance Technique for Commercial Aerospace: Utilization of Approximate Computing
-
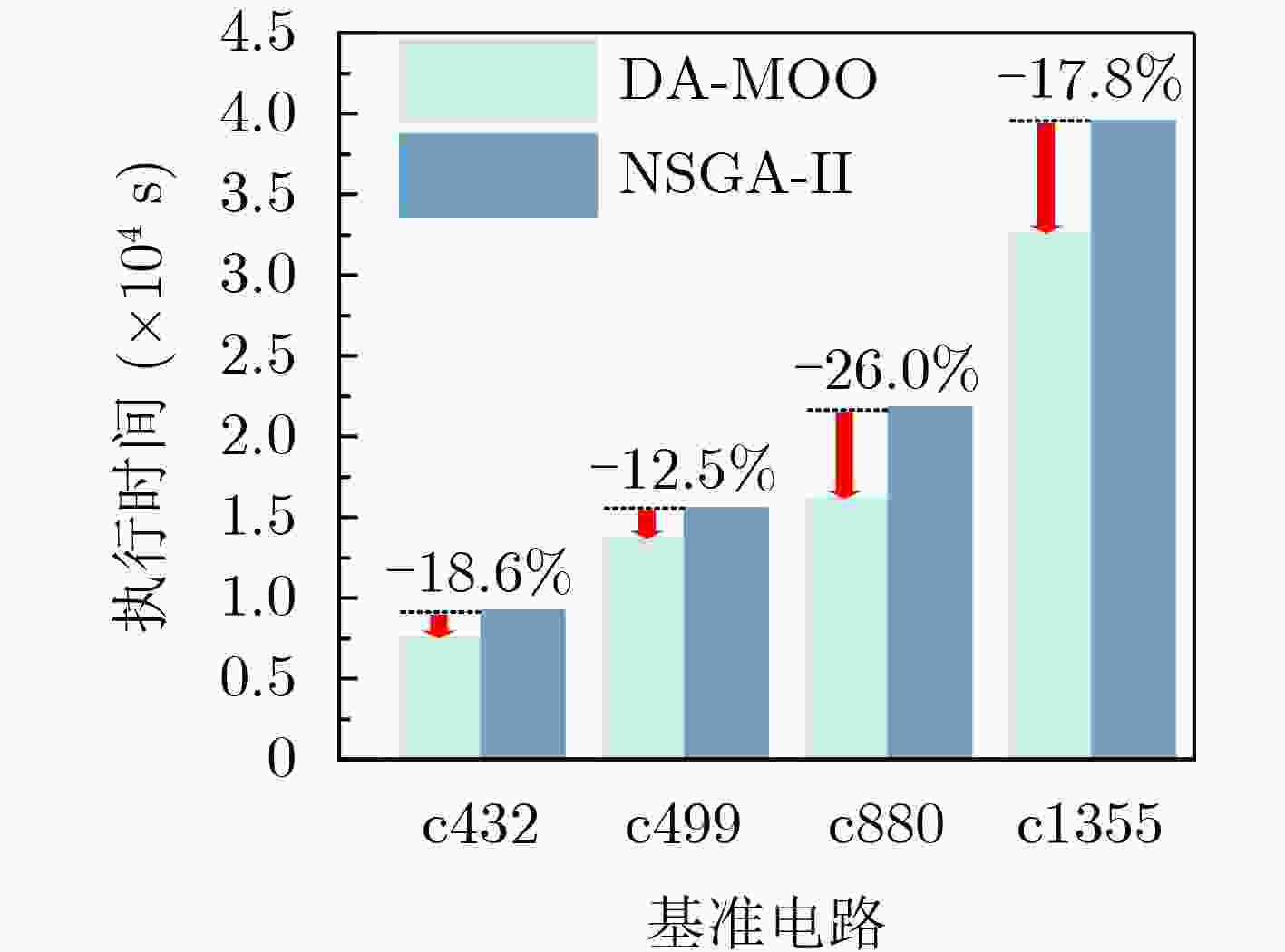
摘要: 三模冗余(TMR)作为如今集成电路可靠性领域中最为常用且有效的软错误加固技术,在满足高容错要求之时,不可避免地牺牲了庞大的硬件损耗。为实现面积、功耗等硬件性能和容错电路加固能力的折中考虑,适应低成本高可靠性加固的时代需求,针对基于近似计算的三模冗余加固技术(ATMR)进行研究,该文提出一种基于近似门单元(ApxLib)的动态调整多目标优化框架(ApxLib+DAMOO)。首先,其基本优化框架采用非支配排序遗传算法(NSGA-II)实现, 通过极性分析与预创建的近似库对电路实现快速近似。随后,该框架提出动态概率调整和极性扩张两种创新机制,根据可测性分析对遗传算法中门单元的突变概率进行动态更新,对双向门单元进行定向识别和重构,以实现寻优效率和寻优效果的双重优化。实验结果表明,该文提出的优化框架与传统NSGA-II相比,在相同硬件损耗下可实现最大10%~20%的额外软错误率(SER)降低,且其执行时间平均降低18.7%。Abstract: Triple Modular Redundancy (TMR), as the most prevalent and effective technique for soft error mitigation technique, inevitably incurs substantial hardware overhead while meeting high fault-tolerance requirements. To achieve the trade-off between area, power and fault coverage and meet the requirement of low-cost and high-reliability circuit design, Approximate Triple Modular Redundancy (ATMR) is investigated and a Dynamic Adjustment Multi-Objective Optimization Framework based on Approximate Gate Library (ApxLib+DAMOO) is investigated. The basic optimization framework employs Non-dominated Sorting Genetic Algorithm II (NSGA-II), achieving rapidly approximation through parity analysis and the pre-established ApxLib. Subsequently, the framework introduces two novel mechanisms: dynamic probability adjustment and parity expansion. The first mechanism dynamically updates the mutation probability of gates in the genetic algorithm based on testability analysis, while the second mechanism performs recognition and reconstruction for binate gates to achieve dual optimization of efficiency and effectiveness in optimization. Experimental results indicate that the proposed optimization framework achieves an additional Soft Error Rate (SER) reduction of up to 10%~20% compared to traditional NSGA-II with the same hardware overhead, while reducing 18.7% of execution time reduction averagely.
-
表 1 可测性分析与突变概率转换表
近似选项 可控性 可观察性 可测性 突变概率 g1_under_apx 0.2500 0.25 0.0625 0.461 g2_under_apx 0.3750 0.50 0.1875 0.155 g1_over_apx 0.7500 0.25 0.1875 0.155 g2_over_apx 0.6250 0.50 0.3125 0.093 g3_under_apx 0.3125 1.00 0.3125 0.093 g3_over_apx 0.6875 1.00 0.6875 0.043 表 2 图7所示电路的向上近似突变概率表
近似选项 突变概率 g2_under_apx 0.439 g1_over_apx 0.439 g3_over_apx 0.122 表 3 基准电路信息
基准电路 #输入数量 #输出数量 #门单元数量 c432 36 7 160 c499 41 32 202 c880 60 26 383 c1355 41 32 546 表 4 基准电路加固结果比较(%)
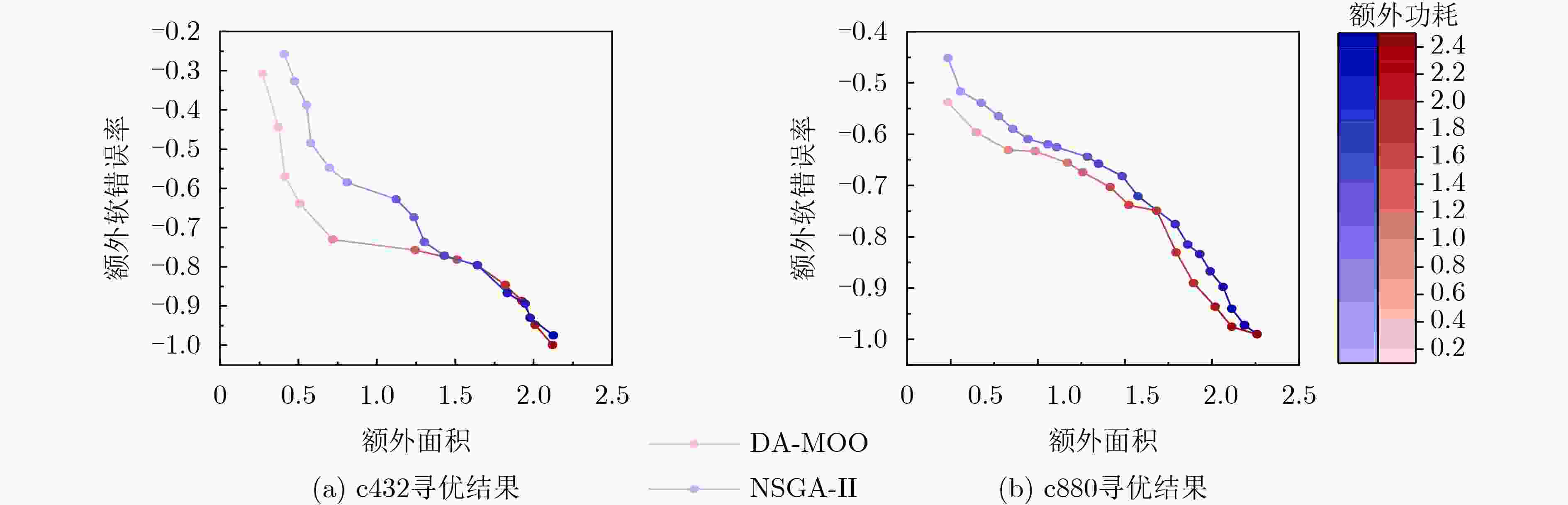
电路 DA-MOO NSGA-II TMR 面积(+) 功耗(+) 软错误率(–) 面积(+) 功耗(+) 软错误率(–) 面积(+) 功耗(+) 软错误率(–) c432 128.2 138.0 71.9 130.4 138.4 73.7 220.8 237.5 100 c499 158.3 159.3 78.3 153.8 164.2 75.7 231.7 221.1 100 c880 141.8 153.7 70.3 163.4 169.8 71.8 226.0 243.0 100 c1355 131.8 114.4 73.6 133.6 117.1 72.3 231.7 220.0 100 均值 140.0 141.4 73.5 145.3 147.4 73.4 227.6 230.4 100 表 5 c880应用DA-MOO的最终加固方案(%)
ATMR电路 额外面积
损耗额外功耗
损耗软错误率 非保护
输出占比未加固电路 0 0 100.0 100.0 ATMR1 46.9 37.4 53.6 52.1 ATMR2 83.3 90.6 36.9 34.6 ATMR3 125.9 125.6 32.6 15.8 ATMR4 152.4 167.6 26.2 13.9 ATMR5 179.5 179.1 17.1 11.8 ATMR6 190.0 195.7 10.5 7.3 ATMR7 201.9 214.1 6.4 4.9 ATMR8 211.5 229.6 2.5 2.3 TMR 226.0 243.0 0 0 -
[1] LI Yan, CHEN Chao, CHENG Xu, et al. DMBF: Design metrics balancing framework for soft-error-tolerant digital circuits through bayesian optimization[J]. IEEE Transactions on Circuits and Systems I: Regular Papers, 2023, 70(10): 4015–4027. doi: 10.1109/TCSI.2023.3302341. [2] PHILIP A S and SREEKALA K S. The ramification of single event transient effect on efficient charge recovery logic circuit[C]. 2022 International Conference on Innovative Trends in Information Technology, Kottayam, India, 2022: 1–4. doi: 10.1109/ICITIIT54346.2022.9744208. [3] CHEN Z F, LAI Yusheng, HUANG Chengming, et al. Process and simulation design of Silicon-on-Insulator (SOI) NMOS[C]. 2023 IEEE Nanotechnology Materials and Devices Conference, Paestum, Italy, 2023: 313–317. doi: 10.1109/NMDC57951.2023.10344290. [4] YUE Hengshan, WEI Xiaohui, TAN Jingweijia, et al. Eff-ECC: Protecting GPGPUs register file with a unified energy-efficient ECC mechanism[J]. IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, 2022, 41(7): 2080–2093. doi: 10.1109/TCAD.2021.3104529. [5] ZHOU Quming and MOHANRAM K. Gate sizing to radiation harden combinational logic[J]. IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, 2006, 25(1): 155–166. doi: 10.1109/TCAD.2005.853696. [6] YAN Aibin, FAN Zhengzheng, DING Liang, et al. Cost-effective and highly reliable circuit-components design for safety-critical applications[J]. IEEE Transactions on Aerospace and Electronic Systems, 2022, 58(1): 517–529. doi: 10.1109/TAES.2021.3103586. [7] CHEN Ke, LIU Weiqiang, and LOMBARDI F. Approximate arithmetic circuits: Design and applications[M]. LIU Weiqiang and LOMBARDI F. Approximate Computing[M]. Cham: Springer, 2022: 3–21. doi: 10.1007/978-3-030-98347-5_1. [8] NARASIMHAM B, LUK H, PAONE C, et al. Scaling trends and the effect of process variations on the soft error rate of advanced FinFET SRAMs[C]. 2023 IEEE International Reliability Physics Symposium, Monterey, USA, 2023: 1–4. doi: 10.1109/IRPS48203.2023.10118025. [9] GOMES I A C, MARTINS M G A, REIS A I, et al. Exploring the use of approximate TMR to mask transient faults in logic with low area overhead[J]. Microelectronics Reliability, 2015, 55(9/10): 2072–2076. doi: 10.1016/j.microrel.2015.06.125. [10] SIERAWSKI B D, BHUVA B L, and MASSENGILL L W. Reducing soft error rate in logic circuits through approximate logic function[J]. IEEE Transactions on Nuclear Science, 2006, 53(6): 3417–3421. doi: 10.1109/TNS.2006.884352. [11] ARIFEEN T, HASSAN A S, and LEE J A. Approximate triple modular redundancy: A survey[J]. IEEE Access, 2020, 8: 139851–139867. doi: 10.1109/ACCESS.2020.3012673. [12] GOMES I A C, MARTINS M, KASTENSMIDT F L, et al. Methodology for achieving best trade-off of area and fault masking coverage in ATMR[C]. The 15th Latin American Test Workshop - LATW, Fortaleza, Brazil, 2014: 1–6. doi: 10.1109/LATW.2014.6841916. [13] ARIFEEN T, HASSAN A S, MORADIAN H, et al. Probing approximate TMR in error resilient applications for better design tradeoffs[C]. 2016 Euromicro Conference on Digital System Design, Limassol, Cyprus, 2016: 637–640. doi: 10.1109/DSD.2016.57. [14] ALBANDES I, SERRANO-CASES A, SÁNCHEZ-CLEMENTE A J, et al. Improving approximate-TMR using multi-objective optimization genetic algorithm[C]. The IEEE 19th Latin-American Test Symposium, Sao Paulo, Brazil, 2018: 1–6. doi: 10.1109/LATW.2018.8349665. [15] SÁNCHEZ-CLEMENTE A, ENTRENA L, and GARCÍA-VALDERAS M. Error masking with approximate logic circuits using dynamic probability estimations[C]. 2014 IEEE 20th International On-Line Testing Symposium, Platja d’Aro, Spain, 2014: 134–139. doi: 10.1109/IOLTS.2014.6873685. [16] VERMA S, PANT M, and SNASEL V. A comprehensive review on NSGA-II for multi-objective combinatorial optimization problems[J]. IEEE Access, 2021, 9: 57757–57791. doi: 10.1109/ACCESS.2021.3070634. [17] ALBANDES I, MARTINS M, CUENCA-ASENSI S, et al. Building ATMR circuits using approximate library and heuristic approaches[J]. Microelectronics Reliability, 2019, 97: 24–30. doi: 10.1016/j.microrel.2019.04.002. [18] BRGLEZ F. On testability analysis of combinational networks[J]. IEEE International Symposium on Circuits and Systems, 1984, 1984(1): 221–225. [19] MANSKE G B, FARIAS C R, BUTZEN P F, et al. A fast approximate function generation method to ATMR architecture[C]. 2022 IEEE 13th Latin America Symposium on Circuits and System, Puerto Varas, Chile, 2022: 1–4. doi: 10.1109/LASCAS53948.2022.9789047. -





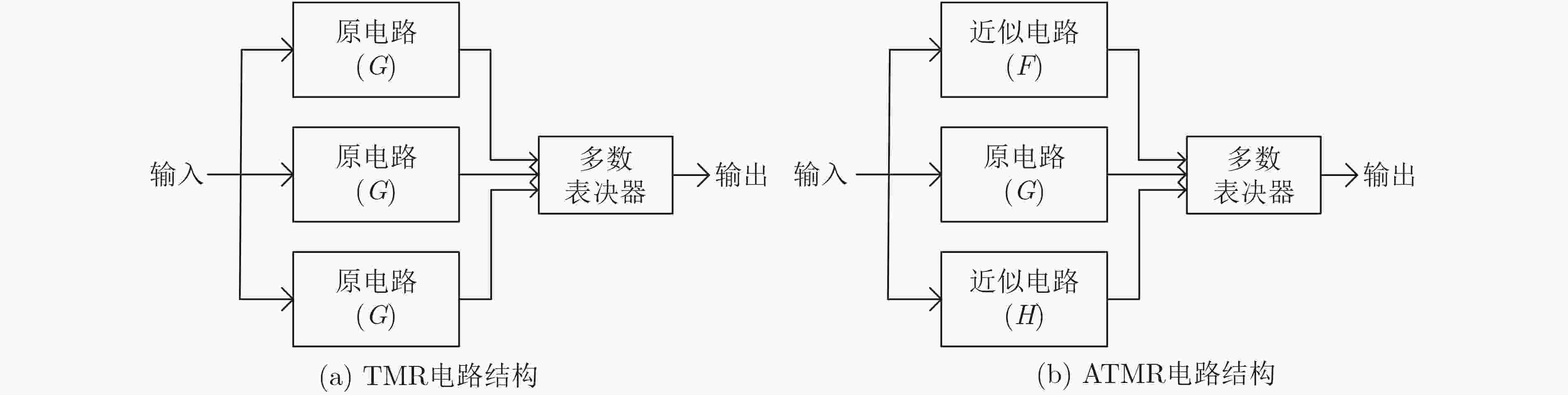
 下载:
下载:
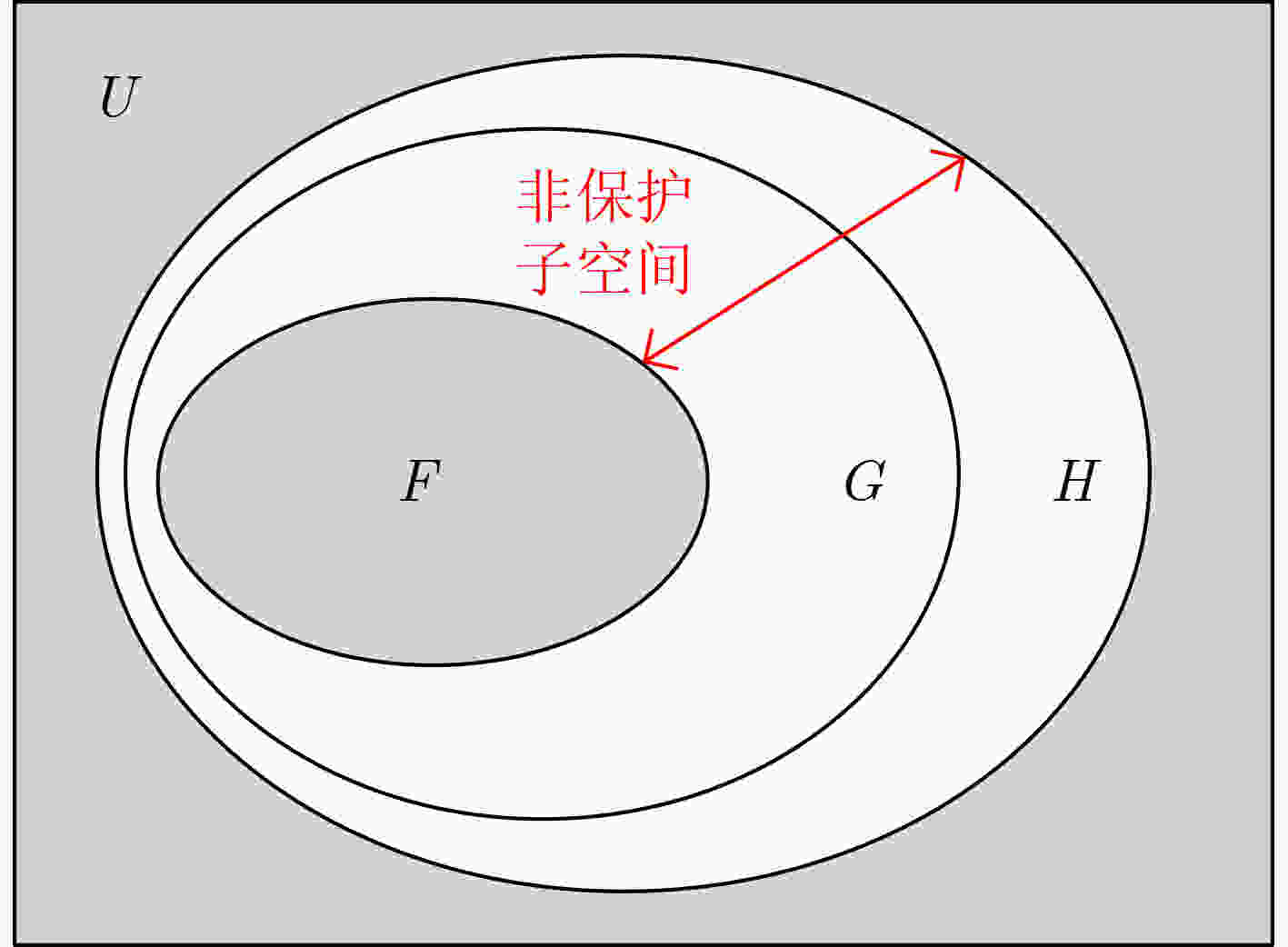

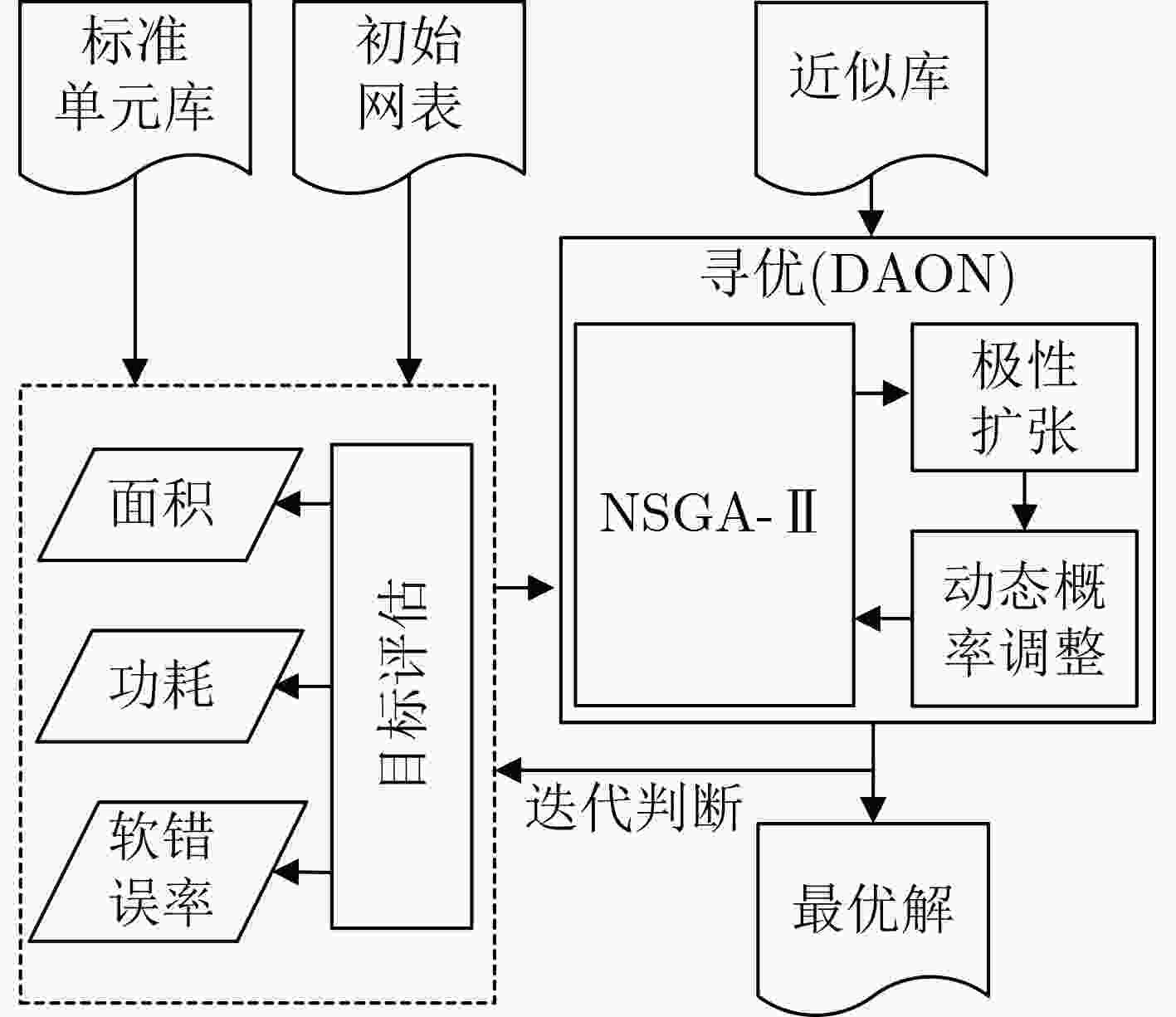

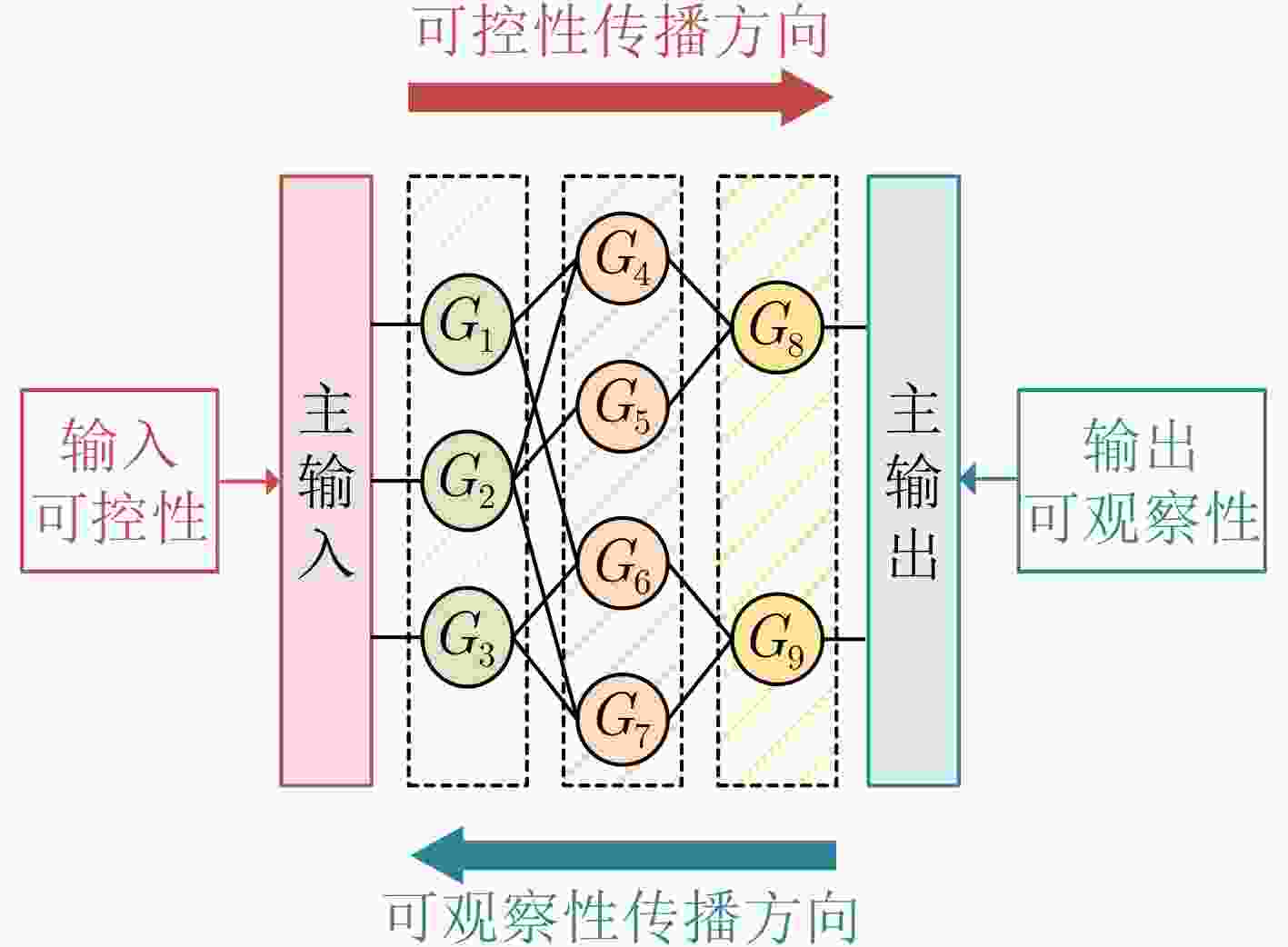



 下载:
下载:
