强稀疏低副瓣近场聚焦稀疏阵列三维成像

杨磊; 宋昊; 申瑞阳; 陈英杰; 胡仲伟; 霍鑫; 邢孟道

doi:10.11999/JEIT231278

强稀疏低副瓣近场聚焦稀疏阵列三维成像

doi: 10.11999/JEIT231278

1.
中国民航大学电子信息与自动化学院天津 300300
2.
西安电子科技大学雷达信号处理国家重点实验室西安 710071

基金项目: 国家自然科学基金(62271487)

详细信息

作者简介:
杨磊：男，教授，研究方向为高分辨SAR成像及机器学习理论应用

宋昊：男，硕士生，研究方向为毫米波成像与稀疏阵列构型设计

申瑞阳：男，硕士生，研究方向为毫米波成像与稀疏阵列构型设计

陈英杰：男，硕士生，研究方向为毫米波成像与稀疏阵列构型设计

胡仲伟：男，讲师，研究方向为高分辨SAR成像及优化学习理论

霍鑫：男，硕士生，研究方向为毫米波成像与稀疏阵列构型设计

邢孟道：男，教授，研究方向为雷达成像、动目标检测

通讯作者:
杨磊 email:　yanglei840626@163.com

中图分类号: TN957
计量
- 文章访问数: 155
- HTML全文浏览量: 59
- PDF下载量: 36
- 被引次数: 0
出版历程
- 收稿日期: 2023-11-20
- 修回日期: 2024-11-10
- 网络出版日期: 2024-11-19
- 刊出日期: 2025-12-01

High Sparsity and Low Sidelobe Near-field Focused Sparse Array for Three-Dimensional Imagery

1.
College of Electronic Information and Automation, Civil Aviation University of China, Tianjin 300300, China
2.
National Laboratory of Radar Signal Processing, Xidian University, Xi’an 710071, China

Funds: The National Natural Science Foundation of China (62271487)

摘要

摘要: 在主动式电扫描毫米波安检成像中，均匀阵列天线存在成本受限以及复杂度高等瓶颈问题，难以在实际工程中大规模运用。由此，该文提出一种强稀疏低副瓣的近场聚焦稀疏阵列设计方法，并进一步利用改进3维时域成像算法实现高精度3维重建。首先，以近场聚焦位置以及峰值旁瓣电平为约束，以权向量的$ {\ell _p} $(0<p<1)范数正则化为目标函数，构建近场聚焦稀疏阵列天线优化模型。然后，通过引入辅助变量，建立旁瓣及聚焦位置约束与辅助变量间的等价代换模型，解决阵列权向量目标函数与复杂约束耦合带来的求解难题，通过等价代换思想对模型化简并求解。接着，采用复数求导结合启发式近似方法对阵列激励以及位置进行优化选择。最后，利用交替方向多乘子法(ADMM)实现聚焦位置、峰值旁瓣约束以及阵列激励协同求解，通过改进3维时域成像算法实现稀疏阵列3维成像。仿真模拟实验结果显示，该方法可以在满足阵列天线辐射特性以及近场聚焦条件下，以更少的阵元数目获得更低的旁瓣电平。此外，采用实测数据验证稀疏阵列改进3维时域成像算法高精度、高效率的优势。
- 近场成像 /
- 稀疏阵列 /
- 3维成像 /
- 交替方向多乘子法
Abstract: In active electrical scanning millimeter-wave security imaging, the uniform array antenna has the bottleneck of uncontrolled cost and high complexity, which is difficult to be widely applied in practices. To this end, a near-field focused sparse array design algorithm for high sparsity and low sidelobes is proposed in this paper. It applies an improved three dimensional (3D) time-domain imaging algorithm to achieve high-accuracy 3D reconstruction. Firstly, the near-field focusing sparse array antenna model is constructed by taking the near-field focusing position and peak sidelobe level as constraints, where the $ {\ell _p} $(0<p<1) norm of the weight vector regularization is established as the objective function. Secondly, by introducing auxiliary variables and establishing equivalent substitution models between sidelobe and focus position constraints and auxiliary variables, the problem of solving the array weight vector in the coupling of the objective function and complex constraints is developed. The model is simplified and solved through the idea of equivalent substitution. Then, the array excitation and position are optimized using a combination of complex number differentiation and heuristic approximation methods. Finally, the Alternating Direction Method of Multipliers (ADMM) is employed to achieve the focus position, peak sidelobe constraint, and array excitation in a cooperative manner. The sparse array 3D imaging is realized by improving the 3D time-domain imaging algorithm. The experimental results show that the proposed method is capable of obtaining lower sidelobe level with fewer array elements under the condition of satisfying the radiation characteristics of array antenna and near-field focusing. Applying raw millimeter-wave data, the advantages of sparse array 3D time-domain imaging algorithm are verified in terms of high accuracy and high efficiency.
- Near field imaging /
- Sparse array /
- Three-dimensional imaging /
- Alternating Direction Method of Multipliers (ADMM)

HTML全文

图 1 圆柱体扫描毫米波安检成像几何示意图

下载: 全尺寸图片幻灯片

图 2 笛卡尔坐标系下近场线性阵列天线模型

下载: 全尺寸图片幻灯片

图 3 距离-高度维局部极坐标网格

下载: 全尺寸图片幻灯片

图 4 3维场景成像切片划分

下载: 全尺寸图片幻灯片

图 5 不同算法下天线方向图对比

下载: 全尺寸图片幻灯片

图 6 阵元位置分布及其对应激励值

下载: 全尺寸图片幻灯片

图 7 辅助变量收敛曲线

下载: 全尺寸图片幻灯片

图 8 均匀阵列与稀疏阵列成像结果对比

下载: 全尺寸图片幻灯片

图 9 均匀阵列与稀疏阵列点目标成像结果剖面图

下载: 全尺寸图片幻灯片

1 稀疏阵列优化算法

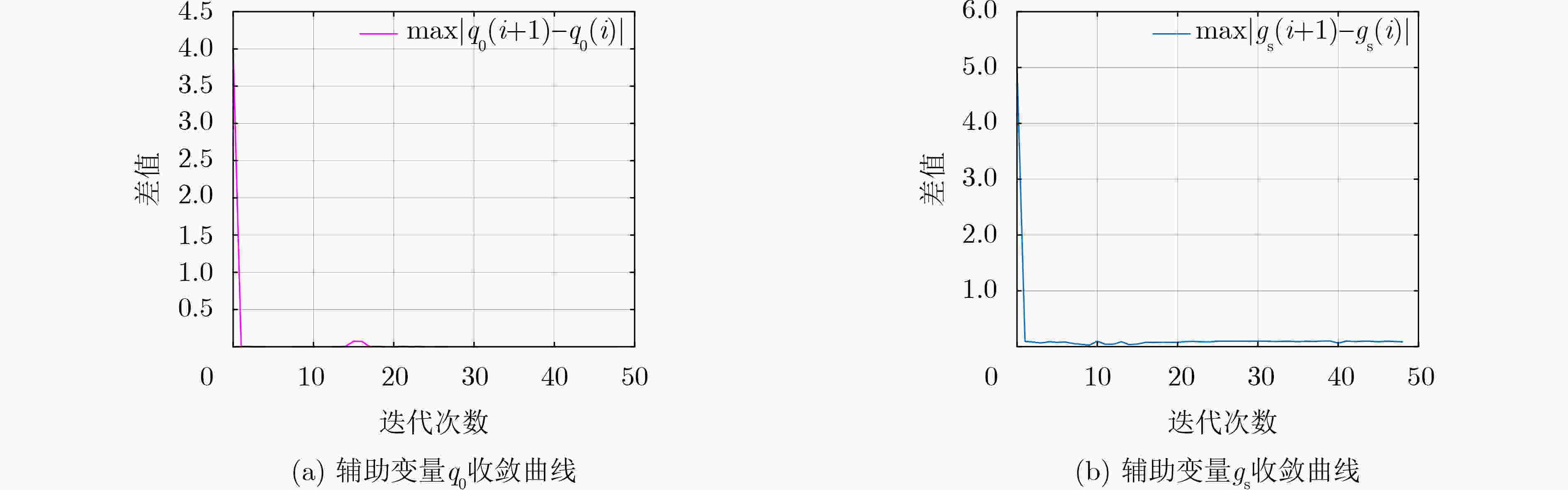
(1)初始化：$ {{\boldsymbol{\gamma}} ^{\mathrm{r}}}(0) $, $ {{\boldsymbol{\gamma}} ^{\mathrm{i}}}(0) $, $ {{\boldsymbol{\varsigma}} ^{\mathrm{r}}}(0) $, $ {{\boldsymbol{\varsigma}} ^{\mathrm{i}}}(0) $, $ {\boldsymbol{w}}(0) $，给定循环的迭代　次数$ K $, $ N $
(2) for $ i = 0,1, \cdots ,K $
步骤1　得到$ {q_0}(i + 1) $和$ {g_s}(i + 1) $通过式(12)–式(16)
步骤2　求解$ {\boldsymbol{w}}(i + 1) $
for $ k = 0,1, \cdots ,N $
(1)得到关于$ {\boldsymbol{w}} $非线性方程通过式(17)–式(21)
(2)确定$ {{\boldsymbol{w}}^{(k)}}(i + 1) $通过式(22)
End for $ k = N $
步骤3　通过式(23)更新$ {{\boldsymbol{\gamma}} ^{\mathrm{r}}}(i + 1) $, $ {{\boldsymbol{\gamma}} ^{\mathrm{i}}}(i + 1) $, $ {{\boldsymbol{\varsigma}} ^{\mathrm{r}}}(i + 1) $, $ {{\boldsymbol{\varsigma}} ^{\mathrm{i}}}(i + 1) $
end for $ i = K $
得到最终阵列权值向量的结果$ {\boldsymbol{w}} $

下载: 导出CSV

表 1 圆周柱面阵列天线实测数据参数

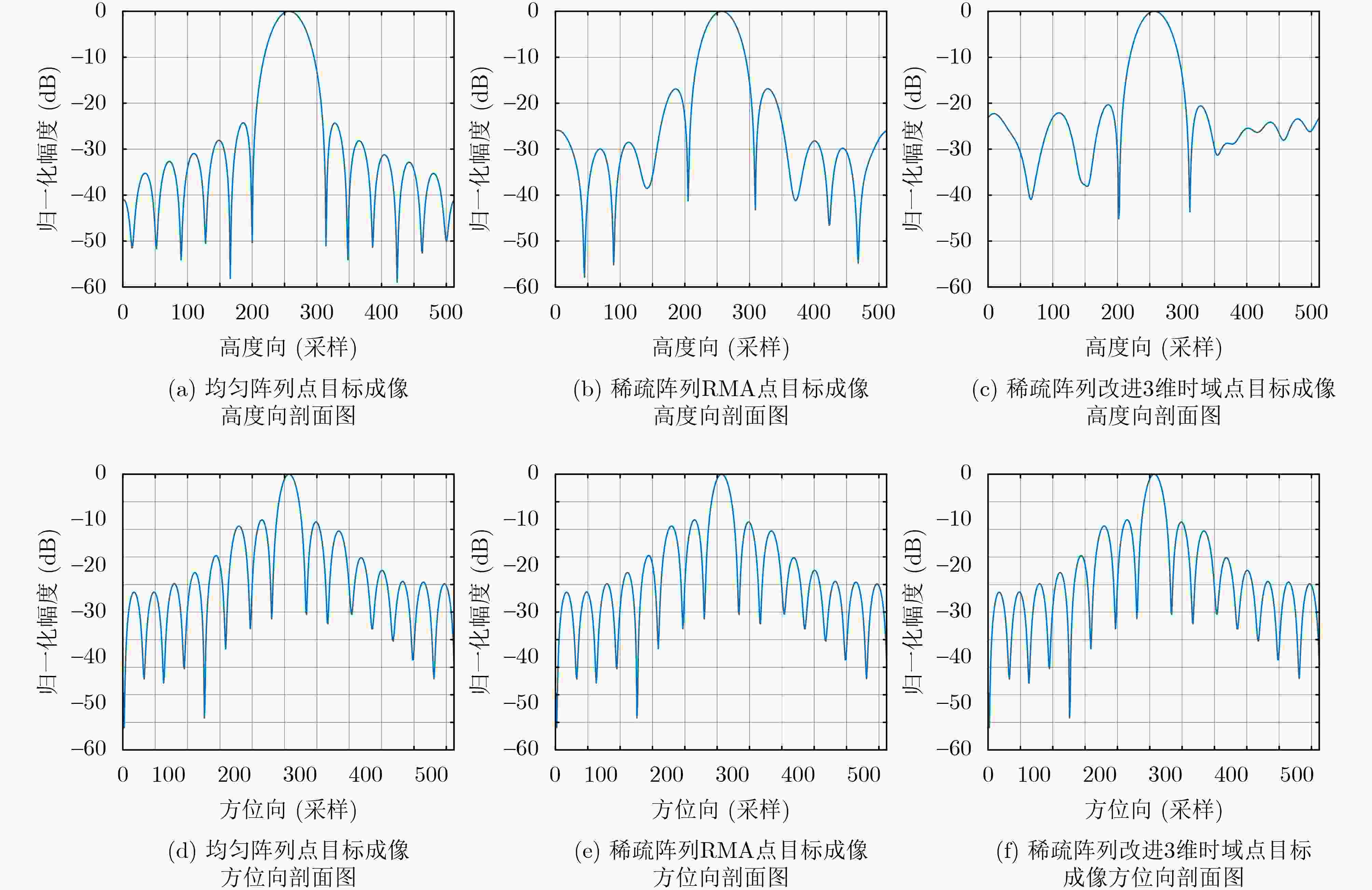
雷达参数	数值	雷达参数	数值	雷达参数	数值
系统工作带宽	6.5 GHz	方位/俯仰波束角	55°/55°	旋转次数	314
工作频率	27 GHz	单脉冲采样点数	64	单次旋转角度	0.2867°
目标距离	0.4～0.8 m	阵元间距	0.0052 m	旋转半径	0.628 m

下载: 导出CSV

表 2 均匀阵列与稀疏阵列点目标成像结果剖面图定量分析

点目标高度向成像结果	峰值旁瓣比(dB)	高度向分辨率(mm)
均匀阵列成像	–24.27	7.76
稀疏阵列RMA成像	–16.82	7.76
稀疏阵列改进3维时域成像	–20.32	7.76

下载: 导出CSV

参考文献(24)

[1]	冯辉, 涂昊, 高炳西, 等. 被动毫米波太赫兹人体成像关键技术进展[J]. 激光与红外, 2020, 50(11): 1395–1401. doi: 10.3969/j.issn.1001-5078.2020.11.018. FENG Hui, TU Hao, GAO Bingxi, et al. Progress on key technologies of passive millimeter wave and terahertz imaging for human body screening[J]. Laser & Infrared, 2020, 50(11): 1395–1401. doi: 10.3969/j.issn.1001-5078.2020.11.018.
[2]	李连伟, 秦世引. 基于轻量级U-Net深度学习的人体安检隐匿违禁物的实时检测[J]. 电子与信息学报, 2022, 44(10): 3435–3446. doi: 10.11999/JEIT210787. LI Lianwei and QIN Shiyin. Real-time detection of hiding contraband in human body during the security check based on lightweight U-Net with deep learning[J]. Journal of Electronics & Information Technology, 2022, 44(10): 3435–3446. doi: 10.11999/JEIT210787.
[3]	CHENG Yayun, YOU Yan, ZHU Dong, et al. Reflection removal using dual-polarization and saliency in millimeter-wave and terahertz imaging[J]. IEEE Transactions on Geoscience and Remote Sensing, 2021, 59(11): 9439–9447. doi: 10.1109/TGRS.2021.3049554.
[4]	SUN Peng, LIU Ting, CHEN Xiaotong, et al. Multi-source aggregation transformer for concealed object detection in millimeter-wave images[J]. IEEE Transactions on Circuits and Systems for Video Technology, 2022, 32(9): 6148–6159. doi: 10.1109/TCSVT.2022.3161815.
[5]	庞育才, 刘松. 基于改进人工蜂群算法的MIMO雷达稀疏阵列优化[J]. 系统工程与电子技术, 2018, 40(5): 1026–1030. doi: 10.3969/j.issn.1001-506X.2018.05.10. PANG Yucai and LIU Song. Optimization of MIMO radar sparse array based on modified artificial bee colony[J]. Systems Engineering and Electronics, 2018, 40(5): 1026–1030. doi: 10.3969/j.issn.1001-506X.2018.05.10.
[6]	黎子皓, 郝程鹏, 闫晟. 稀疏直线阵列优化设计算法综述[J]. 中国传媒大学学报(自然科学版), 2021, 28(4): 20–32. doi: 10.16196/j.cnki.issn.1673-4793.2021.04.003. LI Zihao, HAO Chengpeng, and YAN Sheng. Review of algorithms for designing sparse linear arrays[J]. Journal of Communication University of China (Science and Technology), 2021, 28(4): 20–32. doi: 10.16196/j.cnki.issn.1673-4793.2021.04.003.
[7]	孔玥, 邱明华, 黄晟, 等. 基于凸优化理论的可扫描稀疏阵列综合[J]. 雷达与对抗, 2020, 40(3): 33–37. doi: 10.19341/j.cnki.issn.1009-0401.2020.03.008. KONG Yue, QIU Minghua, HUANG Sheng, et al. Synthesis of steerable sparse arrays based on convex optimization theory[J]. RADAR & ECM, 2020, 40(3): 33–37. doi: 10.19341/j.cnki.issn.1009-0401.2020.03.008.
[8]	LI Pengfa, QU Shiwei, YANG Shiwen, et al. Focused array antenna based on subarrays[J]. IEEE Antennas and Wireless Propagation Letters, 2017, 16: 888–891. doi: 10.1109/LAWP.2016.2613887.
[9]	SUN Guilin and ZHU Qi. The design of a focused sparse microstrip antenna array[C]. 2016 IEEE International Symposium on Antennas and Propagation, Fajardo, USA, 2016: 515–516. doi: 10.1109/APS.2016.7695966.
[10]	HUANG Zixuan, CHENG Yujian, and YANG Haining. Synthesis of sparse near-field focusing antenna arrays with accurate control of focal distance by reweighted l₁ norm optimization[J]. IEEE Transactions on Antennas and Propagation, 2021, 69(5): 3010–3014. doi: 10.1109/TAP.2020.3025242.
[11]	陈鹭伟, 罗迎, 倪嘉成, 等. 基于深度展开的SAR大斜视RD成像算法[J]. 空军工程大学学报, 2022, 23(4): 43–50. doi: 10.3969/j.issn.2097-1915.2022.04.007. CHEN Luwei, LUO Ying, NI Jiacheng, et al. A novel range-Doppler imaging method for highly squinted SAR based on deep unfolded net[J]. Journal of Air Force Engineering University, 2022, 23(4): 43–50. doi: 10.3969/j.issn.2097-1915.2022.04.007.
[12]	陈权, 刘文康, 孙光才, 等. 基于超大幅宽的高轨SAR加速BP成像方法[J]. 电子与信息学报, 2022, 44(9): 3136–3143. doi: 10.11999/JEIT210560. CHEN Quan, LIU Wenkang, SUN Guangcai, et al. An Accelerated back-projection algorithm based on large swath for geosynchronous-earch-orbit SAR imaging[J]. Journal of Electronics & Information Technology, 2022, 44(9): 3136–3143. doi: 10.11999/JEIT210560.
[13]	董祺, 杨泽民, 孙光才, 等. 子场景处理的弹载前斜视SAR时域成像算法[J]. 系统工程与电子技术, 2017, 39(5): 1013–1018. doi: 10.3969/j.issn.1001-506X.2017.05.10. DONG Qi, YANG Zemin, SUN Guangcai, et al. Missile-borne forward squint SAR time-domain imaging algorithm based on sub-region processing[J]. Systems Engineering and Electronics, 2017, 39(5): 1013–1018. doi: 10.3969/j.issn.1001-506X.2017.05.10.
[14]	杨磊, 王腾腾, 陈英杰, 等. 低秩矩阵补全高分辨SAR成像特征重建[J]. 电子与信息学报, 2023, 45(8): 2965–2974. doi: 10.11999/JEIT220992. YANG Lei, WANG Tengteng, CHEN Yingjie, et al. Feature reconstruction of high resolution SAR imagery based on low rank matrix completion[J]. Journal of Electronics & Information Technology, 2023, 45(8): 2965–2974. doi: 10.11999/JEIT220992.
[15]	谢朋飞, 张磊, 吴振华. 融合ω-K和BP算法的圆柱扫描毫米波三维成像算法[J]. 雷达学报, 2018, 7(3): 387–394. doi: 10.12000/JR17112. XIE Pengfei, ZHANG Lei, and WU Zhenhua. A three-dimensional imaging algorithm fusion with ω-K and BP algorithm for millimeter-wave cylindrical scanning[J]. Journal of Radars, 2018, 7(3): 387–394. doi: 10.12000/JR17112.
[16]	LIANG Junli, ZHANG Xuan, SO H C, et al. Sparse array beampattern synthesis via alternating direction method of multipliers[J]. IEEE Transactions on Antennas and Propagation, 2018, 66(5): 2333–2345. doi: 10.1109/TAP.2018.2811778.
[17]	郑美燕. 基于矩阵束方法的天线阵列优化[D]. [硕士论文], 电子科技大学, 2013. ZHENG Meiyan. Sparse antenna array synthesis using matrix pencil method[D]. [Master dissertation], University of Electronic Science and Technology of China, 2013.
[18]	WANG Xinkuan and WANG Guibao. A hybrid method based on the iterative Fourier transform and the differential evolution for pattern synthesis of sparse linear arrays[J]. International Journal of Antennas and Propagation, 2018, 2018: 6309192. doi: 10.1155/2018/6309192.
[19]	TENG Duo, LI Yatian, YANG Hu, et al. Genetic algorithm for sparse optimization of mills cross array used in underwater acoustic imaging[J]. Journal of Marine Science and Engineering, 2022, 10(2): 155. doi: 10.3390/jmse10020155.
[20]	CHATTERJEE A, MAHANTI G K, and MAHANTI A. Synthesis of thinned concentric ring array antenna in predefined phi-planes using binary firefly and binary particle swarm optimization algorithm[J]. International Journal of Numerical Modelling: Electronic Networks, Devices and Fields, 2015, 28(2): 164–174. doi: 10.1002/jnm.1994.
[21]	HUANG Zixuan and CHENG Yujian. Near-field pattern synthesis for sparse focusing antenna arrays based on Bayesian compressive sensing and convex optimization[J]. IEEE Transactions on Antennas and Propagation, 2018, 66(10): 5249–5257. doi: 10.1109/TAP.2018.2860044.
[22]	王洪雁, 于若男. 基于稀疏和低秩恢复的稳健DOA估计方法[J]. 电子与信息学报, 2020, 42(3): 589–596. doi: 10.11999/JEIT190263. WANG Hongyan and YU Ruonan. Sparse and low rank recovery based robust DOA estimation method[J]. Journal of Electronics & Information Technology, 2020, 42(3): 589–596. doi: 10.11999/JEIT190263.
[23]	ZHAO Xiaobin, LI Wei, ZHANG Mengmeng, et al. Adaptive iterated shrinkage thresholding-based L_p-norm sparse representation for hyperspectral imagery target detection[J]. Remote Sensing, 2020, 12(23): 3991. doi: 10.3390/rs12233991.
[24]	杨磊, 陈英杰, 王腾腾, 等. 旅客人身时频调和型毫米波三维重建[J]. 红外与毫米波学报, 2023, 42(3): 327–338. doi: 10.11972/j.issn.1001-9014.2023.03.006. YANG Lei, CHEN Yingjie, WANG Tengteng, et al. Three-dimensional reconstruction algorithm for passengers based on time-frequency coordination[J]. Journal of Infrared and Millimeter Waves, 2023, 42(3): 327–338. doi: 10.11972/j.issn.1001-9014.2023.03.006.