Secret Sharing: Design of Higher-Order Masking S-box and Secure Multiplication in Galois Field
-
摘要: 在信息时代,信息安全是最不能忽视的重要问题,对密码设备的攻击和防护是该领域的研究热点。近年来,多种对密码设备的攻击已为人所知,其目的都是为了获取设备中的密钥,在众多攻击中,功耗侧信道攻击是最受关注的攻击技术之一 。掩码技术是对抗功耗侧信道攻击的有效方法,然而随着攻击手段的不断进步,1阶掩码的防护已经不足以应对2阶及以上的功耗分析攻击,因此对高阶掩码的研究具有重要的意义。为了提升加密电路抗攻击能力,该文基于秘密共享的思想,对分组密码算法的S盒变换实施了高阶掩码防护——共享型掩码,并基于Ishai等人在Crypto 2003上发表的安全方案(ISW框架)提出了有限域安全乘法的通用设计方法。通过实验表明,该文提出的共享型掩码方案不影响加密算法的功能,同时能抵御1阶和2阶相关功耗分析攻击。Abstract: In the information era, information security is the priority that cannot be ignored. Attacks and protection against password devices are research hotspots in this field. In recent years, various attacks on cryptographic devices have become well-known, all aimed at obtaining keys from the device. Among these attacks, power side channel attack is one of the most concerned attack techniques. Mask technology is an effective method to combat power side channel attacks, however, with the continuous progress of attack methods, the protection of first-order mask is no longer sufficient to cope with second-order and higher order power analysis attack, so the research on higher-order mask has considerable significance. To enhance the encryption circuit’s capability of anti-attack, high-order masking schemes: N-share masking is implemented on S-box in this paper, and a universal design method for galois field secure multiplication is proposed, which is based on the secure scheme published by Ishai et al. at Crypto 2003 (ISW framework). Through experiments, it has been shown that the encryption scheme adopted in this paper does not affect the functionality of the encryption algorithm, and can resist first-order and second-order correlation power analysis attack.
-
Key words:
- Block cipher algorithm /
- S-box /
- N-share mask /
- Galois field multiplication
-
1 确定下标(i,j)所属集合
输入:软件上定义的GF(28)乘法:Gfmult。 输出:集合Uk,k=0,1,2,3,4,5,6,7。 (1) for ( k=0; k<7; k++ ) do (2) Uk=$\varnothing $; (3) for ( j=0; j<7; j++ ) do (4) b=2 j; (5) for ( i=0; i<7; i++ ) do (6) a=2i; (7) if (Gfmult(a,b)的二进制表示的第k位等于1) then (8) Uk=Uk ∪ {(i,j)}; //有限域上乘积的某一比特等于1,将下标加入对应的集合 (9) end if (10) end for (11) end for (12) end for (13) return Uk,k=0,1,2,3,4,5,6,7; 表 1 下标$(i,j)$分布表
ai c7 c6 c5 c4 c3 c2 c1 c0 bj b0 7 6 5 4 3 2 1 0 b1 6 5 4 3,7 2,7 1 0,7 7 b2 5 4 3,7 2,6,7 1,6 0,7 6,7 6 b3 4 3,7 2,6,7 1,5,6 0,5,7 6,7 5,6 5 b4 3,7 2,6,7 1,5,6 0,4,5,7 4,6,7 5,6 4,5 4 b5 2,6,7 1,5,7 0,4,5,7 3,4,6 3,5,6,7 4,5 3,4,7 3,7 b6 1,5,6 0,4,5,7 3,4,6 2,3,5 2,4,5,6,7 3,4,7 2,3,6 2,6,7 b7 0,4,5,7 3,4,6 2,3,5 1,2,4,7 1,3,4,5,6,7 2,3,6 1,2,5,7 1,5,6 -
[1] 王永娟, 樊昊鹏, 代政一, 等. 侧信道攻击与防御技术研究进展[J]. 计算机学报, 2023, 46(1): 202–228. doi: 10.11897/SP.J.1016.2023.00202.WANG Yongjuan, FAN Haopeng, DAI Zhengyi, et al. Advances in side channel attacks and countermeasures[J]. Chinese Journal of Computers, 2023, 46(1): 202–228. doi: 10.11897/SP.J.1016.2023.00202. [2] HASNAIN A, ASFIA Y, and KHAWAJA S G. Power profiling-based side-channel attacks on FPGA and Countermeasures: A survey[C]. The 2nd International Conference on Digital Futures and Transformative Technologies (ICoDT2), Rawalpindi, Pakistan, 2022: 106–113. doi: 10.1109/ICoDT255437.2022.9787473. [3] KOCHER P, JAFFE J, and JUN B. Differential power analysis[C]. The 19th Annual International Cryptology Conference on Advances in Cryptology - CRYPTO’99, Santa Barbara, USA, 1999: 388–397. doi: 10.1007/3-540-48405-1_25. [4] BRIER E, CLAVIER C, and OLIVIER F. Correlation power analysis with a leakage model[C]. The 6th International Workshop on Cryptographic Hardware and Embedded Systems, Cambridge, USA, 2004: 16–29. doi: 10.1007/978-3-540-28632-5_2. [5] CHARI S, JUTLA C S, RAO J R, et al. Towards sound approaches to counteract power-analysis attacks[C]. The 19th Annual International Cryptology Conference on Advances in Cryptology - CRYPTO’99, Santa Barbara, USA, 1999: 398–412. doi: 10.1007/3-540-48405-1_26. [6] GOLIĆ J D and TYMEN C. Multiplicative masking and power analysis of AES[C]. The 4th International Workshop on Cryptographic Hardware and Embedded Systems - CHES 2002, Redwood Shores, USA, 2002: 198–212. doi: 10.1007/3-540-36400-5_16. [7] ISHAI Y, SAHAI A, and WAGNER D. Private circuits: Securing hardware against probing attacks[C]. The 23rd Annual International Cryptology Conference on Advances in Cryptology -- CRYPTO 2003, Santa Barbara, USA, 2003: 463–481. doi: 10.1007/978-3-540-45146-4_27. [8] RIVAIN M and PROUFF E. Provably secure higher-order masking of AES[C]. The 12th International Conference on Cryptographic Hardware and Embedded Systems - CHES 2010, Santa Barbara, USA, 2010: 413–427. doi: 10.1007/978-3-642-15031-9_28. [9] KIM H S, HONG S, and LIM J. A fast and provably secure higher-order masking of AES S-Box[C]. The 13th International Workshop on Cryptographic Hardware and Embedded Systems – CHES 2011, Nara, Japan, 2011: 95–107. doi: 10.1007/978-3-642-23951-9_7. [10] TAOUIL M, ALJUFFRI A, and HAMDIOU S. Power side channel attacks: Where are we standing?[C]. The 16th International Conference on Design & Technology of Integrated Systems in Nanoscale Era (DTIS), Montpellier, France, 2021: 1–6. doi: 10.1109/DTIS53253.2021.9505075. [11] SINGHA T B, PALATHINKAL R P, and AHAMED S R. Securing AES designs against power analysis attacks: A survey[J]. IEEE Internet of Things Journal, 2023, 10(16): 14332–14356. doi: 10.1109/JIOT.2023.3265683. [12] XU Yongkang, DENG Feng, XU Weihan, et al. Unified coprocessor for high-speed AES-128 and SM4 encryption[C]. The IEEE 6th Advanced Information Technology, Electronic and Automation Control Conference (IAEAC), Beijing, China, 2022: 640–644. doi: 10.1109/IAEAC54830.2022.9929737. [13] SATOH A, MORIOKA S, TAKANO K, et al. A compact rijndael hardware architecture with S-Box optimization[C]. The 7th International Conference on the Theory and Application of Cryptology and Information Security: Advances in Cryptology, Gold Coast, Australia, 2001: 239–254. doi: 10.1007/3-540-45682-1_15. [14] WOLKERSTORFER J, OSWALD E, and LAMBERGER M. An ASIC implementation of the AES SBoxes[C]. The Cryptographer’s Track at the RSA Conference 2002, San Jose, USA, 2002: 29–52. doi: 10.1007/3-540-45760-7_6. [15] CANRIGHT D. A very compact Rijndael S-box[C]. Cryptographic Hardware and Embedded Systems – CHES 2005, Edinburgh, UK, 2005: 441–455. [16] IYER V, WANG Meizhi, KULKARNI J, et al. A systematic evaluation of EM and power side-channel analysis attacks on AES implementations[C]. 2021 IEEE International Conference on Intelligence and Security Informatics (ISI), San Antonio, USA, 2021: 46–51. doi: 10.1109/ISI53945.2021.9624778. [17] 段晓毅, 王思翔, 崔琦, 等. 一种带掩码AES算法的高阶差分功耗分析攻击方案[J]. 计算机工程, 2017, 43(10): 120–125. doi: 10.3969/j.issn.1000-3428.2017.10.021.DUAN Xiaoyi, WANG Sixiang, CUI Qi, et al. A high-order differential power analysis attack scheme with Masked AES algorithm[J]. Computer Engineering, 2017, 43(10): 120–125. doi: 10.3969/j.issn.1000-3428.2017.10.021. [18] 郭筝, 杨正文, 张效林, 等. 一种基于乘法掩码的AES 防护方案[J]. 密码学报, 2023, 10(1): 209–218. doi: 10.13868/j.cnki.jcr.000590.GUO Zheng, YANG Zhengwen, ZHANG Xiaolin, et al. A side-channel countermeasure for AES based on multiplication mask[J]. Journal of Cryptologic Research, 2023, 10(1): 209–218. doi: 10.13868/j.cnki.jcr.000590. [19] 郭志鹏. 高阶掩码防护方案设计及安全检测技术研究[D]. [博士论文], 武汉大学, 2019.GUO Zhipeng. Design of high-order masking scheme and security detection technology[D]. [Ph. D. dissertation], Wuhan University, 2019. [20] RAMEZANPOUR K, AMPADU P, and DIEHL W. RS-mask: Random space masking as an integrated countermeasure against power and fault analysis[C]. 2020 IEEE International Symposium on Hardware Oriented Security and Trust (HOST), San Jose, USA, 2020: 176–187. doi: 10.1109/HOST45689.2020.9300266. -






 下载:
下载:



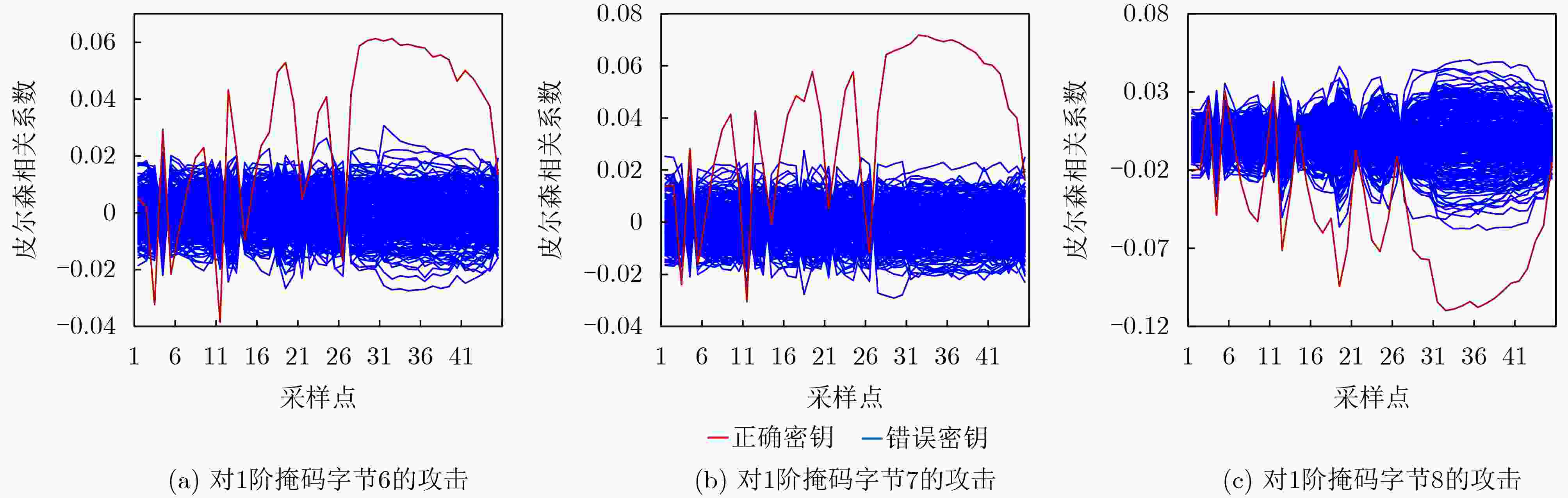




 下载:
下载:
