基于亚稳态叠加单元的高吞吐量真随机数发生器设计

倪天明; 俞俊勇; 彭青松; 聂牧

doi:10.11999/JEIT231166

基于亚稳态叠加单元的高吞吐量真随机数发生器设计

doi: 10.11999/JEIT231166

倪天明^{1, 2, 3},
俞俊勇^{1, 2, 3},
彭青松⁴,
聂牧^{1, 2, 3, ,}

1.
安徽工程大学集成电路学院芜湖 241000
2.
安徽省车载显示集成系统工程研究中心芜湖 241000
3.
触控显示材料与器件安徽省联合共建学科重点实验室芜湖 241000
4.
合肥工业大学微电子学院合肥 230000

基金项目: 国家自然科学基金(62174001, 62274052, 61974001, 62311540021)，安徽省自然科学基金(2208085J02)，安徽省重点研发(202104b11020032)，安徽省高校优秀科研创新团队(2022AH010059)，安徽省教育厅杰出青年学者基金(2022AH020014)

详细信息

作者简介:
倪天明：男，教授，研究方向为集成电路容错设计、数字集成电路抗辐射加固设计及硬件安全

俞俊勇：男，硕士生，研究方向为硬件安全

彭青松：男，硕士生，研究方向为硬件安全

聂牧：男，博士，讲师，研究方向为机器学习与晶圆检测

通讯作者:
聂牧　niemu@seu.edu.cn

中图分类号: TN402
计量
- 文章访问数: 393
- HTML全文浏览量: 129
- PDF下载量: 53
- 被引次数: 0
出版历程
- 收稿日期: 2023-10-26
- 修回日期: 2024-01-26
- 网络出版日期: 2024-02-03
- 刊出日期: 2024-05-30

Design of High Throughput True Random Number Generator Based on Metastability Superposition Cells

NI Tianming^{1, 2, 3},
YU Junyong^{1, 2, 3},
PENG Qingsong⁴,
NIE Mu^{1, 2, 3
, ,}

1.
School of Integrated Circuits, Anhui Polytechnic University, Wuhu 241000, China
2.
Anhui Engineering Research Center of Vehicle Display Integrated Systems, Wuhu 241000, China
3.
Anhui Province Joint Key Laboratory of Touch Display Materials and Devices, Wuhu 241000, China
4.
School of Microelectronics, Hefei University of Technology, Hefei 230000, China

Funds: The National Natural Science Foundation of China (62174001, 62274052, 61974001, 62311540021), Anhui Provincial Natural Science Foundation (2208085J02), The Key Research and Development Projects in Anhui Province (202104b11020032), The Excellent Scientific Research and Innovation Teams of Anhui Province (2022AH010059), The Distinguished Young Scholar Fund of Anhui Provincial Department of Education (2022AH020014)

摘要

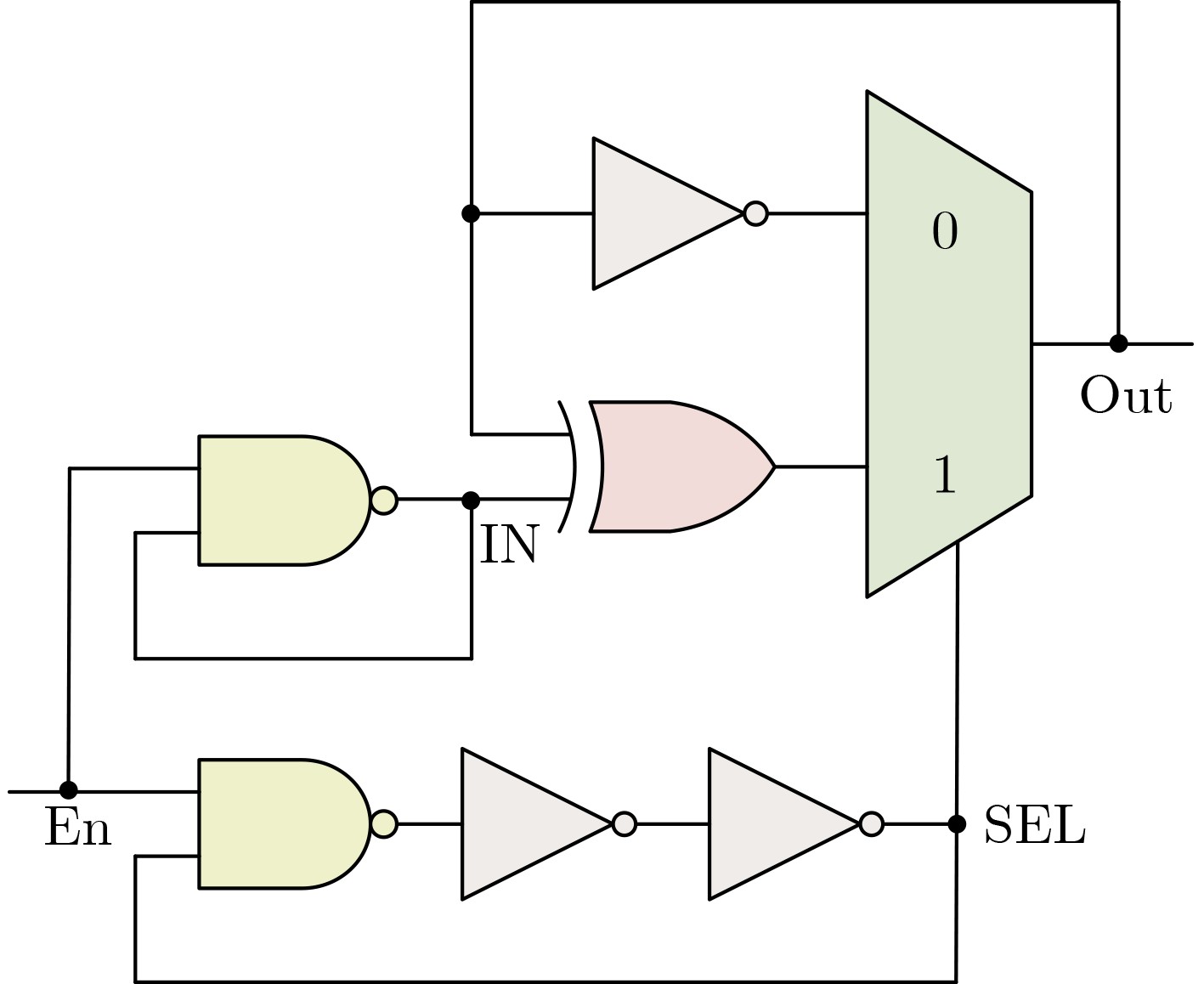
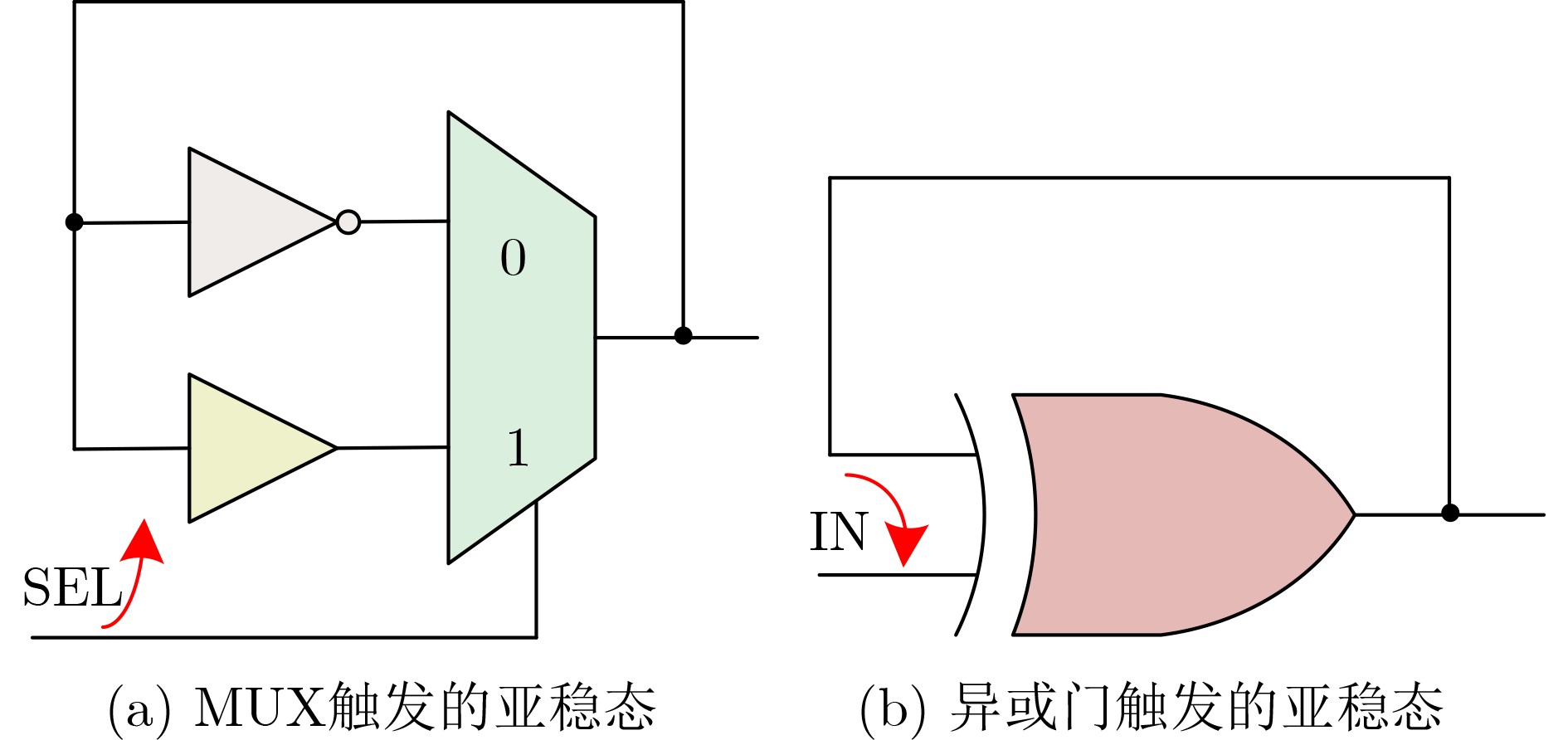
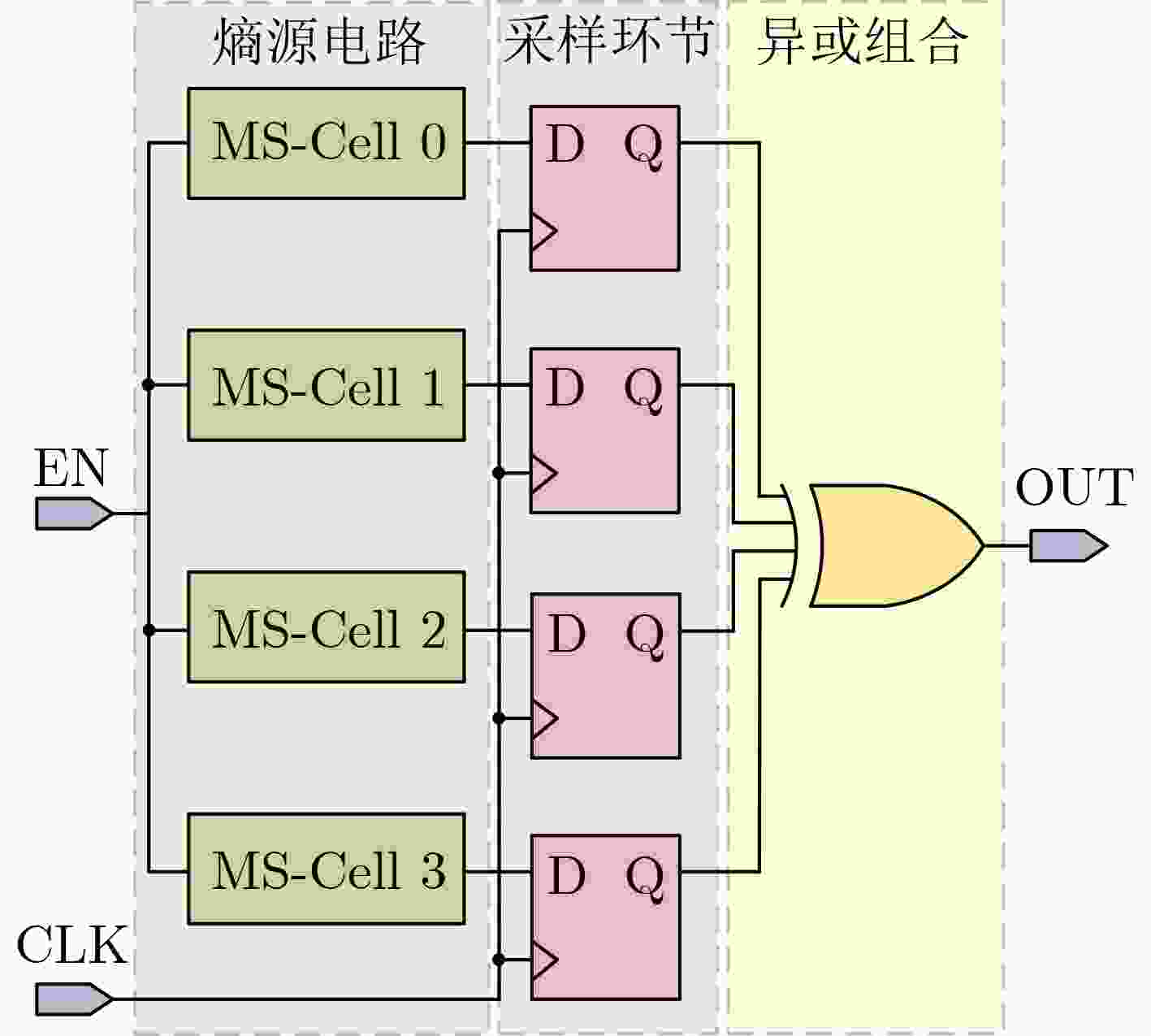
摘要: 真随机数发生器(TRNG)作为一类重要的硬件安全原语，在密钥生成、初始化向量和协议中的身份认证等加密领域得到应用。为设计出高吞吐量的轻量级TRNG，该文研究了利用多路选择器(MUX)和异或门(XOR gate)的开关特性来产生亚稳态的方法，提出一种基于亚稳态叠加单元(MS-cell)的TRNG(MS-TRNG)设计。它将MUX和异或门触发的亚稳态进行叠加，从而提高TRNG的熵。所提TRNG分别在Xilinx Virtex-7和Xilinx Artix-7 FPGA开发板中实现，无需后处理电路。与其他先进的TRNG相比，所提TRNG具有最高的吞吐量和极低的硬件开销，并且它所生成的随机序列通过了NIST测试和一系列性能测试。
- 真随机数发生器 /
- 熵源叠加 /
- 亚稳态 /
- 吞吐量
Abstract: True Random Number Generator (TRNG), as an important hardware security primitive, is used in key generation, initialization vector and identity authentication in protocols. In order to design a lightweight TRNG with high throughput, the method of generating metastability is studied by using the switching characteristics of MUltipleXer (MUX) and XOR gate, and a TRNG design based on Metastability Superposition (MS-TRNG) cell (MS-cell) is proposed. It superimposes MUX and XOR gate guided metastases, thereby increasing the entropy of TRNG. The proposed TRNG is implemented in Xilinx Virtex-7 and Xilinx Artix-7 FPGA development boards, respectively, without the need for post-processing circuits. Compared to other advanced TRNGS, the proposed TRNG has the highest throughput and extremely low hardware overhead, and the random sequences it generates pass NIST testing and a series of performance tests.
- True Random Number Generator(TRNG) /
- Entropy source superposition /
- Metastability /
- Throughput

HTML全文

图 1 一种流行的亚稳态电路模型

下载: 全尺寸图片幻灯片

图 2 采用MUX实现的基于亚稳态的TRNG

下载: 全尺寸图片幻灯片

图 3 异或门的开关特性

下载: 全尺寸图片幻灯片

图 4 采用异或门实现的基于亚稳态的TRNG

下载: 全尺寸图片幻灯片

图 5 MS-cell电路图

下载: 全尺寸图片幻灯片

图 6 两类数字元件触发的亚稳态

下载: 全尺寸图片幻灯片

图 7 抖动的累积效应

下载: 全尺寸图片幻灯片

图 8 异或组合结构

下载: 全尺寸图片幻灯片

图 9 退化后的异或函数

下载: 全尺寸图片幻灯片

图 10 MS-TRNG的完整结构

下载: 全尺寸图片幻灯片

图 11 10⁶位输出序列的偏差测试

下载: 全尺寸图片幻灯片

图 12 6次重启动测试结果

下载: 全尺寸图片幻灯片

图 13 10⁶位输出序列的自相关测试

下载: 全尺寸图片幻灯片

图 14 不同电压下NIST测试结果

下载: 全尺寸图片幻灯片

图 15 不同温度下NIST测试结果

下载: 全尺寸图片幻灯片

表 1 MS-cell的工作模式

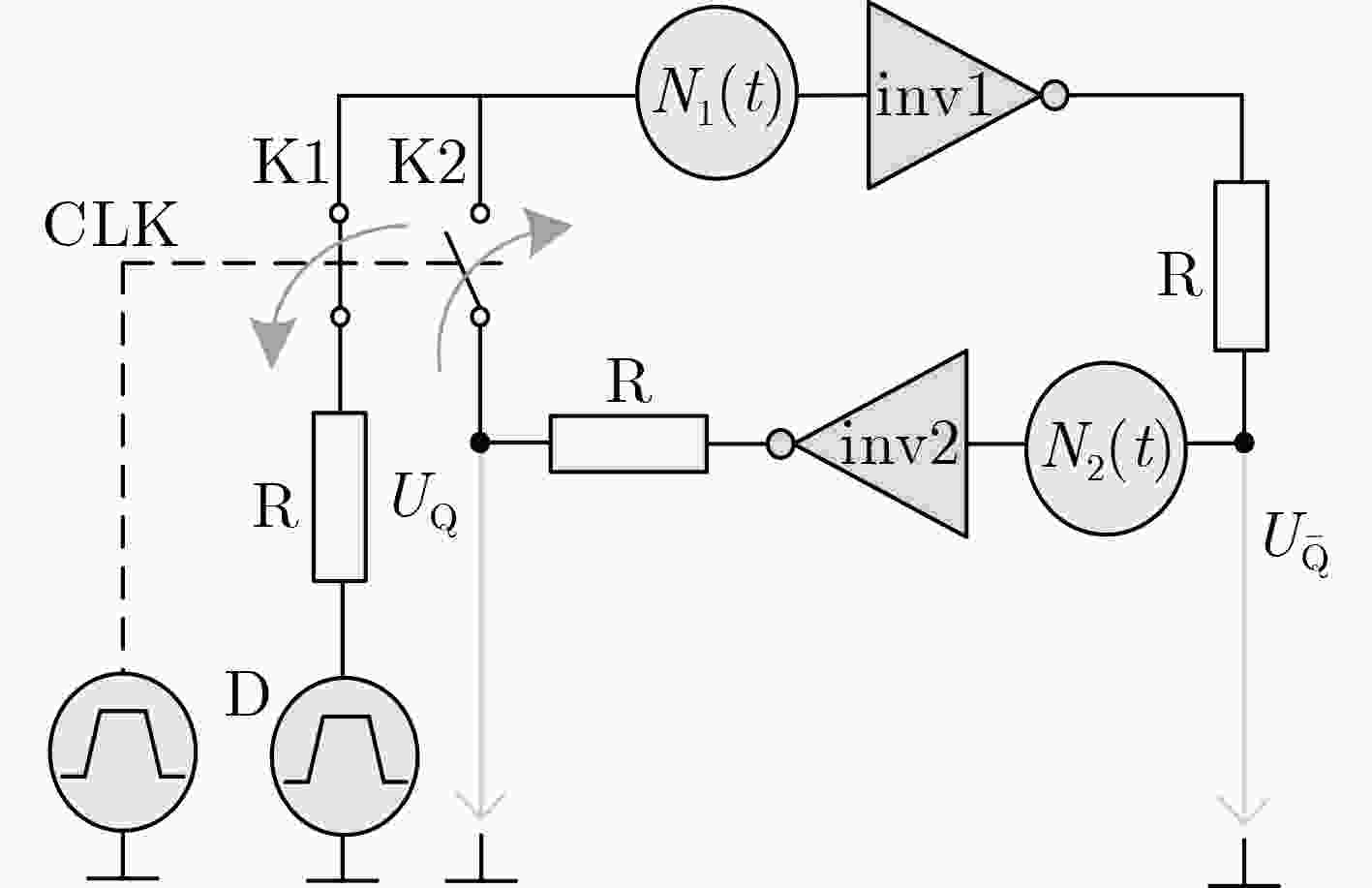
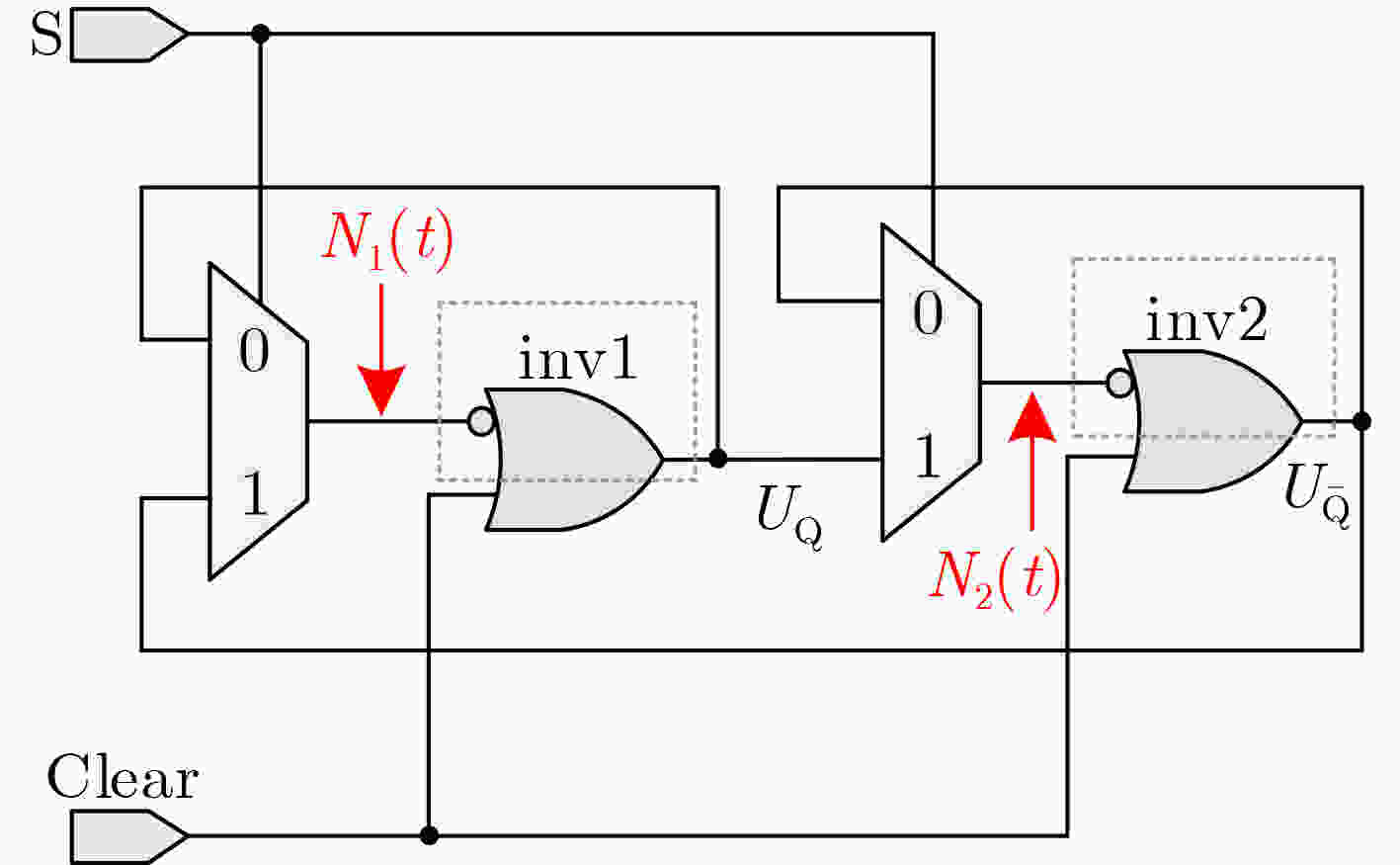
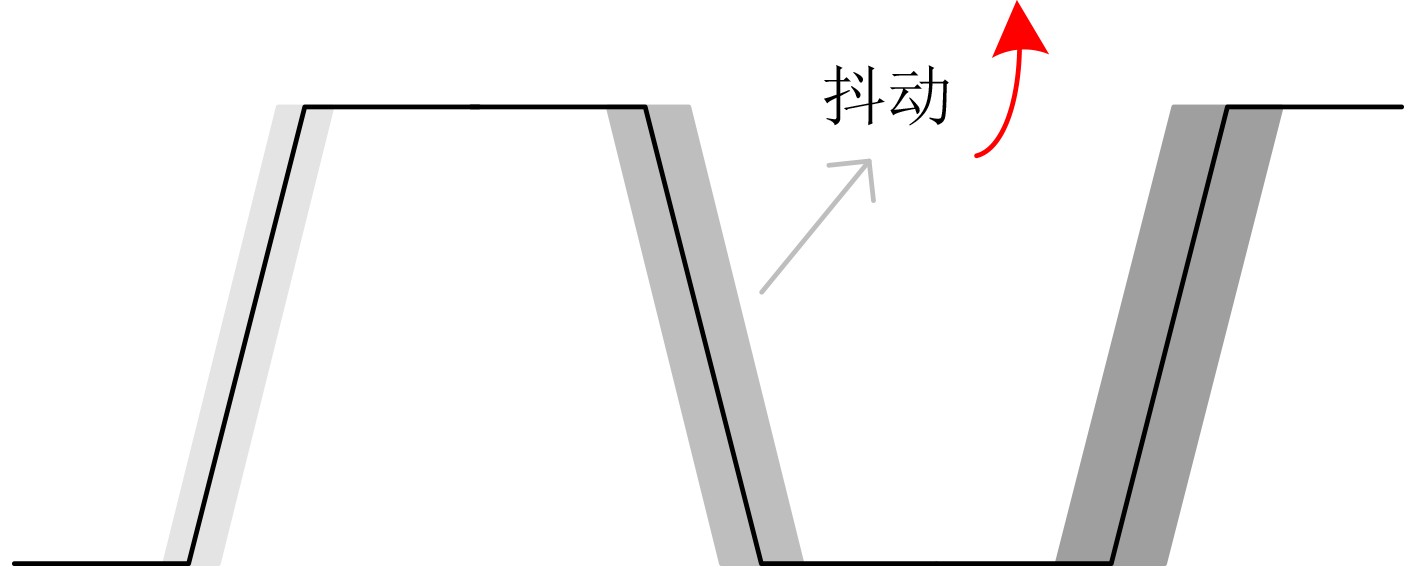
SEL脉冲	IN脉冲	熵源
↘	×	反相器触发的抖动
0	×	反相器触发的抖动
↗	↘	MUX与异或门触发的亚稳态叠加
↗	0	MUX触发的亚稳态
↗	↗	异或门触发的抖动
↗	1	异或门触发的抖动
1	↘	异或门触发的亚稳态
1	0	无熵源(保持)
1	↗	异或门触发的抖动
1	1	异或门触发的抖动

下载: 导出CSV

表 2 NIST SP 800-22测试结果

测试项目	Artix-7			Virtex-7
测试项目	P值	通过率	总体	P值	通过率	总体
近似熵检测	0.503917	99	通过	0.509126	98	通过
块内频数检测	0.510257	100	通过	0.480771	98	通过
累加和检测	0.537681	100	通过	0.466125	98	通过
离散傅里叶变换检测	0.454209	99	通过	0.522061	100	通过
频率检测	0.546769	99	通过	0.460289	98	通过
线性复杂度检测	0.461250	99	通过	0.474038	98	通过
块内最长运行检测	0.510434	100	通过	0.522953	99	通过
非重叠模板匹配检测	0.495718	99	通过	0.500575	99	通过
重叠模板匹配检测	0.465718	99	通过	0.507311	99	通过
随机偏移检测	0.271823	98	通过	0.310572	99	通过
随机偏移变化检测	0.270109	99	通过	0.315353	98	通过
2元矩阵秩检测	0.526488	98	通过	0.495522	100	通过
运行检测	0.550720	97	通过	0.554121	98	通过
序列检测	0.496321	97	通过	0.515058	100	通过
通用统计检测	0.478454	100	通过	0.476515	99	通过

下载: 导出CSV

表 3 NIST SP 800-90B Non-IID测试结果

测试项目	Artix-7		Virtex-7
测试项目	P (max)	h-min	P (max)	h-min
最频值	0.501712	0.995069	0.501694	0.995120
碰撞	0.537109	0.896712	0.539062	0.891476
马尔可夫	4.0306e–39	0.996439	4.4813e–39	0.995244
压缩	0.5	1	0.506836	0.980409
元组	0.526629	0.925141	0.519390	0.945111
最长重复字串长度	0.502963	0.991475	0.501607	0.995369
多个MCW	0.501673	0.995182	0.500678	0.998046
滞后	0.500954	0.997251	0.500901	0.997404
多个MMC	0.500685	0.998025	0.501520	0.995621
LZ78Y算法	0.501425	0.995896	0.500968	0.997211

下载: 导出CSV

表 4 NIST SP 800-90B IID测试结果

测试项目	Artix-7 Result	Virtex-7 Result
IID 置换检验	通过	通过
卡方独立检验	通过	通过
卡方拟合优度检验	通过	通过
最长重复字串长度测试	通过	通过
重启动测试	通过	通过
最小熵测试	0.995069	0.995120

下载: 导出CSV

表 5 与其他先进TRNG的对比

方法	熵源	硬件资源	吞吐量(Mbit/s)	功耗(mW)	后处理电路
[9]	抖动	50LUTs/79FFs	280.0	–	有
[12]	抖动	56LUTs/19FFs	100.0	1.150	有
[14]	抖动	24LUTs/2FFs	290.0	3703.000	无
[16]	抖动	32LUTs/55FFs/33Slices	12.5	9.514	无
[19]	亚稳态	38LUTs/121FFs/38Slices	300.0	119.000	有
[24]	抖动+亚稳态	271LUTs/199Cells	1.0	90.000	有
[25]	抖动+亚稳态	36LUTs/0FFs	12.5	–	无
[26]	抖动	37LUTs/25FFs	160.0	–	无
本文	抖动+亚稳态	29LUTs/4FFs	500.0	123.000	无

下载: 导出CSV

参考文献(26)

[1]	CORRIGAN-GIBBS H, MU W, BONEH D, et al. Ensuring high-quality randomness in cryptographic key generation[C]. 2013 ACM SIGSAC Conference on Computer & Communications Security, Berlin, Germany, 2013: 685–696. doi: 10.1145/2508859.2516680.
[2]	CHAKRABORTY S, GARG A, and SURI M. True random number generation from commodity NVM chips[J]. IEEE Transactions on Electron Devices, 2020, 67(3): 888–894. doi: 10.1109/TED.2019.2963203.
[3]	YANG Bohan, ROŽIC V, GRUJIC M, et al. ES-TRNG: A high-throughput, low-area true random number generator based on edge sampling[J]. IACR Transactions on Cryptographic Hardware and Embedded Systems, 2018, 2018(3): 267–292. doi: 10.13154/tches.v2018.i3.267-292.
[4]	TANG Qianying, KIM B, LAO Yingjie, et al. True random number generator circuits based on single- and multi-phase beat frequency detection[C]. IEEE 2014 Custom Integrated Circuits Conference, San Jose, USA, 2014: 1–4. doi: 10.1109/CICC.2014.6946136.
[5]	ROBOSON S, LEUNG B, and GONG G. Truly random number generator based on a ring oscillator utilizing last passage time[J]. IEEE Transactions on Circuits and Systems II:Express Briefs, 2014, 61(12): 937–941. doi: 10.1109/TCSII.2014.2362715.
[6]	KWOK S H M and LAM E Y. FPGA-based high-speed true random number generator for cryptographic applications[C]. 2006 IEEE Region 10 Conference, Hong Kong, China, 2006: 1–4. doi: 10.1109/TENCON.2006.344013.
[7]	FISCHER V, DRUTAROVSKÝ M, ŠIMKA M, et al. High performance true random number generator in Altera stratix FPLDs[C]. 14th International Conference and Field Programmable Logic and Application, Leuven, Belgium, 2004: 555–564. doi: 10.1007/978-3-540-30117-2_57.
[8]	MEITEI H B and KUMAR M. FPGA implantations of TRNG architecture using ADPLL based on FIR filter as a loop filter[J]. SN Applied Sciences, 2022, 4(4): 96. doi: 10.1007/s42452-022-04981-6.
[9]	LIN Jianming, WANG Yonggang, ZHAO Zelong, et al. A new method of true random number generation based on Galois ring oscillator with event sampling architecture in FPGA[C]. 2020 IEEE International Instrumentation and Measurement Technology Conference, Dubrovnik, Croatia, 2020: 1–6. doi: 10.1109/I2MTC43012.2020.9129357.
[10]	GOLIC J D J. New methods for digital generation and postprocessing of random data[J]. IEEE Transactions on Computers, 2006, 55(10): 1217–1229. doi: 10.1109/TC.2006.164.
[11]	DICHTL M. Fibonacci ring oscillators as true random number generators—a security risk[J]. IACR Cryptology ePrint Archive, 2015, 2015: 270.
[12]	WANG Xinyu, LIANG Huaguo, WANG Yanjie, et al. High-throughput portable true random number generator based on jitter-latch structure[J]. IEEE Transactions on Circuits and Systems I:Regular Papers, 2021, 68(2): 741–750. doi: 10.1109/TCSI.2020.3037173.
[13]	GU Haoang, DENG Fangyu, WANG Qin, et al. A four-phase self-timed ring based true random number generator on FPGA[C]. 2022 IEEE 16th International Conference on Solid-State & Integrated Circuit Technology (ICSICT), Nangjing, China, 2022: 1–3. doi: 10.1109/ICSICT55466.2022.9963322.
[14]	CUI Jianguo, YI Maoxiang, CAO Di, et al. Design of true random number generator based on multi-stage feedback ring oscillator[J]. IEEE Transactions on Circuits and Systems II:Express Briefs, 2022, 69(3): 1752–1756. doi: 10.1109/TCSII.2021.3111049.
[15]	PARK J, KIM B, and SIM J Y. A PVT-tolerant oscillation-collapse-based true random number generator with an odd number of inverter stages[J]. IEEE Transactions on Circuits and Systems II:Express Briefs, 2022, 69(10): 4058–4062. doi: 10.1109/TCSII.2022.3184950.
[16]	GRUJIĆ M and VERBAUWHEDE I. TROT: A three-edge ring oscillator based true random number generator with time-to-digital conversion[J]. IEEE Transactions on Circuits and Systems I: Regular Papers, 2022, 69(6): 2435–2448. doi: 10.1109/TCSI.2022.3158022.
[17]	DI PATRIZIO STANCHIERI G, DE MARCELLIS A, PALANGE E, et al. A true random number generator architecture based on a reduced number of FPGA primitives[J]. AEU - International Journal of Electronics and Communications, 2019, 105: 15–23. doi: 10.1016/j.aeue.2019.03.006.
[18]	MAJZOOBI M, KOUSHANFAR F, and DEVADAS S. FPGA-based true random number generation using circuit metastability with adaptive feedback control[C]. 13th International Workshop on Cryptographic Hardware and Embedded Systems, Nara, Japan, 2011: 17–32. doi: 10.1007/978-3-642-23951-9_2.
[19]	FRUSTACI F, SPAGNOLO F, PERRI S, et al. A high-speed FPGA-based true random number generator using metastability with clock managers[J]. IEEE Transactions on Circuits and Systems II:Express Briefs, 2023, 70(2): 756–760. doi: 10.1109/TCSII.2022.3211278.
[20]	WIECZOREK P Z. Dual-metastability FPGA-based true random number generator[J]. Electronics Letters, 2013, 49(12): 744–745. doi: 10.1049/el.2012.4126.
[21]	VON NEUMANN J. Various techniques used in connection with random digits[J]. National Bureau of Standards Applied Mathematics Series, 1951, 12: 36–38.
[22]	WIECZOREK P Z. An FPGA implementation of the resolve time-based true random number generator with quality control[J]. IEEE Transactions on Circuits and Systems I:Regular Papers, 2014, 61(12): 3450–3459. doi: 10.1109/TCSI.2014.2338615.
[23]	JIN Liyu, YI Maoxiang, XIAO Yuan, et al. A dynamically reconfigurable entropy source circuit for high-throughput true random number generator[J]. Microelectronics Journal, 2023, 133: 105690. doi: 10.1016/j.mejo.2023.105690.
[24]	WIECZOREK P Z. Lightweight TRNG based on multiphase timing of bistables[J]. IEEE Transactions on Circuits and Systems I:Regular Papers, 2016, 63(7): 1043–1054. doi: 10.1109/tcsi.2016.2555248.
[25]	DELLA SALA R, BELLIZIA D, and SCOTTI G. High-throughput FPGA-compatible TRNG architecture exploiting multistimuli metastable cells[J]. IEEE Transactions on Circuits and Systems I:Regular Papers, 2022, 69(12): 4886–4897. doi: 10.1109/TCSI.2022.3199218.
[26]	MEI Faqiang, ZHANG Lei, GU Chongyan, et al. A highly flexible lightweight and high speed true random number generator on FPGA[C]. 2018 IEEE Computer Society Annual Symposium on VLSI (ISVLSI), Hong Kong, China, 2018: 399–404. doi: 10.1109/ISVLSI.2018.00079.