多子阵合成孔径声纳距离-多普勒成像算法

张学波; 王砚梅; 杨家崇; 沈文彦; 孙海信

doi:10.11999/JEIT231160

多子阵合成孔径声纳距离-多普勒成像算法

doi: 10.11999/JEIT231160

1.
海底鹰深海科技股份有限公司昆明 650000
2.
厦门大学信息学院厦门 361005

基金项目: 国家自然科学基金(61971362, 62271426)，福建省自然科学基金 (2020J01003)

详细信息

作者简介:
张学波：男，博士，高级工程师，研究方向为水声信号处理

王砚梅：女，高级工程师，研究方向为水声信号处理

杨家崇：男，高级工程师，研究方向为电路与系统

沈文彦：男，高级工程师，研究方向为水声工程

孙海信：男，博士，教授，研究方向为水声信号处理

通讯作者:
孙海信　hxsun@xmu.edu.cnn

中图分类号: TN911.7
计量
- 文章访问数: 252
- HTML全文浏览量: 142
- PDF下载量: 49
- 被引次数: 0
出版历程
- 收稿日期: 2023-10-25
- 修回日期: 2024-01-25
- 网络出版日期: 2024-02-29
- 刊出日期: 2024-05-30

Range-Doppler Imaging Algorithm for Multireceiver Synthetic Aperture Sonar

1.
Whale Wave Technology Inc., Kunming 650000, China
2.
School of informatics, Xiamen University, Xiamen 361005, China

Funds: The National Natural Science Foundation of China (61971362, 62271426), The Natural Science Foundation of Fujian Province (2020J01003)

摘要

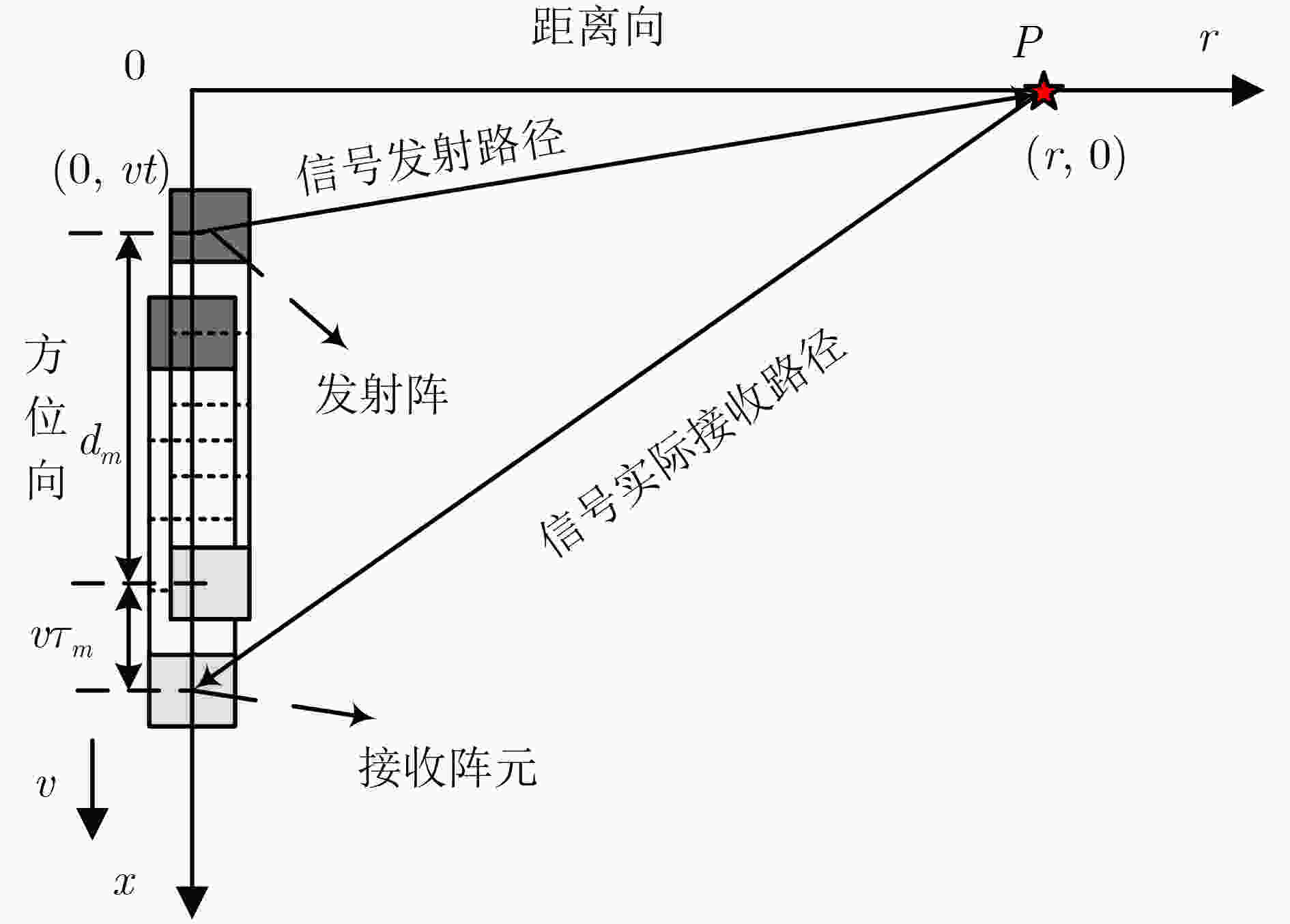
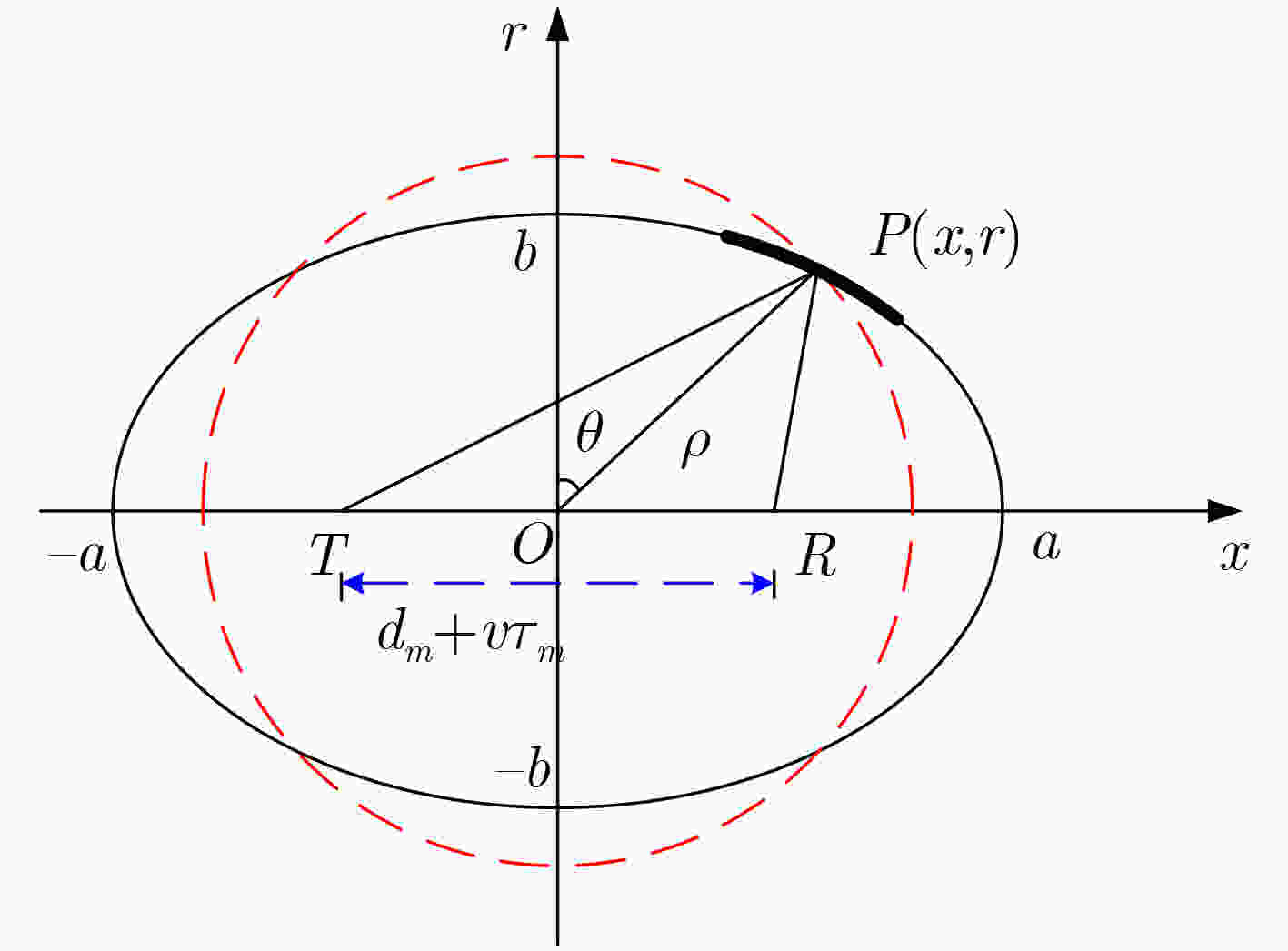
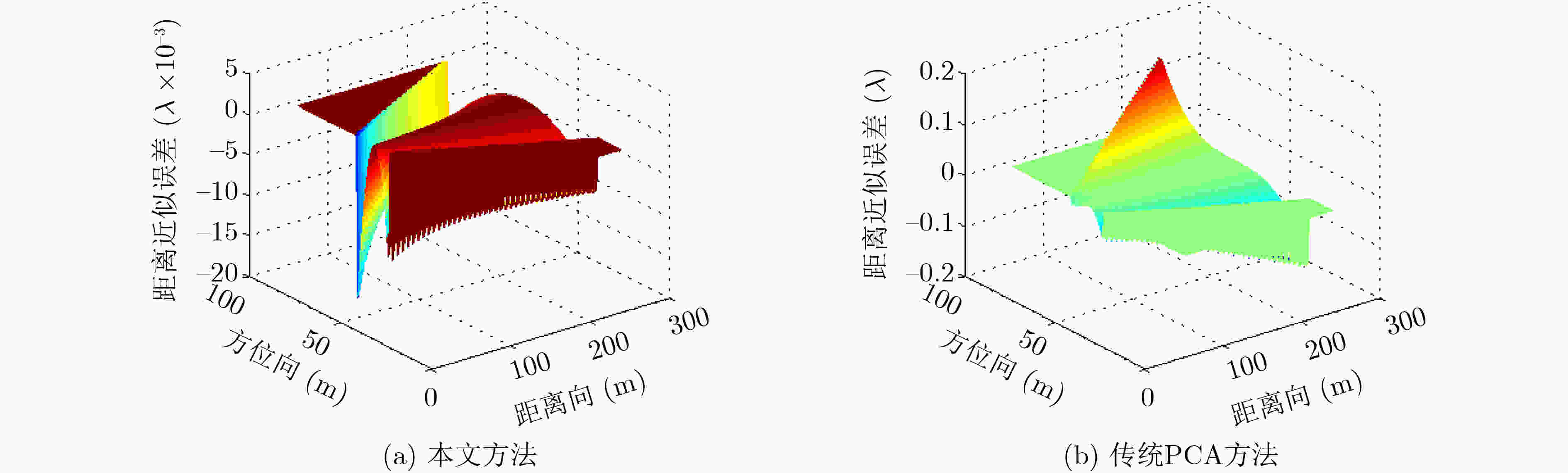
摘要: 基于相位中心近似(PCA)的传统多子阵合成孔径声纳(SAS)成像方法忽略了近似误差的方位空变性，使得分布式目标的聚焦结果发生畸变。为解决这个问题，该文从收发阵元空间分置采样与相位中心近似采样的几何模型出发推导了一种考虑近似误差方位空变性的双程斜距历程，并将多子阵合成孔径声纳2维频域系统函数分解为收发分置畸变项和类收发合置项。在此基础上，采用复数相乘、插值实现收发分置畸变项的补偿，并利用距离-多普勒算法进行成像处理。相对传统方法，该文方法在整个测绘带内的近似误差更小，不会带来方位向上的位置偏移，能得到与真实目标位置一致的成像结果。
- 多接收阵合成孔径声纳 /
- 相位中心近似 /
- 方位空变性 /
- 距离-多普勒算法
Abstract: Traditional multireceiver Synthetic Aperture Sonar (SAS) imaging algorithms based on Phase Center Approximation (PCA) neglect the spatial variance of approximation error in the azimuth dimension. The distortion would be introduced in the focused results of distributed. To solve this problem, a two-way slant range considering the azimuth variance of approximation error is deduced based on the geometry models of transmitter/receiver bistatic sampling and PCA sampling. The system function in the 2D frequency domain is further decomposed into transmitter/receiver bistatic deformation term and quasi monostatic term. Based on that, the complex multiplication and interpolation are adopted to compensate the bistatic deformation term. Then, the range-Doppler imaging algorithm is used to focus the targets. Compared to traditional methods, much smaller appropriation error across the whole mapping swath is obtained by using the proposed method. Besides, the position deviation in the azimuth dimension is not introduced by the proposed method. The imaging result which is identical to practical target position can be obtained.
- Multireceiver Synthetic Aperture Sonar (SAS) /
- Phase Center Approximation(PCA) /
- Azimuth spatial variance /
- Range-Doppler algorithm

HTML全文

图 1 多接收阵SAS系统成像几何

下载: 全尺寸图片幻灯片

图 2 相位中心近似法的几何解释

下载: 全尺寸图片幻灯片

图 3 近似误差

下载: 全尺寸图片幻灯片

图 4 点目标成像结果在方位向的剖面

下载: 全尺寸图片幻灯片

图 5 湖试数据成像结果

下载: 全尺寸图片幻灯片

图 6 方位向剖面

下载: 全尺寸图片幻灯片

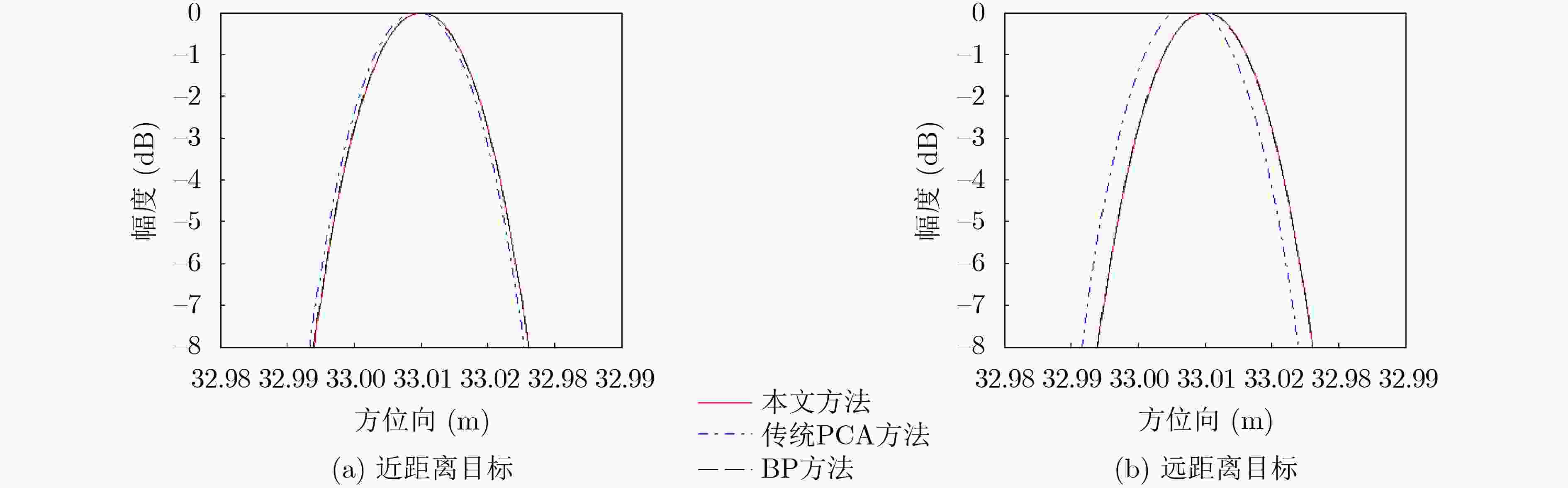
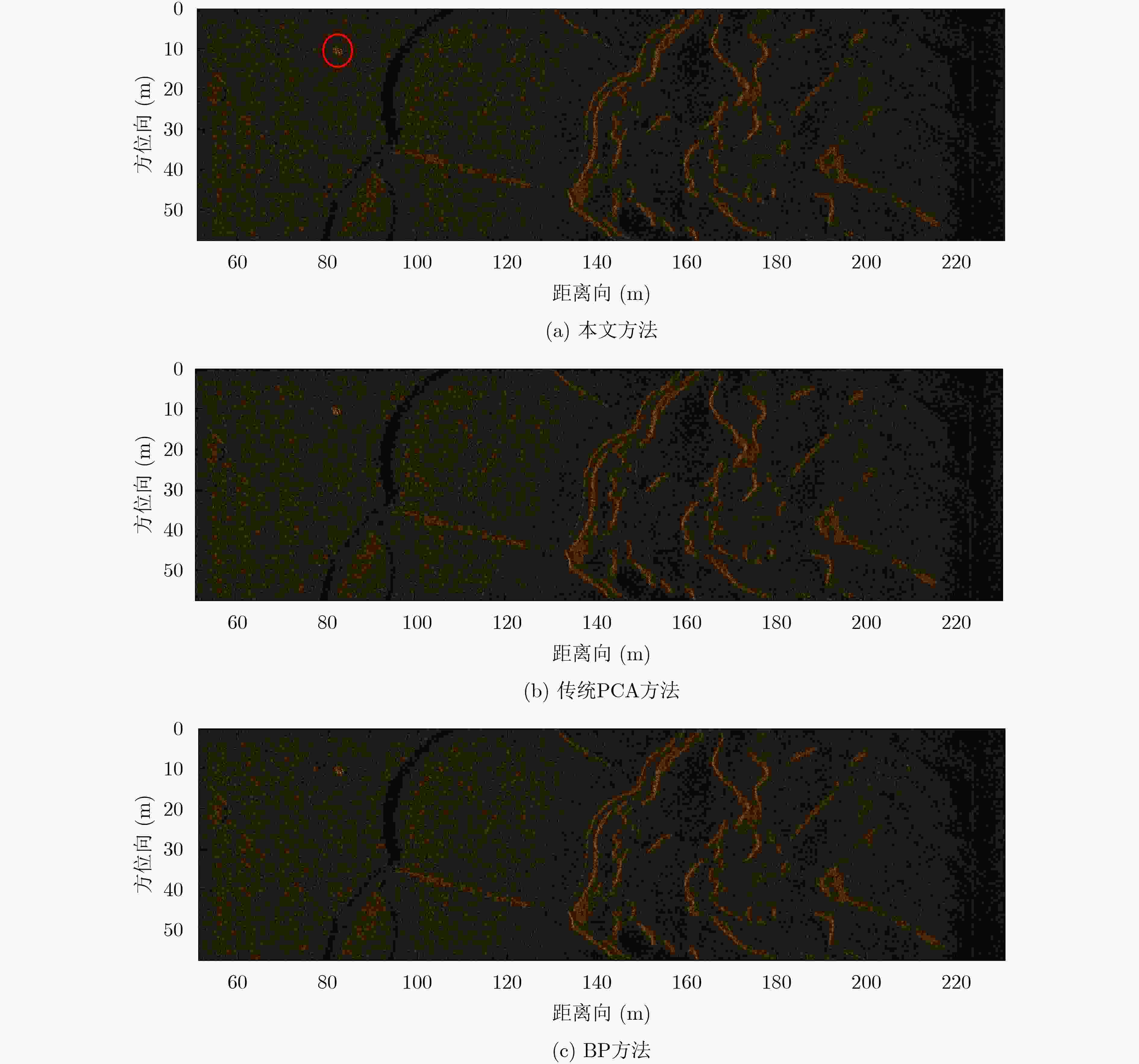
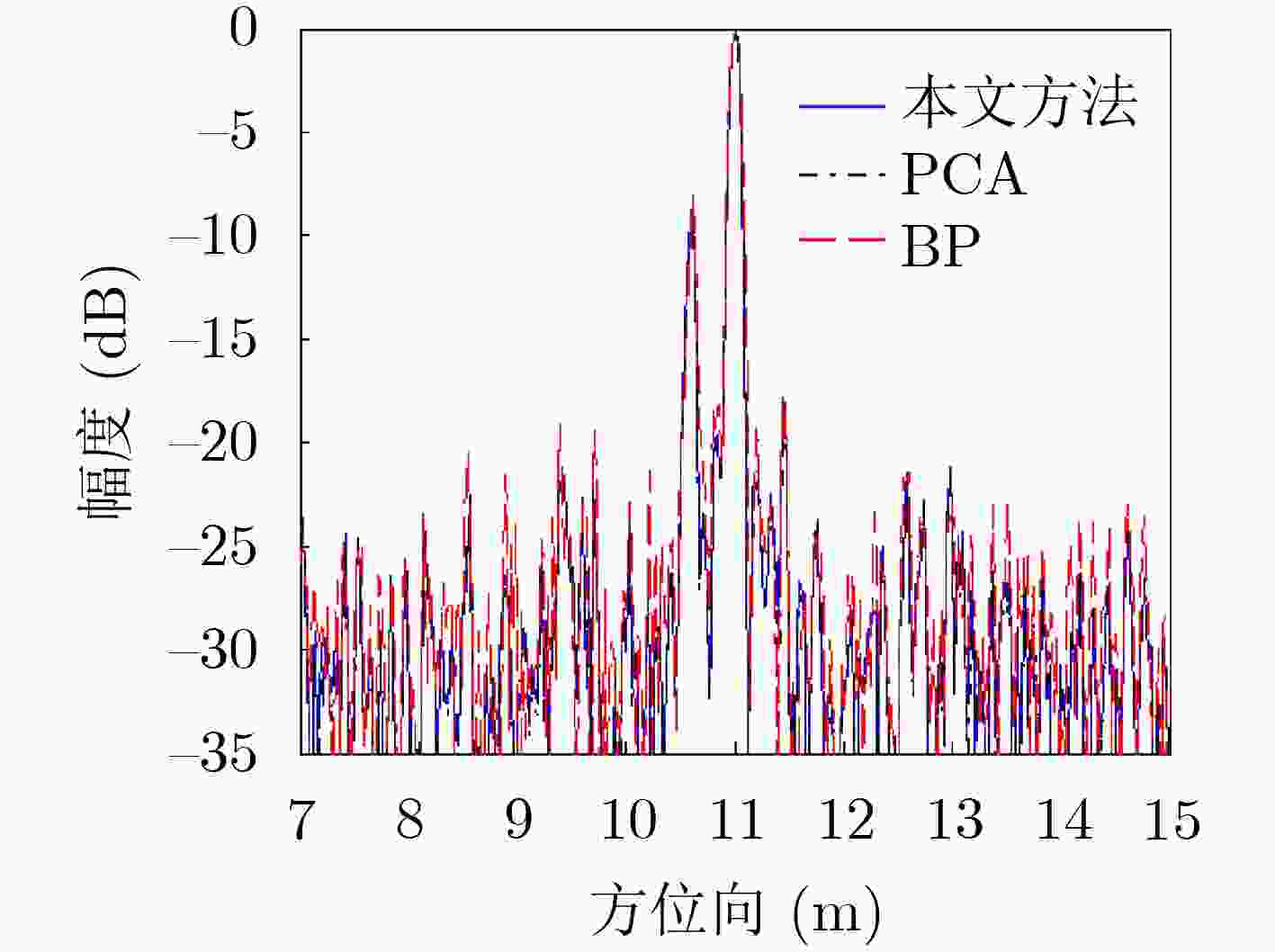
表 1 成像结果性能统计(dB)

	传统PCA方法		本文方法		BP算法
	PSLR	ISLR	PSLR	ISLR	PSLR	ISLR
近距离目标	–14.04	–10.51	–14.53	–10.65	–14.73	–10.71
远距离目标	–13.41	–9.53	–14.37	–10.57	–14.51	–10.58

下载: 导出CSV

参考文献(19)

[1]	THOMAS B and HUNTER A. Coherence-induced bias reduction in synthetic aperture sonar along-track micronavigation[J]. IEEE Journal of Oceanic Engineering, 2022, 47(1): 162–178. doi: 10.1109/JOE.2021.3103264.
[2]	YANG Peixuan. An imaging algorithm for high-resolution imaging sonar system[J]. Multimedia Tools and Applications, 2023. doi: 10.1007/s11042-023-16757-0.
[3]	PATE D J, COOK D A, and DONNELL B N O. Estimation of synthetic aperture resolution by measuring point scatterer responses[J]. IEEE Journal of Oceanic Engineering, 2022, 47(2): 457–471. doi: 10.1109/JOE.2021.3128414.
[4]	GERG I D and COTNER C F. A perceptual metric prior on deep latent space improves out-of-distribution synthetic aperture sonar image classification[C]. 2023 IEEE International Geoscience and Remote Sensing Symposium, Pasadena, USA, 2023: 6576–6579. doi: 10.1109/IGARSS52108.2023.10283358.
[5]	WANG Meng and HUANG Pan. A multireceiver SAS imaging algorithm and optimization[J]. IEEE Access, 2023, 11: 75112–75120. doi: 10.1109/ACCESS.2023.3297138.
[6]	WILLIAMS D P. On the use of tiny convolutional neural networks for human-expert-level classification performance in sonar imagery[J]. IEEE Journal of Oceanic Engineering, 2021, 46(1): 236–260. doi: 10.1109/JOE.2019.2963041.
[7]	NADIMI N, JAVIDAN R, and LAYEGHI K. Efficient detection of underwater natural gas pipeline leak based on synthetic aperture sonar (SAS) systems[J]. Journal of Marine Science and Engineering, 2021, 9(11): 1273. doi: 10.3390/jmse9111273.
[8]	CHOI H M, YANG H S, and SEONG W J. Compressive underwater sonar imaging with synthetic aperture processing[J]. Remote Sensing, 2021, 13(10): 1924. doi: 10.3390/rs13101924.
[9]	杨磊, 王腾腾, 陈英杰, 等. 低秩矩阵补全高分辨SAR成像特征重建[J]. 电子与信息学报, 2023, 45(8): 2965–2974. doi: 10.11999/JEIT220992. YANG Lei, WANG Tengteng, CHEN Yingjie, et al. Feature Reconstruction of high resolution SAR imagery based on low rank matrix completion[J]. Journal of Electronics & Information Technology, 2023, 45(8): 2965–2974. doi: 10.11999/JEIT220992.
[10]	别博文, 刘江, 孙光才, 等. 基于奇异值分解的低轨星载双基调频连续波SAR成像方法[J]. 电子与信息学报, 2023, 45(7): 2502–2510. doi: 10.11999/JEIT220757. BIE Bowen, LIU Jiang, SUN Guangcai, et al. Low-orbit bistatic frequency modulated continuous wave SAR imaging method based on singular value decomposition[J]. Journal of Electronics & Information Technology, 2023, 45(7): 2502–2510. doi: 10.11999/JEIT220757.
[11]	闵林, 刘向前, 郝晓龙, 等. 基于低秩汉克尔矩阵重构技术的星载间断调频连续波SAR成像方法[J]. 电子与信息学报, 2023, 45(4): 1285–1292. doi: 10.11999/JEIT220239. MIN Lin, LIU Xiangqian, HAO Xiaolong, et al. Spaceborne interrupted frequency modulate continuous wave SAR imaging based on low-rank Hankel matrix reconstruction technique[J]. Journal of Electronics & Information Technology, 2023, 45(4): 1285–1292. doi: 10.11999/JEIT220239.
[12]	GOUGH P T, HAYES M P, and WILKINSON D R. An efficient image reconstruction algorithm for a multiple hydrophone array synthetic aperture sonar[C]. The 5th European Conference on Underwater Acoustics, Lyon, France, 2000: 395–400.
[13]	BONIFANT W W, RICHARDS M A, and MCCLELLAN J H. Interferometric height estimation of the seafloor via synthetic aperture sonar in the presence of motion errors[J]. IEE Proceedings - Radar, Sonar and Navigation, 2000, 147(6): 322–330. doi: 10.1049/ip-rsn:20000618.
[14]	GOUGH P T and HAYES M P. Fast Fourier techniques for SAS imagery[C]. The Europe Oceans 2005, Brest, France, 2005: 563–568. doi: 10.1109/OCEANSE.2005.1511776.
[15]	CALLOW H J, HAYES M P, and GOUGH P T. Motion-compensation improvement for widebeam, multiple-receiver SAS systems[J]. IEEE Journal of Oceanic Engineering, 2009, 34(3): 262–268. doi: 10.1109/JOE.2009.2014659.
[16]	HUANG Pan and YANG Peixuan. Synthetic aperture imagery for high-resolution imaging sonar[J]. Frontiers in Marine Science, 2022, 9: 1049761. doi: 10.3389/fmars.2022.1049761.
[17]	ZHANG Xuebo, CHEN Xiaohui, and QU Wu. Influence of the stop-and-hop assumption on synthetic aperture sonar imagery[C]. The IEEE 17th International Conference on Communication Technology (ICCT), Chengdu, China, 2017: 1601–1607. doi: 10.1109/ICCT.2017.8359901.
[18]	ZHANG Xuebo, WU Haoran, SUN Haixin, et al. Multireceiver SAS imagery based on monostatic conversion[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2021, 14: 10835–10853. doi: 10.1109/JSTARS.2021.3121405.
[19]	ZHANG Xuebo and YANG Peixuan. Back projection algorithm for multi-receiver synthetic aperture sonar based on two interpolators[J]. Journal of Marine Science and Engineering, 2022, 10(6): 718. doi: 10.3390/jmse10060718.