A Multi-party Vertically Partitioned Data Synthesis Mechanism with Personalized Differential Privacy
-
摘要: 当今时代,随着大数据技术的飞速发展和数据量的持续增加,大量数据不断被不同的公司或者机构收集,把来自不同公司或机构的数据聚合起来并发布,有助于更好地提供服务、支持决策。然而他们各自的数据中可能包含敏感程度不同的隐私信息,所以在聚合发布各方数据时需要满足个性化隐私保护要求。针对个性化隐私保护的多方数据聚合发布问题,该文提出满足个性化差分隐私的多方垂直划分数据合成机制(PDP-MVDS)。该机制通过生成低维边缘分布实现对高维数据的降维,用低维边缘分布更新随机初始的数据集,最终发布和各方的真实聚合数据集分布近似的合成数据集;同时通过划分隐私预算实现个性化差分隐私保护,利用安全点积协议和门限Paillier加密保证各方数据在聚合过程中的隐私性,利用分布式拉普拉斯机制有效保护了多方聚合边缘分布的隐私。该文通过严格的理论分析证明了PDP-MVDS能够确保每个参与方数据和发布数据集的安全。最后,在公开数据集上进行了实验评估,实验结果表明PDP-MVDS机制能够以低开销生成高效用的多方合成数据集。Abstract: In today’s era, with the rapid development of big data technology and the continuous increase in data volume, large amounts of data are constantly collected by different companies or institutions, aggregating and publishing data owned by different companies or institutions helps to better provide services and support decision-making. However, their respective data may contain privacy information with different degrees of sensitivity, thus personalized privacy protection requirements need to be met while aggregating and publishing data from all parties. To solve the problem of multi-party data publication while ensuring that different privacy protection needs of all parties are met, a Multi-party Vertically partitioned Data Synthesis mechanism with Personalized Differential Privacy (PDP-MVDS) is proposed. Low-dimensional marginal distributions are firstly generated to reduce the dimension of high-dimensional data, then a randomly initialized dataset with these marginal distributions are updated, and finally a synthesized dataset whose distribution is similar to that of the real aggregated dataset from all parties is published. Personalized differential privacy protection is achieved by dividing the privacy budget; Secure scalar product protocol and threshold Paillier encryption algorithm are used to ensure the privacy of each party’s data in the aggregation process; Distributed Laplace perturbation mechanism is used to effectively protect the privacy of marginal distributions that aggregated from those parties. Through rigorous theoretical analysis, it is proved that PDP-MVDS can ensure the security of each participant’s data and the finally published dataset. Furthermore, the experimental results on public datasets show that PDP-MVDS mechanism can obtain a multi-party synthesized dataset with high utility under low overhead.
-
表 1 参与方${P_k}$的重要参数
参与方 服从$N\left( {0,\sqrt {{\lambda / 2}} } \right)$
分布的变量Pailler的解密私钥份额 ${P_k}$ $Y_{1k}$, $Y_{2k}$, $Y_{3k}$, $Y_{4k}$ ${\lambda _{k,t}}$($t \in \left\{ {1,2, \cdots ,K} \right\}\backslash k$) ${\tau _k}$ 1 计算跨数据集属性对IInDif*的算法
输入:属性$a$的加噪1维频数分布${\boldsymbol{N}}_a^*$,属性$b$的加噪1维频数分布${\boldsymbol{N}}_b^*$,属性$a$的取值集合${\boldsymbol{A}}$,属性$b$的取值集合${\boldsymbol{B}}$,需要合成的数据集的
记录数$n$,${P_x}$的私钥${\lambda _{x,y}}$,${P_y}$的私钥${\lambda _{y,x}}$。输出:跨数据集属性对$\left( {a,b} \right)$的加噪IInDif:$ {\text{IInDi}}{{\text{f}}_{a,b}}^* $。 1 对于每个$i \in {\boldsymbol{A}}$, $j \in {\boldsymbol{B}}$: 2 ${P_x}$和${P_y}$执行SSPP,协议执行后,${P_x}$得到${S_x}$,${P_y}$得到${S_y}$,其中${S_x} + {S_y} = {N_{a = i,b = j}}$; 3 ${P_x}$和${P_y}$分别用Paillier密码系统对${S_x}$, ${S_y}$进行加密得到${{C}}\left[ {{S_x}} \right]$, ${{C}}\left[ {{S_y}} \right]$,并把${{C}}\left[ {{S_x}} \right]$, ${{C}}\left[ {{S_y}} \right]$, $N_{a = i}^*$, $N_{b = j}^*$发给半可信第三方S; 4 S用Paillier公钥得到密文${{C}}\left[ {N_{a = i}^* \times N_{b = j}^*} \right]$,并利用Paillier密码系统的同态性计算${{C}}\left[ t \right]= {{{{C}}\left[ {N_{a = i}^* \times N_{b = j}^*} \right]} \mathord{\left/ {\vphantom {{{{C}}\left[ {N_{a = i}^* \times N_{b = j}^*} \right]} {{{\left( {{{C}}\left[ {{S_x}} \right] \times {{C}}\left[ {{S_y}} \right]} \right)}^n}}}} \right. } {{{\left( {{{C}}\left[ {{S_x}} \right] \times {{C}}\left[ {{S_y}} \right]} \right)}^n}}} =$
$ {\rm{C}}\left[ {N_{a = i}^* \times N_{b = j}^* - n \times {N_{a = i,b = j}}} \right] $,接着随机选择一个大于0的整数$r$并计算${{C}}{\left[ t \right]^r} = {{C}}\left[ {t \times r} \right]$,然后把${{C}}{\left[ t \right]^r}$发给${P_x}$和${P_y}$;5 ${P_x}$和${P_y}$利用私钥${\lambda _{x,y}}$, ${\lambda _{y,x}}$,协作对${{C}}{\left[ t \right]^r}$进行解密,得到$t \times r$,若$t \times r \ge 0$,则向S发送sign=1,若$t \times r < 0$,则向S发送
sign=–1;6 S接收sign,若sign=1,S令${c_{i,j}} = {{C}}\left[ t \right]$,若sign=–1,S用Paillier公钥对0进行加密得到${{C}}\left[ 0 \right]$,并计算${c_{i,j}} = {{{{C}}\left[ 0 \right]} \mathord{\left/ {\vphantom {{{{C}}\left[ 0 \right]} {{{C}}\left[ t \right]}}} \right. } {{{C}}\left[ t \right]}}$; 7 ${P_x}$和${P_y}$在S的帮助下,利用DLPA生成噪声${{C}}\left[ \eta \right]$;$ {{E}}_{{t}}={{E}}_{{t}}\left({l}\right) $ 8 S先计算$ {{C}}\left[ {{\mathrm{sum}}} \right] = {\left( {\prod\nolimits_{i,j} {{c_{i,j}}} } \right)^{{1 \mathord{\left/ {\vphantom {1 n}} \right. } n}}} $,再计算${{C}}\left[ {{\mathrm{sum}}} \right] \times {{C}}\left[ \eta \right]$并将其发给${P_x}$和${P_y}$; 9 ${P_x}$和${P_y}$利用私钥${\lambda _{x,y}}$, ${\lambda _{y,x}}$,协作对${{C}}\left[ {{\mathrm{sum}}} \right] \times {{C}}\left[ \eta \right]$进行解密,得到$ {\text{IInDi}}{{\text{f}}_{a,b}}^* $; 2 选择属性对的算法
输入:属性对的个数$m$,参与方的个数$K$,隐私预算集$\{ \rho _2^1,\rho _2^2, \cdots ,\rho _2^K\} $,比例因子$\mu \in (0,1)$,各参与方手中的属性对标号集合
${{\boldsymbol{I}}_k} = \{ {A_{k - 1}} + 1,{A_{k - 1}} + 2, \cdots ,{A_k}\} $(${A_0} = 0$),每个属性对的值域基数$ {{c}}_{{i}}\left({i}\in \left\{1,2,\cdots ,{M}\right\}\right) $($i \in \left\{ {1,2, \cdots ,m} \right\}$),依赖误差
$ {\varPhi _i} \approx {\text{IInDi}}{{\text{f}}_i}^* $。输出:被选择属性对的序号集$ {{\boldsymbol{X}}} $(${\boldsymbol{X}} = \bigcup\nolimits_{k = 1}^K {{{\boldsymbol{X}}_k}} $)。 1 ${\boldsymbol{X}} = {\boldsymbol{\varnothing}} $,${{\boldsymbol{X}}_k} = \varnothing $($k \in \{ 1,2, \cdots ,K\} $),$t = 0$,${E_0} = \displaystyle\sum\nolimits_{i \in \bar {\boldsymbol{X}}} {{\varPhi _i}} $;//初始化参数 2 while True: 3 for $k = 1$ to $K$: 4 每个${P_o}(o \ne k)$计算每个属于${{\boldsymbol{X}}_o}$的属性对$s$的隐私预算:${\varepsilon _s} = \frac{{c_s^{2/3}}}{{\displaystyle\sum\nolimits_{j \in {{\boldsymbol{X}}_o}} {c_j^{2/3}} }} \times \rho _2^o \times (1 - \mu )$,并计算
${\varPsi _o} = \displaystyle\sum\nolimits_{s \in {{\boldsymbol{X}}_o}} {{c_s} \times \sqrt {{1 \mathord{\left/ {\vphantom {1 {(\pi \times {\varepsilon _s})}}} \right. } {(\pi \times {\varepsilon _s})}}} } $,把$ {\Psi _o} $, $ {\varPhi _o} = \displaystyle\sum\nolimits_{i \in {{\boldsymbol{I}}_o}\backslash {{\boldsymbol{X}}_o}} {{\varPhi _i}} $发给${P_k}$;5 对于${{\boldsymbol{I}}_k}$中每个不属于${{\boldsymbol{X}}_k}$的属性对$ i \in {{\boldsymbol{I}}_k}\backslash {{\boldsymbol{X}}_k} $: 6 ${P_k}$为每个$ h \in {{\boldsymbol{X}}_k} \cup \left\{ i \right\} $计算${\varepsilon _h} = \frac{{c_h^{2/3}}}{{\displaystyle\sum\nolimits_{j \in {{\boldsymbol{X}}_k} \cup \{ i\} } {c_j^{2/3}} }} \times \rho _2^k \times (1 - \mu )$,然后计算
${E_t}(i) = \displaystyle\sum\nolimits_{h \in {{\boldsymbol{X}}_k} \cup \{ i\} } {{c_h} \times \sqrt {{1 \mathord{\left/ {\vphantom {1 {(\pi \times {\varepsilon _h})}}} \right. } {(\pi \times {\varepsilon _h})}}} } + \displaystyle\sum\nolimits_{j \in {{\boldsymbol{I}}_k}\backslash {{\boldsymbol{X}}_k}\backslash \{ i\} } {{\varPhi _j}} + \displaystyle\sum\nolimits_{o \ne k} {{\varPsi _o}} + \displaystyle\sum\nolimits_{o \ne k} {{\varPhi _o}} $;7 每个${P_k}$($ k\in \{1,2,\cdots ,K\} $)选出$ E_t^k(l) = \min \left\{ {E_t^k(i)|i \in {{\boldsymbol{I}}_k}\backslash {{\boldsymbol{X}}_k}} \right\} $,然后进行比较,得到$ E_t^x(l) = \min \left\{ {E_t^1(l),E_t^2(l), \cdots ,E_t^K(l)} \right\} $; 8 ${E_t} = {E_t}(l)$ 9 if ${E_t} \ge {E_{t - 1}}$: 10 Break; 11 ${P_x}$进行操作:${\boldsymbol{X}} = {\boldsymbol{X}} \cup \{ l\} $,${{\boldsymbol{X}}_x} = {{\boldsymbol{X}}_x} \cup \{ l\} $; 12 $t = t + 1$; 3 方案的整体流程
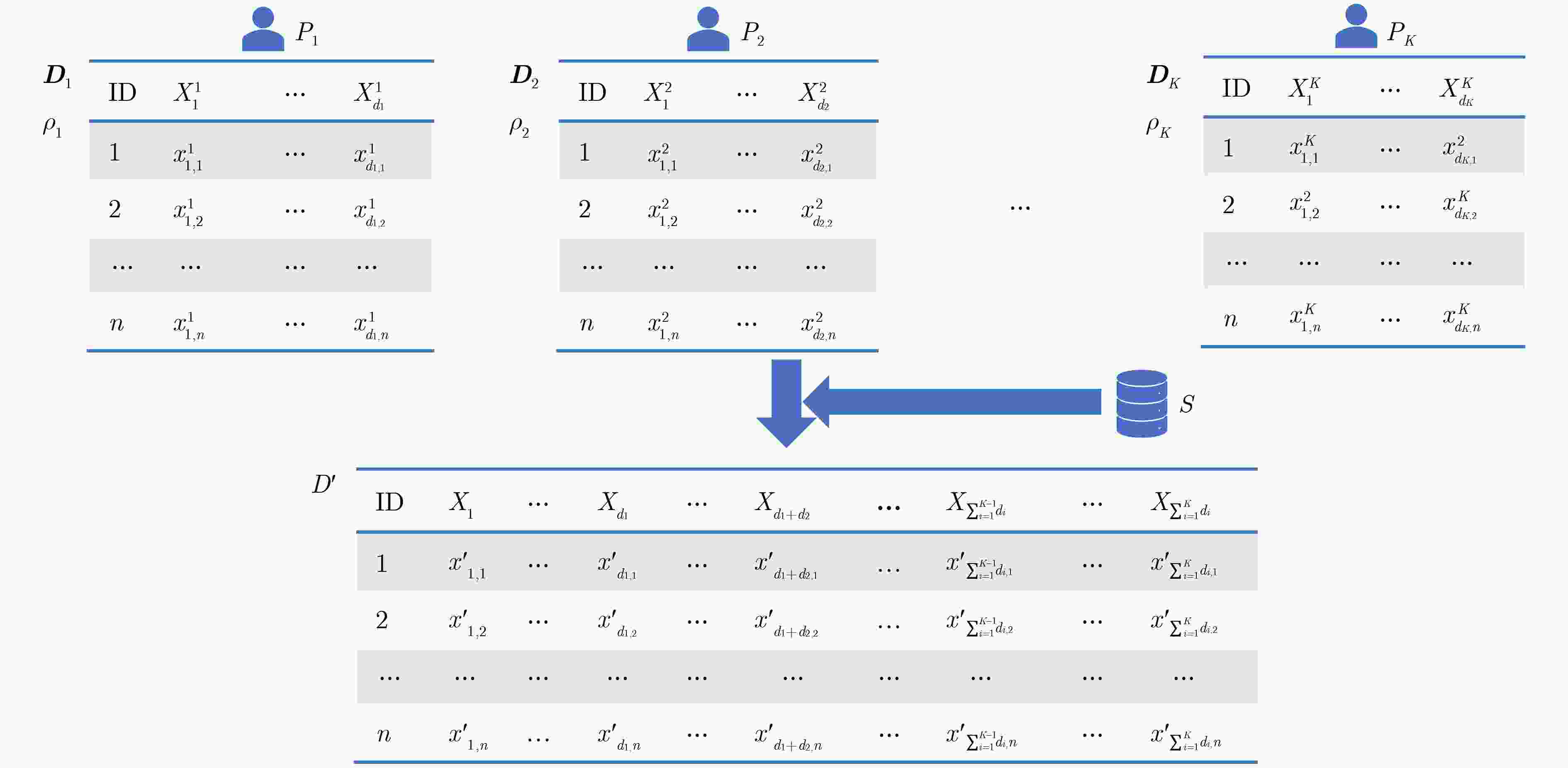
输入:$K$个数据集${{\boldsymbol{D}}_1},{{\boldsymbol{D}}_2}, \cdots ,{{\boldsymbol{D}}_K}$及其对应的隐私预算${\rho _1},{\rho _2}, \cdots ,{\rho _K}$。 输出:合成的整体数据集$ {{\boldsymbol{D}}_s} $。 //预处理并计算加噪1维分布 1 for $k = 1$ to $K$: 2 ${P_k}$对$ {{\boldsymbol{D}}_k} $进行预处理; 3 ${P_k}$以$\rho _1^k = 0.1 \times {\rho _k}$,的隐私预算,用拉普拉斯机制计算$ {{\boldsymbol{D}}_k} $中所有属性的加噪1维边缘频数分布$ ({\boldsymbol{N}}_X^*)_{1 - {\text{way}}}^k $($X$属于$ {{\boldsymbol{D}}_k} $的属性集
${{\boldsymbol{\chi }}_k}$);//选择属性对 4 各个参与方${P_k}$以$\rho _2^k = 0.1 \times {\rho _k}$的隐私预算,用算法2共同选择属性对; //合并属性对并加噪 5 某一个参与方${P_x}$对选出的属性对进行合并,得到多属性组合集${\boldsymbol{Z}}$; 6 各个参与方${P_k}$以$\rho _3^k = 0.8 \times {\rho _k}$的隐私预算,用SSPP和DLPA共同计算${\boldsymbol{Z}}$中每个${{\boldsymbol{Z}}_i} \in {\boldsymbol{Z}}$的加噪低维边缘频数分布; //后处理并合成数据集 7 某一个参与方${P_x}$对得到的加噪低维边缘频数分布进行后处理,并初始化一个数据集$ {{\boldsymbol{D}}_0} $,根据后处理后的加噪低维边缘频数分布对其进
行更新,得到$ {{\boldsymbol{D}}_s} $;表 2 实验用到的数据集的详细信息
数据集 记录数 属性数 数据集大小(MB) Adult 48842 15 5.07 Big5 19719 57 2.21 -
[1] 唐朋. 满足差分隐私的多方数据发布技术研究[D]. [博士论文], 北京邮电大学, 2019.TANG Peng. Research on differentially private multi-party data publishing[D]. [Ph. D. dissertation], Beijing University of Posts and Telecommunications, 2019. [2] DWORK C. Differential privacy[C]. 33rd International Colloquium on Automata, Languages and Programming, Venice, Italy, 2006: 1–12. doi: 10.1007/11787006_1. [3] ZHANG Jun, CORMODE G, PROCOPIUC C M, et al. PrivBayes: Private data release via Bayesian networks[J]. ACM Transactions on Database Systems, 2017, 42(4): 25. doi: 10.1145/3134428. [4] CHEN Rui, XIAO Qian, ZHANG Yu, et al. Differentially private high-dimensional data publication via sampling-based inference[C]. Proceedings of the 21th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Sydney, Australia, 2015: 129–138. doi: 10.1145/2783258.2783379. [5] CAI Kuntai, LEI Xiaoyu, WEI Jianxin, et al. Data synthesis via differentially private Markov random fields[J]. Proceedings of the VLDB Endowment, 2021, 14(11): 2190–2202. doi: 10.14778/3476249.3476272. [6] ZHANG Zhikun, WANG Tianhao, LI Ninghui, et al. PrivSyn: Differentially private data synthesis[C]. 30th USENIX Security Symposium, Berkeley, USA, 2021: 929–946. [7] CHENG Wenqing, WEN Ruxue, HUANG Haojun, et al. OPTDP: Towards optimal personalized trajectory differential privacy for trajectory data publishing[J]. Neurocomputing, 2022, 472: 201–211. doi: 10.1016/j.neucom.2021.04.137. [8] 张星, 张兴, 王晴阳. DP-IMKP: 满足个性化差分隐私的数据发布保护方法[J]. 计算机工程与应用, 2023, 59(10): 288–298. doi: 10.3778/j.issn.1002-8331.2201-0457.ZHANG Xing, ZHANG Xing, and WANG Qingyang. DP-IMKP: Data publishing protection method for personalized differential privacy[J]. Computer Engineering and Applications, 2023, 59(10): 288–298. doi: 10.3778/j.issn.1002-8331.2201-0457. [9] ZHU Hui, YIN Fan, PENG Shuangrong, et al. Differentially private hierarchical tree with high efficiency[J]. Computers & Security, 2022, 118: 102727. doi: 10.1016/j.cose.2022.102727. [10] ALHADIDI D, MOHAMMED N, FUNG B C M, et al. Secure distributed framework for achieving ε-differential privacy[C]. 12th International Symposium on Privacy Enhancing Technologies, Vigo, Spain, 2012: 120–139. doi: 10.1007/978-3-642-31680-7_7. [11] CHENG Xiang, TANG Peng, SU Sen, et al. Multi-party high-dimensional data publishing under differential privacy[J]. IEEE Transactions on Knowledge and Data Engineering, 2020, 32(8): 1557–1571. doi: 10.1109/TKDE.2019.2906610. [12] GU Zhen, ZHANG Kejia, and ZHANG Guoyin. Multiparty data publishing via blockchain and differential privacy[J]. Security and Communication Networks, 2022, 2022: 5612794. doi: 10.1155/2022/5612794. [13] TANG Peng, CHEN Rui, SU Sen, et al. Multi-party sequential data publishing under differential privacy[J]. IEEE Transactions on Knowledge and Data Engineering, 2023, 35(9): 9562–9577. doi: 10.1109/TKDE.2023.3241661. [14] MOHAMMED N, ALHADIDI D, FUNG B C M, et al. Secure two-party differentially private data release for vertically partitioned data[J]. IEEE Transactions on Dependable and Secure Computing, 2014, 11(1): 59–71. doi: 10.1109/TDSC.2013.22. [15] TANG Peng, CHENG Xiang, SU Sen, et al. Differentially private publication of vertically partitioned data[J]. IEEE Transactions on Dependable and Secure Computing, 2021, 18(2): 780–795. doi: 10.1109/TDSC.2019.2905237. [16] 张小玉. 基于差分隐私的异构多属性数据发布方法研究[D]. [硕士论文], 南京航空航天大学, 2022.ZHANG Xiaoyu. Research on heterogeneous multi-attribute data publishing method based on differential privacy[D]. [Master dissertation], Nanjing University of Aeronautics and Astronautics, 2022. [17] WANG Rong, FUNG B C M, ZHU Yan, et al. Differentially private data publishing for arbitrarily partitioned data[J]. Information Sciences, 2021, 553: 247–265. doi: 10.1016/j.ins.2020.10.051. [18] BUN M and STEINKE T. Concentrated differential privacy: Simplifications, extensions, and lower bounds[C]. 14th International Conference on Theory of Cryptography, Beijing, China, 2016: 635–658. doi: 10.1007/978-3-662-53641-4_24. [19] JORGENSEN Z, YU Ting, and CORMODE G. Conservative or liberal? Personalized differential privacy[C]. 2015 IEEE 31st International Conference on Data Engineering, Seoul, Korea (South), 2015: 1023–1034. doi: 10.1109/ICDE.2015.7113353. [20] RASTOGI V and NATH S. Differentially private aggregation of distributed time-series with transformation and encryption[C]. Proceedings of the 2010 ACM SIGMOD International Conference on Management of Data, Indianapolis, USA, 2010: 735–746. doi: 10.1145/1807167.1807247. [21] FOUQUE P A, POUPARD G, and STERN J. Sharing decryption in the context of voting or lotteries[C]. 4th International Conference on Financial Cryptography, Anguilla, British West Indies, 2001: 90–104. doi: 10.1007/3-540-45472-1_7. [22] GOETHALS B, LAUR S, LIPMAA H, et al. On private scalar product computation for privacy-preserving data mining[C]. 7th International Conference on Information Security and Cryptology, Seoul, Korea (South), 2005: 104–120. doi: 10.1007/11496618_9. [23] UCI machine learning repository[EB/OL]. http://archive.ics.uci.edu/ml/datasets.html. [24] EB/OL]. http://personality-testing.info/_rawdata/. [25] TSYBAKOV A B. Introduction to Nonparametric Estimation[M]. New York: Springer, 2009. -





 下载:
下载:


 下载:
下载:
