A High Precision Direction of Arrival Estimation Method Applied to Semi-Coprime Arrays
-
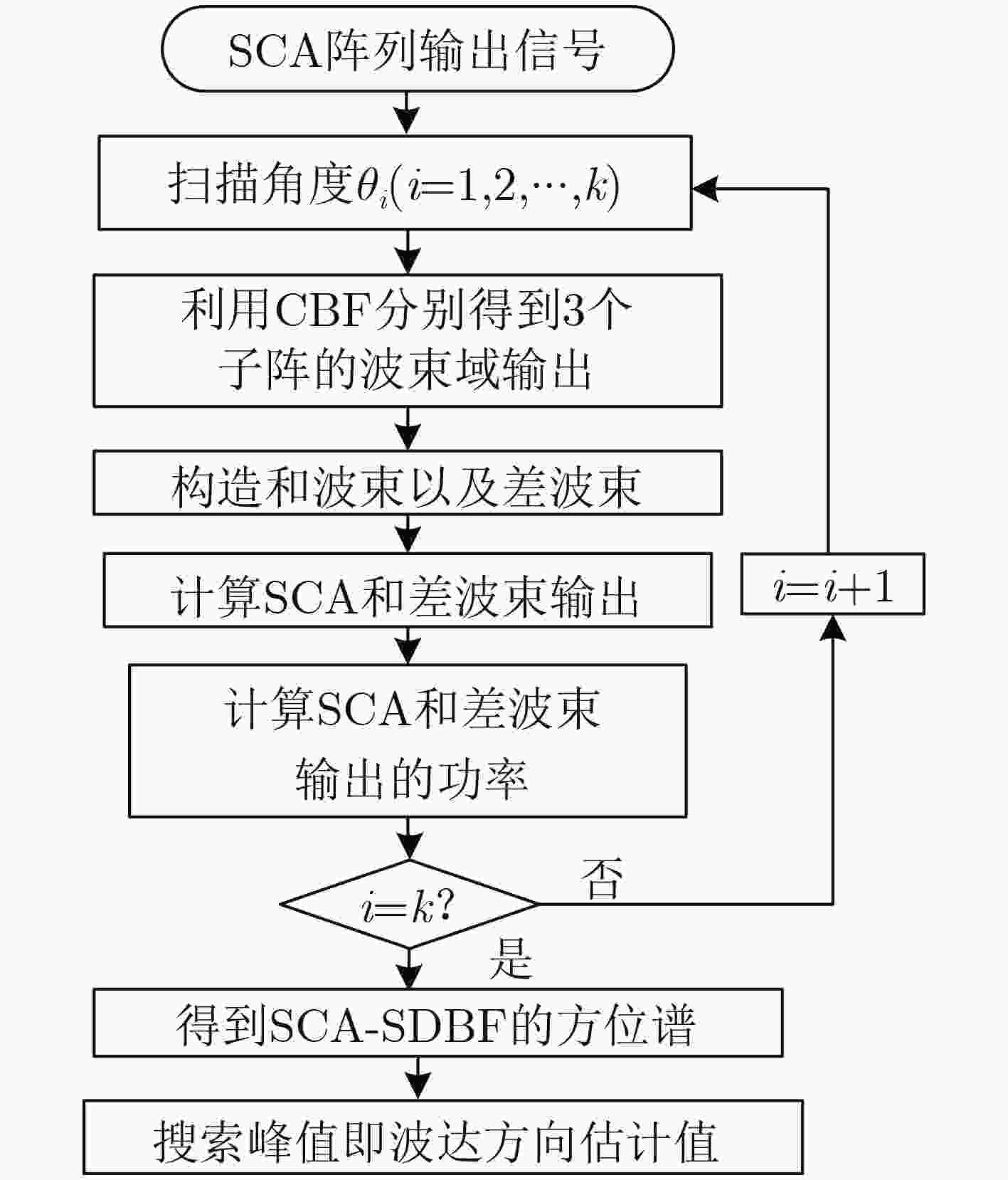
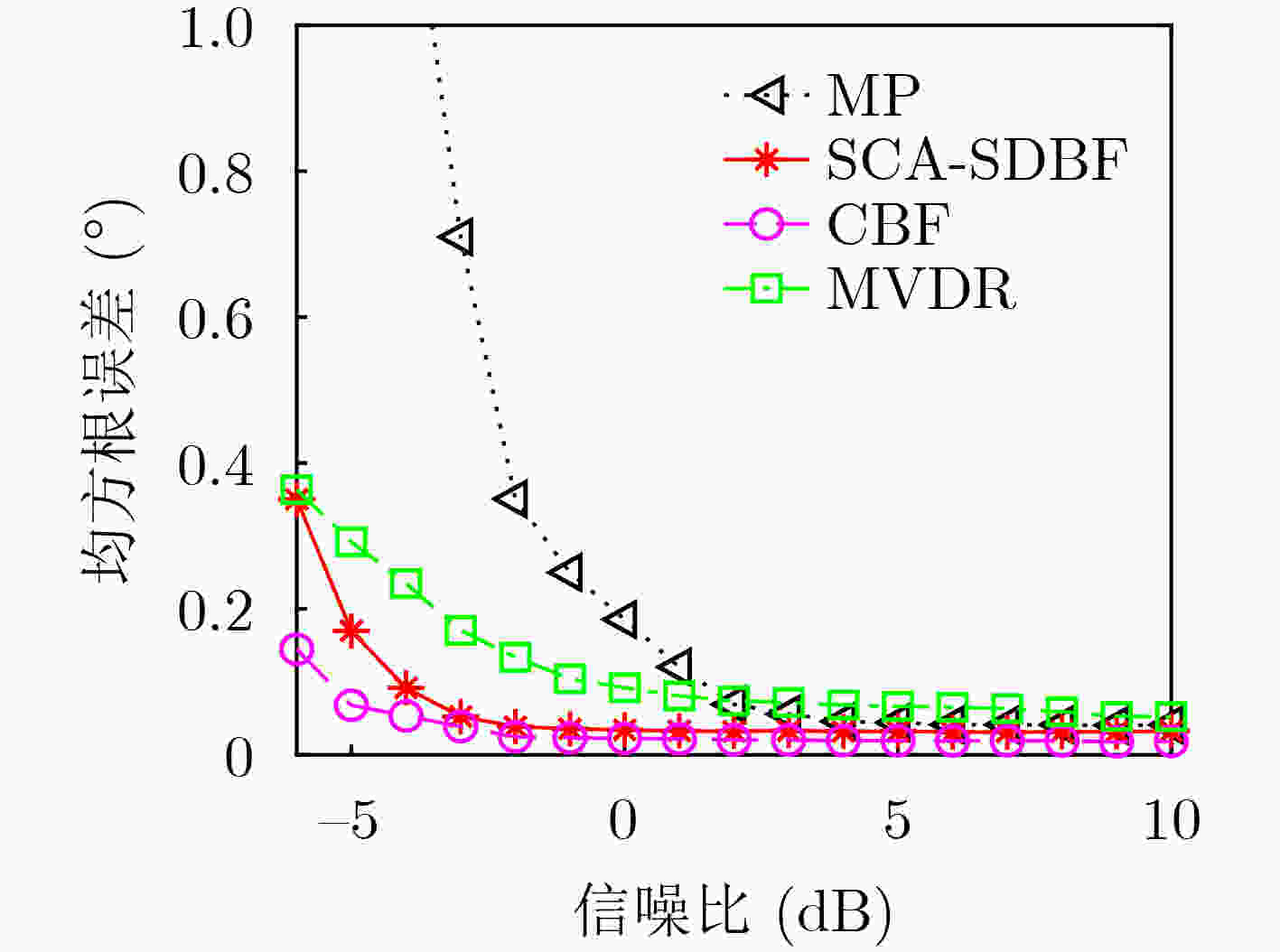
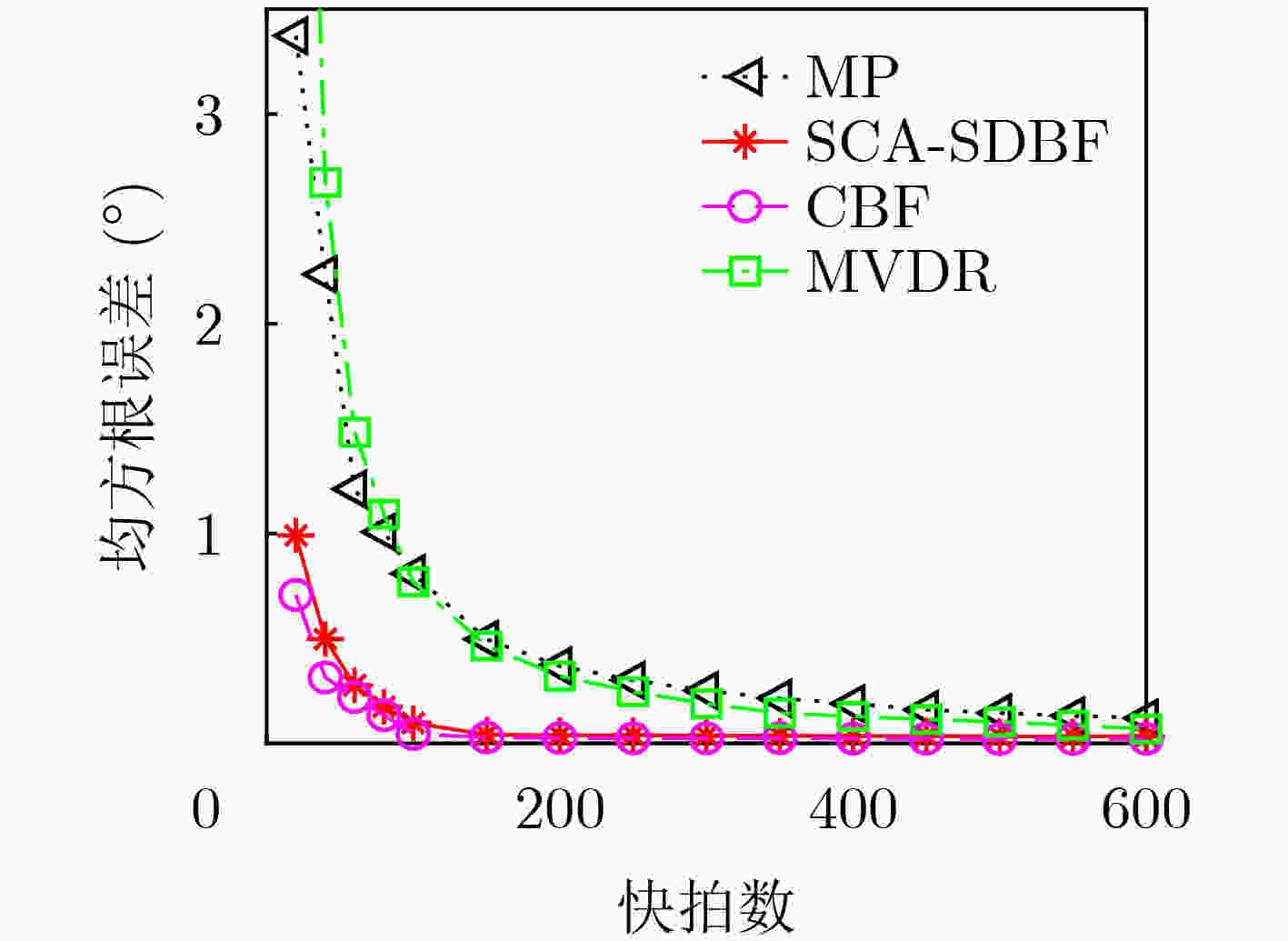
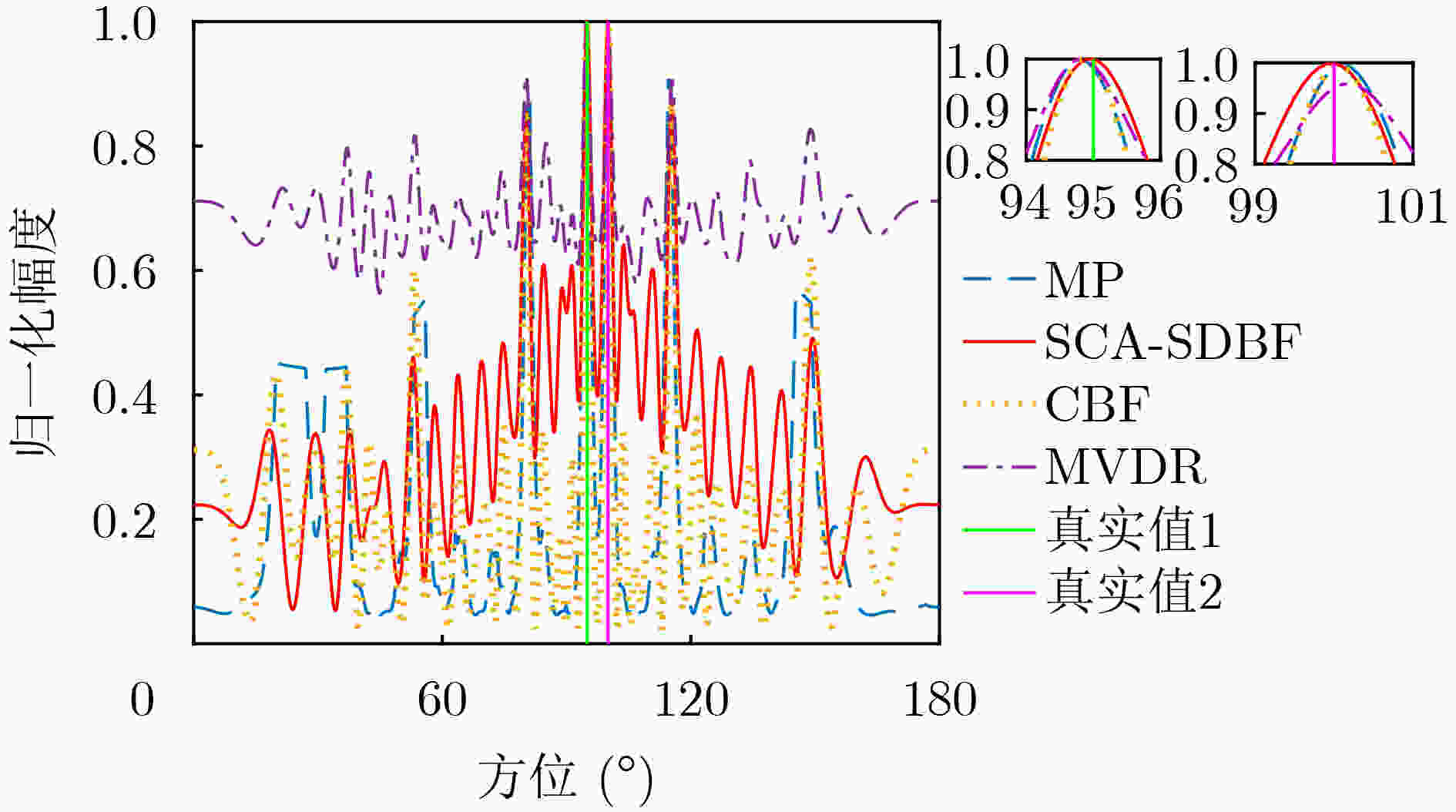
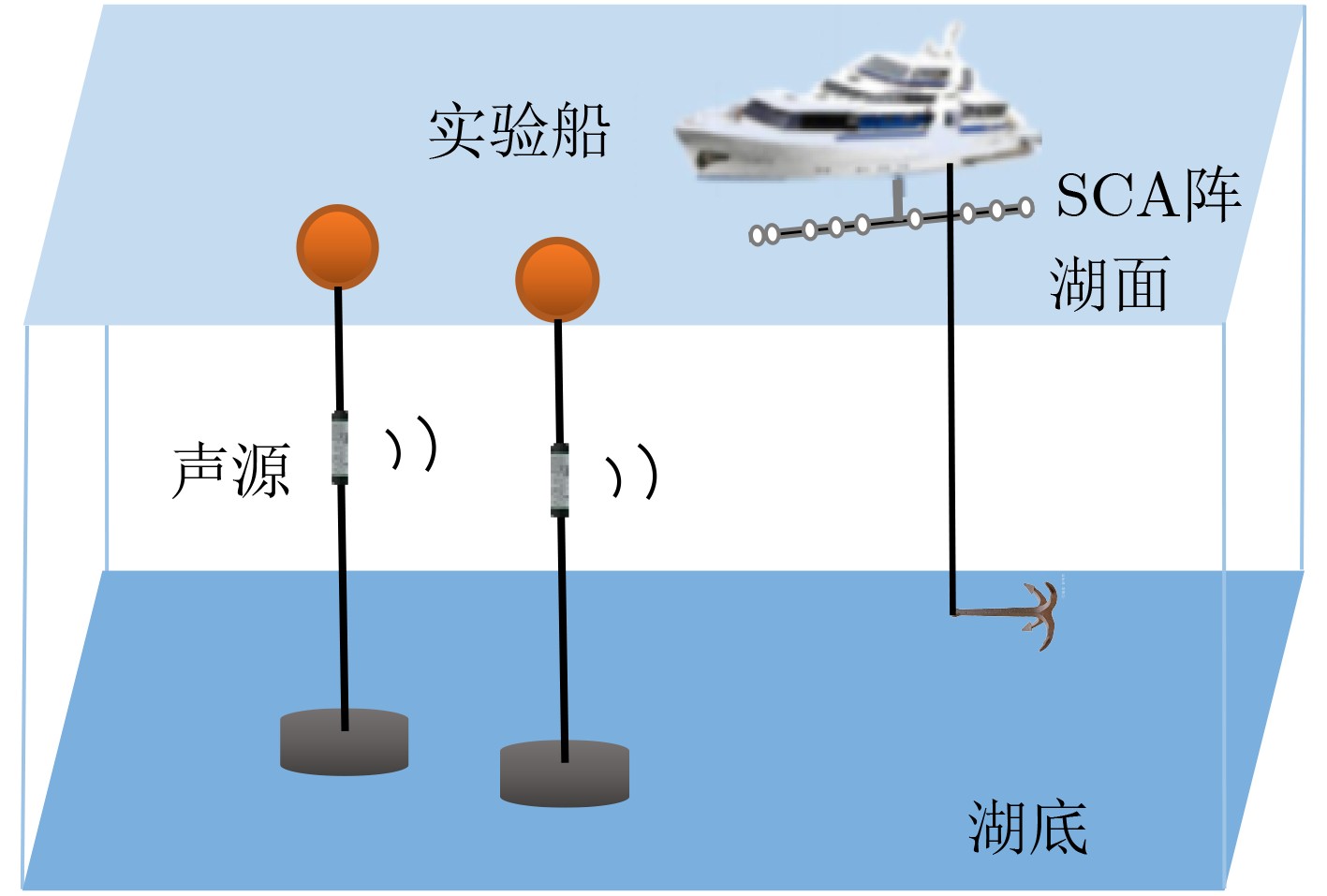
摘要: 在半互质阵列(SCA)下,经典波达方向估计(DoA)算法在面对邻近相干信源时估计性能退化。为了解决该问题,该文提出一种适用于半互质阵列的高精度波达方向估计方法。首先,将半互质阵划分为3个均匀线阵并利用常规波束形成算法对子阵1、子阵2和子阵3的阵列输出信号进行处理;然后,对子阵3的输出信号进行加权后与子阵1,2的输出信号加和构建和波束,利用子阵1与子阵2的输出信号做差构建差波束;最后,将上述和差波束做差得到最终输出信号,计算最终信号的功率得到方位谱。该方法基于半互质阵列特点构建和差波束,充分利用了3个子阵的重叠阵元实现估计精度的提高。通过仿真和湖上实测数据验证表明,该方法可以适用于半互质阵列实现波达方向估计,并且在面对邻近相干信源时其波达方向估计性能优于最小方差无失真估计算法(MVDR)和最小处理算法(MP)。Abstract: For Semi-Coprime Arrays (SCA), the performance of classical Direction of Arrival (DoA) estimation algorithm degrades under the presence of coherent adjacent sources. To address this problem, a high-precison DoA estimation method for SCA is proposed. Firstly, the array is divided into three subarrays (Subarray 1 to 3 respectively). And conventional beamforming algorithm is applied to obtain the signals of the three subarrays, respectively. Then, the output signal of subarray 3 is weighted and added to the output signals of subarray 1 and 2 to construct one sum beam. Meanwhile, the difference between output signals of subarray 1 and subarray 2 is used to construct one difference beam. Finally, the final output signal is obtained by the sum beam signal and the difference beam signal. The azimuth spectrum is the power of the final output signal. This method is based on the characteristic of SCA arrays to construct sum beam and difference beam, fully utilizing the overlapping sensors of the three subarrays to improve estimation accuracy. Simulations and lake experiments are implemented to validate the effectiveness for the proposed method used for DoA estimation in SCA. The proposed method performs better than the existing approaches, such as Minimum Variance Distortionless Response (MVDR) and Min Processing (MP) when facing adjacent coherent sources.
-
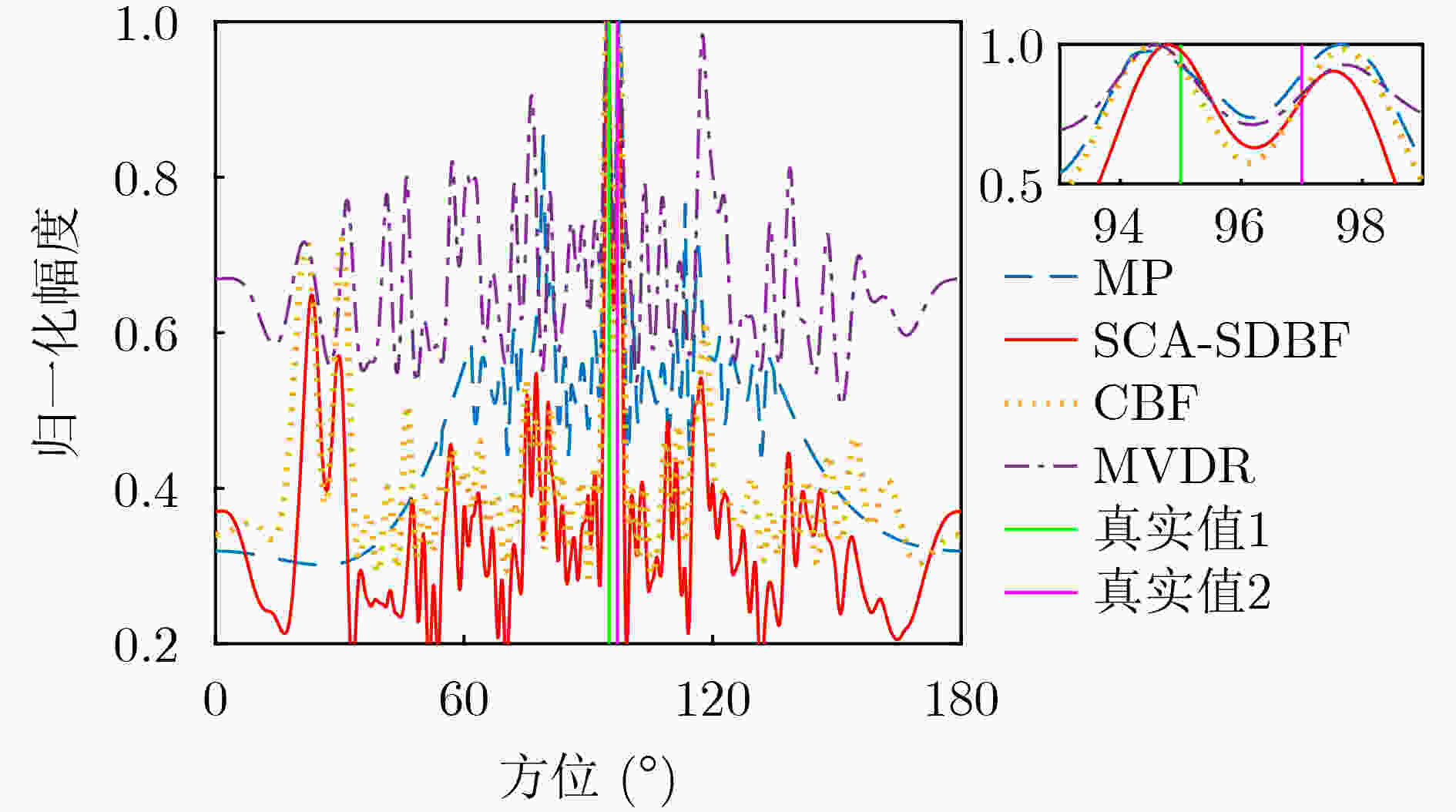
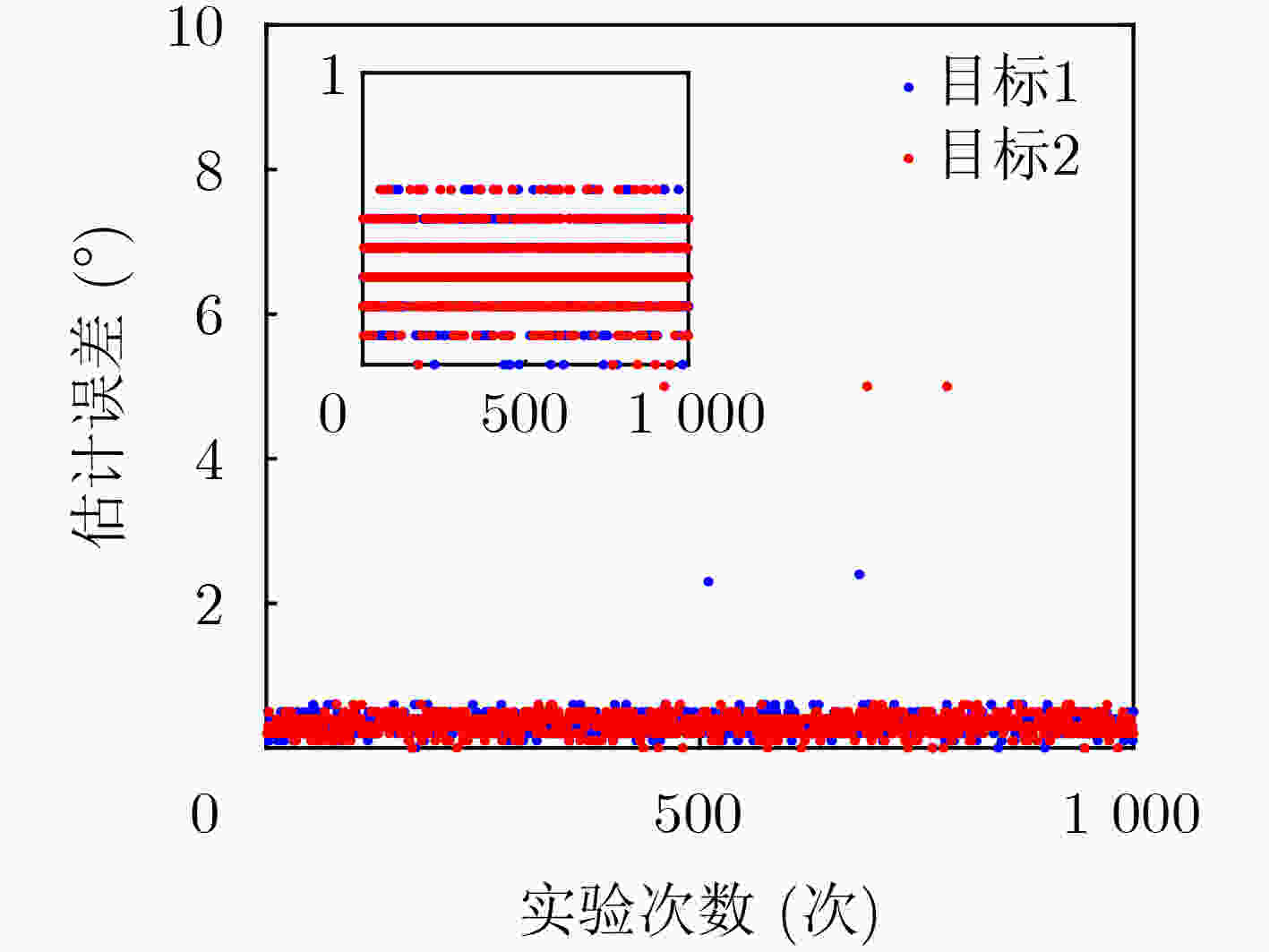
表 1 4种算法正确估计概率及正确估计时的均方根误差
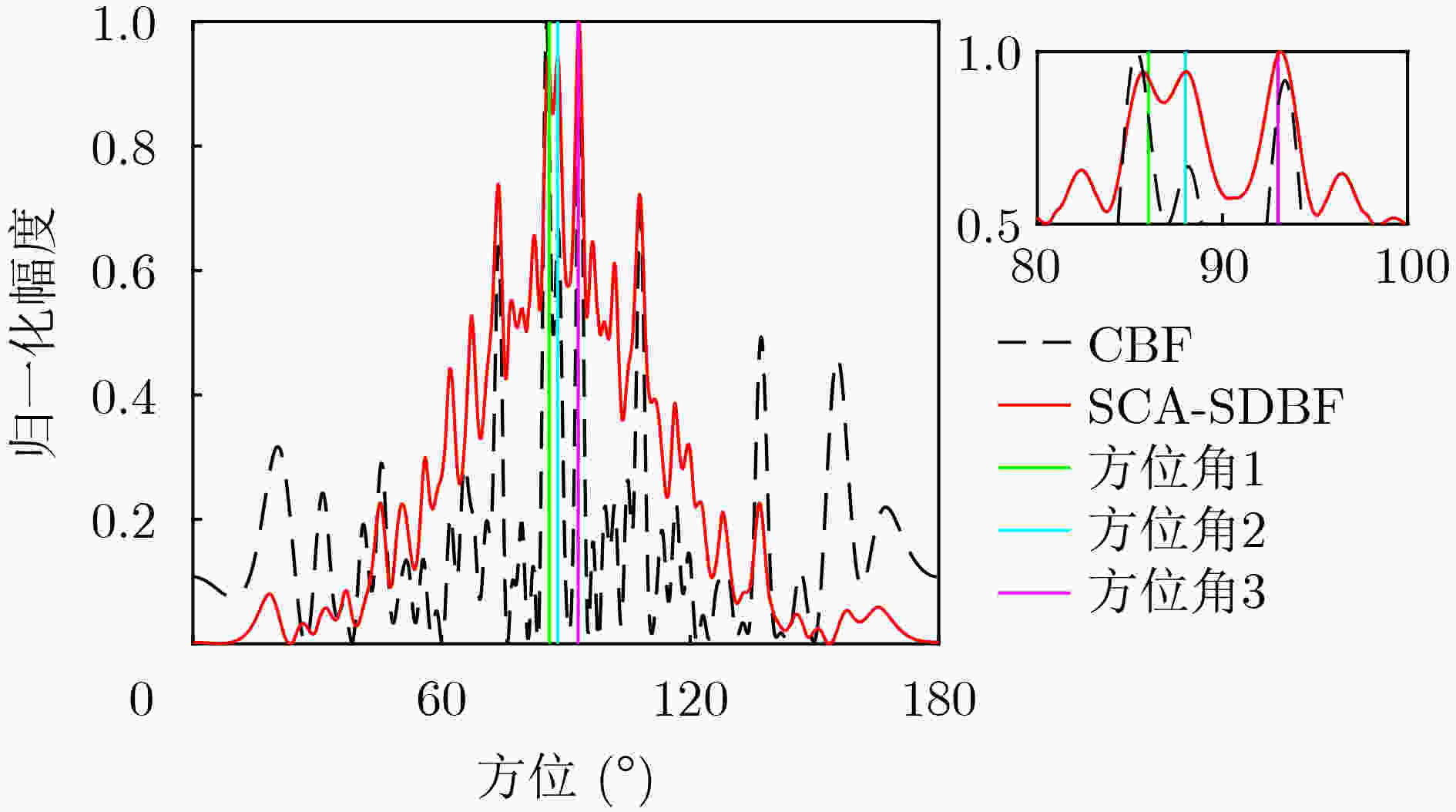
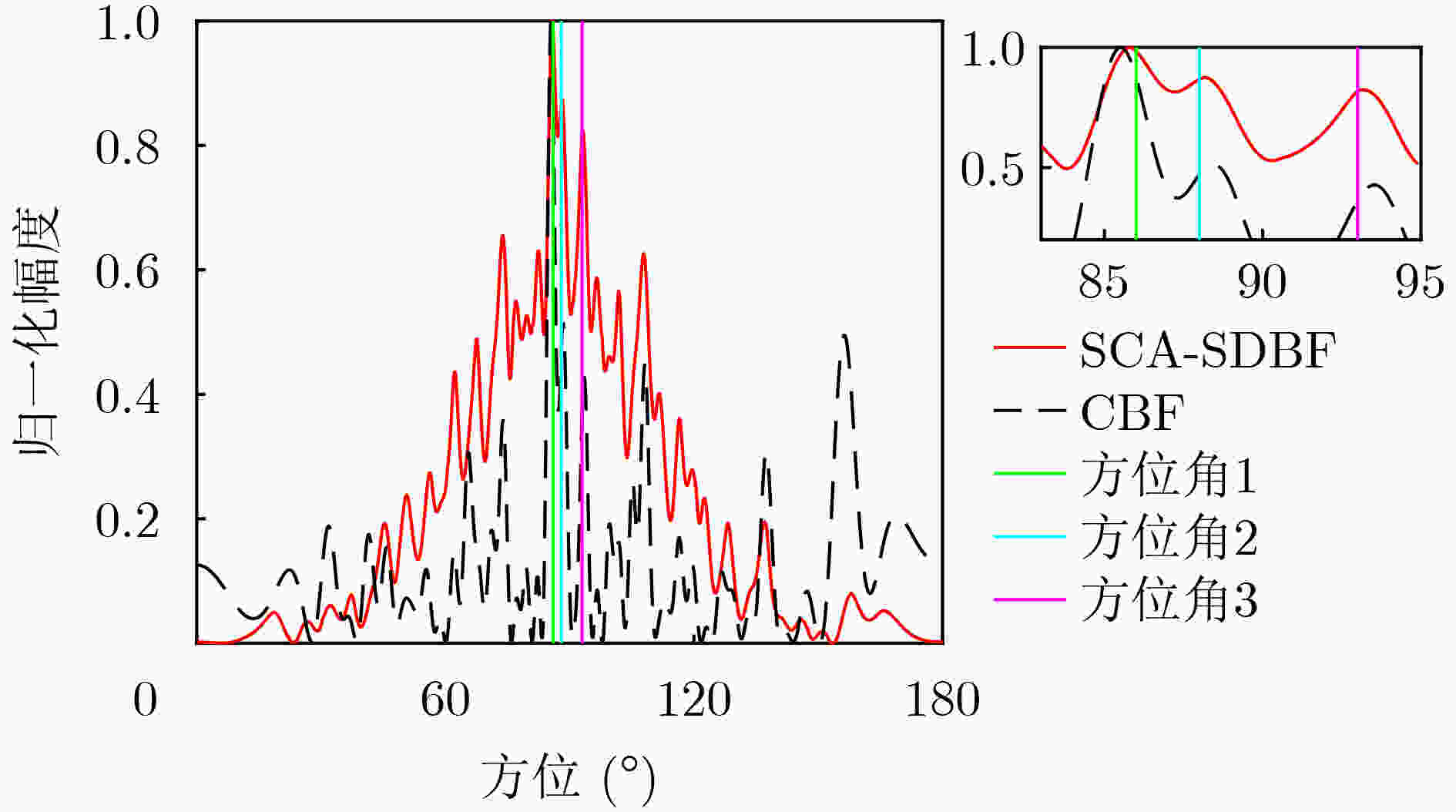
估计算法 正确估计概率(%) 估计误差(°) MP 88.9 0.508 5 MVDR 81.6 0.568 3 CBF 99.6 0.527 8 SCA-SDBF 99.1 0.352 4 -
[1] FUCHS J, KASPER A, LÜBKE M, et al. High-resolution direction-of-arrival estimation using distributed radar sensors[C]. 2022 IEEE Radio and Wireless Symposium (RWS), Las Vegas, USA, 2022: 53–56. doi: 10.1109/RWS53089.2022.9719971. [2] 谭鹏, 胡博, 张友文, 等. 交叉验证多路径匹配追踪水声矢量阵稀疏方位估计[J]. 声学学报, 2022, 47(5): 557–567. doi: 10.15949/j.cnki.0371-0025.2022.05.014.TAN Peng, HU Bo, ZHANG Youwen, et al. Multipath matching pursuit using a cross-validation technique for sparse direction-of-arrival estimation with an acoustic vector array[J]. Acta Acustica, 2022, 47(5): 557–567. doi: 10.15949/j.cnki.0371-0025.2022.05.014. [3] 张豪, 甄冬, 刘英辉, 等. 采用四阶累积量多重矩阵重构的低信噪比相干声源波达方向估计[J]. 声学学报, 2023, 48(2): 337–346. doi: 10.15949/j.cnki.0371-0025.2023.02.004.ZHANG Hao, ZHEN Dong, LIU Yinghui, et al. Fourth-order cumulant multiple matrix reconstruction to estimate direction of arrival for coherent sound source under low signal-to-noise ratio[J]. Acta Acustica, 2023, 48(2): 337–346. doi: 10.15949/j.cnki.0371-0025.2023.02.004. [4] SHAFIN R, LIU Lingjia, ZHANG Jianzhong, et al. DoA estimation and capacity analysis for 3-D Millimeter wave massive-MIMO/FD-MIMO OFDM systems[J]. IEEE Transactions on Wireless Communications, 2016, 15(10): 6963–6978. doi: 10.1109/TWC.2016.2594173. [5] WANG Lei, REN Chunhui, LIU Renting, et al. Direction-of-arrival estimation for nested array using mixed-resolution ADCs[J]. IEEE Communications Letters, 2022, 26(8): 1868–1872. doi: 10.1109/LCOMM.2022.3178617. [6] MOFFET A. Minimum-redundancy linear arrays[J]. IEEE Transactions on Antennas and Propagation, 1968, 16(2): 172–175. doi: 10.1109/TAP.1968.1139138. [7] PAL P and VAIDYANATHAN P P. Nested arrays: A novel approach to array processing with enhanced degrees of freedom[J]. IEEE Transactions on Signal Processing, 2010, 58(8): 4167–4181. doi: 10.1109/TSP.2010.2049264. [8] VAIDYANATHAN P P and PAL P. Sparse sensing with co-prime samplers and arrays[J]. IEEE Transactions on Signal Processing, 2011, 59(2): 573–586. doi: 10.1109/TSP.2010.2089682. [9] ADHIKARI K. Beamforming with semi-coprime arrays[J]. The Journal of the Acoustical Society of America, 2019, 145(5): 2841–2850. doi: 10.1121/1.5100281. [10] SCHENCK D, MESTRE X, and PESAVENTO M. Probability of resolution of MUSIC and g-MUSIC: An asymptotic approach[J]. IEEE Transactions on Signal Processing, 2022, 70: 3566–3581. doi: 10.1109/TSP.2022.3178820. [11] YANG Zai. Nonasymptotic performance analysis of ESPRIT and spatial-smoothing ESPRIT[J]. IEEE Transactions on Information Theory, 2023, 69(1): 666–681. doi: 10.1109/TIT.2022.3199405. [12] KRIM H and VIBERG M. Two decades of array signal processing research: The parametric approach[J]. IEEE Signal Processing Magazine, 1996, 13(4): 67–94. doi: 10.1109/ 79.526899. [13] CAPON J. High-resolution frequency-wavenumber spectrum analysis[J]. Proceedings of the IEEE, 1969, 57(8): 1408–1418. doi: 10.1109/PROC.1969.7278. [14] SCHMIDT R. Multiple emitter location and signal parameter estimation[J]. IEEE Transactions on Antennas and Propagation, 1986, 34(3): 276–280. doi: 10.1109/TAP.1986.1143830. [15] ROY R and KAILATH T. ESPRIT-estimation of signal parameters via rotational invariance techniques[J]. IEEE Transactions on Acoustics, Speech, and Signal Processing, 1989, 37(7): 984–995. doi: 10.1109/29.32276. [16] 聂良春. 超波束(HBF)用于波束锐化[J]. 声学技术, 2008, 27(6): 892–895.NIE Liangchun. Hyper beamforming (HBF) technique for beam narrowing[J]. Technical Acoustics, 2008, 27(6): 892–895. [17] FRIEDLANDER B and WEISS A J. Direction finding in the presence of mutual coupling[J]. IEEE Transactions on Antennas and Propagation, 1991, 39(3): 273–284. doi: 10.1109/8.76322. -






 下载:
下载:
















 下载:
下载:
