6G New Time-delay Doppler Communication Paradigm: Technical Advantages, Design Challenges, Applications and Prospects of OTFS
-
摘要: 在未来的通信网络中,被广泛期待的第6代移动通信系统(The Sixth Generation of Mobile Communications System, 6G)技术将面临诸多挑战,其中包括在高速移动场景下的超高可靠通信问题。正交时频空间(Orthogonal Time Frequency Space, OTFS)调制技术克服了传统通信系统在高速移动环境下多径和多普勒效应的影响,为实现 6G 超高可靠通信提供了新的可能性。该文首先介绍了OTFS的基本原理、数学模型、干扰与优势分析。然后,归纳分析了OTFS技术在同步、信道估计、信号检测技术上的研究现状。接着,从车联网、无人机、卫星通信、海洋通信4个典型应用场景分析了OTFS的应用趋势。最后,从降低多维匹配滤波器、相位解调和信道估计、硬件实现的复杂度和提高对时频资源的高度利用4个角度探讨了未来研究OTFS需要克服的困难和挑战。Abstract: In the future communication network, the sixth generation mobile communication system technology(6G), which is widely expected, will face many challenges, including the issue of ultra-reliable communication in high-speed mobile scenarios. Orthogonal Time Frequency Space (OTFS) modulation technology overcomes the multi-path and Doppler effects of traditional communication systems in high-speed mobile environments, and provides a new possibility for realizing 6G ultra-reliable communication. This paper first introduces the basic principle, mathematical model, interference and advantage analysis of OTFS. Then, the research status of OTFS technology in synchronization, channel estimation and signal detection is summarized and analyzed. Subsequently, the application trend of OTFS is analyzed from four typical application scenarios of vehicle networking, unmanned aerial vehicle, satellite communication and marine communication. Finally, the difficulties and challenges to be overcome in future OTFS research are discussed from four aspects: reducing multi-dimensional matching filter, phase demodulation and channel estimation, hardware implementation complexity and improving the high utilization of time-frequency resources.
-
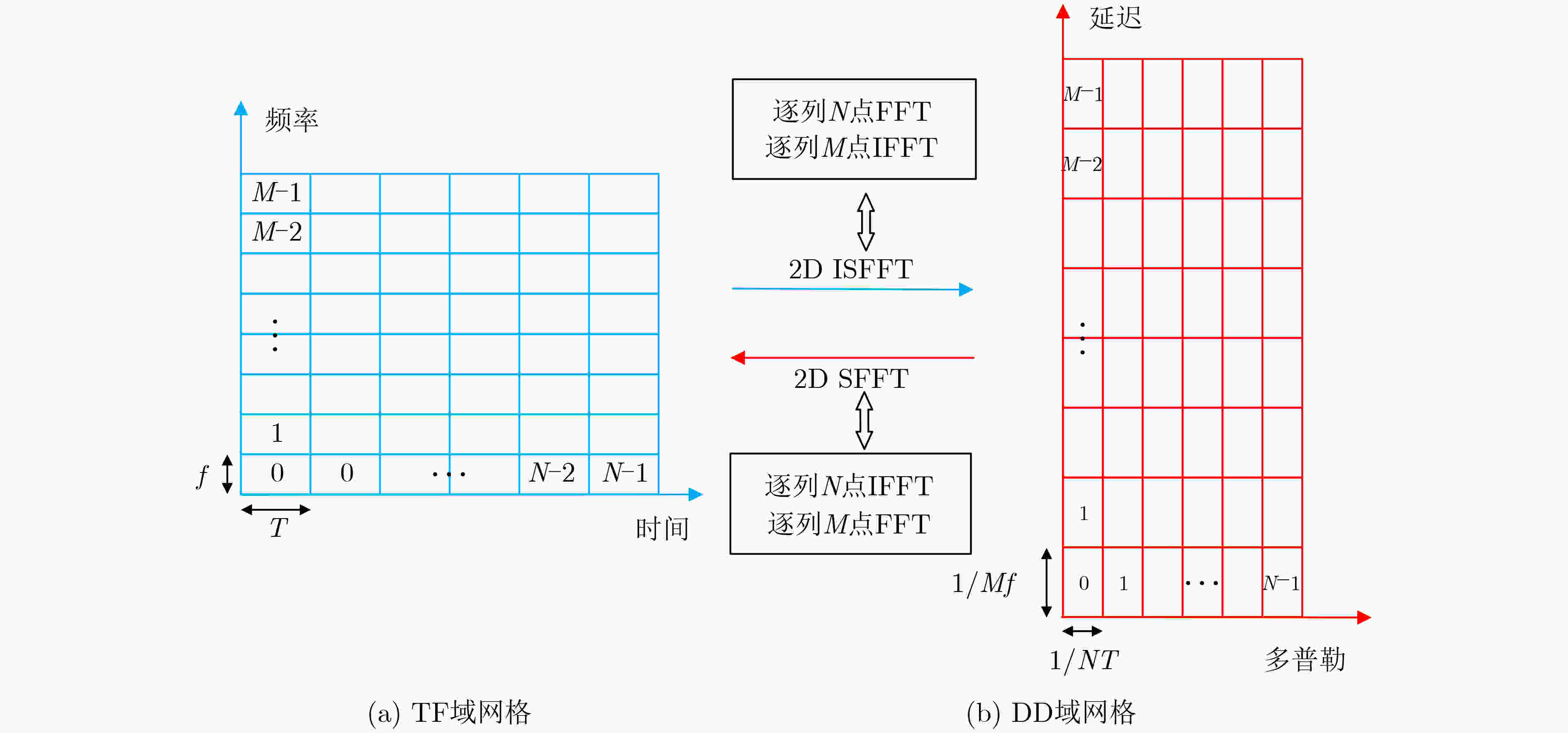
图 1 TF域和DD域平面网格的描述[15]
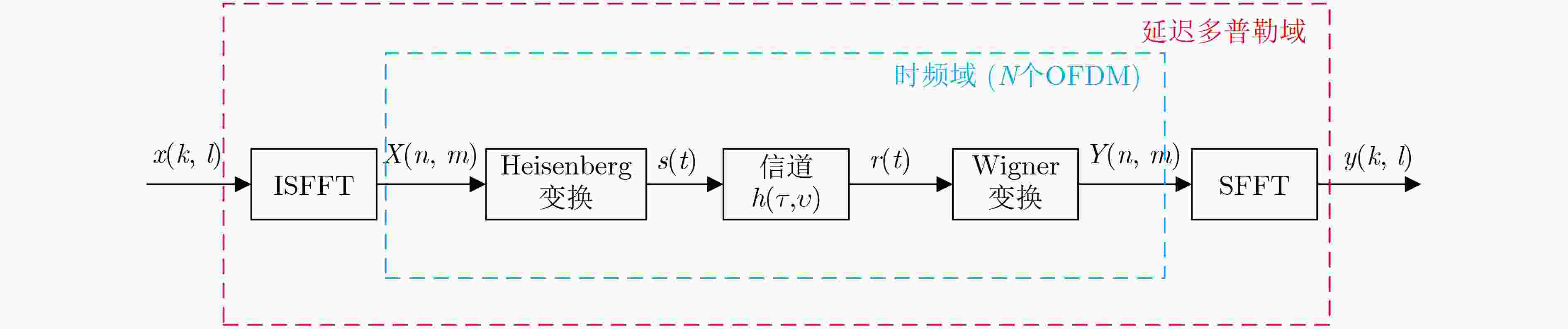
图 2 OTFS系统框图[14]
图 3 用于同步的OTFS框架结构[16]
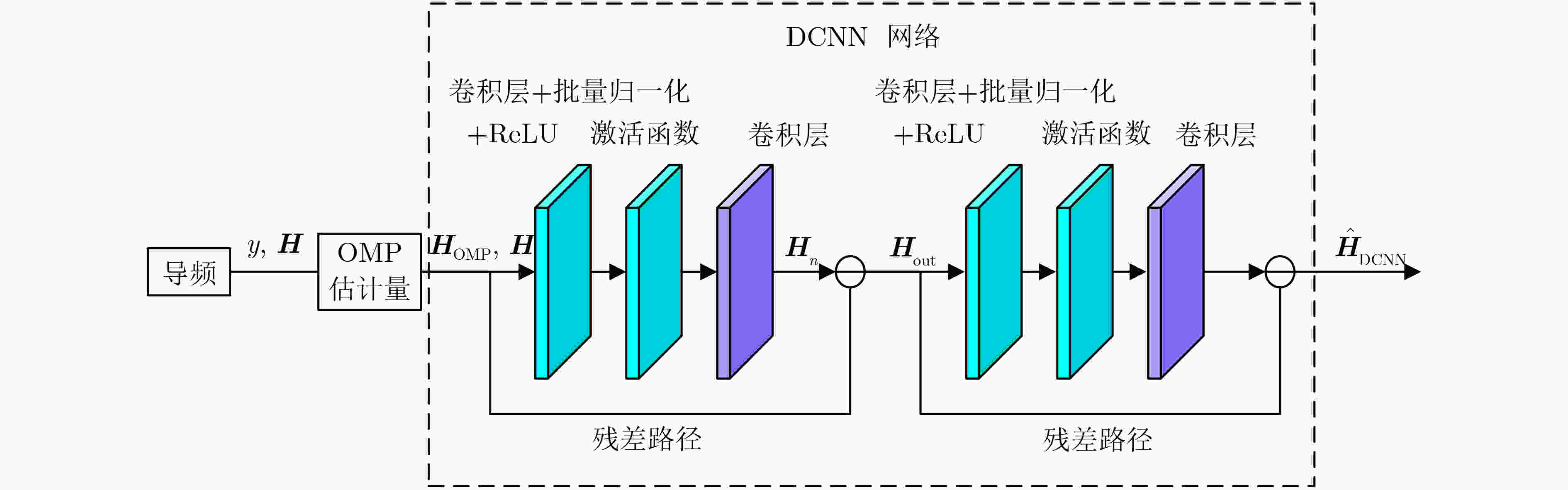
图 4 基于CNN的OTFS信道估计方法结构图[37]
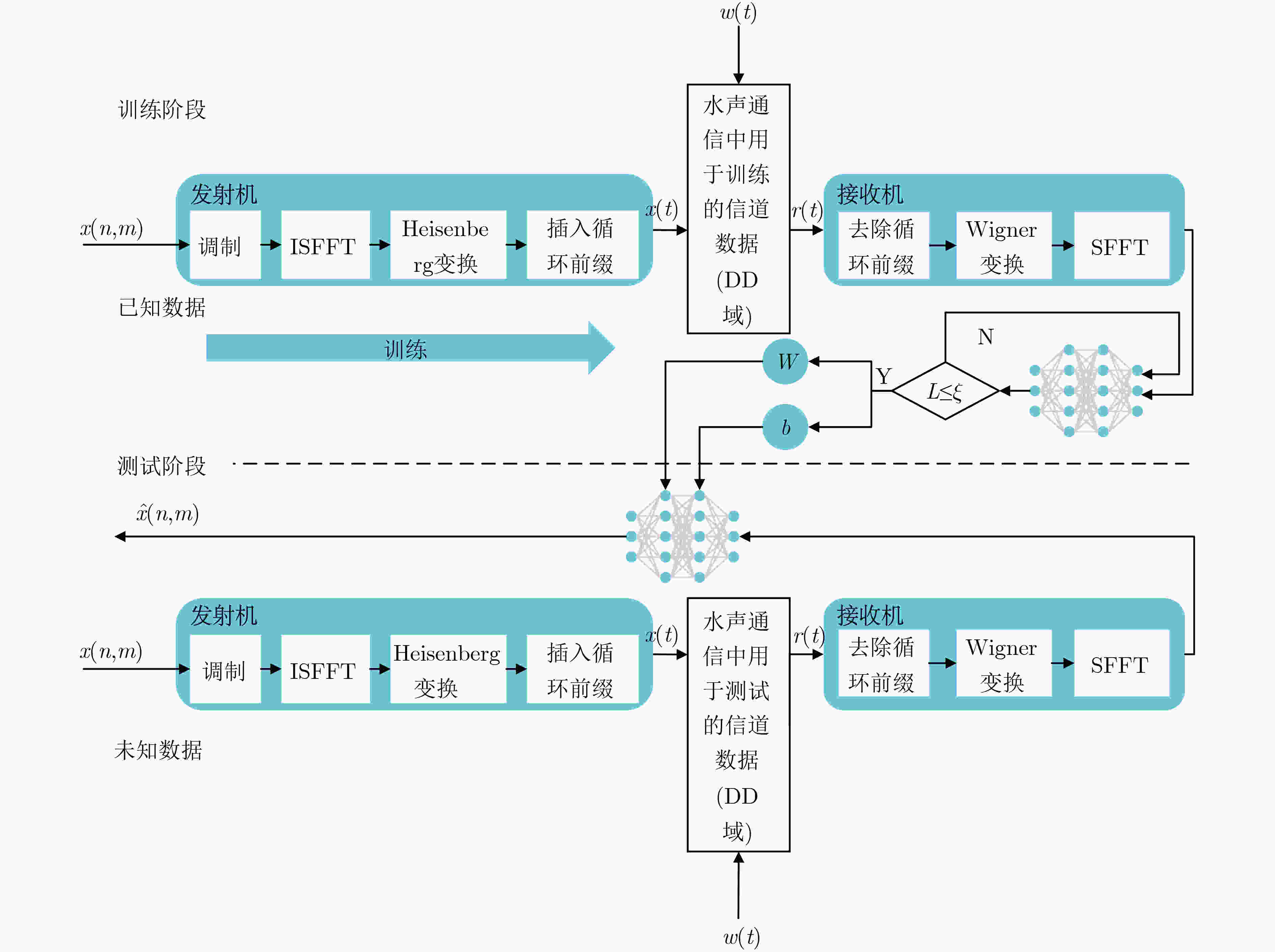
图 5 基于DNN的OTFS信号检测方法结构图[15]
表 1 面向OTFS调制系统的同步方法
表 2 基于AI的OTFS信道估计算法
文献 网络结构 算法名称 基准算法 算法效果 [31] SBL 基于SBL的BCE算法 EP辅助信道估计算法[41]、基于最小二乘的BCE 在信道路径未知情况下,所提算法仍然可以对路径的数量和位置进行准确估计,有效提高了接收机性能。对算法进行复杂度分析和仿真分析,所提算法在复杂度、误码率和NMSE性能方面比基准算法更具优越性。 [32] SBL SBL-EM OMP-CE, GP-CE[41] 通过详尽的模拟分析,验证了所提出的信道估计方案在信道恢复误差、导频成本和导频功率等方面的优越性。 [33] SBL 基于SBL的1维、2维离网信道估计算法 并网OMP[42]、离网NOMP[43]、传统脉冲[44]、传统脉冲+ DC窗[44] 所提出的离网信道CS方案相对于并网方法,在虚拟采样分辨率较低的情况下,也能显著提高OTFS系统的CE精度。基于1维离网SBL的CE方案通过解耦时延和多普勒估计,实现了优异的性能,而所提出的2维离网方案计算复杂度更低。进一步采用数据辅助CE可以提升对未知数据符号干扰的鲁棒性,从而在无保护空间的情况下进一步提升CE性能。 [34] SBL 基于2维离网分解和SBL组合的信道估计 传统OTFS信道估计算法[45]、基于SBL的1维、2维离网信道估计算
法[33]、基于双分数模型的算法[33]仿真结果表明,所提方案比现有的基于双分数模型的方法具有更高的精度和更低的计算成本。 [35] SBL BSBL-BR PP-GP[43], SBL-EM[32], BSBL w/o BR[46], BOMP[47] 不同于传统的BSBL方法,BSBL-BR采用迭代更新非稀疏块的大小来提高信道估计精度。仿真结果表明,所提方法比基准算法具有更加优异的估计误差和噪声鲁棒性。 [36] ResNet 基于修正ResNet的联合信道估计和信号检测方案 嵌入式导频信道估计[41]+MMSE信号检测算法[48]、嵌入式导频信道估计[41]+MP信号检测算法[21] 与基准算法相比,所提方法具有更强的鲁棒性和良好的泛化能力,其算法复杂度得到降低,误码率性能也增加了约2dB。 [37] CNN 基于DCNN 的信道估计 OMP、基于导频的信道估计算法 与基准算法比较,此方法复杂度更低,对不同的车速具有较好的鲁棒性,满足了高精度信道估计。 [38] DRDN 一种数据驱动的DRDN信道估计方法 最小二乘估计器、线性最小均方
误差估计器、OMP、
基于阈值的算法在复杂噪声环境下,与基准算法相比,此算法在OTFS系统信道估计中具有更强的盲去噪能力。 [39] DRSN 基于DRSN的信道估计 最小二乘估计器、线性最小均方
误差估计器、OMP、
基于阈值的算法仿真结果表明,即使在没有先验知识的情况下,所提的算法性能依然可以接近于经典算法。相比基准算法,该算法在复杂的噪声场景下性能显著更优。 [40] RNN 基于RNN的信道估计 独有导频架构的信道估计算法[49]、嵌入式导频架构的信道估计算法[41] 与基准算法相比,所提出的方法有着更好的最小均方误差性能和误码率性能。 表 3 基于DL的OTFS信号检测算法
文献 算法类型 算法名称 基准算法 数据驱动/
模型驱动算法效果 [15] DNN 基于DNN的UWA OTFS通信信号检测算法 线性最小均方误差、迫零算法、匹配滤波器 数据驱动 仿真表明所提算法比基准算法的误码率更低且具有非线性映射的优势有利于对DD域中的数据进行拟合。除此外,所提方法对多径和多普勒效应具有很好的鲁棒性。 [52] DNN 用于OTFS信号检测的低复杂度延迟多普勒符号DNN算法 全DNN、最大似然 数据驱动 在误码率、复杂度方面,所提算法均优于基准算法。 [53] DNN 基于DNN的RIS辅助OTFS系统信号检测算法 最小均方误差、迫零算法、MP 数据驱动 仿真表明,此算法能够比基准算法以更低的信噪比提供无限低的误码率。 [54] MatNet OTFS-MatNet 最小均方误差、DR-DNN[60]、符号DNN[52] 数据驱动 所提算法在误码率性能改进和减少训练样本方面与基准算法相比具有显著的优势。 [55] CNN 基于2D CNN的OTFS系统信号检测算法 最优最大后验、线性最小均方误差、MP 数据驱动 所提算法的性能优于MP检测器,与最优最大后验检测器的性能近乎相同,但所提算法的时间复杂度很低。 [56] CNN 存在HI时的基于 DL 的 OTFS 信号检测 最小均方误差[61]、MP[21] 数据驱动 仿真表明所提算法比带有和不带有HI的传统MP、最小均方误差检测器都有更好的误码率性能。 [57] NN ViterbiNet 最小均方误差、MRC[62]、MP[21]、
FC-DNN[60]模型驱动 仿真验证了所提算法的鲁棒性。因为ViterbiNet是模型驱动的网络,因此仅仅要求小尺寸的神经网络和少量的训练数据也能够达到不错的性能。 [58] GNN 一种高效的GNN辅助检测算法 最小均方误差[63]、
MP[21]、GAMP[64]、GAMP-NET[65]模型驱动 仿真表明所提算法比基准算法的误码率性能更优。 [59] EP-Net 用于OTFS信号检测的EP辅助模型驱动深度学习算法 最小均方误差[49]、MP[67]、JMPA[64]、GAMP[64]、OAMP[66]、OAMP-Net[66]、EP[67] 模型驱动 仿真表明所提算法比传统的EP算法
具有更加显著的性能。 -
[1] GUO Fengxian, YU F R, ZHANG Heli, et al. Enabling massive IoT toward 6G: A comprehensive survey[J]. IEEE Internet of Things Journal, 2021, 8(15): 11891–11915. doi: 10.1109/JIOT.2021.3063686. [2] SALH A, AUDAH L, SHAH N S M, et al. A survey on deep learning for ultra-reliable and low-latency communications challenges on 6G wireless systems[J]. IEEE Access, 2021, 9: 55098–55131. doi: 10.1109/ACCESS.2021.3069707. [3] LV Zhihan, LOU Ranran, LI Jinhua, et al. Big data analytics for 6G-enabled massive internet of things[J]. IEEE Internet of Things Journal, 2021, 8(7): 5350–5359. doi: 10.1109/JIOT.2021.3056128. [4] ALSAEDI W K, AHMADI H, KHAN Z, et al. Spectrum options and allocations for 6G: A regulatory and standardization review[J]. IEEE Open Journal of the Communications Society, 2023, 4: 1787–1812. doi: 10.1109/OJCOMS.2023.3301630. [5] BANAFAA M, SHAYEA I, DIN J, et al. 6G mobile communication technology: Requirements, targets, applications, challenges, advantages, and opportunities[J]. Alexandria Engineering Journal, 2023, 64: 245–274. doi: 10.1016/j.aej.2022.08.017. [6] ABASI A K, ALOQAILY M, OUNI B, et al. A survey on securing 6G wireless communications based optimization techniques[C]. Proceedings of 2023 International Wireless Communications and Mobile Computing, Marrakesh, Morocco, 2023: 216–223. doi: 10.1109/IWCMC58020.2023.10183210. [7] CUI Huanxi, ZHANG Jun, GENG Yuhui, et al. Space-air-ground integrated network (SAGIN) for 6G: Requirements, architecture and challenges[J]. China Communications, 2022, 19(2): 90–108. doi: 10.23919/JCC.2022.02.008. [8] CHANG Luyi, ZHANG Zhe, LI Pei, et al. 6G-enabled edge AI for metaverse: Challenges, methods, and future research directions[J]. Journal of Communications and Information Networks, 2022, 7(2): 107–121. doi: 10.23919/JCIN.2022.9815195. [9] 程翔, 张浩天, 杨宗辉, 等. 车联网通信感知一体化研究: 现状与发展趋势[J]. 通信学报, 2022, 43(8): 188–202. doi: 10.11959/j.issn.1000-436x.2022137.CHENG Xiang, ZHANG Haotian, YANG Zonghui, et al. Integrated sensing and communications for Internet of vehicles: Current status and development trend[J]. Journal on Communications, 2022, 43(8): 188–202. doi: 10.11959/j.issn.1000-436x.2022137. [10] LI Qingyu, GONG Yi, WANG Jianyu, et al. Exploring the performance of receiver algorithm in OTFS based on CNN[C]. Proceedings of 2022 IEEE International Conference on Communications Workshops, Seoul, Republic of Korea, 2022: 957–962. doi: 10.1109/ICCWorkshops53468.2022.9814529. [11] REDDY C S, PRIYA P, SEN D, et al. Spectral efficient modem design with OTFS modulation for vehicular-IoT system[J]. IEEE Internet of Things Journal, 2023, 10(3): 2444–2458. doi: 10.1109/JIOT.2022.3211531. [12] WEI Zhiqiang, YUAN Weijie, LI Shuangyang, et al. Orthogonal time-frequency space modulation: A promising next-generation waveform[J]. IEEE Wireless Communications, 2021, 28(4): 136–144. doi: 10.1109/MWC.001.2000408. [13] XIAO Lixia, LI Shuo, QIAN Ying, et al. An overview of OTFS for internet of things: Concepts, benefits, and challenges[J]. IEEE Internet of Things Journal, 2022, 9(10): 7596–7618. doi: 10.1109/JIOT.2021.3132606. [14] LI Mao, LIU Wei, and LEI Jing. A review on orthogonal time–frequency space modulation: State-of-art, hotspots and challenges[J]. Computer Networks, 2023, 224: 109597. doi: 10.1016/j.comnet.2023.109597. [15] ZHANG Shumin, ZHANG Yuzhi, CHANG Jiazheng, et al. DNN-based signal detection for underwater OTFS systems[C]. Proceedings of 2022 IEEE/CIC International Conference on Communications in China, Sanshui, Foshan, China, 2022: 348–352. doi: 10.1109/ICCCWorkshops55477.2022.9896695. [16] KHAN M S, KIM Y J, SULTAN Q, et al. Downlink synchronization for OTFS-based cellular systems in high doppler environments[J]. IEEE Access, 2021, 9: 73575–73589. doi: 10.1109/ACCESS.2021.3079429. [17] GAO Ziqiang, DENG Xiong, ZOU Xihua, et al. Orthogonal time frequency space modulation in wideband Doppler channel[C]. Proceedings of the 48th Annual Conference of the IEEE Industrial Electronics Society, Brussels, Belgium, 2022: 1–6. doi: 10.1109/IECON49645.2022.9968556. [18] TUSHA A and ARSLAN H. Low complex inter-doppler interference mitigation for OTFS systems via global receiver windowing[J]. IEEE Transactions on Vehicular Technology, 2023, 72(6): 7685–7698. doi: 10.1109/TVT.2023.3243577. [19] CHENNIAPPAN P, PRASANA S, DEEPA D, et al. Performance analysis of Orthogonal Time Frequency Space (OTFS) modulation technique in massive MIMO system for high-speed communication[J]. AIP Conference Proceedings, 2023, 2725(1): 060003. doi: 10.1063/5.0125238. [20] CAUS M, SHAAT M, PÉREZ-NEIRA A I, et al. Reliability oriented OTFS-based LEO satellites joint transmission scheme[C]. Proceedings of 2022 IEEE Globecom Workshops, Rio de Janeiro, Brazil, 2022: 1406–1412. doi: 10.1109/GCWkshps56602.2022.10008593. [21] RAVITEJA P, PHAN K T, HONG Yi, et al. Interference cancellation and iterative detection for orthogonal time frequency space modulation[J]. IEEE Transactions on Wireless Communications, 2018, 17(10): 6501–6515. doi: 10.1109/TWC.2018.2860011. [22] JIN Chenxi, BIE Zhisong, LIN Xuehong, et al. A simple two-stage equalizer for OTFS with rectangular windows[J]. IEEE Communications Letters, 2021, 25(4): 1158–1162. doi: 10.1109/LCOMM.2020.3043841. [23] 尉志青, 冯志勇, 李怡恒, 等. 太赫兹通信感知一体化波形: 现状与展望[J]. 通信学报, 2022, 43(1): 3–10. doi: 10.11959/j.issn.1000-436x.2022007.WEI Zhiqing, FENG Zhiyong, LI Yiheng, et al. Terahertz joint communication and sensing waveform: Status and prospect[J]. Journal on Communications, 2022, 43(1): 3–10. doi: 10.11959/j.issn.1000-436x.2022007. [24] THAJ T and VITERBO E. OTFS modem SDR implementation and experimental study of receiver impairment effects[C]. Proceedings of 2019 IEEE International Conference on Communications Workshops, Shanghai, China, 2019: 1–6. doi: 10.1109/ICCW.2019.8757167. [25] MOZAFFARI TAZEHKAND B, AGHDAM M R G, VAKILIAN V, et al. Novel successive interference cancellation (SIC) with low-complexity for GFDM systems[J]. IEEE Access, 2022, 10: 40063–40072. doi: 10.1109/ACCESS.2022.3167051. [26] BEMANI A, KSAIRI N, and KOUNTOURIS M. Affine frequency division multiplexing for next generation wireless communications[J]. IEEE Transactions on Wireless Communications, 2023, 22(11): 8214–8229. doi: 10.1109/TWC.2023.3260906. [27] SINHA A K, MOHAMMED S K, RAVITEJA P, et al. OTFS based random access preamble transmission for high mobility scenarios[J]. IEEE Transactions on Vehicular Technology, 2020, 69(12): 15078–15094. doi: 10.1109/TVT.2020.3034130. [28] BAYAT M and FARHANG A. Time and frequency synchronization for OTFS[J]. IEEE Wireless Communications Letters, 2022, 11(12): 2670–2674. doi: 10.1109/LWC.2022.3214002. [29] 肖之长, 彭丽, 张沉思, 等. 基于导频辅助的OTFS载波同步技术[J]. 无线电通信技术, 2021, 47(3): 315–318. doi: 10.3969/j.issn.1003-3114.2021.03.010.XIAO Zhichang, PENG Li, ZHANG Chensi, et al. Pilot-aided OTFS carrier synchronization technology[J]. Radio Communications Technology, 2021, 47(3): 315–318. doi: 10.3969/j.issn.1003-3114.2021.03.010. [30] 邢旺, 唐晓刚, 周一青, 等. 面向OTFS的时延-多普勒域信道估计方法综述[J]. 通信学报, 2022, 43(12): 188–201. doi: 10.11959/j.issn.1000-436x.2022224.XING Wang, TANG Xiaogang, ZHOU Yiqing, et al. Survey of channel estimation method in delay-Doppler domain for OTFS[J]. Journal on Communications, 2022, 43(12): 188–201. doi: 10.11959/j.issn.1000-436x.2022224. [31] LIAO Yong and LI Xue. Joint multi-domain channel estimation based on sparse Bayesian learning for OTFS system[J]. China Communications, 2023, 20(1): 14–23. doi: 10.23919/JCC.2023.01.002. [32] ZHAO Lei, GAO Wenjing, and GUO Wenbin. Sparse Bayesian learning of delay-Doppler channel for OTFS system[J]. IEEE Communications Letters, 2020, 24(12): 2766–2769. doi: 10.1109/LCOMM.2020.3021120. [33] WEI Zhiqiang, YUAN Weijie, LI Shuangyang, et al. Off-grid channel estimation with sparse Bayesian learning for OTFS systems[J]. IEEE Transactions on Wireless Communications, 2022, 21(9): 7407–7426. doi: 10.1109/TWC.2022.3158616. [34] WANG Qianli, LIANG Yu, ZHANG Zhengquan, et al. 2D off-grid decomposition and SBL combination for OTFS channel estimation[J]. IEEE Transactions on Wireless Communications, 2023, 22(5): 3084–3098. doi: 10.1109/TWC.2022.3215991. [35] ZHAO Lei, YANG J, LIU Yueliang, et al. Block sparse Bayesian learning-based channel estimation for MIMO-OTFS systems[J]. IEEE Communications Letters, 2022, 26(4): 892–896. doi: 10.1109/LCOMM.2022.3144674. [36] 周硕, 周一青, 张冲, 等. ResNet使能的OTFS联合信道估计和信号检测[J]. 西安电子科技大学学报, 2023, 50(3): 19–30. doi: 10.19665/j.issn1001-2400.2023.03.002.ZHOU Shuo, ZHOU Yiqing, ZHANG Chong, et al. ResNet enabled joint channel estimation and signal detection for OTFS[J]. Journal of Xidian University, 2023, 50(3): 19–30. doi: 10.19665/j.issn1001-2400.2023.03.002. [37] HE Bangwei, BAI Zhiquan, MA Yuanyuan, et al. Denoising CNN based channel estimation for vehicular OTFS communication system[C]. Proceedings of the 25th International Conference on Advanced Communication Technology, Pyeongchang, Republic of Korea, 2023: 54–58. doi: 10.23919/ICACT56868.2023.10079625. [38] ZHANG Xiaoqi, YUAN Weijie, and LIU Chang. Deep residual learning for OTFS channel estimation with arbitrary noise[C]. Proceedings of 2022 IEEE/CIC International Conference on Communications in China, Sanshui, Foshan, China, 2022: 320–324. doi: 10.1109/ICCCWorkshops55477.2022.9896721. [39] ZHANG Xiaoqi, YUAN Weijie, LIU Chang, et al. Deep learning with a self-adaptive threshold for OTFS channel estimation[C]. Proceedings of 2022 International Symposium on Wireless Communication Systems, Hangzhou, China, 2022: 1–5. doi: 10.1109/ISWCS56560.2022.9940260. [40] MATTU S R and CHOCKALINGAM A. An RNN based DD channel estimator for OTFS with embedded pilots[C]. Proceedings of 2022 IEEE 33rd Annual International Symposium on Personal, Indoor and Mobile Radio Communications, Kyoto, Japan, 2022: 457–462. doi: 10.1109/PIMRC54779.2022.9977831. [41] RAVITEJA P, PHAN K T, and HONG Yi. Embedded pilot-aided channel estimation for OTFS in delay–Doppler channels[J]. IEEE Transactions on Vehicular Technology, 2019, 68(5): 4906–4917. doi: 10.1109/TVT.2019.2906357. [42] SHEN Wenqian, DAI Linglong, AN Jianping, et al. Channel estimation for orthogonal time frequency space (OTFS) massive MIMO[J]. IEEE Transactions on Signal Processing, 2019, 67(16): 4204–4217. doi: 10.1109/TSP.2019.2919411. [43] LI Muye, ZHANG Shun, GAO Feifei, et al. A new path division multiple access for the massive MIMO-OTFS networks[J]. IEEE Journal on Selected Areas in Communications, 2021, 39(4): 903–918. doi: 10.1109/JSAC.2020.3018826. [44] WEI Zhiqiang, YUAN Weijie, LI Shuangyang, et al. Transmitter and receiver window designs for orthogonal time-frequency space modulation[J]. IEEE Transactions on Communications, 2021, 69(4): 2207–2223. doi: 10.1109/TCOMM.2021.3051386. [45] QIAN Ying, XIAO Lixia, and JIANG Tao. SM-STBC aided orthogonal time frequency space modulation[C]. Proceedings of 2022 IEEE Wireless Communications and Networking Conference, Austin, USA, 2022: 2172–2177. doi: 10.1109/WCNC51071.2022.9771767. [46] PRASAD R, MURTHY C R, and RAO B D. Joint channel estimation and data detection in MIMO-OFDM systems: A sparse Bayesian learning approach[J]. IEEE Transactions on Signal Processing, 2015, 63(20): 5369–5382. doi: 10.1109/TSP.2015.2451071. [47] LI Haifeng and WEN Jinming. A new analysis for support recovery with block orthogonal matching pursuit[J]. IEEE Signal Processing Letters, 2019, 26(2): 247–251. doi: 10.1109/LSP.2018.2885919. [48] SURABHI G D and CHOCKALINGAM A. Low-complexity linear equalization for OTFS modulation[J]. IEEE Communications Letters, 2020, 24(2): 330–334. doi: 10.1109/LCOMM.2019.2956709. [49] KOLLENGODE RAMACHANDRAN M and CHOCKALINGAM A. MIMO-OTFS in high-doppler fading channels: Signal detection and channel estimation[C]. Proceedings of 2018 IEEE Global Communications Conference, Abu Dhabi, United Arab Emirates, 2018: 206–212. doi: 10.1109/GLOCOM.2018.8647394. [50] ZHENG Jieheng, ZHANG Lin, LI Yan, et al. An orthogonal time frequency space modulation based differential chaos shift keying transceiver for reliable communications[C]. Proceedings of 2023 IEEE 97th Vehicular Technology Conference, Florence, Italy, 2023: 1–5. doi: 10.1109/VTC2023-Spring57618.2023.10201217. [51] 梁应敞, 谭俊杰, NIYATO D. 智能无线通信技术研究概况[J]. 通信学报, 2020, 41(7): 1–17. doi: 10.11959/j.issn.1000-436x.2020145.LIANG Yingchang, TAN Junjie, and NIYATO D. Overview on intelligent wireless communication technology[J]. Journal on Communications, 2020, 41(7): 1–17. doi: 10.11959/j.issn.1000-436x.2020145. [52] NAIKOTI A and CHOCKALINGAM A. Low-complexity delay-Doppler symbol DNN for OTFS signal detection[C]. Proceedings of 2021 IEEE 93rd Vehicular Technology Conference, Helsinki, Finland, 2021: 1–6. doi: 10.1109/VTC2021-Spring51267.2021.9448630. [53] ABID M H, TALIN I A, and KADIR M I. Reconfigurable intelligent surface-aided orthogonal time frequency space and its deep learning-based signal detection[J]. IEEE Access, 2023, 11: 47321–47338. doi: 10.1109/ACCESS.2023.3273297. [54] CHENG Qingqing, SHI Zhenguo, YUAN Jinhong, et al. Environment-robust signal detection for OTFS systems using deep learning[C]. Proceedings of 2022 IEEE Global Communications Conference, Rio de Janeiro, Brazil, 2022: 47321–47338. doi: 10.1109/GLOBECOM48099.2022.10000940. [55] ENKU Y K, BAI Baoming, WAN Fei, et al. Two-dimensional convolutional neural network-based signal detection for OTFS systems[J]. IEEE Wireless Communications Letters, 2021, 10(11): 2514–2518. doi: 10.1109/LWC.2021.3106039. [56] SINGH A, SHARMA S, DEKA K, et al. DL-based OTFS signal detection in presence of hardware impairments[J]. IEEE Wireless Communications Letters, 2023, 12(9): 1533–1537. doi: 10.1109/LWC.2023.3281790. [57] GONG Yi, LI Qingyu, MENG Fanke, et al. ViterbiNet-based signal detection for OTFS system[J]. IEEE Communications Letters, 2023, 27(3): 881–885. doi: 10.1109/LCOMM.2023.3237719. [58] ZHANG Xufan, ZHANG Shengyu, XIAO Lixia, et al. Graph neural network assisted efficient signal detection for OTFS systems[J]. IEEE Communications Letters, 2023, 27(8): 2058–2062. doi: 10.1109/LCOMM.2023.3286800. [59] LI Shuo, DING Chao, XIAO Lixia, et al. Expectation propagation aided model driven learning for OTFS signal detection[J]. IEEE Transactions on Vehicular Technology, 2023, 72(9): 12407–12412. doi: 10.1109/TVT.2023.3268231. [60] LI Qingyu, GONG Yi, MENG Fanke, et al. Data-driven receiver for OTFS system with deep learning[C]. Proceedings of the 7th IEEE International Conference on Network Intelligence and Digital Content, Beijing, China, 2021: 172–176. doi: 10.1109/IC-NIDC54101.2021.9660432. [61] LI Qi, YUAN Jinhong, and LIN Hai. Iterative MMSE detection for orthogonal time frequency space modulation[C]. Proceedings of 2022 IEEE International Conference on Communications Workshops, Seoul, Republic of Korea, 2022: 1–6. doi: 10.1109/ICCWorkshops53468.2022.9814638. [62] THAJ T and VITERBO E. Low complexity iterative rake decision feedback equalizer for zero-padded OTFS systems[J]. IEEE Transactions on Vehicular Technology, 2020, 69(12): 15606–15622. doi: 10.1109/TVT.2020.3044276. [63] TIWARI S, DAS S S, and RANGAMGARI V. Low complexity LMMSE Receiver for OTFS[J]. IEEE Communications Letters, 2019, 23(12): 2205–2209. doi: 10.1109/LCOMM.2019.2945564. [64] XIANG Luping, LIU Yusha, YANG Lieliang, et al. Gaussian approximate message passing detection of orthogonal time frequency space modulation[J]. IEEE Transactions on Vehicular Technology, 2021, 70(10): 10999–11004. doi: 10.1109/TVT.2021.3102673. [65] ZHANG Xufan, XIAO Lixia, LI Shuo, et al. Gaussian AMP aided model-driven learning for OTFS system[J]. IEEE Communications Letters, 2022, 26(12): 2949–2953. doi: 10.1109/LCOMM.2022.3206414. [66] HE Hengtao, WEN Chaokai, JIN Shi, et al. Model-driven deep learning for MIMO detection[J]. IEEE Transactions on Signal Processing, 2020, 68: 1702–1715. doi: 10.1109/TSP.2020.2976585. [67] LI Hua, DONG Yuanyuan, GONG Caihong, et al. Low complexity receiver via expectation propagation for OTFS modulation[J]. IEEE Communications Letters, 2021, 25(10): 3180–3184. doi: 10.1109/LCOMM.2021.3101827. [68] IMT-2030 (6G)推进组. 6G网络架构愿景与关键技术展望白皮书[R]. IMT-2030 (6G), 2021.IMT-2030(6G) Promotion Group. 6G network architecture vision and key technology outlook white paper[R]. IMT-2030 (6G), 2021. [69] XU Weilin, HE Yating, ZHAI Shenghua, et al. Discussion on network communication technology of unmanned cluster[C]. Proceedings of 2022 10th International Conference on Information Systems and Computing Technology, Guilin, China, 2022: 48–52. doi: 10.1109/ISCTech58360.2022.00014. [70] CHU T M C, ZEPERNICK H J, WESTERHAGEN A, et al. Performance assessment of OTFS modulation in high Doppler airborne communication networks[J]. Mobile Networks and Applications, 2022, 27(4): 1746–1756. doi: 10.1007/s11036-022-01928-4. [71] RAVITEJA P, VITERBO E, and HONG Yi. OTFS performance on static multipath channels[J]. IEEE Wireless Communications Letters, 2019, 8(3): 745–748. doi: 10.1109/LWC.2018.2890643. [72] ALBANESE A, SCIANCALEPORE V, and COSTA-PÉREZ X. First responders got wings: UAVs to the rescue of localization operations in beyond 5G systems[J]. IEEE Communications Magazine, 2021, 59(11): 28–34. doi: 10.1109/MCOM.101.2100273. [73] VAEZI M, AZARI A, KHOSRAVIRAD S R, et al. Cellular, wide-area, and non-terrestrial IoT: A survey on 5G advances and the road toward 6G[J]. IEEE Communications Surveys & Tutorials, 2022, 24(2): 1117–1174. doi: 10.1109/COMST.2022.3151028. [74] ALSABAH M, NASER M A, MAHMMOD B M, et al. 6G wireless communications networks: A comprehensive survey[J]. IEEE Access, 2021, 9: 148191–148243. doi: 10.1109/ACCESS.2021.3124812. [75] WANG Jiawei, JIANG Chunxiao, and KUANG Linling. High-mobility satellite-UAV communications: Challenges, solutions, and future research trends[J]. IEEE Communications Magazine, 2022, 60(5): 38–43. doi: 10.1109/MCOM.001.2100850. [76] VAN WALREE P A. Propagation and scattering effects in underwater acoustic communication channels[J]. IEEE Journal of Oceanic Engineering, 2013, 38(4): 614–631. doi: 10.1109/JOE.2013.2278913. [77] JOSHI M, PUNJABI G, SAINATH B, et al. Comparative performance investigation of MIMO-OTFS and MIMO-OFDM using deep neural network modeling[C]. Proceedings of 2021 IEEE 18th India Council International Conference, Guwahati, India, 2021: 1–6. doi: 10.1109/INDICON52576.2021.9691490. [78] QU Huiyang, LIU Guanghui, ZHANG Lei, et al. Low-dimensional subspace estimation of continuous-Doppler-spread channel in OTFS systems[J]. IEEE Transactions on Communications, 2021, 69(7): 4717–4731. doi: 10.1109/TCOMM.2021.3072744. [79] XIAO Zhenyu, YANG Junyi, MAO Tianqi, et al. LEO satellite access network (LEO-SAN) towards 6G: Challenges and approaches[J]. IEEE Wireless Communications, 2024, 31(2): 89–96. doi: 10.1109/MWC.011.2200310. [80] SUN Teng, LV Jiebiao, and ZHOU Tao. A transformer-based channel estimation method for OTFS systems[J]. Entropy, 2023, 25(10): 1423. doi: 10.3390/e25101423. [81] LONG Fei, NIU Kai, and LIN Jiaru. Joint channel estimation and equalization for OTFS based on EP[C]. Proceedings of 2021 IEEE Global Communications Conference, Madrid, Spain, 2021: 1–6. doi: 10.1109/GLOBECOM46510.2021.9685527. [82] TUSHA A, ALTHUNIBAT S, HASNA M O, et al. Exploiting user diversity in OTFS transmission for beyond 5G wireless systems[J]. IEEE Wireless Communications Letters, 2022, 11(8): 1689–1693. doi: 10.1109/LWC.2022.3174455. [83] MOHAMMED S K. Time-domain to delay-Doppler domain conversion of OTFS signals in very high mobility scenarios[J]. IEEE Transactions on Vehicular Technology, 2021, 70(6): 6178–6183. doi: 10.1109/TVT.2021.3071942. [84] BALAKRISHNAN S and EDDINGTON C. Efficient DSP algorithm development for FPGA and ASIC technologies[C]. Proceedings of 2007 IFIP International Conference on Very Large Scale Integration, Atlanta, USA, 2007: 168–171. doi: 10.1109/VLSISOC.2007.4402492. -





 下载:
下载:



 下载:
下载:
