一种基于三角数分解的可配置2-D卷积器优化方法

黄继业; 肖强; 田大海; 高明裕; 王俊帆; 董哲康; 黄汐威

doi:10.11999/JEIT231123

一种基于三角数分解的可配置2-D卷积器优化方法

doi: 10.11999/JEIT231123

黄继业^{1, 2},
肖强^{1, 2},
田大海¹,
高明裕^{1, 2},
王俊帆^{1, 2, ,},
董哲康^{1, 2, 3},
黄汐威¹

1.
杭州电子科技大学电子信息学院杭州 310018
2.
浙江省装备电子研究重点实验室杭州 310018
3.
浙江大学电气工程学院杭州 310027

基金项目: 国家重点研发计划(2022YFD2000100)

详细信息

作者简介:
黄继业：男，教授，研究方向为EDA技术(FPGA算法加速)、嵌入式系统(工业控制、机器视觉)

肖强：男，硕士生，研究方向为FPGA算法加速和图像处理

田大海：男，硕士生，研究方向为FPGA算法加速和图像处理

高明裕：男，教授，研究方向为汽车电子、智慧交通、算法加速等

王俊帆：女，博士生，研究方向为智慧交通、人工神经网络等

董哲康：男，副教授，研究方向为忆阻器及忆阻系统、人工神经网络等

黄汐威：男，教授，研究方向为人工智能、EDA技术(IC)等

通讯作者:
王俊帆　wangjunfan@hdu.edu.cn

中图分类号: TN492;TP391.6
计量
- 文章访问数: 201
- HTML全文浏览量: 119
- PDF下载量: 35
- 被引次数: 0
出版历程
- 收稿日期: 2023-10-17
- 修回日期: 2024-02-03
- 网络出版日期: 2024-02-20
- 刊出日期: 2024-07-29

A Reconfigurable 2-D Convolver Based on Triangular Numbers Decomposition

HUANG Jiye^{1, 2},
XIAO Qiang^{1, 2},
TIAN Dahai¹,
GAO Mingyu^{1, 2},
WANG Junfan^{1, 2
, ,},
DONG Zhekang^{1, 2, 3},
HUANG Xiwei¹

1.
School of Electronic Information, Hangzhou Dianzi University, Hangzhou 310018, China
2.
Zhejiang Provincial Key Lab of Equipment Electronics, Hangzhou 310027, China
3.
College of Electrical Engineering, Zhejiang University, Hangzhou 310027, China

Funds: The National Key Research and Development Program (2022YFD2000100)

摘要

摘要: 多尺寸2-D卷积通过特征提取在检测、分类等计算机视觉任务中发挥着重要作用。然而，目前缺少一种高效的可配置2-D卷积器设计方法，这限制了卷积神经网络(CNN)模型在边缘端的部署和应用。该文基于乘法管理以及奇平方数的三角数分解方法，提出一种高性能、高适应性的卷积核尺寸可配置的2-D卷积器。所提2-D卷积器包含一定数量的处理单元(PE)以及相应的控制单元，前者负责运算任务，后者负责管理乘法运算的组合，二者结合以实现不同尺寸的卷积。具体地，首先根据应用场景确定一个奇数列表，列表中为2-D卷积器所支持的尺寸，并利用三角数分解得到对应的三角数列表；其次，根据三角数列表和计算需求，确定PE的总数量；最后，基于以小凑大的方法，确定PE的互连方式，完成电路设计。该可配置2-D卷积器通过Verilog硬件描述语言(HDL)设计实现，由Vivado 2022.2在XCZU7EG板卡上进行仿真和分析。实验结果表明，相比同类方法，该文所提可配置2-D卷积器，乘法资源利用率得到显著提升，由20%～50%提升至89%，并以514个逻辑单元实现1 500 MB/s的吞吐率，具有广泛的适用性。
- 2-D卷积器 /
- 可配置架构 /
- 乘法管理 /
- 三角数分解
Abstract: Two-Dimensional (2-D) convolution with different kernel sizes enriches the overall performance in computer vision tasks. Currently, there is a lack of an efficient design method of reconfigurable 2-D convolver, which limits the deployment of Convolution Neural Network (CNN) models at the edge. In this paper, a new approach based on multiplication management and triangular numbers decomposition is proposed. The proposed 2-D convolver includes a certain number of Processing Elements (PE) and corresponding control units, where the former is responsible for computing tasks and the latter manages the combination of multiplication operations to achieve different convolution sizes. Specifically, an odd number list is determined based on the application scenario, which represents the supported sizes of the 2-D convolutional kernel. The corresponding triangular number list is obtained using the triangular numbers decomposition method. Then, the total number of PEs is determined based on the triangular number list and computational requirements. Finally, the corresponding control units and the interconnection of PEs are determined by the addition combinations of triangular numbers. The proposed reconfigurable 2-D convolver is designed by Verilog Hardware Description Language (HDL) and implemented by Vivado 2022.2 software on the XCZU7EG board. Compared with similar methods, the proposed 2-D convolver significantly improves the efficiency of multiplication resources, increasing from 20%～50% to 89%, and achieves a throughput of 1 500 MB/s with 514 logic units, thereby demonstrating its wide applicability.
- 2-D convolver /
- Reconfigurable architecture /
- Multiplication management /
- Triangular numbers decomposition

HTML全文

图 1 可配置2-D卷积器技术路线图

下载: 全尺寸图片幻灯片

图 2 PE加法组合方式(含3$* $3卷积)

下载: 全尺寸图片幻灯片

图 3 PE加法组合方式(不含3$* $3卷积，取公倍数)

下载: 全尺寸图片幻灯片

图 4 可配置2-D卷积器PE电路图

下载: 全尺寸图片幻灯片

图 5 加法电路图

下载: 全尺寸图片幻灯片

图 6 寄存器阵列设计优化流程图

下载: 全尺寸图片幻灯片

图 7 寄存器阵列-PE连接关系示意图

下载: 全尺寸图片幻灯片

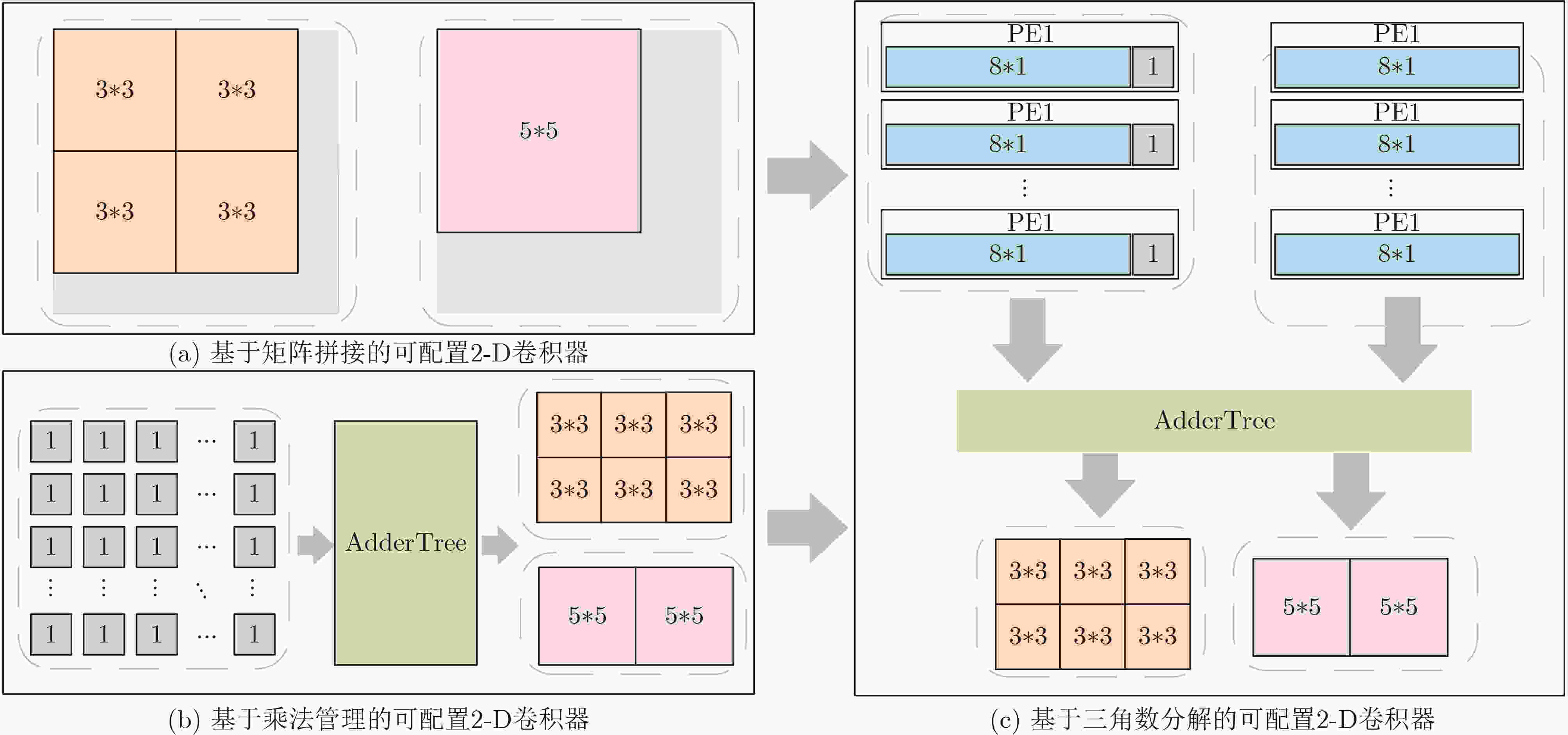
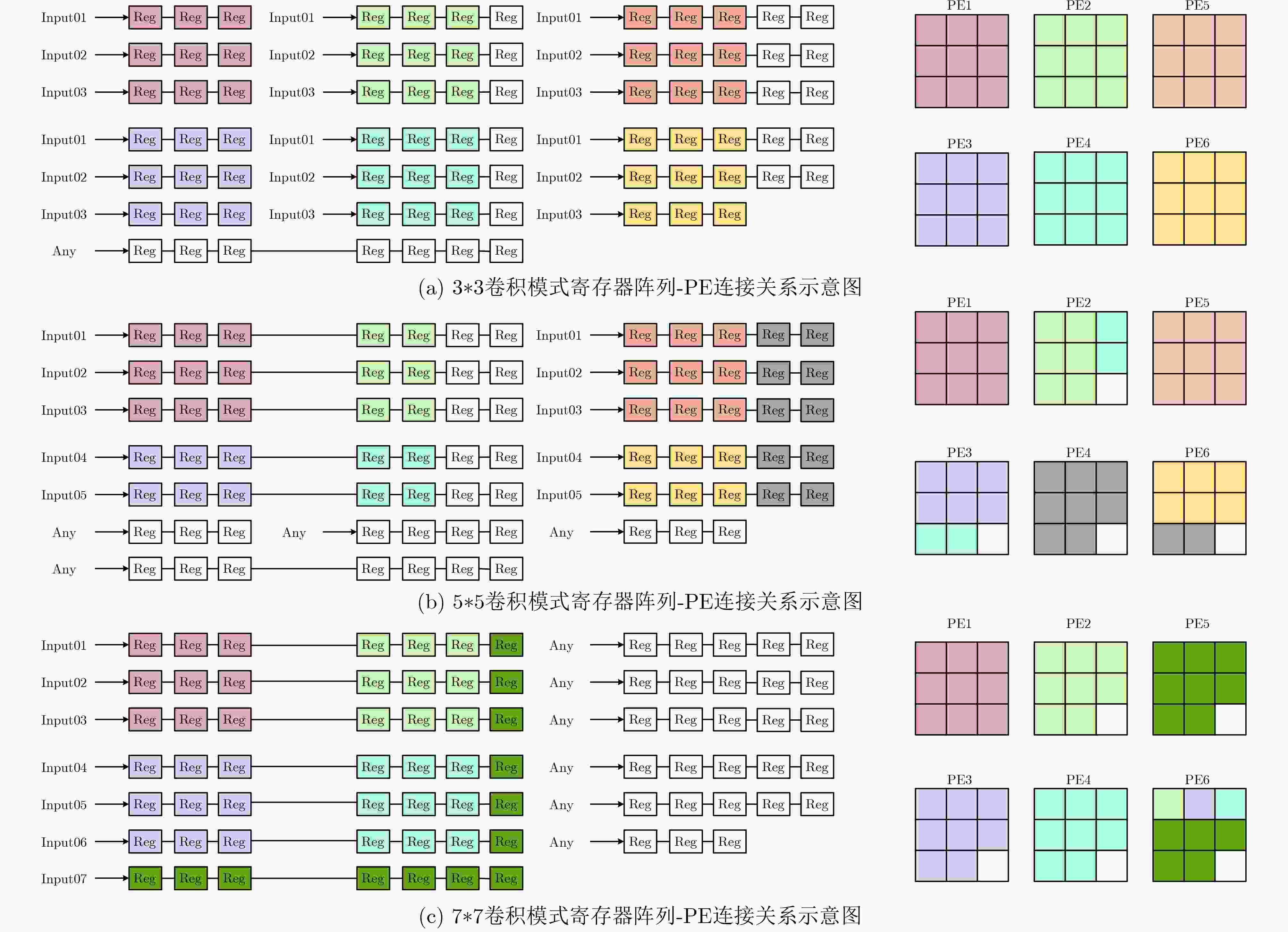
1 基于三角数分解的卷积计算方法

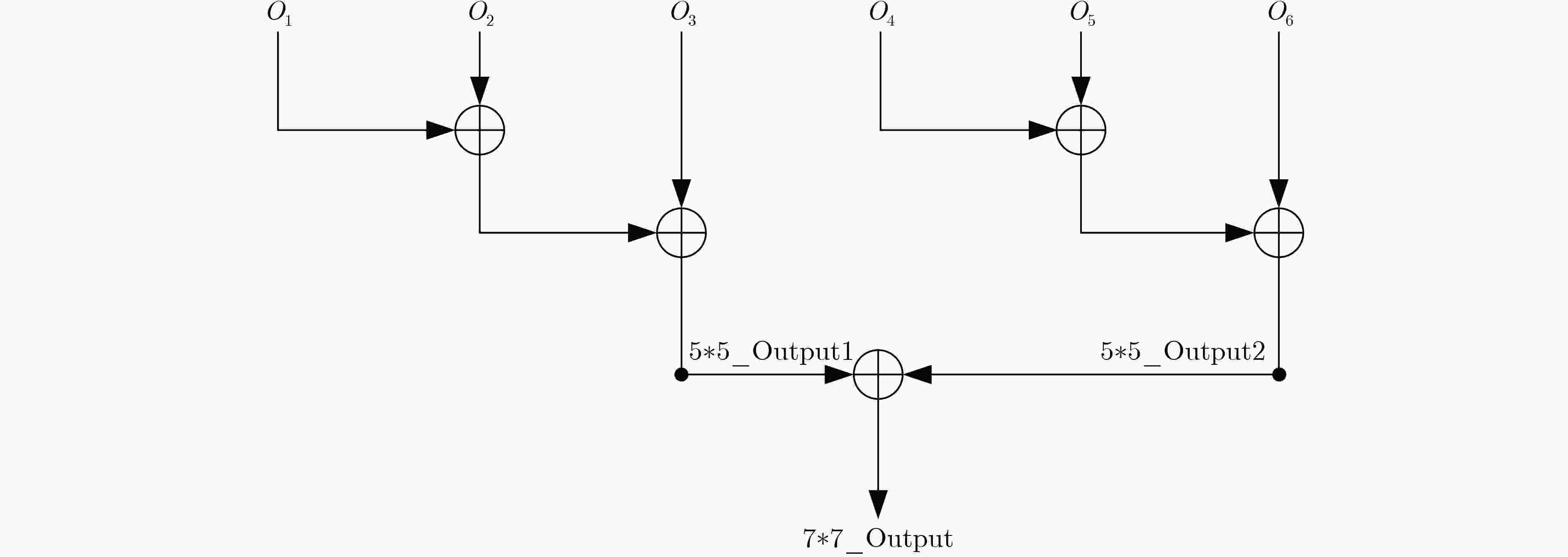
(1) 输入：input_H1[m]/ input_H2：(2k+1)$* $(2k+1)卷积的输入像素，由H1部分及H2部分组成
(2) 　　kernel_H1[m]/ kernel_H2：输入像素的对应卷积核系数
(3) 输出：num_H1：H1运算的数量，每个H1包含8个元素，即8次乘法和7次加法
(4) 　　conv_out：卷积结果，由num_H1个H1运算与一个H2运算组成，H2为单次乘法
(5) num_H1 = k$* $(k+1)/2;
(6) for m = [1:k$* $(k+1)/2]
(7) 　conv_out += kernel_H1[m] $\oplus $ input_H1[m];
(8) 　conv_out += kernel_H2 * input_H2;

下载: 导出CSV

表 1 不同实现方法的乘法资源利用率及成本对比

	矩阵填零	矩阵拼接	乘法管理	三角数分解
乘法资源利用率	$k_{\min }^2/k_{\max }^2$	$k_m^2/k_{\max }^2$	100%	$(8{T_{\max }} + 1)/({T_{\max }}/{T_{\min }} + 8{T_{\max }})$
成本	低	低	高	较高

下载: 导出CSV

表 2 乘法资源利用率对比(%)

卷积核尺寸	本文	矩阵填零	矩阵拼接^[22]	文献[29]
3$* $3	100.00	7.44	66.94	100.00
5$* $5	92.59	20.66	82.64	67.40
7$* $7	90.74	40.50	40.50	75.64
9$* $9	90.00	66.94	66.94	NR
11$* $11	89.63	100.00	100.00	83.20

下载: 导出CSV

表 3 资源使用及性能对比

参数/指标		三角数分解	三角数分解(优化)	乘法管理	矩阵拼接^[22]*1	文献[23]	文献[29]	文献[30]
参数/指标		XCZU7EG	XCZU7EG	XCZU7EG	XCZU7EG	XCV2000e	Z-7045	Z-7045
时钟(MHz)		250	250	250	250	28.6	140	125
FF		3980	3028	5618	2387	NR^*2	NR	NR
LUT		1 896	1772	3520	1316	NR	NR	NR
DSP		54	54	54	49	NR	576	855
Area		514	458	799	371	7262	NR	NR
3$* $3(PPC)		6	6	6	4	4	NR	NR
5$* $5(PPC)		2	2	2	1	1	NR	NR
7$* $7(PPC)		1	1	1	1	NS*²	NR	NR
吞吐率(GOPS)		25.50	25.50	25.50	17.00	0.23	129.73	155.81
吞吐密度(×10^–3)		1.89	1.89	1.89	1.39	NR	1.58	1.45
单位资源使用量 (3$* $3)	FF	663.33	504.67	936.33	596.75	NR	NR	NR
	LUT	316	295.33	586.67	329	NR	NR	NR
	DSP	9	9	9	12.25	NR	NR	NR
	Area	85.67	76.33	133.17	92.75	1815.5	NR	NR
单位资源使用量 (5$* $5)	FF	1 990	1514	2809	2387	NR	NR	NR
	LUT	948	886	1760	1316	NR	NR	NR
	DSP	27	27	27	49	NR	NR	NR
	Area	257	229	399.5	371	7262	NR	NR
单位资源使用量 (7$* $7)	FF	3980	3028	5618	2387	NS	NR	NR
	LUT	1 896	1772	3520	1316	NS	NR	NR
	DSP	54	54	54	49	NS	NR	NR
	Area	514	458	799	371	NS	NR	NR
1. 该数据由文献[22]的复现版本提供，由于本文对比时包含了更多电路模块，且受硬件平台和输入位宽不同的影响，与原文献中的数据存在差异。2. NR：未报告， NS：不支持。

下载: 导出CSV

表 4 可配置2-D卷积器设计复杂度对比

	本文	矩阵填零	矩阵拼接^[22]	文献[23]	文献[29]
PE种类	2种	1种	多种	1种	1种
组合方式	三角数加法	固定	嵌套的矩阵拼接	矩阵拼接	矩阵拼接

下载: 导出CSV

参考文献(30)

[1]	GUO Liang. SAR image classification based on multi-feature fusion decision convolutional neural network[J]. IET Image Processing, 2022, 16(1): 1–10. doi: 10.1049/ipr2.12323.
[2]	LI Guoqing, ZHANG Jingwei, ZHANG Meng, et al. Efficient depthwise separable convolution accelerator for classification and UAV object detection[J]. Neurocomputing, 2022, 490: 1–16. doi: 10.1016/j.neucom.2022.02.071.
[3]	ZHU Wei, ZHANG Hui, EASTWOOD J, et al. Concrete crack detection using lightweight attention feature fusion single shot multibox detector[J]. Knowledge-Based Systems, 2023, 261: 110216. doi: 10.1016/j.knosys.2022.110216.
[4]	DONG Zhekang, JI Xiaoyue, LAI C S, et al. Design and implementation of a flexible neuromorphic computing system for affective communication via memristive circuits[J]. IEEE Communications Magazine, 2023, 61(1): 74–80. doi: 10.1109/mcom.001.2200272.
[5]	GAO Mingyu, SHI Jie, DONG Zhekang, et al. A Chinese dish detector with modified YOLO v3[C]. 7th International Conference on Intelligent Equipment, Robots, and Vehicles, Hangzhou, China, 2021: 174–183. doi: 10.1007/978-981-16-7213-2_17.
[6]	GAO Mingyu, CHEN Chao, SHI Jie, et al. A multiscale recognition method for the optimization of traffic signs using GMM and category quality focal loss[J]. Sensors, 2020, 20(17): 4850. doi: 10.3390/s20174850.
[7]	GADEKALLU T R, SRIVASTAVA G, LIYANAGE M, et al. Hand gesture recognition based on a harris hawks optimized convolution neural network[J]. Computers and Electrical Engineering, 2022, 100: 107836. doi: 10.1016/j.compeleceng.2022.107836.
[8]	JI Xiaoyue, DONG Zhekang, HAN Yifeng, et al. A brain-inspired hierarchical interactive in-memory computing system and its application in video sentiment analysis[J]. IEEE Transactions on Circuits and Systems for Video Technology, 2023, 33(12): 7928–7942. doi: 10.1109/tcsvt.2023.3275708.
[9]	COPE B. Implementation of 2D Convolution on FPGA, GPU and CPU[J]. Imperial College Report, 2006.
[10]	JUNG G C, PARK S M, and KIM J H. Efficient VLSI architectures for convolution and lifting based 2-D discrete wavelet transform[C]. 10th Asia-Pacific Conference on Advances in Computer Systems Architecture, Singapore, 2005: 795–804. doi: 10.1007/11572961_65.
[11]	MOHANTY B K and MEHER P K. New scan method and pipeline architecture for VLSI implementation of separable 2-D FIR filters without transposition[C]. TENCON 2008–2008 IEEE Region 10 Conference, Hyderabad, India, 2008: 1–5. doi: 10.1109/tencon.2008.4766758.
[12]	BOSI B, BOIS G, and SAVARIA Y. Reconfigurable pipelined 2-D convolvers for fast digital signal processing[J]. IEEE Transactions on Very Large Scale Integration (VLSI) Systems, 1999, 7(3): 299–308. doi: 10.1109/92.784091.
[13]	ZHANG Hui, XIA Mingxin, and HU Guangshu. A multiwindow partial buffering scheme for FPGA-based 2-D convolvers[J]. IEEE Transactions on Circuits and Systems II:Express Briefs, 2007, 54(2): 200–204. doi: 10.1109/tcsii.2006.886898.
[14]	CARDELLS-TORMO F, MOLINET P L, SEMPERE-AGULLO J, et al. Area-efficient 2D shift-variant convolvers for FPGA-based digital image processing[C]. International Conference on Field Programmable Logic and Applications, 2005, Tampere, Finland, 2005: 578–581. doi: 10.1109/fpl.2005.1515789.
[15]	DI CARLO S, GAMBARDELLA G, INDACO M, et al. An area-efficient 2-D convolution implementation on FPGA for space applications[C]. 2011 IEEE 6th International Design and Test Workshop (IDT), Beirut, Lebanon, 2011: 88–92. doi: 10.1109/idt.2011.6123108.
[16]	KALBASI M and NIKMEHR H. A classified and comparative study of 2-D convolvers[C]. 2020 International Conference on Machine Vision and Image Processing (MVIP), Qom, Iran, 2020: 1–5. doi: 10.1109/MVIP49855.2020.9116874.
[17]	WANG Junfan, CHEN Yi, DONG Zhekang, et al. Improved YOLOv5 network for real-time multi-scale traffic sign detection[J]. Neural Computing and Applications, 2023, 35(10): 7853–7865. doi: 10.1007/s00521-022-08077-5.
[18]	MA Yuliang, ZHU Zhenbin, DONG Zhekang, et al. Multichannel retinal blood vessel segmentation based on the combination of matched filter and U-net network[J]. BioMed Research International, 2021, 2021: 5561125. doi: 10.1155/2021/5561125.
[19]	董哲康, 杜晨杰, 林辉品, 等. 基于多通道忆阻脉冲耦合神经网络的多帧图像超分辨率重建算法[J]. 电子与信息学报, 2020, 42(4): 835–843. doi: 10.11999/JEIT190868. DONG Zhekang, DU Chenjie, LIN Huipin, et al. Multi-channel memristive pulse coupled neural network based multi-frame images super-resolution reconstruction algorithm[J]. Journal of Electronics & Information Technology, 2020, 42(4): 835–843. doi: 10.11999/JEIT190868.
[20]	SZEGEDY C, LIU Wei, JIA Yangqing, et al. Going deeper with convolutions[C]. 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, USA, 2015: 1–9. doi: 10.1109/cvpr.2015.7298594.
[21]	TAN Mingxing and LE Q V. MixConv: Mixed depthwise convolutional kernels[C]. 30th British Machine Vision Conference, Cardiff, UK, 2019: 74.
[22]	DEHGHANI A, KAVARI A, KALBASI M, et al. A new approach for design of an efficient FPGA-based reconfigurable convolver for image processing[J]. The Journal of Supercomputing, 2022, 78(2): 2597–2615. doi: 10.1007/s11227-021-03963-6.
[23]	PERRI S, LANUZZA M, CORSONELLO P, et al. A high-performance fully reconfigurable FPGA-based 2D convolution processor[J]. Microprocessors and Microsystems, 2005, 29(8/9): 381–391. doi: 10.1016/j.micpro.2004.10.004.
[24]	WANG Wulun and SUN Guolin. A DSP48-based reconfigurable 2-D convolver on FPGA[C]. 2019 International Conference on Virtual Reality and Intelligent Systems (ICVRIS), Jishou, China, 2019: 342–345. doi: 10.1109/icvris.2019.00089.
[25]	FONS F, FONS M, and CANTÓ E. Run-time self-reconfigurable 2D convolver for adaptive image processing[J]. Microelectronics Journal, 2011, 42(1): 204–217. doi: 10.1016/j.mejo.2010.08.008.
[26]	MA Zhaobin, YANG Yang, LIU Yunxia, et al. Recurrently decomposable 2-D Convolvers for FPGA-based digital image processing[J]. IEEE Transactions on Circuits and Systems II:Express Briefs, 2016, 63(10): 979–983. doi: 10.1109/TCSII.2016.2536202.
[27]	CABELLO F, LEÓN J, IANO Y, et al. Implementation of a fixed-point 2D Gaussian filter for image processing based on FPGA[C]. 2015 Signal Processing: Algorithms, Architectures, Arrangements, and Applications (SPA), Poznan, Poland, 2015: 28–33. doi: 10.1109/SPA.2015.7365108.
[28]	CHEEMALAKONDA S, CHAGARLAMUDI S, DASARI B, et al. Area efficient 2D FIR filter architecture for image processing applications[C]. 2022 6th International Conference on Devices, Circuits and Systems (ICDCS), Coimbatore, India, 2022: 337–341. doi: 10.1109/ICDCS54290.2022.9780828.
[29]	JIA Han, REN Daming, and ZOU Xuecheng. An FPGA-based accelerator for deep neural network with novel reconfigurable architecture[J]. IEICE Electronics Express, 2021, 18(4): 20210012. doi: 10.1587/elex.18.20210012.
[30]	VENIERIS S I and BOUGANIS C S. fpgaConvNet: Mapping regular and irregular convolutional neural networks on FPGAs[J]. IEEE Transactions on Neural Networks and Learning Systems, 2019, 30(2): 326–342. doi: 10.1109/tnnls.2018.2844093.