多蛇形机器人编队路径跟踪控制

郝爽; 何玉鹏; 陈继尧; 王铮

doi:10.11999/JEIT231004

多蛇形机器人编队路径跟踪控制

doi: 10.11999/JEIT231004

郝爽^1, ,,
何玉鹏²,
陈继尧³,
王铮⁴

1.
上海交通大学安泰经济与管理学院上海 200030
2.
国网宁夏电力有限公司银川 750001
3.
国网宁东供电公司银川 750411
4.
国网宁夏电力有限公司经济技术研究院银川 750002

详细信息

作者简介:
郝爽：男，博士，研究方向为蛇形机器人运动规划

何玉鹏：男，硕士，研究方向为蛇形机器人运动控制

陈继尧：男，硕士，研究方向为输变电设备运检

王铮：男，硕士，研究方向为电力工程经济研究

通讯作者:
郝爽　sjtu-haos@sjtu.edu.cn

中图分类号: TN962; TP242; TH39
计量
- 文章访问数: 223
- HTML全文浏览量: 144
- PDF下载量: 35
- 被引次数: 0
出版历程
- 收稿日期: 2023-09-14
- 修回日期: 2024-01-22
- 网络出版日期: 2024-03-06
- 刊出日期: 2024-07-29

Formation Path-following Control of Multi-snake Robots

1.
Antai College of Economics & Management, Shanghai Jiao Tong University, Shanghai 200030, China
2.
State Grid Ningxia Electric Power Co., Ltd., Yinchuan 750001, China
3.
Ningdong Power Supply Company, State Grid Ningxia Electric Power Co., Ltd., Yinchuan 750411, China
4.
Eco-tech Research Institute, State Grid Ningxia Electric Power Co., Ltd., Yinchuan 750002, China

摘要

摘要: 为了实现多个蛇形机器人的编队控制，该文提出一种基于误差约束的抗干扰路径跟随方法。该方法使用高度耦合的动态频率补偿器来调整每个机器人的运动速度，以确保编队成员之间位置和速度的一致性。在动力学控制中，通过障碍函数的等效原则消除了虚拟变量的奇异现象，提高了路径跟随的稳定性。此外，该文设计了模型不确定性和外界干扰的预测值，以此来提前补偿机器人的关节偏移量和扭矩输入，从而进一步提高了跟随误差的收敛速度和稳态性能。最后，利用Lyapunov理论证明了该方法的一致最终有界性(UUB)。仿真数据表明，相对于其他经典方法，该文所提模型和控制策略具有更高的跟随精度。
- 抗干扰 /
- 障碍李雅普诺夫函数 /
- 误差约束 /
- 编队控制 /
- 多蛇形机器人
Abstract: To achieve formation control of multiple snake robots, an error-constrained anti-interference path-following method is proposed in this paper. A highly coupled dynamic frequency compensator is used to adjust the motion speed of each robot to ensure consistency in the position and velocity of the formation members. In dynamic control, the singularity phenomenon of virtual variables is eliminated by the equivalent principle of barrier functions, improving the stability of path following. In addition, predictive values for model uncertainty and external interference are designed to pre-compensate for joint offsets and torque inputs of the robots, further improving the convergence rate and steady-state performance of the following errors. Finally, the Lyapunov theory is used to prove the Uniform Ultimate Boundedness (UUB) of this system. Simulation data demonstrate that the proposed method and control strategy have higher following accuracy compared to other classic methods.
- Anti-disturbance /
- Barrier Lyapunov theory /
- Error constraint /
- Formation control /
- Multi-snake robots

HTML全文

图 1 蛇形机器人连杆实际运动模型

下载: 全尺寸图片幻灯片

图 2 编队控制流程

下载: 全尺寸图片幻灯片

图 3 蛇形机器人编队运动路径

下载: 全尺寸图片幻灯片

图 4 蛇形机器人编队的位置误差

下载: 全尺寸图片幻灯片

图 5 蛇形机器人编队的方向角误差

下载: 全尺寸图片幻灯片

图 6 第1个蛇形机器人的关节角误差

下载: 全尺寸图片幻灯片

图 7 运动速度和速度误差

下载: 全尺寸图片幻灯片

图 8 第1个蛇形机器人的关节扭矩输入

下载: 全尺寸图片幻灯片

表 1 变量的定义

参数名	符号	参数名	符号
连杆个数	$ N $	第i个连杆的扭矩输入	$ {u}_{i} $
关节个数	$ N-1 $	粘滞摩擦系数	$ {\lambda }_{1},{\lambda }_{2} $
连杆质量	$ m $	关节旋转系数	$ {c}_{t},{c}_{p} $
连杆长度	$ 2h $	切向速度	$ {v}_{t}\in \mathbb{R} $
第i个连杆在xOy中的质心位置	$ ({p}_{xi},{p}_{yi}) $	法向速度	$ {v}_{n}\in \mathbb{R} $
第i个连杆在tRn中的质心位置	$ ({p}_{ti},{p}_{ni}) $	方向角速度	$ {v}_{\theta }\in \mathbb{R} $
第i个连杆在xOy中的位置	$ ({x}_{i},{y}_{i}) $	关节角速度	$ {v}_{\phi }\in {\mathbb{R}}^{N-1} $
第i个连杆在tRn中的位置	$ ({t}_{i},{n}_{i}) $	连杆的扰动速度	$ {d}_{\theta }\in \mathbb{R} $
第i个连杆的方向角	$ {\theta }_{i} $	关节的扰动速度	$ {d}_{\phi }\in {\mathbb{R}}^{N-1} $
第i个连杆的关节角	$ {\phi }_{i} $

下载: 导出CSV

表 2 参数取值

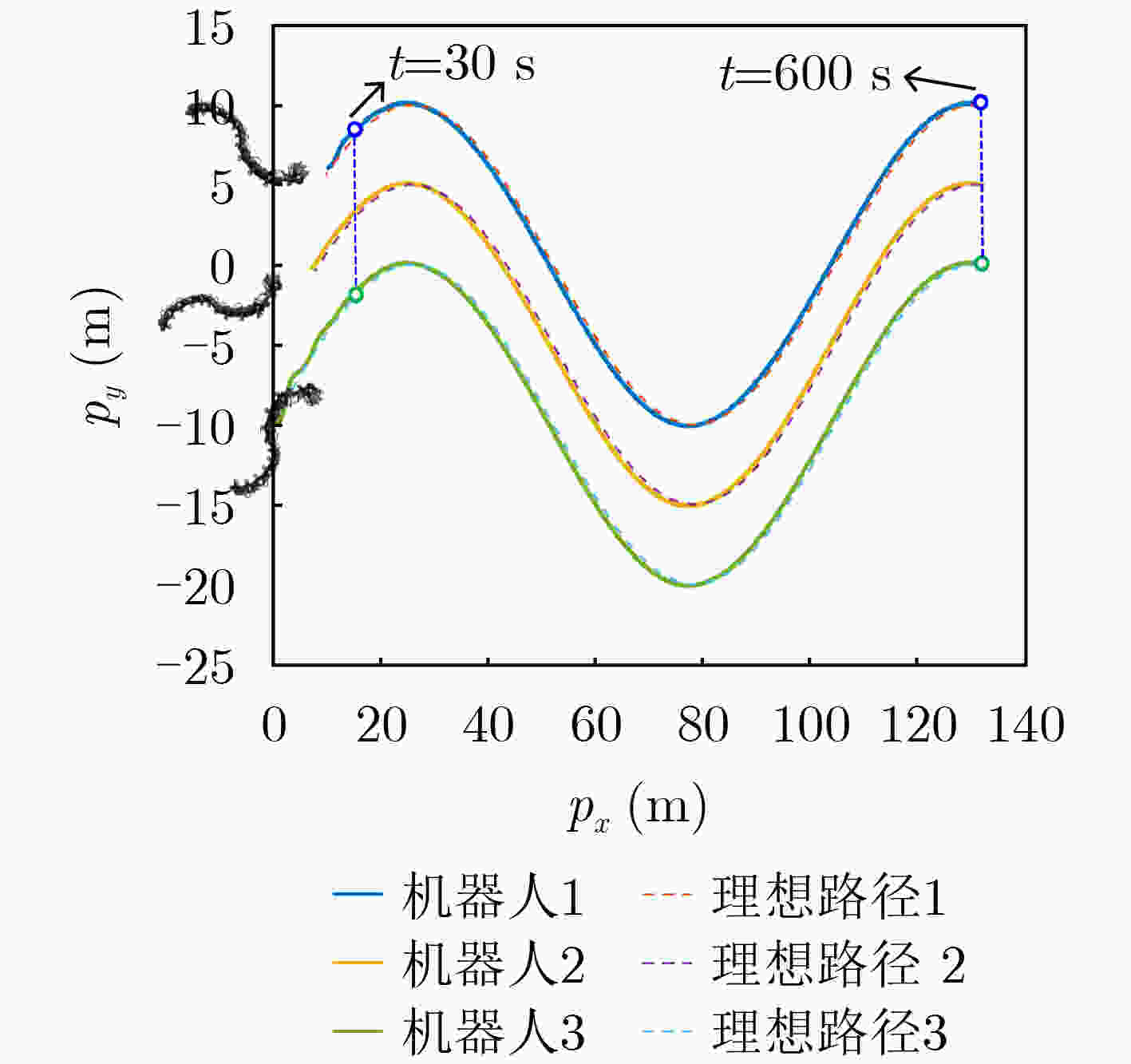
参数	数值	参数	数值	参数	数值	参数	数值	参数	数值	参数	数值
$ m $	0.2	$ h $	0.145	$ {\sigma }_{11} $	0.1	$ {\sigma }_{3} $	5	$ ({p}_{x1},{p}_{y1}) $	(0, 5)	$ {\phi }_{0}\left(0\right) $	0
$ N $	10	$ {b}_{1i} $	20	$ {\sigma }_{22} $	0.2	$ {\sigma }_{4} $	3	$ ({p}_{x2},{p}_{y2}) $	(0, –2.5)	$ {v}_{\theta }\left(0\right) $	0
$ {c}_{t} $	1	$ {c}_{1i} $	0.1	$ {\sigma }_{33} $	0.1	$ {\rho }_{\theta } $	2	$ ({p}_{x3},{p}_{y3}) $	(0, –10)	$ {v}_{\phi i}\left(0\right) $	0
$ {c}_{p} $	3	$ {g}_{1} $	1	$ {\sigma }_{44} $	0.2	$ {\rho }_{\phi } $	2	$ {p}_{t}\left(0\right) $	0.001	$ {\sigma }_{\theta } $	0.1
$ {\lambda }_{1} $	0.5	$ {g}_{2} $	0.5	$ {\sigma }_{1} $	5	$ a $	0.04	$ {v}_{t}\left(0\right) $	0.14	$ {\sigma }_{\phi } $	0.1
$ {\lambda }_{2} $	20	$ {g}_{3} $	0.01	$ {\sigma }_{2} $	3	$ \delta $	0.698	$ {v}_{n}\left(0\right) $	0	$ \varDelta $	1.5

下载: 导出CSV

参考文献(30)

[1]	LI Dongfang, ZHANG Binxin, XIU Yang, et al. Snake robots play an important role in social services and military needs[J]. The Innovation, 2022, 3(6): 100333. doi: 10.1016/j.xinn.2022.100333.
[2]	朱威, 郭宪, 方勇纯, 等. 可重构模块化蛇形机器人研制及多运动模态研究[J]. 信息与控制, 2020, 49(1): 69–77. doi: 10.13976/j.cnki.xk.2020.9481. ZHU Wei, GUO Xian, FANG Yongchun, et al. Development of a reconfigurable modular snake-like robot and research on multiple motion modes[J]. Information and Control, 2020, 49(1): 69–77. doi: 10.13976/j.cnki.xk.2020.9481.
[3]	LI Dongfang, DENG Hongbin, PAN Zhenhua, et al. Collaborative obstacle avoidance algorithm of multiple bionic snake robots in fluid based on IB-LBM[J]. ISA Transactions, 2022, 122: 271–280. doi: 10.1016/j.isatra.2021.04.048.
[4]	WANG Xiangyu, LIU Weiming, WU Quanwei, et al. A modular optimal formation control scheme of multiagent systems with application to multiple mobile robots[J]. IEEE Transactions on Industrial Electronics, 2022, 69(9): 9331–9341. doi: 10.1109/TIE.2021.3114732.
[5]	TAKAOKA S, YAMADA H, and HIROSE S. Snake-like active wheel robot ACM-R4.1 with joint torque sensor and limiter[C]. The 2011 IEEE/RSJ International Conference on Intelligent Robots and Systems, San Francisco, USA, 2011: 1081–1086. doi: 10.1109/IROS.2011.6094475.
[6]	陈培民, 王汝贵, 李欣蓬. 蛇形机器人平面-空间运动步态规划[J]. 机械设计与研究, 2022, 38(6): 34–39,45. doi: 10.13952/j.cnki.jofmdr.2022.0203. CHEN Peimin, WANG Rugui, and LI Xinpeng. Planar-space motion gait planning of snake robot[J]. Machine Design and Research, 2022, 38(6): 34–39,45. doi: 10.13952/j.cnki.jofmdr.2022.0203.
[7]	郁树梅, 马书根, 李斌, 等. 蛇形机器人步态产生及步态分析[J]. 机器人, 2011, 33(3): 371–378. doi: 10.3724/SP.J.1218.2011.00371. YU Shumei, MA Shugen, LI Bin, et al. Gait generation and analysis for snake-like robots[J]. Robot, 2011, 33(3): 371–378. doi: 10.3724/SP.J.1218.2011.00371.
[8]	ZHAO Wei, WANG Jiangbei, and FEI Yanqiong. A multigait continuous flexible snake robot for locomotion in complex terrain[J]. IEEE/ASME Transactions on Mechatronics, 2022, 27(5): 3751–3761. doi: 10.1109/TMECH.2021.3131766.
[9]	LIU Xiongding, LIN Guangjie, and WEI Wu. Adaptive transition gait planning of snake robot based on polynomial interpolation method[J]. Actuators, 2022, 11(8): 222. doi: 10.3390/act11080222.
[10]	REZAPOUR E, PETTERSEN K Y, LILJEBÄCK P, et al. Path following control of planar snake robots using virtual holonomic constraints: Theory and experiments[J]. Robotics and Biomimetics, 2014, 1(1): 3. doi: 10.1186/s40638-014-0003-6.
[11]	REZAPOUR E, HOFMANN A, PETTERSEN K Y, et al. Virtual holonomic constraint based direction following control of planar snake robots described by a simplified model[C]. IEEE Conference on Control Applications, Juan Les Antibes, France, 2014: 1064–1071. doi: 10.1109/CCA.2014.6981476.
[12]	KELASIDI E, LILJEBACK P, PETTERSEN K Y, et al. Integral line-of-sight guidance for path following control of underwater snake robots: Theory and experiments[J]. IEEE Transactions on Robotics, 2017, 33(3): 610–628. doi: 10.1109/TRO.2017.2651119.
[13]	KELASIDI E, MOE S, PETTERSEN K Y, et al. Path following, obstacle detection and obstacle avoidance for thrusted underwater snake robots[J]. Frontiers in Robotics and AI, 2019, 6: 57. doi: 10.3389/frobt.2019.00057.
[14]	张丹凤, 李斌, 常健. 基于角度对称性调节的蛇形机器人路径跟随方法[J]. 机器人, 2019, 41(6): 788–794,833. doi: 10.13973/j.cnki.robot.180768. ZHANG Danfeng, LI Bin, and CHANG Jian. Path following method for snake robot based on the angle symmetry adjustment[J]. Robot, 2019, 41(6): 788–794,833. doi: 10.13973/j.cnki.robot.180768.
[15]	CAO Zhengcai, ZHANG Dong, HU Biao, et al. Adaptive path following and locomotion optimization of snake-like robot controlled by the central pattern generator[J]. Complexity, 2019, 2019: 8030374. doi: 10.1155/2019/8030374.
[16]	ZHANG Dong, YUAN Hao, and CAO Zhengcai. Environmental adaptive control of a snake-like robot with variable stiffness actuators[J]. IEEE/CAA Journal of Automatica Sinica, 2020, 7(3): 745–751. doi: 10.1109/JAS.2020.1003144.
[17]	LI Dongfang, PAN Zhenhua, DENG Hongbin, et al. Adaptive path following controller of a multijoint snake robot based on the improved serpenoid curve[J]. IEEE Transactions on Industrial Electronics, 2022, 69(4): 3831–3842. doi: 10.1109/TIE.2021.3075851.
[18]	李东方, 杨弘晟, 邓宏彬, 等. 蛇形机器人跟踪误差预测的自适应轨迹跟踪控制器[J]. 仪器仪表学报, 2021, 42(11): 267–278. doi: 10.19650/j.cnki.cjsi.J2108438. LI Dongfang, YANG Hongsheng, DENG Hongbin, et al. Adaptive trajectory tracking controller for snake robot tracking error prediction[J]. Chinese Journal of Scientific Instrument, 2021, 42(11): 267–278. doi: 10.19650/j.cnki.cjsi.J2108438.
[19]	REZAPOUR E, PETTERSEN K Y, GRAVDAHL J T, et al. Formation control of underactuated bio-inspired snake robots[J]. Artificial Life and Robotics, 2016, 21(3): 282–294. doi: 10.1007/s10015-016-0297-2.
[20]	HUANG Zipeng, BAUER R, and PAN Yajun. Event-triggered formation tracking control with application to multiple mobile robots[J]. IEEE Transactions on Industrial Electronics, 2023, 70(1): 846–854. doi: 10.1109/TIE.2022.3146582.
[21]	DAI Shilu, HE Shude, LIN Hai, et al. Platoon formation control with prescribed performance guarantees for USVs[J]. IEEE Transactions on Industrial Electronics, 2018, 65(5): 4237–4246. doi: 10.1109/TIE.2017.2758743.
[22]	DAI Shilu, HE Shude, CHEN Xin, et al. Adaptive leader–follower formation control of nonholonomic mobile robots with prescribed transient and steady-state performance[J]. IEEE Transactions on Industrial Informatics, 2020, 16(6): 3662–3671. doi: 10.1109/TII.2019.2939263.
[23]	CHEN B S, WANG Chunping, and LEE M Y. Stochastic robust team tracking control of multi-UAV networked system under Wiener and Poisson random fluctuations[J]. IEEE Transactions on Cybernetics, 2021, 51(12): 5786–5799. doi: 10.1109/TCYB.2019.2960104.
[24]	黄兵, 肖云飞, 冯元, 等. 无人艇全分布式动态事件触发编队控制[J]. 控制理论与应用, 2023, 40(8): 1479–1487. doi: 10.7641/CTA.2022.11067. HUANG Bing, XIAO Yunfei, FENG Yuan, et al. Fully distributed dynamic event-triggered formation control for multiple unmanned surface vehicles[J]. Control Theory & Applications, 2023, 40(8): 1479–1487. doi: 10.7641/CTA.2022.11067.
[25]	TAKEUCHI S. Some double-angle formulas related to a generalized lemniscate function[J]. The Ramanujan Journal, 2021, 56(2): 753–761. doi: 10.1007/s11139-021-00395-x.
[26]	王芳, 高雅丽, 张政, 等. 输出误差约束下四旋翼无人机预定性能反步控制[J]. 控制与决策, 2021, 36(5): 1059–1068. doi: 10.13195/j.kzyjc.2019.1249. WANG Fang, GAO Yali, ZHANG Zheng, et al. Prescribed performance backstepping control for quadrotor UAV with output error constraint[J]. Control and Decision, 2021, 36(5): 1059–1068. doi: 10.13195/j.kzyjc.2019.1249.
[27]	ZERAICK MONTEIRO N and RODRIGUES MAZORCHE S. Limitations and applications in a fractional Barbalat’s Lemma[J]. Fractional Calculus and Applied Analysis, 2023, 26(1): 253–275. doi: 10.1007/s13540-022-00111-6.
[28]	李新凯, 张宏立, 范文慧. 基于时变障碍李雅普诺夫函数的变体无人机有限时间控制[J]. 自动化学报, 2022, 48(8): 2062–2074. doi: 10.16383/j.aas.c200712. LI Xinkai, ZHANG Hongli, and FAN Wenhui. Finite-time control for morphing aerospace vehicle based on time-varying barrier Lyapunov function[J]. Acta Automatica Sinica, 2022, 48(8): 2062–2074. doi: 10.16383/j.aas.c200712.
[29]	TANWAR D V, KUMAR M, and TIWARI A K. Lie symmetries, invariant solutions and phenomena dynamics of Boiti–Leon–pempinelli system[J]. Physica Scripta, 2022, 97(7): 075209. doi: 10.1088/1402-4896/ac76eb.
[30]	SUN Wenbing and LIU Qiong. Hadamard type local fractional integral inequalities for generalized harmonically convex functions and applications[J]. Mathematical Methods in the Applied Sciences, 2020, 43(9): 5776–5787. doi: 10.1002/mma.6319.